Evaluating the Performance of a Climate-Driven Mortality Model during Heat Waves and Cold Spells in Europe
Abstract
:1. Introduction
2. Experimental Section
2.1. Mortality, Population and Climate Data
2.2. Estimation of the Temperature-Mortality Relationship
3. Results and Discussion
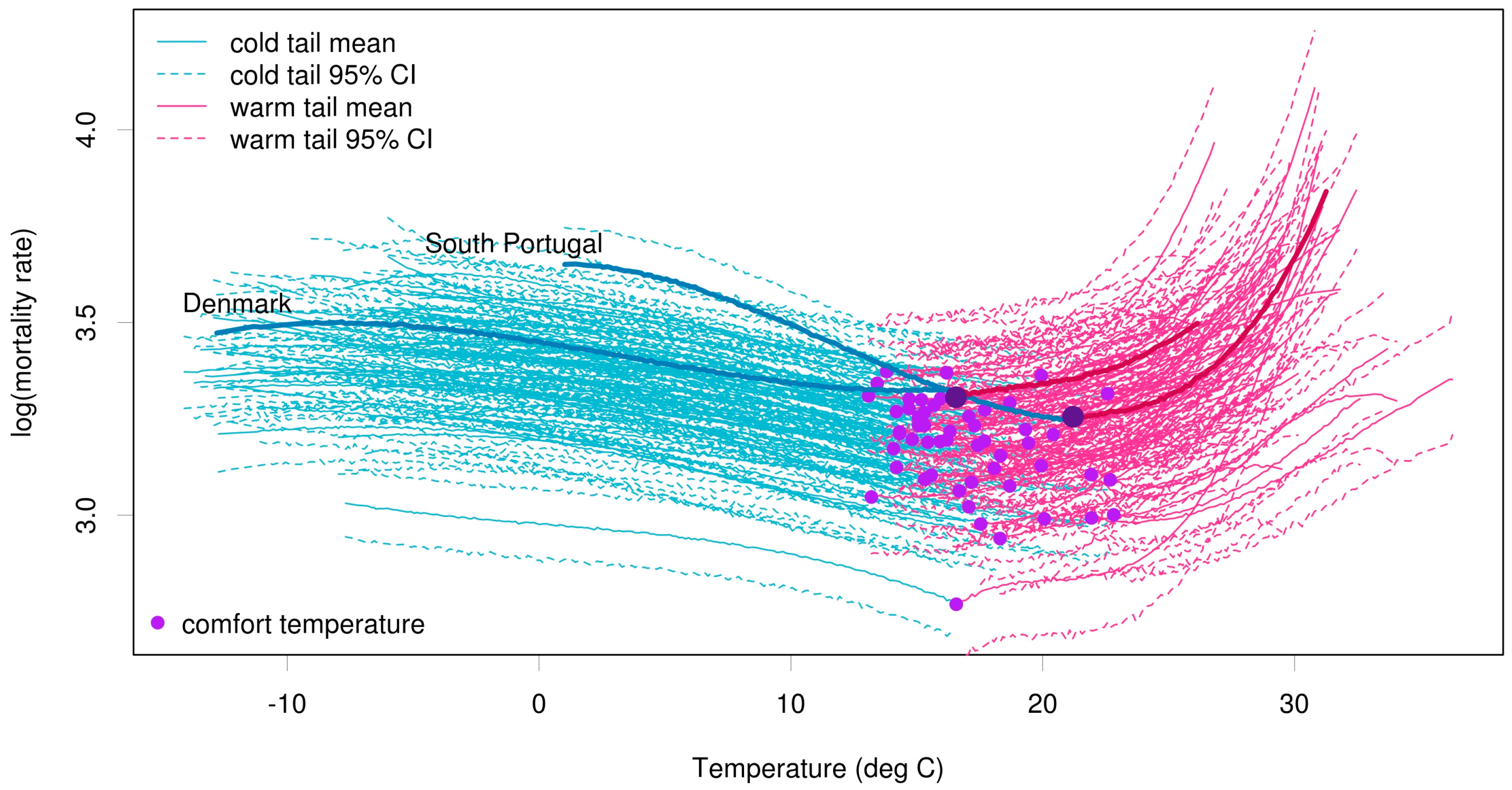
3.1. Temperature and Mortality Curves
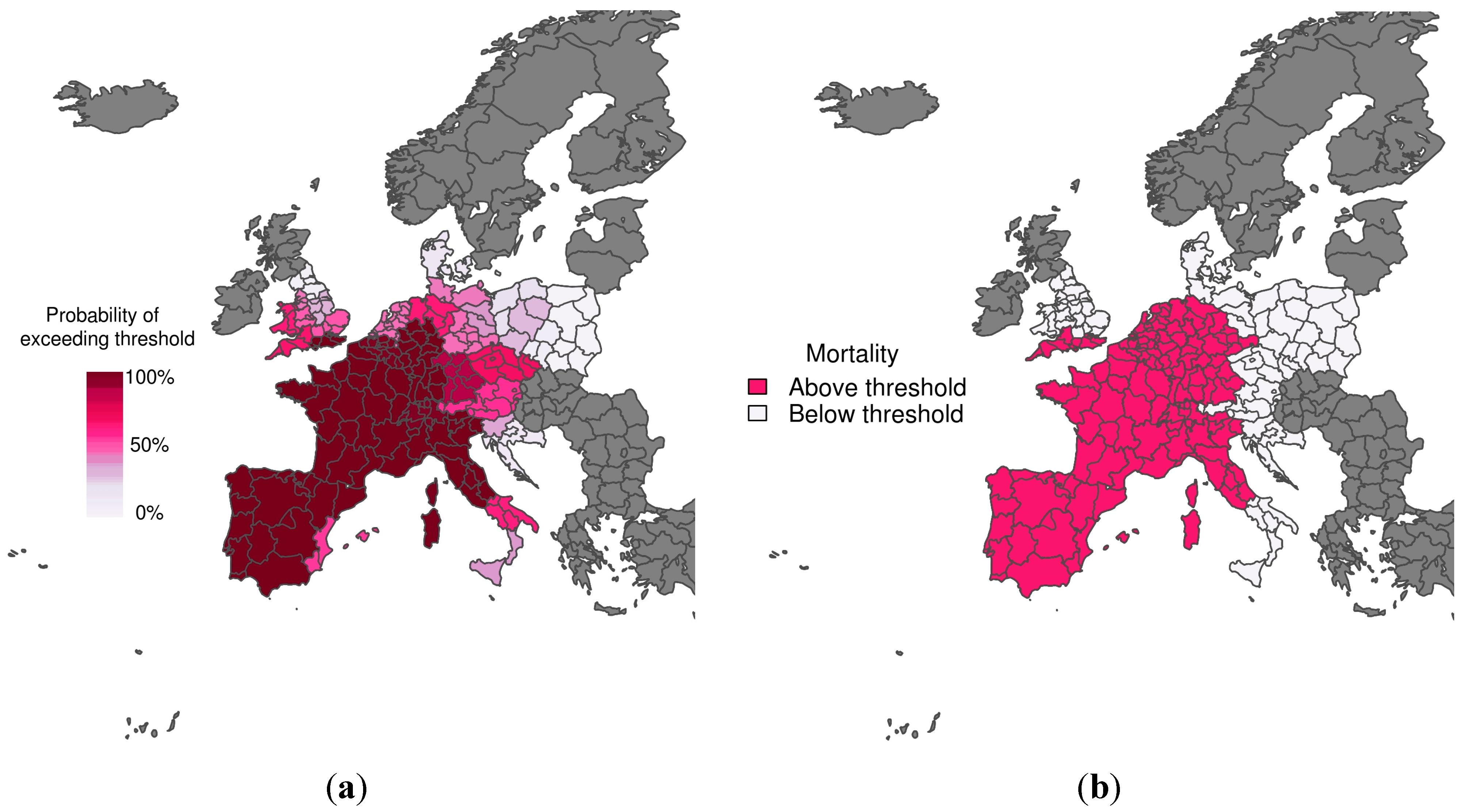
3.2. Probability of Exceeding Emergency Mortality Thresholds
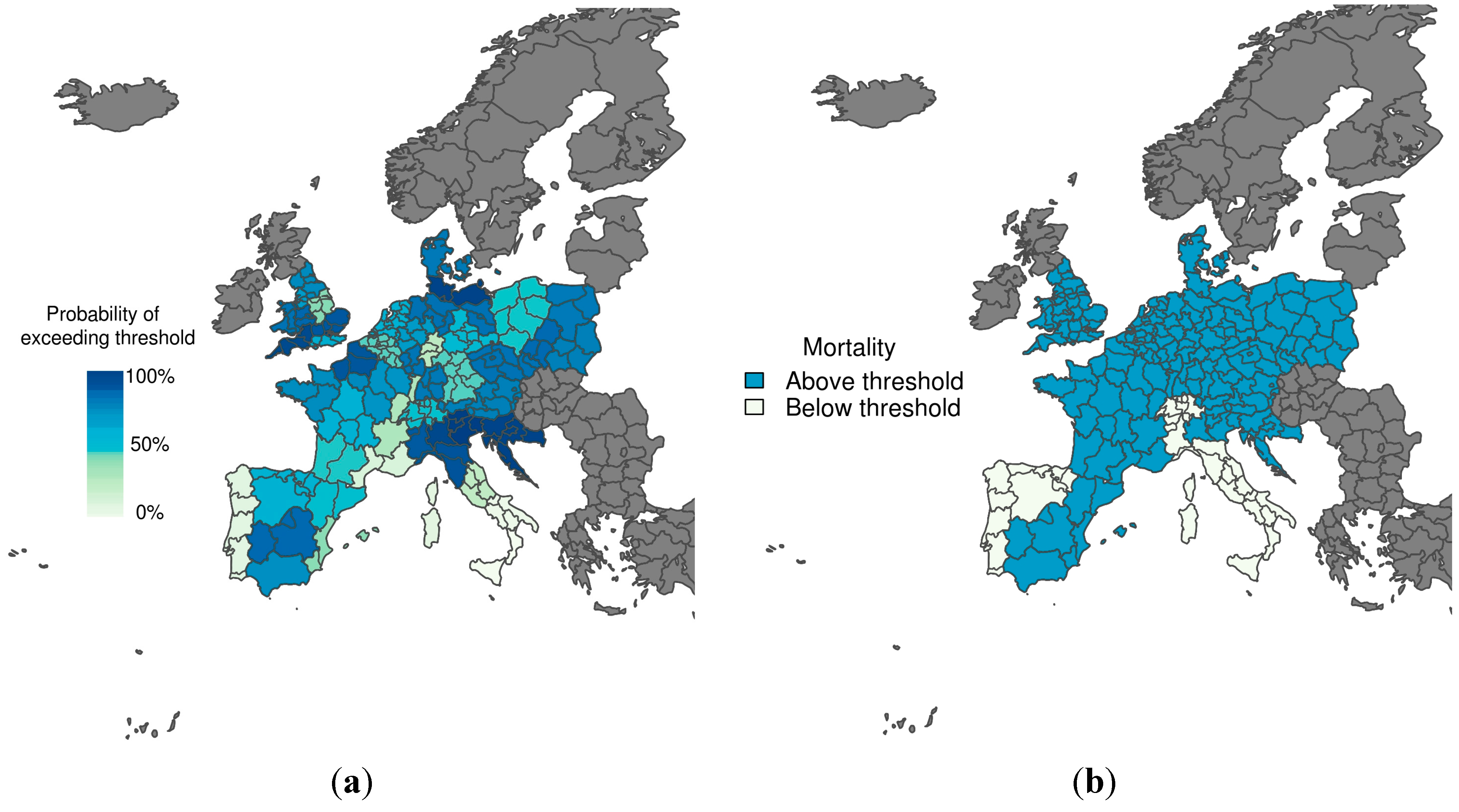
3.3. Assessment of Probability Decision Thresholds
| Scenario | Emergency Threshold Defined for Each Region Using Daily Data 1998–2003 | ROC Score | Probability Decision Threshold | Hit Rate | False Alarm Rate | Proportion Correct |
|---|---|---|---|---|---|---|
| Heat wave 1–15 August 2003 | 75th percentile of mortality distribution given that temperature is warmer than the comfort temperature. | 97% | 70% | 85% | 5% | 89% |
| 30% | 100% | 55% | 80% | |||
| Cold spell 1–15 January 2003 | 75th percentile of mortality distribution given that temperature is colder than the comfort temperature. | 78% | 70% | 66% | 20% | 69% |
| 30% | 93% | 40% | 87% |
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Barriopedro, D.; Fischer, E.M.; Luterbacher, J.; Trigo, R.M.; García-Herrera, R. The hot summer of 2010: Redrawing the temperature record map of Europe. Science 2011, 332, 220–224. [Google Scholar] [CrossRef] [PubMed]
- Luterbacher, J.; Dietrich, D.; Xoplaki, E.; Grosjean, M.; Wanner, H. European seasonal and annual temperature variability, trends, and extremes since 1500. Science 2004, 303, 1499–1503. [Google Scholar] [CrossRef] [PubMed]
- Ballester, J.; Robine, J.-M.; Herrmann, F.R.; Rodó, X. Long-term projections and acclimatization scenarios of temperature-related mortality in Europe. Nat. Commun. 2011, 2. [Google Scholar] [CrossRef]
- Robine, J.-M.; Cheung, S.L.K.; le Roy, S.; van Oyen, H.; Griffiths, C.; Michel, J.-P.; Herrmann, F.R. Death toll exceeded 70,000 in Europe during the summer of 2003. C. R. Biol. 2008, 331, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Matthies, F.; Bickler, G.; Marín, N.C.; Hales, S. Heat-Health Action Plans: Guidance; World Health Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Bouchama, A.; Knochel, J.P. Heat stroke. N. Engl. J. Med. 2002, 346, 1978–1988. [Google Scholar] [CrossRef] [PubMed]
- Robine, J.-M.; Michel, J.-P.; Herrmann, F. Excess male mortality and age-specific mortality trajectories under different mortality conditions: A lesson from the heat wave of summer 2003. Mech. Ageing Dev. 2012, 133, 378–386. [Google Scholar] [CrossRef] [PubMed]
- Madrigano, J.; Mittleman, M.A.; Baccarelli, A.; Goldberg, R.; Melly, S.; von Klot, S.; Schwartz, J. Temperature, myocardial infarction, and mortality: Effect modification by individual and area-level characteristics. Epidemiol. Camb. Mass 2013, 24. [Google Scholar] [CrossRef]
- Monteiro, A.; Carvalho, V.; Oliveira, T.; Sousa, C. Excess mortality and morbidity during the July 2006 heat wave in Porto, Portugal. Int. J. Biometeorol. 2013, 57, 155–167. [Google Scholar] [CrossRef] [PubMed]
- McGuinn, L.; Hajat, S.; Wilkinson, P.; Armstrong, B.; Anderson, H.; Monk, V.; Harrison, R. Ambient temperature and activation of implantable cardioverter defibrillators. Int. J. Biometeorol. 2013, 57, 655–662. [Google Scholar] [CrossRef] [PubMed]
- Callaly, E.; Mikulich, O.; Silke, B. Increased winter mortality: The effect of season, temperature and deprivation in the acutely ill medical patient. Eur. J. Intern. Med. 2013, 24, 546–551. [Google Scholar] [CrossRef] [PubMed]
- Keatinge, W.; Donaldson, G. Cold exposure and winter mortality from ishaemic heart disease cerebrovascular disease respiratory disease and all causes in warm and cold regions of Europe. Lancet 1997, 349, 1341–1346. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, S.; Pan, X.; Tong, S.; Jaakkola, J.J.; Gasparrini, A.; Guo, Y.; Wang, S. The effects of ambient temperature on cerebrovascular mortality: An epidemiologic study in four climatic zones in China. Environ. Health 2014, 13. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Acebo, I.; Llorca, J.; Dierssen, T. Cold-related mortality due to cardiovascular diseases, respiratory diseases and cancer: A case-crossover study. Public Health 2013, 127, 252–258. [Google Scholar] [CrossRef] [PubMed]
- Hong, Y.-C.; Rha, J.-H.; Lee, J.-T.; Ha, E.-H.; Kwon, H.-J.; Kim, H. Ischemic stroke associated with decrease in temperature. Epidemiology 2003, 14, 473–478. [Google Scholar] [PubMed]
- Stewart, S.; McIntyre, K.; Capewell, S.; McMurray, J.J. Heart failure in a cold climate: Seasonal variation in heart failure-related morbidity and mortality. J. Amer. Coll. Cardiol. 2002, 39, 760–766. [Google Scholar] [CrossRef]
- Vasconcelos, J.; Freire, E.; Almendra, R.; Silva, G.L.; Santana, P. The impact of winter cold weather on acute myocardial infarctions in Portugal. Environ. Pollut. 2013, 183, 14–18. [Google Scholar] [CrossRef] [PubMed]
- Carder, M.; McNamee, R.; Beverland, I.; Elton, R.; Cohen, G.; Boyd, J.; Agius, R. The lagged effect of cold temperature and wind chill on cardiorespiratory mortality in Scotland. Occup. Environ. Med. 2005, 62, 702–710. [Google Scholar] [CrossRef] [PubMed]
- Conlon, K.C.; Rajkovich, N.B.; White-Newsome, J.L.; Larsen, L.; O’Neill, M.S. Preventing cold-related morbidity and mortality in a changing climate. Maturitas 2011, 69, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Kysely, J.; Pokorna, L.; Kyncl, J.; Kriz, B. Excess cardiovascular mortality associated with cold spells in the Czech Republic. BMC Public Health 2009, 9. [Google Scholar] [CrossRef] [PubMed]
- Stocker, T.; Qin, D.; Plattner, G.; Tignor, M.; Allen, S.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P. IPCC, 2013: Summary for policymakers. In Climate Change 2013: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Meehl, G.A.; Tebaldi, C. More intense, more frequent, and longer lasting heat waves in the 21st century. Science 2004, 305, 994–997. [Google Scholar] [CrossRef] [PubMed]
- Ballester, J.; Rodó, X.; Giorgi, F. Future changes in Central Europe heat waves expected to mostly follow summer mean warming. Clim. Dyn. 2010, 35, 1191–1205. [Google Scholar] [CrossRef]
- Ciscar, J.-C.; Feyen, L.; Soria, A.; Lavalle, C.; Raes, F.; Perry, M.; Nemry, F.; Demirel, H.; Rozsai, M.; Dosio, A.; et al. Climate Impacts in Europe—The JRC PESETA II Project; JRC-IPTS Working Papers, Joint Research Centre, Institute for Prospective and Technological Studies. Available online: http://EconPapers.repec.org/RePEc:ipt:iptwpa:jrc87011 (accessed on 22 January 2015).
- Kovats, S.; Lloyd, S.; Hunt, A.; Watkiss, P. The ClimateCost Project. Final Report. Volume 1: Europe; Watkiss, P., Ed.; Stockholm Environment Institute: Stockholm, Sweden, 2011. [Google Scholar]
- Kovats, R.S.; Hajat, S. Heat stress and public health: A critical review. Annu. Rev. Public Health 2008, 29, 41–55. [Google Scholar] [CrossRef] [PubMed]
- Healy, J.D. Excess winter mortality in Europe: A cross country analysis identifying key risk factors. J. Epidemiol. Community Health 2003, 57, 784–789. [Google Scholar] [CrossRef] [PubMed]
- Lowe, D.; Ebi, K.L.; Forsberg, B. Heatwave early warning systems and adaptation advice to reduce human health consequences of heatwaves. Int. J. Environ. Res. Public Health 2011, 8, 4623–4648. [Google Scholar] [CrossRef] [PubMed]
- Rodó, X.; Baert, E.; Comin, F. Variations in seasonal rainfall in Southern Europe during the present century: Relationships with the North Atlantic Oscillation and the El Niño-Southern Oscillation. Clim. Dyn. 1997, 13, 275–284. [Google Scholar] [CrossRef]
- Van Oldenborgh, G.; Burgers, G.; Tank, A. On the El Niño teleconnection to spring precipitation in Europe. Int. J. Climatol. 2000, 20, 565–574. [Google Scholar] [CrossRef]
- Doblas-Reyes, F.J.; García-Serrano, J.; Lienert, F.; Biescas, A.P.; Rodrigues, L.R. Seasonal climate predictability and forecasting: Status and prospects. Wiley Interdiscip. Rev. Clim. Chang. 2013, 4, 245–268. [Google Scholar] [CrossRef]
- Hewitt, C.; Buontempo, C.; Newton, P. Using climate Predictions to better serve society’s needs. Eos Trans. Amer. Geophys. Union 2013, 94, 105–107. [Google Scholar] [CrossRef]
- Matthies, F.; Menne, B. Prevention and management of health hazards related to heatwaves. Int. J. Circumpolar Health 2009, 68, 8–22. [Google Scholar] [CrossRef] [PubMed]
- Matthies, F.; Menne, B. Improving Public Health Responses to Extreme Weather/Heat-Waves—EuroHEAT; World Health Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Dee, D.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Michelozzi, P.; Accetta, G.; de Sario, M.; D’Ippoliti, D.; Marino, C.; Baccini, M.; Biggeri, A.; Anderson, H.R.; Katsouyanni, K.; Ballester, F.; et al. High temperature and hospitalizations for cardiovascular and respiratory causes in 12 European cities. Amer. J. Respir. Crit. Care Med. 2009, 179, 383–389. [Google Scholar] [CrossRef]
- Smoyer, K.E.; Rainham, D.G.; Hewko, J.N. Heat-stress-related mortality in five cities in Southern Ontario: 1980–1996. Int. J. Biometeorol. 2000, 44, 190–197. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, M.S.; Zanobetti, A.; Schwartz, J. Modifiers of the temperature and mortality association in seven U.S. cities. Amer. J. Epidemiol. 2003, 157, 1074–1082. [Google Scholar] [CrossRef]
- Michelozzi, P.; de Sario, M.; Accetta, G.; de’ Donato, F.; Kirchmayer, U.; D’Ovidio, M.; Perucci, C.A. Temperature and summer mortality: Geographical and temporal variations in four Italian cities. J. Epidemiol. Community Health 2006, 60, 417–423. [Google Scholar] [CrossRef] [PubMed]
- Huynen, M.-M.; Martens, P.; Schram, D.; Weijenberg, M.P.; Kunst, A.E. The impact of heat waves and cold spells on mortality rates in the Dutch population. Environ. Health Perspect. 2001, 109, 463–470. [Google Scholar] [CrossRef] [PubMed]
- McMichael, A.J.; Woodruff, R.E.; Hales, S. Climate change and human health: Present and future risks. Lancet 2006, 367, 859–869. [Google Scholar] [CrossRef] [PubMed]
- Christidis, N.; Donaldson, G.C.; Stott, P.A. Causes for the recent changes in cold-and heat-related mortality in England and Wales. Clim. Change 2010, 102, 539–553. [Google Scholar] [CrossRef]
- Huang, C.; Barnett, A.G.; Wang, X.; Tong, S. Effects of extreme temperatures on years of life lost for cardiovascular deaths: A time series study in Brisbane, Australia. Circ. Cardiovasc. Qual. Outcomes 2012, 5, 609–614. [Google Scholar] [CrossRef] [PubMed]
- Curriero, F.C.; Heiner, K.S.; Samet, J.M.; Zeger, S.L.; Strug, L.; Patz, J.A. Temperature and mortality in 11 cities of the eastern United States. Amer. J. Epidemiol. 2002, 155, 80–87. [Google Scholar] [CrossRef]
- Ostro, B.; Barrera-Gómez, J.; Ballester, J.; Basagaña, X.; Sunyer, J. The impact of future summer temperature on public health in Barcelona and Catalonia, Spain. Int. J. Biometeorol. 2012, 56, 1135–1144. [Google Scholar] [CrossRef] [PubMed]
- Davis, R.E.; Knappenberger, P.C.; Novicoff, W.M.; Michaels, P.J. Decadal changes in summer mortality in U.S. cities. Int. J. Biometeorol. 2003, 47, 166–175. [Google Scholar] [PubMed]
- Sherwood, S.C.; Huber, M. An adaptability limit to climate change due to heat stress. Proc. Natl. Acad. Sci. USA 2010, 107, 9552–9555. [Google Scholar] [CrossRef] [PubMed]
- Keatinge, W.; Donaldson, G.; Cordioli, E.; Martinelli, M.; Kunst, A.; Mackenbach, J.; Nayha, S.; Vuori, I. Heat related mortality in warm and cold regions of Europe: Observational study. BMJ 2000, 321, 670–673. [Google Scholar] [CrossRef] [PubMed]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B Stat. Methodol. 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Martins, T.G.; Simpson, D.; Lindgren, F.; Rue, H. Avard Bayesian computing with INLA: New features. Comput. Stat. Data Anal. 2013, 67, 68–83. [Google Scholar] [CrossRef]
- Nájera, J.; Kouznetsov, R.; Delacollete, C. Malaria Epidemics: Detection and Control, Forecasting and Prevention. Geneva; World Health Organizaton: Geneva, Switzerland, 1998. Available online: http://www.rollbackmalaria.org/docs/najera_epidemics/naj_toc htm (accessed on 12 October 2010).
- Soares, M.B.; Dessai, S. On the use and potential use of seasonal to decadal climate predictions for decision-making in Europe. In European Geophysical Union General Assembly Conference Abstracts; Copernicus Publications: Göttingen, Germany, 2014; Volume 16, p. 12907. [Google Scholar]
- Mason, S.J.; Graham, N.E. Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation. Q. J. R. Meteorol. Soc. 2002, 128, 2145–2166. [Google Scholar] [CrossRef]
- Braga, A.L.F.; Zanobetti, A.; Schwartz, J. The time course of weather-related deaths. Epidemiology 2001, 12, 662–667. [Google Scholar] [CrossRef] [PubMed]
- Hajat, S.; Kovats, R.S.; Lachowycz, K. Heat-related and cold-related deaths in England and Wales: Who is at risk? Occup. Environ. Med. 2007, 64, 93–100. [Google Scholar] [CrossRef] [PubMed]
- Donaldson, G.; Keatinge, W. Excess winter mortality: Influenza or cold stress? Observational study. BMJ 2002, 324, 89–90. [Google Scholar] [CrossRef] [PubMed]
- Keatinge, W. Winter mortality and its causes. Int. J. Circumpolar Health 2002, 61, 292–299. [Google Scholar] [CrossRef] [PubMed]
- Benmarhnia, T.; Oulhote, Y.; Petit, C.; Lapostolle, A.; Chauvin, P.; Zmirou-Navier, D.; Deguen, S. Chronic air pollution and social deprivation as modifiers of the association between high temperature and daily mortality. Environ. Health 2014, 13, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Howieson, S.G.; Hogan, M. Multiple deprivation and excess winter deaths in Scotland. J. R. Soc. Promot. Health 2005, 125, 18–22. [Google Scholar] [CrossRef] [PubMed]
- Rosenthal, J.K.; Kinney, P.L.; Metzger, K.B. Intra-urban vulnerability to heat-related mortality in New York City, 1997–2006. Health Place 2014, 30, 45–60. [Google Scholar] [CrossRef] [PubMed]
- Rey, G.; Fouillet, A.; Bessemoulin, P.; Frayssinet, P.; Dufour, A.; Jougla, E.; Hémon, D. Heat exposure and socio-economic vulnerability as synergistic factors in heat-wave-related mortality. Eur. J. Epidemiol. 2009, 24, 495–502. [Google Scholar] [CrossRef] [PubMed]
- Goodman, P.G.; Dockery, D.W.; Clancy, L. Cause-specific mortality and the extended effects of particulate pollution and temperature exposure. Environ. Health Perspect. 2004, 112, 179–185. [Google Scholar] [CrossRef] [PubMed]
- Magariño, M.E.; Cofiño, A.; Bedia, J.; Vega, M.; Fernández, J.; Manzanas, R.; Gutiérrez, J.M. The ECOMS user data gateway: Homogeneous seasonal-to-decadal forecast data access for end-users. In European Geophysical Union General Assembly Conference Abstracts; Copernicus Publications: Göttingen, Germany, 2014; Volume 16, p. 14992. [Google Scholar]
- Hewitt, C.; Mason, S.; Walland, D. The global framework for climate services. Nat. Clim. Chang. 2012, 2, 831–832. [Google Scholar] [CrossRef]
- Shumake-Guillemot, J.; Campbell-Lendrum, D.; Abrahams, J.; MacPherson, J.; Hossain, R.; Villalobos, E.; Menne, B.; Kootval, H.; Malone, L.; Connor, S.; et al. Health Exemplar to the User Interface Platform of the Global Framework for Climate Services; World Meteorological Organization: Geneva, Switzerland, 2014. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lowe, R.; Ballester, J.; Creswick, J.; Robine, J.-M.; Herrmann, F.R.; Rodó, X. Evaluating the Performance of a Climate-Driven Mortality Model during Heat Waves and Cold Spells in Europe. Int. J. Environ. Res. Public Health 2015, 12, 1279-1294. https://doi.org/10.3390/ijerph120201279
Lowe R, Ballester J, Creswick J, Robine J-M, Herrmann FR, Rodó X. Evaluating the Performance of a Climate-Driven Mortality Model during Heat Waves and Cold Spells in Europe. International Journal of Environmental Research and Public Health. 2015; 12(2):1279-1294. https://doi.org/10.3390/ijerph120201279
Chicago/Turabian StyleLowe, Rachel, Joan Ballester, James Creswick, Jean-Marie Robine, François R. Herrmann, and Xavier Rodó. 2015. "Evaluating the Performance of a Climate-Driven Mortality Model during Heat Waves and Cold Spells in Europe" International Journal of Environmental Research and Public Health 12, no. 2: 1279-1294. https://doi.org/10.3390/ijerph120201279
APA StyleLowe, R., Ballester, J., Creswick, J., Robine, J.-M., Herrmann, F. R., & Rodó, X. (2015). Evaluating the Performance of a Climate-Driven Mortality Model during Heat Waves and Cold Spells in Europe. International Journal of Environmental Research and Public Health, 12(2), 1279-1294. https://doi.org/10.3390/ijerph120201279






