NMR-Based Configurational Assignments of Natural Products: Gibbs Sampling and Bayesian Inference Using Floating Chirality Distance Geometry Calculations
Abstract
:1. Introduction
2. Results and Discussion
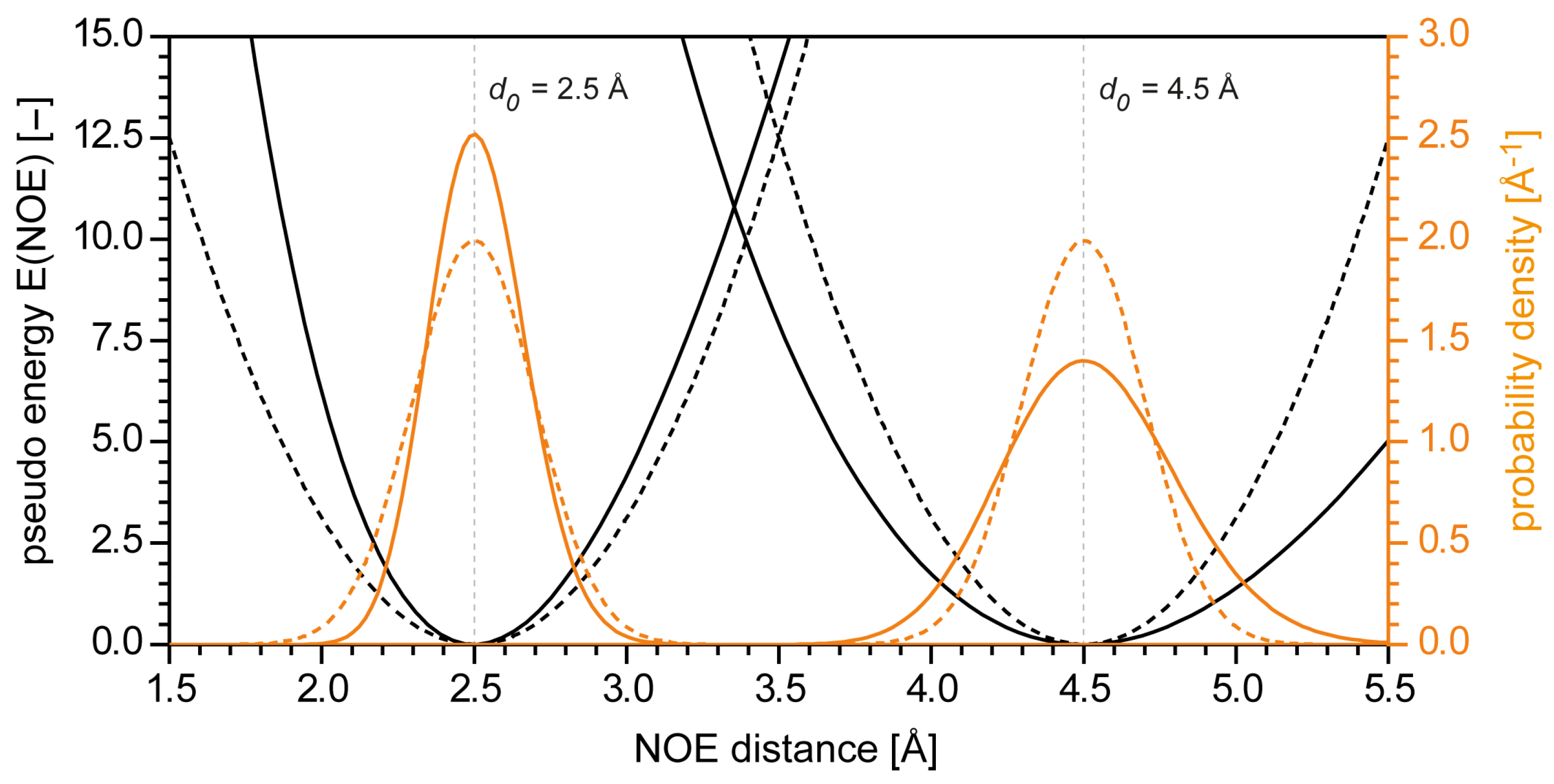
2.1. NMR Restraints in Distance Geometry Calculations
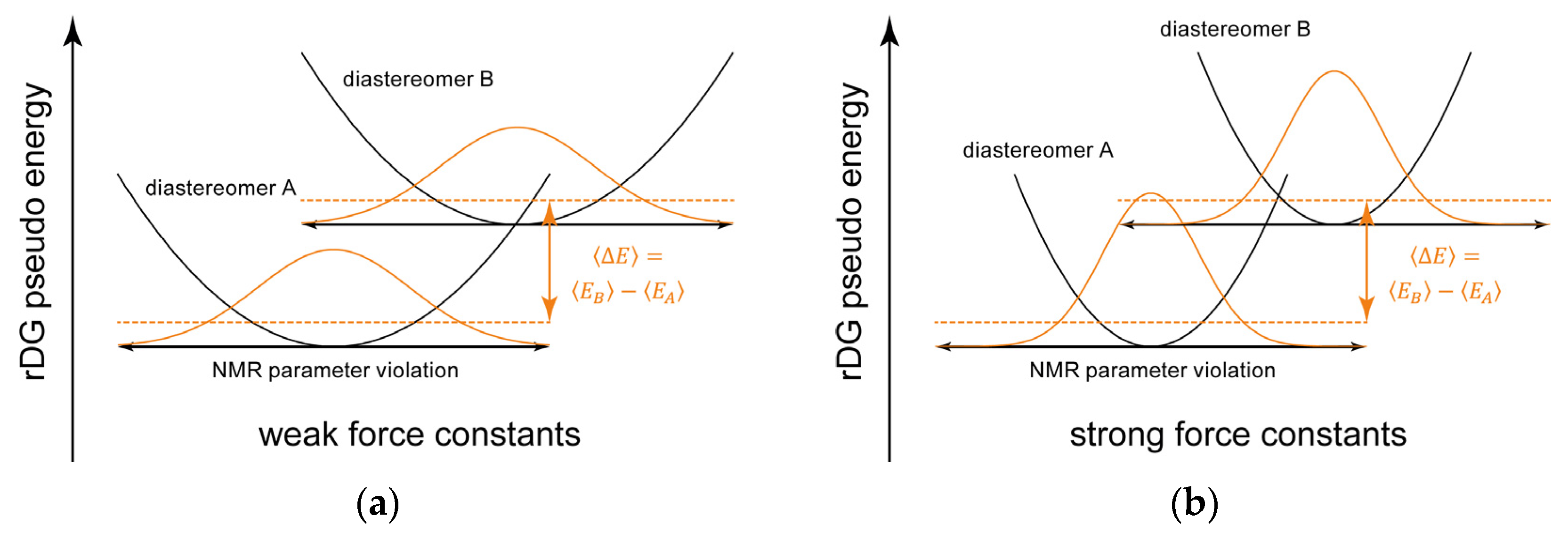
2.2. Bayesian Inference from RDC-Driven rDG Calculations
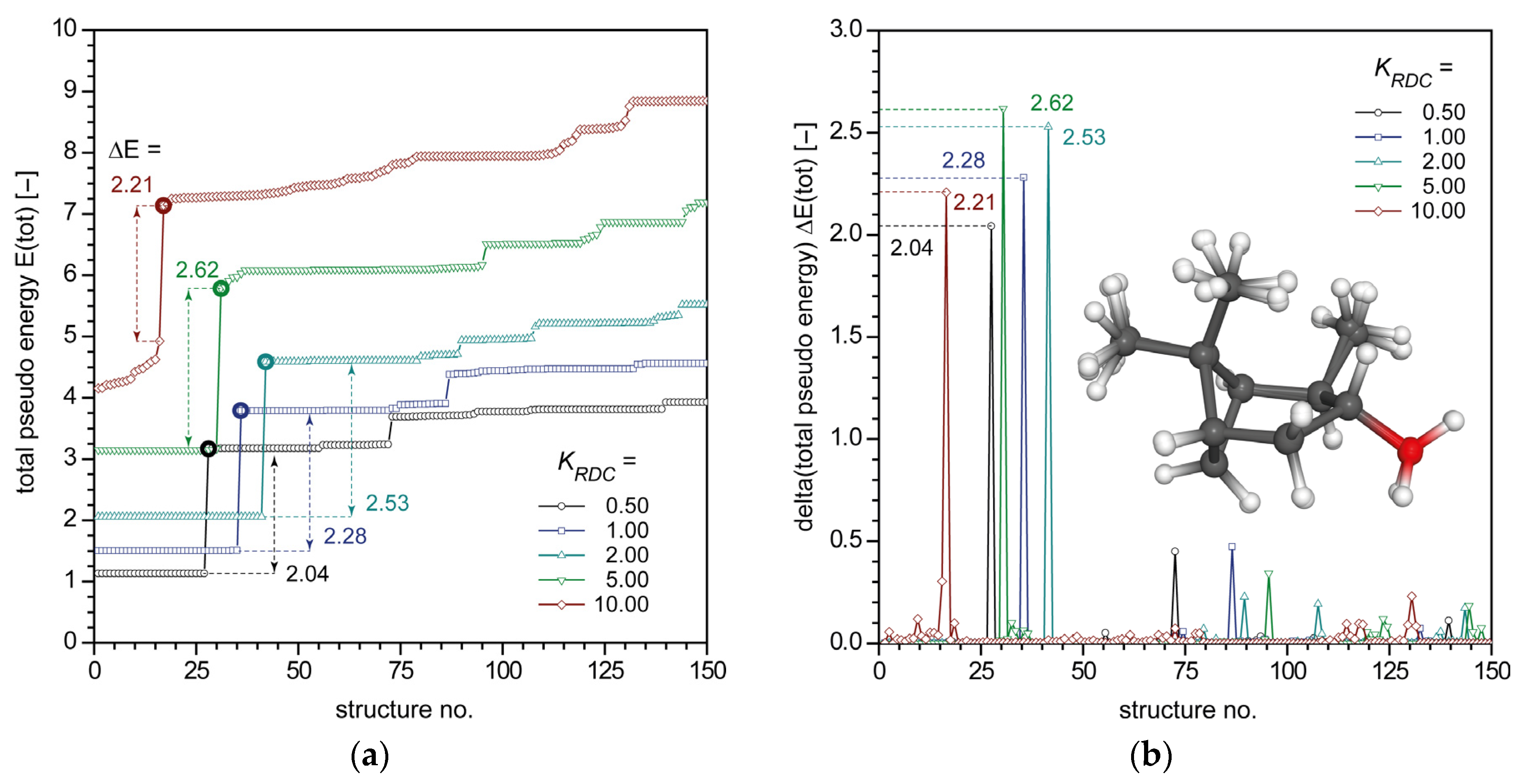
2.3. RDC-Driven rDG Calculations of IPC (1)
2.4. rDG Calculations Using Combined NOE and RDC Restraints
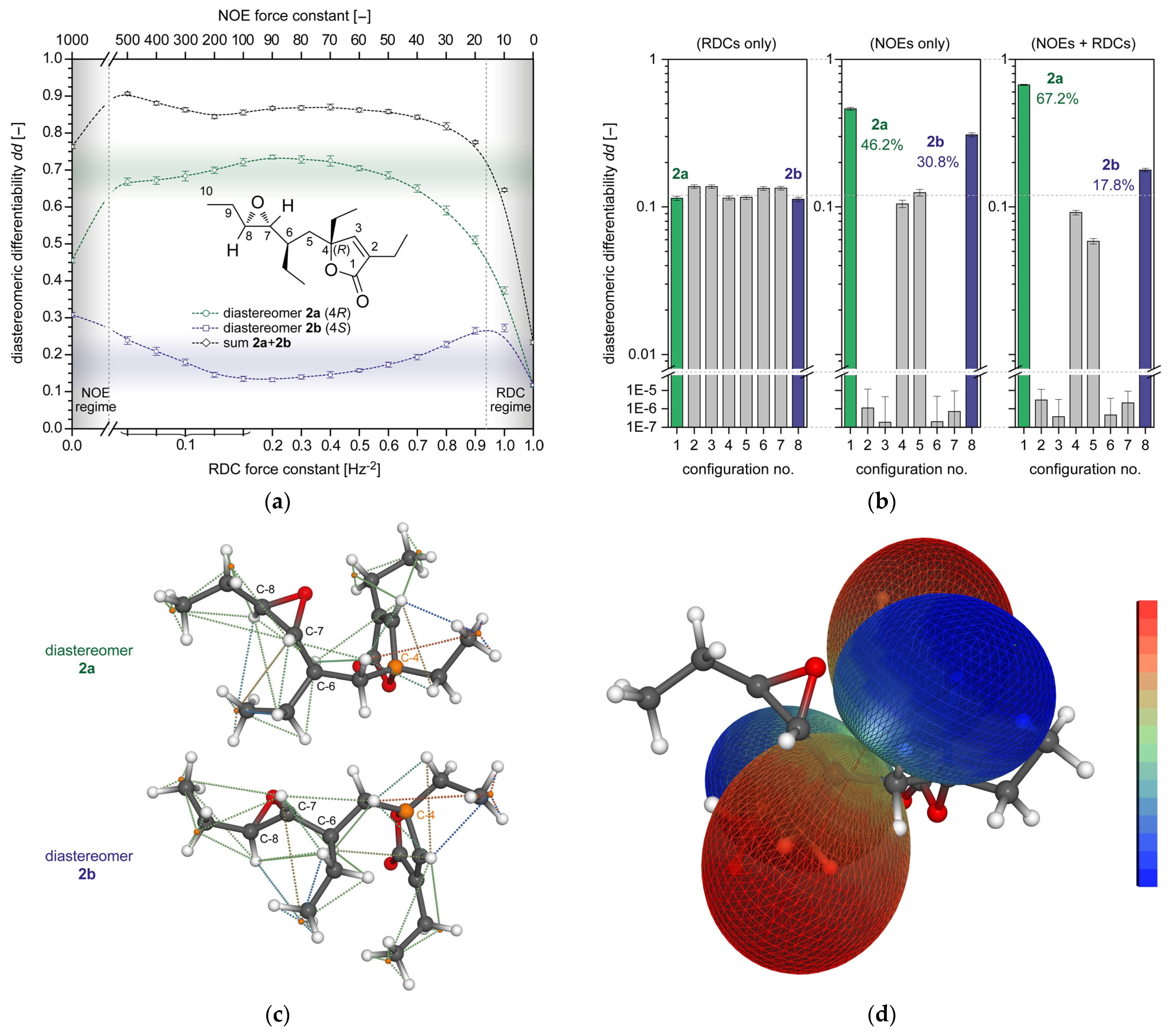
2.4.1. Plakilactone H (2)
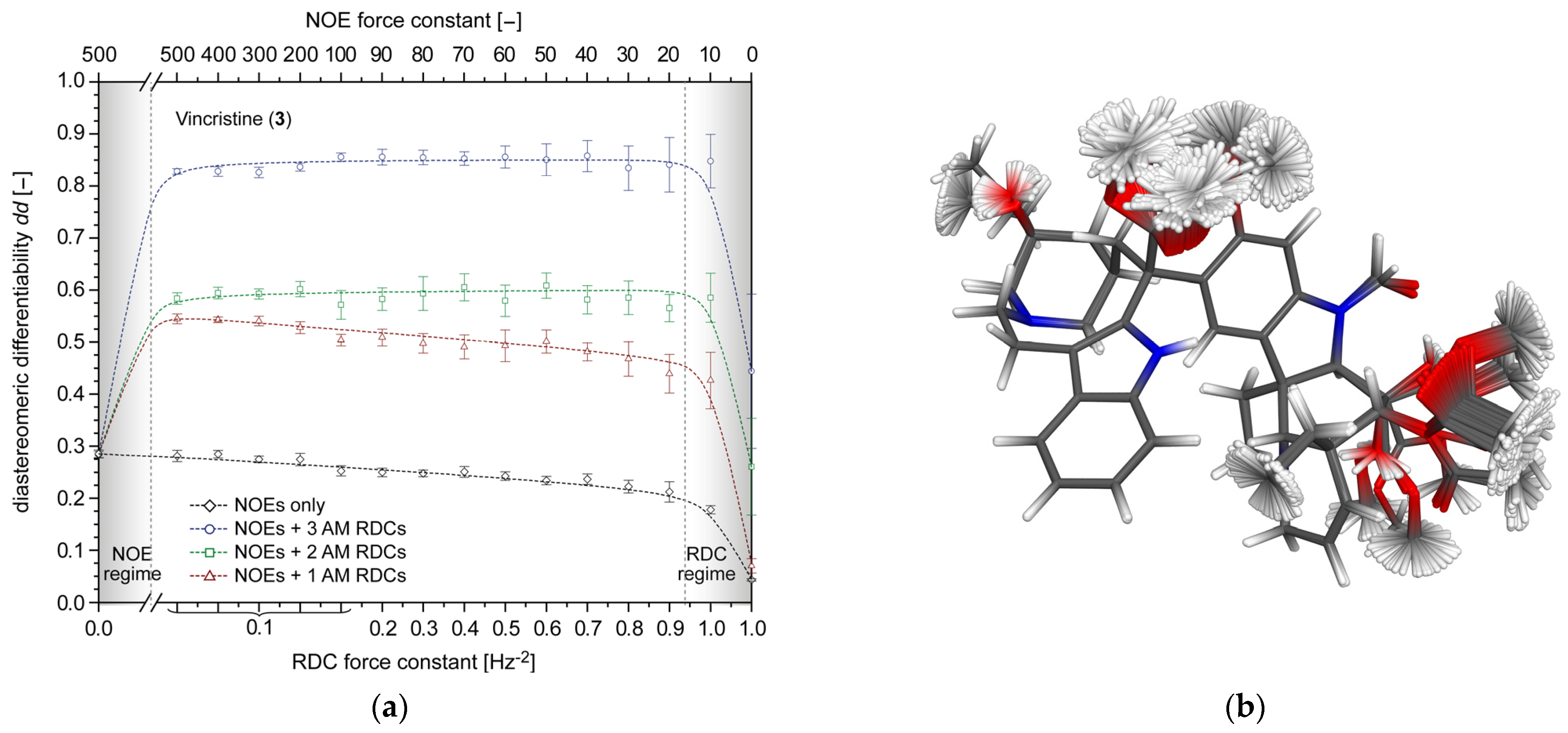
2.4.2. Vincristine (3)
3. Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Elyashberg, M.; Argyropoulos, D. Computer Assisted Structure Elucidation (CASE): Current and Future Perspectives. Magn. Reson. Chem. 2021, 59, 669–690. [Google Scholar] [CrossRef] [PubMed]
- Koos, M.R.M.; Navarro-Vázquez, A.; Anklin, C.; Gil, R.R. Computer-Assisted 3D Structure Elucidation (CASE-3D): The Structural Value of 2JCH in Addition to 3JCH Coupling Constants. Angew. Chem. Int. Ed. 2020, 59, 3938–3941. [Google Scholar] [CrossRef]
- Liu, Y.; Navarro-Vázquez, A.; Gil, R.R.; Griesinger, C.; Martin, G.E.; Williamson, R.T. Application of anisotropic NMR parameters to the confirmation of molecular structure. Nat. Protoc. 2019, 14, 217–247. [Google Scholar] [CrossRef]
- Milanowski, D.J.; Oku, N.; Cartner, L.K.; Bokesch, H.R.; Williamson, R.T.; Saurí, J.; Liu, Y.; Blinov, K.A.; Ding, Y.; Li, X.-C.; et al. Unequivocal determination of caulamidines A and B: Application and validation of new tools in the structure elucidation tool box. Chem. Sci. 2018, 9, 307–314. [Google Scholar] [CrossRef] [Green Version]
- Navarro-Vázquez, A.; Gil, R.R.; Blinov, K. Computer-Assisted 3D Structure Elucidation (CASE-3D) of Natural Products Combining Isotropic and Anisotropic NMR Parameters. J. Nat. Prod. 2018, 81, 203–210. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Saurí, J.; Mevers, E.; Peczuh, M.W.; Hiemstra, H.; Clardy, J.; Martin, G.E.; Williamson, R.T. Unequivocal determination of complex molecular structures using anisotropic NMR measurements. Science 2017, 356, 5349. [Google Scholar] [CrossRef] [Green Version]
- Troche-Pesqueira, E.; Anklin, C.; Gil, R.R.; Navarro-Vázquez, A. Computer-Assisted 3D Structure Elucidation of Natural Products using Residual Dipolar Couplings. Angew. Chem. Int. Ed. 2017, 56, 3660–3664. [Google Scholar] [CrossRef]
- Buevich, A.V.; Elyashberg, M.E. Synergistic Combination of CASE Algorithms and DFT Chemical Shift Predictions: A Powerful Approach for Structure Elucidation, Verification, and Revision. J. Nat. Prod. 2016, 79, 3105–3116. [Google Scholar] [CrossRef] [PubMed]
- Elyashberg, M. Identification and structure elucidation by NMR spectroscopy. TrAC Trends Anal. Chem. 2015, 69, 88–97. [Google Scholar] [CrossRef]
- Smurnyy, Y.D.; Blinov, K.A.; Churanova, T.S.; Elyashberg, M.E.; Williams, A.J. Toward More Reliable 13C and 1H Chemical Shift Prediction: A Systematic Comparison of Neural-Network and Least-Squares Regression Based Approaches. J. Chem. Inf. Model. 2008, 48, 128–134. [Google Scholar] [CrossRef]
- Smurnyy, Y.D.; Elyashberg, M.E.; Blinov, K.A.; Lefebvre, B.A.; Martin, G.E.; Williams, A.J. Computer-aided determination of relative stereochemistry and 3D models of complex organic molecules from 2D NMR spectra. Tetrahedron 2005, 61, 9980–9989. [Google Scholar] [CrossRef]
- Lindel, T.; Junker, J.; Köck, M. COCON: From NMR Correlation Data to Molecular Constitutions. J. Mol. Model. 1997, 3, 364–368. [Google Scholar] [CrossRef]
- Lindel, T.; Junker, J.; Köck, M. 2D-NMR-guided constitutional analysis of organic compounds employing the computer program COCON. Eur. J. Org. Chem. 1999, 573–577. [Google Scholar] [CrossRef]
- Meiler, J.; Köck, M. Novel methods of automated structure elucidation based on13C NMR spectroscopy. Magn. Reson. Chem. 2004, 42, 1042–1045. [Google Scholar] [CrossRef]
- Ermanis, K.; Parkes, K.E.B.; Agback, T.; Goodman, J.M. Expanding DP4: Application to drug compounds and automation. Org. Biomol. Chem. 2016, 14, 3943–3949. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Marcarino, M.O.; Zanardi, M.M.; Sarotti, A.M. The Risks of Automation: A Study on DFT Energy Miscalculations and Its Consequences in NMR-based Structural Elucidation. Org. Lett. 2020, 22, 3561–3565. [Google Scholar] [CrossRef]
- Nicolaou, K.C.; Snyder, S.A. Chasing Molecules That Were Never There: Misassigned Natural Products and the Role of Chemical Synthesis in Modern Structure Elucidation. Angew. Chem. Int. Ed. 2005, 44, 1012–1044. [Google Scholar] [CrossRef]
- Maier, M.E. Structural revisions of natural products by total synthesis. Nat. Prod. Rep. 2009, 26, 1105–1124. [Google Scholar] [CrossRef] [PubMed]
- Köck, M.; Grube, A.; Seiple, I.B.; Baran, P.S. The Pursuit of Palau’amine. Angew. Chem. Int. Ed. 2007, 46, 6586–6594. [Google Scholar] [CrossRef]
- Suyama, T.L.; Gerwick, W.H.; McPhail, K.L. Survey of marine natural product structure revisions: A synergy of spectroscopy and chemical synthesis. Bioorgan. Med. Chem. 2011, 19, 6675–6701. [Google Scholar] [CrossRef] [Green Version]
- Chhetri, B.K.; Lavoie, S.; Sweeney-Jones, A.M.; Kubanek, J. Recent trends in the structural revision of natural products. Nat. Prod. Rep. 2018, 35, 514–531. [Google Scholar] [CrossRef] [PubMed]
- Vögeli, B. The nuclear Overhauser effect from a quantitative perspective. Prog. Nucl. Magn. Reson. Spectrosc. 2014, 78, 1–46. [Google Scholar] [CrossRef] [Green Version]
- Neuhaus, D.; Williamson, M.P. The Nuclear Overhauser Effect in Structural and Conformational Analysis; Wiley-VCH: Weinheim, Germany, 2000. [Google Scholar]
- Lesot, P.; Aroulanda, C.; Berdagué, P.; Meddour, A.; Merlet, D.; Farjon, J.; Giraud, N.; Lafon, O. Multinuclear NMR in polypeptide liquid crystals: Three fertile decades of methodological developments and analytical challenges. Prog. Nucl. Magn. Reson. Spectrosc. 2020, 116, 85–154. [Google Scholar] [CrossRef]
- Kummerlöwe, G.; Luy, B. Residual Dipolar Couplings for the Configurational and Conformational Analysis of Organic Molecules. Annu. Rep. NMR Spectrosc. 2009, 68, 193–232. [Google Scholar]
- Kummerlöwe, G.; Luy, B. Residual dipolar couplings as a tool in determining the structure of organic molecules. TrAC Trends Anal. Chem. 2009, 28, 483–493. [Google Scholar] [CrossRef]
- Li, G.W.; Liu, H.; Qiu, F.; Wang, X.-J.; Lei, X.-X. Residual Dipolar Couplings in Structure Determination of Natural Products. Nat. Prod. Bioprospecting 2018, 8, 279–295. [Google Scholar] [CrossRef] [Green Version]
- Luy, B. Disinction of enantiomers by NMR spectroscopy using chiral orienting media. J. Indian Inst. Sci. 2010, 90, 119–132. [Google Scholar]
- Navarro-Vázquez, A.; Berdagué, P.; Lesot, P. Integrated Computational Protocol for the Analysis of Quadrupolar Splittings from Natural-Abundance Deuterium NMR Spectra in (Chiral) Oriented Media. ChemPhysChem 2017, 18, 1252–1266. [Google Scholar] [CrossRef] [PubMed]
- Lesot, P.; Aroulanda, C.; Zimmermann, H.; Luz, Z. Enantiotopic discrimination in the NMR spectrum of prochiral solutes in chiral liquid crystals. Chem. Soc. Rev. 2015, 44, 2330–2375. [Google Scholar] [CrossRef]
- Lesot, P.; Gil, R.R.; Berdagué, P.; Navarro-Vázquez, A. Deuterium Residual Quadrupolar Couplings: Crossing the Current Frontiers in the Relative Configuration Analysis of Natural Products. J. Nat. Prod. 2020, 83, 3141–3148. [Google Scholar] [CrossRef]
- Nath, N.; Fuentes-Monteverde, J.C.; Pech-Puch, D.; Rodríguez, J.; Jiménez, C.; Noll, M.; Kreiter, A.; Reggelin, M.; Navarro-Vázquez, A.; Griesinger, C. Relative configuration of micrograms of natural compounds using proton residual chemical shift anisotropy. Nat. Commun. 2020, 11, 4372. [Google Scholar] [CrossRef]
- Lesot, P.; Berdagué, P.; Silvestre, V.; Remaud, G. Exploring the enantiomeric 13C position-specific isotope fractionation: Challenges and anisotropic NMR-based analytical strategy. Anal. Bioanal. Chem. 2021, 413, 6379–6392. [Google Scholar] [CrossRef] [PubMed]
- Li, X.-L.; Chi, L.-P.; Navarro-Vázquez, A.; Hwang, S.; Schmieder, P.; Li, X.M.; Li, X.; Yang, S.-Q.; Lei, X.; Wang, B.-G.; et al. Stereochemical Elucidation of Natural Products from Residual Chemical Shift Anisotropies in a Liquid Crystalline Phase. J. Am. Chem. Soc. 2019, 142, 2301–2309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Recchia, M.J.J.; Cohen, R.D.; Liu, Y.; Sherer, E.C.; Harper, J.K.; Martin, G.E.; Williamson, R.T. “One-Shot” Measurement of Residual Chemical Shift Anisotropy Using Poly-γ-benzyl-l-glutamate as an Alignment Medium. Org. Lett. 2020, 22, 8850–8854. [Google Scholar] [CrossRef] [PubMed]
- Hallwass, F.; Teles, R.R.; Hellemann, E.; Griesinger, C.; Gil, R.R.; Navarro-Vázquez, A. Measurement of residual chemical shift anisotropies in compressed polymethylmethacrylate gels. Automatic compensation of gel isotropic shift contribution. Magn. Reson. Chem. 2018, 56, 321–328. [Google Scholar] [CrossRef]
- Nath, N.; Schmidt, M.; Gil, R.R.; Williamson, R.T.; Martin, G.E.; Navarro-Vázquez, A.; Griesinger, C.; Liu, Y. Determination of Relative Configuration from Residual Chemical Shift Anisotropy. J. Am. Chem. Soc. 2016, 138, 9548–9556. [Google Scholar] [CrossRef]
- Hallwass, F.; Schmidt, M.; Sun, H.; Mazur, A.; Kummerlöwe, G.; Luy, B.; Navarro-Vázquez, A.; Griesinger, C.; Reinscheid, U.M. Residual Chemical Shift Anisotropy (RCSA): A Tool for the Analysis of the Configuration of Small Molecules. Angew. Chem. Int. Ed. 2011, 50, 9487–9490. [Google Scholar] [CrossRef]
- Schmidts, V. Perspectives in the application of residual dipolar couplings in the structure elucidation of weakly aligned small molecules. Magn. Reson. Chem. 2017, 55, 54–60. [Google Scholar] [CrossRef]
- Schwab, M.; Herold, D.; Thiele, C.M. Polyaspartates as Thermoresponsive Enantiodifferentiating Helically Chiral Alignment Media for Anisotropic NMR Spectroscopy. Chem. A Eur. J. 2017, 23, 14576–14584. [Google Scholar] [CrossRef]
- Schwab, M.; Schmidts, V.; Thiele, C.M. Thermoresponsive Alignment Media in NMR Spectroscopy: Helix Reversal of a Copolyaspartate at Ambient Temperatures. Chem. A Eur. J. 2018, 24, 14373–14377. [Google Scholar] [CrossRef]
- Hirschmann, M.; Schirra, D.S.; Thiele, C.M. Copolyaspartates: Uncovering Simultaneous Thermo and Magnetoresponsiveness. Macromolecules 2021, 54, 1648–1656. [Google Scholar] [CrossRef]
- Knoll, K.; Leyendecker, M.; Thiele, C.M. L-Valine Derivatised 1,3,5-Benzene-Tricarboxamides as Building Blocks for a New Supramolecular Organogel-Like Alignment Medium. Eur. J. Org. Chem. 2019, 2019, 720–727. [Google Scholar] [CrossRef]
- Li, G.-W.; Cao, J.-M.; Zong, W.; Hu, L.; Hu, M.-L.; Lei, X.; Sun, H.; Tan, R.X. Helical Polyisocyanopeptides as Lyotropic Liquid Crystals for Measuring Residual Dipolar Couplings. Chem. A Eur. J. 2017, 23, 7653–7656. [Google Scholar] [CrossRef] [PubMed]
- Lei, X.; Qiu, F.; Sun, H.; Bai, L.; Wang, W.-X.; Xiang, W.; Xiao, H. A Self-Assembled Oligopeptide as a Versatile NMR Alignment Medium for the Measurement of Residual Dipolar Couplings in Methanol. Angew. Chem. Int. Ed. 2017, 56, 12857–12861. [Google Scholar] [CrossRef]
- Qin, S.Y.; Jiang, Y.; Sun, H.; Liu, H.; Zhang, A.Q.; Lei, X. Measurement of Residual Dipolar Couplings of Organic Molecules in Multiple Solvent Systems Using a Liquid-Crystalline-Based Medium. Angew. Chem. Int. Ed. 2020, 59, 17097–17103. [Google Scholar] [CrossRef]
- Navarro-Vázquez, A. When not to rely on Boltzmann populations. Automated CASE-3D structure elucidation of hyacinthacines through chemical shift differences. Magn. Reson. Chem. 2020, 58, 139–144. [Google Scholar] [CrossRef]
- Cornilescu, G.; Alvarenga, R.F.R.; Wyche, T.P.; Bugni, T.S.; Gil, R.R.; Cornilescu, C.C.; Westler, W.M.; Markley, J.L.; Schwieters, C.D. Progressive Stereo Locking (PSL): A Residual Dipolar Coupling Based Force Field Method for Determining the Relative Configuration of Natural Products and Other Small Molecules. ACS Chem. Biol. 2017, 12, 2157–2163. [Google Scholar] [CrossRef] [Green Version]
- Kaptein, R.; Zuiderweg, E.R.P.; Scheek, R.M.; Boelens, R.; van Gunsteren, W.F. A protein structure from nuclear magnetic resonance data: Lac Repressor headpiece. J. Mol. Biol. 1985, 182, 179–182. [Google Scholar] [CrossRef]
- Clore, G.M.; Gronenborn, A.M.; Brunger, A.T.; Karplus, M. Solution conformation of a heptadecapeptide comprising the DNA binding helix F of the cyclic AMP receptor protein of Escherichia coli: Combined use of 1H nuclear magnetic resonance and restrained molecular dynamics. J. Mol. Biol. 1985, 186, 435–455. [Google Scholar] [CrossRef]
- Reggelin, M.; Hoffmann, H.; Köck, M.; Mierke, D.F. Determination of conformation and relative configuration of a small, rapidly tumbling molecule in solution by combined application of NOESY and restrained MD calculations. J. Am. Chem. Soc. 1992, 114, 3272–3277. [Google Scholar] [CrossRef]
- Di Pietro, M.E.; Tzvetkova, P.; Gloge, T.; Sternberg, U.; Luy, B. Fundamental and practical aspects of molecular dynamics using tensorial orientational constraints. Liq. Cryst. 2020, 47, 2043–2057. [Google Scholar] [CrossRef]
- Di Pietro, M.E.; Sternberg, U.; Luy, B. Molecular Dynamics with Orientational Tensorial Constraints: A New Approach to Probe the Torsional Angle Distributions of Small Rotationally Flexible Molecules. J. Phys. Chem. B 2019, 123, 8480–8491. [Google Scholar] [CrossRef]
- Tzvetkova, P.; Sternberg, U.; Gloge, T.; Navarro-Vázquez, A.; Luy, B. Configuration determination by residual dipolar couplings: Accessing the full conformational space by molecular dynamics with tensorial constraints. Chem. Sci. 2019, 10, 8774–8791. [Google Scholar] [CrossRef] [PubMed]
- Sternberg, U.; Witter, R. Molecular dynamics simulations on PGLa using NMR orientational constraints. J. Biomol. NMR 2015, 63, 265–274. [Google Scholar] [CrossRef]
- Sternberg, U.; Witter, R.; Ulrich, A.S. All-atom molecular dynamics simulations using orientational constraints from anisotropic NMR samples. J. Biomol. NMR 2007, 38, 23–39. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Azurmendi, H.F.; Bush, C.A. Tracking Alignment from the Moment of Inertia Tensor (TRAMITE) of Biomolecules in Neutral Dilute Liquid Crystal Solutions. J. Am. Chem. Soc. 2002, 124, 2426–2427. [Google Scholar] [CrossRef]
- Ozenne, V.; Bauer, F.; Salmon, L.; Huang, J.-R.; Jensen, M.R.; Segard, S.; Bernado, P.; Charavay, C.; Blackledge, M. Flexible-meccano: A tool for the generation of explicit ensemble descriptions of intrinsically disordered proteins and their associated experimental observables. Bioinformatics 2012, 28, 1463–1470. [Google Scholar] [CrossRef] [PubMed]
- Tomba, G.; Camilloni, C.; Vendruscolo, M. Determination of the conformational states of strychnine in solution using NMR residual dipolar couplings in a tensor-free approach. Methods 2018, 148, 4–8. [Google Scholar] [CrossRef]
- Camilloni, C.; Vendruscolo, M. A Tensor-Free Method for the Structural and Dynamical Refinement of Proteins using Residual Dipolar Couplings. J. Phys. Chem. B 2015, 119, 653–661. [Google Scholar] [CrossRef] [PubMed]
- Grube, A.; Köck, M. Structural assignment of tetrabromostyloguanidine: Does the relative configuration of the palau’amines need revision? Angew. Chem. Int. Ed. 2007, 46, 2320–2324. [Google Scholar] [CrossRef]
- Köck, M.; Reggelin, M.; Immel, S. The Advanced Floating Chirality Distance Geometry Approach―How Anisotropic NMR Parameters Can Support the Determination of the Relative Configuration of Natural Products. Mar. Drugs 2020, 18, 330. [Google Scholar] [CrossRef] [PubMed]
- De Opakua, A.I.; Klama, F.; Ndukwe, I.; Martin, G.E.; Williamson, R.T.; Zweckstetter, M. Determination of Complex Small-Molecule Structures Using Molecular Alignment Simulation. Angew. Chem. Int. Ed. 2020, 59, 6172–6176. [Google Scholar] [CrossRef] [PubMed]
- De Opakua, A.I.; Zweckstetter, M. Extending the applicability of P3D for structure determination of small molecules. Magn. Reson. 2021, 2, 105–116. [Google Scholar] [CrossRef]
- Roth, F.A.; Schmidts, V.; Thiele, C.M. TITANIA: Model-Free Interpretation of Residual Dipolar Couplings in the Context of Organic Compounds. J. Org. Chem. 2021, 86, 15387–15402. [Google Scholar] [CrossRef] [PubMed]
- Roth, F.A.; Schmidts, V.; Rettig, J.; Thiele, C.M. Model Free Analysis of Experimental Residual Dipolar Couplings in Small Organic Compounds. Phys. Chem. Chem. Phys. 2022. accepted. [Google Scholar] [CrossRef]
- Havel, T.F.; Kuntz, I.D.; Crippen, G.M. The theory and practice of distance geometry. Bull. Math. Biol. 1983, 45, 665–720. [Google Scholar] [CrossRef]
- Kaptein, R.; Boelens, R.; Scheek, R.M.; van Gunsteren, W.F. Protein structures from NMR. Biochemistry 1988, 27, 5389–5395. [Google Scholar] [CrossRef]
- De Vlieg, J.; Scheek, R.M.; van Gunsteren, W.F.; Berendsen, H.J.C.; Kaptein, R.; Thomason, J. Combined procedure of distance geometry and restrained molecular dynamics techniques for protein structure determination from nuclear magnetic resonance data: Application to the DNA binding domain of lac repressor from Escherichia coli. Proteins: Struct. Funct. Bioinform. 1988, 3, 209–218. [Google Scholar] [CrossRef]
- Crippen, G.M.; Havel, T.F. Distance Geometry and Molecular Conformation; Research Studies Press: Taunton, UK, 1988. [Google Scholar]
- Crippen, G.M. A novel approach to calculation of conformation: Distance geometry. J. Comput. Phys. 1977, 24, 96–107. [Google Scholar] [CrossRef]
- Mierke, D.F.; Reggelin, M. Simultaneous determination of conformation and configuration using distance geometry. J. Org. Chem. 1992, 57, 6365–6367. [Google Scholar] [CrossRef]
- Köck, M.; Griesinger, C. FAST NOESY Experiments—An Approach for Fast Structure Determination. Angew. Chem. Int. Ed. 1994, 33, 332–334. [Google Scholar] [CrossRef]
- Köck, M.; Junker, J. How Many NOE Derived Restraints Are Necessary for a Reliable Determination of the Relative Configuration of an Organic Compound? Application to a Model System. J. Org. Chem. 1997, 62, 8614–8615. [Google Scholar] [CrossRef]
- Köck, M.; Junker, J. Determination of the Relative Configuration of Organic Compounds Using NMR and DG: A Systematic Approach for a Model System. J. Mol. Model. 1997, 3, 403–407. [Google Scholar] [CrossRef]
- Immel, S.; Köck, M.; Reggelin, M.K. Configurational Analysis by Residual Dipolar Coupling Driven Floating Chirality Distance Geometry Calculations. Chem. A Eur. J. 2018, 24, 13918–13930. [Google Scholar] [CrossRef]
- Köck, M.; Reggelin, M.; Immel, S. Model-Free Approach for the Configurational Analysis of Marine Natural Products. Mar. Drugs 2021, 19, 283. [Google Scholar] [CrossRef] [PubMed]
- Cornilescu, G.; Marquardt, J.L.; Ottiger, M.; Bax, A. Validation of Protein Structure from Anisotropic Carbonyl Chemical Shifts in a Dilute Liquid Crystalline Phase. J. Am. Chem. Soc. 1998, 120, 6836–6837. [Google Scholar] [CrossRef]
- Immel, S.; Köck, M.; Reggelin, M. Configurational analysis by residual dipolar couplings: A critical assessment of diastereomeric differentiabilities. Chirality 2019, 31, 384–400. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- De Melo Sousa, C.M.; Giordani, R.B.; de Almeida, W.A.M.; Griesinger, C.; Gil, R.R.; Navarro-Vázquez, A.; Hallwass, F. Effect of the solvent on the conformation of monocrotaline as determined by isotropic and anisotropic NMR parameters. Magn. Reson. Chem. 2021, 59, 561–568. [Google Scholar] [CrossRef] [Green Version]
- Zweckstetter, M.; Bax, A. Evaluation of uncertainty in alignment tensors obtained from dipolar couplings. J. Biomol. NMR 2002, 23, 127–137. [Google Scholar] [CrossRef]
- Losonczi, J.A.; Andrec, M.; Fischer, M.W.F.; Prestegard, J.H. Order Matrix Analysis of Residual Dipolar Couplings Using Singular Value Decomposition. J. Magn. Reson. 1999, 138, 334–342. [Google Scholar] [CrossRef] [Green Version]
- Reggelin, M.K.; Immel, S. Configurational Analysis by Residual Dipolar Couplings: Critical Assessment of “Structural Noise” from Thermal Vibrations. Angew. Chem. Int. Ed. 2021, 60, 3412–3416. [Google Scholar] [CrossRef] [PubMed]
- Holak, T.A.; Gondol, D.; Otlewski, J.; Wilusz, T. Determination of the complete three-dimensional structure of the trypsin inhibitor from squash seeds in aqueous solution by nuclear magnetic resonance and a combination of distance geometry and dynamical simulated annealing. J. Mol. Biol. 1989, 210, 635–648. [Google Scholar] [CrossRef]
- Köck, M.; Schmidt, G.; Seiple, I.B.; Baran, P.S. Configurational Analysis of Tetracyclic Dimeric Pyrrole–Imidazole Alkaloids Using a Floating Chirality Approach. J. Nat. Prod. 2012, 75, 127–130. [Google Scholar] [CrossRef] [Green Version]
- Weber, P.L.; Morrison, R.; Hare, D. Determining stereo-specific proton nuclear magnetic resonance assignments from distance geometry calculations. J. Mol. Biol. 1988, 204, 483–487. [Google Scholar] [CrossRef]
- Scheek, R.M.; van Gunsteren, W.F.; Kaptein, R. Molecular dynamics simulation techniques for determination of molecular structures from nuclear magnetic resonance data. Methods Enzymol. 1989, 177, 204–218. [Google Scholar] [CrossRef] [PubMed]
- Kinz-Thompson, C.D.; Ray, K.K.; Gonzalez, R.L. Bayesian Inference: The Comprehensive Approach to Analyzing Single-Molecule Experiments. Annu. Rev. Biophys. 2021, 50, 191–208. [Google Scholar] [CrossRef] [PubMed]
- Von Toussaint, U. Bayesian inference in physics. Rev. Mod. Phys. 2011, 83, 943–999. [Google Scholar] [CrossRef] [Green Version]
- Hibbert, D.B.; Armstrong, N. An introduction to Bayesian methods for analyzing chemistry data: Part II: A review of applications of Bayesian methods in chemistry. Chemom. Intell. Lab. Syst. 2009, 97, 211–220. [Google Scholar] [CrossRef]
- Stephen, M.S. The Epic Story of Maximum Likelihood. Stat. Sci. 2007, 22, 598–620. [Google Scholar] [CrossRef]
- Cheeseman, P.; Stutz, J. On the Relationship between Bayesian and Maximum Entropy Inference. AIP Conf. Proc. 2004, 735, 445–461. [Google Scholar] [CrossRef] [Green Version]
- Pressé, S.; Ghosh, K.; Lee, J.; Dill, K.A. Principles of maximum entropy and maximum caliber in statistical physics. Rev. Mod. Phys. 2013, 85, 1115–1141. [Google Scholar] [CrossRef] [Green Version]
- Habeck, M. Bayesian Modeling of Biomolecular Assemblies with Cryo-EM Maps. Front. Mol. Biosci. 2017, 4, 15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Habeck, M.; Nilges, M.; Rieping, W. Bayesian inference applied to macromolecular structure determination. Phys. Rev. E 2005, 72, 031912. [Google Scholar] [CrossRef]
- Sels, D.; Dashti, H.; Mora, S.; Demler, O.; Demler, E. Quantum approximate Bayesian computation for NMR model inference. Nat. Mach. Intell. 2020, 2, 396–402. [Google Scholar] [CrossRef] [PubMed]
- Riniker, S.; Landrum, G.A. Better Informed Distance Geometry: Using What We Know to Improve Conformation Generation. J. Chem. Inf. Model. 2015, 55, 2562–2574. [Google Scholar] [CrossRef]
- Chan, L.; Hutchison, G.R.; Morris, G.M. Bayesian optimization for conformer generation. J. Cheminform. 2019, 11, 32. [Google Scholar] [CrossRef]
- Chan, L.; Hutchison, G.R.; Morris, G.M. BOKEI: Bayesian optimization using knowledge of correlated torsions and expected improvement for conformer generation. Phys. Chem. Chem. Phys. 2020, 22, 5211–5219. [Google Scholar] [CrossRef]
- Habeck, M.; Nilges, M.; Rieping, W. A unifying probabilistic framework for analyzing residual dipolar couplings. J. Biomol. NMR 2008, 40, 135–144. [Google Scholar] [CrossRef] [Green Version]
- Lincoff, J.; Haghighatlari, M.; Krzeminski, M.; Teixeira, J.M.C.; Gomes, G.-N.W.; Gradinaru, C.C.; Forman-Kay, J.D.; Head-Gordon, T. Extended experimental inferential structure determination method in determining the structural ensembles of disordered protein states. Commun. Chem. 2020, 3, 74. [Google Scholar] [CrossRef] [PubMed]
- Habeck, M.; Rieping, W.; Nilges, M. Weighting of experimental evidence in macromolecular structure determination. Proc. Natl. Acad. Sci. USA 2006, 103, 1756–1761. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Engel, E.A.; Anelli, A.; Hofstetter, A.; Paruzzo, F.; Emsley, L.; Ceriotti, M. A Bayesian approach to NMR crystal structure determination. Phys. Chem. Chem. Phys. 2019, 21, 23385–23400. [Google Scholar] [CrossRef] [Green Version]
- Hofstetter, A.; Balodis, M.; Paruzzo, F.M.; Widdifield, C.M.; Stevanato, G.; Pinon, A.C.; Bygrave, P.J.; Day, G.M.; Emsley, L. Rapid Structure Determination of Molecular Solids Using Chemical Shifts Directed by Unambiguous Prior Constraints. J. Am. Chem. Soc. 2019, 141, 16624–16634. [Google Scholar] [CrossRef]
- Hofstetter, A.; Emsley, L. Positional Variance in NMR Crystallography. J. Am. Chem. Soc. 2017, 139, 2573–2576. [Google Scholar] [CrossRef]
- Bayes, T.; Price, M. An essay towards solving a problem in the doctrine of chances. By the late Rev. Mr. Bayes, F.R.S. communicated by Mr. Price, in a letter to John Canton, A.M.F.R.S. Phil. Trans. R. Soc. Lond. 1763, 53, 370–418. [Google Scholar] [CrossRef]
- Nilges, M.; Habeck, M.; Rieping, W. Probabilistic structure calculation. C. R. Chim. 2008, 11, 356–369. [Google Scholar] [CrossRef]
- Williams, M.N.; Bååth, R.A.; Philipp, M.C. Using Bayes Factors to Test Hypotheses in Developmental Research. Res. Hum. Dev. 2017, 14, 321–337. [Google Scholar] [CrossRef]
- O’Hagan, T. Bayes factors. Significance 2006, 3, 184–186. [Google Scholar] [CrossRef]
- Rieping, W.; Habeck, M.; Nilges, M. Modeling Errors in NOE Data with a Log-normal Distribution Improves the Quality of NMR Structures. J. Am. Chem. Soc. 2005, 127, 16026–16027. [Google Scholar] [CrossRef]
- Di Micco, S.; Zampella, A.; D’Auria, M.V.; Festa, C.; De Marino, S.; Riccio, R.; Butts, C.P.; Bifulco, G. Plakilactones G and H from a marine sponge. Stereochemical determination of highly flexible systems by quantitative NMR-derived interproton distances combined with quantum mechanical calculations of 13C chemical shifts. Beilstein J. Org. Chem. 2013, 9, 2940–2949. [Google Scholar] [CrossRef] [Green Version]
- Moncrief, J.W.; Lipscomb, W.N. Structures of Leurocristine (Vincristine) and Vincaleukoblastine.1 X-Ray Analysis of Leurocristine Methiodide. J. Am. Chem. Soc. 1965, 87, 4963–4964. [Google Scholar] [CrossRef] [PubMed]
- Moncrief, J.W.; Lipscomb, W.N. Structure of leurocristine methiodide dihydrate by anomalous scattering methods: Relation to leurocristine (vincristine) and vincaleukoblastine (vinblastine). Acta Crystallogr. Sect. A 1966, 21, 322–331. [Google Scholar] [CrossRef] [PubMed]
- Kramer, F.; Deshmukh, M.V.; Kessler, H.; Glaser, S.J. Residual dipolar coupling constants: An elementary derivation of key equations. Concepts Magn. Reson. 2004, 21A, 10–21. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Immel, S.; Köck, M.; Reggelin, M. NMR-Based Configurational Assignments of Natural Products: Gibbs Sampling and Bayesian Inference Using Floating Chirality Distance Geometry Calculations. Mar. Drugs 2022, 20, 14. https://doi.org/10.3390/md20010014
Immel S, Köck M, Reggelin M. NMR-Based Configurational Assignments of Natural Products: Gibbs Sampling and Bayesian Inference Using Floating Chirality Distance Geometry Calculations. Marine Drugs. 2022; 20(1):14. https://doi.org/10.3390/md20010014
Chicago/Turabian StyleImmel, Stefan, Matthias Köck, and Michael Reggelin. 2022. "NMR-Based Configurational Assignments of Natural Products: Gibbs Sampling and Bayesian Inference Using Floating Chirality Distance Geometry Calculations" Marine Drugs 20, no. 1: 14. https://doi.org/10.3390/md20010014
APA StyleImmel, S., Köck, M., & Reggelin, M. (2022). NMR-Based Configurational Assignments of Natural Products: Gibbs Sampling and Bayesian Inference Using Floating Chirality Distance Geometry Calculations. Marine Drugs, 20(1), 14. https://doi.org/10.3390/md20010014






