A New Analytic Approximation of Luminosity Distance in Cosmology Using the Parker–Sochacki Method
Abstract
1. Introduction
2. The Parker–Sochacki Method
3. Differential Equation for the Luminosity Distance in a Flat Universe
4. Luminosity Distance in Cosmology
4.1. CDM Cosmological Model
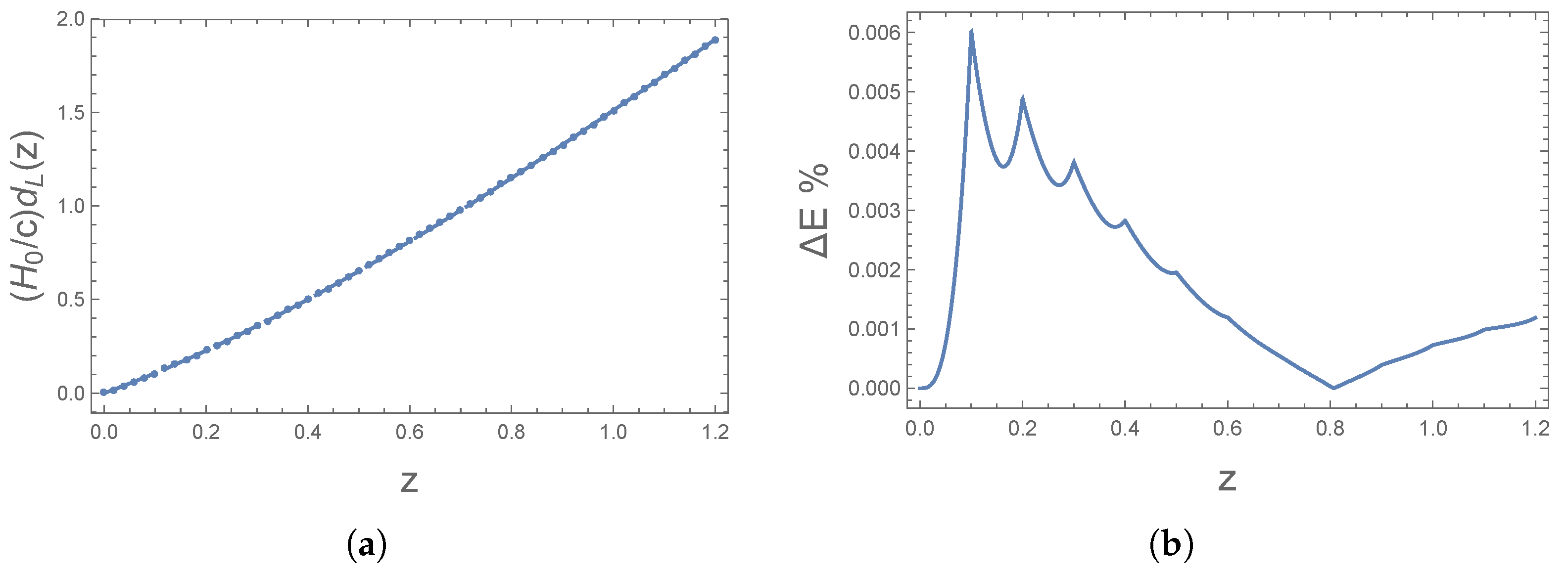
4.2. CPL Cosmological Model
5. Discussion and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Approximate Solutions
Appendix A.1. CDM Cosmological Model
Appendix A.2. CPL Cosmological Model
References
- Lin, W.; Mack, K.J.; Hou, L. Investigating the Hubble constant tension: Two numbers in the standard cosmological model. Astrophys. J. Lett. 2020, 904, L22. [Google Scholar] [CrossRef]
- Fanizza, G. Precision Cosmology and Hubble tension in the era of LSS surveys. arXiv 2021, arXiv:2110.15272v2. [Google Scholar]
- Pen, U.-L. Analytical fit to the luminosity distance for flat cosmologies with a cosmological constant. Astrophys. J. Supp. Ser. 1999, 120, 49–50. [Google Scholar] [CrossRef][Green Version]
- Wickramasinghe, T.; Ukwatta, T.N. An analytical approach for the determination of the luminosity distance in a flat universe with dark energy. Mon. Not. R. Astron. Soc. 2010, 206, 548–550. [Google Scholar] [CrossRef][Green Version]
- Liu, D.-Z.; Ma, C.; Zhang, T.-J.; Yang, Z. Numerical strategies of computing the luminosity distance. Mon. Not. R. Astron. Soc. 2011, 412, 2685–2688. [Google Scholar] [CrossRef]
- Adachi, M.; Kasai, M. An analytical approximation of the luminosity distance in flat cosmologies with a cosmological constant. Prog. Theor. Phys. 2012, 127, 145–152. [Google Scholar] [CrossRef]
- Eisenstein, D.J. An analytic expression for the growth function in a flat universe with a cosmological constant. arXiv 1997, arXiv:astro-ph/9709054. [Google Scholar]
- Mészáros, A.; Řípa, J. A curious relation between the flat cosmological model and the elliptic integral of the first kind. Astron. Astrophys. 2013, 556, A13. [Google Scholar] [CrossRef]
- Zaninetti, L. An analytical solution in the complex plane for the luminosity distance in flat cosmology. J. High. Energy Phys. 2016, 2, 581–586. [Google Scholar] [CrossRef]
- Baes, M.; Camps, P.; van de Putte, D. Analytical expressions and numerical evaluation of the luminosity distance in a flat cosmology. Mon. Not. R. Astron. Soc. 2017, 468, 927–930. [Google Scholar] [CrossRef]
- Clarkson, C.; Zunckel, C. Direct reconstruction of dark energy. Phys. Rev. Lett. 2010, 104, 211301. [Google Scholar] [CrossRef] [PubMed]
- Capozziello, S.; D’Agostino, R.; Luongo, O. High-redshift cosmography: Auxiliary variables versus Pad polynomials. Mon. Not. R. Astron. Soc. 2020, 494, 2576–2590. [Google Scholar] [CrossRef]
- Cattoën, C.; Visser, M. The Hubble series: Convergence properties and redshift variables. Class. Quantum Grav. 2007, 24, 5985–5998. [Google Scholar] [CrossRef]
- Scolnic, D.M.; Jones, D.O.; Rest, A.; Pan, Y.C.; Chornock, R.; Foley, R.J.; Huber, M.E.; Kessler, R.; Narayan, G.; Riess, A.G.; et al. The complete light-curve sample of spectroscopically confirmed SNe Ia from Pan-STARRS1 and cosmological constraints from the combined Pantheon sample. Astrophys. J. 2018, 859, 101. [Google Scholar] [CrossRef]
- Zhou, Y.-N.; Liu, D.-Z.; Zou, X.-B.; Wei, H. New generalizations of cosmography inspired by the Padé approximant. Eur. Phys. J. C 2016, 76, 281. [Google Scholar] [CrossRef]
- Li, S.-Y.; Li, Y.-L.; Zhang, T.-J.; Zhang, T. Model-independent determination of cosmic curvature based on the Padé approximation. Astrophys. J. 2019, 887, 36. [Google Scholar] [CrossRef]
- Wei, H.; Yan, X.-P.; Zhou, Y.-N. Cosmological applications of Padé approximant. J. Cosmol. Astropart. Phys. 2014, 1401, 045. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Analytic approximation of luminosity distance in cosmology via Variational Iteration Method. Univ. J. Comp. Math. 2017, 5, 68–74. [Google Scholar] [CrossRef]
- Yu, B.; Zhang, J.-C.; Zhang, T.-J.; Zhang, T. A new analytical approximation of luminosity distance by optimal HPM-Padé technique. Phys. Dark Univ. 2021, 31, 100772. [Google Scholar] [CrossRef]
- Shchigolev, V.K. Calculating luminosity distance versus redshift in FLRW cosmology via Homotopy Perturbation Method. Grav. Cosmo. 2017, 23, 142–148. [Google Scholar] [CrossRef]
- Shchigolev, V.K. A simple analytic approximation of luminosity distance in FLRW cosmology using Daftardar-Jafari Method. Comp. Sci. Info. Tech. 2020, 8, 43–49. [Google Scholar] [CrossRef]
- Parker, G.E.; Sochacki, J.S. Implementing the Picard iteration. Neural Parallel Sci. Comput. 1996, 4, 97–112. [Google Scholar]
- Parker, G.E.; Sochacki, J.S. A Picard-McLaurin theorem for initial value PDEs. Abstr. Appl. Anal. 2000, 5, 47–63. [Google Scholar] [CrossRef]
- Picard, E. Traite D’Analyse; Gauthier-Villars: Paris, France, 2013; Volume 3, pp. 1922–1928. [Google Scholar]
- Abdelrazik, I.M.; Elkaranshawy, H.A. Extended Parker Sochacki method for Michaelis-Menten enzymatic reaction model. Anal. Biochem. 2016, 496, 50–54. [Google Scholar] [CrossRef] [PubMed]
- Abdelrazik, I.M.; Elkaranshawy, H.A.; Abdelrazek, A.M. Modified Parker-Sochacki method for solving nonlinear oscillators. Mech. Based Des. Struct. Mach. 2017, 45, 239–252. [Google Scholar] [CrossRef]
- Akindeinde, S.O. Parker-Sochacki method for the solution of convective straight fins problem with temperature-dependent thermal conductivity. Int. J. Nonlinear Sci. 2018, 25, 119–128. [Google Scholar]
- Akindeinde, S.O.; Okyere, E. New analytic technique for the solution of nth order nonlinear two-point boundary value problems. Br. J. Math. Comput. Sci. 2016, 15, 1–11. [Google Scholar] [CrossRef]
- Elkaranshawy, H.A.; Abdelrazek, A.M.; Ezzat, H.M. Power series solution to sliding velocity in three-dimensional multibody systems with impact and friction. Int. J. Math. Comput. Phys. Electr. Comput. Eng. 2015, 9, 585–588. [Google Scholar]
- Nakhjiri, N.; Villac, B. Modified Picard integrator for spacefight mechanics. J. Guid. Control Dyn. 2014, 37, 1625–1637. [Google Scholar] [CrossRef]
- Nurminskii, E.; Buryi, A. Parker-Sochacki method for solving systems of ordinary differential equations using graphics processors. Numer. Anal. Appl. 2011, 4, 223. [Google Scholar] [CrossRef]
- Ogundare, B.S.; Akindeinde, S.O.; Adewumi, A.O.; Aderogba, A.A. Improved Parker- Sochacki approach for closed form solution of enzyme catalyzed reaction model. J. Mod. Methods Numer. Math. 2017, 8, 90–98. [Google Scholar] [CrossRef][Green Version]
- Rudmin, J.W. Application of the Parker-Sochacki Method to Celestial Mechanics; Technical Report; James Madison University: Harrisonburg, VA, USA, 1998. [Google Scholar]
- Singarimbun, A.; Fujimitsu, Y.; Djamal, M.; Dewi, R. Pressure transient modeling in geothermal reservoir by using Picard-Mclaurin iteration. Adv. Mater. Res. 2014, 1025–1026, 959–973. [Google Scholar]
- Stewart, R.D.; Bair, W. Spiking neural network simulation: Numerical integration with the Parker-Sochacki method. J. Comput. Neurosci. 2009, 27, 115–133. [Google Scholar] [CrossRef] [PubMed]
- Stewart, R.D.; Bair, W. Spiking neural network simulation: Memory-optimal synaptic event scheduling. J. Comput. Neurosci. 2011, 30, 721–728. [Google Scholar] [CrossRef]
- Szynkiewicz, P. A novel GPU-enabled simulator for large scale spiking neural networks. J. Telecommun. Inf. Technol. 2016, 2, 34–42. [Google Scholar]
- Akindeinde, S.O. A new multistage technique for approximate analytical solution of nonlinear differential equations. Heliyon 2020, 6, e05188. [Google Scholar] [CrossRef]
- Carothers, D.C.; Parker, G.E.; Sochacki, J.S.; Warne, P.G. Some properties of solutions to polynomial systems of differential equations. Electron. J. Differ. Equ. 2005, 2005, 1–17. [Google Scholar]
- Chevallier, M.; Polarski, D. Accelerating universes with scaling dark matter. Int. J. Mod. Phys. D 2001, 10, 213–223. [Google Scholar] [CrossRef]
- Linder, E.V. Exploring the expansion history of the Universe. Phys. Rev. Lett. 2003, 90, 091301. [Google Scholar] [CrossRef]
- Linder, E.V. Probing gravitation, dark energy, and acceleration. Phys. Rev. D 2004, 70, 023511. [Google Scholar] [CrossRef]
- Guenther, J.; Wolf, M. An adaptive, highly accurate and efficient, Parker-Sochacki algorithm for numerical solutions to initial value ordinary differential equation systems. SIAM Undergrad. Res. Online 2019, 12, 257–281. [Google Scholar] [CrossRef]
- Pouly, A.; Graça, D.S. Computational complexity of solving polynomial differential equations over unbounded domains. Theor. Comp. Sci. 2016, 626, 67–82. [Google Scholar] [CrossRef]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of omega and lambda from 42 high-redshift supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Weinberg, S. Gravitation and Cosmology: Principles and Applications of The General Theory of Relativity; John Wiley Press: New York, NY, USA, 1972. [Google Scholar]
- Solà, J.; Gómez-Valent, A.; de Pérez, J. Dynamical dark energy: Scalar fields and running vacuum. Mod. Phys. Lett. A 2017, 32, 1750054. [Google Scholar] [CrossRef]
- Nunes, R.C.; Pan, S.; Abreu, E.N.S.E.M.C. New observational constraints on f(R) gravity from cosmic chronometers. J. Cosmol. Astropart. Phys. 2017, 2017, 005. [Google Scholar] [CrossRef]

| z | ||
|---|---|---|
| ⋮ | ⋮ | |
| z | ||
|---|---|---|
| ⋮ | ⋮ | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sultana, J. A New Analytic Approximation of Luminosity Distance in Cosmology Using the Parker–Sochacki Method. Universe 2022, 8, 300. https://doi.org/10.3390/universe8060300
Sultana J. A New Analytic Approximation of Luminosity Distance in Cosmology Using the Parker–Sochacki Method. Universe. 2022; 8(6):300. https://doi.org/10.3390/universe8060300
Chicago/Turabian StyleSultana, Joseph. 2022. "A New Analytic Approximation of Luminosity Distance in Cosmology Using the Parker–Sochacki Method" Universe 8, no. 6: 300. https://doi.org/10.3390/universe8060300
APA StyleSultana, J. (2022). A New Analytic Approximation of Luminosity Distance in Cosmology Using the Parker–Sochacki Method. Universe, 8(6), 300. https://doi.org/10.3390/universe8060300






