Beyond Black Boxes: Interpretable AI with Explainable Neural Networks (ENNs) for Acute Myocardial Infarction (AMI) Using Common Hematological Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
- Demographic variables: age, gender (0: female, 1: male)
- Hematological parameters: white blood cell (WBC), red blood cell (RBC), hemoglobin (HGB), hematocrit (HCT), mean corpuscular volume (MCV), mean corpuscular hemoglobin (MCH), mean corpuscular hemoglobin concentration (MCHC), red cell distribution width—standard deviation (RDW-SD), red cell distribution width—coefficient of variation (RDW-CV), platelet count (PLT), mean platelet volume (MPV), platelet distribution width (PDW), procalcitonin (PCT), basophil (BA), eosinophil (EO), lymphocyte (LY), monocyte (MO), neutrophil (NEU)
- Derived indices: neutrophil-to-lymphocyte ratio (NEU/LY), platelet-to-lymphocyte ratio (PLT/LY), mean platelet volume-to-lymphocyte ratio (MPV/LY), lymphocyte-to-monocyte ratio (LY/MO)
- Target variable: label (0 = control, 1 = AMI)
2.2. Explainable Artificial Intelligence (XAI) and Neural Network (ENN)
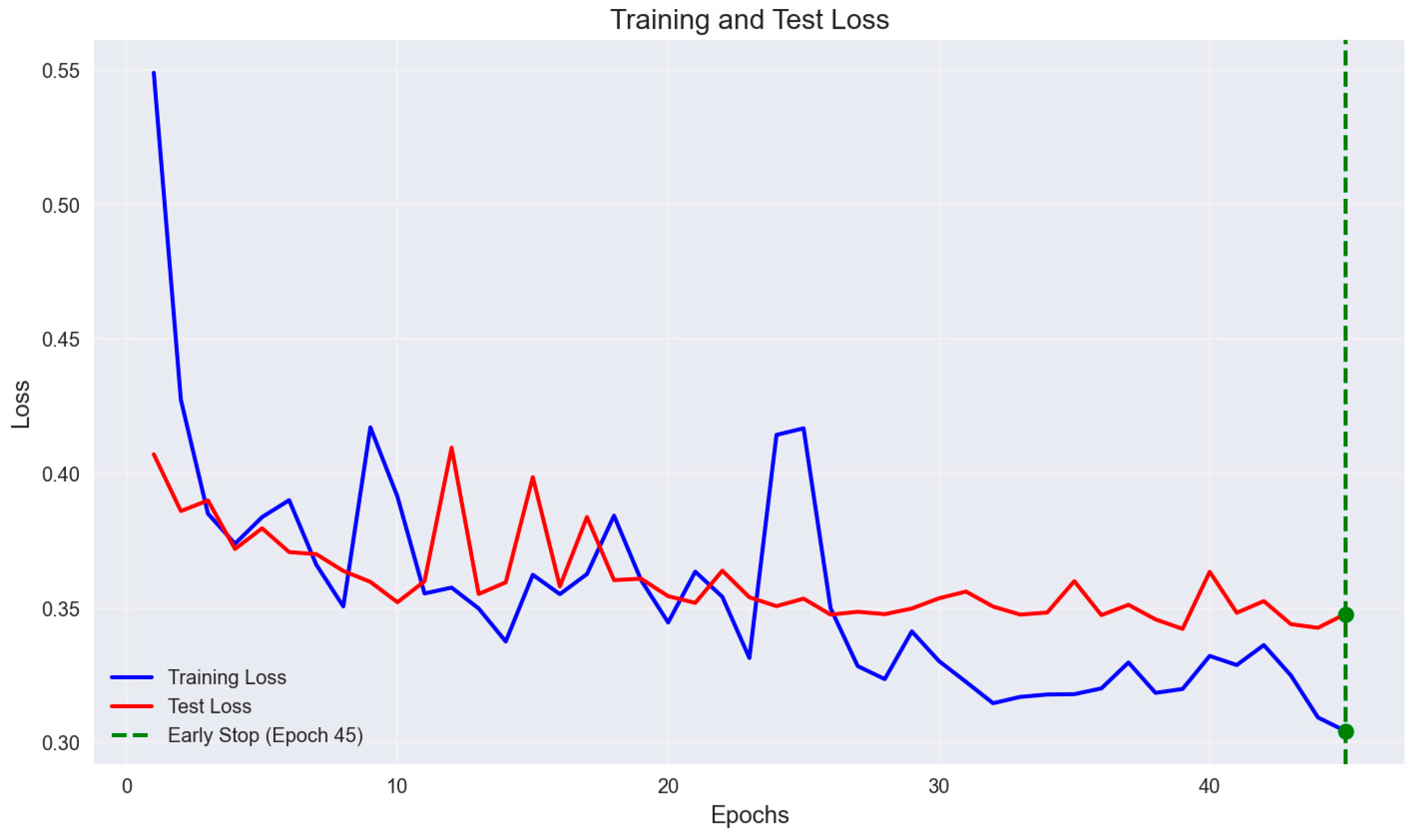
2.3. Modelling
3. Results
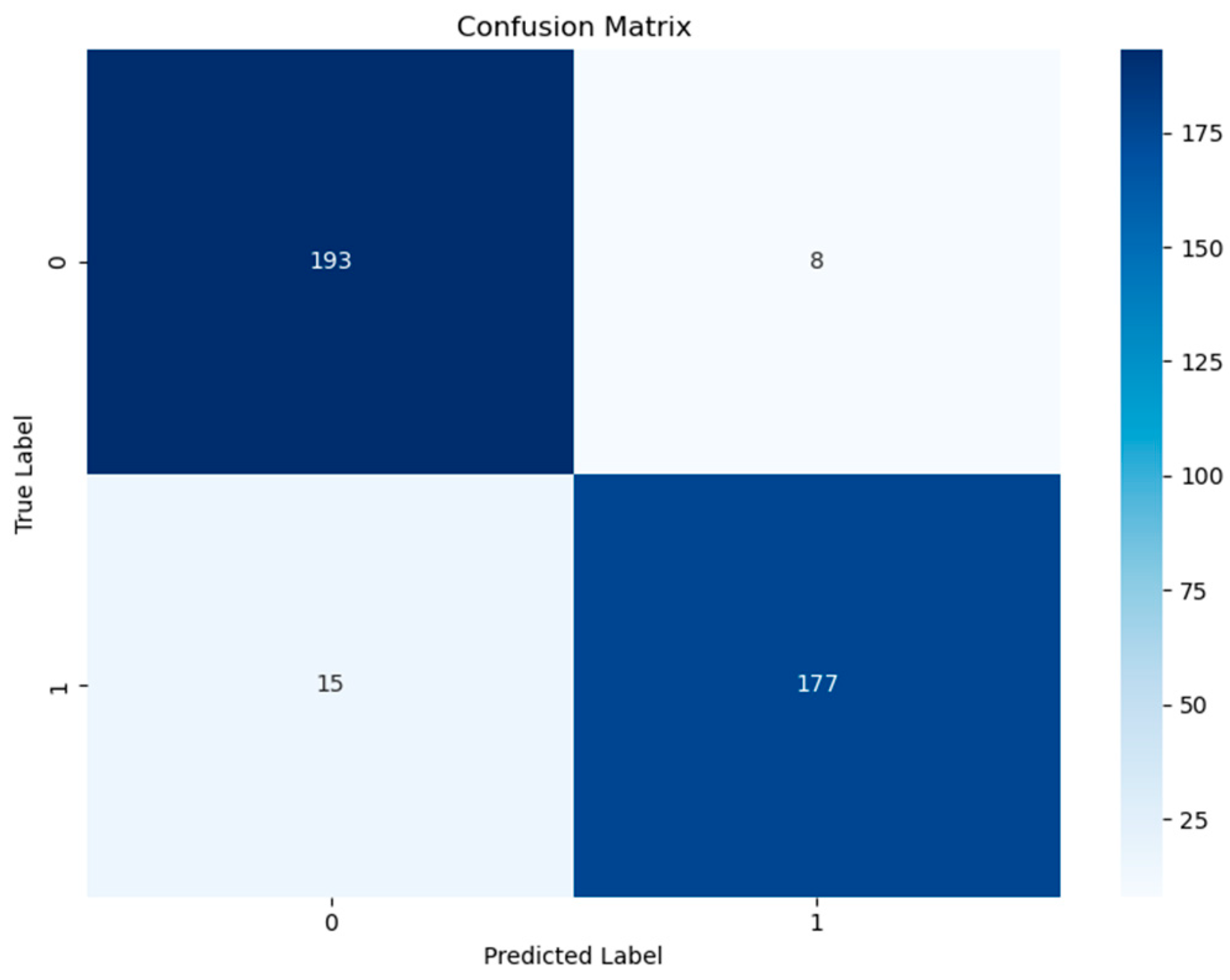
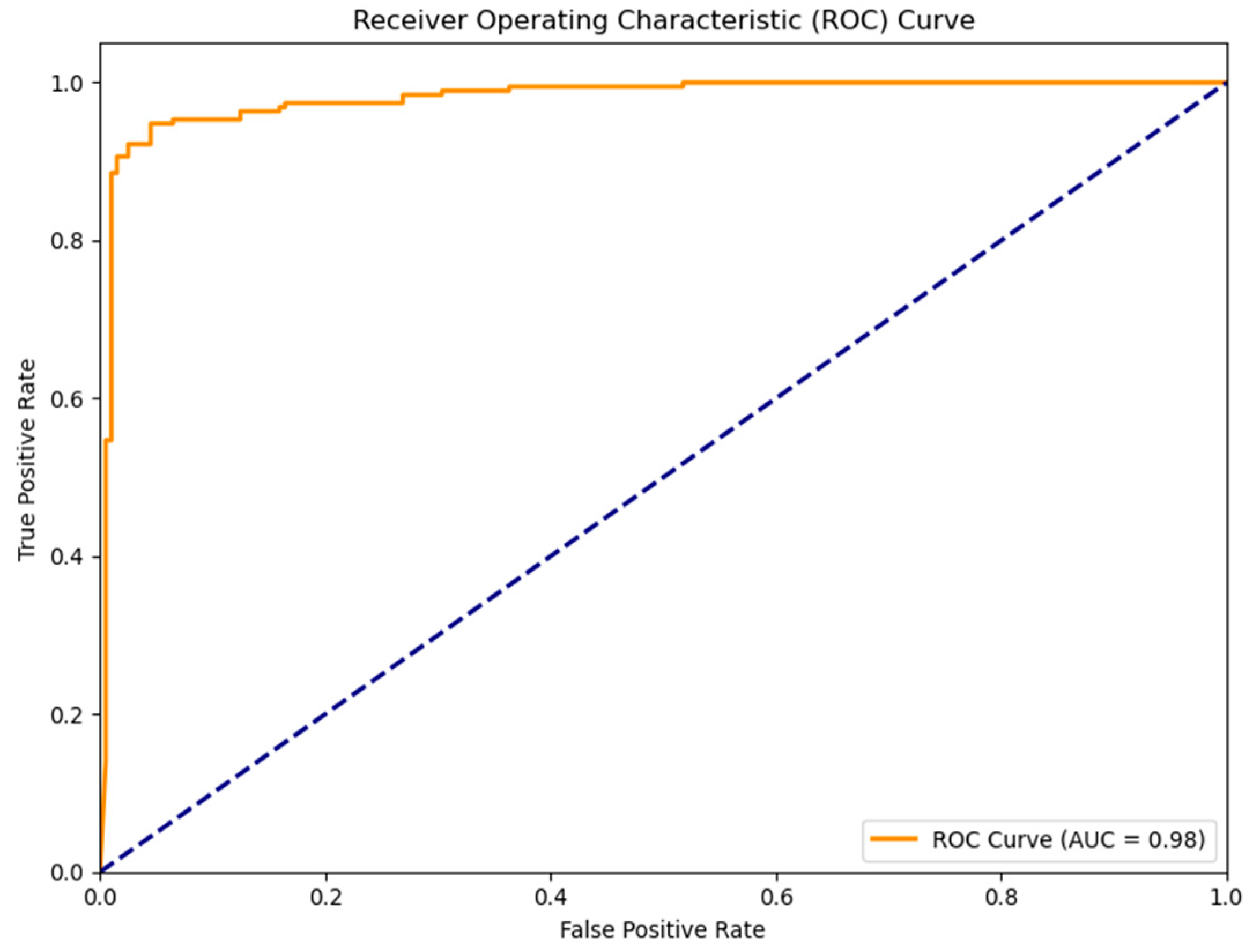
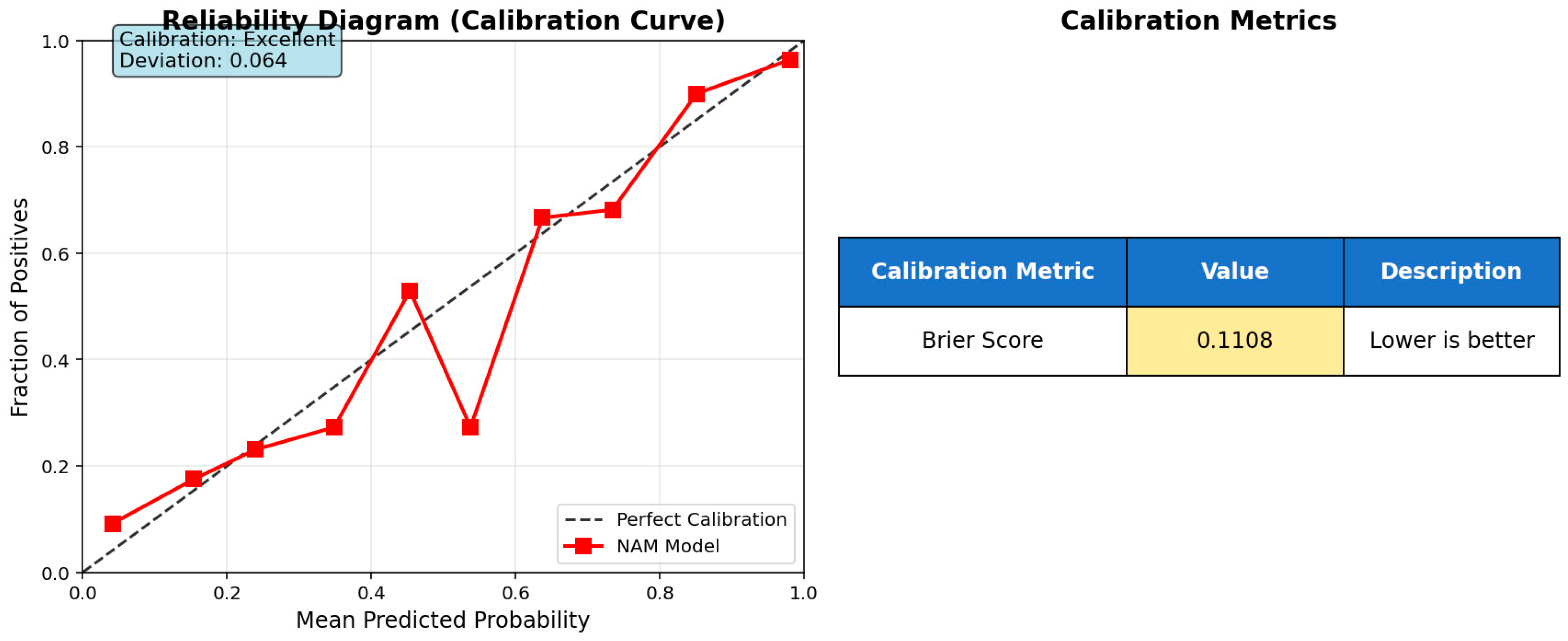
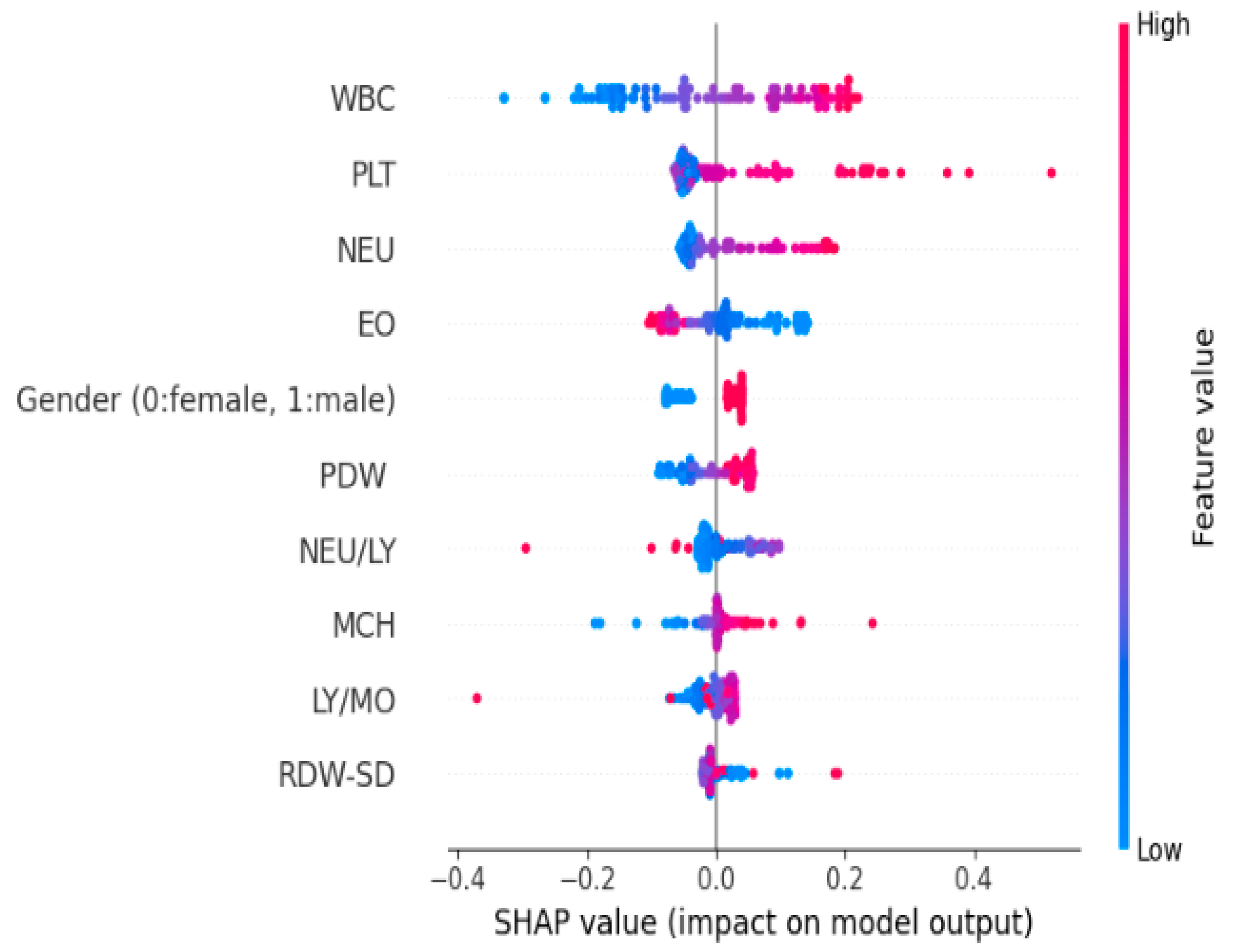
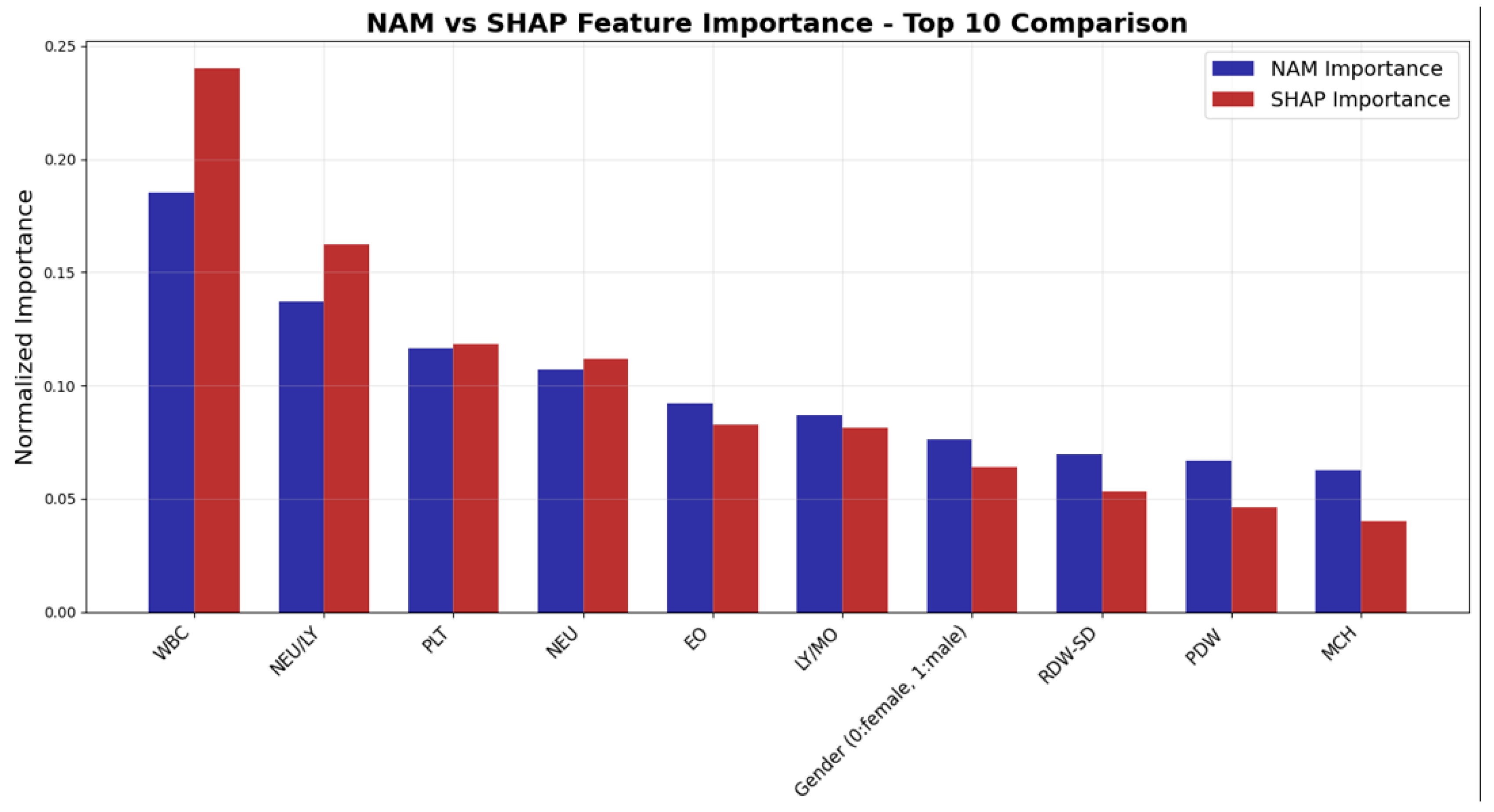
3.1. Modeling for AMI and Control Groups
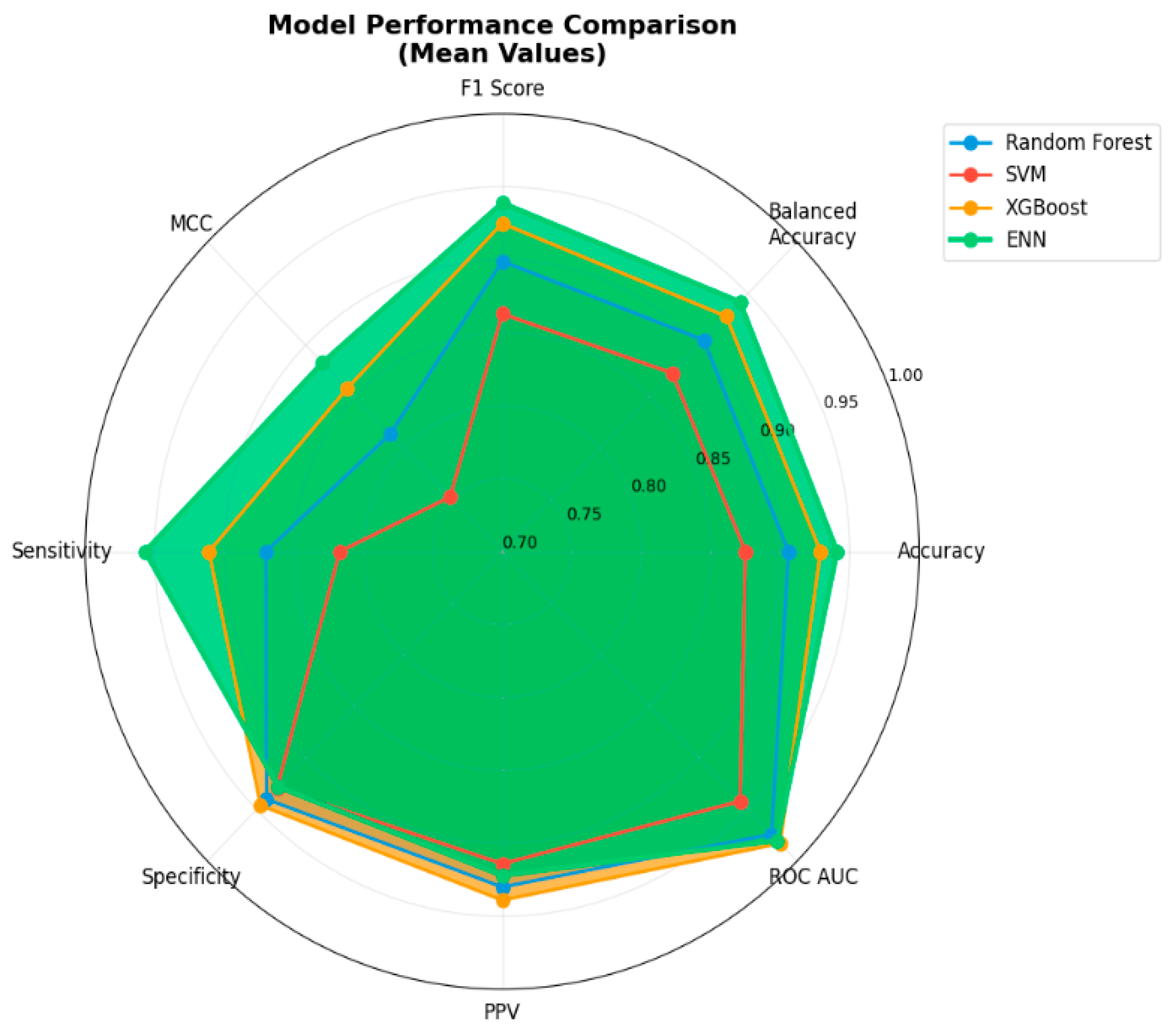
3.2. Comparative Performance Analysis of ENN and Alternative Classifiers for AMI and Control Groups
3.3. Modeling for STEMI and NSTEMI Groups
4. Discussion
Limitation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AMI | Acute Myocardial Infarction |
| SHAP | SHapley Additive exPlanations |
| ENN | Explainable Neural Network |
| NAM | Neural Additive Model |
| STEMI | ST-segment elevation MI |
| NSTEMI | non-ST- segment elevation MI |
References
- Madjid, M.; Fatemi, O. Components of the complete blood count as risk predictors for coronary heart disease: In-depth review and update. Tex. Heart Inst. J. 2013, 40, 17–29. [Google Scholar] [PubMed]
- Arbel, Y.; Finkelstein, A.; Halkin, A.; Birati, E.Y.; Revivo, M.; Zuzut, M.; Shevach, A.; Berliner, S.; Herz, I.; Keren, G.; et al. Neutrophil/lymphocyte ratio is related to the severity of coronary artery disease and clinical outcome in patients undergoing angiography. Atherosclerosis 2012, 225, 456–460. [Google Scholar] [CrossRef] [PubMed]
- Murat, S.N.; Duran, M.; Kalay, N.; Günebakmaz, Ö.; Akpek, M.; Döğer, C.; Elcık, D.; Ocak, A.; Vatankulu, M.A.; Turfan, M.; et al. Relation Between Mean Platelet Volume and Severity of Atherosclerosis in Patients with Acute Coronary Syndromes. Angiology 2012, 64, 131–136. [Google Scholar] [CrossRef]
- Klovaite, J.; Benn, M.; Yazdanyar, S.; Nordestgaard, B.G. High Platelet Volume and Increased Risk of Myocardial Infarction: 39 531 Participants From the General Population. J. Thromb. Haemost. 2011, 9, 49–56. [Google Scholar] [CrossRef]
- Chu, S.; Becker, R.C.; Berger, P.B.; Bhatt, D.L.; Eikelboom, J.W.; Konkle, B.A.; Mohler, E.R.; Reilly, M.P.; Berger, J.S. Mean Platelet Volume as a Predictor of Cardiovascular Risk: A Systematic Review and Meta-analysis. J. Thromb. Haemost. 2010, 8, 148–156. [Google Scholar] [CrossRef] [PubMed]
- Pereg, D.; Berlin, T.; Mosseri, M. Mean Platelet Volume on Admission Correlates with Impaired Response to Thrombolysis in Patients with ST-elevation Myocardial Infarction. Platelets 2010, 21, 117–121. [Google Scholar] [CrossRef]
- Uysal, H.B.; Dağlı, B.; Akgüllü, Ç.; Avcil, M.; Zencir, C.; Ayhan, M.; Sönmez, H.M. Blood Count Parameters Can Predict the Severity of Coronary Artery Disease. Korean J. Intern. Med. 2016, 31, 1093–1100. [Google Scholar] [CrossRef]
- Ayça, B.; Akın, F.; Okuyan, E. Platelet to Lymphocyte Ratio as a Prognostic Marker in Primary Percutaneous Coronary Intervention. Platelets 2015, 26, 816. [Google Scholar] [CrossRef][Green Version]
- Kotla, S.K. Leukocytosis: A Risk Factor for Myocardial Infarction. Res. Rep. Clin. Cardiol. 2012, 3, 23–25. [Google Scholar] [CrossRef]
- Benedek, I.; Benedek, T. Modern Hematology—A Complex Interdisciplinary Tool. J. Interdiscip. Med. 2017, 2, 9–11. [Google Scholar] [CrossRef][Green Version]
- Karakaş, M.S.; Korucuk, N.; Tosun, V.; Altekin, R.E.; Koç, F.; Özbek, S.C.; Özel, D.; Ermiş, C. Red Cell Distribution Width and Neutrophil-to-Lymphocyte Ratio Predict Left Ventricular Dysfunction in Acute Anterior ST-segment Elevation Myocardial Infarction. J. Saudi Heart Assoc. 2016, 28, 152–158. [Google Scholar] [CrossRef][Green Version]
- Lee, J.H.; Yang, D.H.; Jang, S.Y.; Choi, W.S.; Kim, K.H.; Lee, W.K.; Bae, M.H.; Park, H.S.; Cho, Y.; Chae, S.C. Incremental Predictive Value of Red Cell Distribution Width for 12-Month Clinical Outcome After Acute Myocardial Infarction. Clin. Cardiol. 2013, 36, 336–341. [Google Scholar] [CrossRef]
- Abdinur, M.M.A.; Yong, X. Progress in Red Blood Cell Distribution Width and Cardiovascular Diseases. Iosr J. Dent. Med. Sci. 2016, 15, 128–131. [Google Scholar] [CrossRef]
- Hashemi, A.; Gerges, F.; Naqvi, H.R.; Kotlar, I.; Moscatelli, S.; Hashemi, A.; Rustamova, Y.; Almaghraby, A. A Rare Presentation of an Elderly Patient with Acute Lymphocytic Leukemia and Platelet Count of Zero Associated with ST-elevation Myocardial Infarction, Pulmonary Thromboembolism in the Setting of SARS-CoV-2: A Case Report. Egypt. Heart J. 2021, 73, 39. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.Z.; Baqi, A.; Patel, K.; Weinstock, J.; Franklin, S.; Kutalek, S.P. Clinical in-Hospital Outcomes of Acute Myocardial Infarction in Patients with Hematological Malignancies. Cureus 2022, 14, e21627. [Google Scholar] [CrossRef] [PubMed]
- Muñiz, A.E. Myocardial Infarction and Stroke as the Presenting Symptoms of Acute Myeloid Leukemia. J. Emerg. Med. 2012, 42, 651–654. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, R.; Yagin, F.H.; Colak, C.; Toprak, K.; Abdel Samee, N.; Mahmoud, N.F.; Alshahrani, A.A. Analysis of hematological indicators via explainable artificial intelligence in the diagnosis of acute heart failure: A retrospective study. Front. Med. 2024, 11, 1285067. [Google Scholar] [CrossRef]
- Blazek, P.J.; Lin, M.M. Explainable neural networks that simulate reasoning. Nat. Comput. Sci. 2021, 1, 607–618. [Google Scholar] [CrossRef]
- Somani, A.; Horsch, A.; Bopardikar, A.; Prasad, D.K. Propagating Transparency: A Deep Dive Into the Interpretability of Neural Networks. Nord. Mach. Intell. 2024, 4, 1–18. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, A.; Sudjianto, A. Increasing the explainability of neural networks through architectural constraints. arXiv 2019, arXiv:1901.03838. [Google Scholar]
- Zhang, Y.; Tiňo, P.; Leonardis, A.; Tang, K. A survey on neural network interpretability. IEEE Trans. Emerg. Top. Comput. Intell. 2021, 5, 726–742. [Google Scholar] [CrossRef]
- Agarwal, R.; Melnick, L.; Frosst, N.; Lengerich, B.; Zhang, X.; Caruana, R.; Hinton, G.E. Neural Additive Models: Interpretable Machine Learning with Neural Networks. arXiv 2021, arXiv:2004.13912. [Google Scholar]
- Rudin, C. Stop Explaining Black Box Machine Learning Models for High Stakes Decisions and Use Interpretable Models Instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef]
- Ibanez, B.; James, S.; Agewall, S.; Antunes, M.J.; Bucciarelli-Ducci, C.; Bueno, H.; Caforio, A.L.P.; Crea, F.; Goudevenos, J.A.; Halvorsen, S.; et al. 2017 ESC Guidelines for the management of acute myocardial infarction in patients presenting with ST-segment elevation: The Task Force for the management of acute myocardial infarction in patients presenting with ST-segment elevation of the European Society of Cardiology (ESC). Eur. Heart J. 2018, 39, 119–177. [Google Scholar] [CrossRef]
- Tonelli, M.; Sacks, F.; Arnold, M.; Moye, L.; Davis, B.; Pfeffer, M. Relation Between Red Blood Cell Distribution Width and Cardiovascular Event Rate in People with Coronary Disease. Circulation 2008, 117, 163–168. [Google Scholar] [CrossRef]
- Rechciński, T.; Jasińska, A.; Foryś, J.; Krzemińska-Pakuła, M.; Wierzbowska-Drabik, K.; Plewka, M.; Peruga, J.Z.; Kasprzak, J.D. Prognostic value of platelet indices after acute myocardial infarction treated with primary percutaneous coronary intervention. Cardiol. J. 2013, 20, 491–498. [Google Scholar] [CrossRef] [PubMed]
- Fava, C.; Cattazzo, F.; Hu, Z.-D.; Lippi, G.; Montagnana, M. The role of red blood cell distribution width (RDW) in cardiovascular risk assessment: Useful or hype? Ann. Transl. Med. 2019, 7, 581. [Google Scholar] [CrossRef] [PubMed]
- Horne, B.D.; Anderson, J.L.; John, J.M.; Weaver, A.; Bair, T.L.; Jensen, K.R.; Renlund, D.G.; Muhlestein, J.B. Which white blood cell subtypes predict increased cardiovascular risk? J. Am. Coll. Cardiol. 2005, 45, 1638–1643. [Google Scholar] [CrossRef]
- Reddy, S.K.; Shetty, R.; Marupuru, S.; Yedavalli, N.; Shetty, K. Significance of platelet volume indices in STEMI patients: A case-control study. J. Clin. Diagn. Res. JCDR 2017, 11, LC05. [Google Scholar] [CrossRef] [PubMed]
- Dang, P.; Wang, F.; Yu, H. Prognostic potential of neutrophil-to-lymphocyte ratio, platelet to lymphocyte ratio, and monocyte to lymphocyte ratio in acute myocardial infarction patients combined with chronic obstructive pulmonary disease. Front. Cardiovasc. Med. 2024, 11, 1401634. [Google Scholar] [CrossRef]
- Latif, A.; Ahsan, M.J.; Lateef, N.; Kapoor, V.; Fazeel, H.M.; Razzaq, F.; Iftikhar, A.; Ashfaq, M.Z.; Anwer, F.; Mirza, M.; et al. Prognostic Impact of Red Cell Distribution Width on the Development of Contrast-Induced Nephropathy, Major Adverse Cardiac Events, and Mortality in Coronary Artery Disease Patients Undergoing Percutaneous Coronary Intervention. Curr. Cardiol. Rev. 2021, 17, e051121191160. [Google Scholar] [CrossRef] [PubMed]
- Frentiu, A.A.; Mao, K.; Caruana, C.B.; Raveendran, D.; Perry, L.A.; Penny-Dimri, J.C.; Ramson, D.M.; Segal, R.; Bellomo, R.; Smith, J.A. The Prognostic significance of red cell distribution width in cardiac surgery: A systematic review and Meta-analysis. J. Cardiothorac. Vasc. Anesth. 2023, 37, 471–479. [Google Scholar] [CrossRef] [PubMed]
- Yilmaz, R.; Yagin, F.H.; Raza, A.; Colak, C.; Akinci, T.C. Assessment of hematological predictors via explainable artificial intelligence in the prediction of acute myocardial infarction. IEEE Access 2023, 11, 108591–108602. [Google Scholar] [CrossRef]

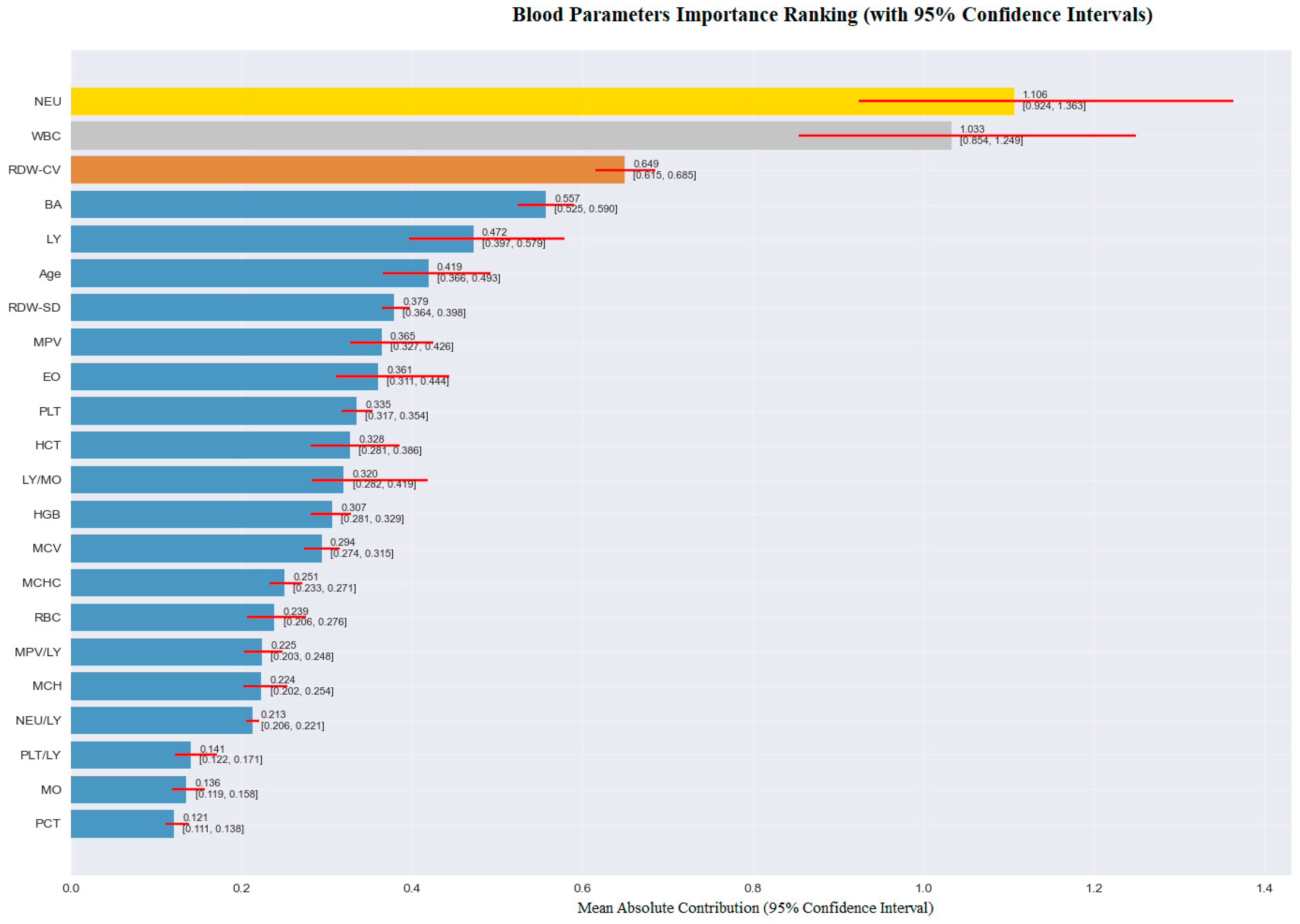

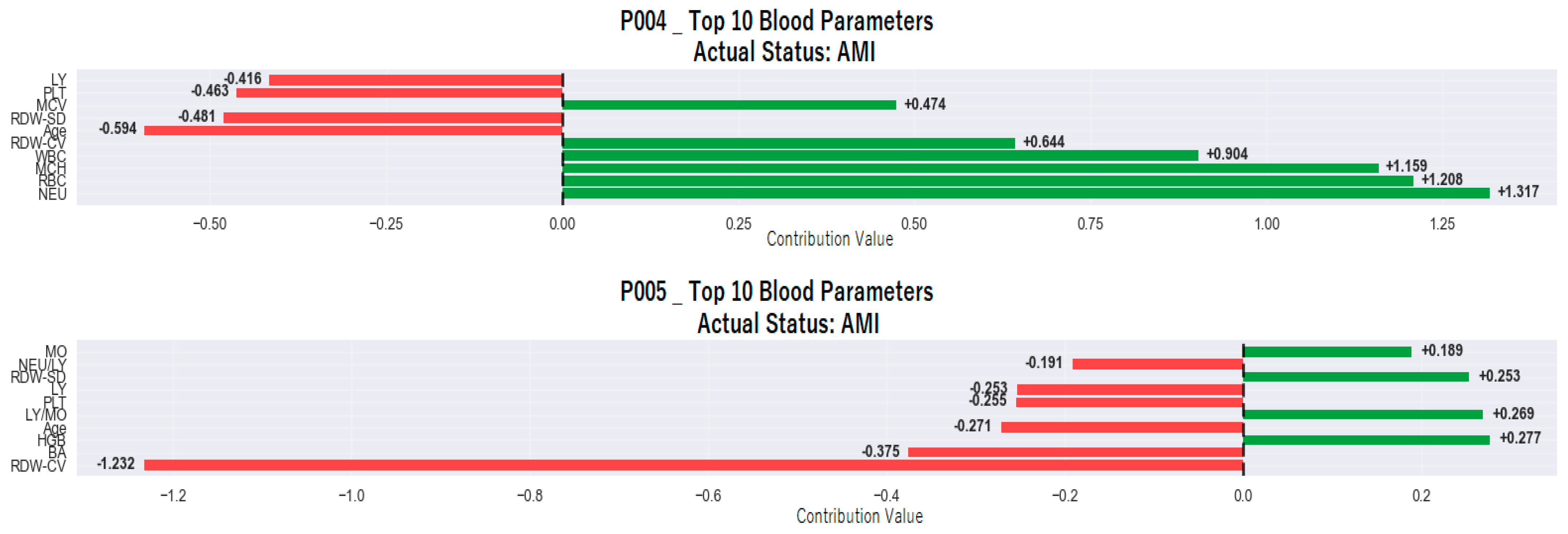
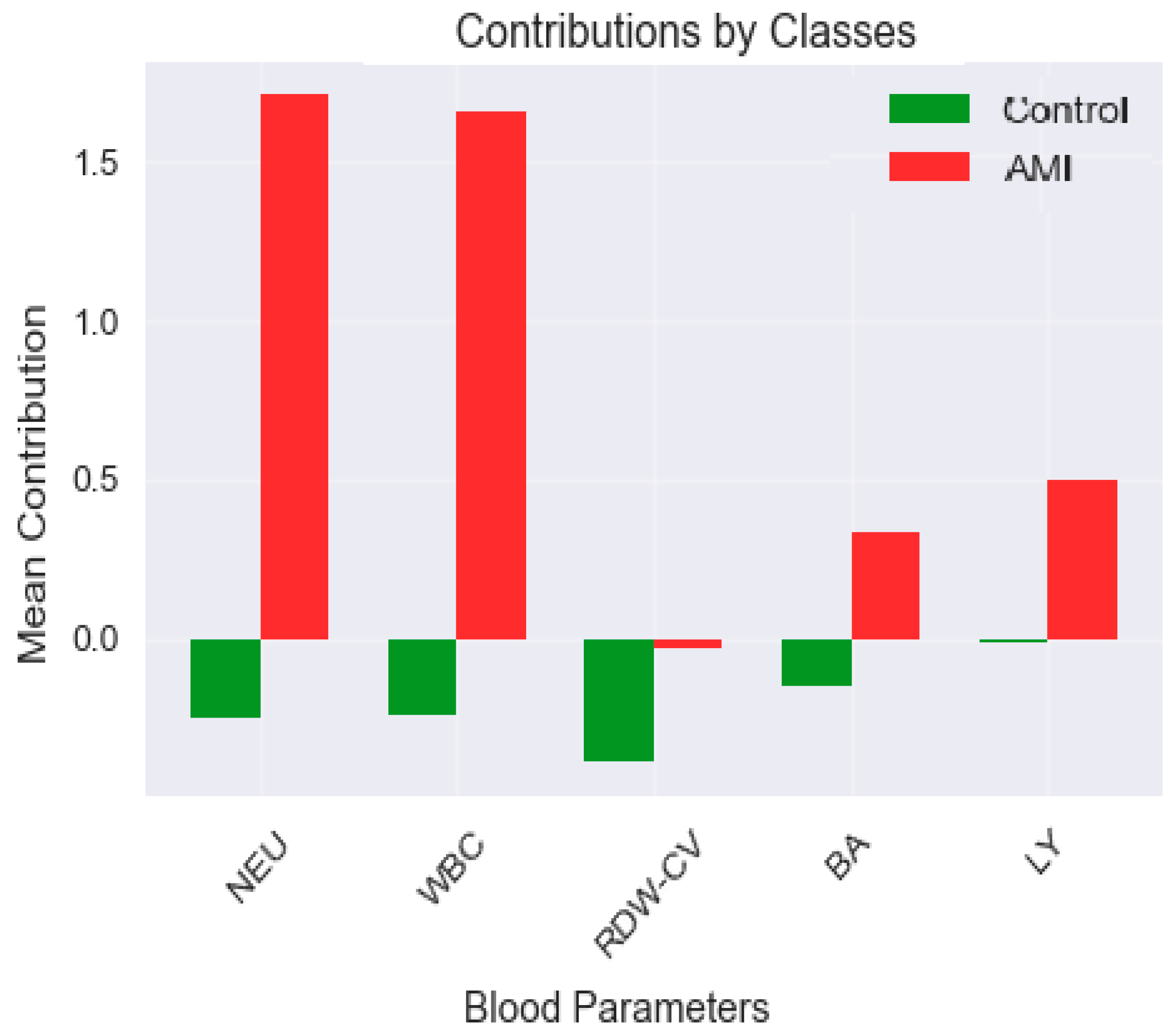
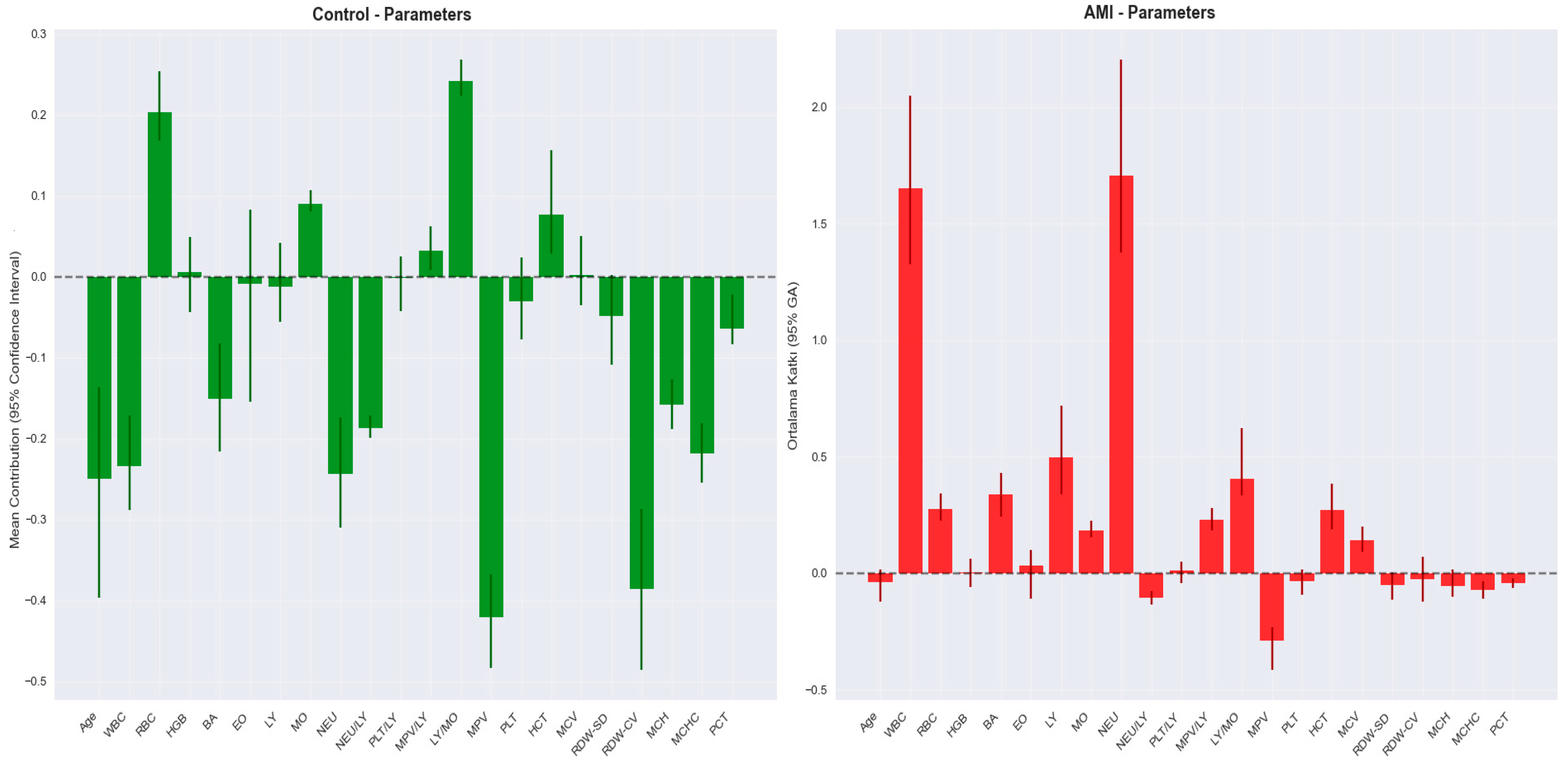
| Variable * | Group | p ** | |
|---|---|---|---|
| Control | AMI | ||
| WBC (103/L) | 7.5 (2.282) | 10.38 (4.5) | <0.001 |
| RBC (1012/L) | 4.7 (0.685) | 4.79 (0.82) | 0.384 |
| HGB (g/dL) | 13.7 (2.125) | 13.9 (2.5) | 0.107 |
| HCT (102/L) | 0.04 (0.04) | 0.06 (0.04) | <0.001 |
| EO (103/L) | 0.13 (0.13) | 0.1 (0.15) | 0.004 |
| LY (103/L) | 2.28 (0.883) | 2.36 (1.76) | 0.077 |
| MO (103/L) | 0.56 (0.215) | 0.7 (0.39) | <0.001 |
| NEU (103/L) | 4.3 (1.745) | 6.45 (3.93) | <0.001 |
| NLR | 1.89 (0.912) | 2.697 (2.23) | <0.001 |
| PLR | 111.462 (52.1) | 102.632 (67.846) | 0.002 |
| MPVLR | 4.32 (1.832) | 3.866 (3.273) | <0.001 |
| SWR | 4.13 (1.735) | 3.526 (2.466) | <0.001 |
| MPV (fL) | 10.1 (1.3) | 9.4 (1.69) | <0.001 |
| PLT (103/L) | 256.5 (84.5) | 253 (92) | 0.499 |
| PDW (%) | 41 (5.625) | 41.2 (6.41) | 0.265 |
| MCV (fL) | 87.2 (5.325) | 86.3 (6.6) | 0.003 |
| RDW-SD | 41 (4.425) | 41.2 (4.7) | 0.117 |
| RDW-CV | 13.2 (1.3) | 13.6 (1.3) | <0.001 |
| MCH (pg) | 29.1 (2.4) | 29.3 (2.8) | 0.095 |
| MCHC (g/dL) | 33.2 (1.9) | 33.9 (1.6) | <0.001 |
| PDW (fL) | 12 (3.625) | 15.9 (5.29) | <0.001 |
| PCT (%) | 0.255 (0.07) | 0.23 (0.09) | <0.001 |
| Performance Metrics | Value | 95% CI Lower Limit | 95% CI Upper Limit |
|---|---|---|---|
| Accuracy | 0.941 | 0.918 | 0.965 |
| Balanced Accuracy | 0.942 | 0.919 | 0.965 |
| F1-Score | 0.939 | 0.915 | 0.963 |
| MCC | 0.883 | 0.852 | 0.915 |
| Sensitivity | 0.957 | 0.917 | 0.981 |
| Specificity | 0.928 | 0.884 | 0.959 |
| Positive Predictive Value | 0.922 | 0.874 | 0.956 |
| Negative Predictive Value | 0.96 | 0.923 | 0.983 |
| Positive Likelihood Ratio | 13.267 | 8.14 | 21.622 |
| Negative Likelihood Ratio | 0.047 | 0.024 | 0.092 |
| Model | Accuracy | Balanced Accuracy | F1-Score | MCC | Sensitivity | Specificity | PPV | NPV | ROC AUC |
|---|---|---|---|---|---|---|---|---|---|
| Random Forest | 0.906 (0.878, 0.935) | 0.905 (0.875, 0.935) | 0.899 (0.866, 0.933) | 0.814 (0.766, 0.860) | 0.870 (0.829, 0.911) | 0.940 (0.907, 0.974) | 0.930 (0.893, 0.968) | 0.887 (0.852, 0.922) | 0.974 (0.953, 0.997) |
| SVM | 0.875 (0.847, 0.904) | 0.873 (0.844, 0.903) | 0.863 (0.830, 0.896) | 0.753 (0.707, 0.800) | 0.817 (0.776, 0.858) | 0.929 (0.896, 0.963) | 0.914 (0.877, 0.952) | 0.847 (0.811, 0.880) | 0.942 (0.920, 0.964) |
| XGBoost | 0.929 (0.902, 0.957) | 0.928 (0.899, 0.959) | 0.925 (0.892, 0.958) | 0.858 (0.811, 0.905) | 0.911 (0.870, 0.952) | 0.946 (0.913, 0.979) | 0.939 (0.902, 0.977) | 0.921 (0.885, 0.956) | 0.983 (0.960, 1.000) |
| ENN | 0.941 (0.918, 0.965) | 0.942 (0.919, 0.965) | 0.939 (0.915, 0.963) | 0.883 (0.852, 0.8915) | 0.957 (0.917, 0.981) | 0.928 (0.884, 0.959) | 0.922 (0.874, 0.9956) | 0.960 (0.923, 0.983) | 0.980 (0.966, 1.000) |
| Performance Metric | Value |
|---|---|
| Doğruluk (Accuracy) | 0.9100 |
| Dengeli Doğruluk (Balanced Accuracy) | 0.9100 |
| Matthews Korelasyon Katsayısı (MCC) | 0.8199 |
| Kesinlik (Precision) | 0.9082 |
| Duyarlılık (Recall/Sensitivity) | 0.9082 |
| F1 Skoru (F1-Score) | 0.9082 |
| ROC Eğrisi Altındaki Alan (ROC-AUC) | 0.9776 |
| Feature | NAM Importance | SHAP Importance |
|---|---|---|
| WBC | 0.188 | 0.240 |
| NEU/LY | 0.138 | 0.168 |
| PLT | 0.118 | 0.120 |
| NEU | 0.108 | 0.115 |
| EO | 0.093 | 0.082 |
| LY/MO | 0.088 | 0.080 |
| Gender (0: female, 1: male) | 0.076 | 0.065 |
| RDW-SD | 0.070 | 0.053 |
| PDW | 0.066 | 0.048 |
| MCH | 0.062 | 0.042 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the Lithuanian University of Health Sciences. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kucukakcali, Z.; Balikci Cicek, I. Beyond Black Boxes: Interpretable AI with Explainable Neural Networks (ENNs) for Acute Myocardial Infarction (AMI) Using Common Hematological Parameters. Medicina 2025, 61, 1552. https://doi.org/10.3390/medicina61091552
Kucukakcali Z, Balikci Cicek I. Beyond Black Boxes: Interpretable AI with Explainable Neural Networks (ENNs) for Acute Myocardial Infarction (AMI) Using Common Hematological Parameters. Medicina. 2025; 61(9):1552. https://doi.org/10.3390/medicina61091552
Chicago/Turabian StyleKucukakcali, Zeynep, and Ipek Balikci Cicek. 2025. "Beyond Black Boxes: Interpretable AI with Explainable Neural Networks (ENNs) for Acute Myocardial Infarction (AMI) Using Common Hematological Parameters" Medicina 61, no. 9: 1552. https://doi.org/10.3390/medicina61091552
APA StyleKucukakcali, Z., & Balikci Cicek, I. (2025). Beyond Black Boxes: Interpretable AI with Explainable Neural Networks (ENNs) for Acute Myocardial Infarction (AMI) Using Common Hematological Parameters. Medicina, 61(9), 1552. https://doi.org/10.3390/medicina61091552






