PyGlaucoMetrics: A Stacked Weight-Based Machine Learning Approach for Glaucoma Detection Using Visual Field Data
Abstract
1. Introduction
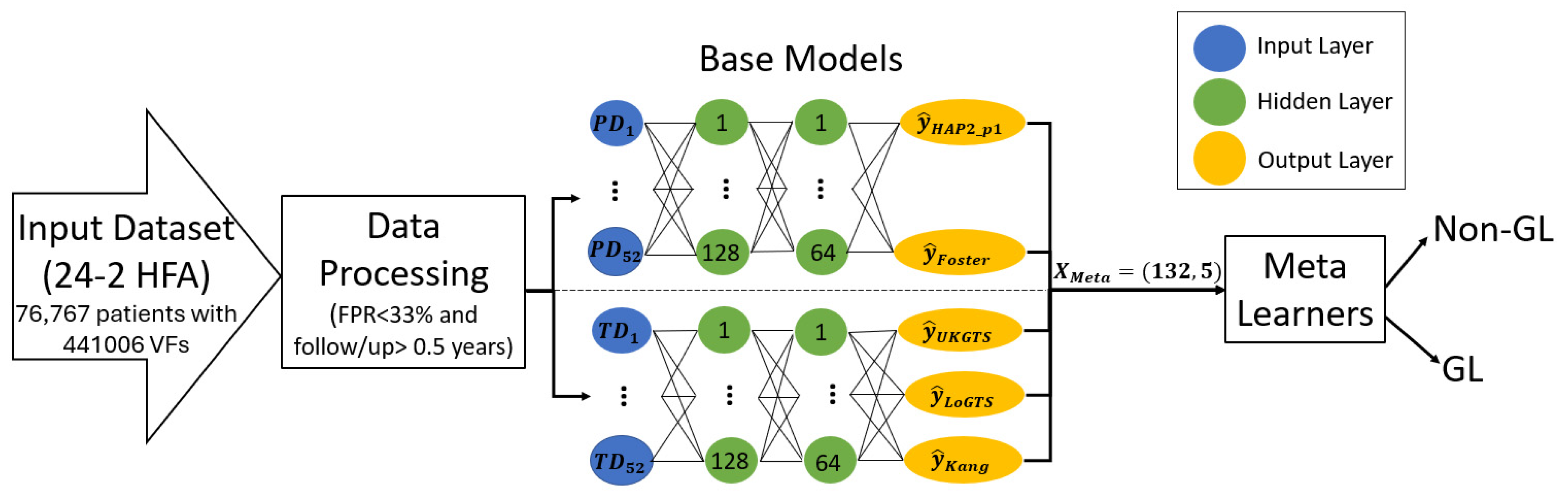
2. Materials and Methods
2.1. Dataset and Clinical Labeling
2.2. Stand-Alone Model Development
2.3. Data Preprocessing and Training Protocol
2.4. The Proposed Meta-Learners
2.5. Statistical Analysis
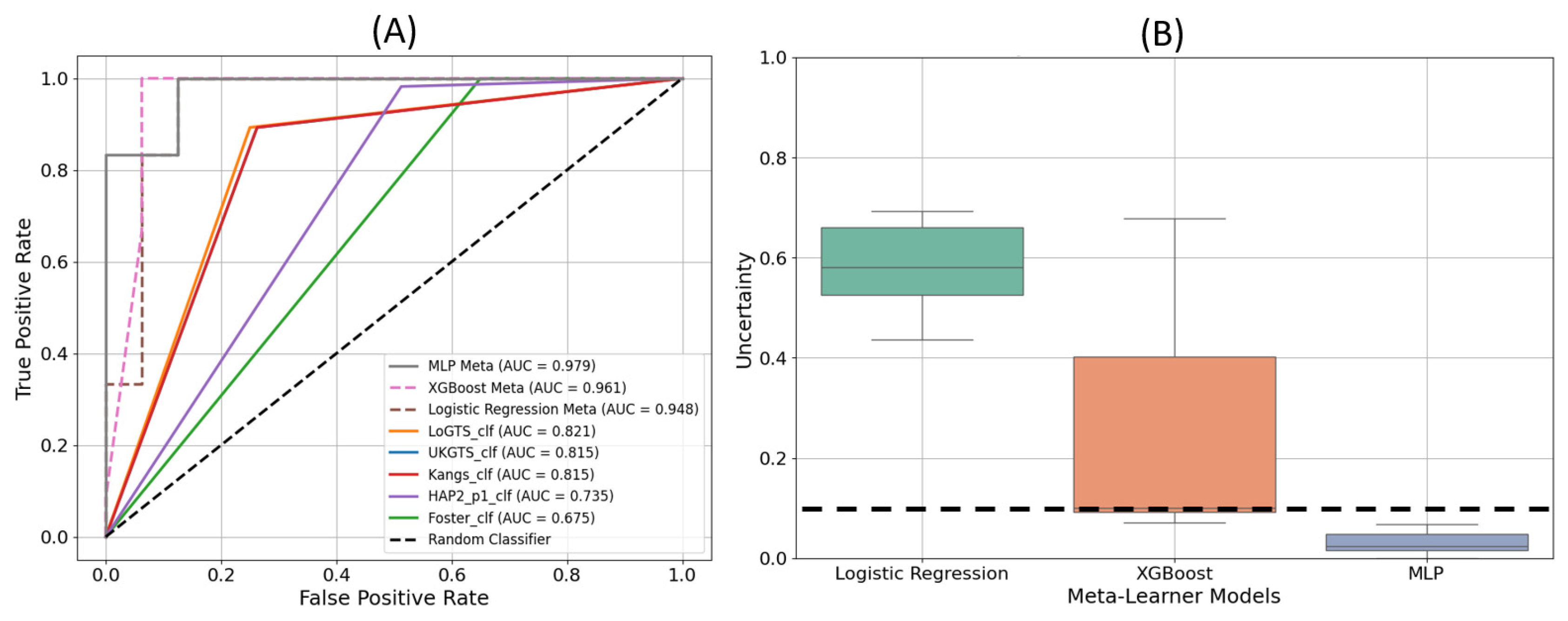
3. Results
3.1. Patients Characteristics
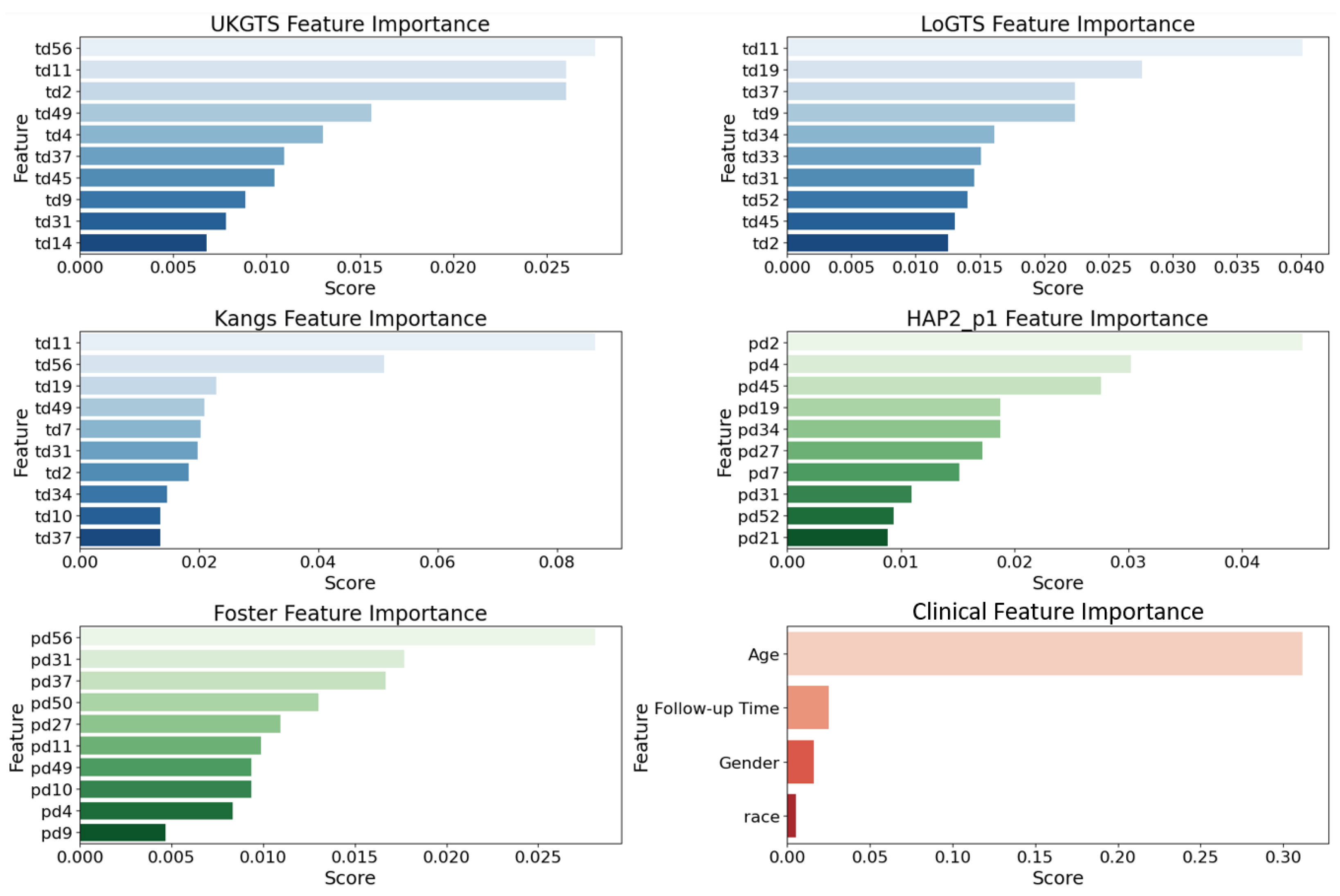
3.2. Permutation Importance Analysis
3.3. Model Execution Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ha, Q. The Number of People with Glaucoma Worldwide in 2010 and 2020. Br. J. Ophthalmol. 2006, 90, 262–267. [Google Scholar]
- Azuara-Blanco, A.; Traverso, C.E. Terminology and Guidelines for Glaucoma; European Glaucoma Society: Savona, Italy, 2020. [Google Scholar]
- Wu, Z.; Medeiros, F.A. Impact of Different Visual Field Testing Paradigms on Sample Size Requirements for Glaucoma Clinical Trials. Sci. Rep. 2018, 8, 4889. [Google Scholar] [CrossRef] [PubMed]
- Elze, T.; Pasquale, L.R.; Shen, L.Q.; Chen, T.C.; Wiggs, J.L.; Bex, P.J. Patterns of Functional Vision Loss in Glaucoma Determined with Archetypal Analysis. J. R. Soc. Interface 2015, 12, 20141118. [Google Scholar] [CrossRef] [PubMed]
- Russell, R.A.; Crabb, D.P.; Malik, R.; Garway-Heath, D.F. The Relationship between Variability and Sensitivity in Large-Scale Longitudinal Visual Field Data. Investig. Ophthalmol. Vis. Sci. 2012, 53, 5985–5990. [Google Scholar] [CrossRef]
- Wall, M.; Woodward, K.R.; Doyle, C.K.; Artes, P.H. Repeatability of Automated Perimetry: A Comparison between Standard Automated Perimetry with Stimulus Size Iii and V, Matrix, and Motion Perimetry. Investig. Ophthalmol. Vis. Sci. 2009, 50, 974–979. [Google Scholar] [CrossRef]
- Christopher, M.; Bowd, C.; Belghith, A.; Goldbaum, M.H.; Weinreb, R.N.; Fazio, M.A.; Girkin, C.A.; Liebmann, J.M.; Zangwill, L.M. Deep Learning Approaches Predict Glaucomatous Visual Field Damage from Oct Optic Nerve Head En Face Images and Retinal Nerve Fiber Layer Thickness Maps. Ophthalmology 2020, 127, 346–356. [Google Scholar] [CrossRef]
- Heijl, A.; Leske, M.C.; Bengtsson, B.; Hyman, L.; Bengtsson, B.; Hussein, M.; Group, E.M.G.T. Reduction of Intraocular Pressure and Glaucoma Progression: Results from the Early Manifest Glaucoma Trial. Arch. Ophthalmol. 2002, 120, 1268–1279. [Google Scholar] [CrossRef]
- Chauhan, B.C.; Garway-Heath, D.F.; Goñi, F.J.; Rossetti, L.; Bengtsson, B.; Viswanathan, A.C.; Heijl, A. Practical Recommendations for Measuring Rates of Visual Field Change in Glaucoma. Br. J. Ophthalmol. 2008, 92, 569–573. [Google Scholar] [CrossRef]
- Moradi, M.; Chen, Y.; Du, X.; Seddon, J.M. Deep Ensemble Learning for Automated Non-Advanced Amd Classification Using Optimized Retinal Layer Segmentation and Sd-Oct Scans. Comput. Biol. Med. 2023, 154, 106512. [Google Scholar] [CrossRef]
- Moradi, M.; Du, X.; Huan, T.; Chen, Y. Feasibility of the Soft Attention-Based Models for Automatic Segmentation of Oct Kidney Images. Biomed. Opt. Express 2022, 13, 2728–2738. [Google Scholar] [CrossRef]
- Ting, D.S.W.; Pasquale, L.R.; Peng, L.; Campbell, J.P.; Lee, A.Y.; Raman, R.; Tan, G.S.W.; Schmetterer, L.; Keane, P.A.; Wong, T.Y. Artificial Intelligence and Deep Learning in Ophthalmology. Br. J. Ophthalmol. 2019, 103, 167–175. [Google Scholar] [CrossRef]
- Moradi, M. Computational Modeling and Machine Learning Methods for Advancing Healthcare: Medical Image Analysis and Model Validation in Kidney Assessment, AMD Detection, and Pulse Oximetry. Ph.D. Thesis, University of Massachusetts Amherst, Amherst, MA, USA, 2024. [Google Scholar]
- Moradi, M.; Du, X.; Chen, Y. Soft Attention-Based U-Net for Automatic Segmentation of Oct Kidney Images. In Proceedings of the Optical Coherence Tomography and Coherence Domain Optical Methods in Biomedicine XXVI, San Francisco, CA, USA, 24–26 January 2022; pp. 106–111. [Google Scholar]
- Moradi, M.; Huan, T.; Chen, Y.; Du, X.; Seddon, J. Ensemble Learning for Amd Prediction Using Retina Oct Scans. Investig. Ophthalmol. Vis. Sci. 2022, 63, 732-F0460. [Google Scholar]
- Artes, P.H.; Nicolela, M.T.; LeBlanc, R.P.; Chauhan, B.C. Visual Field Progression in Glaucoma: Total Versus Pattern Deviation Analyses. Investig. Ophthalmol. Vis. Sci. 2005, 46, 4600–4606. [Google Scholar] [CrossRef] [PubMed]
- Sabharwal, J.; Hou, K.; Herbert, P.; Bradley, C.; Johnson, C.A.; Wall, M.; Ramulu, P.Y.; Unberath, M.; Yohannan, J. A Deep Learning Model Incorporating Spatial and Temporal Information Successfully Detects Visual Field Worsening Using a Consensus Based Approach. Sci. Rep. 2023, 13, 1041. [Google Scholar] [CrossRef] [PubMed]
- Stubeda, H.; Quach, J.; Gao, J.; Shuba, L.M.; Nicolela, M.T.; Chauhan, B.C.; Vianna, J.R. Comparing Five Criteria for Evaluating Glaucomatous Visual Fields. Am. J. Ophthalmol. 2022, 237, 154–163. [Google Scholar] [CrossRef]
- Krupin, T.; Liebmann, J.M.; Greenfield, D.S.; Rosenberg, L.F.; Ritch, R.; Yang, J.W.; Group, L.-P.G.S. The Low-Pressure Glaucoma Treatment Study (Logts): Study Design and Baseline Characteristics of Enrolled Patients. Ophthalmology 2005, 112, 376–385. [Google Scholar] [CrossRef]
- Garway-Heath, D.F.; Lascaratos, G.; Bunce, C.; Crabb, D.P.; Russell, R.A.; Shah, A.; Investigators, U.K.G.T.S. The United Kingdom Glaucoma Treatment Study: A Multicenter, Randomized, Placebo-Controlled Clinical Trial: Design and Methodology. Ophthalmology 2013, 120, 68–76. [Google Scholar] [CrossRef]
- Garway-Heath, D.F.; Crabb, D.P.; Bunce, C.; Lascaratos, G.; Amalfitano, F.; Anand, N.; Azuara-Blanco, A.; Bourne, R.R.; Broadway, D.C.; Cunliffe, I.A. Latanoprost for Open-Angle Glaucoma (Ukgts): A Randomised, Multicentre, Placebo-Controlled Trial. Lancet 2015, 385, 1295–1304. [Google Scholar] [CrossRef]
- Kang, J.H.; Loomis, S.J.; Rosner, B.A.; Wiggs, J.L.; Pasquale, L.R. Comparison of Risk Factor Profiles for Primary Open-Angle Glaucoma Subtypes Defined by Pattern of Visual Field Loss: A Prospective Study. Investig. Ophthalmol. Vis. Sci. 2015, 56, 2439–2448. [Google Scholar] [CrossRef]
- Perkins, T.W. Clinical Decisions in Glaucoma. Arch. Ophthalmol. 1994, 112, 1518–1519. [Google Scholar] [CrossRef]
- Chang, T.C.; Ramulu, P.; Hodapp, E. Clinical Decisions in Glaucoma; Bascom Palmer Eye Institute Miami (FL): Miami, FL, USA, 2016. [Google Scholar]
- Foster, P.J.; Buhrmann, R.; Quigley, H.A.; Johnson, G.J. The Definition and Classification of Glaucoma in Prevalence Surveys. Br. J. Ophthalmol. 2002, 86, 238–242. [Google Scholar] [CrossRef]
- Marín-Franch, I.; Swanson, W.H. The Visualfields Package: A Tool for Analysis and Visualization of Visual Fields. J. Vis. 2013, 13, 10. [Google Scholar] [CrossRef] [PubMed]
- Elze, T.; Li, D.; Choi, E.Y. Cran—Package Vfprogression. 2019. Available online: https://cran.r-project.org/web/packages/vfprogression/index.html (accessed on 25 October 2024).
- LaValley, M.P. Logistic Regression. Circulation 2008, 117, 2395–2399. [Google Scholar] [CrossRef]
- Hatami, F.; Moradi, M. Comparative Analysis of Machine Learning Models for Predicting Viscosity in Tri-N-Butyl Phosphate Mixtures Using Experimental Data. Computation 2024, 12, 133. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T. Xgboost: Extreme Gradient Boosting. R Package Version 0.4-2. 2015. Available online: https://cran.ms.unimelb.edu.au/web/packages/xgboost/vignettes/xgboost.pdf (accessed on 20 February 2025).
- Popescu, M.-C.; Balas, V.E.; Perescu-Popescu, L.; Mastorakis, N. Multilayer Perceptron and Neural Networks. WSEAS Trans. Circuits Syst. 2009, 8, 579–588. [Google Scholar]
- Onyekaba, N.-A.E.; Estrela, T.; Naithani, R.; McCarthy, K.M.; Jammal, A.A.; Medeiros, F.A. Comparison of 10-2 and 24-2 Perimetry to Diagnose Glaucoma Using Oct as an Independent Reference Standard. Ophthalmol. Glaucoma 2023, 6, 187–197. [Google Scholar] [CrossRef] [PubMed]
- Eslami, M.; Kazeminasab, S.; Sharma, V.; Li, Y.; Fazli, M.; Wang, M.; Zebardast, N.; Elze, T. Pyvisualfields: A Python Package for Visual Field Analysis. Transl. Vis. Sci. Technol. 2023, 12, 6. [Google Scholar] [CrossRef]
- Heijl, A.; Lindgren, G.; Olsson, J. The Effect of Perimetric Experience in Normal Subjects. Arch. Ophthalmol. 1989, 107, 81–86. [Google Scholar] [CrossRef]
- Heijl, A.; Patella, V.M. Essential Perimetry: The Field Analyzer Primer; Carl Zeiss Meditec: Jena, Germany, 2002. [Google Scholar]
- Bengtsson, B.; Heijl, A. False-Negative Responses in Glaucoma Perimetry: Indicators of Patient Performance or Test Reliability? Investig. Ophthalmol. Vis. Sci. 2000, 41, 2201–2204. [Google Scholar] [CrossRef]
- Wang, C.; Chen, D.-F.; Shang, X.; Wang, X.; Chu, X.; Hu, C.; Huang, Q.; Cheng, G.; Li, J.; Ren, R. Evaluating Diagnostic Concordance in Primary Open-Angle Glaucoma among Academic Glaucoma Subspecialists. Diagnostics 2024, 14, 2460. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked Generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Gorishniy, Y.; Rubachev, I.; Khrulkov, V.; Babenko, A. Revisiting Deep Learning Models for Tabular Data. Adv. Neural Inf. Process. Syst. 2021, 34, 18932–18943. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.; Bengio, Y. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Volume 1. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System. In Proceedings of the 22nd Acm Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Hosmer, D.W., Jr.; Lemeshow, S.; Sturdivant, R.X. Applied Logistic Regression; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Shwartz-Ziv, R.; Armon, A. Tabular Data: Deep Learning Is Not All You Need. Inf. Fusion 2022, 81, 84–90. [Google Scholar] [CrossRef]
- Karim, F.; Majumdar, S.; Darabi, H.; Harford, S. Multivariate Lstm-Fcns for Time Series Classification. Neural Netw. 2019, 116, 237–245. [Google Scholar] [CrossRef]
- Forchheimer, I.; De Moraes, C.; Teng, C.; Folgar, F.; Tello, C.; Ritch, R.; Liebmann, J. Baseline Mean Deviation and Rates of Visual Field Change in Treated Glaucoma Patients. Eye 2011, 25, 626–632. [Google Scholar] [CrossRef] [PubMed]
- Altmann, A.; Toloşi, L.; Sander, O.; Lengauer, T. Permutation Importance: A Corrected Feature Importance Measure. Bioinformatics 2010, 26, 1340–1347. [Google Scholar] [CrossRef]
- Wu, C.-W.; Shen, H.-L.; Lu, C.-J.; Chen, S.-H.; Chen, H.-Y. Comparison of Different Machine Learning Classifiers for Glaucoma Diagnosis Based on Spectralis Oct. Diagnostics 2021, 11, 1718. [Google Scholar] [CrossRef]
- Masumoto, H.; Tabuchi, H.; Nakakura, S.; Ishitobi, N.; Miki, M.; Enno, H. Deep-Learning Classifier with an Ultrawide-Field Scanning Laser Ophthalmoscope Detects Glaucoma Visual Field Severity. J. Glaucoma 2018, 27, 647–652. [Google Scholar] [CrossRef] [PubMed]
- Quigley, H.A. Glaucoma: Macrocosm to Microcosm the Friedenwald Lecture. Investig. Ophthalmol. Vis. Sci. 2005, 46, 2663–2670. [Google Scholar] [CrossRef]
- Sampaolesi, R.; Sampaolesi, J.R.; Zárate, J. The Glaucomas: Volume Ii-Open Angle Glaucoma and Angle Closure Glaucoma; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 2. [Google Scholar]
- Mikelberg, F.S.; Yidegiligne, H.M.; Schulzer, M. Optic Nerve Axon Count and Won Diameter in Patients with Ocular Hypertension and Normal Visual Fields. Ophthalmology 1995, 102, 342–348. [Google Scholar] [CrossRef]
- Araie, M. Pattern of Visual Field Defects in Normal-Tension and High-Tension Glaucoma. Curr. Opin. Ophthalmol. 1995, 6, 36–45. [Google Scholar] [CrossRef]
- Choi, J.A.; Park, H.-Y.L.; Jung, K.-I.; Hong, K.H.; Park, C.K. Difference in the Properties of Retinal Nerve Fiber Layer Defect between Superior and Inferior Visual Field Loss in Glaucoma. Investig. Ophthalmol. Vis. Sci. 2013, 54, 6982–6990. [Google Scholar] [CrossRef] [PubMed]
- Hayreh, S.S. Anterior Ischemic Optic Neuropathy. Clin. Neurosci. 1997, 4, 251–263. [Google Scholar] [PubMed]
- Hayreh, S.S.; Podhajsky, P.A.; Zimmerman, M.B. Branch Retinal Artery Occlusion: Natural History of Visual Outcome. Ophthalmology 2009, 116, 1188–1194.e4. [Google Scholar] [CrossRef] [PubMed]
- Burlina, P.; Paul, W.; Mathew, P.; Joshi, N.; Pacheco, K.D.; Bressler, N.M. Low-Shot Deep Learning of Diabetic Retinopathy with Potential Applications to Address Artificial Intelligence Bias in Retinal Diagnostics and Rare Ophthalmic Diseases. JAMA Ophthalmol. 2020, 138, 1070–1077. [Google Scholar] [CrossRef]
- Li, S.G.; Spaeth, G.L.; Scimeca, H.A.; Schatz, N.J.; Saving, P.J. Clinical Experiences with the Use of an Automated Perimeter (Otopus) in the Diagnosis and Management of Patients with Glaucoma and Neurologic Diseases. Ophthalmology 1979, 86, 1302–1312. [Google Scholar] [CrossRef]
- Garway–Heath, D.F.; Caprioli, J.; Fitzke, F.W.; Hitchings, R.A. Scaling the Hill of Vision: The Physiological Relationship between Light Sensitivity and Ganglion Cell Numbers. Investig. Ophthalmol. Vis. Sci. 2000, 41, 1774–1782. [Google Scholar]
- Wu, J.-H.; Moghimi, S.; Walker, E.; Nishida, T.; Liebmann, J.M.; Fazio, M.A.; Girkin, C.A.; Zangwill, L.M.; Weinreb, R.N. Time to Glaucoma Progression Detection by Optical Coherence Tomography and Visual Field in Glaucoma Individuals of African Descent. Am. J. Ophthalmol. 2025, 269, 195–204. [Google Scholar] [CrossRef]
- Hasan, M.M.; Phu, J.; Wang, H.; Sowmya, A.; Meijering, E.; Kalloniatis, M. Predicting Visual Field Global and Local Parameters from Oct Measurements Using Explainable Machine Learning. Sci. Rep. 2025, 15, 5685. [Google Scholar] [CrossRef]
- Huang, J.; Galal, G.; Mukhin, V.; Etemadi, M.; Tanna, A.P. Prediction and Detection of Glaucomatous Visual Field Progression Using Deep Learning on Macular Optical Coherence Tomography. J. Glaucoma 2024, 33, 246–253. [Google Scholar] [CrossRef]
- Artes, P.H.; O’Leary, N.; Nicolela, M.T.; Chauhan, B.C.; Crabb, D.P. Visual Field Progression in Glaucoma: What Is the Specificity of the Guided Progression Analysis? Ophthalmology 2014, 121, 2023–2027. [Google Scholar] [CrossRef] [PubMed]
- Wyatt, H.J.; Dul, M.W.; Swanson, W.H. Variability of Visual Field Measurements Is Correlated with the Gradient of Visual Sensitivity. Vis. Res. 2007, 47, 925–936. [Google Scholar] [CrossRef] [PubMed]

| Characteristic | |
|---|---|
| Age at baseline, years, Mean (SD) | 61.86 (17.40) |
| Gender, n (%) | |
| Female | 19,528 (58.06%) |
| Male | 14,109 (41.95%) |
| Race, n (%) | |
| White | 309,516 (70.18%) |
| Black/African Americans | 51,579 (11.70%) |
| Asians | 26,563 (6.02%) |
| American Indian/Alaska Native | 17,564 (3.98%) |
| Others | 33,473 (7.59%) |
| Visual fields (total), n | 340,439 |
| Follow-up time, years, median [IQR] | 2.49 [0.54, 6.22] |
| N of visits per eye, years, Mean (SD) | 5.16 (3.35) |
| MD at baseline, dB, Mean (SD) | |
| Overall | −4.48 (6.49) |
| Mild (MD > −4.20) | −1.13 (1.73) |
| Moderate (−8.17 < MD <= −4.20) | −5.83 (1.12) |
| Severe (MD <= −8.17) | −16.34 (6.70) |
| Classifier | Accuracy (%) | Precision (%) | Sensitivity (%) | F-Score (%) |
|---|---|---|---|---|
| MLP | 96.43 | 92.32 | 100 | 96.01 |
| XGB | 92.86 | 85.71 | 100 | 92.31 |
| LR | 89.29 | 90.91 | 83.33 | 86.96 |
| LoGTS | 87.51 | 76.92 | 90.90 | 83.33 |
| UKGTS | 84.40 | 73.30 | 91.72 | 81.48 |
| Kang | 84.41 | 73.32 | 91.73 | 81.50 |
| HAP2_p1 | 78.14 | 63.22 | 95 | 75.92 |
| Foster | 65.65 | 52.22 | 95.03 | 67.40 |
| Method, Year | Test Type | Accuracy (%) | Precision (%) | Sensitivity (%) | AUC (%) |
|---|---|---|---|---|---|
| MLP Meta-Learner (this study), 2025 | 24-2 VF | 96.43 | 92.32 | 100 | 97.96 |
| Wu et al. [47], C5 Decision Tree, 2021 | 30-2 VF | 87.1 | 84.7 | 88.3 | 94 |
| Masumoto et al. [48], Deep learning model, 2018 | 24-2 VF | NA | 80.2 | 81.3 | 87.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the Lithuanian University of Health Sciences. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moradi, M.; Hashemabad, S.K.; Vu, D.M.; Soneru, A.R.; Fujita, A.; Wang, M.; Elze, T.; Eslami, M.; Zebardast, N. PyGlaucoMetrics: A Stacked Weight-Based Machine Learning Approach for Glaucoma Detection Using Visual Field Data. Medicina 2025, 61, 541. https://doi.org/10.3390/medicina61030541
Moradi M, Hashemabad SK, Vu DM, Soneru AR, Fujita A, Wang M, Elze T, Eslami M, Zebardast N. PyGlaucoMetrics: A Stacked Weight-Based Machine Learning Approach for Glaucoma Detection Using Visual Field Data. Medicina. 2025; 61(3):541. https://doi.org/10.3390/medicina61030541
Chicago/Turabian StyleMoradi, Mousa, Saber Kazeminasab Hashemabad, Daniel M. Vu, Allison R. Soneru, Asahi Fujita, Mengyu Wang, Tobias Elze, Mohammad Eslami, and Nazlee Zebardast. 2025. "PyGlaucoMetrics: A Stacked Weight-Based Machine Learning Approach for Glaucoma Detection Using Visual Field Data" Medicina 61, no. 3: 541. https://doi.org/10.3390/medicina61030541
APA StyleMoradi, M., Hashemabad, S. K., Vu, D. M., Soneru, A. R., Fujita, A., Wang, M., Elze, T., Eslami, M., & Zebardast, N. (2025). PyGlaucoMetrics: A Stacked Weight-Based Machine Learning Approach for Glaucoma Detection Using Visual Field Data. Medicina, 61(3), 541. https://doi.org/10.3390/medicina61030541





