Selection of an Optimal Metabolic Model for Accurately Predicting the Hepatic Clearance of Albumin-Binding-Sensitive Drugs
Abstract
1. Introduction
2. Results
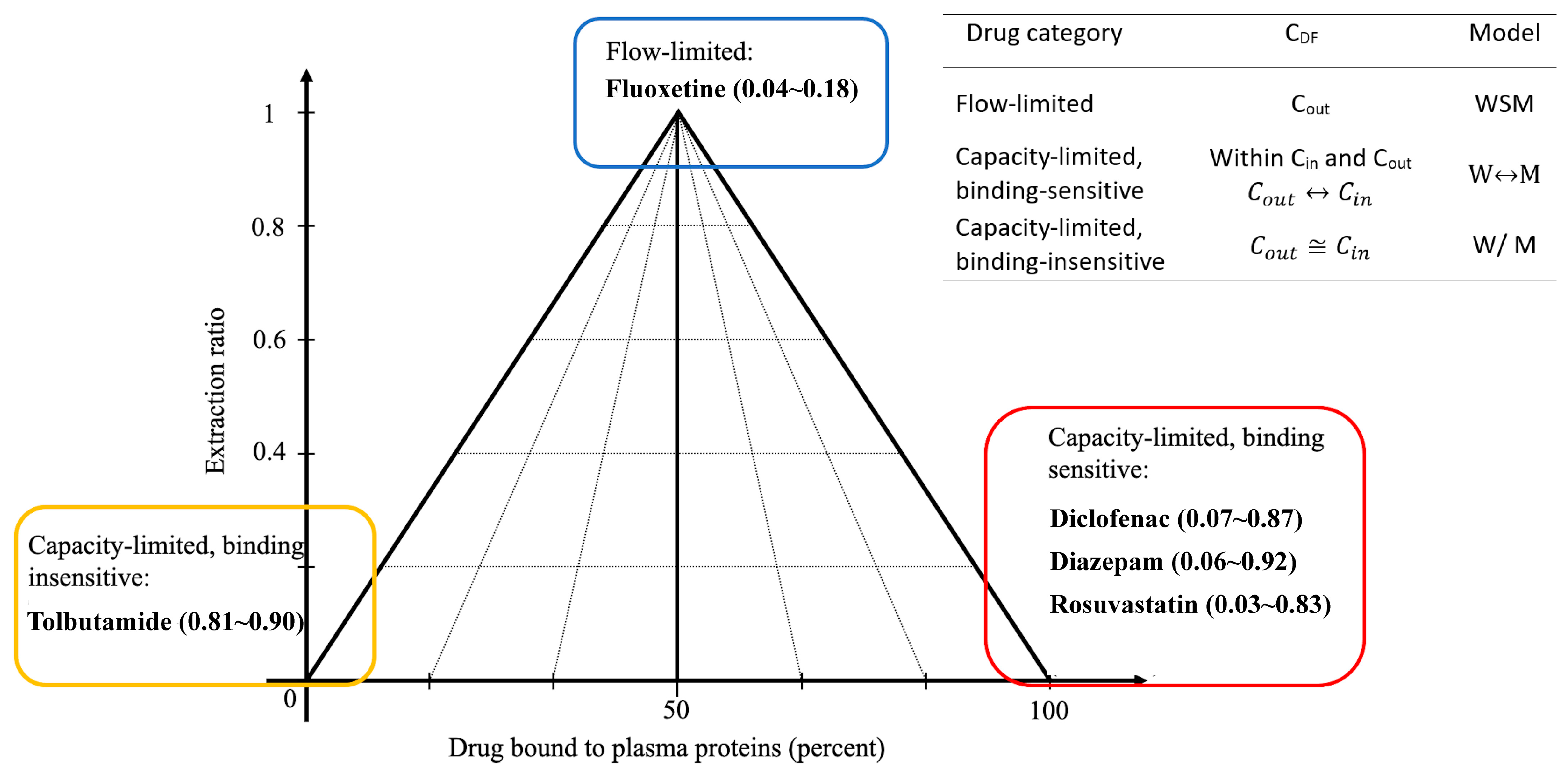
2.1. Logistic Regression Modeling
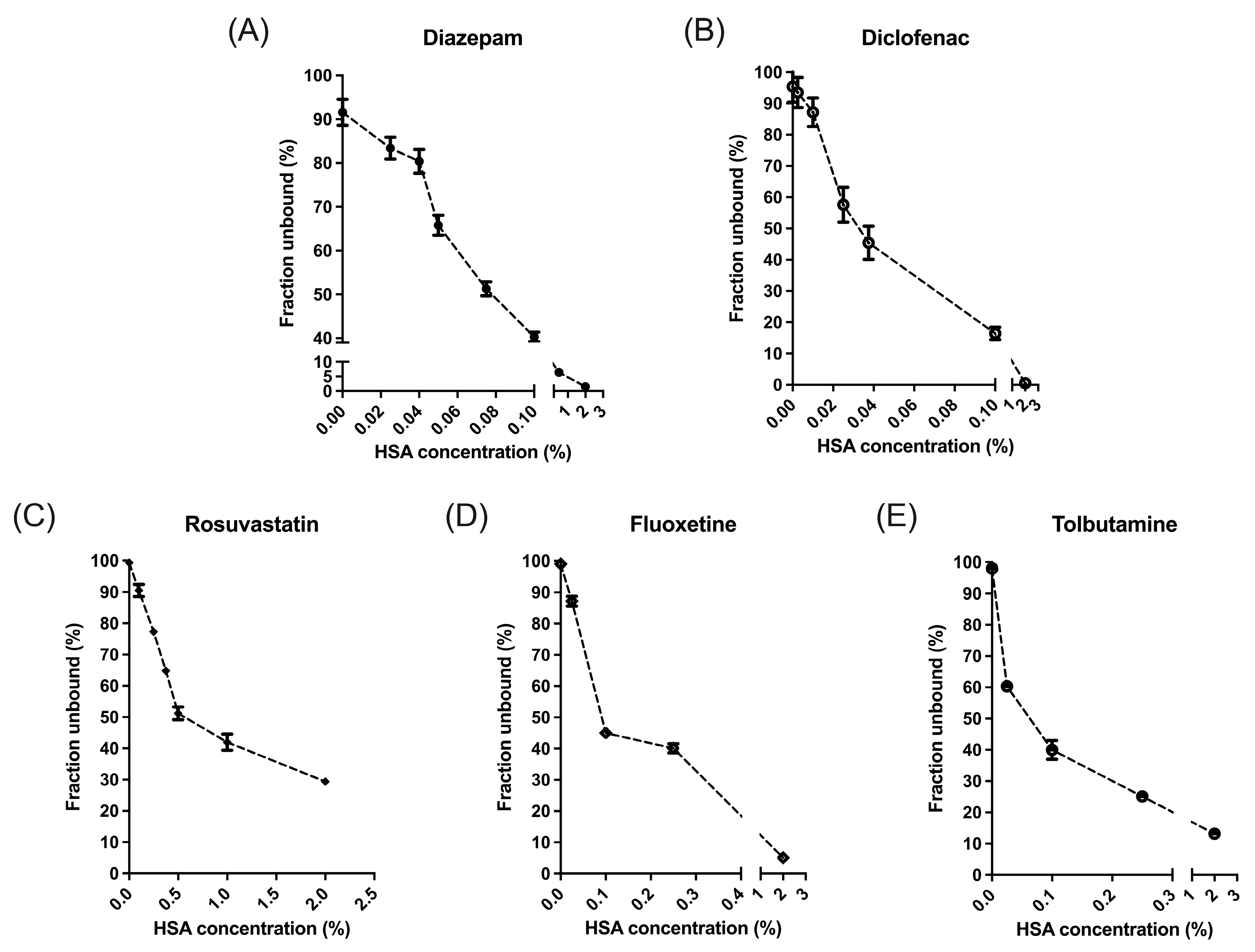
2.2. Equilibrium Dialysis
2.3. Drug Metabolism in IPRL
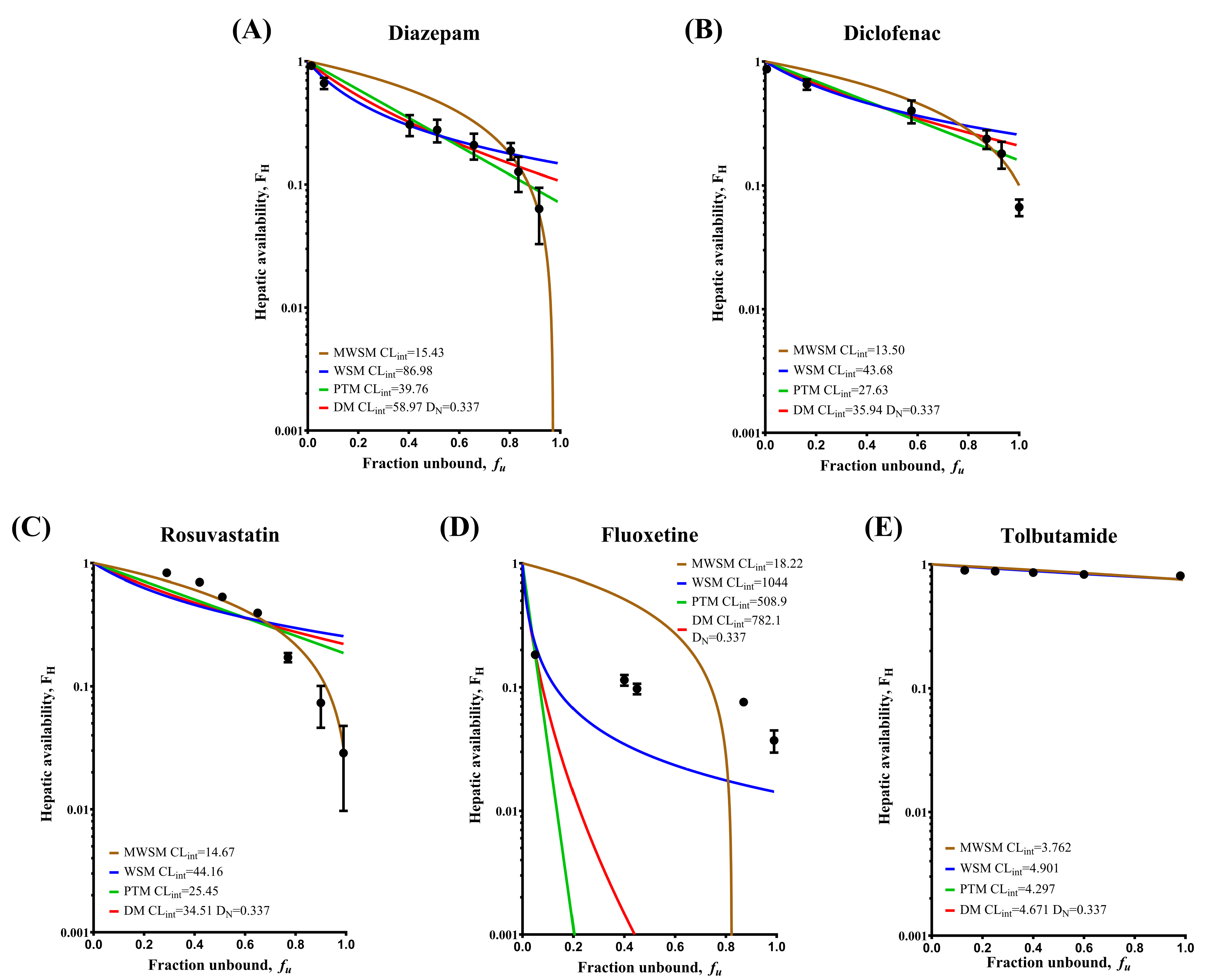
2.4. Fitting the Model-Simulated Curves
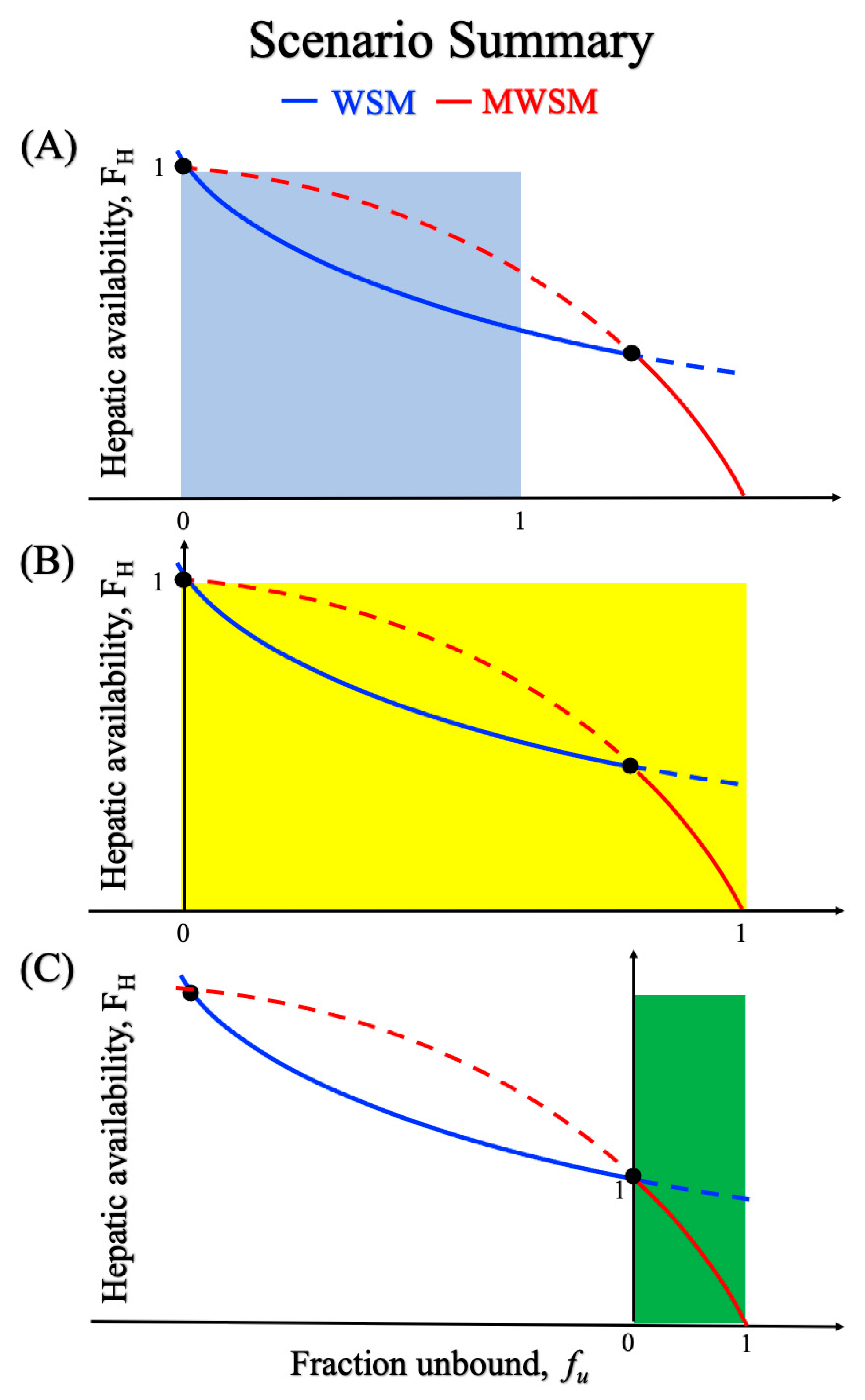
3. Discussion
- When protein binding occurs, does the variation in the concentration of the free drug influence the accuracy of model predictions, and if so, in what way?
- WSM designates Cout as the CDF. What are the reasons behind this choice and what mechanisms could validate this assumption?
- While Equation (10) has long been regarded as practical and intuitive from a macroscopic perspective, questions remain regarding its universal applicability.
4. Materials and Methods
4.1. Logistic Regression Modeling for Hepatic Model Selection
4.2. Chemicals
4.3. Rapid Equilibrium Dialysis
4.4. Surgery and Liver Perfusion
4.5. Sample Preparation and Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CDF | Driving force concentrations |
| CDM | Representative drug concentration in DM |
| CH | Total drug concentration in liver |
| Cin | Drug concentration entering liver |
| CLH | Hepatic clearance |
| CLint | Intrinsic clearance |
| CMWSM | Representative drug concentration in MWSM |
| Cout | Drug concentration exiting liver |
| CPTM | Logarithmic mean drug concentration in PTM |
| CWSM | Representative drug concentration in WSM |
| DM | Dispersion model |
| ER | Extraction ratio |
| FH | Hepatic availability |
| fu | Intravascular fraction of unbound drug |
| fu,E | Extravascular fraction of unbound drug |
| HSA | Human serum albumin |
| IPRL | Isolated perfused rat liver |
| IVIVE | In vitro-to-in vivo extrapolation |
| MWSM | Modified well-stirred model |
| PTM | Parallel-tube model |
| QH | Hepatic blood flow |
| WSM | Well-stirred model |
References
- Rowland, M. Influence of Route of Administration on Drug Availability. J. Pharm. Sci. 1972, 61, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Benet, L.Z.; Sodhi, J.K. Investigating the Theoretical Basis for In Vitro–In Vivo Extrapolation (IVIVE) in Predicting Drug Metabolic Clearance and Proposing Future Experimental Pathways. AAPS J. 2020, 22, 120. [Google Scholar] [CrossRef] [PubMed]
- Chang, T.-Y.; Wang, H.-J.; Hsu, S.-H.; Chang, M.-L.; Kao, L.-T.; Pao, L.-H. Evidence of the Need for Modified Well-Stirred Model in Vitro to in Vivo Extrapolation. Eur. J. Pharm. Sci. 2022, 177, 106268. [Google Scholar] [CrossRef]
- Diaz-Garcia, J.M.; Evans, A.M.; Rowland, M. Application of the Axial Dispersion Model of Hepatic Drug Elimination to the Kinetics of Diazepam in the Isolated Perfused Rat Liver. J. Pharmacokinet. Biopharm. 1992, 20, 171–193. [Google Scholar] [CrossRef]
- Dong, J.; Park, M.S. Discussions on the Hepatic Well-Stirred Model: Re-Derivation from the Dispersion Model and Re-Analysis of the Lidocaine Data. Eur. J. Pharm. Sci. 2018, 124, 46–60. [Google Scholar] [CrossRef]
- Hsu, S.-H.; Cheng, A.-C.; Chang, T.-Y.; Pao, L.-H.; Hsiong, C.-H.; Wang, H.-J. Precisely Adjusting the Hepatic Clearance of Highly Extracted Drugs Using the Modified Well-Stirred Model. Biomed. Pharmacother. 2021, 141, 111855. [Google Scholar] [CrossRef] [PubMed]
- Pang, K.S.; Rowland, M. Hepatic Clearance of Drugs. I. Theoretical Considerations of a “Well-Stirred” Model and a “Parallel Tube” Model. Influence of Hepatic Blood Flow, Plasma and Blood Cell Binding, and the Hepatocellular Enzymatic Activity on Hepatic Drug Clearance. J. Pharmacokinet. Biopharm. 1977, 5, 625–653. [Google Scholar] [CrossRef]
- Pang, K.S.; Rowland, M. Hepatic Clearance of Drugs. II. Experimental Evidence for Acceptance of the “Well-Stirred” Model over the “Parallel Tube” Model Using Lidocaine in the Perfused Rat Liverin Situ Preparation. J. Pharmacokinet. Biopharm. 1977, 5, 655–680. [Google Scholar] [CrossRef]
- Roberts, M.S.; Rowland, M. A Dispersion Model of Hepatic Elimination: 3. Application to Metabolite Formation and Elimination Kinetics. J. Pharmacokinet. Biopharm. 1986, 14, 289–308. [Google Scholar] [CrossRef]
- Rowland, M.; Pang, K.S. Commentary on “The Universally Unrecognized Assumption in Predicting Drug Clearance and Organ Extraction Ratio”. Clin. Pharmacol. Ther. 2018, 103, 386–388. [Google Scholar] [CrossRef]
- Pang, K.S.; Han, Y.R.; Noh, K.; Lee, P.I.; Rowland, M. Hepatic Clearance Concepts and Misconceptions: Why the Well-Stirred Model Is Still Used Even Though It Is Not Physiologic Reality? Biochem. Pharmacol. 2019, 169, 113596. [Google Scholar] [CrossRef]
- Sodhi, J.K.; Wang, H.-J.; Benet, L.Z. Are There Any Experimental Perfusion Data That Preferentially Support the Dispersion and Parallel-Tube Models over the Well-Stirred Model of Organ Elimination? Drug Metab. Dispos. 2020, 48, 537–543. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.-J.; Benet, L.Z. Protein Binding and Hepatic Clearance: Re-Examining the Discrimination between Models of Hepatic Clearance with Diazepam in the Isolated Perfused Rat Liver Preparation. Drug Metab. Dispos. 2019, 47, 1397–1402. [Google Scholar] [CrossRef] [PubMed]
- Paumgartner, G. The Liver. Quantitative Aspects of Structure and Function: 1st International Gstaad Symposium, Organized by the Swiss Society for Gastroenterology, Gstaad, September 1972: Proceedings; Karger Medical and Scientific Publishers: Basel, Switzerland, 1973; ISBN 978-3-318-05184-1. [Google Scholar]
- Robert, M.S.; Rowland, M. Hepatic Eliminatilon—Dispersion Model. J. Pharm. Sci. 1985, 74, 585–587. [Google Scholar] [CrossRef]
- Blaschke, T.F. Protein Binding and Kinetics of Drugs in Liver Diseases. Clin. Pharmacokinet. 1977, 2, 32–44. [Google Scholar] [CrossRef] [PubMed]
- Bteich, M.; Poulin, P.; Piette, S.; Haddad, S. Impact of Extensive Plasma Protein Binding on the In Situ Hepatic Uptake and Clearance of Perampanel and Fluoxetine in Sprague Dawley Rats. J. Pharm. Sci. 2020, 109, 3190–3205. [Google Scholar] [CrossRef]
- Schary, W.L.; Rowland, M. Protein Binding and Hepatic Clearance: Studies with Tolbutamide, a Drug of Low Intrinsic Clearance, in the Isolated Perfused Rat Liver Preparation. J. Pharmacokinet. Biopharm. 1983, 11, 225–243. [Google Scholar] [CrossRef]
- Rowland, M.; Leitch, D.; Fleming, G.; Smith, B. Protein Binding and Hepatic Clearance: Discrimination between Models of Hepatic Clearance with Diazepam, a Drug of High Intrinsic Clearance, in the Isolated Perfused Rat Liver Preparation. J. Pharmacokinet. Biopharm. 1984, 12, 129–147. [Google Scholar] [CrossRef]
- Hussein, Z.; Evans, A.M.; Rowland, M. Physiologic Models of Hepatic Drug Clearance: Influence of Altered Protein Binding on the Elimination of Diclofenac in the Isolated Perfused Rat Liver. J. Pharm. Sci. 1993, 82, 880–885. [Google Scholar] [CrossRef]
- Hanke, N.; Gómez-Mantilla, J.D.; Ishiguro, N.; Stopfer, P.; Nock, V. Physiologically Based Pharmacokinetic Modeling of Rosuvastatin to Predict Transporter-Mediated Drug-Drug Interactions. Pharm. Res. 2021, 38, 1645–1661. [Google Scholar] [CrossRef]
- Luvai, A.; Mbagaya, W.; Hall, A.S.; Barth, J.H. Rosuvastatin: A Review of the Pharmacology and Clinical Effectiveness in Cardiovascular Disease. Clin. Med. Insights Cardiol. 2012, 6, CMC.S4324. [Google Scholar] [CrossRef] [PubMed]
- Wood, F.L.; Houston, J.B.; Hallifax, D. Clearance Prediction Methodology Needs Fundamental Improvement: Trends Common to Rat and Human Hepatocytes/Microsomes and Implications for Experimental Methodology. Drug Metab. Dispos. 2017, 45, 1178–1188. [Google Scholar] [CrossRef] [PubMed]
- Caccia, S.; Cappi, M.; Fracasso, C.; Garattini, S. Influence of Dose and Route of Administration on the Kinetics of Fluoxetine and Its Metabolite Norfluoxetine in the Rat. Psychopharmacology 1990, 100, 509–514. [Google Scholar] [CrossRef]
- Benet, L.; Liu, S.; Wolfe, A. The Universally Unrecognized Assumption in Predicting Drug Clearance and Organ Extraction Ratio. Clin. Pharmacol. Ther. 2018, 103, 521–525. [Google Scholar] [CrossRef]
- Benet, L.; Sodhi, J. Can In Vitro–In Vivo Extrapolation Be Successful? Recognizing the Incorrect Clearance Assumptions. Clin. Pharmacol. Ther. 2021, 111, 1022–1035. [Google Scholar] [CrossRef]
- Cheng, H.-C.; Chen, H.-T.; Chen, H.-Y.; Chou, N.-H.; Wang, H.-J.; Pao, L.-H.; Tang, S.-L. Advancing Hepatic Clearance Prediction across In Vitro, Ex Situ, and In Vivo Systems to Facilitate In Vitro-to-In Vivo Extrapolation. Eur. J. Pharm. Sci. 2025, 212, 107171. [Google Scholar] [CrossRef] [PubMed]
- Banh, H.L.; Burton, M.E.; Sperling, M.R. Interpatient and Intrapatient Variability in Phenytoin Protein Binding. Ther. Drug Monit. 2002, 24, 379. [Google Scholar] [CrossRef]
- Soeters, P.B.; Wolfe, R.R.; Shenkin, A. Hypoalbuminemia: Pathogenesis and Clinical Significance. J. Parenter. Enter. Nutr. 2019, 43, 181–193. [Google Scholar] [CrossRef]
- Ulldemolins, M.; Roberts, J.A.; Rello, J.; Paterson, D.L.; Lipman, J. The Effects of Hypoalbuminaemia on Optimizing Antibacterial Dosing in Critically Ill Patients. Clin. Pharmacokinet. 2011, 50, 99–110. [Google Scholar] [CrossRef]
- Bar-Or, D.; Rael, L.T.; Bar-Or, R.; Slone, D.S.; Craun, M.L. The Formation and Rapid Clearance of a Truncated Albumin Species in a Critically Ill Patient. Clin. Chim. Acta 2006, 365, 346–349. [Google Scholar] [CrossRef]
- Zemlin, A.E.; Burgess, L.J.; Engelbrecht, A. Two Cases of Severe Hypoalbuminemia (<10 g/L). Nutrition 2009, 25, 1006–1010. [Google Scholar] [CrossRef] [PubMed]
- Fagerholm, U. Prediction of Human Pharmacokinetics—Evaluation of Methods for Prediction of Hepatic Metabolic Clearance. J. Pharm. Pharmacol. 2007, 59, 803–828. [Google Scholar] [CrossRef] [PubMed]
- Masimirembwa, C.M.; Bredberg, U.; Andersson, T.B. Metabolic Stability for Drug Discovery and Development. Clin. Pharmacokinet. 2003, 42, 515–528. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, F.; Berellini, G.; Obach, R.S. Trend Analysis of a Database of Intravenous Pharmacokinetic Parameters in Humans for 1352 Drug Compounds. Drug Metab. Dispos. 2018, 46, 1466–1477. [Google Scholar] [CrossRef]
- El-Kattan, A.F.; Varma, M.V.; Steyn, S.J.; Scott, D.O.; Maurer, T.S.; Bergman, A. Projecting ADME Behavior and Drug-Drug Interactions in Early Discovery and Development: Application of the Extended Clearance Classification System. Pharm. Res. 2016, 33, 3021–3030. [Google Scholar] [CrossRef]
| Drug | Percent Better Prediction (BP%) | ||
|---|---|---|---|
| W | S | M | |
| Diazepam | 92.92 | 7.04 | 0.04 |
| Diclofenac | 55.26 | 30.82 | 13.92 |
| Rosuvastatin | 19.95 | 31.46 | 48.59 |
| Concentration Sequences | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|---|
| Drug | |||||||||
| Diazepam a | 0.063 ± 0.031 (15) | 0.127 ± 0.040 (15) | 0.188 ± 0.029 (9) | 0.208 ± 0.050 (15) | 0.277 ± 0.058 (9) | 0.305 ± 0.059 (15) | 0.664 ± 0.070 (6) | 0.920 ± 0.040 (6) | |
| Diclofenac b | 0.067 ± 0.010 (6) | 0.180 ± 0.044 (5) | 0.237 ± 0.041 (6) | 0.400 ± 0.084 (6) | 0.654 ± 0.064 (6) | 0.869 ± 0.039 (4) | - | - | |
| Rosuvastatin c | 0.029 ± 0.019 (12) | 0.073 ± 0.027 (6) | 0.172 ± 0.015 (6) | 0.395 ± 0.015 (6) | 0.533 ± 0.037 (6) | 0.700 ± 0.032 (6) | 0.833 ± 0.039 (4) | - | |
| Fluoxetine d | 0.037 ± 0.008 (7) | 0.076 ± 0.005 (7) | 0.097 ± 0.010 (7) | 0.114 ± 0.011 (7) | 0.183 ± 0.010 (6) | - | - | - | |
| Tolbutamide d | 0.808 ± 0.030 (6) | 0.828 ± 0.025 (6) | 0.858 ± 0.015 (6) | 0.880 ± 0.014 (6) | 0.895 ± 0.014 (6) | - | - | - | |
| Drug | Interval of HSA Concentration (%) | Optimal Model | Modified WSM | WSM | PTM | DM |
|---|---|---|---|---|---|---|
| Diazepam | 0–0.04 | MWSM | 0.0481 | 0.1123 | 0.0894 | 0.1003 |
| 0.04–2 | WSM | 1.5150 | 0.1818 | 0.4375 | 0.2781 | |
| Diclofenac | 0–0.01 | MWSM | 0.0278 | 0.0885 | 0.0702 | 0.0792 |
| 0.025–2 | WSM | 0.2923 | 0.1194 | 0.1790 | 0.1400 | |
| Rosuvastatin | 0–2 | MWSM | 0.2132 | 1.8440 | 1.0670 | 1.4550 |
| Fluoxetine | 0–2 | WSM | 5.9630 | 0.1154 | 0.2096 | 0.2062 |
| Tolbutamide | 0–2 | WSM | 0.0923 | 0.0672 | 0.0790 | 0.0715 |
| Drug | MW a | AlogP a | PSA a | Rotatable Bonds a | HBA a | HBD a | Aromatic Rings a | Heavy Atoms a | Vss b | MRT b | logCLint,u,in-vivo (pred) | fup | Class a | OATP c | P-gp c | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| hep | mic | |||||||||||||||
| Diazepam | 285 | 3.15 | 32.67 | 1 | 3 | 0 | 2 | 20 | 1.00 | 44.00 | 0.93 | 0.95 | 0.021 | N | Without | With |
| Diclofenac | 296 | 4.36 | 49.33 | 4 | 3 | 2 | 2 | 19 | 0.22 | 1.00 | 2.24 | 2.17 | 0.004 | A | Without | Without |
| Rosuvastatin | 482 | 2.4 | 140.9 | 10 | 9 | 3 | 2 | 33 | 1.70 | 2.60 | 1.30 | NF | 0.129 | A | With | Without |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, R.-J.; Hsu, S.-H.; Chen, H.-T.; Chen, W.-H.; Fu, H.-Y.; Chen, H.-Y.; Wang, H.-J.; Tang, S.-L. Selection of an Optimal Metabolic Model for Accurately Predicting the Hepatic Clearance of Albumin-Binding-Sensitive Drugs. Pharmaceuticals 2025, 18, 991. https://doi.org/10.3390/ph18070991
Liang R-J, Hsu S-H, Chen H-T, Chen W-H, Fu H-Y, Chen H-Y, Wang H-J, Tang S-L. Selection of an Optimal Metabolic Model for Accurately Predicting the Hepatic Clearance of Albumin-Binding-Sensitive Drugs. Pharmaceuticals. 2025; 18(7):991. https://doi.org/10.3390/ph18070991
Chicago/Turabian StyleLiang, Ren-Jong, Shu-Hao Hsu, Hsueh-Tien Chen, Wan-Han Chen, Han-Yu Fu, Hsin-Ying Chen, Hong-Jaan Wang, and Sung-Ling Tang. 2025. "Selection of an Optimal Metabolic Model for Accurately Predicting the Hepatic Clearance of Albumin-Binding-Sensitive Drugs" Pharmaceuticals 18, no. 7: 991. https://doi.org/10.3390/ph18070991
APA StyleLiang, R.-J., Hsu, S.-H., Chen, H.-T., Chen, W.-H., Fu, H.-Y., Chen, H.-Y., Wang, H.-J., & Tang, S.-L. (2025). Selection of an Optimal Metabolic Model for Accurately Predicting the Hepatic Clearance of Albumin-Binding-Sensitive Drugs. Pharmaceuticals, 18(7), 991. https://doi.org/10.3390/ph18070991








