Advancing Internal Dosimetry in Personalized Nuclear Medicine: Toward Optimized Radiopharmaceutical Use in Clinical Practice
Abstract
1. Introduction
2. Results
2.1. Absorbed Dose
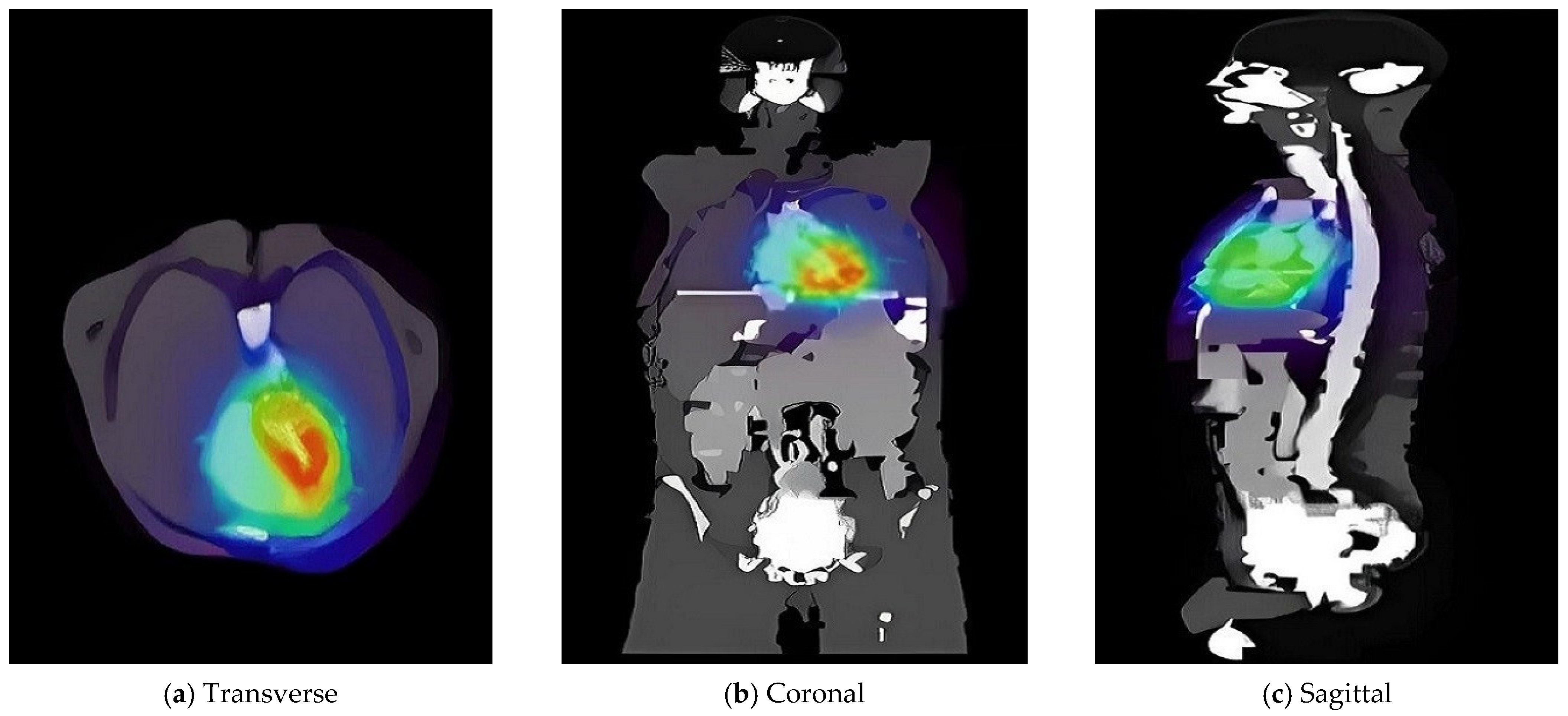
2.2. Zubal Phantom Study Using 18-Fluorine
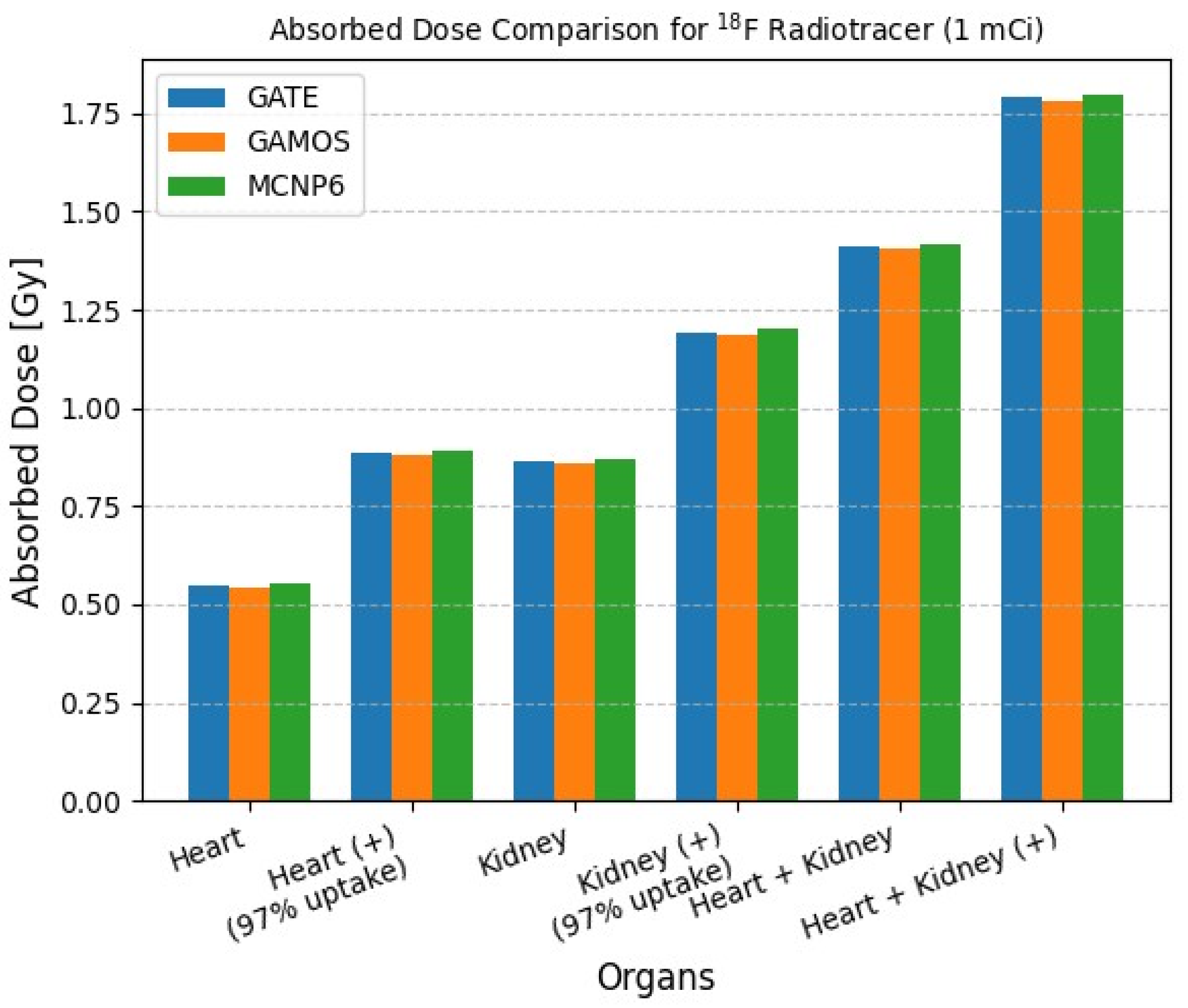
2.3. Dose Estimation Using GATE, GAMOS, and MCNP6 Codes
2.4. Post-Injection Dynamics at Cardiac Rest
3. Discussion
4. Methods and Materials
4.1. Monte Carlo-Based Simulations
4.2. Phantom Configuration and Source Definition
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CT | Computed Tomography |
| GATE | Geant4 Application for Tomographic Emission |
| GAMOS | GEANT4-Based Architecture for Medicine-Oriented Simulations |
| ICRP | International Commission on Radiological Protection |
| MC | Monte Carlo |
| MCNP6 | Monte Carlo N-Particle Code, Version 6 |
| MIBI | Methoxyisobutylisonitrile |
| MIRD | Medical Internal Radiation Dose |
| PET | Positron Emission Tomography |
| RBE | Relative Biological Effectiveness |
| SAF | Specific Absorbed Fraction |
| SPECT | Single Photon Emission Computed Tomography |
| TIAC | Time-Integrated Activity Coefficient |
| VSV | Voxel S-Value |
| ICC | Intraclass Correlation Coefficient |
| 95% CI | Confidence Interval |
| p-value | Probability Value |
| RMSD | Root Mean Square Deviation |
| CV (%) | Coefficient of Variation |
References
- Ebrahimnejad Gorji, K.; Abedi Firouzjah, R.; Khanzadeh, F.; Abdi-Goushbolagh, N.; Banaei, A.; Ataei, G. Estimating the absorbed dose of organs in pediatric imaging of 99mtc-dtpatc-dtpa radiopharmaceutical using mirdose software. J. Biomed. Phys. Eng. 2019, 9, 285. [Google Scholar] [CrossRef]
- Vakili, S.; Shahbazi-Gahrouei, D. Determining the fetal dose in ventilation/perfusion scan using monte carlo simulation. J. Isfahan Med. Sch. 2019, 37, 237–241. [Google Scholar] [CrossRef]
- Pandit-Taskar, N.; Dauer, L.T.; Montgomery, L.; Germain, J.S.; Zanzonico, P.B.; Divgi, C.R. Organ and fetal absorbed dose estimates from 99mtc-sulfur colloid lymphoscintigraphy and sentinel node localization in breast cancer patients. J. Nucl. Med. 2006, 47, 1202–1208. [Google Scholar]
- Khoshyari-morad, Z.; Jahangir, R.; Miri-Hakimabad, H.; Mohammadi, N.; Arabi, H. Monte carlo-based estimation of patient absorbed dose in 99mtc-dmsa,-mag3, and-dtpa spect imaging using the university of florida (uf) phantoms. arXiv 2021, arXiv:2103.00619. [Google Scholar] [CrossRef]
- Einstein, A.J.; Shuryak, I.; Castaño, A.; Mintz, A.; Maurer, M.S.; Bokhari, S. Estimating cancer risk from 99mtc pyrophosphate imaging for transthyretin cardiac amyloidosis. J. Nucl. Cardiol. 2020, 27, 215–224. [Google Scholar] [CrossRef] [PubMed]
- Mattsson, S.; Johansson, L.; Liniecki, J.; Nosske, D.; Stabin, M.; Leide-Svegborn, S.; Taylor, D. Radiation dose to patients from radiopharmaceuticals. In Radiation Protection and Dosimetry, Biological Effects of Radiation, Proceedings of the World Congress on Medical Physics and Biomedical Engineering, Munich, Germany, 7–12 September 2009; Springer: Berlin/Heidelberg, Germany, 2009; Volume 25/3, pp. 474–477. [Google Scholar]
- Ma, H.; Li, S.; Wu, Z.; Liu, J.; Liu, H.; Guo, X. Comparison of 99mtc-n-dbodc5 and 99mtc-mibi of myocardial perfusion imaging for diagnosis of coronary artery disease. BioMed Res. Int. 2013, 2013, 145427. [Google Scholar] [CrossRef][Green Version]
- Boschi, A.; Uccelli, L.; Marvelli, L.; Cittanti, C.; Giganti, M.; Martini, P. Technetium-99m radiopharmaceuticals for ideal myocardial perfusion imaging: Lost and found opportunities. Molecules 2022, 27, 1188. [Google Scholar] [CrossRef] [PubMed]
- Bolch, W.E.; Eckerman, K.F.; Sgouros, G.; Thomas, S.R. Mird pamphlet no. 21: A generalized schema for radiopharmaceutical dosimetry-standardization of nomenclature. J. Nucl. Med. 2009, 50, 477–484. [Google Scholar] [CrossRef] [PubMed]
- Capala, J.; Graves, S.A.; Scott, A.; Sgouros, G.; James, S.S.; Zanzonico, P.; Zimmerman, B.E. Dosimetry for radiopharmaceutical therapy: Current practices and commercial resources. J. Nucl. Med. 2021, 62 (Suppl. 3), 3S–11S. [Google Scholar] [CrossRef]
- Staelens, S.; Buvat, I. Advances in Biomedical Engineering; Elsevier: Amsterdam, The Netherlands, 2009; pp. 177–209. [Google Scholar] [CrossRef]
- Harkness, L.; Arce, P.; Judson, D.; Boston, A.; Boston, H.; Cresswell, J.; Dormand, J.; Jones, M.; Nolan, P.; Sampson, J.; et al. A compton camera application for the gamos geant4-based framework. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2012, 671, 29–39. [Google Scholar] [CrossRef]
- Gasteuil, J.; Noblet, C.; Moreau, M.; Meyer, P. A gate/geant4 monte carlo toolkit for surface dose calculation in vmat breast cancer radiotherapy. Phys. Medica 2019, 61, 112–117. [Google Scholar] [CrossRef]
- Lee, C.; Lodwick, D.; Hurtado, J.; Williams, J.; Bolch, W. Comparative dosimetry of monte carlo-based internal dose calculations for diagnostic nuclear medicine applications: Gate versus mcnp6. Med. Phys. 2015, 42, 905–913. [Google Scholar] [CrossRef]
- Spyridonidis, T.; Papathanasiou, N.; Spyridonidis, J.; Ntzoumani, C.; Spyropoulou, D.; Katsanos, K.; Apostolopoulos, D.J. 90y-microsphere radioembolization: The method, clinical evidence and perspective. Hell. J. Nucl. Med. 2020, 23, 330–338. [Google Scholar] [PubMed]
- Georgiou, M.F.; Nielsen, J.A.; Chiriboga, R.; Kuker, R.A. An artificial intelligence system for optimizing radioactive iodine therapy dosimetry. J. Clin. Med. 2023, 13, 117. [Google Scholar] [CrossRef]
- Cordeiro, L.P.; de Sá, L.V.; Kitamikado, R.A.; Sapienza, M.T.; Bonifacio, D.A.B. Optimized Monte Carlo simulations for voxel-based internal dosimetry. Phys. Med. Biol. 2023, 68, 115004. [Google Scholar] [CrossRef] [PubMed]
- Salari, S.; Khorshidi, A.; Soltani-Nabipour, J. Simulation and assessment of 99mTc absorbed dose into internal organs from cardiac perfusion scan. Nucl. Eng. Technol. 2023, 55, 248–253. [Google Scholar] [CrossRef]
- Grimes, J.; Celler, A. Comparison of internal dose estimates obtained using organ—Level, voxel S value, and Monte Carlo techniques. Med. Phys. 2014, 41, 092501. [Google Scholar] [CrossRef]
- Wrixon, A. New recommendations from the international commission on radiological protection—A review. Phys. Med. Biol. 2008, 53, R41. [Google Scholar] [CrossRef]
- Jan, S.; Benoit, D.; Becheva, E.; Carlier, T.; Cassol, F.; Descourt, P.; Frisson, T.; Grevillot, L.; Guigues, L.; Maigne, L.; et al. Gate v6: A major enhancement of the gate simulation platform enabling modelling of ct and radiotherapy. Phys. Med. Biol. 2011, 56, 881. [Google Scholar] [CrossRef]
- Al-Zain, J.; El Bardouni, T.; Mohammed, M.; El Hajjaji, O. Validation of gamos code based on geant4 monte carlo for a 12 mv saturne43 linac. J. King Saud Univ. Sci. 2019, 31, 500–505. [Google Scholar] [CrossRef]
- Arce, P.; Lagares, J.I.; Harkness, L.; P’erez-Astudillo, D.; Canñadas, M.; Rato, P.; de Prado, M.; Abreu, Y.; de Lorenzo, G.; Kolstein, M.; et al. Gamos: A framework to do geant4 simulations in different physics fields with an user-friendly interface. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2014, 735, 304–313. [Google Scholar] [CrossRef]
- Merai, S.; Benrachi, F.; Laouet, N. External and internal GATE/Geant4 dosimetric calculations on voxelized phantoms. Radiol. Phys. Technol. 2025, 18, 514–522. [Google Scholar] [CrossRef]
- Demir, B.; Kucuk, N.O.; Soydal, C.; Celebioglu, E.C.; Inal, G.; Dursun, E.; Bilgic, M.S.; Oz, D.K.; Elhan, A.H.; Kir, K.M. Comparative voxel-based dosimetry with pre-treatment Tc-99m SPECT/CT and post-treatment Y-90 PET/MRI for radioembolization with Y-90 microspheres. Ann. Nucl. Med. 2025, 39, 716–731. [Google Scholar] [CrossRef]
- Rising, M.E.; Armstrong, J.C.; Bolding, S.R.; Brown, F.B.; Bull, J.S.; Cox, L.J. The MCNP®6 code: A decade of progress. EPJ Nucl. Sci. Technol. 2025, 11, 3. [Google Scholar] [CrossRef]
- Goorley, T.; James, M.; Booth, T.; Brown, F.; Bull, J.; Cox, L.; Durkee, J.; Elson, J.; Fensin, M.; Forster, R.; et al. Features of MCNP6. In SNA+ MC 2013-Joint International Conference on Supercomputing in Nuclear Applications + Monte Carlo; EDP Sciences: Les Ulis, France, 2014; p. 06011. [Google Scholar]
- Zankl, M. Adult male and female reference computational phantoms (icrp publication 110). Jpn. J. Health Phys. 2010, 45, 357–369. [Google Scholar] [CrossRef]
- Ghaly, M.; Du, Y.; Fung, G.S.; Tsui, B.M.; Links, J.M.; Frey, E. Design of a digital phantom population for myocardial perfusion spect imaging research. Phys. Med. Biol. 2014, 59, 2935. [Google Scholar] [CrossRef]
- Rossetti, C.; Vanoli, G.; Paganelli, G.; Kwiatkowski, M.; Zito, F.; Colombo, F.; Bonino, C.; Carpinelli, A.; Casati, R.; Deutsch, K.; et al. Human biodistribution, dosimetry and clinical use of technetium(III)-99m-Q12. J. Nucl. Med. 1994, 35, 1571–1580. [Google Scholar] [PubMed]
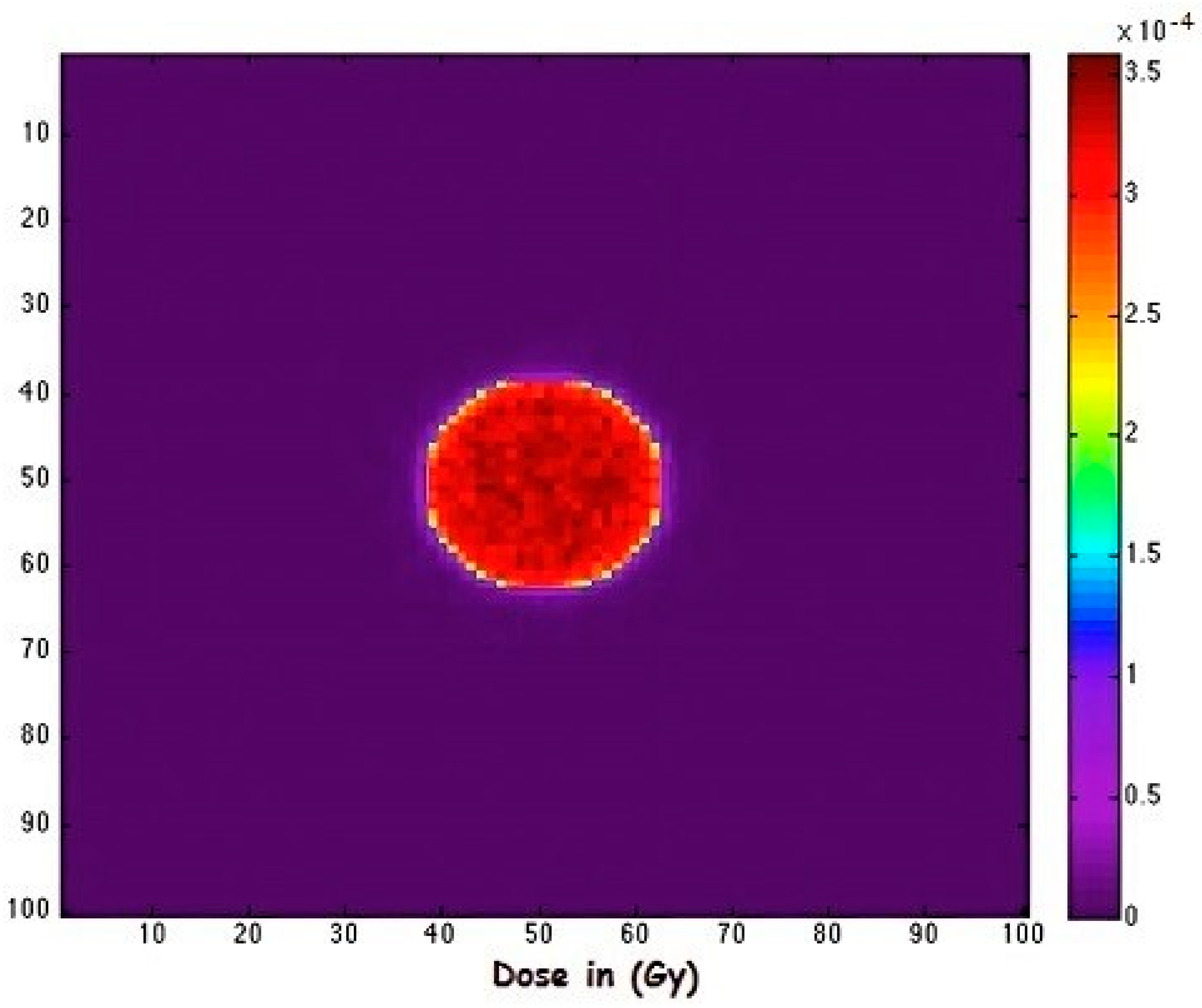
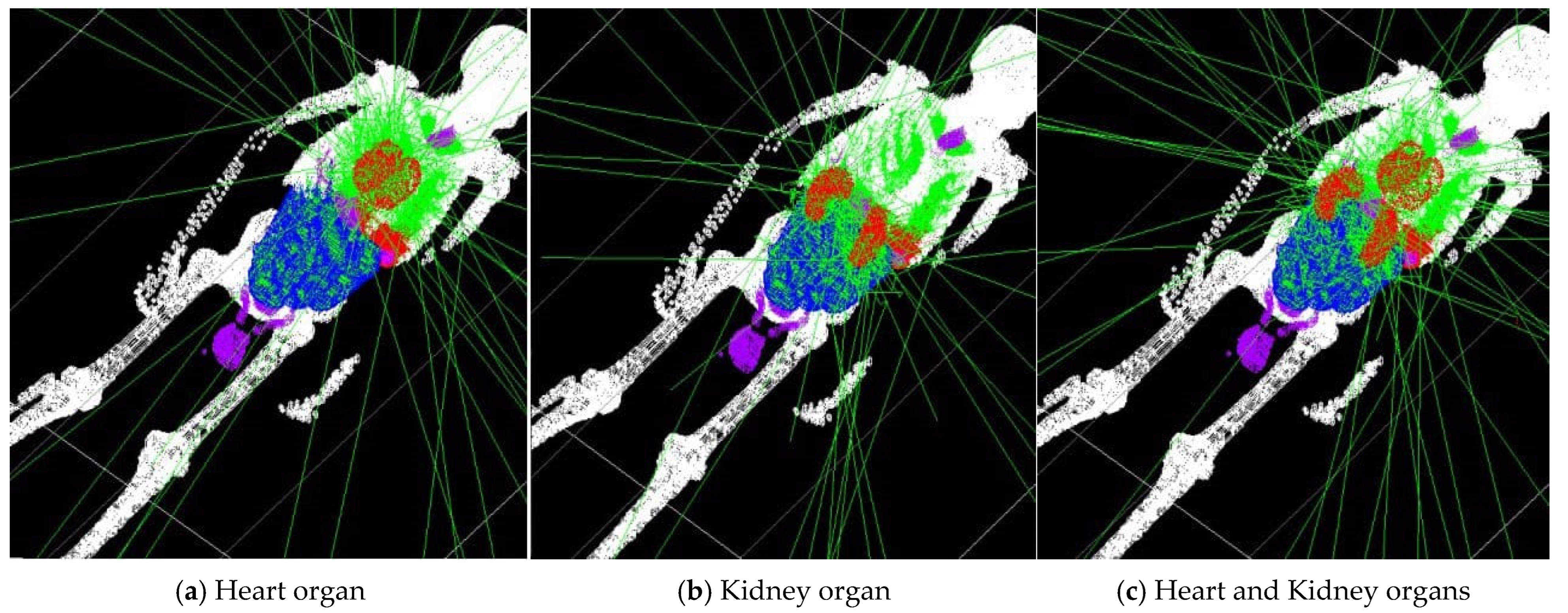
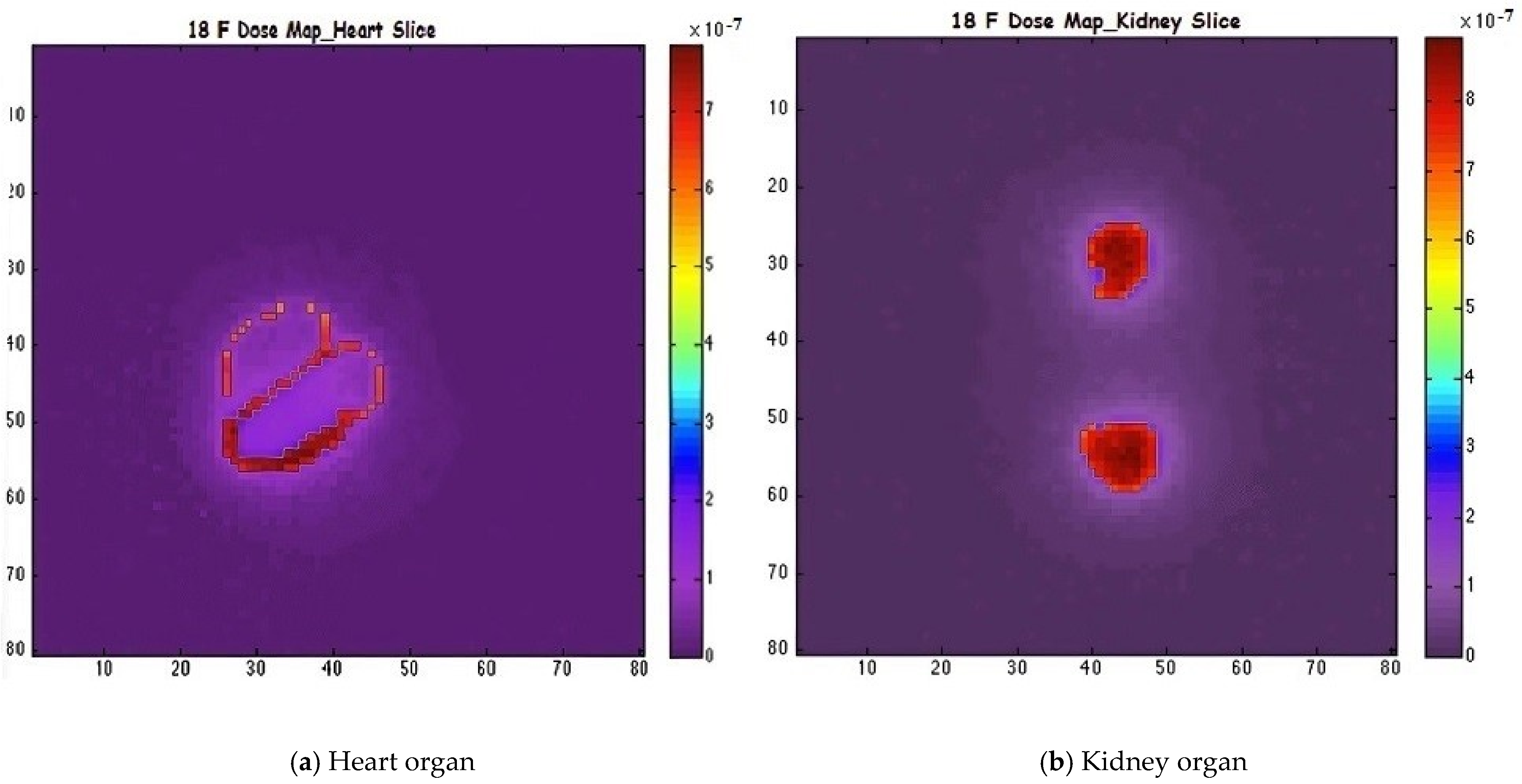


| Isotope | Atomic Number (Z) | Atomic Mass (A) | Ionic Charge (Q) | Excitation Energy (E) [keV] |
|---|---|---|---|---|
| 18F | 9 | 18 | +1 | 0 |
| 90Y | 39 | 90 | +3 | 0 |
| 111mIn | 49 | 111 | +3 | 537 |
| 123I | 53 | 123 | +1 | 0 |
| 131I | 53 | 131 | +1 | 0 |
| 99mTc | 43 | 99 | +1 | 143 |
| 177Lu | 71 | 177 | +3 | 0 |
| 225Ac | 89 | 225 | +3 | 0 |
| Isotope | Emission Type | Energy [keV] | Half-Life | Activity [mCi] | Dose [Gy] | ||
|---|---|---|---|---|---|---|---|
| GATE | GAMOS | MCNP6 | |||||
| 18F | Positron | 249.8 | 109.8 min | 1.0 | 10.75 | 10.68 | 10.81 |
| 90Y | Beta | 934.8 | 64.05 h | 1.0 | 1213.25 | 1207.89 | 1215.34 |
| 111mIn | Gamma | 536.95 | 7.7 min | 1.0 | 178.64 | 177.23 | 179.10 |
| 123I | Gamma | 159 | 13.22 h | 1.0 | 7.63 | 7.58 | 7.69 |
| 131I | Beta | 191.58 | 8.02 d | 1.0 | 952.55 | 948.41 | 955.60 |
| 99mTc | Gamma | 140.5 | 6.006 h | 1.0 | 15.22 | 15.11 | 15.30 |
| Isotope | Source Type | Energy [keV] | Half-Life | Activity [mCi] | Absorbed Dose | ||
|---|---|---|---|---|---|---|---|
| (GATE) [Gy] | (GAMOS) [Gy] | (MCNP6) [Gy] | |||||
| 131I | Radiotracer | – | 8.02 d | 1.0 | 952.55 | 948.60 | 956.80 |
| 131I | Electron (e−) | 191 | 8.02 d | 1.0 | 1034.90 | 1031.20 | 1038.40 |
| 99mTc | Radiotracer | – | 6.006 h | 1.0 | 15.22 | 15.10 | 15.35 |
| 99mTc | Electron (e−) | 1.6 | 6.006 h | 0.74 | 0.3373 | 0.3340 | 0.3405 |
| 99mTc | Electron (e−) | 3.71 | 6.006 h | 0.25 | 0.1460 | 0.1445 | 0.1475 |
| 99mTc | Electron (e−) | 2.2 | 6.006 h | 0.1 | 0.0616 | 0.0608 | 0.0620 |
| 99mTc | Electron (e−) | 15.5 | 6.006 h | 0.02 | 0.0880 | 0.0872 | 0.0890 |
| 99mTc | Electron (e−) | 119 | 6.006 h | 0.088 | 2.5700 | 2.5600 | 2.5800 |
| 99mTc | Electron (e−) | 137 | 6.006 h | 0.014 | 0.5216 | 0.5180 | 0.5250 |
| Organs | Activity | Absorbed Dose | ||
|---|---|---|---|---|
| 3–5 | [18F, mCi] | (GATE) [Gy] | (GAMOS) [Gy] | (MCNP6) [Gy] |
| Heart | 1.0 | 0.5464 | 0.5405 | 0.5510 |
| Heart (+) (97% uptake) | 1.0 | 0.8845 | 0.8790 | 0.8910 |
| Kidney | 1.0 | 0.8650 | 0.8592 | 0.8715 |
| Kidney (+) (97% uptake) | 1.0 | 1.1918 | 1.1850 | 1.2000 |
| Heart + Kidney | 1.0 | 1.4110 | 1.4035 | 1.4180 |
| Heart + Kidney (+) | 1.0 | 1.7905 | 1.7802 | 1.7985 |
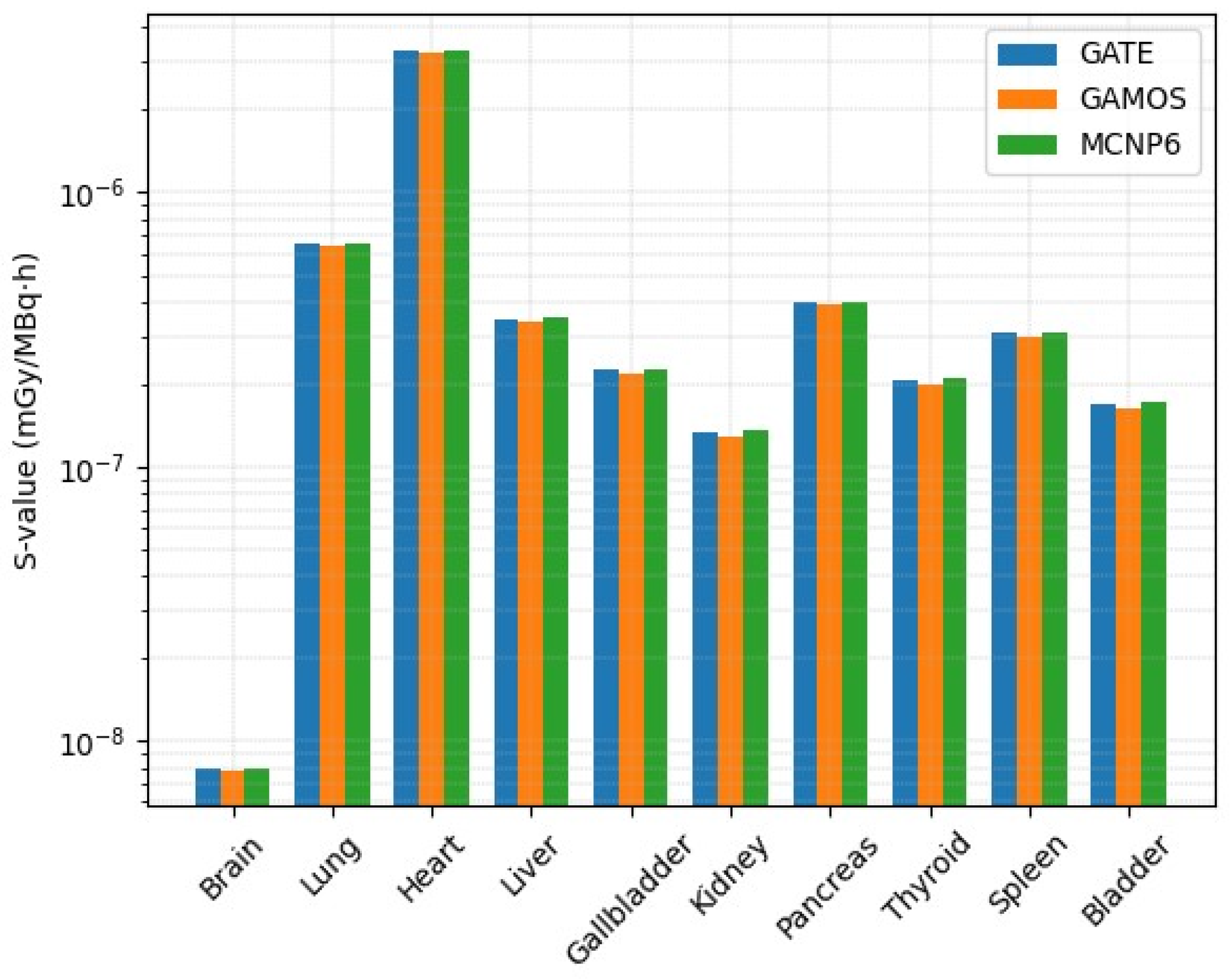
| Organ | S-Value | SAF | Voxel Count | ||||
|---|---|---|---|---|---|---|---|
| 2–4 5–7 | (GATE) | (GAMOS) | (MCNP6) | (GATE) | (GAMOS) | (MCNP6) | |
| Brain | 7.98 × 10−9 | 7.82 × 10−9 | 8.01 × 10−9 | 3.56 × 10−4 | 3.49 × 10−4 | 3.60 × 10−4 | 18,299 |
| Lung | 6.52 × 10−7 | 6.41 × 10−7 | 6.57 × 10−7 | 2.91 × 10−2 | 2.86 × 10−2 | 2.93 × 10−2 | 62,374 |
| Heart (source) | 3.30 × 10−6 | 3.25 × 10−6 | 3.32 × 10−6 | 1.47 × 10−1 | 1.45 × 10−1 | 1.48 × 10−1 | 9354 |
| Liver | 3.47 × 10−7 | 3.38 × 10−7 | 3.50 × 10−7 | 1.55 × 10−2 | 1.51 × 10−2 | 1.57 × 10−2 | 29,277 |
| Gallbladder | 2.26 × 10−7 | 2.18 × 10−7 | 2.28 × 10−7 | 1.01 × 10−2 | 9.7 × 10−3 | 1.02 × 10−2 | 329 |
| Kidney | 1.34 × 10−7 | 1.29 × 10−7 | 1.36 × 10−7 | 5.96 × 10−3 | 5.76 × 10−3 | 6.02 × 10−3 | 7618 |
| Pancreas | 3.97 × 10−7 | 3.88 × 10−7 | 4.00 × 10−7 | 1.77 × 10−2 | 1.73 × 10−2 | 1.79 × 10−2 | 792 |
| Thyroid | 2.08 × 10−7 | 2.01 × 10−7 | 2.10 × 10−7 | 9.29 × 10−3 | 8.97 × 10−3 | 9.40 × 10−3 | 105 |
| Spleen | 3.07 × 10−7 | 2.98 × 10−7 | 3.10 × 10−7 | 1.37 × 10−2 | 1.33 × 10−2 | 1.39 × 10−2 | 5568 |
| Bladder | 1.69 × 10−7 | 1.62 × 10−7 | 1.71 × 10−7 | 4.05 × 10−3 | 3.89 × 10−3 | 4.10 × 10−3 | 3147 |
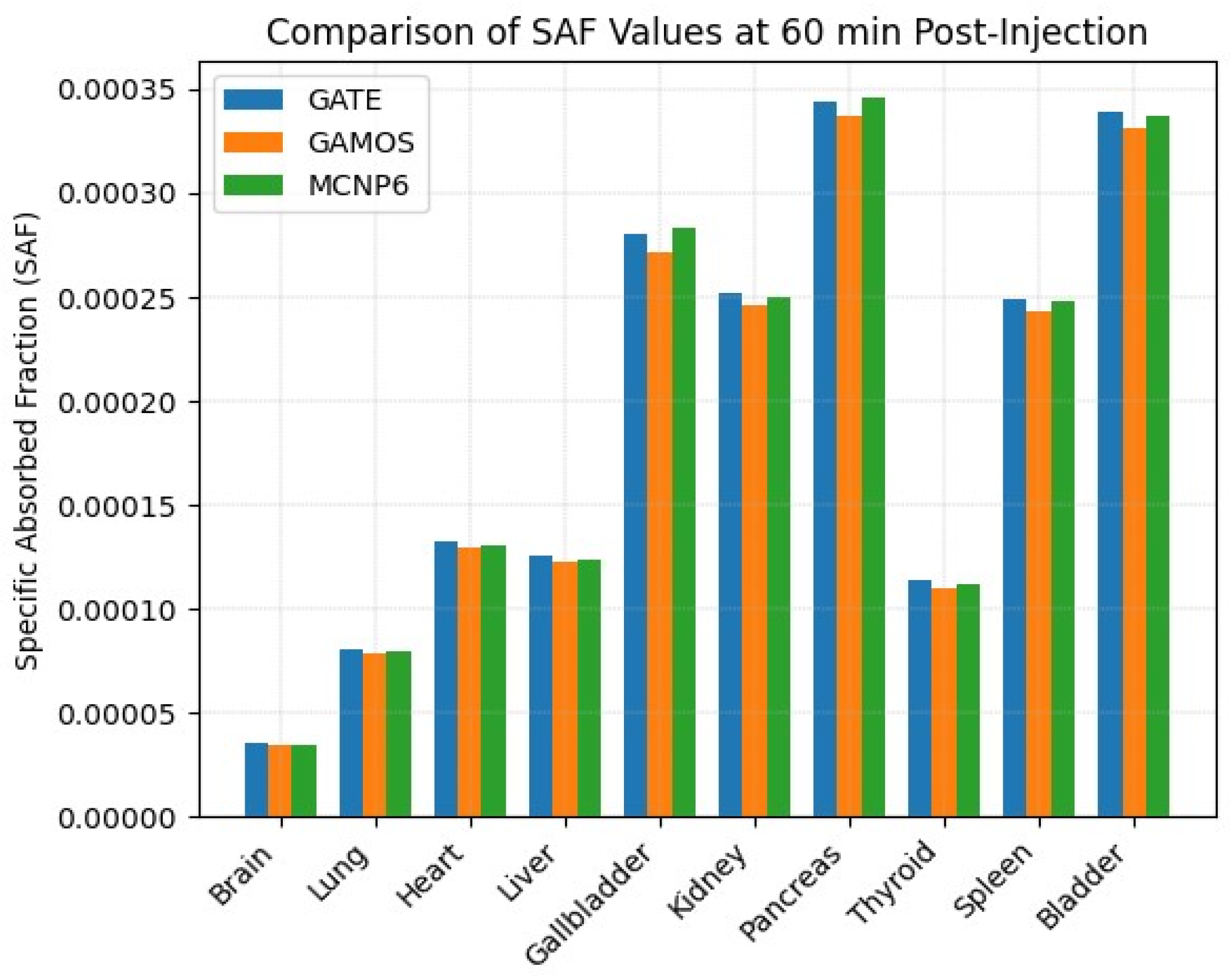
| Organ | Specific-Value | Specific Absorbed Fraction | ||||
|---|---|---|---|---|---|---|
| 2–7 | GATE | GAMOS | MCNP6 | GATE | GAMOS | MCNP6 |
| Brain | 7.97 × 10−10 | 7.75 × 10−10 | 7.69 × 10−10 | 3.56 × 10−5 | 3.46 × 10−5 | 3.44 × 10−5 |
| Lung | 1.81 × 10−9 | 1.77 × 10−9 | 1.79 × 10−9 | 8.08 × 10−5 | 7.90 × 10−5 | 7.95 × 10−5 |
| Heart (source) | 2.98 × 10−9 | 2.91 × 10−9 | 2.95 × 10−9 | 1.33 × 10−4 | 1.30 × 10−4 | 1.31 × 10−4 |
| Liver | 2.82 × 10−9 | 2.75 × 10−9 | 2.80 × 10−9 | 1.26 × 10−4 | 1.23 × 10−4 | 1.24 × 10−4 |
| Gallbladder | 6.26 × 10−9 | 6.10 × 10−9 | 6.31 × 10−9 | 2.80 × 10−4 | 2.72 × 10−4 | 2.83 × 10−4 |
| Kidney | 5.65 × 10−9 | 5.52 × 10−9 | 5.59 × 10−9 | 2.52 × 10−4 | 2.46 × 10−4 | 2.50 × 10−4 |
| Pancreas | 7.71 × 10−9 | 7.55 × 10−9 | 7.75 × 10−9 | 3.44 × 10−4 | 3.37 × 10−4 | 3.46 × 10−4 |
| Thyroid | 2.56 × 10−9 | 2.48 × 10−9 | 2.51 × 10−9 | 1.14 × 10−4 | 1.10 × 10−4 | 1.12 × 10−4 |
| Spleen | 5.59 × 10−9 | 5.45 × 10−9 | 5.62 × 10−9 | 2.49 × 10−4 | 2.43 × 10−4 | 2.48 × 10−4 |
| Bladder | 6.14 × 10−9 | 5.99 × 10−9 | 6.10 × 10−9 | 3.39 × 10−4 | 3.31 × 10−4 | 3.37 × 10−4 |
| Organ | SAF | GATE vs. GAMOS (%) | GATE vs. MCNP6 (%) | S-Value | Diff % | |||
|---|---|---|---|---|---|---|---|---|
| GATE | GAMOS | MCNP6 | GATE | MCNP6 | ||||
| Pancreas | 0.0177 | 0.0173 | 0.0178 | 2.3% | 0.6% | 3.97 × 10−7 | 3.99 × 10−7 | 0.5% |
| Gallbladder | 0.0101 | 0.0097 | 0.0102 | 4.0% | 1.0% | 2.26 × 10−7 | 2.29 × 10−7 | 1.3% |
| Kidney | 0.00596 | 0.00576 | 0.00591 | 3.4% | 0.8% | 1.34 × 10−7 | 1.33 × 10−7 | 0.7% |
| Liver | 0.0155 | 0.0151 | 0.0153 | 2.6% | 1.3% | 3.47 × 10−7 | 3.44 × 10−7 | 0.9% |
| Brain | 3.56 × 10−4 | 3.49 × 10−4 | 3.44 × 10−4 | 2.0% | 3.4% | 7.98 × 10−9 | 7.69 × 10−9 | 3.6% |
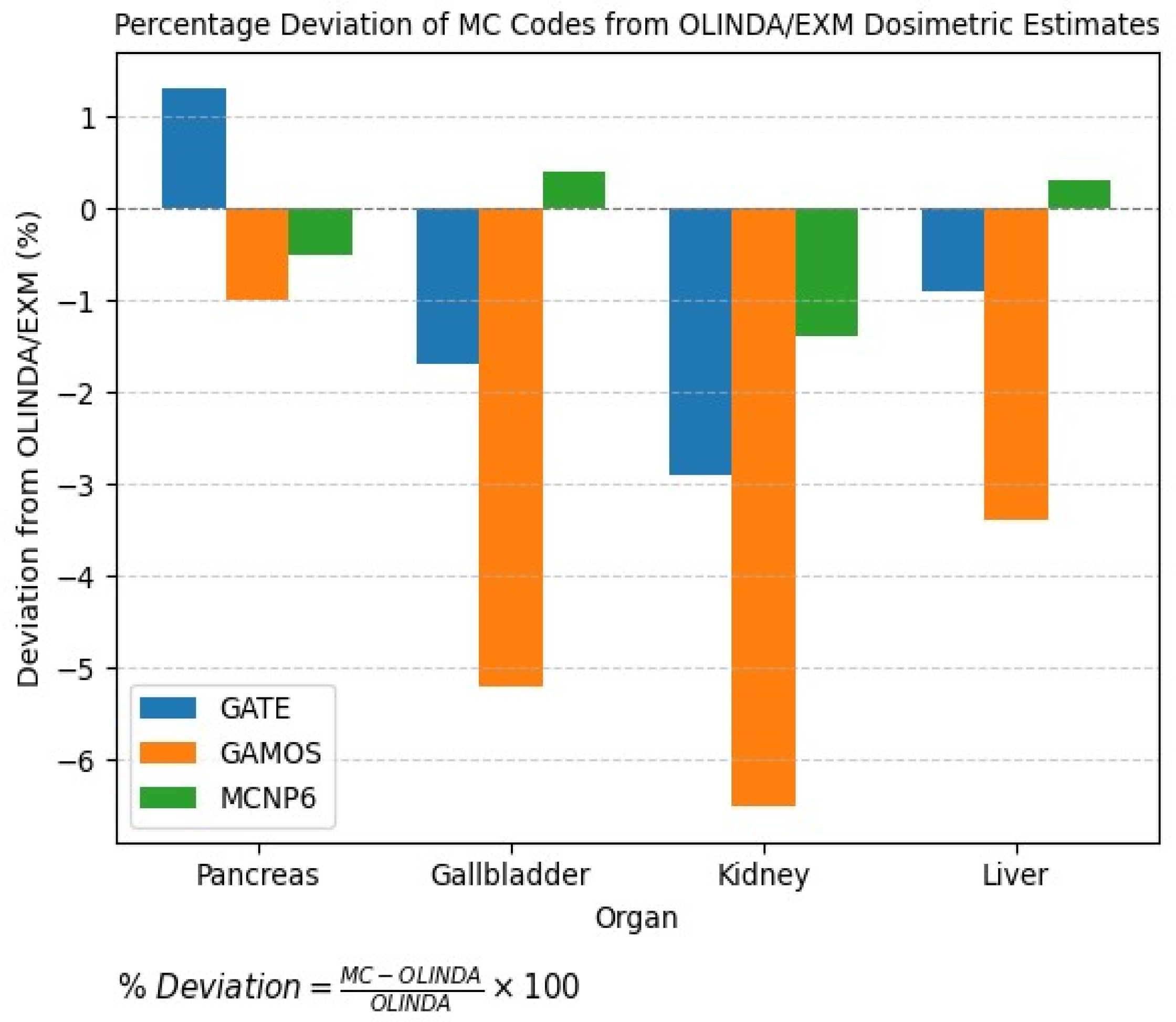
| Organ | OLINDA/EXM (mGy/MBq·h) | GATE (mGy/MBq·h) | Dev. (%) vs. OLINDA | GAMOS (mGy/MBq·h) | Dev. (%) vs. OLINDA | MCNP6 (mGy/MBq·h) | Dev. (%) vs. OLINDA |
|---|---|---|---|---|---|---|---|
| Pancreas | 3.92 × 10−7 | 3.97 × 10−7 | +1.3% | 3.88 × 10−7 | −1.0% | 3.90 × 10−7 | −0.5% |
| Gallbladder | 2.30 × 10−7 | 2.26 × 10−7 | −1.7% | 2.18 × 10−7 | −5.2% | 2.31 × 10−7 | +0.4% |
| Kidney | 1.38 × 10−7 | 1.34 × 10−7 | −2.9% | 1.29 × 10−7 | −6.5% | 1.36 × 10−7 | −1.4% |
| Liver | 3.50 × 10−7 | 3.47 × 10−7 | −0.9% | 3.38 × 10−7 | −3.4% | 3.51 × 10−7 | +0.3% |
| Comparison | ICC | 95% CI | p-Value | Mean Bias | RMSD | CV (%) |
|---|---|---|---|---|---|---|
| GATE vs. GAMOS | 0.998 | (0.994–0.999) | >0.001 | −2.1% | 2.8% | 1.9 |
| GATE vs. MCNP6 | 0.999 | (0.997–1.000) | >0.001 | +0.3% | 1.5% | 1.2 |
| GAMOS vs. MCNP6 | 0.997 | (0.992–0.999) | >0.001 | +2.4% | 3.1% | 2.1 |
| Organ | Activity (%) | Voxel Count | Activity/Voxel (µCi) |
|---|---|---|---|
| Heart (source) | 9.10 | 9345 | 3.60 |
| Lungs | 4.40 | 62,374 | 0.30 |
| Liver | 11.40 | 29,277 | 1.40 |
| Gallbladder | 68.60 | 329 | 771.70 |
| Spleen | 6.40 | 5568 | 4.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshehri, A.H.D. Advancing Internal Dosimetry in Personalized Nuclear Medicine: Toward Optimized Radiopharmaceutical Use in Clinical Practice. Pharmaceuticals 2025, 18, 1741. https://doi.org/10.3390/ph18111741
Alshehri AHD. Advancing Internal Dosimetry in Personalized Nuclear Medicine: Toward Optimized Radiopharmaceutical Use in Clinical Practice. Pharmaceuticals. 2025; 18(11):1741. https://doi.org/10.3390/ph18111741
Chicago/Turabian StyleAlshehri, Ali H. D. 2025. "Advancing Internal Dosimetry in Personalized Nuclear Medicine: Toward Optimized Radiopharmaceutical Use in Clinical Practice" Pharmaceuticals 18, no. 11: 1741. https://doi.org/10.3390/ph18111741
APA StyleAlshehri, A. H. D. (2025). Advancing Internal Dosimetry in Personalized Nuclear Medicine: Toward Optimized Radiopharmaceutical Use in Clinical Practice. Pharmaceuticals, 18(11), 1741. https://doi.org/10.3390/ph18111741






