Protein Representation in Metric Spaces for Protein Druggability Prediction: A Case Study on Aspirin
Abstract
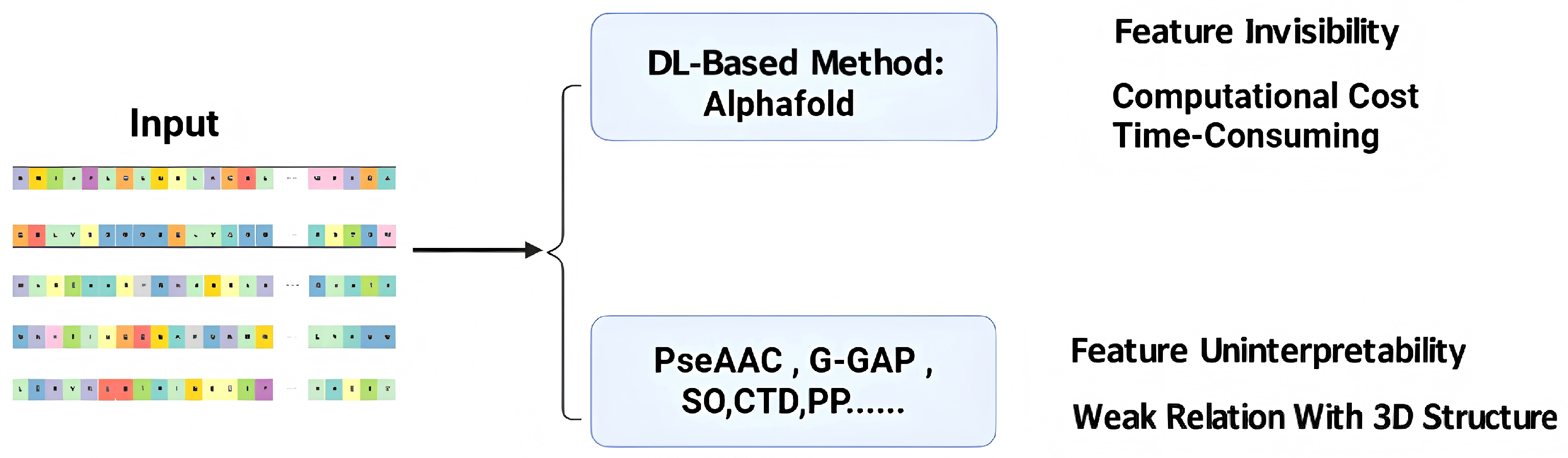
1. Introduction
2. Results
2.1. Case Study: Aspirin
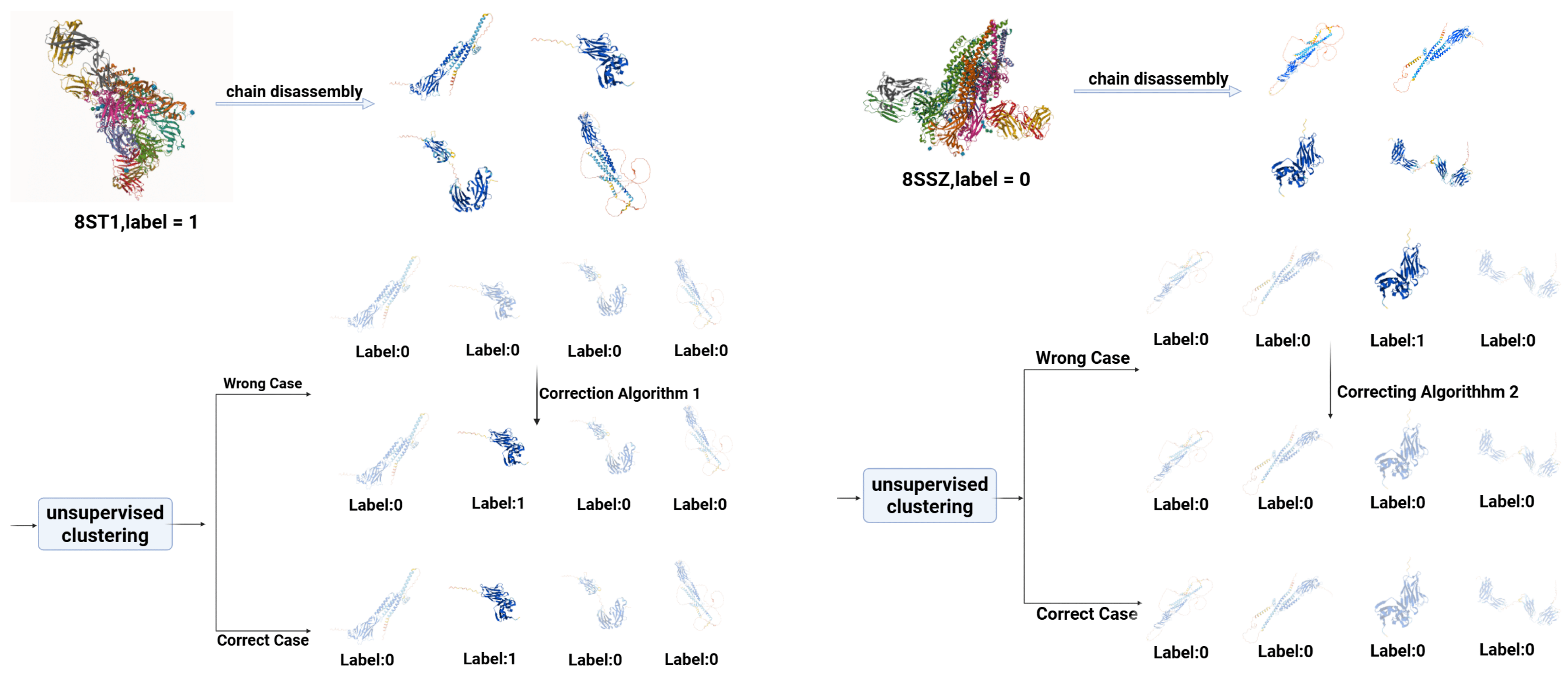
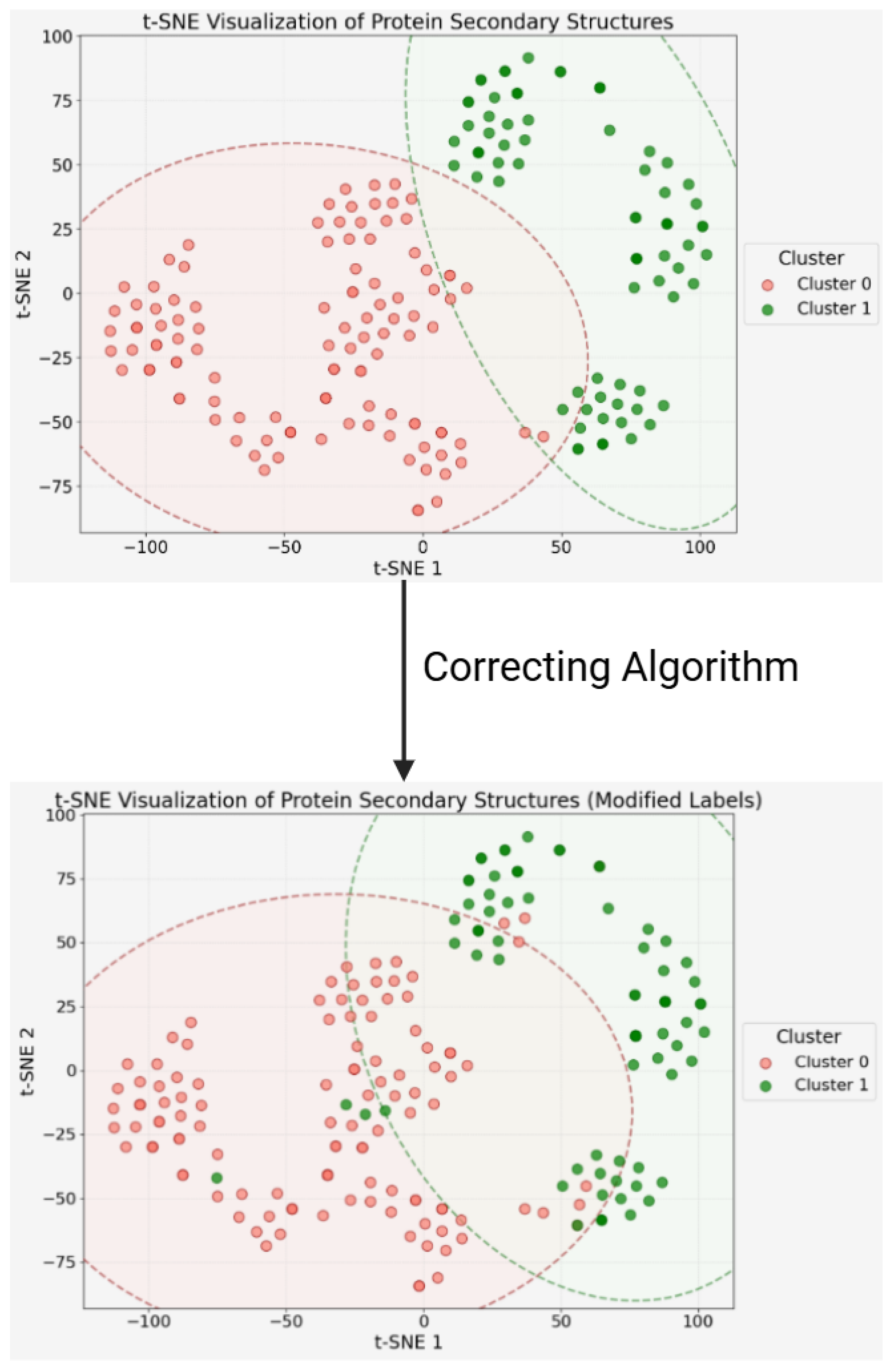
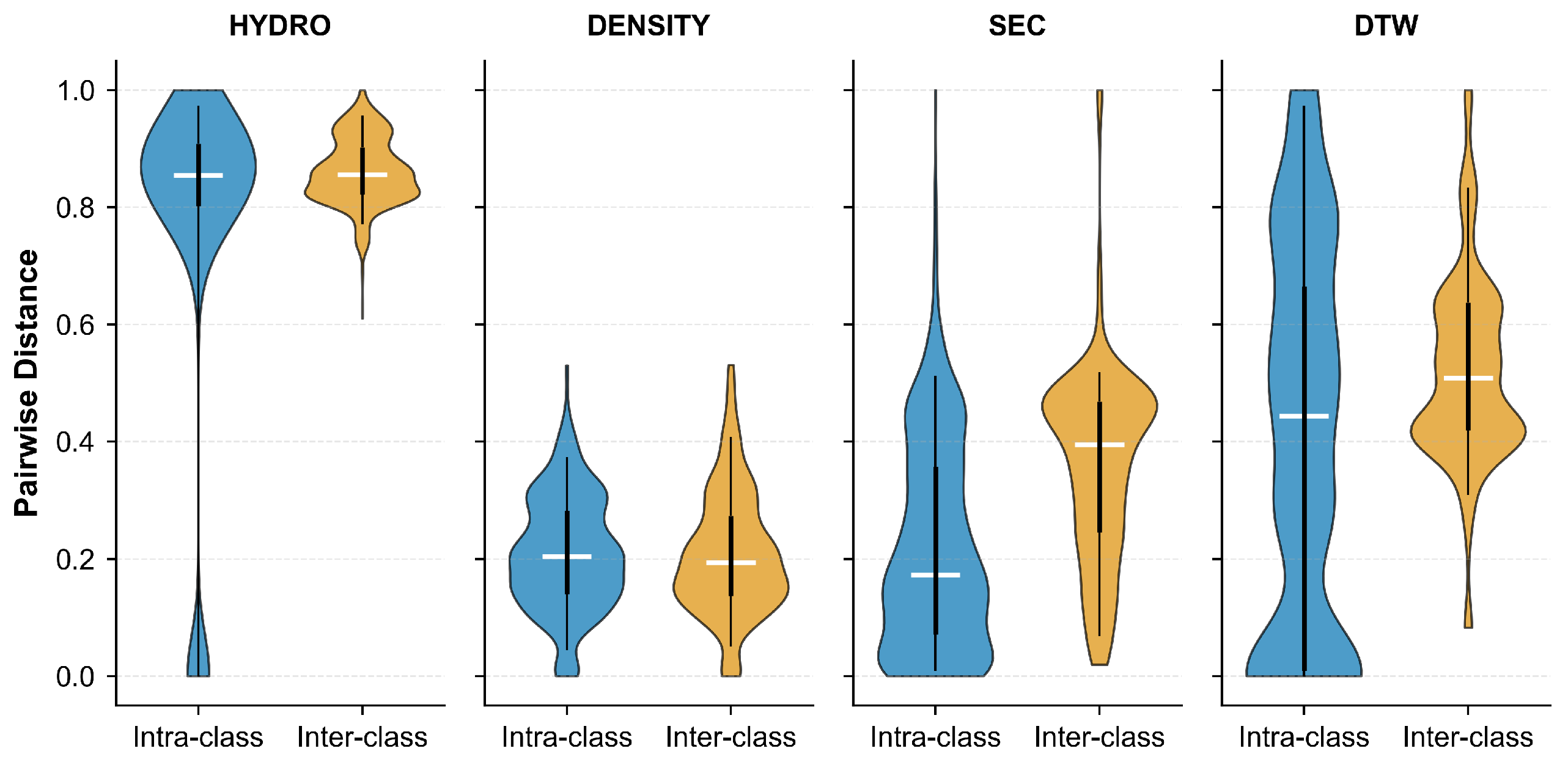
2.1.1. Data Disassembly via Unsupervised Clustering
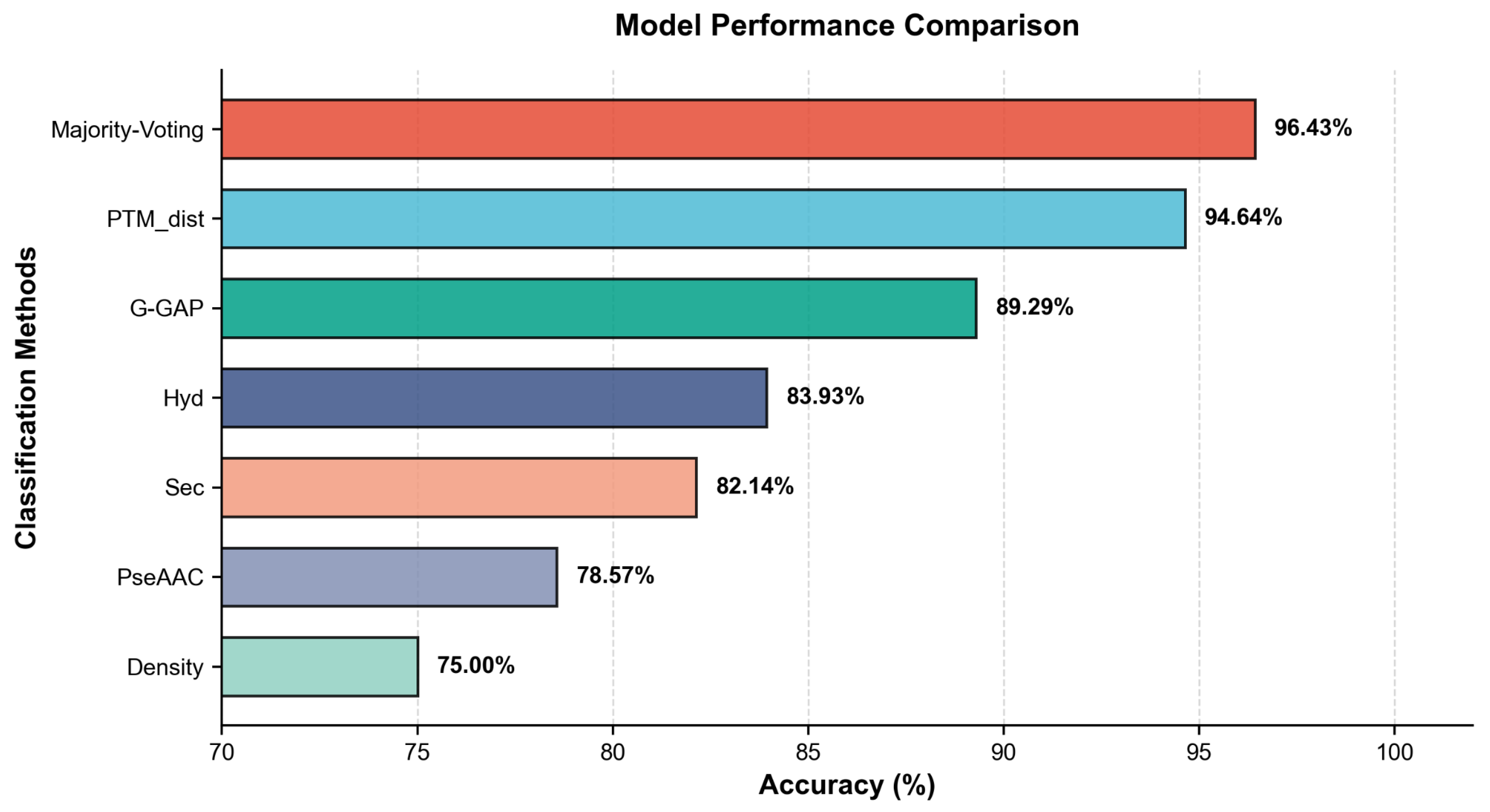
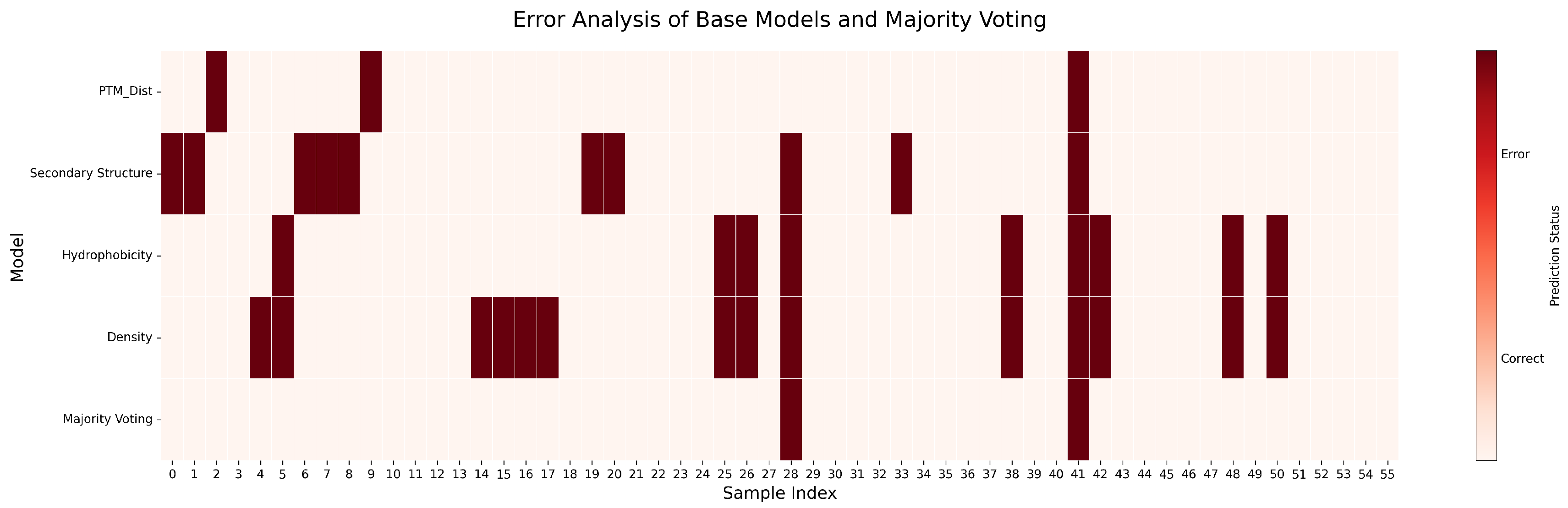
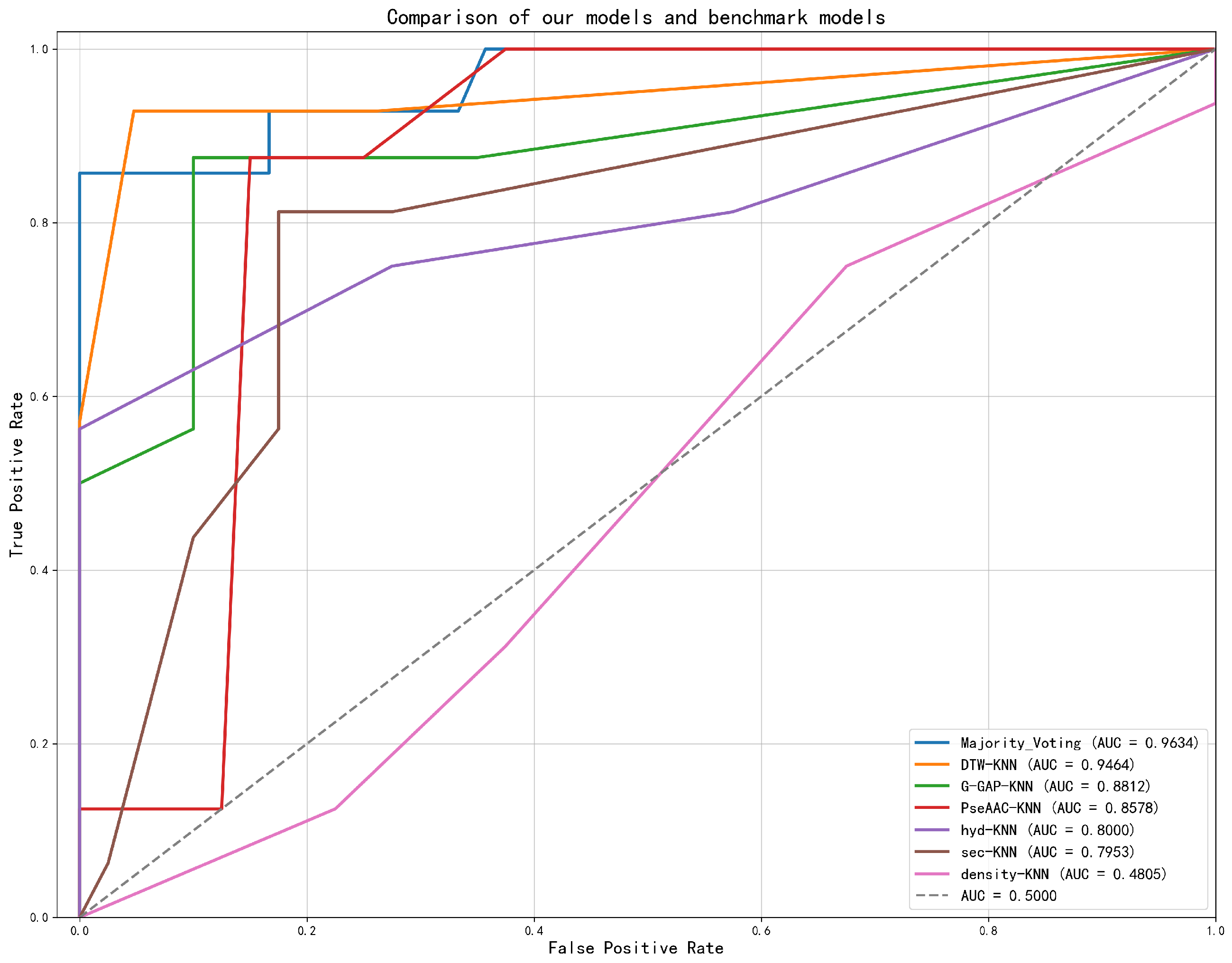
2.1.2. Performance on Single-Chain Protein Dataset
2.1.3. Performance on Whole Protein Dataset
3. Discussion
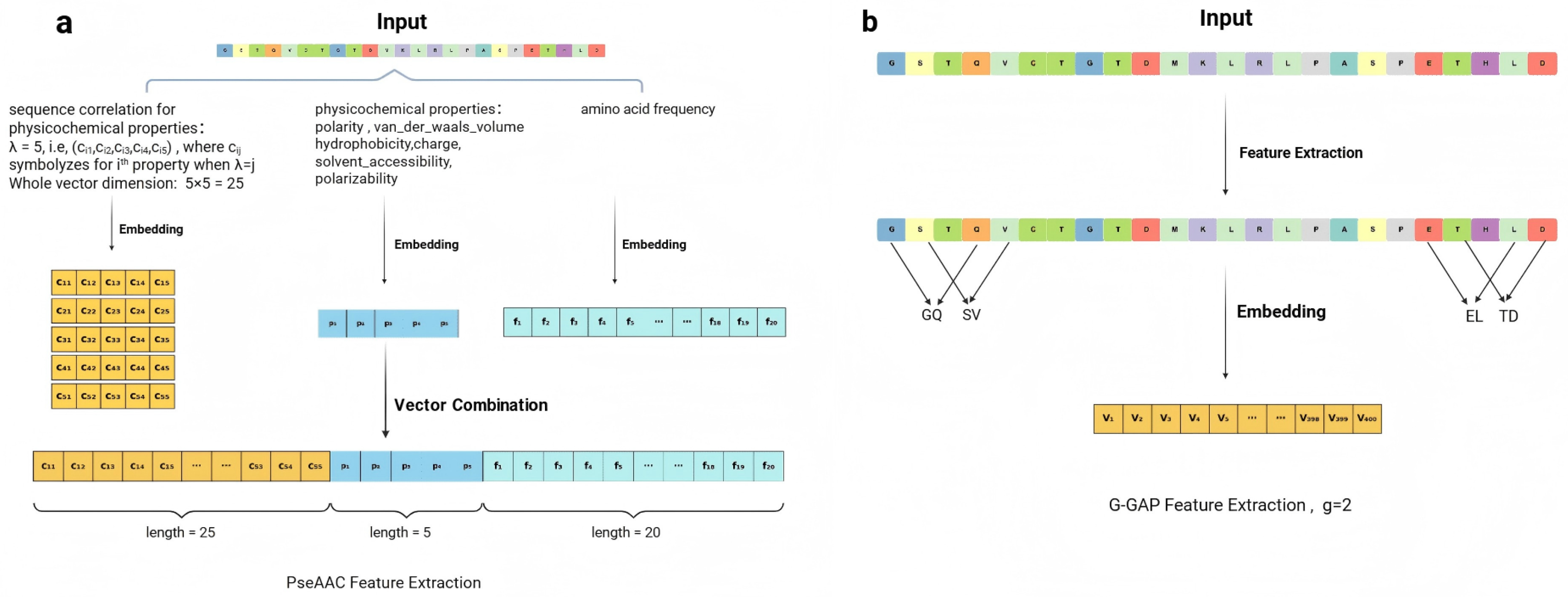
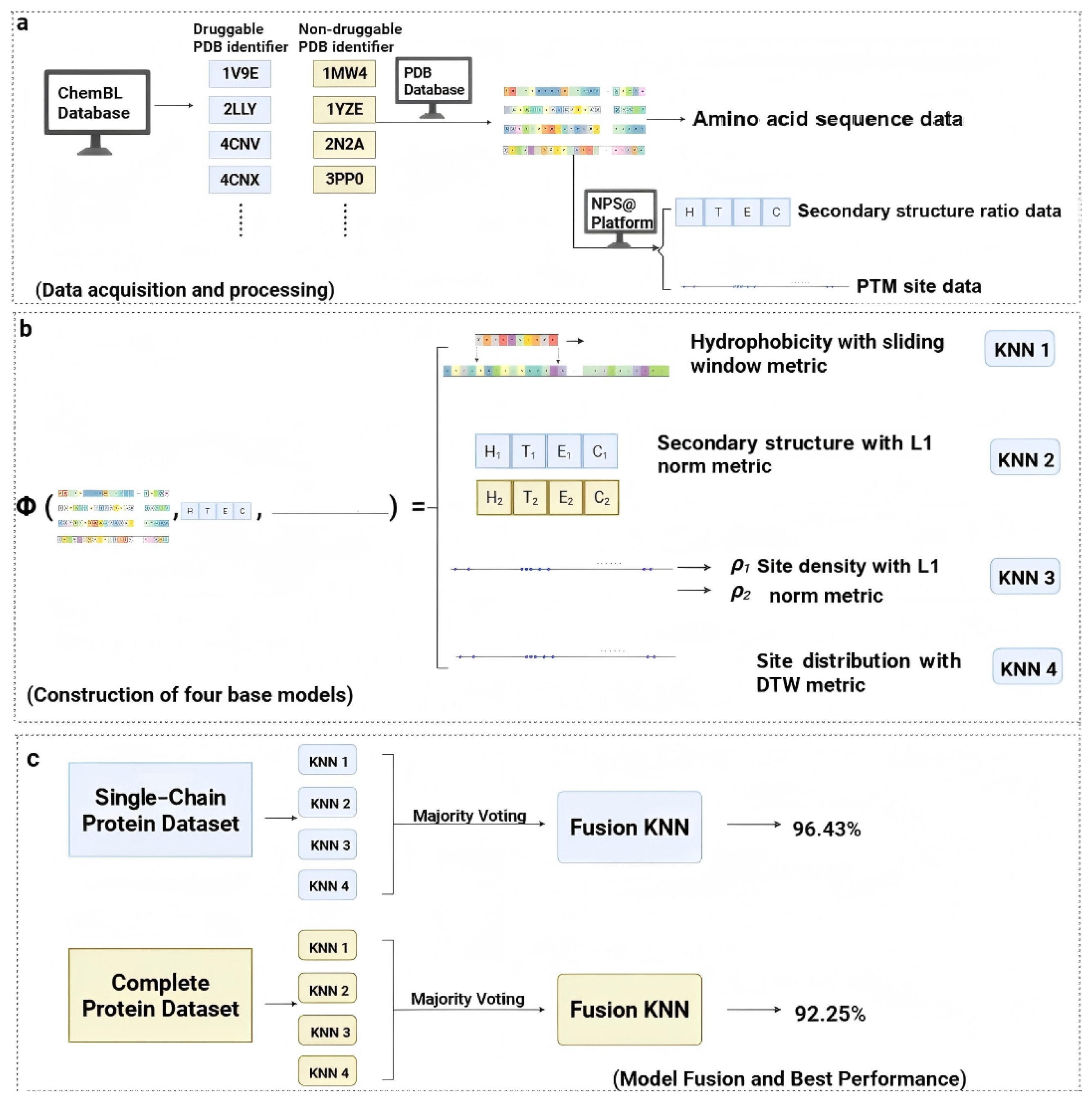
4. Methods and Materials
4.1. Dataset
Aspirin Data Acquisition and Processing
4.2. Constructing Biologically Interpretable Features via Metric Embedding
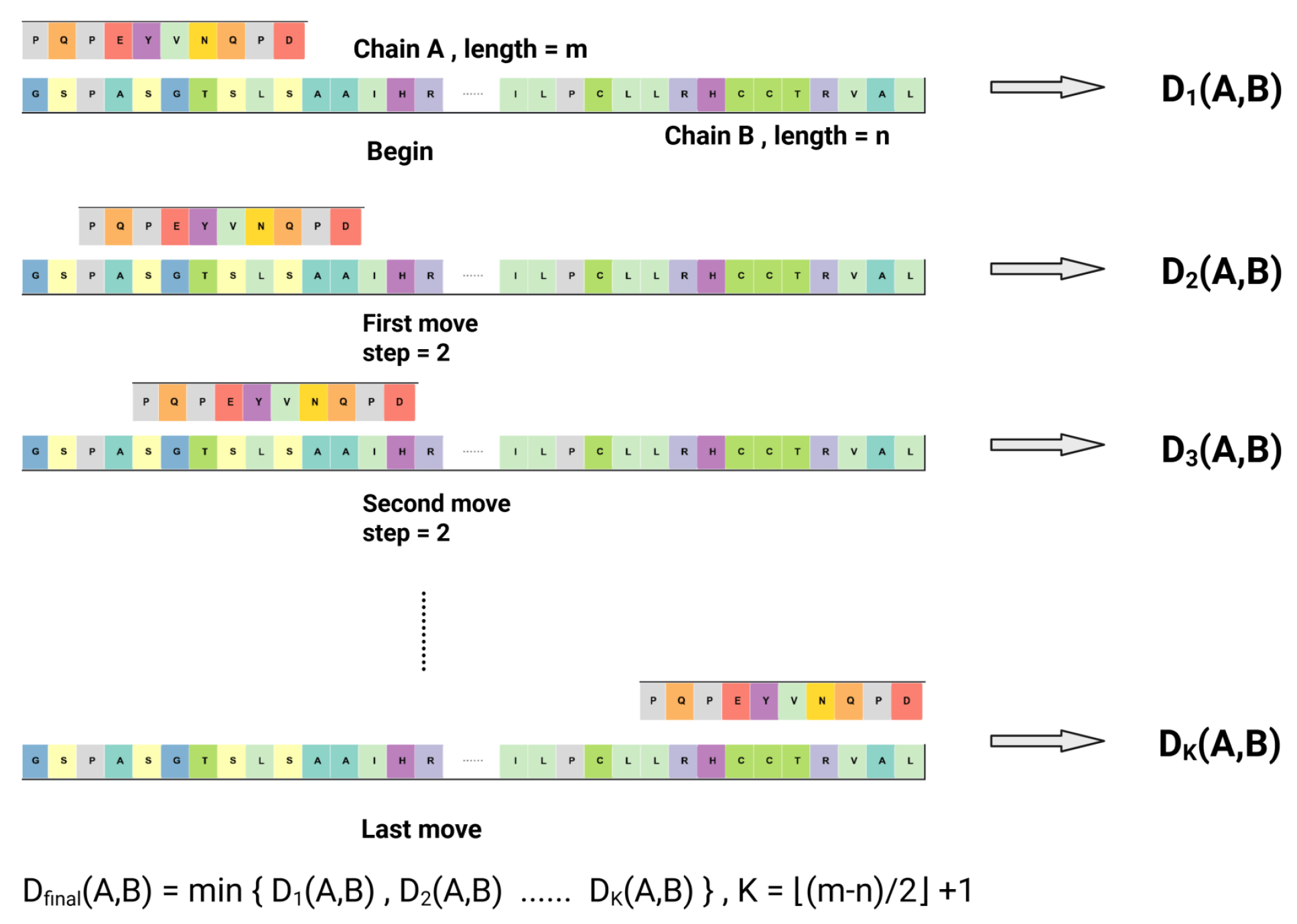
4.2.1. Metric Space : Hydrophobicity Feature via Sliding Window Metric
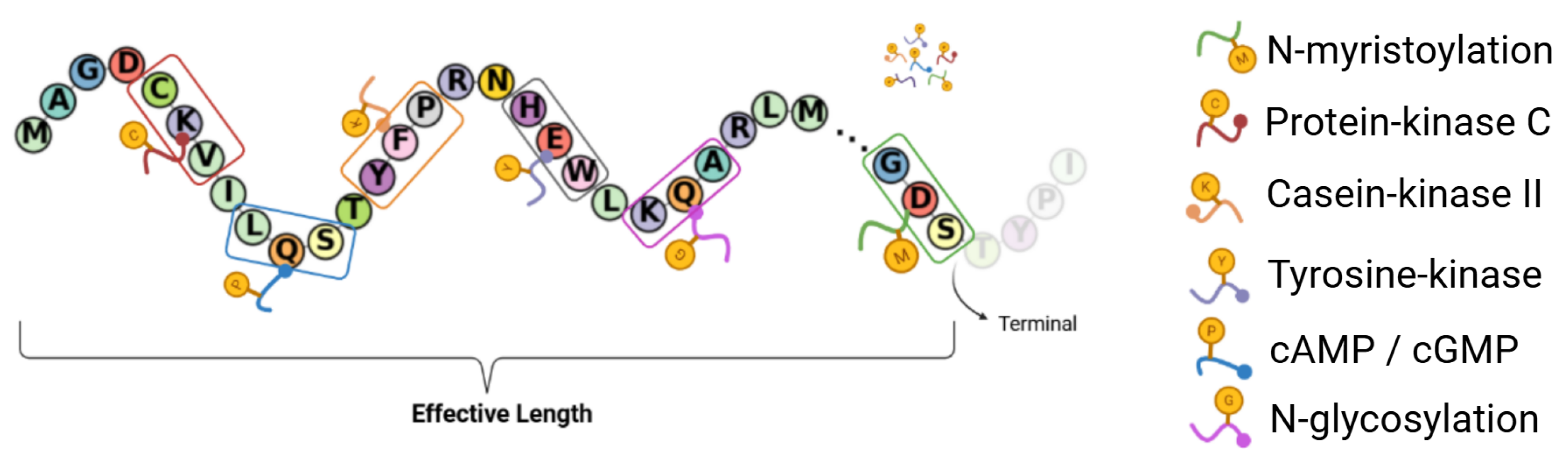
4.2.2. Metric Space : PTM Density and Norm Metric
4.2.3. Metric Space : PTM Distribution via Dynamic Time Warping (DTW) Metric
4.2.4. Metric Space : Secondary Structure Proportion via Norm Metric
4.2.5. Fusion of Metric Space by KNN Model Ensemble
Majority Voting
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PTM | Post-Translational Modification |
| DL | Deep Learning |
| ML | Machine Learning |
| CNN | Convolutional Neural Network |
| AAC | Amino Acid Composition |
| PseAAC | Pseudo-Amino-Acid Composition |
| NLP | Natural Language Processing |
| CTD | Composition–Transition–Distribution |
| HMM | Hidden Markov Model |
| SO | Sequence Order |
| PP | Physicochemical Property |
| KNN | K-Nearest Neighbors |
| KD | Kyte–Doolittle |
| USP | Ubiquitin-Specific Protease |
| DTW | Dynamic Time Warping |
| IDRs | Intrinsically Disordered Regions |
| RF | Random Forest |
| SVM | Support Vector Machine |
| ROC | Receiver Operating Characteristic Curve |
| AUC | Area Under the Curve |
References
- Owens, J. Determining druggability. Nat. Rev. Drug Discov. 2007, 6, 187. [Google Scholar] [CrossRef]
- Padroni, G.; Bikaki, M.; Novakovic, M.; Wolter, A.C.; Rüdisser, S.H.; Gossert, A.D.; Leitner, A.; Allain, F.H. A hybrid structure determination approach to investigate the druggability of the nucleocapsid protein of SARS-CoV-2. Nucleic Acids Res. 2023, 51, 4555–4571. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Yu, Y. Pharmacologically targeting transient receptor potential channels for seizures and epilepsy: Emerging preclinical evidence of druggability. Pharmacol. Ther. 2023, 244, 108384. [Google Scholar] [CrossRef] [PubMed]
- Sutkeviciute, I.; Lee, J.Y.; White, A.D.; Maria, C.S.; Peña, K.A.; Savransky, S.; Doruker, P.; Li, H.; Lei, S.; Kaynak, B.; et al. Precise druggability of the PTH type 1 receptor. Nat. Chem. Biol. 2022, 18, 272–280. [Google Scholar] [CrossRef]
- Hajduk, P.J.; Huth, J.R.; Tse, C. Predicting protein druggability. Drug Discov. Today 2005, 10, 1675–1682. [Google Scholar] [CrossRef]
- Abramson, J.; Adler, J.; Dunger, J.; Evans, R.; Green, T.; Pritzel, A.; Ronneberger, O.; Willmore, L.; Ballard, A.J.; Bambrick, J.; et al. Accurate structure prediction of biomolecular interactions with AlphaFold 3. Nature 2024, 630, 493–500. [Google Scholar] [CrossRef]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Halder, A.; Samantaray, S.; Barbade, S.; Gupta, A.; Srivastava, S. DrugProtAI: A machine learning–driven approach for predicting protein druggability through feature engineering and robust partition-based ensemble methods. Brief. Bioinform. 2025, 26, bbaf330. [Google Scholar] [CrossRef] [PubMed]
- Yu, L.; Xue, L.; Liu, F.; Li, Y.; Jing, R.; Luo, J. The applications of deep learning algorithms on in silico druggable proteins identification. J. Adv. Res. 2022, 41, 219–231. [Google Scholar] [CrossRef]
- Chou, K.C. Some remarks on protein attribute prediction and pseudo amino acid composition. J. Theor. Biol. 2011, 273, 236–247. [Google Scholar] [CrossRef]
- Bonidia, R.P.; Santos, A.P.A.; de Almeida, B.L.; Stadler, P.F.; da Rocha, U.N.; Sanches, D.S.; de Carvalho, A.C. BioAutoML: Automated feature engineering and metalearning to predict noncoding RNAs in bacteria. Brief. Bioinform. 2022, 23, bbac218. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, P.; Li, F.; Marquez-Lago, T.T.; Leier, A.; Revote, J.; Zhu, Y.; Powell, D.R.; Akutsu, T.; Webb, G.I.; et al. iLearn: An integrated platform and meta-learner for feature engineering, machine-learning analysis and modeling of DNA, RNA and protein sequence data. Brief. Bioinform. 2020, 21, 1047–1057. [Google Scholar] [CrossRef]
- Nikam, R.; Gromiha, M.M. Seq2Feature: A comprehensive web-based feature extraction tool. Bioinformatics 2019, 35, 4797–4799. [Google Scholar] [CrossRef]
- Cao, D.S.; Xu, Q.S.; Liang, Y.Z. propy: A tool to generate various modes of Chou’s PseAAC. Bioinformatics 2013, 29, 960–962. [Google Scholar] [CrossRef] [PubMed]
- Xiao, N.; Cao, D.S.; Zhu, M.F.; Xu, Q.S. protr/ProtrWeb: R package and web server for generating various numerical representation schemes of protein sequences. Bioinformatics 2015, 31, 1857–1859. [Google Scholar] [CrossRef]
- Lin, H.; Liu, W.X.; He, J.; Liu, X.H.; Ding, H.; Chen, W. Predicting cancerlectins by the optimal g-gap dipeptides. Sci. Rep. 2015, 5, 16964. [Google Scholar] [CrossRef]
- Chen, Z.; Zhao, P.; Li, F.; Leier, A.; Marquez-Lago, T.T.; Wang, Y.; Webb, G.I.; Smith, A.I.; Daly, R.J.; Chou, K.C.; et al. iFeature: A python package and web server for features extraction and selection from protein and peptide sequences. Bioinformatics 2018, 34, 2499–2502. [Google Scholar] [CrossRef]
- Ofer, D.; Linial, M. ProFET: Feature engineering captures high-level protein functions. Bioinformatics 2015, 31, 3429–3436. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Lee, J.Y.; Liao, L. A new algorithm to train hidden Markov models for biological sequences with partial labels. BMC Bioinform. 2021, 22, 162. [Google Scholar] [CrossRef]
- Faltejsková, K.; Jakubec, D.; Vondrášek, J. Hydrophobic amino acids as universal elements of protein-induced DNA structure deformation. Int. J. Mol. Sci. 2020, 21, 3986. [Google Scholar] [CrossRef]
- Camilloni, C.; Bonetti, D.; Morrone, A.; Giri, R.; Dobson, C.M.; Brunori, M.; Gianni, S.; Vendruscolo, M. Towards a structural biology of the hydrophobic effect in protein folding. Sci. Rep. 2016, 6, 28285. [Google Scholar] [CrossRef]
- Waibl, F.; Fernández-Quintero, M.L.; Wedl, F.S.; Kettenberger, H.; Georges, G.; Liedl, K.R. Comparison of hydrophobicity scales for predicting biophysical properties of antibodies. Front. Mol. Biosci. 2022, 9, 960194. [Google Scholar] [CrossRef]
- Dannenhoffer-Lafage, T.; Best, R.B. A data-driven hydrophobicity scale for predicting liquid–liquid phase separation of proteins. J. Phys. Chem. B 2021, 125, 4046–4056. [Google Scholar] [CrossRef]
- Olsen, J.V.; Blagoev, B.; Gnad, F.; Macek, B.; Kumar, C.; Mortensen, P.; Mann, M. Global, in vivo, and site-specific phosphorylation dynamics in signaling networks. Cell 2006, 127, 635–648. [Google Scholar] [CrossRef]
- Minguez, P.; Parca, L.; Diella, F.; Mende, D.R.; Kumar, R.; Helmer-Citterich, M.; Gavin, A.C.; Van Noort, V.; Bork, P. Deciphering a global network of functionally associated post-translational modifications. Mol. Syst. Biol. 2012, 8, 599. [Google Scholar] [CrossRef]
- Beltrao, P.; Albanèse, V.; Kenner, L.R.; Swaney, D.L.; Burlingame, A.; Villén, J.; Lim, W.A.; Fraser, J.S.; Frydman, J.; Krogan, N.J. Systematic functional prioritization of protein posttranslational modifications. Cell 2012, 150, 413–425. [Google Scholar] [CrossRef]
- Sun, S.C. Deubiquitylation and regulation of the immune response. Nat. Rev. Immunol. 2008, 8, 501–511. [Google Scholar] [CrossRef]
- Iakoucheva, L.M.; Radivojac, P.; Brown, C.J.; O’Connor, T.R.; Sikes, J.G.; Obradovic, Z.; Dunker, A.K. The importance of intrinsic disorder for protein phosphorylation. Nucleic Acids Res. 2004, 32, 1037–1049. [Google Scholar] [CrossRef] [PubMed]
- Orengo, C.A.; Michie, A.D.; Jones, S.; Jones, D.T.; Swindells, M.B.; Thornton, J.M. CATH–a hierarchic classification of protein domain structures. Structure 1997, 5, 1093–1109. [Google Scholar] [CrossRef] [PubMed]
- Dill, K.A.; Bromberg, S.; Yue, K.; Chan, H.S.; Fiebig, K.M.; Yee, D.P.; Thomas, P.D. Principles of protein folding—A perspective from simple exact models. Protein Sci. 1995, 4, 561–602. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Peng, J.; Ma, J.; Xu, J. Protein secondary structure prediction using deep convolutional neural fields. Sci. Rep. 2016, 6, 18962. [Google Scholar] [CrossRef] [PubMed]
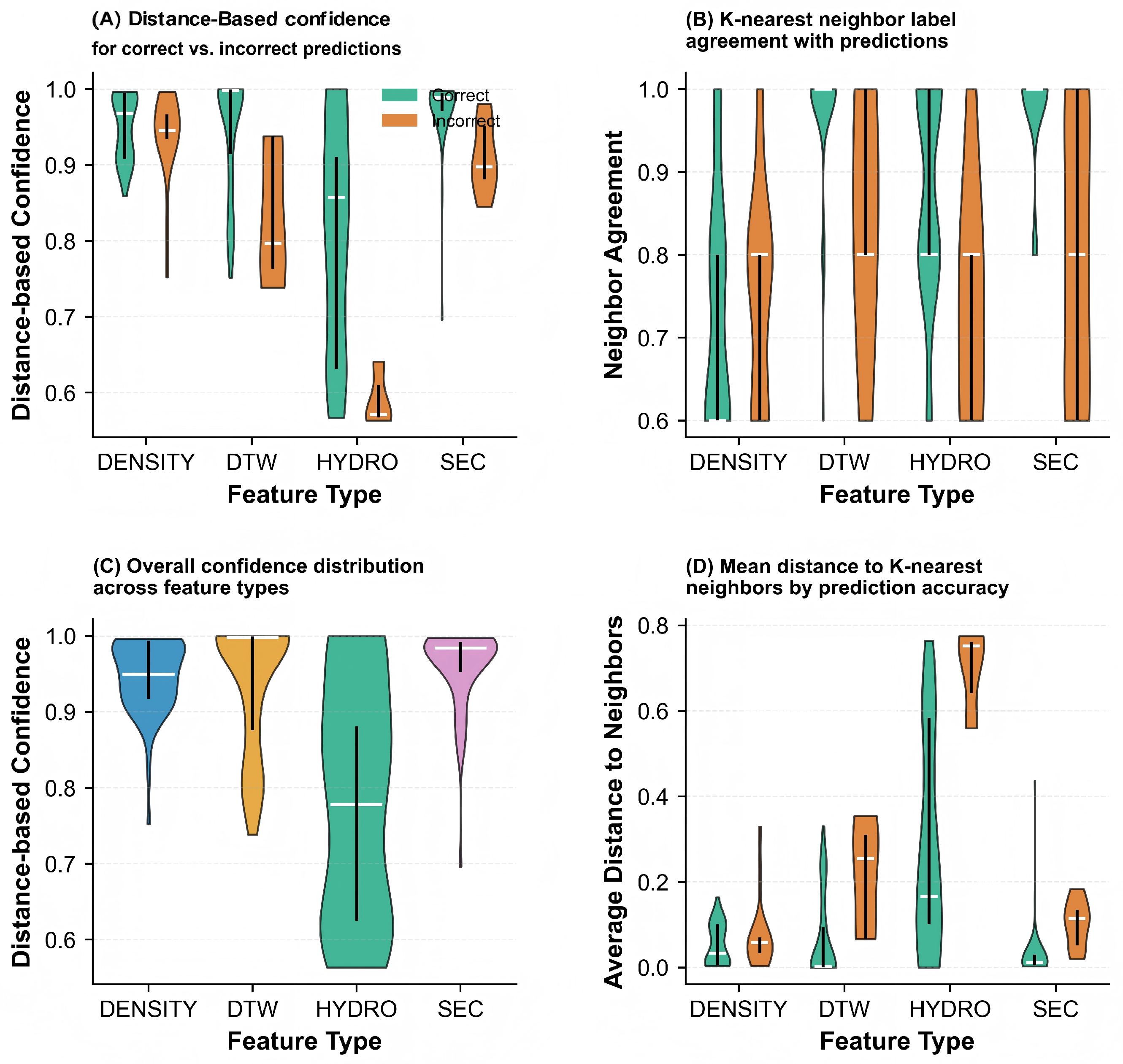
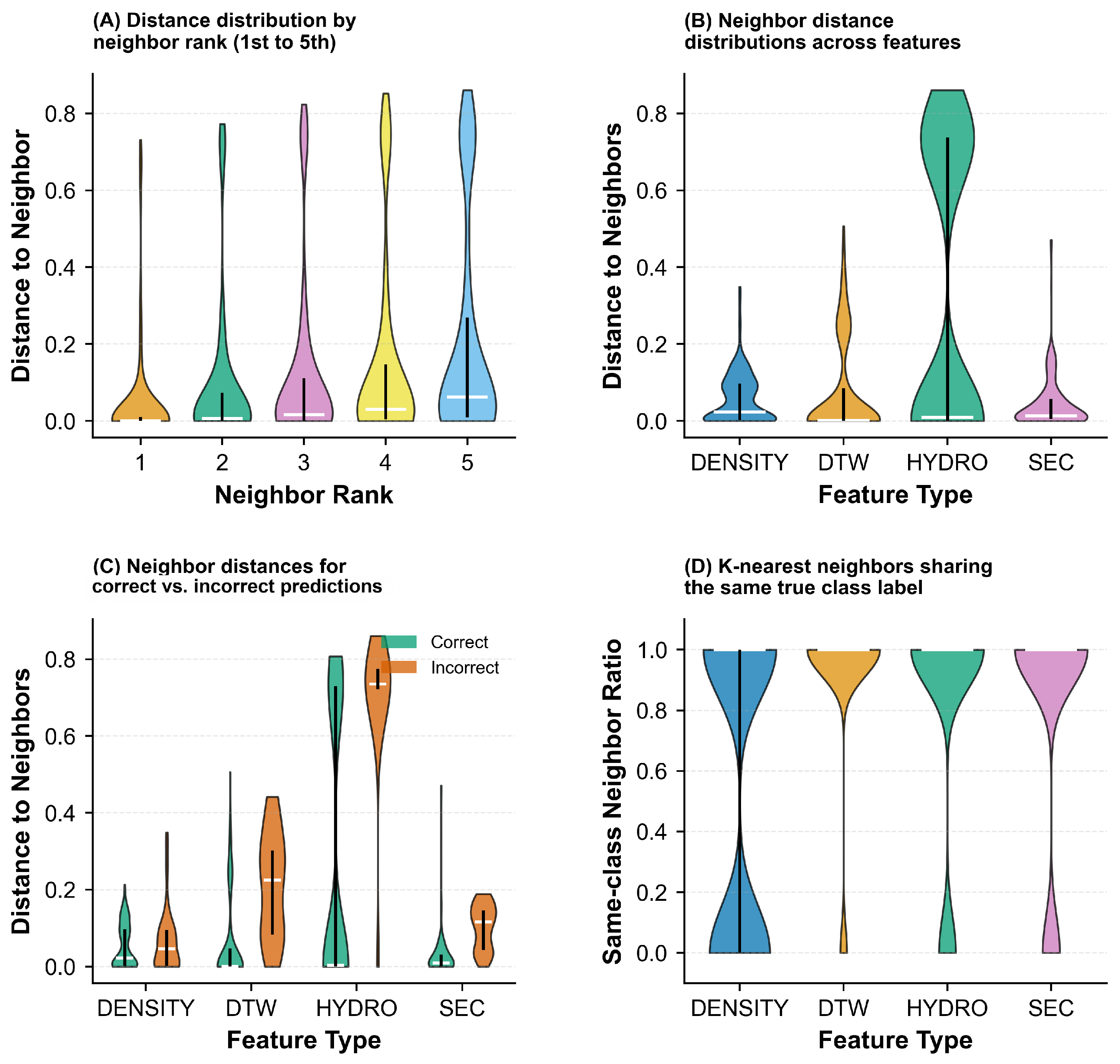
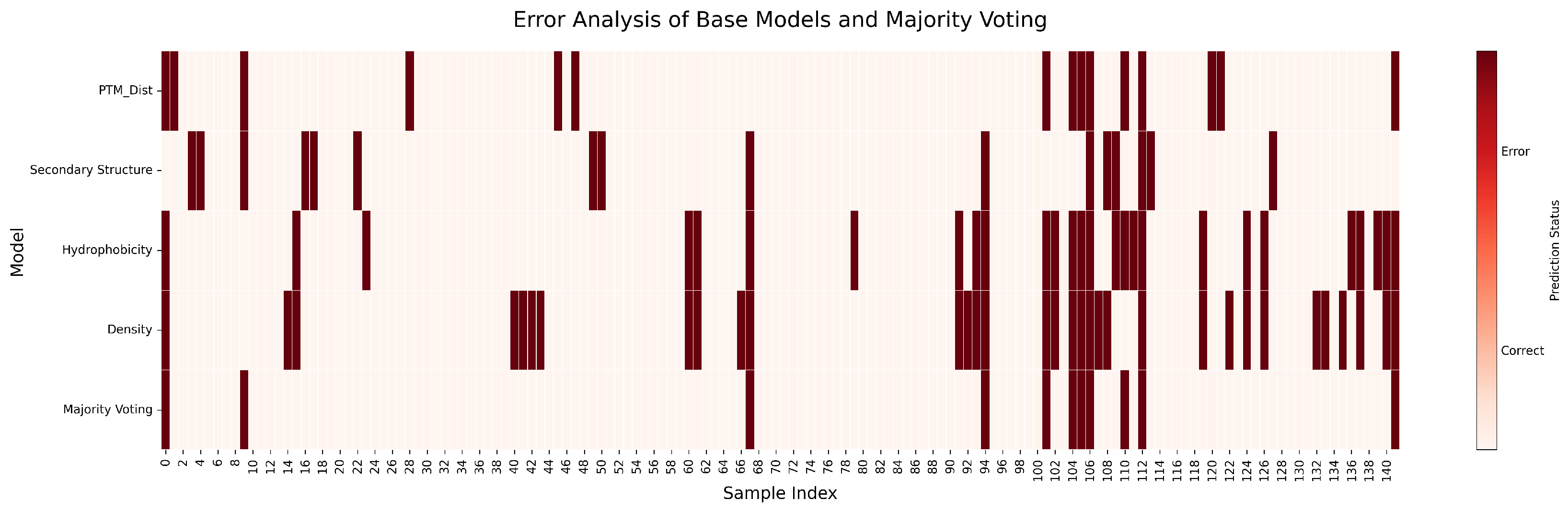
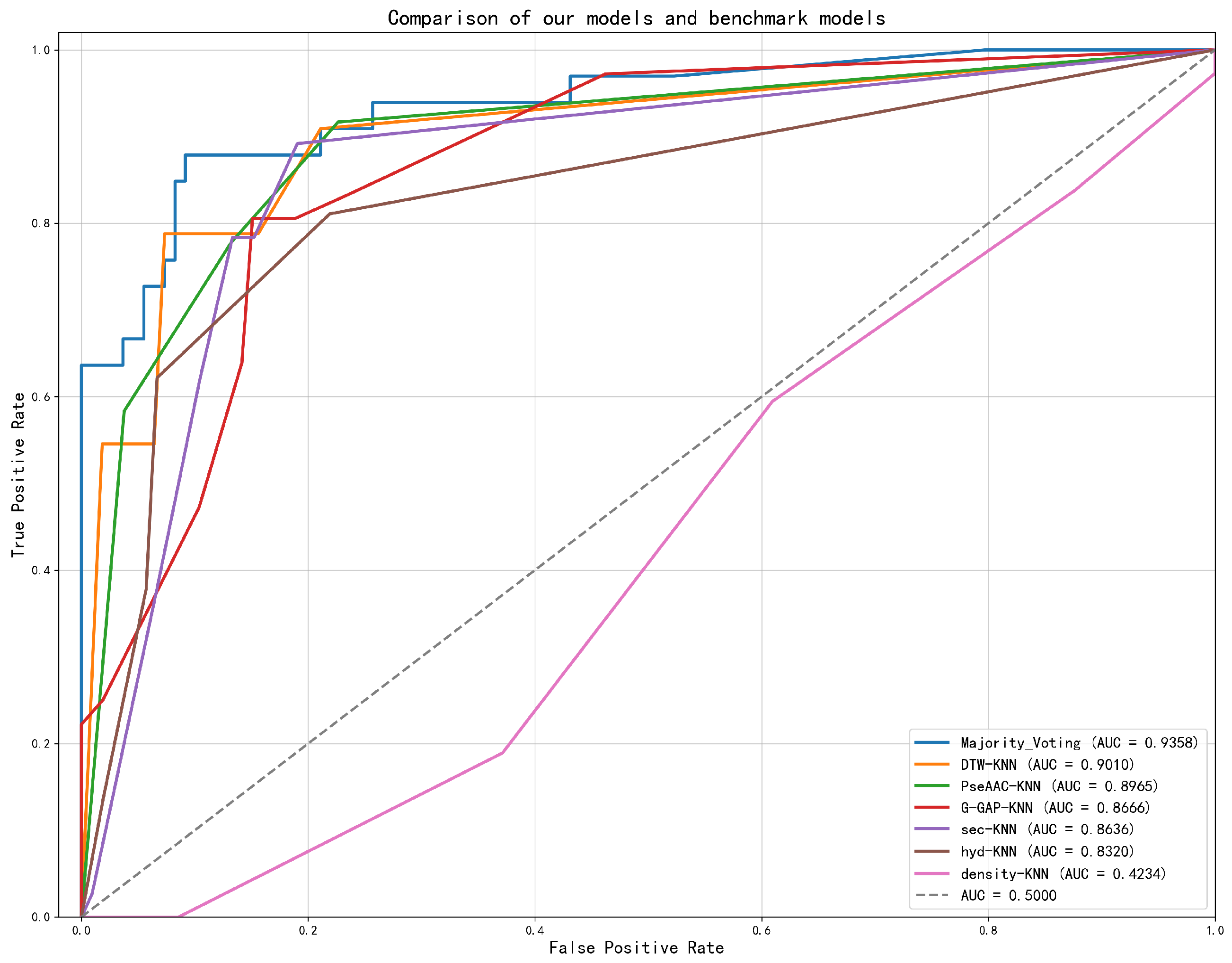
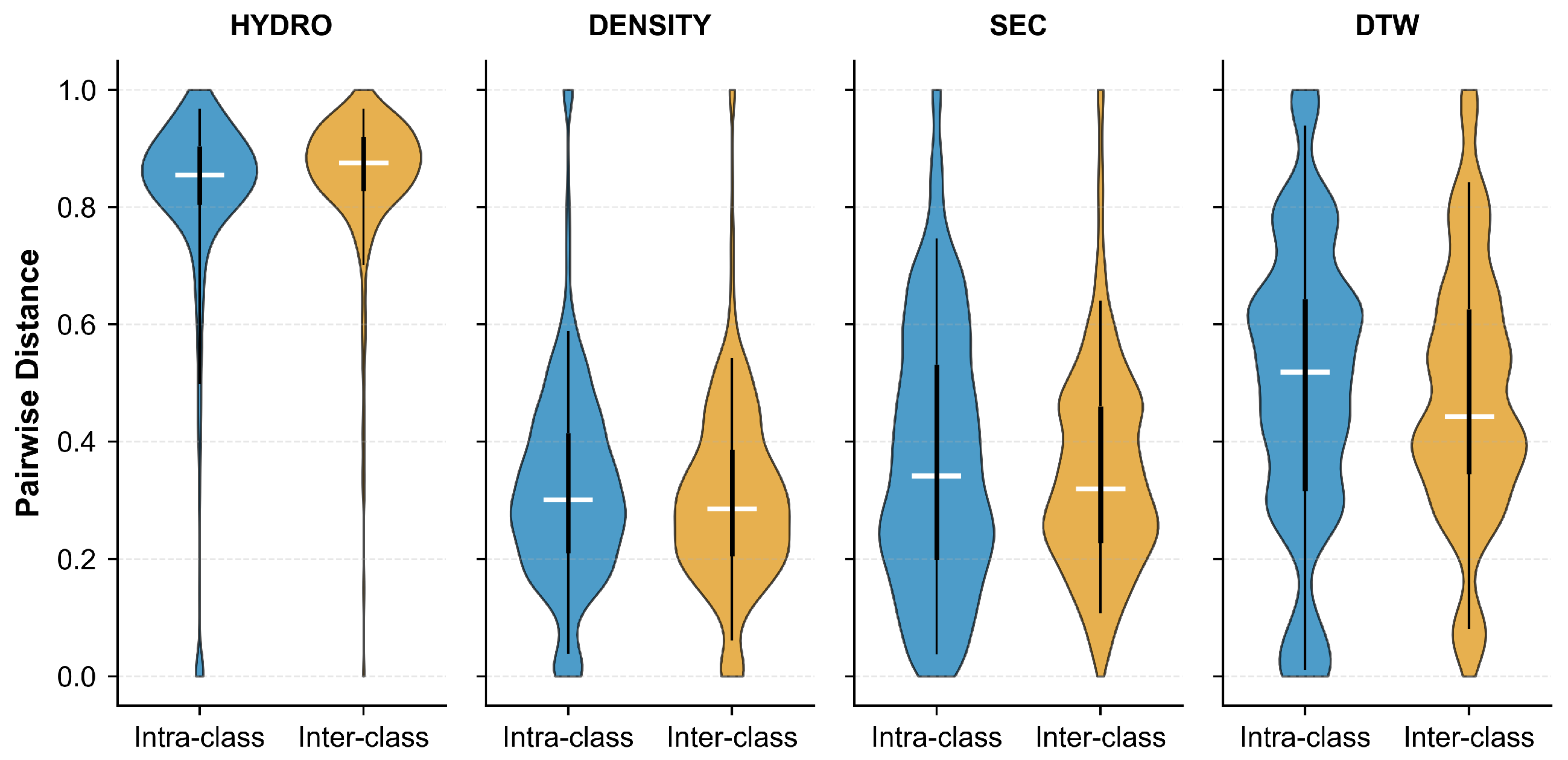
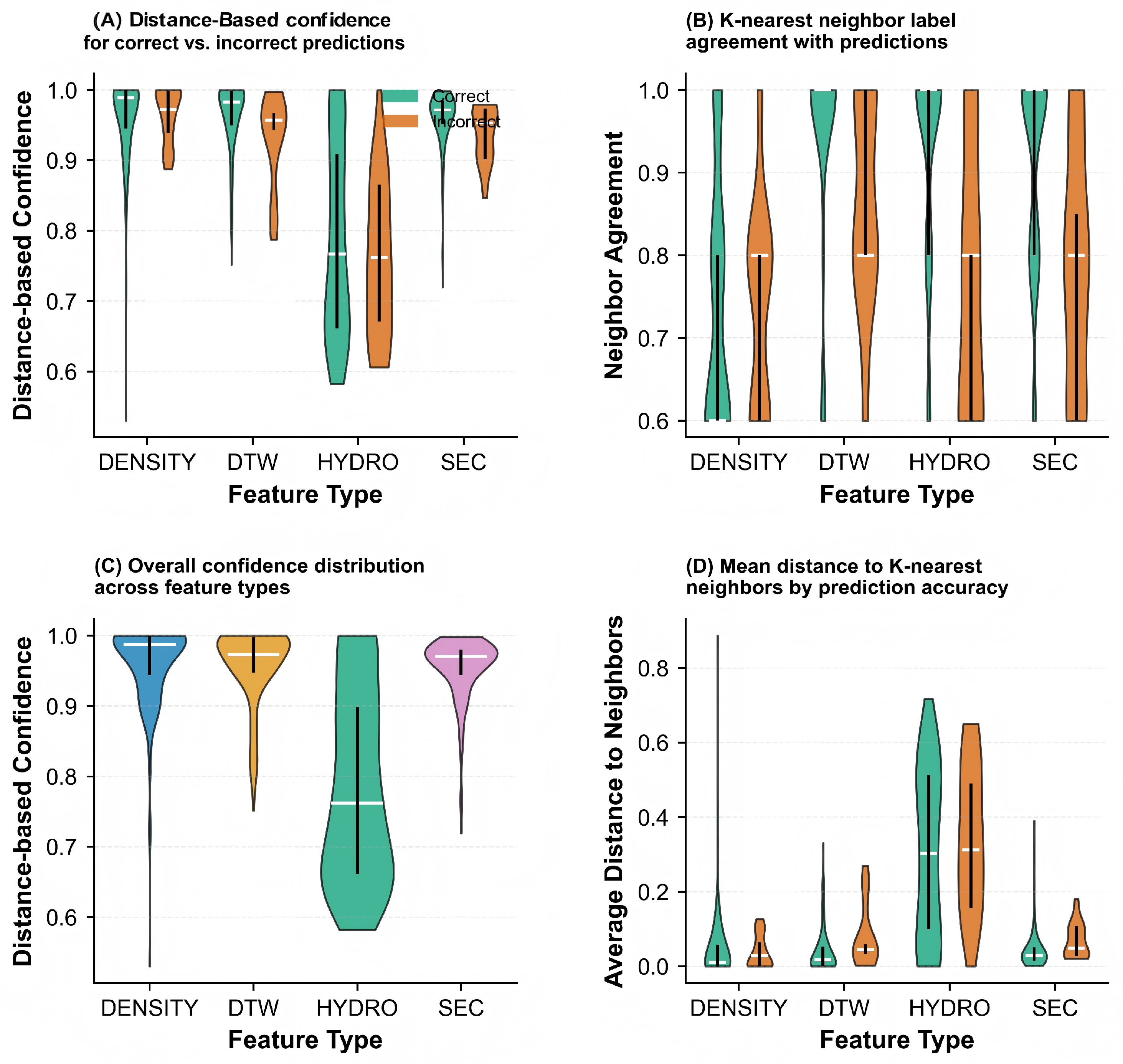
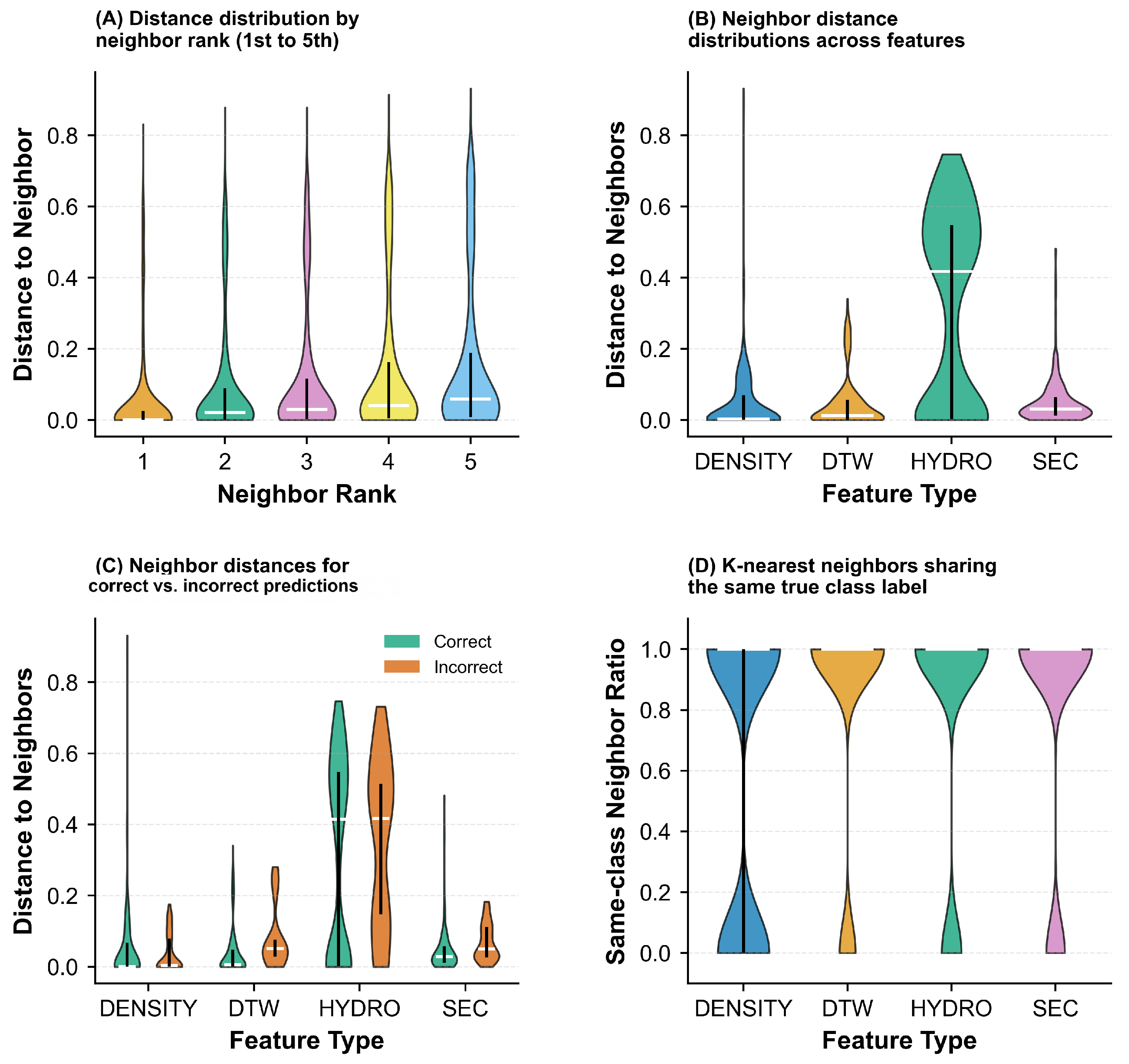

| Labeling Strategy | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) | Acc. (%) |
|---|---|---|---|---|---|
| Full Model (K-Means + Correcting Algorithm) | 92.25 | 92.27 | 85.45 | 88.23 | – |
| Ablated Model (Raw K-Means Only) | 89.44 | 89.23 | 81.92 | 84.70 |
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) |
|---|---|---|---|---|
| Designed Features + Majority Voting | 96.43 | 97.73 | 92.86 | 94.99 |
| PseAAC + KNN | 78.57 | 57.69 | 93.75 | 71.43 |
| PseAAC + Logistic Regression | 94.64 | 88.24 | 93.75 | 90.91 |
| PseAAC + SVM | 94.64 | 93.33 | 87.50 | 90.32 |
| G-GAP + KNN | 89.29 | 77.78 | 87.50 | 82.35 |
| G-GAP + SVM | 94.64 | 100.00 | 81.25 | 89.66 |
| G-GAP + Logistic Regression | 98.21 | 94.12 | 100.00 | 96.97 |
| Method | Accuracy (%) | Precision (%) | Recall (%) | F1 Score (%) |
|---|---|---|---|---|
| Designed Features + Majority Voting | 92.25 | 92.27 | 85.45 | 88.23 |
| PseAAC + KNN | 84.51 | 67.50 | 75.00 | 71.05 |
| PseAAC + Logistic Regression | 82.39 | 62.79 | 75.00 | 68.35 |
| PseAAC + SVM | 88.03 | 77.14 | 75.00 | 76.06 |
| G-GAP + KNN | 83.80 | 64.44 | 80.56 | 71.60 |
| G-GAP + SVM | 88.03 | 80.65 | 69.44 | 74.63 |
| G-GAP + Logistic Regression | 87.32 | 78.12 | 69.44 | 73.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; He, S.; Chen, Y.; Chen, X. Protein Representation in Metric Spaces for Protein Druggability Prediction: A Case Study on Aspirin. Pharmaceuticals 2025, 18, 1711. https://doi.org/10.3390/ph18111711
Xu J, He S, Chen Y, Chen X. Protein Representation in Metric Spaces for Protein Druggability Prediction: A Case Study on Aspirin. Pharmaceuticals. 2025; 18(11):1711. https://doi.org/10.3390/ph18111711
Chicago/Turabian StyleXu, Jiayang, Shuaida He, Yangzhou Chen, and Xin Chen. 2025. "Protein Representation in Metric Spaces for Protein Druggability Prediction: A Case Study on Aspirin" Pharmaceuticals 18, no. 11: 1711. https://doi.org/10.3390/ph18111711
APA StyleXu, J., He, S., Chen, Y., & Chen, X. (2025). Protein Representation in Metric Spaces for Protein Druggability Prediction: A Case Study on Aspirin. Pharmaceuticals, 18(11), 1711. https://doi.org/10.3390/ph18111711






