Model-Informed Drug Development: In Silico Assessment of Drug Bioperformance following Oral and Percutaneous Administration
Abstract
1. Introduction
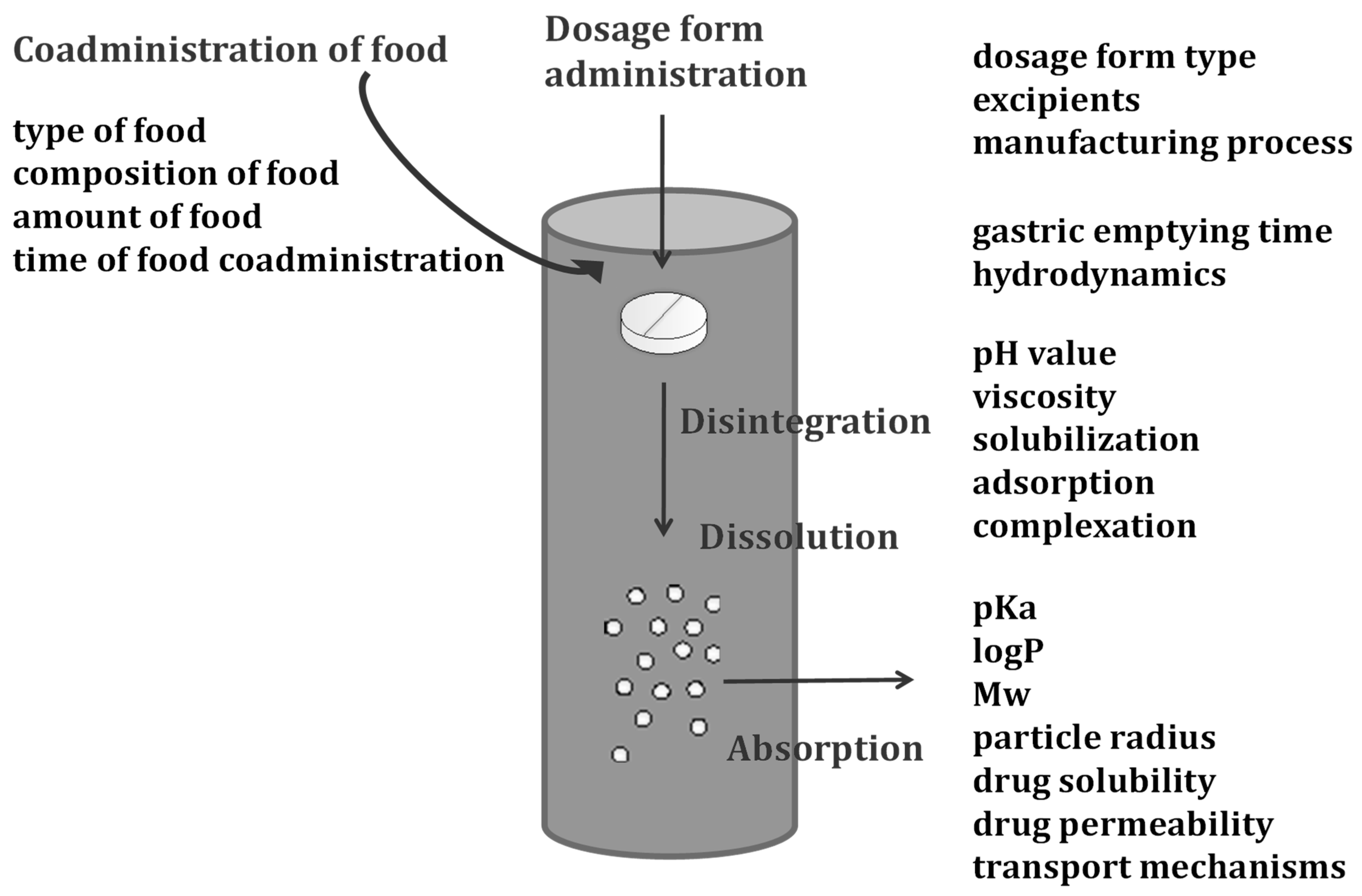
2. Interpretation of Oral Drug Dissolution, Permeation, and Absorption within Physiologically-Based Biopharmaceutics Modeling
3. Drug Release Modeling
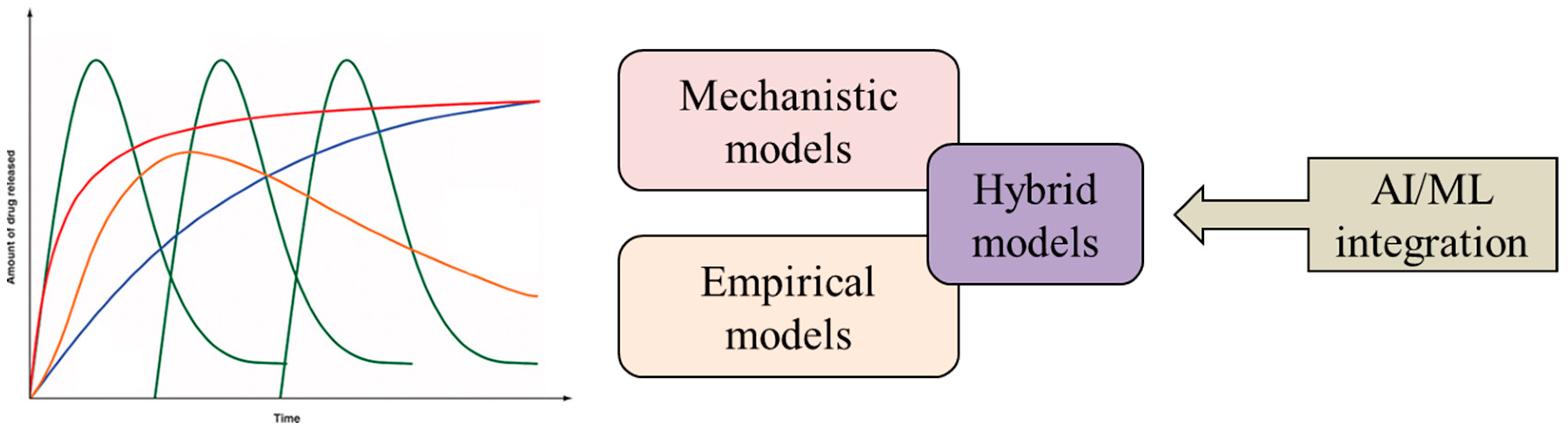
3.1. Other Contemporary Approaches to Drug Release Modeling
3.1.1. Artificial Intelligence and Machine Learning Algorithms in Drug Release Modeling
3.1.2. Hybrid Drug Release Models
3.2. Estimation of Drug Dissolution
4. In Silico Modeling of Oral Drug Permeation and Absorption
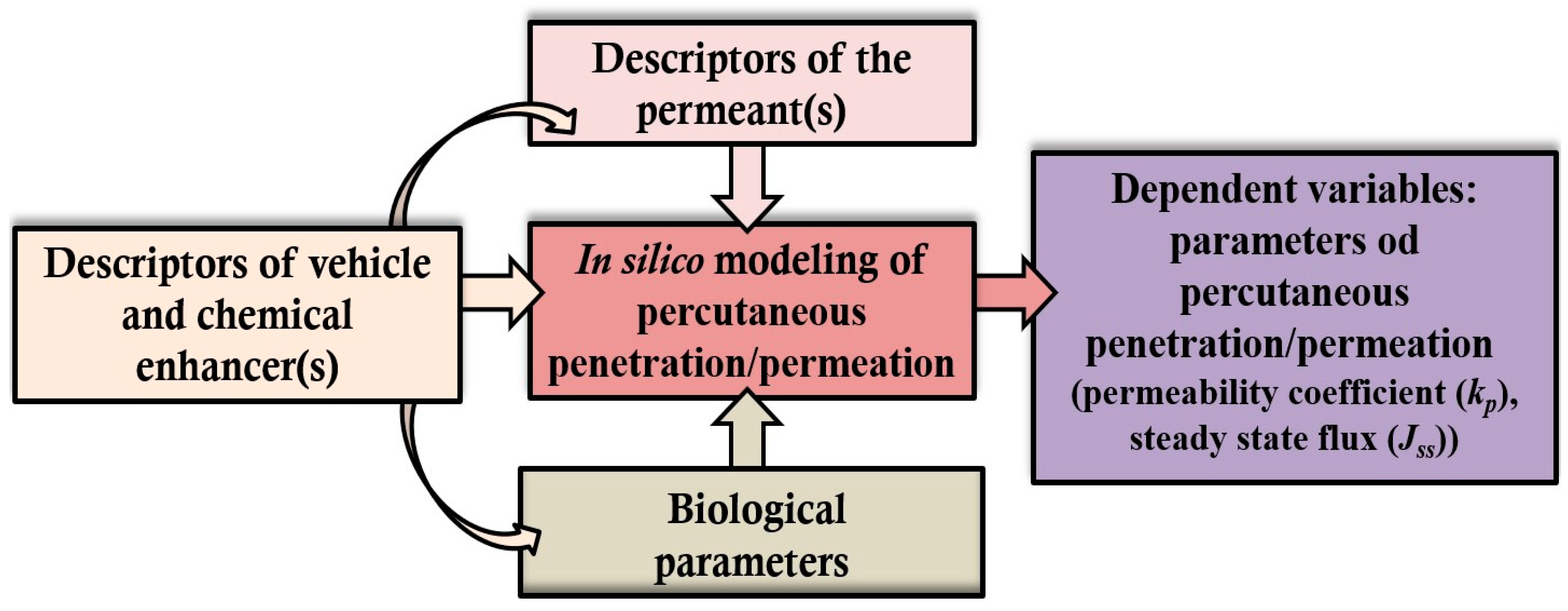
5. In Silico Modeling of Percutaneous Drug Permeation
5.1. QSPR/QSAR Models
| In Silico Model | Considered Descriptors | In Silico Evaluated Percutaneous Permeability | References |
|---|---|---|---|
| QSPR | logP and molecular size (MV or MW) | logP and MW of a single permeant from aqueous solution correlated well with logkp | [185,199] |
| QSPR | 47 descriptors from relevant physico-chemical parameters of 114 drugs | Hydrophobicity and the molecular size of the penetrant affected logkp | [200] |
| QSPR | Lipid solubility of 13 corticosteroids and sex steroids | The predicted flux of steroids was not accurate | [201] |
| QSPR | MV, logP, and MP | The accuracy in the predicted permeability logkp was demonstrated with 60 molecules, including small molecules and steroids | [181] |
| QSAR | Hydrophobicity, molecular size, and hydrogen bonding of 158 compounds | The descriptors provided an excellent fit to the permeability data for most compounds except hydrocortisone derivatives | [195] |
| QSPR | logP, MW, MV, and the melting point of betamethasone dipropionate, clobetasol propionate, fluorouracil, flurandrenolide, ketoconazole, lidocaine, metronidazole, tacrolimus monohydrate and tazarotene (formulated in propylene glycol and commercial formulations) | The QSPR models were useful for skin permeability assessment, although discrepancies were observed for tazarotene, tacrolimus, ketoconazole, and metronidazole | [200] |
| QSPR | MW, logP, and δ (assuming the penetration of drugs with logP > 2 and <2 via nonpolar and polar pathways, respectively) of 13 non-steroidal anti-inflammatory drugs (NSAIDs), and biological parameters (TEWL, HD, SB, RVM, and EL) of individual skin samples | Inclusion of δ and biological parameters improved statistically the QSPR model for predicting logkp of NSAIDs with logP < 2 | [197] |
| QSPR/QSAR integrated with molecular docking | MW, MV, predicted logP, total polarity surface, and hydrogen bond of the phytosterols (campesterol, β-sitosterol, and stigmasterol) | The predicted logkp was the greatest for β-sitosterol, followed by campesterol and stigmasterol. The in vivo study (mice) confirms the capacity of topically applied β-sitosterol as an antipsoriatic agent | [182] |
| QSPR/QSAR integrated with molecular docking | Molecular size (the number of resveratrol subunits) and physico-chemical properties (MV, logP, hydrogen bond (H-bond) number, and total surface polarity) of resveratrol and its oligomers | Oligomers with higher numbers of subunits have higher docking scores and are predicted to bind stratum corneum lipids more strongly; ε-viniferin was identified as a promising antipsoriatic agent that accumulated at higher levels in psoriasis-like mouse skin | [183] |
| QSAR | logP of the drug (haloperidol) and descriptors of 49 terpenes (MW, logP, boiling point, melting point, the terpene type, and the functional group of each enhancer) | The ideal terpene enhancer for haloperidol has at least one or combinations of the following properties: larger logP, liquid state at room temperature, with an ester or aldehyde (but not acid) functional group, and is neither a triterpene nor tetraterpene | [193] |
| Membrane-interaction QSAR (MI-QSAR) | MI-QSAR descriptor (the difference in the integrated cylindrical distribution functions over the phospholipid monolayer model, in and out of the presence of the skin penetration enhancer (ΔΣh(r)) developed for two datasets of 61 and 42 penetration enhancers | Explained 70–80% of the variance in skin penetration enhancement across each of the two training sets to predict skin permeability enhancement for hydrocortisone and hydrocortisone acetate | [202] |
| QSPR | Donor/acceptor interactions, van der Waals forces, HBD–π interactions, and hydrogen bonding in complexes of four APIs (5-fluorouracil, hydrocortisone, estradiol, and diclofenac sodium) and 34 terpenes | The satisfactory correlation between the predicted molecular properties of modeled complexes or examined terpenes and the permeation enhancement effects | [203] |
| ANN-based QSAR | logP, MW, steric energy, van der Waals area, van der Waals volume, dipole moment, highest occupied molecular orbital, and lowest unoccupied molecular orbital of 35 newly synthesized O-ethylmenthol derivatives | logP, steric energy, and the lowest unoccupied molecular orbital significantly affected the prediction of ketoprofen enhancement factor (penetration rate with enhancer:penetration rate without enhancer) (Ef) and total irritation score (TIS) | [204] |
| ANN and RSM | Vehicle composition (water (W), ethanol (E), propylene glycol (P), their binary and ternary mixtures) | RSM and ANN coincided very well in the prediction of the most suitable mixtures (W:E:P (20:60:20), W:E (40:60), and W:P (50:50)) to increase flux and reduce lag time of percutaneously applied melatonin | [205] |
| ANN and differential evolution (DE)) | Statistically significant descriptors of potential permeability enhancers of insulin included: average 1-electron reactivity index for a carbon atom, minimum 1-electron reactivity index for an oxygen atom, Kier and Hall index (order 1), RNCS relative negative charged SA (SAMNEG*RNCG) [Zefirov’s PC], and total dipole of the molecule. | The compounds with greater hydrophobicity and reactivity, as well as low dipole moments and capacity to form intermolecular bonds with stratum corneum lipids, could be promising insulin-specific permeability enhancers | [206] |
5.2. MD Simulations
5.3. In Silico Modeling of Skin Permeation in the Presence of Permeation Enhancers
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, Y.; Zhu, H.; Madabushi, R.; Liu, Q.; Huang, S.M.; Zineh, I. Model-informed drug development: Current US regulatory practice and future considerations. Clin. Pharmacol. Ther. 2019, 105, 899–911. [Google Scholar] [CrossRef] [PubMed]
- Model-Informed Drug Development Paired Meeting Program. Available online: https://www.fda.gov/drugs/development-resources/model-informed-drug-development-paired-meeting-program (accessed on 13 August 2023).
- Cvijić, S.; Ignjatović, J.; Parojčić, J.; Ibrić, S. The emerging role of physiologically-based pharmacokinetic/biopharmaceutics modeling in formulation development. Arh. Farm. 2021, 71, 318–335. [Google Scholar] [CrossRef]
- Cumming, J.G.; Davis, A.M.; Muresan, S.; Haeberlein, M.; Chen, H. Chemical predictive modelling to improve compound quality. Nat. Rev. Drug Discov. 2013, 12, 948–962. [Google Scholar] [CrossRef] [PubMed]
- Kostewicz, E.S.; Aarons, L.; Bergstrand, M.; Bolger, M.B.; Galetin, A.; Hatley, O.; Jamei, M.; Lloyd, R.; Pepin, X.; Rostami-Hodjegan, A.; et al. PBPK models for the prediction of in vivo performance of oral dosage forms. Eur. J. Pharm. Sci. 2014, 57, 300–321. [Google Scholar] [CrossRef] [PubMed]
- Valerio, L.G., Jr. Application of advanced in silico methods for predictive modeling and information integration. Expert Opin. Drug Met. 2012, 8, 395–398. [Google Scholar] [CrossRef] [PubMed]
- Bermejo, M.; Hens, B.; Dickens, J.; Mudie, D.; Paixão, P.; Tsume, Y.; Shedden, K.; Amidon, G.L. A mechanistic physiologically-based biopharmaceutics modeling (PBBM) approach to assess the in vivo performance of an orally administered drug product: From IVIVC to IVIVP. Pharmaceutics 2020, 12, 74. [Google Scholar] [CrossRef] [PubMed]
- Grimstein, M.; Yang, Y.; Zhang, X.; Grillo, J.; Huang, S.M.; Zineh, I.; Wang, Y. Physiologically based pharmacokinetic modeling in regulatory science: An update from the US Food and Drug Administration’s Office of Clinical Pharmacology. J. Pharm. Sci. 2019, 108, 21–25. [Google Scholar] [CrossRef]
- Luzon, E.; Blake, K.; Cole, S.; Nordmark, A.; Versantvoort, C.; Berglund, E.G. Physiologically based pharmacokinetic modeling in regulatory decision-making at the European Medicines Agency. Clin. Pharmacol. Ther. 2017, 102, 98–105. [Google Scholar] [CrossRef]
- Karnati, P.; Murthy, A.; Gundeti, M.; Ahmed, T. Modelling Based Approaches to Support Generic Drug Regulatory Submissions-Practical Considerations and Case Studies. AAPS J. 2023, 25, 63. [Google Scholar] [CrossRef]
- Krstevska, A.; Đuriš, J.; Ibrić, S.; Cvijić, S. In-depth analysis of physiologically based pharmacokinetic (PBPK) modeling utilization in different application fields using text mining tools. Pharmaceutics 2022, 15, 107. [Google Scholar] [CrossRef]
- Miller, N.A.; Reddy, M.B.; Heikkinen, A.T.; Lukacova, V.; Parrott, N. Physiologically based pharmacokinetic modelling for first-in-human predictions: An updated model building strategy illustrated with challenging industry case studies. Clin. Pharmacokinet. 2019, 58, 727–746. [Google Scholar] [CrossRef] [PubMed]
- Feng, K.; Leary, R.H. Toward personalized medicine with physiologically based pharmacokinetic modeling. Int. J. Pharmacokinet. 2017, 2, 1–4. [Google Scholar] [CrossRef][Green Version]
- Hartmanshenn, C.; Scherholz, M.; Androulakis, I.P. Physiologically-based pharmacokinetic models: Approaches for enabling personalized medicine. J. Pharmacokinet. Phar. 2016, 43, 481–504. [Google Scholar] [CrossRef] [PubMed]
- Marsousi, N.; Desmeules, J.A.; Rudaz, S.; Daali, Y. Usefulness of PBPK modeling in incorporation of clinical conditions in personalized medicine. J. Pharm. Sci. 2017, 106, 2380–2391. [Google Scholar] [CrossRef]
- Lin, L.; Wong, H. Predicting oral drug absorption: Mini review on physiologically-based pharmacokinetic models. Pharmaceutics 2017, 9, 41. [Google Scholar] [CrossRef] [PubMed]
- Markl, D.; Zeitler, J.A. A review of disintegration mechanisms and measurement techniques. Pharm. Res. 2017, 34, 890–917. [Google Scholar] [CrossRef] [PubMed]
- DDDPlusTM. Available online: https://www.simulations-plus.com/software/dddplus/ (accessed on 13 August 2023).
- Massimo, G.; Santi, P.; Colombo, G.; Nicoli, S.; Zani, F.; Colombo, P.; Bettini, R. The suitability of disintegrating force kinetics for studying the effect of manufacturing parameters on spironolactone tablet properties. AAPS PharmSciTech 2003, 4, 50–56. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug dissolution. Int. J. Pharm. 2013, 453, 12–24. [Google Scholar] [CrossRef]
- Takano, R.; Sugano, K.; Higashida, A.; Hayashi, Y.; Machida, M.; Aso, Y.; Yamashita, S. Oral absorption of poorly water-soluble drugs: Computer simulation of fraction absorbed in humans from a miniscale dissolution test. Pharm. Res. 2006, 23, 1144–1156. [Google Scholar] [CrossRef]
- Gan, Y.; Baak, J.P.; Chen, T.; Ye, H.; Liao, W.; Lv, H.; Wen, C.; Zheng, S. Supersaturation and Precipitation Applicated in Drug Delivery Systems: Development Strategies and Evaluation Approaches. Molecules 2023, 28, 2212. [Google Scholar] [CrossRef]
- O’Dwyer, P.J.; Litou, C.; Box, K.J.; Dressman, J.B.; Kostewicz, E.S.; Kuentz, M.; Reppas, C. In vitro methods to assess drug precipitation in the fasted small intestine—A PEARRL review. J. Pharm. Pharmacol. 2019, 71, 536–556. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Spivey, N.; Silchenko, S.; Gonzalez-Alvarez, I.; Bermejo, M.; Hidalgo, I.J. A differential equation based modelling approach to predict supersaturation and in vivo absorption from in vitro dissolution-absorption system (idas2) data. Eur. J. Pharm. Biopharm. 2021, 165, 1–12. [Google Scholar] [CrossRef]
- Kambayashi, A.; Yasuji, T.; Dressman, J.B. Prediction of the precipitation profiles of weak base drugs in the small intestine using a simplified transfer (“dumping”) model coupled with in silico modeling and simulation approach. Eur. J. Pharm. Biopharm. 2016, 103, 95–103. [Google Scholar] [CrossRef] [PubMed]
- Kleppe, M.S.; Forney-Stevens, K.M.; Haskell, R.J.; Bogner, R.H. Mathematical models to explore potential effects of supersaturation and precipitation on oral bioavailability of poorly soluble drugs. AAPS J. 2015, 17, 902–917. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Chirumamilla, S.K.; Banala, V.T.; Jamei, M.; Turner, D.B. Mechanistic PBPK modelling to predict the advantage of the salt form of a drug when dosed with acid reducing agents. Pharmaceutics 2021, 13, 1169. [Google Scholar] [CrossRef] [PubMed]
- Hens, B.; Pathak, S.M.; Mitra, A.; Patel, N.; Liu, B.; Patel, S.; Jamei, M.; Brouwers, J.; Augustijns, P.; Turner, D.B. In silico modeling approach for the evaluation of gastrointestinal dissolution, supersaturation, and precipitation of posaconazole. Mol. Pharm. 2017, 14, 4321–4333. [Google Scholar] [CrossRef] [PubMed]
- Jakubiak, P.; Wagner, B.; Grimm, H.P.; Petrig-Schaffland, J.; Schuler, F.; Alvarez-Sánchez, R. Development of a unified dissolution and precipitation model and its use for the prediction of oral drug absorption. Mol. Pharm. 2016, 13, 586–598. [Google Scholar] [CrossRef]
- Patel, S.; Zhu, W.; Xia, B.; Sharma, N.; Hermans, A.; Ehrick, J.D.; Kesisoglou, F.; Pennington, J. Integration of precipitation kinetics from an in vitro, multicompartment transfer system and mechanistic oral absorption modeling for pharmacokinetic prediction of weakly basic drugs. J. Pharm. Sci. 2019, 108, 574–583. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Ito, S.; Itai, S.; Yamamoto, K. Physicochemical properties and bioavailability of carbamazepine polymorphs and dihydrate. Int. J. Pharm. 2000, 193, 137–146. [Google Scholar] [CrossRef]
- Maragos, S.; Archontaki, H.; Macheras, P.; Valsami, G. Effect of cyclodextrin complexation on the aqueous solubility and solubility/dose ratio of praziquantel. AAPS PharmSciTech 2009, 10, 1444–1451. [Google Scholar] [CrossRef]
- Saokham, P.; Muankaew, C.; Jansook, P.; Loftsson, T. Solubility of cyclodextrins and drug/cyclodextrin complexes. Molecules 2018, 23, 1161. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Orton, E.; Vemuri, N.M. Predicting solubility in multiple nonpolar drugs–cyclodextrin system. J. Pharm. Sci. 2002, 91, 2301–2306. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Guo, R.; Zong, Q.; Ling, G. Application of Molecular Docking in Elaborating Molecular Mechanisms and Interactions of Supramolecular Cyclodextrin. Carbohydr. Polym. 2022, 276, 118644. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Nath, S.; Singh, T.S.; Chattopadhyay, N. Cavity Size Dependent Stoichiometry of Probe–Cyclodextrin Complexation: Experimental and Molecular Docking Demonstration. J. Photochem. Photobiol. A Chem. 2020, 388, 112158. [Google Scholar] [CrossRef]
- Mithani, S.D.; Bakatselou, V.; TenHoor, C.N.; Dressman, J.B. Estimation of the increase in solubility of drugs as a function of bile salt concentration. Pharm. Res. 1996, 13, 163–167. [Google Scholar] [CrossRef] [PubMed]
- Bakatselou, V.; Oppenheim, R.C.; Dressman, J.B. Solubilization and wetting effects of bile salts on the dissolution of steroids. Pharm. Res. 1991, 8, 1461–1469. [Google Scholar] [CrossRef] [PubMed]
- Kesisoglou, F.; Wu, Y. Understanding the effect of API properties on bioavailability through absorption modeling. AAPS J. 2008, 10, 516–525. [Google Scholar] [CrossRef] [PubMed]
- Mathias, N.R.; Crison, J. The use of modeling tools to drive efficient oral product design. AAPS J. 2012, 14, 591–600. [Google Scholar] [CrossRef]
- Wei, H.; Dalton, C.; Di Maso, M.; Kanfer, I.; Löbenberg, R. Physicochemical characterization of five glyburide powders: A BCS based approach to predict oral absorption. Eur. J. Pharm. Biopharm. 2008, 69, 1046–1056. [Google Scholar] [CrossRef]
- Lu, A.T.; Frisella, M.E.; Johnson, K.C. Dissolution modeling: Factors affecting the dissolution rates of polydisperse powders. Pharm. Res. 1993, 10, 1308–1314. [Google Scholar] [CrossRef]
- Dali, M.V.; Carstensen, J.T. Effect of change in shape factor of a single crystal on its dissolution behavior. Pharm. Res. 1996, 13, 155–162. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Glennon, B.; He, Y.; Donnellan, P. Dissolution kinetics of a bcs class ii active pharmaceutical ingredient: Diffusion-based model validation and prediction. ACS Omega 2021, 6, 8056–8067. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Jia, X.; Li, Y.; Amador, C.; Ding, Y. CFD-DNS simulation of irregular-shaped particle dissolution. Particuology 2020, 50, 144–155. [Google Scholar] [CrossRef]
- Zhang, K.; Zhou, Z.Q.; Han, P.D.; Sun, Z.G.; Xi, G. Dissolution characteristics of solutes with different shapes using the moving particle semi-implicit method. Phys. Fluids 2022, 34, 117104. [Google Scholar] [CrossRef]
- Assunção, M.; Vynnycky, M.; Moroney, K.M. On the dissolution of a solid spherical particle. Phys. Fluids 2023, 35, 053605. [Google Scholar] [CrossRef]
- Gigliobianco, M.R.; Casadidio, C.; Censi, R.; Di Martino, P. Nanocrystals of poorly soluble drugs: Drug bioavailability and physicochemical stability. Pharmaceutics 2018, 10, 134. [Google Scholar] [CrossRef]
- Wu, Y.; Loper, A.; Landis, E.; Hettrick, L.; Novak, L.; Lynn, K.; Chen, C.; Thompson, K.; Higgins, R.; Batra, U.; et al. The role of biopharmaceutics in the development of a clinical nanoparticle formulation of MK-0869: A Beagle dog model predicts improved bioavailability and diminished food effect on absorption in human. Int. J. Pharm. 2004, 285, 135–146. [Google Scholar] [CrossRef]
- Zhang, H.; Xia, B.; Sheng, J.; Heimbach, T.; Lin, T.H.; He, H.; Wang, Y.; Novick, S.; Comfort, A. Application of physiologically based absorption modeling to formulation development of a low solubility, low permeability weak base: Mechanistic investigation of food effect. AAPS PharmSciTech 2014, 15, 400–406. [Google Scholar] [CrossRef]
- Colombo, G.; Politis, S.; Rossi, A. Technologies and Mechanisms for Oral Modified Release by Monolithic and Multiparticulate Delivery Systems. In Oral Drug Delivery for Modified Release Formulations; Kostewicz, E.S., Vertzoni, M., Benson, H.A., Roberts, M.S., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 119–136. [Google Scholar] [CrossRef]
- Peppas, N.A.; Narasimhan, B. Mathematical models in drug delivery: How modeling has shaped the way we design new drug delivery systems. J. Control Release 2014, 190, 75–81. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Modeling of diffusion controlled drug delivery. J. Control Release 2012, 161, 351–362. [Google Scholar] [CrossRef]
- Jain, A.; King, D.; Pontrelli, G.; McGinty, S. Controlling release from encapsulated drug-loaded devices: Insights from modeling the dissolution front propagation. J. Control Release 2023, 360, 225–235. [Google Scholar] [CrossRef]
- Chakravarty, K.; Dalal, D.C. A two-phase model for drug release from microparticles with combined effects of solubilisation and recrystallisation. Math. Biosci. 2016, 272, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Ye, Z.; Gao, H.; Ouyang, D. Computational pharmaceutics-A new paradigm of drug delivery. J. Control Release 2021, 338, 119–136. [Google Scholar] [CrossRef] [PubMed]
- Siepmann, J.; Streubel, A.; Peppas, N.A. Understanding and predicting drug delivery from hydrophilic matrix tablets using the “sequential layer” model. Pharm. Res. 2002, 19, 306–314. [Google Scholar] [CrossRef] [PubMed]
- Geraili, A.; Mequanint, K. Systematic studies on surface erosion of photocrosslinked polyanhydride tablets and data correlation with release kinetic models. Polymers 2020, 12, 1105. [Google Scholar] [CrossRef] [PubMed]
- Rizwan, M.; Yahya, R.; Hassan, A.; Yar, M.; Azzahari, A.D.; Selvanathan, V.; Sonsudin, F.; Abouloula, C.N. pH sensitive hydrogels in drug delivery: Brief history, properties, swelling, and release mechanism, material selection and applications. Polymers 2017, 9, 137. [Google Scholar] [CrossRef] [PubMed]
- Kashkooli, F.M.; Soltani, M.; Souri, M. Controlled anti-cancer drug release through advanced nano-drug delivery systems: Static and dynamic targeting strategies. J. Control Release 2020, 327, 316–349. [Google Scholar] [CrossRef]
- Kashkooli, F.M.; Jakhmola, A.; Hornsby, T.K.; Tavakkoli, J.J.; Kolios, M.C. Ultrasound-mediated nano drug delivery for treating cancer: Fundamental physics to future directions. J. Control Release 2023, 355, 552–578. [Google Scholar] [CrossRef]
- Iturrioz-Rodríguez, N.; Correa-Duarte, M.A.; Fanarraga, M.L. Controlled drug delivery systems for cancer based on mesoporous silica nanoparticles. Int. J. Nanomed. 2019, 14, 3389–3401. [Google Scholar] [CrossRef]
- Davoodi, P.; Lee, L.Y.; Xu, Q.; Sunil, V.; Sun, Y.; Soh, S.; Wang, C.H. Drug delivery systems for programmed and on-demand release. Adv. Drug Deliv. Rev. 2018, 132, 104–138. [Google Scholar] [CrossRef]
- Sirousazar, M. Mathematical modeling of drug release in a phase-transient temperature-responsive drug delivery system in spherical coordinates. J. Macromol. Sci. B 2019, 58, 890–907. [Google Scholar] [CrossRef]
- Kubinski, A.M.; Shivkumar, G.; Georgi, R.A.; George, S.; Reynolds, J.; Sosa, R.D.; Ju, T.R. Predictive Drug Release Modeling Across Dissolution Apparatuses I and II using Computational Fluid Dynamics. J. Pharm. Sci. 2023, 112, 808–819. [Google Scholar] [CrossRef]
- Lou, H.; Hageman, M.J. Investigating the Influence of Tablet Location Inside Dissolution Test Apparatus on Polymer Erosion and Drug Release of a Surface-Erodible Sustained-Release Tablet Using Computational Simulation Methods. AAPS PharmSciTech 2021, 22, 99. [Google Scholar] [CrossRef]
- Walsh, J.P.; Ghadiri, M.; Shirazian, S. CFD approach for simulation of API release from solid dosage formulations. J. Mol. Liq. 2020, 317, 113899. [Google Scholar] [CrossRef]
- Schütt, M.; Stamatopoulos, K.; Batchelor, H.K.; Simmons, M.J.; Alexiadis, A. Modelling and Simulation of the Drug Release from a Solid Dosage Form in the Human Ascending Colon: The Influence of Different Motility Patterns and Fluid Viscosities. Pharmaceutics 2021, 13, 859. [Google Scholar] [CrossRef] [PubMed]
- D’Arcy, D.M.; Healy, A.M.; Corrigan, O.I. Towards determining appropriate hydrodynamic conditions for in vitro in vivo correlations using computational fluid dynamics. Eur. J. Pharm. Sci. 2009, 37, 291–299. [Google Scholar] [CrossRef] [PubMed]
- D’Arcy, D.M.; Corrigan, O.I.; Healy, A.M. Evaluation of hydrodynamics in the basket dissolution apparatus using computational fluid dynamics—Dissolution rate implications. Eur. J. Pharm. Sci. 2006, 27, 259–267. [Google Scholar] [CrossRef] [PubMed]
- D’Arcy, D.M.; Liu, B.; Bradley, G.; Healy, A.M.; Corrigan, O.I. Hydrodynamic and species transfer simulations in the USP 4 dissolution apparatus: Considerations for dissolution in a low velocity pulsing flow. Pharm. Res. 2010, 27, 246–258. [Google Scholar] [CrossRef]
- Kalný, M.; Grof, Z.; Štěpánek, F. Microstructure based simulation of the disintegration and dissolution of immediate release pharmaceutical tablets. Powder Technol. 2021, 377, 257–268. [Google Scholar] [CrossRef]
- Kimber, J.A.; Kazarian, S.G.; Štěpánek, F. DEM simulation of drug release from structurally heterogeneous swelling tablets. Powder Technol. 2013, 248, 68–76. [Google Scholar] [CrossRef]
- Ranjan, A.; Jha, P.K. Studying drug release through polymeric controlled release formulations in United States pharmacopoeia 2 apparatus using multiphysics simulation and experiments. Mol. Pharm. 2021, 18, 2600–2611. [Google Scholar] [CrossRef] [PubMed]
- van Haaren, C.; De Bock, M.; Kazarian, S.G. Advances in ATR-FTIR Spectroscopic Imaging for the Analysis of Tablet Dissolution and Drug Release. Molecules 2023, 28, 4705. [Google Scholar] [CrossRef]
- Velasco, D.; Danoux, C.B.; Redondo, J.A.; Elvira, C.; San Roman, J.; Wray, P.S.; Kazarian, S.G. pH-sensitive polymer hydrogels derived from morpholine to prevent the crystallization of ibuprofen. J. Control Release 2011, 149, 140–145. [Google Scholar] [CrossRef] [PubMed]
- Zahoor, F.D.; Mader, K.T.; Timmins, P.; Brown, J.; Sammon, C. Investigation of within-tablet dynamics for extended release of a poorly soluble basic drug from hydrophilic matrix tablets using ATR–FTIR imaging. Mol. Pharm. 2020, 17, 1090–1099. [Google Scholar] [CrossRef] [PubMed]
- Wray, P.; Li, J.; Li, L.Q.; Kazarian, S.G. Combined Study of Biphasic and Zero-Order Release Formulations with Dissolution Tests and ATR–FTIR Spectroscopic Imaging. J. Pharm. Sci. 2014, 103, 1995–2004. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.G.; Park, Y.S.; Jeong, J.H.; Kwon, Y.B.; Shin, D.H.; Kim, J.Y.; Rhee, Y.S.; Park, E.S.; Kim, D.W.; Park, C.W. Physicochemical properties and drug-release mechanisms of dual-release bilayer tablet containing mirabegron and fesoterodine fumarate. Drug Des. Dev. Ther. 2019, 13, 2459–2474. [Google Scholar] [CrossRef] [PubMed]
- Hifumi, H.; Ewing, A.V.; Kazarian, S.G. ATR-FTIR spectroscopic imaging to study the drying and dissolution of pharmaceutical polymer-based films. Int. J. Pharm. 2016, 515, 57–68. [Google Scholar] [CrossRef] [PubMed]
- Kimber, J.A.; Kazarian, S.G.; Štěpánek, F. Modelling of pharmaceutical tablet swelling and dissolution using discrete element method. Chem. Eng. Sci. 2012, 69, 394–403. [Google Scholar] [CrossRef]
- Brown, B.; Ward, A.; Fazili, Z.; Østergaard, J.; Asare-Addo, K. Application of UV dissolution imaging to pharmaceutical systems. Adv. Drug Deliv. Rev. 2021, 177, 113949. [Google Scholar] [CrossRef]
- Pudlas, M.; Kyeremateng, S.O.; Williams, L.A.; Kimber, J.A.; van Lishaut, H.; Kazarian, S.G.; Woehrle, G.H. Analyzing the impact of different excipients on drug release behavior in hot-melt extrusion formulations using FTIR spectroscopic imaging. Eur. J. Pharm. Sci. 2015, 67, 21–31. [Google Scholar] [CrossRef]
- Lizoňová, D.; Mužík, J.; Šoltys, M.; Beránek, J.; Kazarian, S.G.; Štěpánek, F. Molecular-level insight into hot-melt loading and drug release from mesoporous silica carriers. Eur. J. Pharm. Biopharm. 2018, 130, 327–335. [Google Scholar] [CrossRef] [PubMed]
- Ewing, A.V.; Biggart, G.D.; Hale, C.R.; Clarke, G.S.; Kazarian, S.G. Comparison of pharmaceutical formulations: ATR-FTIR spectroscopic imaging to study drug-carrier interactions. Int. J. Pharm. 2015, 495, 112–121. [Google Scholar] [CrossRef] [PubMed]
- Ward, A.; Walton, K.; Mawla, N.; Kaialy, W.; Liu, L.; Timmins, P.; Conway, B.R.; Asare-Addo, K. Development of a novel method utilising dissolution imaging for the measurement of swelling behaviour in hydrophilic matrices. Int. J. Pharm. X 2019, 1, 100013. [Google Scholar] [CrossRef] [PubMed]
- Østergaard, J. UV imaging in pharmaceutical analysis. J. Pharmaceut. Biomed. 2018, 147, 140–148. [Google Scholar] [CrossRef] [PubMed]
- Ward, A.; Walton, K.; Stoycheva, S.; Wallis, M.; Adebisi, A.; Nep, E.; Ngwuluka, N.C.; Shaboun, S.; Smith, A.M.; Conway, B.R.; et al. The use of visible and UV dissolution imaging for the assessment of propranolol hydrochloride in liquisolid compacts of Sesamum radiatum gum. J. Drug Deliv. Sci. Technol. 2020, 56, 101511. [Google Scholar] [CrossRef]
- Zarmpi, P.; Flanagan, T.; Meehan, E.; Mann, J.; Fotaki, N. Surface dissolution UV imaging for characterization of superdisintegrants and their impact on drug dissolution. Int. J. Pharm. 2020, 577, 119080. [Google Scholar] [CrossRef]
- Park, C.; Lee, J.H.; Jin, G.; Ngo, H.V.; Park, J.B.; Tran, T.T.; Tran, P.H.; Lee, B.J. Release kinetics of hydroxypropyl methylcellulose governing drug release and hydrodynamic changes of matrix tablet. Curr. Drug Deliv. 2022, 19, 520–533. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, X.; Ouyang, D.; Williams, R.O., III. Emerging artificial intelligence (AI) technologies used in the development of solid dosage forms. Pharmaceutics 2022, 14, 2257. [Google Scholar] [CrossRef]
- Wang, S.; Di, J.; Wang, D.; Dai, X.; Hua, Y.; Gao, X.; Zheng, A.; Gao, J. State-of-the-art review of artificial neural networks to predict, characterize and optimize pharmaceutical formulation. Pharmaceutics 2022, 14, 183. [Google Scholar] [CrossRef]
- Hassanzadeh, P.; Atyabi, F.; Dinarvand, R. The significance of artificial intelligence in drug delivery system design. Adv. Drug Deliv. Rev. 2019, 151, 169–190. [Google Scholar] [CrossRef]
- Djuriš, J.; Kurćubić, I.; Ibrić, S. Review of machine learning algorithms application in pharmaceutical technology. Arch. Pharm. 2021, 71, 302–317. [Google Scholar] [CrossRef]
- Sabaghi, M.; Tavasoli, S.; Hoseyni, S.Z.; Mozafari, M.R.; Degraeve, P.; Katouzian, I. A critical review on approaches to regulate the release rate of bioactive compounds from biopolymeric matrices. Food Chem. 2022, 382, 132411. [Google Scholar] [CrossRef]
- Sousa, A.S.; Serra, J.; Estevens, C.; Costa, R.; Ribeiro, A.J. A quality by design approach in oral extended release drug delivery systems: Where we are and where we are going? J. Pharm. Investig. 2023, 53, 269–306. [Google Scholar] [CrossRef]
- Vora, L.K.; Gholap, A.D.; Jetha, K.; Thakur, R.R.S.; Solanki, H.K.; Chavda, V.P. Artificial Intelligence in Pharmaceutical Technology and Drug Delivery Design. Pharmaceutics 2023, 15, 1916. [Google Scholar] [CrossRef]
- Gao, H.; Wang, W.; Dong, J.; Ye, Z.; Ouyang, D. An integrated computational methodology with data-driven machine learning, molecular modeling and PBPK modeling to accelerate solid dispersion formulation design. Eur. J. Pharm. Biopharm. 2021, 158, 336–346. [Google Scholar] [CrossRef] [PubMed]
- Elbadawi, M.; Gustaffson, T.; Gaisford, S.; Basit, A.W. 3D printing tablets: Predicting printability and drug dissolution from rheological data. Int. J. Pharm. 2020, 590, 119868. [Google Scholar] [CrossRef] [PubMed]
- Nagy, B.; Petra, D.; Galata, D.L.; Démuth, B.; Borbás, E.; Marosi, G.; Nagy, Z.K.; Farkas, A. Application of artificial neural networks for Process Analytical Technology-based dissolution testing. Int. J. Pharm. 2019, 567, 118464. [Google Scholar] [CrossRef] [PubMed]
- Greenberg, Z.F.; Graim, K.S.; He, M. Towards artificial intelligence-enabled extracellular vesicle precision drug delivery. Adv. Drug Deliv. Rev. 2023, 199, 114974. [Google Scholar] [CrossRef]
- Yokoyama, R.; Kimura, G.; Huwyler, J.; Hosoya, K.I.; Puchkov, M. Impact of insoluble separation layer mechanical properties on disintegration and dissolution kinetics of multilayer tablets. Pharmaceutics 2020, 12, 495. [Google Scholar] [CrossRef]
- Sivasankaran, S.; Jonnalagadda, S. Levonorgestrel loaded biodegradable microparticles for injectable contraception: Preparation, characterization and modelling of drug release. Int. J. Pharm. 2022, 624, 121994. [Google Scholar] [CrossRef]
- Pishnamazi, M.; Ismail, H.Y.; Shirazian, S.; Iqbal, J.; Walker, G.M.; Collins, M.N. Application of lignin in controlled release: Development of predictive model based on artificial neural network for API release. Cellulose 2019, 26, 6165–6178. [Google Scholar] [CrossRef]
- The Use of Physiologically Based Pharmacokinetic Analyses—Biopharmaceutics Applications for Oral Drug Product Development, Manufacturing Changes, and Controls. Guidance for Industry. Available online: https://www.fda.gov/media/142500/download (accessed on 13 August 2023).
- Culen, M.; Rezacova, A.; Jampilek, J.; Dohnal, J. Designing a dynamic dissolution method: A review of instrumental options and corresponding physiology of stomach and small intestine. J. Pharm. Sci. 2013, 102, 2995–3017. [Google Scholar] [CrossRef] [PubMed]
- Fotaki, N.; Vertzoni, M. Biorelevant dissolution methods and their applications in in vitro-in vivo correlations for oral formulations. Open Drug Deliv. J. 2010, 4, 2–13. [Google Scholar] [CrossRef]
- Grady, H.; Elder, D.; Webster, G.K.; Mao, Y.; Lin, Y.; Flanagan, T.; Mann, J.; Blanchard, A.; Cohen, M.J.; Lin, J.; et al. Industry’s view on using quality control, biorelevant, and clinically relevant dissolution tests for pharmaceutical development, registration, and commercialization. J. Pharm. Sci. 2018, 107, 34–41. [Google Scholar] [CrossRef] [PubMed]
- Hens, B.; Sinko, P.D.; Job, N.; Dean, M.; Al-Gousous, J.; Salehi, N.; Ziff, R.M.; Tsume, Y.; Bermejo, M.; Paixao, P.; et al. Formulation predictive dissolution (fPD) testing to advance oral drug product development: An introduction to the US FDA funded ‘21st Century BA/BE’ project. Int. J. Pharm. 2018, 548, 120–127. [Google Scholar] [CrossRef] [PubMed]
- Klein, S. The use of biorelevant dissolution media to forecast the in vivo performance of a drug. AAPS J. 2010, 12, 397–406. [Google Scholar] [CrossRef]
- Kostewicz, E.S.; Abrahamsson, B.; Brewster, M.; Brouwers, J.; Butler, J.; Carlert, S.; Dickinson, P.A.; Dressman, J.; Holm, R.; Klein, S.; et al. In vitro models for the prediction of in vivo performance of oral dosage forms. Eur. J. Pharm. Sci. 2014, 57, 342–366. [Google Scholar] [CrossRef]
- Markopoulos, C.; Andreas, C.J.; Vertzoni, M.; Dressman, J.; Reppas, C. In-vitro simulation of luminal conditions for evaluation of performance of oral drug products: Choosing the appropriate test media. Eur. J. Pharm. Biopharm. 2015, 93, 173–182. [Google Scholar] [CrossRef]
- Reppas, C.; Vertzoni, M. Biorelevant in-vitro performance testing of orally administered dosage forms. J. Pharm. Pharmacol. 2012, 64, 919–930. [Google Scholar] [CrossRef]
- Silva, D.A.; Al-Gousous, J.; Davies, N.M.; Chacra, N.B.; Webster, G.K.; Lipka, E.; Amidon, G.; Löbenberg, R. Simulated, biorelevant, clinically relevant or physiologically relevant dissolution media: The hidden role of bicarbonate buffer. Eur. J. Pharm. Biopharm. 2019, 142, 8–19. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, L.; Shao, X. Applications of bio-predictive dissolution tools for the development of solid oral dosage forms: Current industry experience. Drug Dev. Ind. Pharm. 2022, 48, 79–97. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Huo, M.; Zhou, J.; Zou, A.; Li, W.; Yao, C.; Xie, S. DDSolver: An add-in program for modeling and comparison of drug dissolution profiles. AAPS J. 2010, 12, 263–271. [Google Scholar] [CrossRef] [PubMed]
- The Simcyp™ In Vitro Data Analysis (SIVA) Toolkit. Available online: https://www.certara.com/software/simcyp-in-vitro-data-analysis-toolkit-siva/ (accessed on 13 August 2023).
- Almukainzi, M.; Okumu, A.; Wei, H.; Löbenberg, R. Simulation of in vitro dissolution behavior using DDDPlus™. AAPS PharmSciTech 2015, 16, 217–221. [Google Scholar] [CrossRef] [PubMed]
- Fiolka, T.; Van Den Abeele, J.; Augustijns, P.; Arora, S.; Dressman, J. Biorelevant two-stage in vitro testing for rDCS classification and in PBPK modeling–case example ritonavir. J. Pharm. Sci. 2020, 109, 2512–2526. [Google Scholar] [CrossRef] [PubMed]
- Loisios-Konstantinidis, I.; Cristofoletti, R.; Fotaki, N.; Turner, D.B.; Dressman, J. Establishing virtual bioequivalence and clinically relevant specifications using in vitro biorelevant dissolution testing and physiologically-based population pharmacokinetic modeling. case example: Naproxen. Eur. J. Pharm. Sci. 2020, 143, 105170. [Google Scholar] [CrossRef] [PubMed]
- Kollipara, S.; Bhattiprolu, A.K.; Boddu, R.; Ahmed, T.; Chachad, S. Best practices for integration of dissolution data into physiologically based biopharmaceutics models (PBBM): A biopharmaceutics modeling scientist perspective. AAPS PharmSciTech 2023, 24, 59. [Google Scholar] [CrossRef]
- Pathak, S.M.; Schaefer, K.J.; Jamei, M.; Turner, D.B. Biopharmaceutic IVIVE—Mechanistic modeling of single-and two-phase in vitro experiments to obtain drug-specific parameters for incorporation into PBPK models. J. Pharm. Sci. 2019, 108, 1604–1618. [Google Scholar] [CrossRef]
- Carapeto, G.V.; Duque, M.D.; Issa, M.G.; Ferraz, H.G. Development of Biopredictive Dissolution Method for Extended-Release Desvenlafaxine Tablets. Pharmaceutics 2023, 15, 1544. [Google Scholar] [CrossRef]
- Ghate, V.M.; Chaudhari, P.; Lewis, S.A. Physiologically based pharmacokinetic (PBPK) modelling for in vitro-in vivo extrapolation: Emphasis on the use of dissolution data. Dissol. Technol. 2019, 26, 18–27. [Google Scholar] [CrossRef]
- Golhar, A.; Pillai, M.; Dhakne, P.; Rajput, N.; Jadav, T.; Sengupta, P. Progressive tools and critical strategies for development of best fit PBPK model aiming better in vitro-in vivo correlation. Int. J. Pharm. 2023, 643, 123267. [Google Scholar] [CrossRef]
- Grbic, S.; Parojcic, J.; Ibric, S.; Djuric, Z. In vitro–in vivo correlation for gliclazide immediate-release tablets based on mechanistic absorption simulation. AAPS PharmSciTech 2011, 12, 165–171. [Google Scholar] [CrossRef] [PubMed]
- O’Dwyer, P.J.; Box, K.J.; Imanidis, G.; Vertzoni, M.; Reppas, C. On the usefulness of four in vitro methods in assessing the intraluminal performance of poorly soluble, ionisable compounds in the fasted state. Eur. J. Pharm. Sci. 2022, 168, 106034. [Google Scholar] [CrossRef] [PubMed]
- Okumu, A.; DiMaso, M.; Löbenberg, R. Dynamic dissolution testing to establish in vitro/in vivo correlations for montelukast sodium, a poorly soluble drug. Pharm. Res. 2008, 25, 2778–2785. [Google Scholar] [CrossRef] [PubMed]
- Otsuka, K.; Shono, Y.; Dressman, J. Coupling biorelevant dissolution methods with physiologically based pharmacokinetic modelling to forecast in-vivo performance of solid oral dosage forms. J. Pharm. Pharmacol. 2013, 65, 937–952. [Google Scholar] [CrossRef] [PubMed]
- Stillhart, C.; Pepin, X.; Tistaert, C.; Good, D.; Van Den Bergh, A.; Parrott, N.; Kesisoglou, F. PBPK absorption modeling: Establishing the in vitro–in vivo link—Industry perspective. AAPS J. 2019, 21, 19. [Google Scholar] [CrossRef]
- Tsume, Y.; Ashworth, L.; Bermejo, M.; Cheng, J.; Cicale, V.; Dressman, J.; Fushimi, M.; Gonzalez-Alvarez, I.; Guo, Y.; Jankovsky, C.; et al. Harmonizing Biopredictive Methodologies Through the Product Quality Research Institute (PQRI) Part I: Biopredictive Dissolution of Ibuprofen and Dipyridamole Tablets. AAPS J. 2023, 25, 45. [Google Scholar] [CrossRef]
- Wei, H.; Löbenberg, R. Biorelevant dissolution media as a predictive tool for glyburide a class II drug. Eur. J. Pharm. Sci. 2006, 29, 45–52. [Google Scholar] [CrossRef]
- Lee, M.H.; Ta, G.H.; Weng, C.F.; Leong, M.K. In silico prediction of intestinal permeability by hierarchical support vector regression. Int. J. Mol. Sci. 2020, 21, 3582. [Google Scholar] [CrossRef]
- MembranePlus™. Available online: https://www.simulations-plus.com/software/membraneplus/ (accessed on 13 August 2023).
- Balimane, P.V.; Chong, S.; Morrison, R.A. Current methodologies used for evaluation of intestinal permeability and absorption. J. Pharmacol. Toxicol. 2000, 44, 301–312. [Google Scholar] [CrossRef]
- Bergström, C.A.; Holm, R.; Jørgensen, S.A.; Andersson, S.B.; Artursson, P.; Beato, S.; Borde, A.; Box, K.; Brewster, M.; Dressman, J.; et al. Early pharmaceutical profiling to predict oral drug absorption: Current status and unmet needs. Eur. J. Pharm. Sci. 2014, 57, 173–199. [Google Scholar] [CrossRef]
- Dahlgren, D.; Lennernäs, H. Intestinal permeability and drug absorption: Predictive experimental, computational and in vivo approaches. Pharmaceutics 2019, 11, 411. [Google Scholar] [CrossRef] [PubMed]
- O’Shea, J.P.; Augustijns, P.; Brandl, M.; Brayden, D.J.; Brouwers, J.; Griffin, B.T.; Holm, R.; Jacobsen, A.C.; Lennernäs, H.; Vinarov, Z.; et al. Best practices in current models mimicking drug permeability in the gastrointestinal tract-An UNGAP review. Eur. J. Pharm. Sci. 2022, 170, 106098. [Google Scholar] [CrossRef] [PubMed]
- Sarmento, B.; Andrade, F.; Silva, S.B.D.; Rodrigues, F.; das Neves, J.; Ferreira, D. Cell-based in vitro models for predicting drug permeability. Expert Opin. Drug Met. 2012, 8, 607–621. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Shrestha, N.; Préat, V.; Beloqui, A. An overview of in vitro, ex vivo and in vivo models for studying the transport of drugs across intestinal barriers. Adv. Drug Deliv. Rev. 2021, 175, 113795. [Google Scholar] [CrossRef]
- Lennernäs, H.; Ahrenstedt, Ö.; Hällgren, R.; Knutson, L.; Ryde, M.; Paalzow, L.K. Regional jejunal perfusion, a new in vivo approach to study oral drug absorption in man. Pharm. Res. 1992, 9, 1243–1251. [Google Scholar] [CrossRef]
- Riedmaier, A.E.; DeMent, K.; Huckle, J.; Bransford, P.; Stillhart, C.; Lloyd, R.; Alluri, R.; Basu, S.; Chen, Y.; Dhamankar, V.; et al. Use of physiologically based pharmacokinetic (PBPK) modeling for predicting drug-food interactions: An industry perspective. AAPS J. 2020, 22, 123. [Google Scholar] [CrossRef]
- Zakeri-Milani, P.; Valizadeh, H.; Tajerzadeh, H.; Azarmi, Y.; Islambolchilar, Z.; Barzegar, S.; Barzegar-Jalali, M. Predicting human intestinal permeability using single-pass intestinal perfusion in rat. J. Pharm. Pharm. Sci. 2007, 10, 368–379. [Google Scholar]
- Avdeef, A.; Bendels, S.; Di, L.; Faller, B.; Kansy, M.; Sugano, K.; Yamauchi, Y. PAMPA—Critical factors for better predictions of absorption. J. Pharm. Sci. 2007, 96, 2893–2909. [Google Scholar] [CrossRef]
- Cao, X.; Gibbs, S.T.; Fang, L.; Miller, H.A.; Landowski, C.P.; Shin, H.C.; Lennernas, H.; Zhong, Y.; Amidon, G.L.; Yu, L.X.; et al. Why is it challenging to predict intestinal drug absorption and oral bioavailability in human using rat model. Pharm. Res. 2006, 23, 1675–1686. [Google Scholar] [CrossRef]
- Larregieu, C.A.; Benet, L.Z. Drug discovery and regulatory considerations for improving in silico and in vitro predictions that use Caco-2 as a surrogate for human intestinal permeability measurements. AAPS J. 2013, 15, 483–497. [Google Scholar] [CrossRef]
- Sun, D.; Lennernas, H.; Welage, L.S.; Barnett, J.L.; Landowski, C.P.; Foster, D.; Fleisher, D.; Lee, K.D.; Amidon, G.L. Comparison of human duodenum and Caco-2 gene expression profiles for 12,000 gene sequences tags and correlation with permeability of 26 drugs. Pharm. Res. 2002, 19, 1400–1416. [Google Scholar] [CrossRef] [PubMed]
- Dahlgren, D.; Roos, C.; Lundqvist, A.; Abrahamsson, B.; Tannergren, C.; Hellström, P.M.; Sjögren, E.; Lennernas, H. Regional intestinal permeability of three model drugs in human. Mol. Pharm. 2016, 13, 3013–3021. [Google Scholar] [CrossRef] [PubMed]
- Markovic, M.; Zur, M.; Dahan, A.; Cvijić, S. Biopharmaceutical characterization of rebamipide: The role of mucus binding in regional-dependent intestinal permeability. Eur. J. Pharm. Sci. 2020, 152, 105440. [Google Scholar] [CrossRef] [PubMed]
- Tannergren, C.; Jadhav, H.; Eckernäs, E.; Fagerberg, J.; Augustijns, P.; Sjögren, E. Physiologically based biopharmaceutics modeling of regional and colon absorption in humans. Eur. J. Pharm. Biopharm. 2023, 186, 144–159. [Google Scholar] [CrossRef] [PubMed]
- Agoram, B.; Woltosz, W.S.; Bolger, M.B. Predicting the impact of physiological and biochemical processes on oral drug bioavailability. Adv. Drug Deliv. Rev. 2001, 50, S41–S67. [Google Scholar] [CrossRef] [PubMed]
- Reddy, M.B.; Bolger, M.B.; Fraczkiewicz, G.; Del Frari, L.; Luo, L.; Lukacova, V.; Mitra, A.; Macwan, J.S.; Mullin, J.M.; Parrott, N.; et al. PBPK Modeling as a Tool for Predicting and Understanding Intestinal Metabolism of Uridine 5′-Diphospho-glucuronosyltransferase Substrates. Pharmaceutics 2021, 13, 1325. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.; Lee, S.L.; Yu, L.X. Mechanistic approaches to predicting oral drug absorption. AAPS J. 2009, 11, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Macheras, P.; Karalis, V.; Valsami, G. Keeping a critical eye on the science and the regulation of oral drug absorption: A review. J. Pharm. Sci. 2013, 102, 3018–3036. [Google Scholar] [CrossRef]
- Wang, K.; Amidon, G.L.; Smith, D.E. Physiological Dynamics in the Upper Gastrointestinal Tract and the Development of Gastrointestinal Absorption Models for the Immediate-Release Oral Dosage Forms in Healthy Adult Human. Pharm. Res. 2023, 40, 2607–2626. [Google Scholar] [CrossRef]
- Lawrence, X.Y.; Lipka, E.; Crison, J.R.; Amidon, G.L. Transport approaches to the biopharmaceutical design of oral drug delivery systems: Prediction of intestinal absorption. Adv. Drug Deliv. Rev. 1996, 19, 359–376. [Google Scholar] [CrossRef]
- Jamei, M.; Turner, D.; Yang, J.; Neuhoff, S.; Polak, S.; Rostami-Hodjegan, A.; Tucker, G. Population-based mechanistic prediction of oral drug absorption. AAPS J. 2009, 11, 225–237. [Google Scholar] [CrossRef] [PubMed]
- Willmann, S.; Schmitt, W.; Keldenich, J.; Lippert, J.; Dressman, J.B. A physiological model for the estimation of the fraction dose absorbed in humans. J. Med. Chem. 2004, 47, 4022–4031. [Google Scholar] [CrossRef] [PubMed]
- Kuentz, M. Drug absorption modeling as a tool to define the strategy in clinical formulation development. AAPS J. 2008, 10, 473–479. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sjögren, E.; Thorn, H.; Tannergren, C. In silico modeling of gastrointestinal drug absorption: Predictive performance of three physiologically based absorption models. Mol. Pharm. 2016, 13, 1763–1778. [Google Scholar] [CrossRef]
- Abduljalil, K.; Cain, T.; Humphries, H.; Rostami-Hodjegan, A. Deciding on success criteria for predictability of pharmacokinetic parameters from in vitro studies: An analysis based on in vivo observations. Drug Metab. Dispos. 2014, 42, 1478–1484. [Google Scholar] [CrossRef] [PubMed]
- Sager, J.E.; Yu, J.; Ragueneau-Majlessi, I.; Isoherranen, N. Physiologically based pharmacokinetic (PBPK) modeling and simulation approaches: A systematic review of published models, applications, and model verification. Drug Metab. Dispos. 2015, 43, 1823–1837. [Google Scholar] [CrossRef] [PubMed]
- Shebley, M.; Sandhu, P.; Emami Riedmaier, A.; Jamei, M.; Narayanan, R.; Patel, A.; Peters, S.A.; Reddy, V.P.; Zheng, M.; de Zwart, L.; et al. Physiologically based pharmacokinetic model qualification and reporting procedures for regulatory submissions: A consortium perspective. Clin. Pharmacol. Ther. 2018, 104, 88–110. [Google Scholar] [CrossRef]
- Sugano, K. Lost in modelling and simulation? ADMET DMPK 2021, 9, 75–109. [Google Scholar] [CrossRef]
- Phatale, V.; Vaiphei, K.K.; Jha, S.; Patil, D.; Agrawal, M.; Alexander, A. Overcoming skin barriers through advanced transdermal drug delivery approaches. J. Control Release 2022, 351, 361–380. [Google Scholar] [CrossRef]
- Machado, A.C.H.R.; Lopes, P.S.; Raffier, C.P.; Haridass, I.N.; Roberts, M.; Grice, J.; Leite-Silva, V.R. Skin penetration. In Cosmetic Science and Technology: Theoretical Principles and Applications; Sakamoto, K., Lochhead, R.Y., Maibach, H.I., Yamashita, Y., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 741–755. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Garg, A. An insight of techniques for the assessment of permeation flux across the skin for optimization of topical and transdermal drug delivery systems. J. Drug Deliv. Sci. Technol. 2021, 62, 102355. [Google Scholar] [CrossRef]
- Flaten, G.E.; Palac, Z.; Engesland, A.; Filipović-Grčić, J.; Vanić, Ž.; Škalko-Basnet, N. In vitro skin models as a tool in optimization of drug formulation. Eur. J. Pharm. Sci. 2015, 75, 10–24. [Google Scholar] [CrossRef] [PubMed]
- Yoshimatsu, H.; Ishii, K.; Konno, Y.; Satsukawa, M.; Yamashita, S. Prediction of human percutaneous absorption from in vitro and in vivo animal experiments. Int. J. Pharm. 2017, 534, 348–355. [Google Scholar] [CrossRef] [PubMed]
- Ashrafi, P.; Moss, G.P.; Wilkinson, S.C.; Davey, N.; Sun, Y. The application of machine learning to the modelling of percutaneous absorption: An overview and guide. SAR QSAR Environ. Res. 2015, 26, 181–204. [Google Scholar] [CrossRef] [PubMed]
- Biondo, N.E.; Argenta, D.F.; Rauber, G.S.; Caon, T. How to define the experimental conditions of skin permeation assays for drugs presenting biopharmaceutical limitations? The experience with testosterone. Int. J. Pharm. 2021, 607, 120987. [Google Scholar] [CrossRef] [PubMed]
- Roy, A.; Nair, S.; Sen, N.; Soni, N.; Madhusudhan, M.S. In silico methods for design of biological therapeutics. Methods 2017, 131, 33–65. [Google Scholar] [CrossRef] [PubMed]
- Anissimov, Y.G.; Jepps, O.G.; Dancik, Y.; Roberts, M.S. Mathematical and pharmacokinetic modelling of epidermal and dermal transport processes. Adv. Drug Deliv. Rev. 2013, 65, 169–190. [Google Scholar] [CrossRef] [PubMed]
- Burli, A.; Law, R.M.; Rodriguez, J.; Maibach, H.I. Organic compounds percutaneous penetration in vivo in man: Relationship to mathematical predictive model. Regul. Toxicol. Pharm. 2020, 112, 104614. [Google Scholar] [CrossRef]
- Chen, L.; Han, L.; Saib, O.; Lian, G. In silico prediction of percutaneous absorption and disposition kinetics of chemicals. Pharm. Res. 2015, 32, 1779–1793. [Google Scholar] [CrossRef]
- Fatemi, M.H.; Malekzadeh, H. In silico prediction of dermal penetration rate of chemicals from their molecular structural descriptors. Environ. Toxicol. Pharmacol. 2012, 34, 297–306. [Google Scholar] [CrossRef]
- Naegel, A.; Heisig, M.; Wittum, G. Detailed modeling of skin penetration—An overview. Adv. Drug Deliv. Rev. 2013, 65, 191–207. [Google Scholar] [CrossRef]
- Moss, G.P.; Wilkinson, S.C.; Sun, Y. Mathematical modelling of percutaneous absorption. Curr. Opin. Colloid Interface Sci. 2012, 17, 166–172. [Google Scholar] [CrossRef]
- Goyal, N.; Thatai, P.; Sapra, B. Surging footprints of mathematical modeling for prediction of transdermal permeability. As. J. Pharm. Sci. 2017, 12, 299–325. [Google Scholar] [CrossRef] [PubMed]
- Pecoraro, B.; Tutone, M.; Hoffman, E.; Hutter, V.; Almerico, A.M.; Traynor, M. Predicting skin permeability by means of computational approaches: Reliability and caveats in pharmaceutical studies. J. Chem. Inf. Model. 2019, 59, 1759–1771. [Google Scholar] [CrossRef]
- Barratt, M.D. Quantitative structure-activity relationships for skin permeability. Toxicol. In Vitro 1995, 9, 27–37. [Google Scholar] [CrossRef] [PubMed]
- Chang, Z.Y.; Chen, C.W.; Tsai, M.J.; Chen, C.C.; Alshetaili, A.; Hsiao, Y.T.; Fang, J.Y. The elucidation of structure–activity and structure-permeation relationships for the cutaneous delivery of phytosterols to attenuate psoriasiform inflammation. Int. Immunopharmacol. 2023, 119, 110202. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.Y.; Lin, Y.K.; Yang, S.C.; Alalaiwe, A.; Lin, C.J.; Fang, J.Y.; Lin, C.F. Percutaneous absorption of resveratrol and its oligomers to relieve psoriasiform lesions: In silico, in vitro and in vivo evaluations. Int. J. Pharm. 2020, 585, 119507. [Google Scholar] [CrossRef] [PubMed]
- Mitragotri, S.; Anissimov, Y.G.; Bunge, A.L.; Frasch, H.F.; Guy, R.H.; Hadgraft, J.; Kasting, G.B.; Lane, M.E.; Roberts, M.S. Mathematical models of skin permeability: An overview. Int. J. Pharm. 2011, 418, 115–129. [Google Scholar] [CrossRef]
- Potts, R.O.; Guy, R.H. Predicting skin permeability. Pharm. Res. 1992, 9, 663–669. [Google Scholar] [CrossRef]
- Flynn, G.L. Physicochemical determinants of skin absorption. In Principles of Route-to Route Extrapolation for Risk Assessment; Garrity, T.R., Henry, C.J., Eds.; Elsevier: New York, NY, USA, 1990; pp. 93–127. [Google Scholar]
- US EPA. Risk Assessment Guidance for Superfund. In Human Health Evaluation Manual (Part E, Supplemental Guidance for Dermal Risk Assessment); Final; United States Environmental Protection Agency, Office of Superfund Remediation and Technology Innovation: Washington, DC, USA, 2004; Volume I, pp. 1–156. [Google Scholar]
- Burli, A.; Law, R.M.; Maibach, H.I. Ability of mathematical models to predict human in vivo percutaneous penetration of steroids. Regul. Toxicol. Pharmacol. 2021, 126, 105041. [Google Scholar] [CrossRef]
- Potts, R.O.; Guy, R.H. A predictive algorithm for skin permeability: The effects of molecular size and hydrogen bond activity. Pharm. Res. 1995, 12, 1628–1633. [Google Scholar] [CrossRef]
- Lien, E.J.; Gaot, H. QSAR Analysis of Skin Permeability of Various Drugs in Man as Compared to in Vivo and in Vitro Studies in Rodents. Pharm. Res. 1995, 12, 583–587. [Google Scholar] [CrossRef] [PubMed]
- Chang, Y.C.; Chen, C.P.; Chen, C.C. Predicting skin permeability of chemical substances using a quantitative structure-activity relationship. Procedia Eng. 2012, 45, 875–879. [Google Scholar] [CrossRef]
- Cronin, M.T.D.; Dearden, J.C.; Moss, G.P.; Murray-Dickson, G. Investigation of the mechanism of flux across human skin in vitro by quantitative structure–permeability relationships. Eur. J. Pharm. Sci. 1999, 7, 325–330. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.; Yap, C.W.; Lim, P.F.C.; Chen, Y.Z.; Ho, P.C.; Chan, Y.W.; Wong, G.P.; Chan, S.Y. Formulation development of transdermal dosage forms: Quantitative structure-activity relationship model for predicting activities of terpenes that enhance drug penetration through human skin. J. Control Release 2007, 120, 211–219. [Google Scholar] [CrossRef] [PubMed]
- Neely, B.J.; Madihally, S.V.; Robinson, R.L., Jr.; Gasem, K.A. Nonlinear quantitative structure-property relationship modeling of skin permeation coefficient. J. Pharm. Sci. 2009, 98, 4069–4084. [Google Scholar] [CrossRef] [PubMed]
- Patel, H.; ten Berge, W.; Cronin, M.T. Quantitative structure–activity relationships (QSARs) for the prediction of skin permeation of exogenous chemicals. Chemosphere 2002, 48, 603–613. [Google Scholar] [CrossRef]
- Magnusson, B.M.; Pugh, W.J.; Roberts, M.S. Simple rules defining the potential of compounds for transdermal delivery or toxicity. Pharm. Res. 2004, 21, 1047–1054. [Google Scholar] [CrossRef]
- Liou, Y.B.; Ho, H.O.; Yang, C.J.; Lin, Y.K.; Sheu, M.T. Construction of a quantitative structure-permeability relationship (QSPR) for the transdermal delivery of NSAIDs. J. Control Release 2009, 138, 260–267. [Google Scholar] [CrossRef]
- Lian, G.; Chen, L.; Han, L. An evaluation of mathematical models for predicting skin permeability. J. Pharm. Sci. 2008, 97, 584–598. [Google Scholar] [CrossRef]
- Mitragotri, S. A theoretical analysis of permeation of small hydrophobic solutes across the stratum corneum based on Scaled Particle Theory. J. Pharm. Sci. 2002, 91, 744–752. [Google Scholar] [CrossRef]
- Alonso, C.; Carrer, V.; Espinosa, S.; Zanuy, M.; Cordoba, M.; Vidal, B.; Domínguez, M.; Godessart, N.; Coderch, L.; Pont, M. Prediction of the skin permeability of topical drugs using in silico and in vitro models. Eur. J. Pharm. Sci. 2019, 136, 104945. [Google Scholar] [CrossRef] [PubMed]
- Cleek, R.L.; Bunge, A.L. A new method for estimating dermal absorption from chemical exposure. 1. General approach. Pharm. Res. 1993, 10, 497–506. [Google Scholar] [CrossRef] [PubMed]
- Zheng, T.; Hopfinger, A.J.; Esposito, E.X.; Liu, J.; Tseng, Y.J. Membrane-Interaction Quantitative Structure-Activity Relationship (MI-QSAR) Analyses of Skin Penetration Enhancers. J. Chem. Infor. Model. 2008, 48, 1238–1256. [Google Scholar] [CrossRef] [PubMed]
- Drakulić, B.J.; Juranić, I.O.; Erić, S.; Zloh, M. Role of complexes formation between drugs and penetration enhancers in transdermal delivery. Int. J. Pharm. 2008, 363, 40–49. [Google Scholar] [CrossRef] [PubMed]
- Obata, Y.; Li, C.J.; Fujikawa, M.; Takayama, K.; Sato, H.; Higashiyama, K.; Isowa, K.; Nagai, T. Evaluation and structure–activity relationship of synthesized cyclohexanol derivatives on percutaneous absorption of ketoprofen using artificial neural network. Int. J. Pharm. 2001, 212, 223–231. [Google Scholar] [CrossRef] [PubMed]
- Kandimalla, K.K.; Kanikkannan, N.; Singh, M. Optimization of a vehicle mixture for the transdermal delivery of melatonin using artificial neural networks and response surface method. J. Control Release 1999, 61, 71–82. [Google Scholar] [CrossRef] [PubMed]
- Yerramsetty, K.M.; Neely, B.J.; Madihally, S.V.; Gasem, K.A.M. A skin permeability model of insulin in the presence of chemical penetration enhancer. Int. J. Pharm. 2010, 388, 13–23. [Google Scholar] [CrossRef]
- Keurentjes, A.J.; Maibach, H.I. Percutaneous penetration of drugs applied in transdermal delivery systems: An in vivo based approach for evaluating computer generated penetration models. Regul. Toxicol. Pharmacol. 2019, 108, 104428. [Google Scholar] [CrossRef]
- Vidović, D.; Milošević, N.; Pavlović, N.; Todorović, N.; Panić, J.Č.; Kovačević, S.; Banjac, M.K.; Podunavac-Kuzmanović, S.; Banjac, N.; Trišović, N.; et al. Predicting percutaneous permeation for new succinimide derivatives by in vitro and in silico models. J. Mol. Struc. 2023, 1274, 134516. [Google Scholar] [CrossRef]
- SwissADME. Available online: http://www.swissadme.ch/ (accessed on 1 September 2023).
- Pires, D.E.; Blundell, T.L.; Ascher, D.B. pkCSM: Predicting small-molecule pharmacokinetic and toxicity properties using graph-based signatures. J. Med. Chem. 2015, 58, 4066–4072. [Google Scholar] [CrossRef]
- PreADMET. Available online: https://preadmet.qsarhub.com/ (accessed on 1 September 2023).
- Wu, Y.W.; Ta, G.H.; Lung, Y.C.; Weng, C.F.; Leong, M.K. In Silico Prediction of Skin Permeability Using a Two-QSAR Approach. Pharmaceutics 2022, 14, 961. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.L.; Lyu, Y.C.; Leong, M.K. In silico prediction of the mutagenicity of nitroaromatic compounds using a novel two-QSAR approach. Toxicol. In Vitro 2017, 40, 102–114. [Google Scholar] [CrossRef] [PubMed]
- Leong, M.K.; Chen, Y.M.; Chen, T.H. Prediction of human cytochrome P450 2B6-substrate interactions using hierarchical support vector regression approach. J. Comput. Chem. 2009, 30, 1899–1909. [Google Scholar] [CrossRef] [PubMed]
- Soriano-Meseguer, S.; Fuguet, E.; Port, A.; Rosés, M. Optimization of experimental conditions for skin-PAMPA measurements. ADMET DMPK 2020, 8, 16–28. [Google Scholar] [CrossRef] [PubMed]
- Skin Permeation Calculator. Available online: https://www.cdc.gov/niosh/topics/skin/skinpermcalc.html (accessed on 1 September 2023).
- PreADMET. Available online: https://preadmet.webservice.bmdrc.org/ (accessed on 1 September 2023).
- Allen, D.G.; Rooney, J.; Kleinstreuer, N.; Lowit, A.; Perron, M. Retrospective analysis of dermal absorption triple pack data. ALTEX 2021, 38, 463–476. [Google Scholar] [CrossRef] [PubMed]
- Notman, R.; Anwar, J. Breaching the skin barrier—Insights from molecular simulation of model membranes. Adv. Drug Deliv. Rev. 2013, 65, 237–250. [Google Scholar] [CrossRef] [PubMed]
- Gupta, R.; Sridhar, D.B.; Rai, B. Molecular dynamics simulation study of permeation of molecules through skin lipid bilayer. J. Phys. Chem. B 2016, 120, 8987–8996. [Google Scholar] [CrossRef]
- MacDermaid, C.M.; Hall, K.W.; DeVane, R.H.; Klein, M.L.; Fiorin, G. Coexistence of lipid phases stabilizes interstitial water in the outer layer of mammalian skin. Biophys. J. 2020, 118, 1588–1601. [Google Scholar] [CrossRef]
- Rocco, P.; Cilurzo, F.; Minghetti, P.; Vistoli, G.; Pedretti, A. Molecular Dynamics as a tool for in silico screening of skin permeability. Eur. J. Pharm. Sci. 2017, 106, 328–335. [Google Scholar] [CrossRef]
- Piasentin, N.; Lian, G.; Cai, Q. In Silico Prediction of Stratum Corneum Partition Coefficients via COSMOmic and Molecular Dynamics Simulations. J. Phys. Chem. B 2023, 127, 2719–2728. [Google Scholar] [CrossRef]
- Lundborg, M.; Wennberg, C.; Lidmar, J.; Hess, B.; Lindahl, E.; Norlén, L. Skin permeability prediction with MD simulation sampling spatial and alchemical reaction coordinates. Biophys. J. 2022, 121, 3837–3849. [Google Scholar] [CrossRef] [PubMed]
- Machado, N.C.F.; dos Santos, L.; Carvalho, B.G.; Singh, P.; Soto, C.T.; Azoia, N.G.; Cavaco-Paulo, A.; Martin, A.A.; Favero, P.P. Assessment of penetration of Ascorbyl Tetraisopalmitate into biological membranes by molecular dynamics. Comput. Biol. Med. 2016, 75, 151–159. [Google Scholar] [CrossRef] [PubMed]
- Rim, J.E.; Pinsky, P.M.; van Osdol, W.W. Multiscale modeling framework of transdermal drug delivery. Ann. Biomed. Eng. 2009, 37, 1217–1229. [Google Scholar] [CrossRef]
- Li, N.; Quan, P.; Wan, X.; Liu, C.; Liu, X.; Fang, L. Mechanistic insights of the enhancement effect of sorbitan monooleate on olanzapine transdermal patch both in release and percutaneous absorption processes. Eur. J. Pharm. Sci. 2017, 107, 138–147. [Google Scholar] [CrossRef] [PubMed]
- Arellano, A.; Santoyo, S.; Martin, C.; Ygartua, P. Enhancing effect of terpenes on the in vitro percutaneous absorption of diclofenac sodium. Int. J. Pharm. 1996, 130, 141–145. [Google Scholar] [CrossRef]
- El-Kattan, A.F.; Asbill, C.S.; Michniak, B.B. The effect of terpene enhancer lipophilicity on the percutaneous permeation of hydrocortisone formulated in HPMC gel systems. Int. J. Pharm. 2000, 198, 179–189. [Google Scholar] [CrossRef] [PubMed]
- Ghafourian, T.; Zandasrar, P.; Hamishekar, H.; Nokhodchi, A. The effect of penetration enhancers on drug delivery through skin: A QSAR study. J. Control Release 2004, 99, 113–125. [Google Scholar] [CrossRef]
- Moghimi, H.R.; Williams, A.C.; Barry, B.W. Enhancement by terpenes of 5-fluorouracil permeation through the stratum comeum: Model solvent approach. J. Pharm. Pharmacol. 1998, 50, 955–964. [Google Scholar] [CrossRef]
- Williams, A.C.; Barry, B.W. The enhancement index concept applied to terpene penetration enhancers for human skin and model lipophilic (oestradiol) and hydrophilic (5-fluorouracil) drugs. Int. J. Pharm. 1991, 74, 157–168. [Google Scholar] [CrossRef]
- Djekic, L. Computer-aided formulation development of microemulsion systems. In Computer-Aided Applications in Pharmaceutical Technology, 2nd ed.; Djuris, J., Ed.; Woodhead Publishing Elsevier: Sawston, UK, 2023; pp. 41–59. [Google Scholar]
- Djekic, L.; Ibric, S.; Primorac, M. The application of artificial neural networks in the prediction of microemulsion phase boundaries in PEG-8 caprylic/capric glycerides based systems. Int. J. Pharm. 2008, 361, 41–46. [Google Scholar] [CrossRef]
- Chen, L.J.; Lian, G.P.; Han, L.J. Prediction of human skin permeability using artificial neural network (ANN) modeling 1. Acta Pharmacol. Sin. 2007, 28, 591–600. [Google Scholar] [CrossRef] [PubMed]
- Değim, T.; Hadgraft, J.; İlbasmiş, S.; Özkan, Y. Prediction of skin penetration using artificial neural network (ANN) modeling. J. Pharm. Sci. 2003, 92, 656–664. [Google Scholar] [CrossRef] [PubMed]
- Saini, S.; Singh, S.K.; Garg, A.; Khanna, K.; Shandil, A.; Mishra, D.N. Prediction of skin penetration using artificial neural network. Int. J. Eng. Sci. Technol. 2010, 2, 1526–1531. [Google Scholar]
- Takahara, J.; Takayama, K.; Isowa, K.; Nagai, T. Multi-objective simultaneous optimization based on artificial neural network in a ketoprofen hydrogel formula containing O-ethylmenthol as a percutaneous absorption enhancer. Int. J. Pharm. 1997, 158, 203–210. [Google Scholar] [CrossRef]
- Takayama, K.; Takahara, J.; Fujikawa, M.; Ichikawa, H.; Nagai, T. Formula optimization based on artificial neural networks in transdermal drug delivery. J. Control Release 1999, 62, 161–170. [Google Scholar] [CrossRef]
- Iyer, M.; Zheng, T.; Hopfinger, A.J.; Tseng, Y.J. QSAR analyses of skin penetration enhancers. J. Chem. Inf. Model. 2007, 47, 1130–1149. [Google Scholar] [CrossRef]
- Iyer, M.; Mishra, R.; Han, Y.; Hopfinger, A.J. Predicting blood–brain barrier partitioning of organic molecules using membrane–interaction QSAR analysis. Pharm. Res. 2002, 19, 1611–1621. [Google Scholar] [CrossRef]
| Name | Equation | Denotations |
|---|---|---|
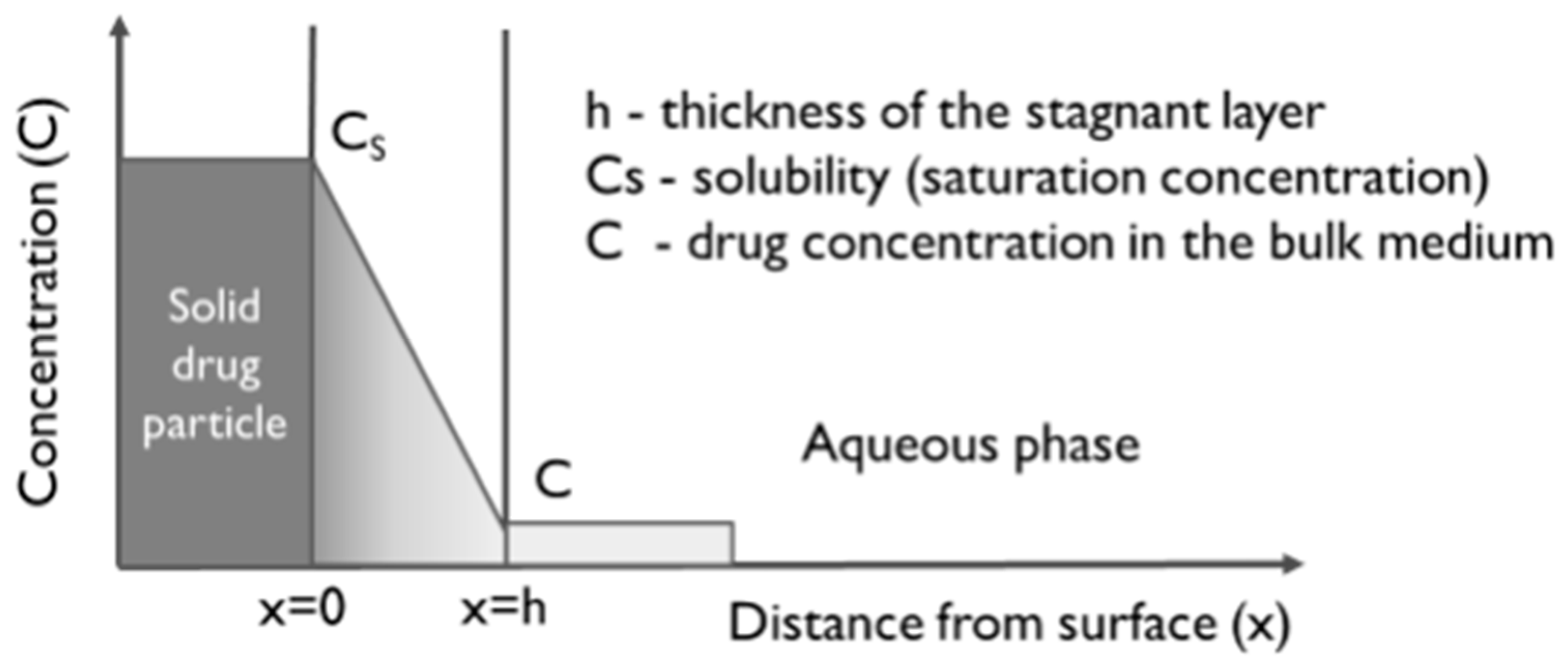
| Nernst–Brunner equation | Mdissol—dissolved amount of drug t—time Cs—solubility (saturation concentration) Ct—drug concentration in solution at time t D—diffusion coefficient h—diffusion layer thickness A—effective surface area ρ—particle density r—spherical particle radius s—shape factor L—particle length d—particle diameter Mundissol—undissolved amount of drug at time t Mundissol(0)—initial amount of the solid drug z *—hybrid dissolution parameter | |
| Johnson equation | ||
| Wang–Flanagan equation | ||
| z-parameter equation * |
| Device Type | Slab | Sphere | Cylinder |
|---|---|---|---|
| Reservoir device with non-constant activity source < | |||
| Reservoir device with constant activity source > | |||
| Matrix systems as monolithic solutions < | |||
| Matrix systems as monolithic dispersions > |
| Delivery System Geometry | Release Mechanism | ||
|---|---|---|---|
| Thin Film | Cylinder | Slab | |
| 0.5 0.5 < < 1.0 | 0.45 0.45 < < 0.89 | 0.43 0.43 < < 0.85 | Fickian diffusion Anomalous transport (combined mechanisms) |
| 1.0 | 0.89 | 0.85 | Case II transport (usually synchronized swelling and erosion of polymers) |
| >1.0 | >0.89 | >0.85 | Super Case II transport |
| Method | API, Delivery System/Dosage Form | Studied Process | References |
|---|---|---|---|
| ATR-FTIR * imaging | Ibuprofen (acid and salt formulations) in amorphous solid dispersions produced through hot-melt extrusion with copovidone and Soluplus® | Interaction of different forms of ibuprofen with polymers: in extrudates with its acidic form, ibuprofen was found to interact with polymers by forming hydrogen bonds, resulting in more sustained drug release. | [83] |
| Ibuprofen (crystalline and amorphous form) in physical mixtures (PM) and hot-melt loaded (HML) mesoporous silica microparticles | Based on the chemical images, the faster release of amorphous ibuprofen from HML tablets compared to crystalline ibuprofen in PM tablets was observed. Ibuprofen dissolved from the PM tablets was adsorbed on the surface of the silica particles. | [84] | |
| Indomethacin formulated with nicotinamide, urea, and mannitol in different ratios | The observed changes in the release kinetics of indomethacin (from first-order to zero-order) can be interpreted from the results of the spatial distribution of the components during the dissolution. | [85] | |
| UV-Vis imaging system | Placebo hydrophilic matrix tablets made of two HPMC ** grades | The swelling behavior of hydrophilic matrices of two HPMC grades with different particle morphology and using two compression forces. | [86] |
| Metformin extended-release tablets | The release of metformin and the swelling of the polymer matrix were monitored simultaneously (at 255 nm and 520 nm, respectively). | [87] | |
| Propranolol formulated in liqui-solid compacts of Sesamum radiatum gum | Differences in the release behavior of propranolol from physical mixtures and liqui-solid formulations were observed. | [88] | |
| UV-imaging system | Tablets with paracetamol or carbamazepine were formulated with super disintegrants (sodium starch glycolate or croscarmellose sodium) | The influence of the properties of the active substance and the properties and variability of the excipients on the release of the drug were investigated. | [89] |
| NIR ***-imaging system | Paracetamol in hydrophilic matrix tablets | Coupling hydrodynamic studies with NIR chemical imaging and dissolution data provided new insights into the mechanisms of drug release. | [90] |
| Process | Equation | Denotations |
|---|---|---|
| Passive diffusion | (Fick´s first law of diffusion) | dM/dt—drug diffusion rate D—diffusion coefficient A—membrane surface area h—membrane thickness C1—concentration in the GI lumen C2—concentration in the blood P—partition coefficient between the lipid membrane and GI fluids V—uptake rate Vmax—maximum uptake rate Km—Michaelis–Menten constant Csubs—substrate concentration Ppara—paracellular permeability ε—porosity δ—pore length F(r/R)—Renkin function r—drug molecular radius R—radius of the pore κ(z)—electrochemical energy function (for the charged species with z valence) |
(Modified Fick´s first law of diffusion) | ||
| Active transport | (Michaelis-Menten equation) | |
| Convective (paracellular) transport | (Adson equation) |
| Method | Equation | Denotations |
|---|---|---|
| Non-cell-based methods (e.g., PAMPA * test) | Papp—apparent permeability coefficient Peff—effective permeability dQ/dt—permeability rate A—membrane surface area C0—initial drug concentration Q—perfusion flow rate Cin′—inlet drug concentrations adjusted for water transport Cout′—outlet drug concentrations adjusted for water transport R—radius of the perfused intestinal segment L—length of the perfused intestinal segment | |
| Cell-based methods (e.g., Caco-2 cells **, MDCK cells ***) | ||
| Animal models (e.g., rat) | ||
| Human studies (e.g., Loc-I-Gut [141]) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Djuris, J.; Cvijic, S.; Djekic, L. Model-Informed Drug Development: In Silico Assessment of Drug Bioperformance following Oral and Percutaneous Administration. Pharmaceuticals 2024, 17, 177. https://doi.org/10.3390/ph17020177
Djuris J, Cvijic S, Djekic L. Model-Informed Drug Development: In Silico Assessment of Drug Bioperformance following Oral and Percutaneous Administration. Pharmaceuticals. 2024; 17(2):177. https://doi.org/10.3390/ph17020177
Chicago/Turabian StyleDjuris, Jelena, Sandra Cvijic, and Ljiljana Djekic. 2024. "Model-Informed Drug Development: In Silico Assessment of Drug Bioperformance following Oral and Percutaneous Administration" Pharmaceuticals 17, no. 2: 177. https://doi.org/10.3390/ph17020177
APA StyleDjuris, J., Cvijic, S., & Djekic, L. (2024). Model-Informed Drug Development: In Silico Assessment of Drug Bioperformance following Oral and Percutaneous Administration. Pharmaceuticals, 17(2), 177. https://doi.org/10.3390/ph17020177