A Density Functional Theory and Information-Theoretic Approach Study of Interaction Energy and Polarizability for Base Pairs and Peptides
Abstract
:1. Introduction
2. Results
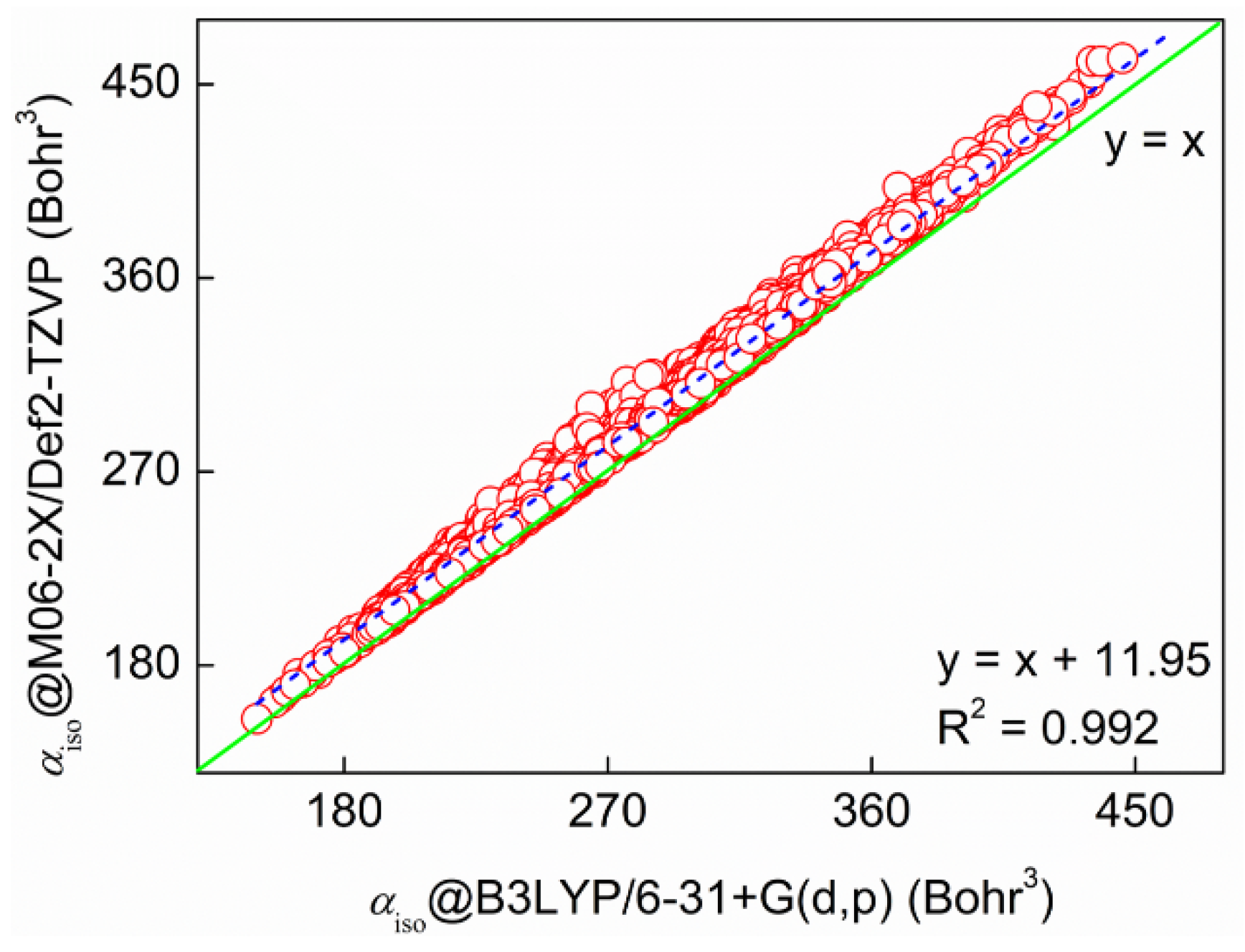
2.1. Validation
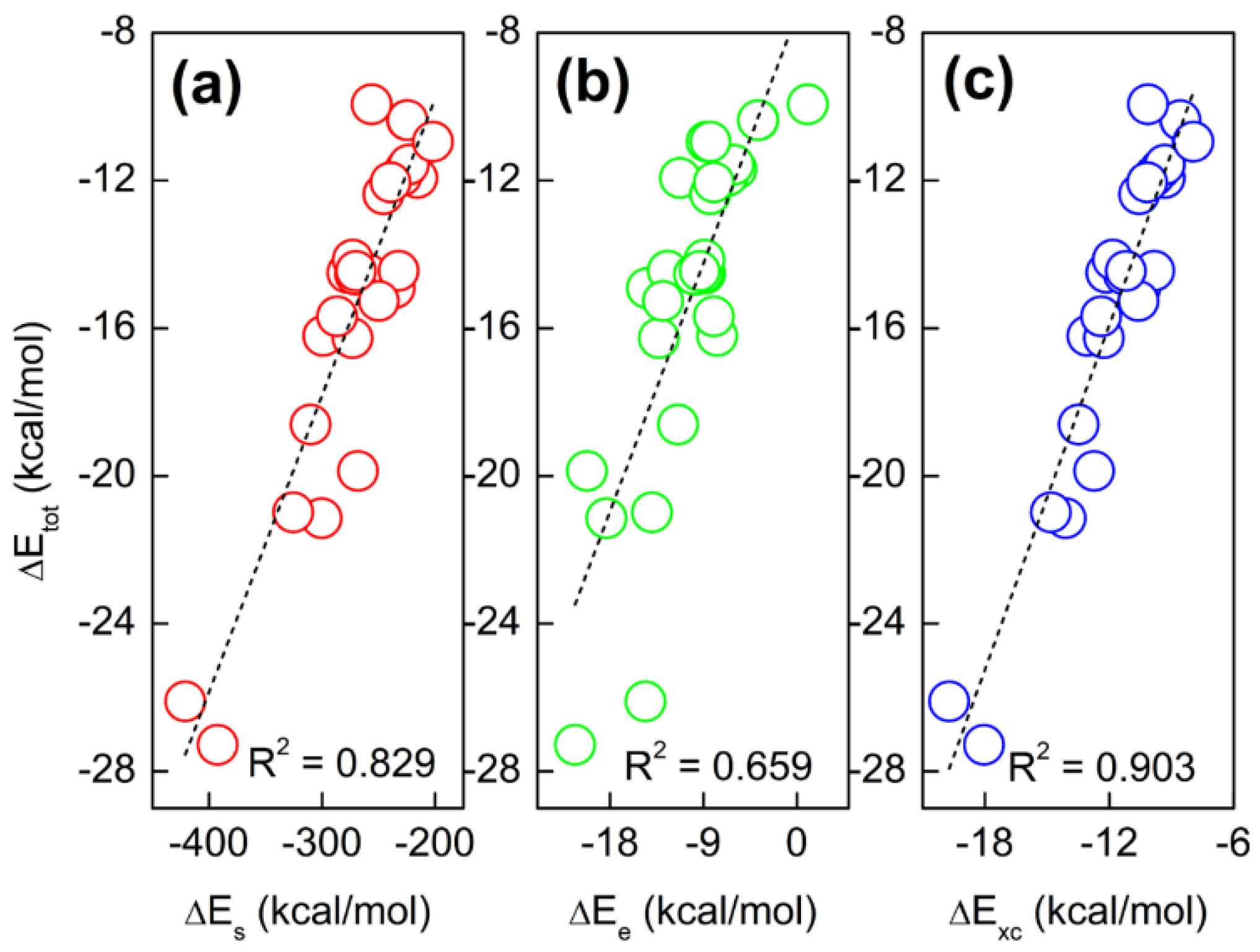
2.2. Total Energy Decomposition of Base Pairs
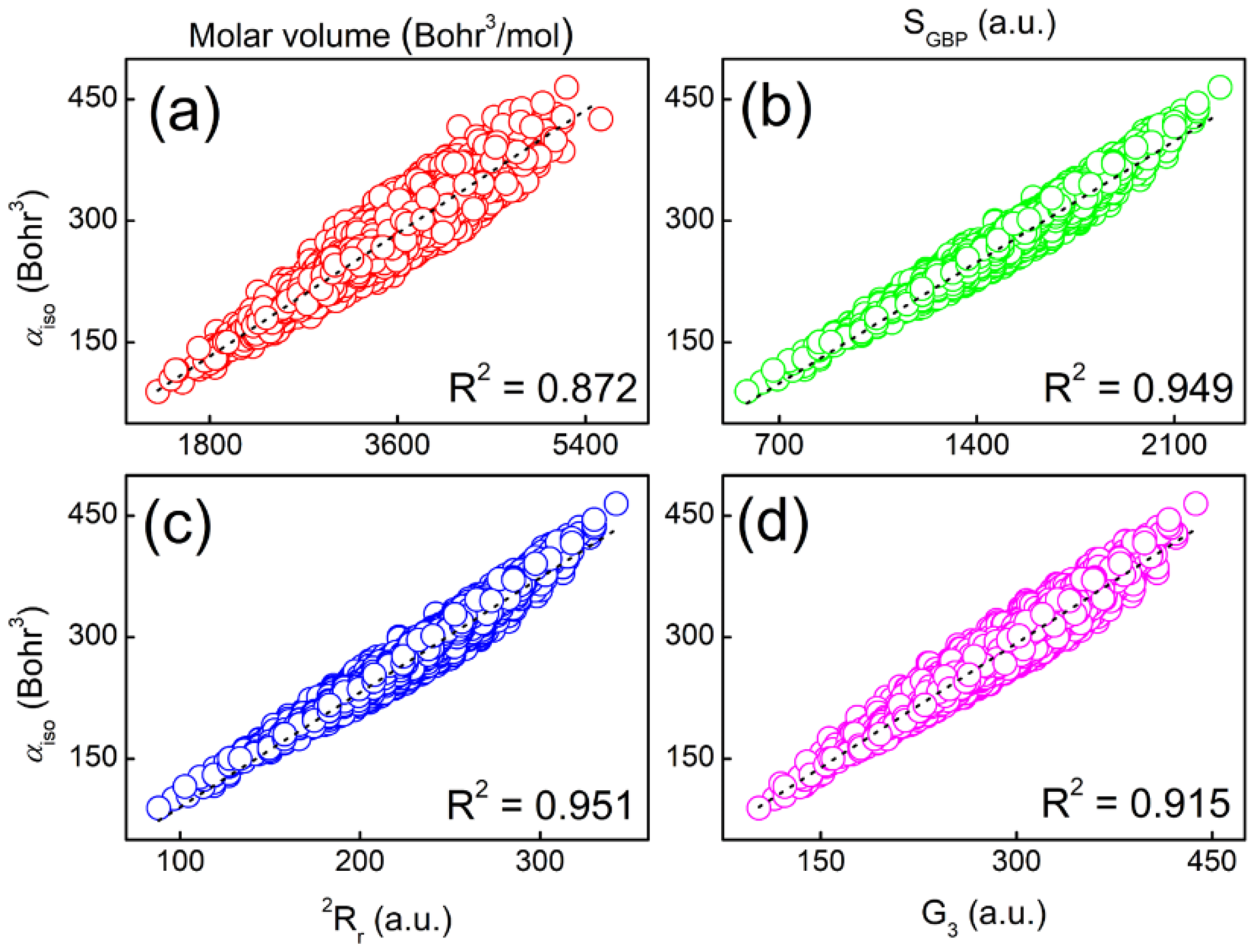
2.3. Molecular Polarizabilities of Base Pairs
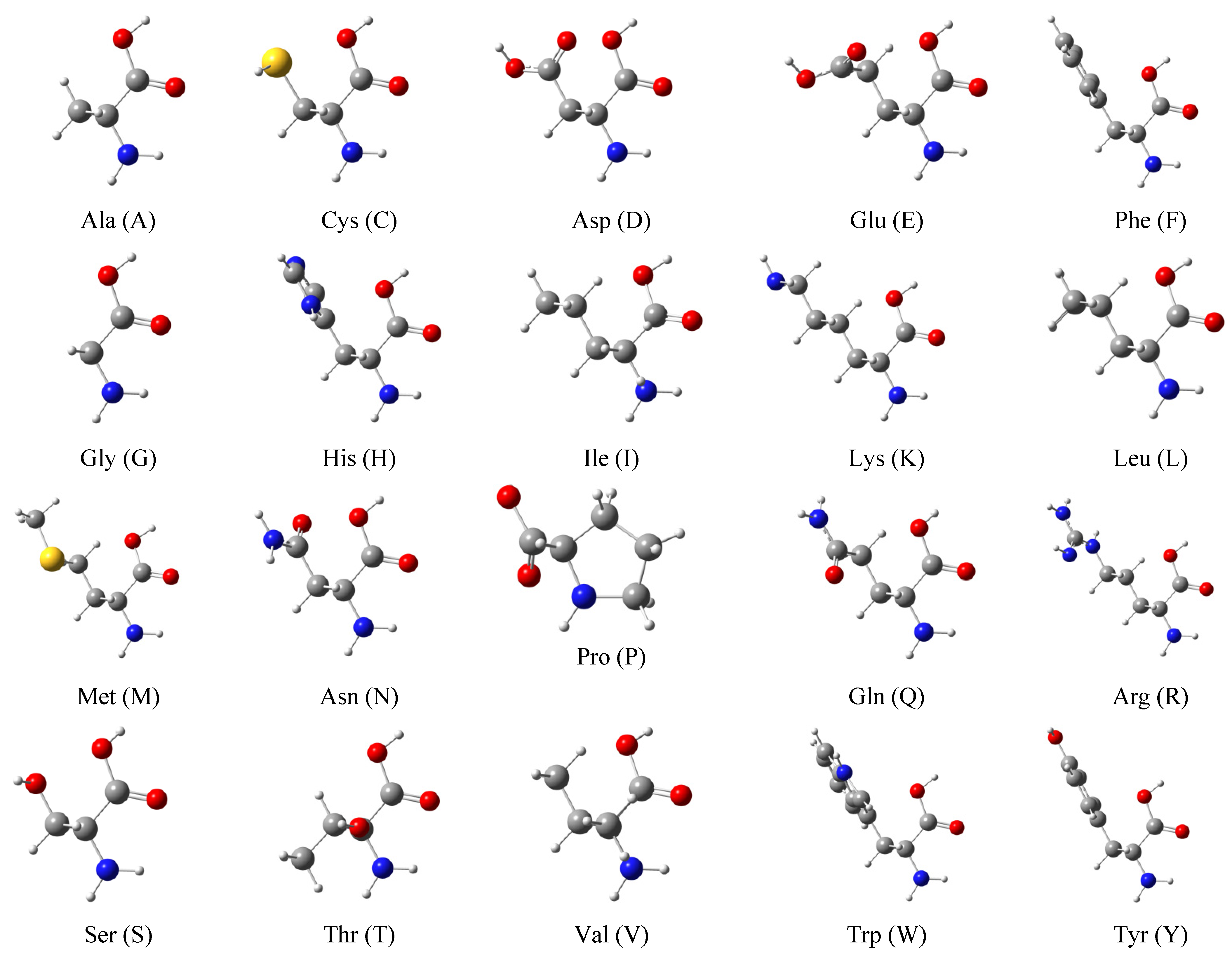
2.4. Molecular Polarizabilities of Amino Acids, Dipeptides and Tripeptides
3. Discussion
4. Materials and Methods
4.1. Energy Decomposition Schemes in DFT
4.2. Information-Theoretic Approach Quantities
4.3. Computational Details
4.3.1. Base Pairs
4.3.2. Amino Acids, Dipeptides, and Tripeptides
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Šponer, J.; Leszczynski, J.; Hobza, P. Structures and Energies of Hydrogen-Bonded DNA Base Pairs. A Nonempirical Study with Inclusion of Electron Correlation. J. Phys. Chem. 1996, 100, 1965–1974. [Google Scholar] [CrossRef]
- Hobza, P.; Šponer, J. Structure, Energetics, and Dynamics of the Nucleic Acid Base Pairs: Nonempirical Ab Initio Calculations. Chem. Rev. 1999, 99, 3247–3276. [Google Scholar] [CrossRef] [PubMed]
- Guerra, C.F.; Bickelhaupt, F.M.; Snijders, J.G.; Baerends, E.J. Hydrogen Bonding in DNA Base Pairs: Reconciliation of Theory and Experiment. J. Am. Chem. Soc. 2000, 122, 4117–4128. [Google Scholar] [CrossRef] [Green Version]
- Parthasarathi, R.; Amutha, R.; Subramanian, V.; Nair, B.U.; Ramasami, T. Bader’s and Reactivity Descriptors’ Analysis of DNA Base Pairs. J. Phys. Chem. A 2004, 108, 3817–3828. [Google Scholar] [CrossRef]
- Toczyłowski, R.R.; Cybulski, S.M. An Analysis of the Interactions between Nucleic Acid Bases: Hydrogen-Bonded Base Pairs. J. Phys. Chem. A 2003, 107, 418–426. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W.T. Density Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1989. [Google Scholar]
- Liu, S.B. Steric effect: A quantitative description from density functional theory. J. Chem. Phys. 2007, 126, 244103. [Google Scholar] [CrossRef] [PubMed]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Fisher, R.A. Theory of statistical estimation. Math. Proc. Camb. Philos. Soc. 1925, 22, 700–725. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, S.K.; Berkowitz, M.; Parr, R.G. Transcription of ground-state density-functional theory into a local thermodynamics. Proc. Natl. Acad. Sci. USA 1984, 81, 8028–8031. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.B.; Rong, C.Y.; Wu, Z.M.; Lu, T. Rényi entropy, Tsallis entropy and Onicescu information energy in density functional reactivity theory. Acta Phys. Chim. Sin. 2015, 31, 2057–2063. [Google Scholar] [CrossRef]
- Kullback, S. Information Theory and Statistics; Dover Publications: Mineola, NY, USA, 1997. [Google Scholar]
- Liu, S.B. Identity for Kullback-Leibler divergence in density functional reactivity theory. J. Chem. Phys. 2019, 151, 141103. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, D.B.; Lu, T.; Liu, S.B.; Rong, C.Y. Quantifications and Applications of Relative Fisher Information in Density Functional Theory. J. Phys. Chem. A 2021, 125, 3802–3811. [Google Scholar] [CrossRef]
- McWeeny, R. Some recent advances in density matrix theory. Rev. Mod. Phys. 1960, 32, 335–369. [Google Scholar] [CrossRef]
- Langhoff, P.W.; Karplus, M.; Hurst, R.P. Approximations to Hartree—Fock Perturbation Theory. J. Chem. Phys. 1966, 44, 505–514. [Google Scholar] [CrossRef]
- Colwell, S.M.; Murray, C.W.; Handy, N.C.; Amos, R.D. The determination of hyperpolarisabilities using density functional theory. Chem. Phys. Lett. 1993, 210, 261–268. [Google Scholar] [CrossRef]
- Grisafi, A.; Wilkins, D.M.; Csányi, G.; Ceriotti, M. Symmetry-Adapted Machine Learning for Tensorial Properties of Atomistic Systems. Phys. Rev. Lett. 2018, 120, 036002. [Google Scholar] [CrossRef] [Green Version]
- Wilkins, D.M.; Grisafi, A.; Yang, Y.; Lao, K.U.; DiStasio, R.A., Jr.; Ceriotti, M. Accurate molecular polarizabilities with coupled cluster theory and machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 3401–3406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, V.H.A.; Lunghi, A. Predicting tensorial molecular properties with equivariant machine learning models. Phys. Rev. B 2022, 105, 165131. [Google Scholar] [CrossRef]
- Amin, M.; Samy, H.; Küpper, J. Robust and Accurate Computational Estimation of the Polarizability Tensors of Macromolecules. J. Phys. Chem. Lett. 2019, 10, 2938–2943. [Google Scholar] [CrossRef] [Green Version]
- Hait, D.; Head-Gordon, M. How accurate are static polarizability predictions from density functional theory? An assessment over 132 species at equilibrium geometry. Phys. Chem. Chem. Phys. 2018, 20, 19800–19810. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yanai, T.; Tew, D.; Handy, N. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6169. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-Range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [Green Version]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian-basis sets for molecular calculations. 1. Second row atoms, Z = 11 ‒ 18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Dunning, T.H., Jr. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- McMeekin, T.L.; Groves, M.L.; Wilensky, M. Refractive indices of proteins in relation to amino acid composition and specific volume. Biochem. Biophys. Res. Commun. 1962, 7, 151–156. [Google Scholar] [CrossRef]
- Krishtal, A.; Senet, P.; Alsenoy, C.V. Local softness, softness dipole, and polarizabilities of functional groups: Application to the side chains of the 20 amino acids. J. Chem. Phys. 2009, 131, 044312. [Google Scholar] [CrossRef] [Green Version]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Simon, S.; Duran, M.; Dannenberg, J.J. How does basis set superposition error change the potential surfaces for hydrogen-bonded dimers? J. Chem. Phys. 1996, 105, 11024–11031. [Google Scholar] [CrossRef] [Green Version]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theoret. Chim. Acta 1977, 44, 129–138. [Google Scholar] [CrossRef]
- Becke, A.D. A multicenter numerical integration scheme for polyatomic molecules. J. Chem. Phys. 1988, 88, 2547–2553. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Nagle, J.K. 2018 Table of static dipole polarizabilities of the neutral elements in the periodic table. Mol. Phys. 2018, 117, 1200–1225. [Google Scholar] [CrossRef] [Green Version]
- Szabó, P.; Góger, S.; Charry, J.; Karimpour, M.R.; Fedorov, D.V.; Tkatchenko, A. Four-Dimensional Scaling of Dipole Polarizability in Quantum Systems. Phys. Rev. Lett. 2022, 128, 070602. [Google Scholar] [CrossRef] [PubMed]
- Condon, E.U. Handbook of Physics; Condon, E.U., Odishaw, H., Eds.; McGraw-Hill: New York, NY, USA, 1958; pp. 4–22. [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 2nd ed.; Wiley: New York, NY, USA, 1975; pp. 60–62. [Google Scholar]
- Dmitrieva, I.K.; Plindov, G.I. Dipole Polarizability, Radius and Ionization Potential for Atomic Systems. Phys. Scr. 1983, 27, 402. [Google Scholar] [CrossRef]
- Gough, K.M. Theoretical analysis of molecular polarizabilities and polarizability derivatives in hydrocarbons. J. Chem. Phys. 1989, 91, 2424–2432. [Google Scholar] [CrossRef]
- Laidig, K.E.; Bader, R.F.W. Properties of atoms in molecules: Atomic polarizabilities. J. Chem. Phys. 1990, 93, 7213–7224. [Google Scholar] [CrossRef]
- Brinck, T.; Murray, J.S.; Politzer, P. Polarizability and volume. J. Chem. Phys. 1993, 98, 4305–4306. [Google Scholar]
- Politzer, P.; Jin, P.; Murray, J.S. Atomic polarizability, volume and ionization energy. J. Chem. Phys. 2002, 117, 8197–8202. [Google Scholar] [CrossRef]
- Blair, S.A.; Thakkar, A.J. Relating polarizability to volume, ionization energy, electronegativity, hardness, moments of momentum, and other molecular properties. J. Chem. Phys. 2014, 141, 074306. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, W.; Fang, T. An Efficient Fragment-Based Approach for Predicting the Ground-State Energies and Structures of Large Molecules. J. Am. Chem. Soc. 2005, 127, 7215–7226. [Google Scholar] [PubMed]
- Li, W.; Li, S.; Jiang, Y. Generalized Energy-Based Fragmentation Approach for Computing the Ground-State Energies and Properties of Large Molecules. J. Phys. Chem. A 2007, 111, 2193–2199. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Li, W.; Ma, J. Generalized Energy-Based Fragmentation Approach and Its Applications to Macromolecules and Molecular Aggregates. Acc. Chem. Res. 2014, 47, 2712–2720. [Google Scholar]
- Li, W.; Dong, H.; Ma, J.; Li, S. Structures and Spectroscopic Properties of Large Molecules and Condensed-Phase Systems Predicted by Generalized Energy-Based Fragmentation Approach. Acc. Chem. Res. 2021, 54, 169–181. [Google Scholar] [CrossRef]
- Jayatilaka, D.; Jha, K.K.; Munshi, P. Is it Reasonable to Obtain Information on the Polarizability and Hyperpolarizability Only from the Electron Density? Aust. J. Chem. 2018, 71, 295–306. [Google Scholar] [CrossRef]
- Rong, C.Y.; Wang, B.; Zhao, D.B.; Liu, S.B. Information-Theoretic approach in density functional theory and its recent applications to chemical problems. WIREs Comput. Mol. Sci. 2020, 10, e1461. [Google Scholar] [CrossRef]
- Liu, S.B. On the relationship between densities of Shannon entropy and Fisher information for atoms and molecules. J. Chem. Phys. 2007, 126, 191107. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.B. Homochirality Originates from Handedness of Helices. J. Phys. Chem. Lett. 2020, 11, 8690–8696. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.B. Principle of Chirality Hierarchy in Three-Blade Propeller Systems. J. Phys. Chem. Lett. 2021, 12, 8720–8725. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.; Millam, J. (Eds.) GaussView, Version 5; Semichem Inc.: Shawnee, KS, USA, 2009. [Google Scholar]
- Tian, C.; Kasavajhala, K.; Belfon, K.A.A.; Raguette, L.; Huang, H.; Migues, A.N.; Bickel, J.; Wang, Y.; Pincay, J.; Wu, Q.; et al. ff19SB: Amino-Acid-Specific Protein Backbone Parameters Trained against Quantum Mechanics Energy Surfaces in Solution. J. Chem. Theory Comput. 2020, 16, 528–552. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Adelman, S.; Doll, J. Generalized Langevin equation approach for atom/solid-surface scattering: General formulation for classical scattering off harmonic solids. J. Chem. Phys. 1976, 64, 2375–2388. [Google Scholar] [CrossRef]
- Feller, S.E.; Zhang, Y.; Pastor, R.W.; Brooks, B.R. Constant pressure molecular dynamics simulation: The Langevin piston method. J. Chem. Phys. 1995, 103, 4613–4621. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N·log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef] [Green Version]
- Goetz, A.W.; Williamson, M.J.; Xu, D.; Poole, D.; Le Grand, S.; Walker, R.C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 1. Generalized Born. J. Chem. Theory Comput. 2012, 8, 1542–1555. [Google Scholar] [CrossRef]
- Salomon-Ferrer, R.; Goetz, A.W.; Poole, D.; Le Grand, S.; Walker, R.C. Routine microsecond molecular dynamics simulations with AMBER on GPUs. 2. Explicit solvent Particle Mesh Ewald. J. Chem. Theory Comput. 2013, 9, 3878–3888. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Lu, T.; Chen, F.W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]


| Methods | 6-311G(d,p) | Def2-SVP | Def2-TZVP | aug-cc-pVTZ | ||||
|---|---|---|---|---|---|---|---|---|
| MUE c | MSE d | MUE | MSE | MUE | MSE | MUE | MSE | |
| M06-2X | −15.3 | 15.3 | −18.4 | 18.4 | −8.9 | 8.9 | −3.7 | 3.8 |
| B3LYP | −10.7 | 10.7 | −13.6 | 13.6 | −4.6 | 4.6 | −0.3 | 1.6 |
| CAM-B3LYP | −13.9 | 13.9 | −1.3 | 2.2 | −7.8 | 7.8 | −4.6 | 4.6 |
| PBE0 | −12.4 | 12.4 | −15.2 | 15.2 | −6.0 | 6.0 | −1.9 | 2.6 |
| ωB97XD | −14.2 | 14.2 | −17.1 | 17.1 | −8.1 | 8.1 | −5.1 | 5.2 |
| MP2 b | −15.6 | 15.6 | ||||||
| Base Pair | ΔTs | ΔEx | ΔEc | ΔExc | ΔEe | ΔEs | ΔEq | ΔE |
|---|---|---|---|---|---|---|---|---|
| C-G-WC | 12.1 | −1.5 | −16.6 | −18.0 | −21.4 | −392.3 | 386.4 | −27.3 |
| G-G-1 | 8.2 | −2.4 | −17.4 | −19.7 | −14.6 | −421.0 | 409.4 | −26.1 |
| C-HX | 11.3 | −0.4 | −13.7 | −14.1 | −18.4 | −300.3 | 297.5 | −21.1 |
| T-G-3 | 7.8 | −1.6 | −13.2 | −14.8 | −14.0 | −325.5 | 318.5 | −21.0 |
| G-G-3 | 6.3 | −0.9 | −12.5 | −13.5 | −11.5 | −310.0 | 302.9 | −18.6 |
| C-C-1 | 13.1 | 0.3 | −13.0 | −12.7 | −20.2 | −268.2 | 268.6 | −19.9 |
| T-G-1 | 4.5 | −0.8 | −12.3 | −13.1 | −7.7 | −298.9 | 290.4 | −16.2 |
| A-G-1 | 9.3 | 1.2 | −13.5 | −12.3 | −13.3 | −273.0 | 270.0 | −16.3 |
| T-G-2 | 4.7 | −0.6 | −11.8 | −12.4 | −8.0 | −286.7 | 279.1 | −15.7 |
| C-A-1 | 10.1 | 0.8 | −11.3 | −10.5 | −14.5 | −235.8 | 235.4 | −14.9 |
| T-A-H | 6.3 | 0.8 | −12.0 | −11.2 | −9.6 | −270.3 | 265.4 | −14.5 |
| T-A-RH | 6.2 | 0.8 | −12.0 | −11.2 | −9.4 | −270.0 | 264.9 | −14.4 |
| C-G-1 | 5.6 | 0.2 | −11.4 | −11.2 | −8.8 | −259.9 | 254.2 | −14.5 |
| C-A-2 | 7.8 | 1.5 | −11.3 | −9.8 | −12.4 | −232.2 | 230.2 | −14.4 |
| FU-A | 6.7 | 0.6 | −12.7 | −12.1 | −9.1 | −277.6 | 272.2 | −14.5 |
| T-A-WC | 6.7 | 0.8 | −12.1 | −11.3 | −9.9 | −270.7 | 266.0 | −14.5 |
| U-A | 6.6 | 0.7 | −12.5 | −11.8 | −8.9 | −272.9 | 267.6 | −14.1 |
| A-G-3 | 8.2 | 2.0 | −12.6 | −10.6 | −12.9 | −249.8 | 247.5 | −15.3 |
| T-A-RWC | 6.1 | 0.8 | −12.0 | −11.2 | −9.4 | −269.9 | 264.9 | −14.4 |
| A-A-1 | 8.7 | 0.9 | −10.2 | −9.3 | −11.3 | −215.8 | 215.1 | −11.9 |
| A-G-4 | 1.9 | 1.5 | −10.1 | −8.6 | −3.7 | −224.8 | 218.1 | −10.4 |
| C-T-2 | 6.5 | 1.3 | −11.9 | −10.6 | −8.4 | −245.6 | 241.6 | −12.4 |
| A-A-2 | 5.7 | 1.4 | −9.3 | −8.0 | −8.7 | −202.1 | 199.8 | −10.9 |
| T-T-1 | 3.6 | 0.1 | −9.7 | −9.5 | −5.8 | −226.1 | 220.3 | −11.7 |
| T-T-2 | 4.6 | 0.0 | −9.8 | −9.8 | −6.7 | −229.4 | 224.1 | −11.9 |
| T-T-3 | 3.8 | 0.2 | −9.5 | −9.3 | −6.1 | −223.2 | 217.7 | −11.6 |
| C-T-1 | 6.1 | 1.5 | −11.7 | −10.2 | −8.0 | −239.4 | 235.3 | −12.0 |
| A-G-2 | 1.9 | 1.5 | −10.1 | −8.6 | −3.7 | −224.4 | 217.8 | −10.4 |
| A-A-3 | 5.3 | 1.4 | −9.3 | −7.9 | −8.3 | −201.8 | 199.2 | −10.9 |
| G-G-4 | −0.9 | 0.8 | −11.0 | −10.1 | 1.1 | −256.2 | 245.2 | −9.9 |
| Base Pair | Polar | Vol | SS | IF | SGBP | E2 | E3 | rR2 | rR3 | G1 | G2 | G3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C-G-WC | 170.2 | 1984.1 | 99.2 | 5854.3 | 924.3 | 866.2 | 48,121.2 | 138.8 | 143.9 | −22.5 | 9.3 | 169.0 |
| G-G-1 | 197.2 | 1954.2 | 109.9 | 6775.8 | 1060.1 | 1002.5 | 55,241.1 | 159.1 | 164.8 | −23.4 | 8.7 | 194.8 |
| C-HX | 159.1 | 1863.3 | 93.6 | 5514.6 | 870.1 | 814.0 | 45,149.3 | 130.6 | 135.6 | −23.6 | 11.2 | 157.8 |
| T-G-3 | 180.1 | 2060.0 | 105.0 | 6215.6 | 978.7 | 927.0 | 53,287.8 | 147.0 | 152.7 | −26.6 | 12.1 | 177.2 |
| G-G-3 | 194.4 | 2184.6 | 110.2 | 6777.3 | 1060.3 | 1002.5 | 55,250.6 | 159.1 | 164.9 | −23.6 | 8.7 | 194.0 |
| C-C-1 | 144.9 | 1731.0 | 88.8 | 4934.0 | 788.7 | 730.0 | 41,006.7 | 118.5 | 123.3 | −21.5 | 9.9 | 142.1 |
| T-G-1 | 177.3 | 2058.5 | 105.1 | 6216.0 | 978.7 | 926.9 | 53,282.0 | 147.0 | 152.7 | −26.7 | 12.5 | 177.1 |
| A-G-1 | 191.7 | 2146.7 | 108.8 | 6327.7 | 1005.6 | 921.3 | 48,236.1 | 151.0 | 156.6 | −24.7 | 10.6 | 186.1 |
| T-G-2 | 177.2 | 2016.1 | 105.1 | 6216.1 | 978.8 | 926.9 | 53,283.8 | 147.0 | 152.7 | −26.7 | 12.3 | 177.0 |
| C-A-1 | 165.7 | 1707.8 | 98.2 | 5406.3 | 869.9 | 785.1 | 41,120.1 | 130.7 | 135.9 | −23.5 | 10.5 | 159.8 |
| T-A-H | 169.8 | 2060.1 | 103.7 | 5766.3 | 924.1 | 845.6 | 46,267.5 | 138.9 | 144.5 | −27.5 | 13.9 | 169.1 |
| T-A-RH | 169.6 | 1997.3 | 103.8 | 5766.3 | 924.1 | 845.7 | 46,272.0 | 138.9 | 144.5 | −27.5 | 13.8 | 169.0 |
| C-G-1 | 147.8 | 1899.5 | 99.6 | 5856.5 | 924.6 | 866.3 | 48,137.5 | 138.8 | 144.0 | −22.8 | 9.7 | 167.6 |
| C-A-2 | 164.4 | 1810.0 | 98.2 | 5406.4 | 869.9 | 785.1 | 41,118.5 | 130.7 | 135.9 | −23.6 | 10.8 | 159.9 |
| FU-A | 158.2 | 1839.0 | 90.1 | 6089.2 | 925.1 | 933.8 | 59,941.1 | 138.6 | 143.4 | −23.2 | 10.5 | 162.2 |
| T-A-WC | 169.7 | 1950.4 | 103.7 | 5766.3 | 924.1 | 845.6 | 46,264.0 | 138.9 | 144.5 | −27.5 | 14.0 | 169.1 |
| U-A | 157.9 | 1892.1 | 93.6 | 5514.7 | 870.1 | 814.0 | 45,157.7 | 130.6 | 135.6 | −23.7 | 11.0 | 157.6 |
| A-G-3 | 190.2 | 2205.6 | 108.9 | 6328.0 | 1005.6 | 921.4 | 48,248.3 | 151.0 | 156.6 | −24.8 | 10.1 | 186.1 |
| T-A-RWC | 169.7 | 2093.3 | 103.8 | 5766.3 | 924.1 | 845.7 | 46,279.4 | 138.9 | 144.5 | −27.5 | 13.4 | 169.0 |
| A-A-1 | 186.9 | 2020.8 | 107.6 | 5878.4 | 951.0 | 840.0 | 41,215.1 | 142.9 | 148.5 | −25.5 | 12.0 | 177.5 |
| A-G-4 | 189.6 | 2119.7 | 109.0 | 6328.3 | 1005.7 | 921.3 | 48,241.8 | 151.0 | 156.6 | −24.7 | 10.4 | 185.3 |
| C-T-2 | 150.7 | 1701.9 | 94.4 | 5294.8 | 843.0 | 790.8 | 46,189.2 | 126.7 | 131.9 | −25.7 | 12.1 | 150.9 |
| A-A-2 | 185.3 | 2157.6 | 107.7 | 5878.6 | 951.0 | 840.0 | 41,219.9 | 142.9 | 148.5 | −25.6 | 11.8 | 177.6 |
| T-T-1 | 158.4 | 1822.9 | 100.1 | 5655.5 | 897.3 | 851.3 | 51,315.6 | 135.0 | 140.6 | −29.8 | 16.3 | 159.7 |
| T-T-2 | 158.2 | 1918.8 | 100.1 | 5655.5 | 897.3 | 851.2 | 51,313.7 | 134.9 | 140.6 | −29.8 | 16.5 | 159.7 |
| T-T-3 | 158.7 | 1961.9 | 100.1 | 5655.5 | 897.3 | 851.3 | 51,318.3 | 135.0 | 140.6 | −29.8 | 16.0 | 159.8 |
| C-T-1 | 150.3 | 1874.4 | 94.4 | 5294.9 | 843.0 | 790.7 | 46,172.2 | 126.7 | 131.9 | −25.7 | 12.9 | 150.8 |
| A-G-2 | 189.6 | 2023.7 | 109.0 | 6328.3 | 1005.7 | 921.2 | 48,235.2 | 151.0 | 156.6 | −24.7 | 10.7 | 185.4 |
| A-A-3 | 185.3 | 2114.5 | 107.7 | 5878.6 | 951.0 | 840.0 | 41,217.5 | 142.9 | 148.5 | −25.6 | 11.9 | 177.4 |
| G-G-4 | 195.4 | 2115.8 | 110.3 | 6777.9 | 1060.4 | 1002.5 | 55,256.4 | 159.0 | 164.7 | −23.7 | 9.2 | 193.4 |
| R2 | 1.000 | 0.632 | 0.834 | 0.722 | 0.824 | 0.544 | 0.048 | 0.826 | 0.828 | 0.007 | 0.141 | 0.904 |
| Base Pair | αiso | Other Work a | This Work | ||
|---|---|---|---|---|---|
| Becke | Hirshfeld | avg. | G3 | ||
| C-G-WC | 170.2 | 128.7 | 188.1 | 158.4 | 169.0 |
| G-G-1 | 197.2 | 144.9 | 213.1 | 179.0 | 194.8 |
| C-HX | 159.1 | 122.0 | 177.4 | 149.7 | 157.8 |
| T-G-3 | 180.1 | 135.3 | 198.3 | 166.8 | 177.2 |
| G-G-3 | 194.4 | 145.2 | 212.6 | 178.9 | 194.0 |
| C-C-1 | 144.9 | 112.9 | 163.1 | 138.0 | 142.1 |
| T-G-1 | 177.3 | 135.5 | 198.2 | 166.9 | 177.1 |
| A-G-1 | 191.7 | 142.3 | 207.9 | 175.1 | 186.1 |
| T-G-2 | 177.2 | 135.5 | 198.3 | 166.9 | 177.0 |
| C-A-1 | 165.7 | 126.2 | 182.9 | 154.5 | 159.8 |
| T-A-H | 169.8 | 132.3 | 193.4 | 162.8 | 169.1 |
| T-A-RH | 169.6 | 132.3 | 193.4 | 162.9 | 169.0 |
| C-G-1 | 169.9 | 129.2 | 187.5 | 158.4 | 167.7 |
| C-A-2 | 164.4 | 126.3 | 183.2 | 154.7 | 159.9 |
| FU-A | 158.2 | 122.1 | 177.8 | 150.0 | 162.2 |
| T-A-WC | 169.7 | 132.3 | 193.4 | 162.8 | 169.1 |
| U-A | 157.9 | 122.0 | 177.4 | 149.7 | 157.6 |
| A-G-3 | 190.2 | 142.4 | 208.0 | 175.2 | 186.1 |
| T-A-RWC | 169.7 | 132.3 | 193.4 | 162.9 | 169.0 |
| A-A-1 | 186.9 | 139.4 | 202.6 | 171.0 | 177.5 |
| A-G-4 | 189.6 | 142.5 | 207.5 | 175.0 | 185.3 |
| C-T-2 | 150.7 | 119.3 | 173.4 | 146.4 | 150.9 |
| A-A-2 | 185.3 | 139.5 | 202.8 | 171.2 | 177.6 |
| T-T-1 | 158.4 | 125.8 | 183.6 | 154.7 | 159.7 |
| T-T-2 | 158.2 | 125.8 | 183.6 | 154.7 | 159.7 |
| T-T-3 | 158.7 | 125.8 | 183.7 | 154.7 | 159.8 |
| C-T-1 | 150.3 | 119.4 | 173.4 | 146.4 | 150.8 |
| A-G-2 | 189.6 | 142.5 | 207.5 | 175.0 | 185.4 |
| A-A-3 | 185.3 | 139.5 | 202.8 | 171.2 | 177.4 |
| G-G-4 | 195.4 | 145.5 | 212.1 | 178.8 | 193.4 |
| MUE(%) b | −23.4 | 11.6 | −5.9 | −1.2 | |
| MSE(%) c | 23.4 | 11.6 | 5.9 | 1.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Liu, S.; Chen, D. A Density Functional Theory and Information-Theoretic Approach Study of Interaction Energy and Polarizability for Base Pairs and Peptides. Pharmaceuticals 2022, 15, 938. https://doi.org/10.3390/ph15080938
Zhao D, Liu S, Chen D. A Density Functional Theory and Information-Theoretic Approach Study of Interaction Energy and Polarizability for Base Pairs and Peptides. Pharmaceuticals. 2022; 15(8):938. https://doi.org/10.3390/ph15080938
Chicago/Turabian StyleZhao, Dongbo, Shubin Liu, and Dahua Chen. 2022. "A Density Functional Theory and Information-Theoretic Approach Study of Interaction Energy and Polarizability for Base Pairs and Peptides" Pharmaceuticals 15, no. 8: 938. https://doi.org/10.3390/ph15080938
APA StyleZhao, D., Liu, S., & Chen, D. (2022). A Density Functional Theory and Information-Theoretic Approach Study of Interaction Energy and Polarizability for Base Pairs and Peptides. Pharmaceuticals, 15(8), 938. https://doi.org/10.3390/ph15080938






