Abstract
This study constructs a machine learning method to simultaneously analyze the thermodynamic behavior of many polymer–drug systems. The solubility temperature of Acetaminophen, Celecoxib, Chloramphenicol, D-Mannitol, Felodipine, Ibuprofen, Ibuprofen Sodium, Indomethacin, Itraconazole, Naproxen, Nifedipine, Paracetamol, Sulfadiazine, Sulfadimidine, Sulfamerazine, and Sulfathiazole in 1,3-bis[2-pyrrolidone-1-yl] butane, Polyvinyl Acetate, Polyvinylpyrrolidone (PVP), PVP K12, PVP K15, PVP K17, PVP K25, PVP/VA, PVP/VA 335, PVP/VA 535, PVP/VA 635, PVP/VA 735, Soluplus analyzes from a modeling perspective. The least-squares support vector regression (LS-SVR) designs to approximate the solubility temperature of drugs in polymers from polymer and drug types and drug loading in polymers. The structure of this machine learning model is well-tuned by conducting trial and error on the kernel type (i.e., Gaussian, polynomial, and linear) and methods used for adjusting the LS-SVR coefficients (i.e., leave-one-out and 10-fold cross-validation scenarios). Results of the sensitivity analysis showed that the Gaussian kernel and 10-fold cross-validation is the best candidate for developing an LS-SVR for the given task. The built model yielded results consistent with 278 experimental samples reported in the literature. Indeed, the mean absolute relative deviation percent of 8.35 and 7.25 is achieved in the training and testing stages, respectively. The performance on the largest available dataset confirms its applicability. Such a reliable tool is essential for monitoring polymer–drug systems’ stability and deliverability, especially for poorly soluble drugs in polymers, which can be further validated by adopting it to an actual implementation in the future.
1. Introduction
Enhancing the deliverability of poorly water-soluble solid drugs has always been challenging for researchers engaged in pharmaceutical synthesis [1,2]. Various strategies, including applying nanotechnology [3], nanosuspension [4], nanomedicine [5], solid dispersion [6], surfactants in solid dispersion [7], mesoporous silica material [8], and diverse solution media (such as supercritical [9,10], ionic [11], eutectic [12], the polymer [13]) have already been tried in the field of drug synthesis/formulation. Utilizing the amorphous form of drugs instead of their crystalline structures (i.e., ASD: amorphous solid dispersions) has also gained tremendous attention as a practical path to improve the deliverability and dissolution rate of poorly soluble drugs [14,15]. Dispersing and stabilizing the amorphous form of drugs in polymeric carriers is a well-established class of this ASD scenario [16,17,18,19]. Molecularly dispersing amorphous drugs in polymeric carriers with a higher glass transition temperature (GTT) increases the mixture’s GTT [20], enhances apparent solubility [21], and improves thermodynamic stability [22]. Some researchers also claimed that polymeric carrier selection is the most critical factor in the ASD scenario [23]. Furthermore, drug–polymer miscibility is likely the most important influential factor in achieving amorphous solid dispersion stability [21].
Therefore, reliable insights into drug solubility in polymeric carriers are necessary for successfully implementing the ASD scenario [22,24,25,26,27,28]. The polymer–drug solubility curve is also significant for selecting appropriate polymers for the ASD process and determining the maximum drug loading in the polymeric carrier without the risk of crystallization [28]. Indeed, the drug stability primarily depends on the drug solubility in polymers at the storage temperature [24,29]. To reach a thermodynamically stable formulation, a drug loading in a polymeric carrier should be smaller or at least equal to the drug solubility in the polymer at the storage temperature [24]. In addition, the drug solubility in polymeric media is of interest in the design of pharmaceutical formulation and purification equipment [30]. The drug solubility in polymers is determined by measuring the temperature and the solution dosage at a system equilibrium state [25]. Experimental measurement of the drug solubility is a well-established method in this regard [31,32]. Laboratory measurements of the drug solubility in polymeric carriers is a challenging task due to the unavailability of the standard procedure [25], the high viscosity of polymers [24,33], the difficulty of reaching the equilibrium condition [28], and the consuming time [27].
Therefore, researchers suggested several correlations to estimate the solubility temperature of ibuprofen and naproxen in Soluplus [24] and the miscibility of curcumin in polyvinyl pyrrolidone, hydroxypropyl methylcellulose, and polyethylene glycol [34]. Knopp et al., developed a model utilizing statistical analysis to compare the effect of preparation methods on indomethacin-Polyvinylpyrrolidone solubility curves [35]. The solubility parameter (originally introduced by Hildebrand [36] and then modified by Hansen [37]) is another approach for theoretically determining drug–polymer miscibility. Recently, Mamidi and Rohera constructed the thermodynamic phase diagram of drug–polymer systems using the melting-point depression data, Gordon–Taylor equation, and the Flory–Huggins theory [21]. Such a correlation is only valid for an investigated polymer–drug medium and potentially presents high uncertainty for other polymer–drug systems. To the authors’ best knowledge, the literature has constructed no general empirical, intelligent, or mathematical model for approximating a broad range of polymer–drug systems. Building a universal model helps find the best polymer for drug carriers among different candidates.
Consequently, designing a reliable LS-SVR model to estimate the equilibrium behavior of a wide range of drugs in different polymers is the main objective of the current research. Furthermore, it is necessary to engineer the LS-SVR structure systematically. The suggested LS-SVR can easily produce the solubility curve of a drug in the polymer as a function of drug and polymer type and drug load in the polymer. In addition, this study:
- (a)
- Introduces the most general model to estimate the solubility of drugs in polymers.
- (b)
- Saves time and money by replacing experimental analysis with a straightforward model.
- (c)
- Offers a route for choosing the most suitable polymer for the ASD scenario.
- (d)
- Provides the polymer–drug solubility data for monitoring the solution stability.
2. Data Collection
An experimental database is needed to develop an LS-SVR model to approximate the solubility temperature of drugs in polymers. This database should include the dependent variable (Tsol: solubility temperature) and its related independent variables (i.e., polymer and drug type and drug load in polymers). Table 1 concisely reports polymer–drug systems that will be analyzed in the current study. This table also introduces the names of the drug and polymer based on the original reference, the amount of data, and the range of drug load in polymers and solubility temperature.

Table 1.
Summary of the literature data for the solubility of drugs in polymers.
Since the collected experimental data covers different polymer–drug systems, molecular weights (Mw) of the drug and polymer are selected to help LS-SVRs discriminate between the behavior of various drugs and polymers during the modeling phase.
In summary, the current study includes 16 drugs, 13 polymers, a drug load of 1 to 100 weight percent (wt%) in polymers, and a solubility temperature of 30 to 252.7 °C. It should be mentioned that the composition of polymer–drug mixtures can vary from low (~0 wt%) to high (~100 wt%) dosages of a drug. Indeed, these points indicate the pure polymer and pure drug, respectively. When the drug loading is 100 wt% (i.e., pure drug), the melting temperature is considered as the solubility temperature [25].
The numerical value of experimental data is available in the Supplementary Materials.
Relevancy Analysis
Two well-known relevancy analysis scenarios, i.e., Spearman [38] and Pearson [38], respectively in Equation (1) are applied to quantize the strength and reveal the direction of relationships between Tsol and drug Mw, Tsol and polymer Mw, and Tsol and drug load in a polymer (Figure 1).
where d is the difference between the two ranks of observations and N is the number of available samples. In addition, IV and IVave (Equation (2)) show numerical values of the independent variable and their average, and and (Equation (3)) are numerical values of the solubility temperature and its average.
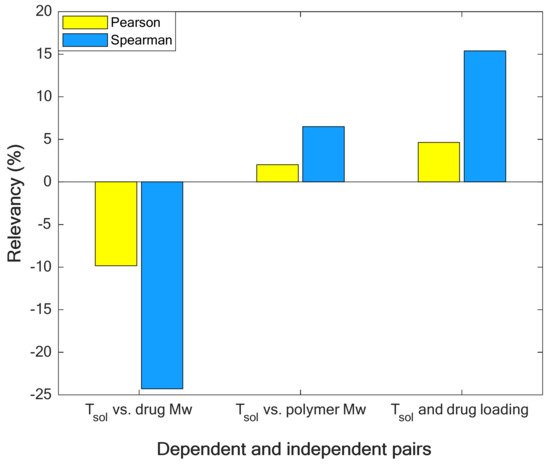
Figure 1.
Quantizing the relevancy (strength and direction of relationship) between solubility temperature and its affecting variables.
Figure 1 approves that increasing the molecular weight of drugs decreases the solubility temperature (negative relevancy value shows an indirect relationship [39]). On the other hand, the molecular weight of polymers and drug load in polymers increase the solubility temperature [40] (positive relevancy value shows a direct relationship [39]). In addition, the molecular weight of drugs is the strongest reducing feature (due to its minimum relevancy value [38]), and drug load is the strongest increasing factor (due to its maximum relevancy value [38]) for the solubility temperature.
3. LS-SVR Description
Machine learning, deep learning, feature selection, and decision-making techniques have a broad range of applications for implementing either classification or approximation [41] tasks in different fields of daily life, science, and technology [42,43,44]. Support vector machine [45] and its derivation (i.e., least-squares support vector regression [46]) have recently gained great attention. These methods transform the experimental data to a multi-dimensional space utilizing the linear, polynomial, and Gaussian kernels (i.e., K) based on Equation (4) [47].
where T is transpose operation, t, d, and are kernel-related parameters.
In the transformed space, it is possible to linearly relate independent and independent variables by Equation (5). w (i.e., weights) and b (bias) are adjustable parameters of LS-SVR method [48].
Then, a combination of simulated annealing and simplex methods tries to adjust weights and biases through solving the following optimization algorithm [48].
4. Results and Discussions
This study aims to determine the best kernel type (Gaussian, polynomial, and linear) and tuning method (leave-one-out and 10-fold cross-validations) of the LS-SVR by trial and error. Hence, it is necessary to adjust the coefficients of the LS-SVR with different kernel types by the leave-one-out and 10-fold cross-validations and compare their accuracy to find the highest accurate topology. MARDP (mean absolute relative deviation percent, Equation (7)), MADP (mean absolute deviation percent, Equation (8)), RMSE (root mean squared error, Equation (9)), and R-value (coefficient of determination, Equation (10)) compare the accuracy of different LS-SVR topologies [49] and help find the best one.
Here, is the predicted solubility temperature by the LS-SVR.
4.1. Constructing the LS-SVR Model
Developing any knowledge-based model needs at least two data collections, i.e., training and testing [50]. Therefore, it is necessary to randomly divide the experimental data into training and testing collections. The former collection is applied to regulate the LS-SVR parameters (known as an LS-SVR training stage). On the other hand, the latter collection is used to appraise the generalization ability of the trained LS-SVR in some unseen situations. This study uses a ratio = 85/15 to allocate the experimental data into the training and testing collections, respectively. Table 2 reports the highest accurate predictions obtained by the LS-SVR models trained by the leave-one-out and 10-fold cross-validation (CV) techniques. The performance of LS-SVRs in the training and testing stages (and the combination of two phases, i.e., overall) has been measured using the aforementioned statistical criteria. The second column of these tables also introduces kernel functions’ adjusted coefficients (t, d, and σ2) and regularization parameter (γ).

Table 2.
The best results obtained by LS-SVRs with different kernel types (leave-one-out CV and 10-fold CV).
The reported results in Table 2 approve that LS-SVRs equipped with the Gaussian and linear kernel functions are the highest and lowest accurate models, respectively.
4.2. Selecting the Best LS-SVR
Although the previous results showed that the Gaussian function provides the LS-SVR with a higher prediction accuracy than the other kernel types, it is better to demonstrate this finding by helping the ranking analysis. This analysis uses Equation (11) to calculate the average rank of each LS-SVR over the four statistical indexes (MARDP, RMSE, MADP, and R-value) [38]. Since ranking analyses have been separately conducted for the training and testing stages (and their combination), it is possible to sort LS-SVRs in different modeling phases.
4.2.1. Selecting the Best Kernel Function
Results of performing the ranking analysis on the priority of LS-SVRs with different kernel functions have been depicted in Figure 2a,b for the leave-one-out CV and 10-fold cross-CV. Thus, LS-SVRs with the Gaussian kernel function achieve the first ranking in the training/testing stages and their combination.
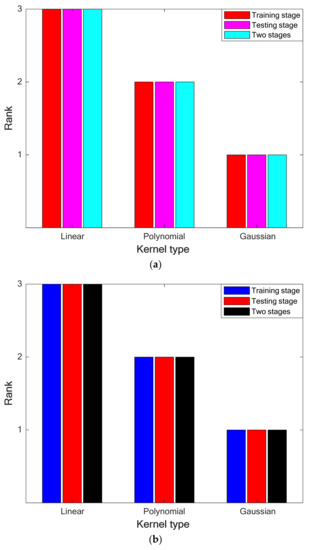
Figure 2.
(a). Performing the ranking analysis on the performance of LS-SVRs with different kernel types (leave-one-out CV). (b). Performing the ranking analysis on the performance of LS-SVRs with different kernel types (10-fold CV).
4.2.2. Selecting the Best Tuning Technique
In this stage, the ranking analysis is applied again to determine the best tuning method of the LS-SVR model. The results of performing the ranking analysis on the priority of leave-one-out and 10-fold CV techniques have been illustrated in Figure 3. It can be concluded that the LS-SVR (with the Gaussian kernel function) trained by the 10-fold cross-validation technique presents the highest accuracy in approximating the solubility temperature of drugs in polymers.
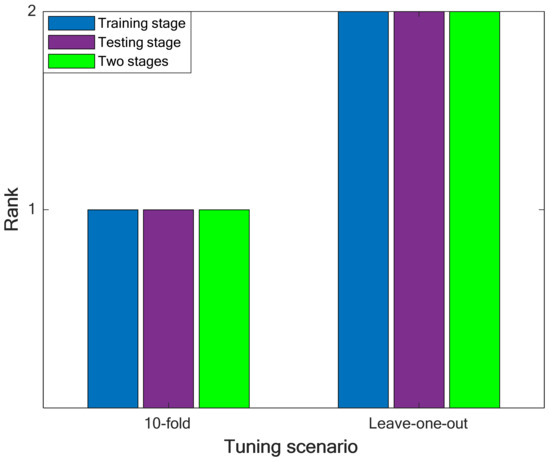
Figure 3.
Performing the ranking analysis on the best results of the leave-one-out and 10-fold cross-validation scenarios.
Although it is possible to extend the LS-SVR model to cover other drug–polymer binary systems, the current version of the LS-SVR model can only be applied to simulate phase equilibria of the involved drug–polymer systems (see Table 1).
4.3. Monitoring the LS-SVR Performance Using Graphical Analyses
4.3.1. Compatibility between Experimental and Calculated Tsol
Equation (12) measures the actual difference (AD) between experimental and approximated values of the drug solubility temperature in polymers.
It is obvious that these observed differences are better to be as small as possible. However, several issues, including the complexity of a considered process/phenomenon, broad ranges of variables, uncertainty in experimental measurements, and modeling error, often result in observing nonzero AD values.
The histogram presentation of the training and testing ADs is shown in Figure 4. This figure indicates that a high percentage of drug solubility temperature in polymers has been estimated with excellent AD values between −20 and 20 °C. In addition, the maximum number of experimental solubility temperatures (~140 training and 30 testing samples) has been computed with the lowest possible AD value (~0 °C). This figure also shows that ~17 experimental solubility samples have been estimated with an AD lower than −40 °C or higher than 40 °C.
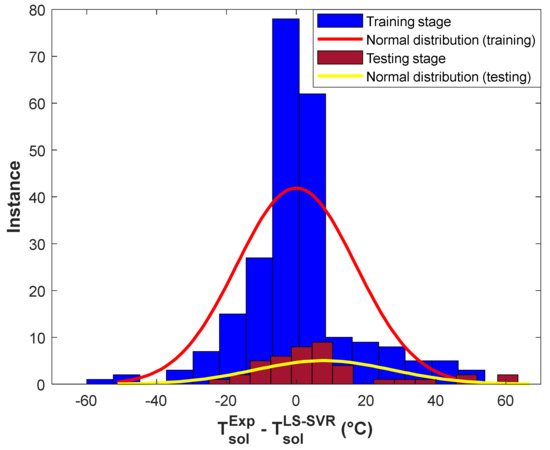
Figure 4.
Histogram of residual errors of the structure-tuned LS-SVR in the training and testing stages.
This section calculates the average value (ADave) and standard deviation (SD) of presented ADs by the structure-tuned LS-SVR using Equations (13) and (14), respectively [38].
The constructed LS-SVR is able to predict 278 solubility temperatures of 16 drugs in 13 polymers with the promising ADave = 1.2 °C and SD = 17.7 °C.
4.3.2. Experimental versus Predicted Tsol in the Training and Testing Stages
Figure 5a,b show the value of experimental solubility temperatures in the training and testing stages of the LS-SVR, respectively. Although the testing group possesses a higher scattering level than the training dataset, it can be seen that both groups are scattered enough to make the modeling hard. Despite this relatively high scattering of experimental solubility temperatures, the constructed LS-SVR properly describes the thermodynamic behavior of polymer–drug systems. The excellent performance of the LS-SVR can be more approved by the values of MARDP, MADP, RMSE, and R reported in the figures’ body.
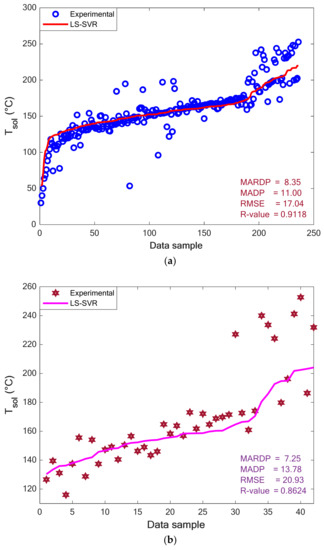
Figure 5.
Experimental and modeling values of the solubility temperature in the (a) training and (b) testing stages.
4.4. Monitoring the LS-SVR Performance Using Trend Analyses
4.4.1. Evaluating the Impact of Drug Type and Its Load in Polymer on the Tsol
The effect of the drugs’ type (i.e., Paracetamol, Celecoxib, and Chloramphenicol) and their loading in Polyvinyl Acetate on the solubility temperature has been depicted in Figure 6. This figure presents experimental as well as modeling values of Tsol versus drug loading. It can be concluded from these profiles that the drug loading in polymers increases the solubility temperature. Increasing the solubility temperature with increasing the drug loading in the polymer is related to the drug–polymer interactions [26]. It is better to recall that the relevancy analyses also anticipated the increasing impact of drug loading in polymers on the solubility temperature (see Section 2). In addition, the drug type also affects the solubility temperature of drugs in a polymer. It is obvious that changing the solute type changes the interaction between the drug–polymer and the observed solubility temperature.
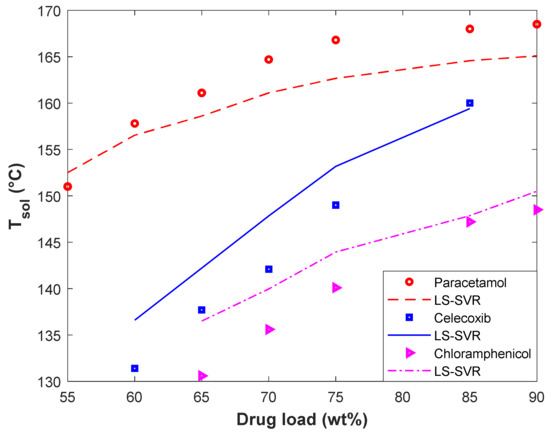
Figure 6.
The effect of drug type and drug load in polyvinyl acetate on the solubility temperature.
From the modeling perspective, the LS-SVR successfully describes the thermodynamic behavior of different polymer–drug systems and discriminates among them. Furthermore, the developed model correctly identifies the direct effect of the drug load on the solubility temperature. The excellent agreement between experimental and predicted solubility temperatures can be more justified by the MARDP of 1.55 (Polyvinyl Acetate-Paracetamol), 2.9 (Polyvinyl Acetate-Celecoxib), and 2.59 (Polyvinyl Acetate-Chloramphenicol).
4.4.2. Evaluating the Impact of Polymer Type on the Tsol
The variation of solubility temperature of D-Mannitol in PVP K12, PVP K15, and VP dimer has been plotted in Figure 7. This figure covers both experimental and modeling Tsol-drug load profiles. It can be viewed that the PVP K12/D-Mannitol and VP dimer/D-Mannitol systems have the highest and lowest solubility temperature, respectively. The acceptable performance of the LS-SVR for predicting the equilibrium behavior of polymer/D-Mannitol systems can be approved by the observed MARDP value of 1.65 (PVP K12/D-Mannitol), 2.84 (PVP K15/D-Mannitol), and 2.34 (VP dimer/D-Mannitol).
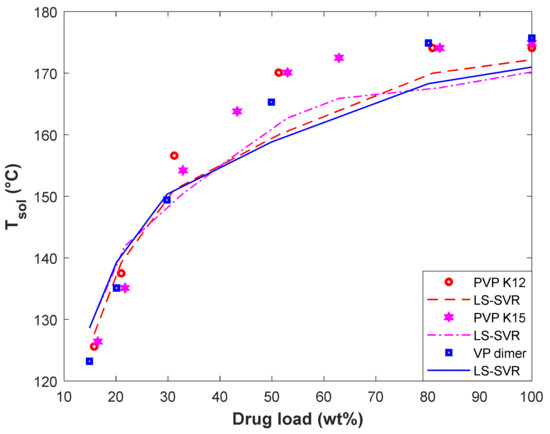
Figure 7.
The effect of polymer type and D-Mannitol load on the solubility temperature.
In addition, both the experimental data and LS-SVR curves in Figure 7 show that the effect of the polymer type on solubility temperature is minor. We recall from Figure 1 that the molecular weight of polymers has a minor effect on the drug solubility temperature. On the other hand, PVP K12, PVP K15, and VP dimer are polyvinyl pyrrolidone-based polymers with different molecular weights. Therefore, it is expected that the solubility temperature of D-Mannitol in these polymers is almost equal.
4.5. Checking the Data Validity
The experimental data may contain different quantities of noise, outliers, and wrong measurements. Human mistakes, instrument defects, and incorrect calibration are the main cause of this data uncertainty. It seems necessary to check the uncertainty level in the analyzed drug–polymer equilibrium samples. Hence, the last analysis of this study utilizes the leverage method to check the experimental database validity. This method uses the standard residual (SR, Equation (15)) against the Hat index (Equation (16)) graph to find both valid and problematic samples [38].
The samples outside the region confined by critical leverage (CL, Equation (17)) and SR = ±3% are outliers, and all others are valid [51].
Figure 8 reveals that 264 valid and 14 problematic samples exist among the 278 experimental datasets. Indeed, 95% of the experimental databank is valid, and only 5% may be outliers. Since the analyzed experimental samples related to drug–polymer equilibrium behavior are almost valid, the extracted LS-SVR model from this databank is also reliable.

Figure 8.
William’s graph to identify outlier as well as valid samples.
5. Conclusions
This study successfully simulated the solubility temperature of 16 drugs in 13 polymeric media by a machine learning technique. The kernel type and tuning method of the LS-SVR have been well-tuned by a systematic combination of statistical and ranking analyses. The results concluded that it is better to equip the LS-SVR with the Gaussian kernel function and adjust its parameters with the 10-fold cross-validation method. The designed LS-SVR predicted the solubility of 278 polymer–drug samples with the MARDP = 8.18, MADP = 11.42, RMSE = 17.69, and R = 0.9037. Since the performance of the LS-SVR model has been validated by the graphical and trend analyses and the utilized experimental database includes 95% valid samples, the suggested model can be readily applied to estimate the solubility temperature of drugs in polymeric media. The relevancy analysis and experimental/modeling profile clarified that the drug solubility temperature in polymers increases by increasing the drug load and the polymer’s molecular weight. On the other hand, the drug’s molecular weight has an inverse relationship with the solubility temperature. This study successfully applied the LS-SVR method to simulate the solubility of different drugs in nonionic polymers. Using machine learning models to estimate the drug solubility in ionic polymers is a good idea to continue this preliminary research study.
Supplementary Materials
The numerical value of independent and dependent variables of the analyzed experimental data can be downloaded at: https://www.mdpi.com/article/10.3390/ph15111405/s1.
Author Contributions
S.S.: Resources, Writing—original draft, Writing—review and editing, Conceptualization. M.A.A.: Writing—original draft, Investigation, and Methodology. T.R.: Writing—original draft, Writing—review and editing, Methodology. F.F.: Writing—original draft, Writing—review and editing, Resources, Investigation. A.K.: Writing—original draft, Investigation, and Methodology. M.E.H.C.: Writing—original draft, Investigation, and Methodology. Z.H.J.: Writing—original draft, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
The publication of this article was funded by the Qatar National Library.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article and Supplementary Materials.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kumar, S.; Dilbaghi, N.; Saharan, R.; Bhanjana, G. Nanotechnology as Emerging Tool for Enhancing Solubility of Poorly Water-Soluble Drugs. Bionanoscience 2012, 2, 227–250. [Google Scholar] [CrossRef]
- Abuzar, S.M.; Hyun, S.M.; Kim, J.H.; Park, H.J.; Kim, M.S.; Park, J.S.; Hwang, S.J. Enhancing the solubility and bioavailability of poorly water-soluble drugs using supercritical antisolvent (SAS) process. Int. J. Pharm. 2018, 538, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Long, X.; Chen, H.; Ji, Z.; Shu, B.; Yue, R.; Liao, Y.; Ma, S.; Qiao, K.; Liu, Y.; et al. Photoclick Reaction Constructs Glutathione-Responsive Theranostic System for Anti-Tuberculosis. Front. Mol. Biosci. 2022, 9, 845179. [Google Scholar] [CrossRef] [PubMed]
- Vedaga, S.B.; Gondkar, S.B.; Saudagar, R.B. Nanosuspension: An Emerging Trend to Improve Solubility of Poorly Water Soluble Drugs. J. Adv. Pharm. Thechnology Res. 2019, 2, 81–87. [Google Scholar] [CrossRef]
- Yang, W.; Liu, W.; Li, X.; Yan, J.; He, W. Turning chiral peptides into a racemic supraparticle to induce the self-degradation of MDM2. J. Adv. Res. 2022; in press. [Google Scholar] [CrossRef] [PubMed]
- Sareen, S.; Joseph, L.; Mathew, G. Improvement in solubility of poor water-soluble drugs by solid dispersion. Int. J. Pharm. Investig. 2012, 2, 12. [Google Scholar] [CrossRef]
- Chaudhari, S.P.; Dugar, R.P. Application of surfactants in solid dispersion technology for improving solubility of poorly water soluble drugs. J. Drug Deliv. Sci. Technol. 2017, 41, 68–77. [Google Scholar] [CrossRef]
- Maleki, A.; Kettiger, H.; Schoubben, A.; Rosenholm, J.M.; Ambrogi, V.; Hamidi, M. Mesoporous silica materials: From physico-chemical properties to enhanced dissolution of poorly water-soluble drugs. J. Control. Release 2017, 262, 329–347. [Google Scholar] [CrossRef]
- Faress, F.; Yari, A.; Kouchi, F.R.; Nezhad, A.S.; Hadizadeh, A.; Bakhtiar, L.S.; Naserzadeh, Y.; Mahmoudi, N. Developing an accurate empirical correlation for predicting anti-cancer drugs’ dissolution in supercritical carbon dioxide. Sci. Rep. 2022, 12, 9380. [Google Scholar] [CrossRef]
- Faraz, O.; Poustchi, M.; Denyani, E.N.; Movahedi, P.; Kouchi, F.R.; Shahriari, R. Thermodynamic modeling of pharmaceuticals solubility in pure, mixed and supercritical solvents. J. Mol. Liq. 2022, 353, 118809. [Google Scholar] [CrossRef]
- Jesus, A.R.; Soromenho, M.R.C.; Raposo, L.R.; Esperança, J.M.S.S.; Baptista, P.V.; Fernandes, A.R.; Reis, P.M. Enhancement of water solubility of poorly water-soluble drugs by new biocompatible N-acetyl amino acid N-alkyl cholinium-based ionic liquids. Eur. J. Pharm. Biopharm. 2019, 137, 227–232. [Google Scholar] [CrossRef]
- Bazzo, G.C.; Pezzini, B.R.; Stulzer, H.K. Eutectic mixtures as an approach to enhance solubility, dissolution rate and oral bioavailability of poorly water-soluble drugs. Int. J. Pharm. 2020, 588, 119741. [Google Scholar] [CrossRef]
- Kazemi, M.; Emami, J.; Hasanzadeh, F.; Minaiyan, M.; Mirian, M.; Lavasanifar, A. Pegylated multifunctional pH-responsive targeted polymeric micelles for ovarian cancer therapy: Synthesis, characterization and pharmacokinetic study. Int. J. Polym. Mater. Polym. Biomater. 2021, 70, 1012–1026. [Google Scholar] [CrossRef]
- Van den Mooter, G. The use of amorphous solid dispersions: A formulation strategy to overcome poor solubility and dissolution rate. Drug Discov. Today Technol. 2012, 9, e79–e85. [Google Scholar] [CrossRef]
- Schittny, A.; Huwyler, J.; Puchkov, M. Mechanisms of increased bioavailability through amorphous solid dispersions: A review. Drug Deliv. 2020, 27, 110–127. [Google Scholar] [CrossRef]
- Meng, F.; Dave, V.; Chauhan, H. Qualitative and quantitative methods to determine miscibility in amorphous drug-polymer systems. Eur. J. Pharm. Sci. 2015, 77, 106–111. [Google Scholar] [CrossRef]
- Rumondor, A.C.F.; Ivanisevic, I.; Bates, S.; Alonzo, D.E.; Taylor, L.S. Evaluation of drug-polymer miscibility in amorphous solid dispersion systems. Pharm. Res. 2009, 26, 2523–2534. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, S.; Wang, S.; Liu, C.; Su, C.; Hageman, M.; Hussain, M.; Haskell, R.; Stefanski, K.; Qian, F. Initial Drug Dissolution from Amorphous Solid Dispersions Controlled by Polymer Dissolution and Drug-Polymer Interaction. Pharm. Res. 2016, 33, 2445–2458. [Google Scholar] [CrossRef]
- Zhang, X.; Qu, Y.Y.; Liu, L.; Qiao, Y.N.; Geng, H.R.; Lin, Y.; Xu, W.; Cao, J.; Zhao, J.Y. Homocysteine inhibits pro-insulin receptor cleavage and causes insulin resistance via protein cysteine-homocysteinylation. Cell Rep. 2021, 37, 109821. [Google Scholar] [CrossRef]
- Asgreen, C.; Knopp, M.M.; Skytte, J.; Löbmann, K. Influence of the polymer glass transition temperature and molecular weight on drug amorphization kinetics using ball milling. Pharmaceutics 2020, 12, 483. [Google Scholar] [CrossRef]
- Mamidi, H.K.; Rohera, B.D. Application of Thermodynamic Phase Diagrams and Gibbs Free Energy of Mixing for Screening of Polymers for Their Use in Amorphous Solid Dispersion Formulation of a Non-Glass-Forming Drug. J. Pharm. Sci. 2021, 110, 2703–2717. [Google Scholar] [CrossRef] [PubMed]
- Caron, V.; Hu, Y.; Tajber, L.; Erxleben, A.; Corrigan, O.I.; McArdle, P.; Healy, A.M. Amorphous solid dispersions of sulfonamide/soluplus® and sulfonamide/PVP prepared by ball milling. AAPS PharmSciTech 2013, 14, 464–474. [Google Scholar] [CrossRef] [PubMed]
- Newman, A.; Nagapudi, K.; Wenslow, R. Amorphous solid dispersions: A robust platform to address bioavailability challenges. Ther. Deliv. 2015, 6, 247–261. [Google Scholar] [CrossRef] [PubMed]
- Kyeremateng, S.O.; Pudlas, M.; Woehrle, G.H. A fast and reliable empirical approach for estimating solubility of crystalline drugs in polymers for hot melt extrusion formulations. J. Pharm. Sci. 2014, 103, 2847–2858. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.E.; Tao, J.; Zhang, G.G.Z.; Yu, L. Solubilities of crystalline drugs in polymers: An improved analytical method and comparison of solubilities of indomethacin and nifedipine in PVP, PVP/VA, and PVAc. J. Pharm. Sci. 2010, 99, 4023–4031. [Google Scholar] [CrossRef]
- Knopp, M.M.; Gannon, N.; Porsch, I.; Rask, M.B.; Olesen, N.E.; Langguth, P.; Holm, R.; Rades, T. A Promising New Method to Estimate Drug-Polymer Solubility at Room Temperature. J. Pharm. Sci. 2016, 105, 2621–2624. [Google Scholar] [CrossRef]
- Knopp, M.M.; Tajber, L.; Tian, Y.; Olesen, N.E.; Jones, D.S.; Kozyra, A.; Löbmann, K.; Paluch, K.; Brennan, C.M.; Holm, R.; et al. Comparative Study of Different Methods for the Prediction of Drug-Polymer Solubility. Mol. Pharm. 2015, 12, 3408–3419. [Google Scholar] [CrossRef]
- Tao, J.; Sun, Y.; Zhang, G.G.Z.; Yu, L. Solubility of small-molecule crystals in polymers: D-Mannitol in PVP, indomethacin in PVP/VA, and nifedipine in PVP/VA. Pharm. Res. 2009, 26, 855–864. [Google Scholar] [CrossRef]
- Wang, X.H.; Xu, S.; Zhou, X.Y.; Zhao, R.; Lin, Y.; Cao, J.; Zang, W.D.; Tao, H.; Xu, W.; Li, M.Q.; et al. Low chorionic villous succinate accumulation associates with recurrent spontaneous abortion risk. Nat. Commun. 2021, 12, 3428. [Google Scholar] [CrossRef]
- Ting, J.M.; Porter, W.W.; Mecca, J.M.; Bates, F.S.; Reineke, T.M. Advances in Polymer Design for Enhancing Oral Drug Solubility and Delivery. Bioconjug. Chem. 2018, 29, 939–952. [Google Scholar] [CrossRef]
- Qu, Y.; Zhao, R.; Zhang, H.; Zhou, Q.; Xu, F.; Zhang, X.; Xu, W.H.; Shao, N.; Zhou, S.X.; Dai, B.; et al. Inactivation of the AMPK–GATA3–ECHS1 Pathway Induces Fatty Acid Synthesis That Promotes Clear Cell Renal Cell Carcinoma Growth. Cancer Res. 2020, 80, 319–333. [Google Scholar] [CrossRef]
- Wang, D.; Wang, F.; Shi, K.H.; Tao, H.; Li, Y.; Zhao, R.; Lu, H.; Duan, W.; Qiao, B.; Zhao, S.M.; et al. Lower Circulating Folate Induced by a Fidgetin Intronic Variant Is Associated with Reduced Congenital Heart Disease Susceptibility. Circulation 2017, 135, 1733–1748. [Google Scholar] [CrossRef]
- Lai, W.F.; Tang, R.; Wong, W.T. Ionically crosslinked complex gels loaded with oleic acid-containing vesicles for transdermal drug delivery. Pharmaceutics 2020, 12, 725. [Google Scholar] [CrossRef]
- Meng, F.; Trivino, A.; Prasad, D.; Chauhan, H. Investigation and correlation of drug polymer miscibility and molecular interactions by various approaches for the preparation of amorphous solid dispersions. Eur. J. Pharm. Sci. 2015, 71, 12–24. [Google Scholar] [CrossRef]
- Knopp, M.M.; Olesen, N.E.; Holm, P.; Löbmann, K.; Holm, R.; Langguth, P.; Rades, T. Evaluation of drug-polymer solubility curves through formal statistical analysis: Comparison of preparation techniques. J. Pharm. Sci. 2015, 104, 44–51. [Google Scholar] [CrossRef]
- Hildebrand, J.H. Solubility of Non-electrolytes. In American Chemical Society Monograph Series, 2nd ed.; Reinhold Pub.: New York, NY, USA, 1936. [Google Scholar]
- Hansen, C.M. The universality of the solubility parameter. Ind. Eng. Chem. Prod. Res. Dev. 1969, 8, 2–11. [Google Scholar] [CrossRef]
- Zhu, X.; Khosravi, M.; Vaferi, B.; Amar, M.N.; Ghriga, M.A.; Mohammed, A.H. Application of machine learning methods for estimating and comparing the sulfur dioxide absorption capacity of a variety of deep eutectic solvents. J. Clean. Prod. 2022, 363, 132465. [Google Scholar] [CrossRef]
- Wang, J.; Ayari, M.A.; Khandakar, A.; Chowdhury, M.E.H.; Zaman, S.M.A.U.; Rahman, T.; Vaferi, B. Estimating the Relative Crystallinity of Biodegradable Polylactic Acid and Polyglycolide Polymer Composites by Machine Learning Methodologies. Polymers 2022, 14, 527. [Google Scholar] [CrossRef]
- Lai, W.F.; Gui, D.; Wong, M.; Döring, A.; Rogach, A.L.; He, T.; Wong, W.T. A self-indicating cellulose-based gel with tunable performance for bioactive agent delivery. J. Drug Deliv. Sci. Technol. 2021, 63, 102428. [Google Scholar] [CrossRef]
- Alibak, A.H.; Khodarahmi, M.; Fayyazsanavi, P.; Alizadeh, S.M.; Hadi, A.J.; Aminzadehsarikhanbeglou, E. Simulation the adsorption capacity of polyvinyl alcohol/carboxymethyl cellulose based hydrogels towards methylene blue in aqueous solutions using cascade correlation neural network (CCNN) technique. J. Clean. Prod. 2022, 337, 130509. [Google Scholar] [CrossRef]
- Song, K.; Wu, D. Shared decision-making in the management of patients with inflammatory bowel disease. World J. Gastroenterol. 2022, 28, 3092–3100. [Google Scholar] [CrossRef] [PubMed]
- Duan, C.; Deng, H.; Xiao, S.; Xie, J.; Li, H.; Zhao, X.; Han, D.; Sun, X.; Lou, X.; Ye, C.; et al. Accelerate gas diffusion-weighted MRI for lung morphometry with deep learning. Eur. Radiol. 2022, 32, 702–713. [Google Scholar] [CrossRef] [PubMed]
- Zou, M.; Yang, Z.; Fan, Y.; Gong, L.; Han, Z.; Ji, L.; Hu, X.; Wu, D. Gut microbiota on admission as predictive biomarker for acute necrotizing pancreatitis. Front. Immunol. 2022, 13, 988326. [Google Scholar] [CrossRef] [PubMed]
- Rafieipour, H.; Zadeh, A.A.; Moradan, A.; Salekshahrezaee, Z. Study of genes associated with Parkinson disease using feature selection. J. Bioeng. Res. 2020, 2, 1–11. [Google Scholar] [CrossRef]
- Suykens, J.A.K.; van Gestel, T.; de Brabanter, J.; de Moor, B.; Vandewalle, J. Least Squares Support Vector Machines; World Scientific Publishing: Singapore, 2002. [Google Scholar]
- Cao, Y.; Kamrani, E.; Mirzaei, S.; Khandakar, A.; Vaferi, B. Electrical efficiency of the photovoltaic/thermal collectors cooled by nanofluids: Machine learning simulation and optimization by evolutionary algorithm. Energy Rep. 2022, 8, 24–36. [Google Scholar] [CrossRef]
- Karimi, M.; Aminzadehsarikhanbeglou, E.; Vaferi, B. Robust intelligent topology for estimation of heat capacity of biochar pyrolysis residues. Meas. J. Int. Meas. Confed. 2021, 183, 109857. [Google Scholar] [CrossRef]
- Hosseini, S.; Vaferi, B. Determination of methanol loss due to vaporization in gas hydrate inhibition process using intelligent connectionist paradigms. Arab. J. Sci. Eng. 2022, 47, 5811–5819. [Google Scholar] [CrossRef]
- Xie, B.; Li, S.; Lv, F.; Liu, C.H.; Wang, G.; Wu, D. A Collaborative Alignment Framework of Transferable Knowledge Extraction for Unsupervised Domain Adaptation. IEEE Trans. Knowl. Data Eng. 2022. [Google Scholar] [CrossRef]
- Moosavi, S.R.; Vaferi, B.; Wood, D.A. Auto-characterization of naturally fractured reservoirs drilled by horizontal well using multi-output least squares support vector regression. Arab. J. Geosci. 2021, 14, 545. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).