Application of RP-18 TLC Retention Data to the Prediction of the Transdermal Absorption of Drugs
Abstract
1. Introduction
2. Results and Discussion
2.1. General Considerations
2.2. Thin Layer Chromatographic Parameters—Extrapolation Methodology
(n = 23, R2 = 0.948, R2adj. = 0.928, F = 48.367, p < 0.00000, se = 0.316)
(n = 60, R2 = 0.731, R2adj. = 0.700, F = 23.994, p < 0.00000, se = 0.572)
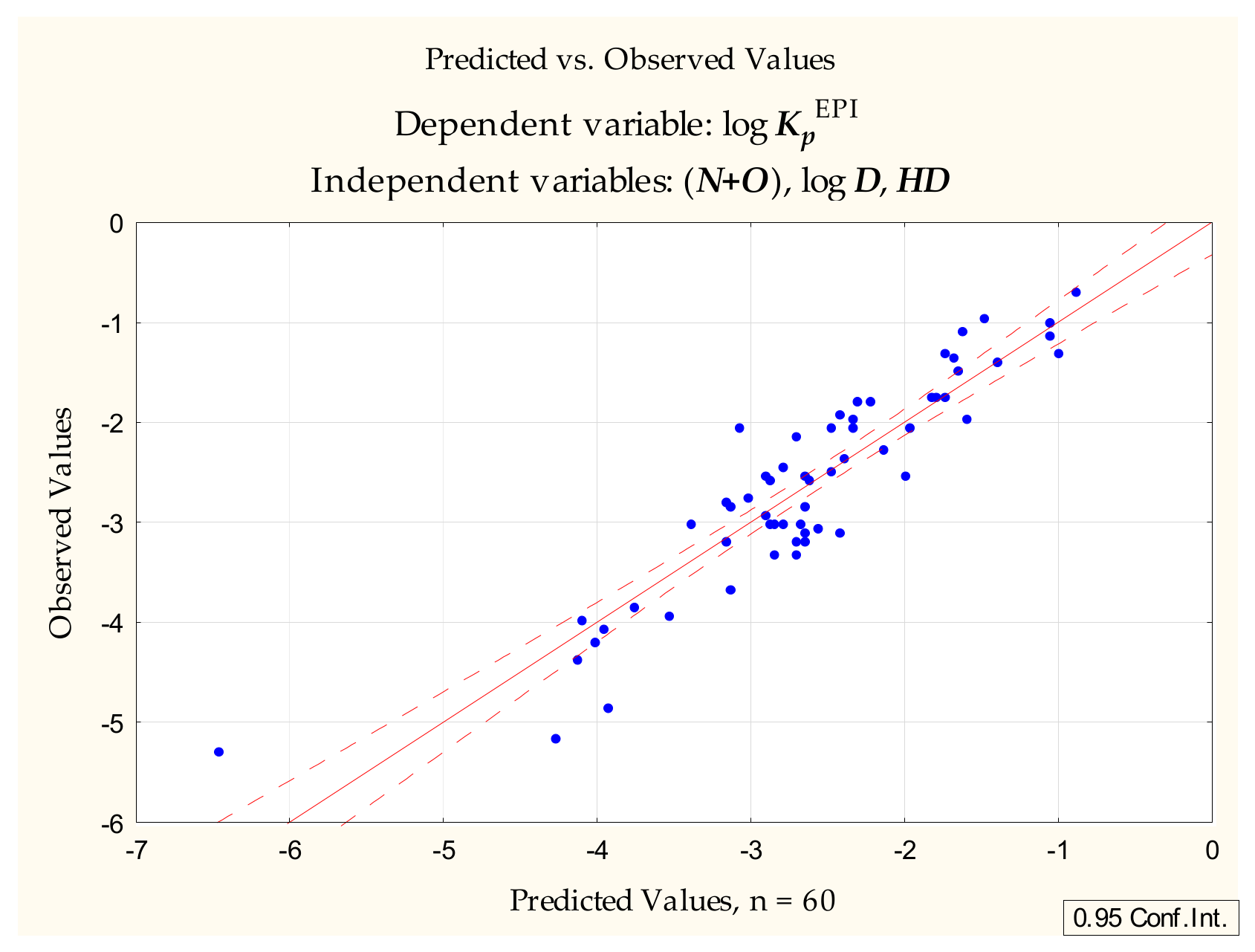
2.3. Single Chromatographic Run Retention Parameters—Rf
(n = 60, R2 = 0.833, R2adj. = 0.824, F = 92.270, p < 0.0000, se = 0.438)
(n = 40, R2 = 0.819, R2adj. = 0.804, F = 54.356, p < 0.00000, se = 0.456)
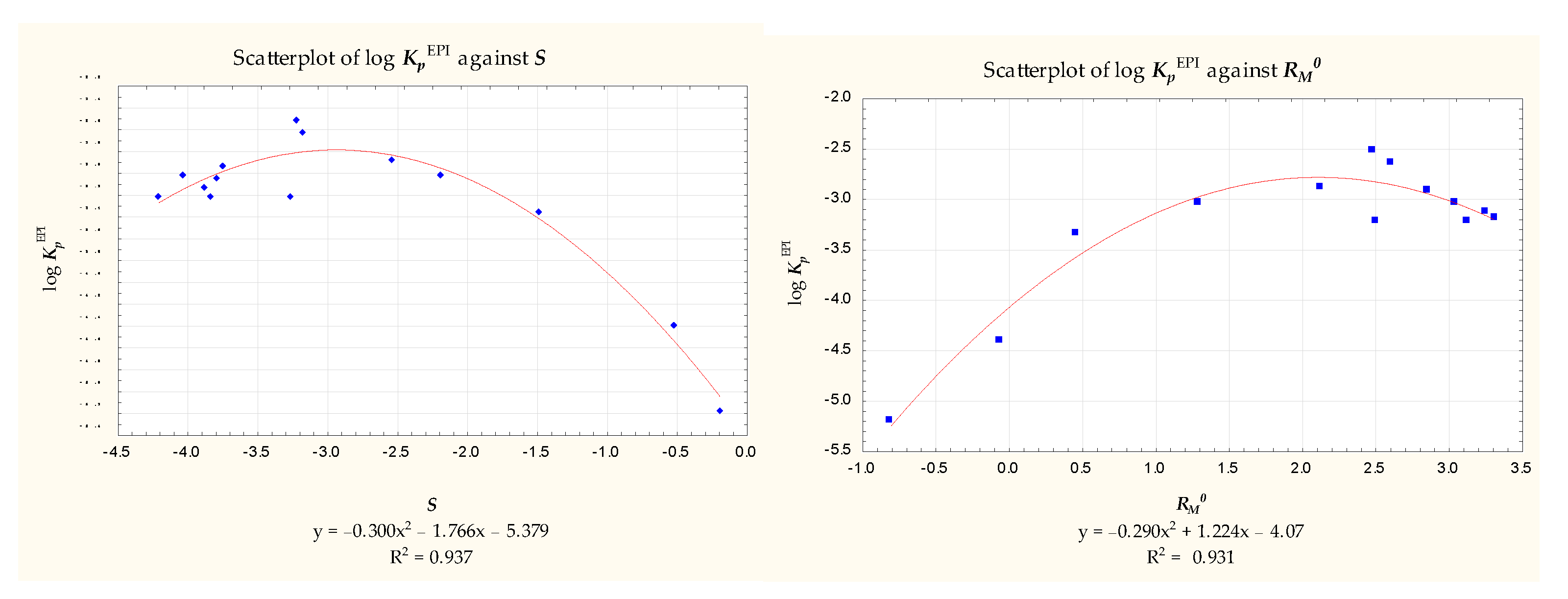
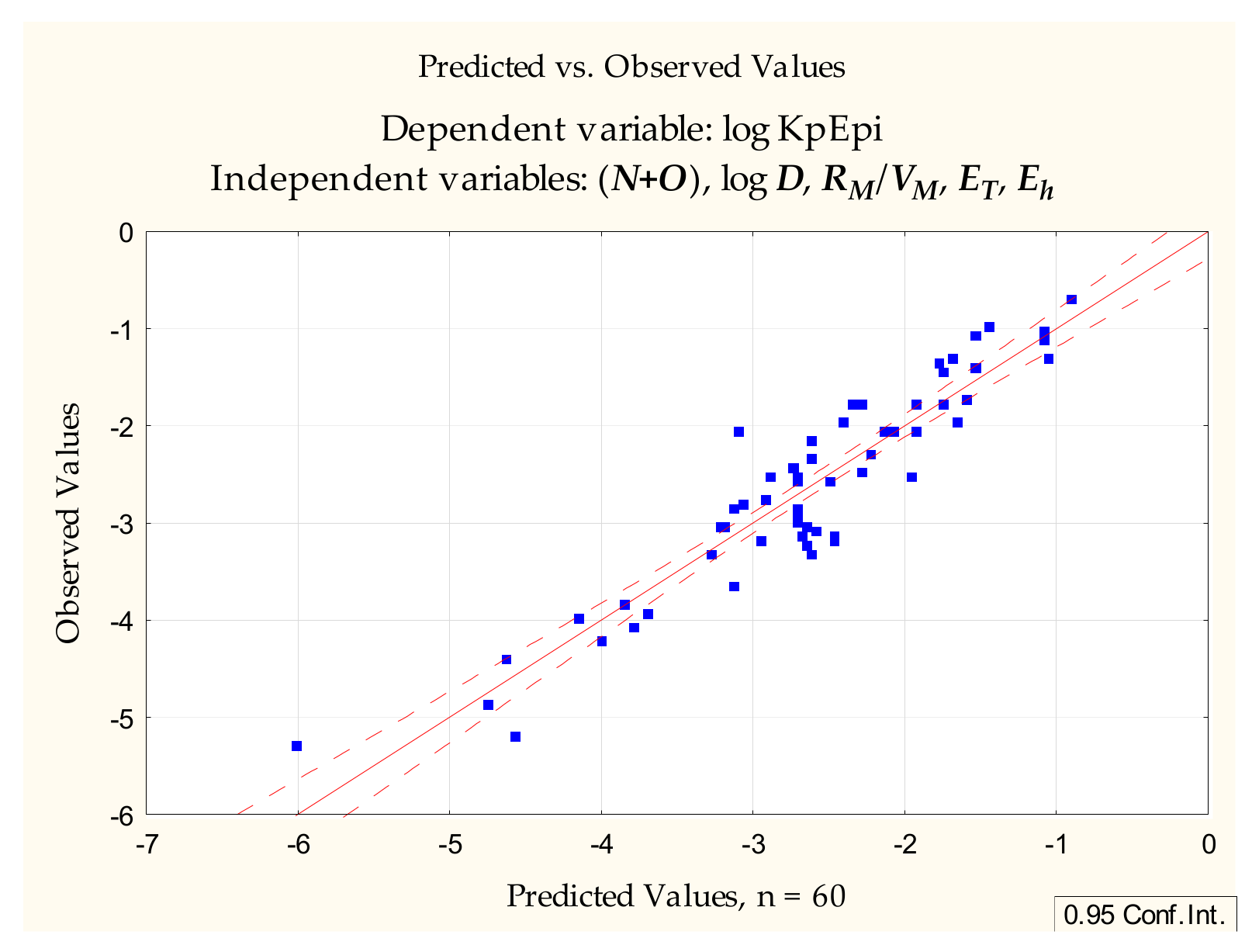
2.4. Single Chromatographic Run Retention Parameters—RM
(n = 60, R2 = 0.868, R2adj. = 0.855, F = 70.869, p < 0.0000, se = 0.397)
(n = 40, R2 = 0.823, R2adj. = 0.797, F = 31.654, p < 0.00000, se = 0.464)
(n = 60, R2 = 0.913, R2adj. = 0.899, F = 66.710, p < 0.0000, se = 0.332)
(n = 40, R2 = 0.863, R2adj. = 0.827, F = 24.361, p < 0.0000, se = 0.428)
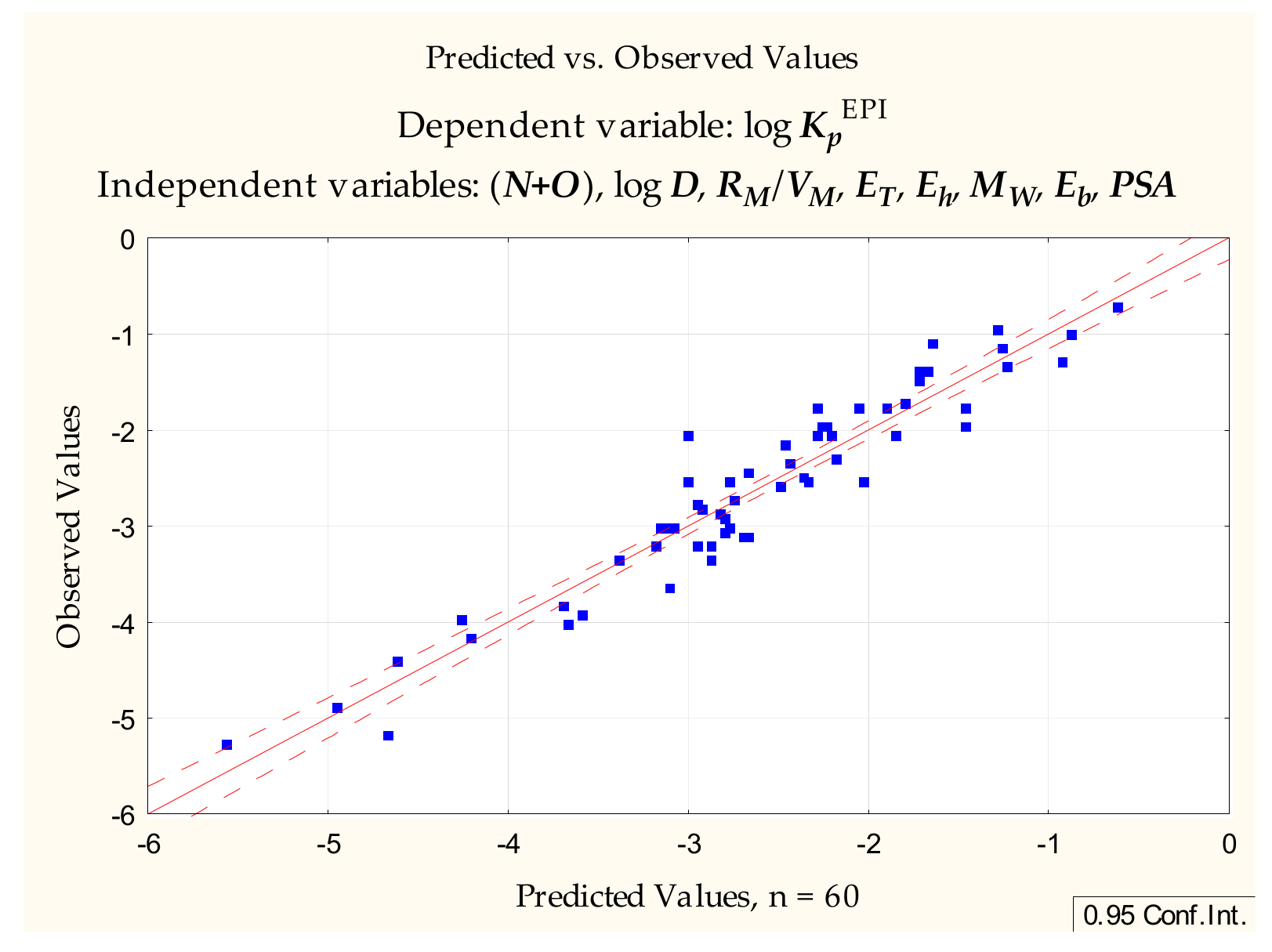
(n = 39, R2 = 0.937, R2adj. = 0.921, F = 56.137, p < 0.0000, se = 0.278)
3. Materials and Methods
3.1. Chemicals
3.2. Thin Layer Chromatography
3.3. Calculated Molecular Descriptors
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Ng, K.W.; Lau, W.M. Skin Deep: The Basics of Human Skin Structure and Drug Penetration. Percutaneous Penetration Enhanc. Chem. Methods Penetration Enhanc. 2015, 3–11. [Google Scholar] [CrossRef]
- Todo, H. Transdermal Permeation of Drugs in Various Animal Species. Pharmaceutics 2017, 9, 33. [Google Scholar] [CrossRef]
- Neupane, R.; Boddu, S.H.S.; Renukuntla, J.; Babu, R.J.; Tiwari, A.K. Alternatives to Biological Skin in Permeation Studies: Current Trends and Possibilities. Pharmaceutics 2020, 12, 152. [Google Scholar] [CrossRef]
- El Tayar, N.; Tsai, R.-S.; Testa, B.; Carrupt, P.-A.; Hansch, C.; Leo, A. Percutaneous Penetration of Drugs: A Quantitative Structure–Permeability Relationship Study. J. Pharm. Sci. 1991, 80, 744–749. [Google Scholar] [CrossRef]
- Anderson, B.D.; Raykar, P.V. Solute Structure-Permeability Relationships in Human Stratum Corneum. J. Investig. Dermatol. 1989, 93, 280–286. [Google Scholar] [CrossRef]
- Potts, R.O.; Guy, R.H. Predicting Skin Permeability. Pharm. Res. 1992, 09, 663–669. [Google Scholar] [CrossRef]
- Potts, R.O.; Guy, R.H. A Predictive Algorithm for Skin Permeability: The Effects of Molecular Size and Hydrogen Bond Activity. Pharm. Res. 1995, 12, 1628–1633. [Google Scholar] [CrossRef] [PubMed]
- Barratt, M.D. Quantitative structure-activity relationships for skin permeability. Toxicol. Vitr. 1995, 9, 27–37. [Google Scholar] [CrossRef]
- Neumann, D.; Kohlbacher, O.; Merkwirth, C.; Lengauer, T. A Fully Computational Model for Predicting Percutaneous Drug Absorption. J. Chem. Inf. Modeling 2006, 46, 424–429. [Google Scholar] [CrossRef]
- Abraham, M.H.; Chadha, H.S.; Mitchell, R.C. The Factors that Influence Skin Penetration of Solutes. J. Pharm. Pharmacol. 1995, 47, 8–16. [Google Scholar] [CrossRef]
- Abraham, M.H.; Martins, F.; Mitchell, R.C. Algorithms For Skin Permeability Using Hydrogen Bond Descriptors: The Problem of Steroids. J. Pharm. Pharmacol. 1997, 49, 858–865. [Google Scholar] [CrossRef]
- Abraham, M.H.; Martins, F. Human Skin Permeation and Partition: General Linear Free-Energy Relationship Analyses. J. Pharm. Sci. 2004, 93, 1508–1523. [Google Scholar] [CrossRef] [PubMed]
- Patel, H.; Berge, W.F.; Cronin, M.T.D. Quantitative structure–activity relationships (QSARs) for the prediction of skin permeation of exogenous chemicals. Chemosphere 2002, 48, 603–613. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Chen, C.-P.; Chen, C.-C. Predicting Skin Permeability of Chemical Substances using a Quantitative Structure-activity Relationship. Procedia Eng. 2012, 45, 875–879. [Google Scholar] [CrossRef]
- Neely, B.J.; Madihally, S.V.; Robinson, R.L.; Gasem, K.A.M. Nonlinear Quantitative Structure-Property Relationship Modeling of Skin Permeation Coefficient. J. Pharm. Sci. 2009, 98, 4069–4084. [Google Scholar] [CrossRef]
- Wilschut, A.; Berge, W.F.; Robinson, P.J.; McKone, T.E. Estimating skin permeation. The validation of five mathematical skin permeation models. Chemosphere 1995, 30, 1275–1296. [Google Scholar] [CrossRef]
- Moss, G.P.; Dearden, J.C.; Patel, H.; Cronin, M.T.D. Quantitative structure–permeability relationships (QSPRs) for percutaneous absorption. Toxicol. Vitr. 2002, 16, 299–317. [Google Scholar] [CrossRef]
- Mitragotri, S.; Anissimov, Y.G.; Bunge, A.L.; Frasch, H.F.; Guy, R.H.; Hadgraft, J.; Kasting, G.B.; Lane, M.E.; Roberts, M.S. Mathematical models of skin permeability: An overview. Int. J. Pharm. 2011, 418, 115–129. [Google Scholar] [CrossRef] [PubMed]
- Fitzpatrick, D.; Corish, J.; Hayes, B. Modelling skin permeability in risk assessment—The future. Chemosphere 2004, 55, 1309–1314. [Google Scholar] [CrossRef]
- Geinoz, S.; Guy, R.H.; Testa, B.; Carrupt, P.-A. Quantitative Structure-Permeation Relationships (QSPeRs) to Predict Skin Permeation: A Critical Evaluation. Pharm. Res. 2004, 21, 83–92. [Google Scholar] [CrossRef]
- Lian, G.; Chen, L.; Han, L. An evaluation of mathematical models for predicting skin permeability. J. Pharm. Sci. 2008, 97, 584–598. [Google Scholar] [CrossRef] [PubMed]
- Alonso, C.; Carrer, V.; Espinosa, S.; Zanuy, M.; Córdoba, M.; Vidal, B.; Domínguez, M.; Godessart, N.; Coderch, L.; Pont, M. Prediction of the skin permeability of topical drugs using in silico and in vitro models. Eur. J. Pharm. Sci. 2019, 136, 104945. [Google Scholar] [CrossRef]
- Lien, E.J.; Gaot, H. QSAR Analysis of Skin Permeability of Various Drugs in Man as Compared to in Vivo and in Vitro Studies in Rodents. Pharm. Res. 1995, 12, 583–587. [Google Scholar] [CrossRef]
- Chen, C.-P.; Chen, C.-C.; Huang, C.-W.; Chang, Y.-C. Evaluating Molecular Properties Involved in Transport of Small Molecules in Stratum Corneum: A Quantitative Structure-Activity Relationship for Skin Permeability. Molecules 2018, 23, 911. [Google Scholar] [CrossRef]
- Mitragotri, S. A theoretical analysis of permeation of small hydrophobic solutes across the stratum corneum based on Scaled Particle Theory. J. Pharm. Sci. 2002, 91, 744–752. [Google Scholar] [CrossRef] [PubMed]
- Sobańska, A.W. Application of planar chromatographic descriptors to the prediction of physicochemical properties and biological activity of compounds. J. Liq. Chromatogr. Relat. Technol. 2018, 41, 255–271. [Google Scholar] [CrossRef]
- Sobańska, A.W.; Brzezińska, E. Phospholipid-based Immobilized Artificial Membrane (IAM) Chromatography: A PowerfulTool to Model Drug Distribution Processes. Curr. Pharm. Des. 2017, 23, 6784–6794. [Google Scholar] [CrossRef]
- Sobańska, A.W.; Brzezińska, E. Application of planar and column micellar liquid chromatography to the prediction of physicochemical properties and biological activity of compounds. J. Liq. Chromatogr. Relat. Technol. 2019, 42, 227–237. [Google Scholar] [CrossRef]
- Jevric, L.R.; Podunavac Kuzmanovic, S.O.; Svarc Gajic, J.V.; Kovacevic, S.; Jovanovic, B.Z. RP- HPTLC Retention Data in Correlation with the In-silico ADME Properties of a Series of s-triazine Derivatives. Iran. J. Pharm. Res. 2014, 13, 1203–1211. [Google Scholar] [CrossRef]
- Kovačević, S.Z.; Jevrić, L.R.; Podunavac Kuzmanović, S.O.; Lončar, E.S. Prediction of In-silico ADME Properties of 1,2-O-Isopropylidene Aldohexose Derivatives. Iran. J. Pharm. Res. 2014, 13, 899–907. [Google Scholar]
- Nasal, A.; Sznitowska, M.; Buciński, A.; Kaliszan, R. Hydrophobicity parameter from high-performance liquid chromatography on an immobilized artificial membrane column and its relationship to bioactivity. J. Chromatogr. A 1995, 692, 83–89. [Google Scholar] [CrossRef]
- Barbato, F.; Cappello, B.; Miro, A.; La Rotonda, M.; Quaglia, F. Chromatographic indexes on immobilized artificial membranes for the prediction of transdermal transport of drugs. II Farm. 1998, 53, 655–661. [Google Scholar] [CrossRef]
- Lázaro, E.; Ràfols, C.; Abraham, M.H.; Rosés, M. Chromatographic Estimation of Drug Disposition Properties by Means of Immobilized Artificial Membranes (IAM) and C18 Columns. J. Med. Chem. 2006, 49, 4861–4870. [Google Scholar] [CrossRef]
- Hidalgo-Rodríguez, M.; Soriano-Meseguer, S.; Fuguet, E.; Ràfols, C.; Rosés, M. Evaluation of the suitability of chromatographic systems to predict human skin permeation of neutral compounds. Eur. J. Pharm. Sci. 2013, 50, 557–568. [Google Scholar] [CrossRef] [PubMed]
- Soriano-Meseguer, S.; Fuguet, E.; Port, A.; Rosés, M. Estimation of skin permeation by liquid chromatography. ADMET DMPK 2018, 6, 140–152. [Google Scholar] [CrossRef]
- Turowski, M.; Kaliszan, R. Keratin immobilized on silica as a new stationary phase for chromatographic modelling of skinpermeation. J. Pharm. Biomed. Anal. 1997, 15, 1325–1333. [Google Scholar] [CrossRef]
- Martínez-Pla, J.J.; Martín-Biosca, Y.; Sagrado, S.; Villanueva-Camañas, R.M.; Medina-Hernández, M.J. Biopartitioning micellar chromatography to predict skin permeability. Biomed. Chromatogr. 2003, 17, 530–537. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Pla, J.; Martin-Biosca, Y.; Sagrado, S.; Villanueva-Camanas, R.; Medina-Hernandez, M. Evaluation of the pH effect of formulations on the skin permeability of drugs by biopartitioning micellar chromatography. J. Chromatogr. A 2004, 1047, 255–262. [Google Scholar] [CrossRef]
- Waters, L.J.; Shahzad, Y.; Stephenson, J. Modelling skin permeability with micellar liquid chromatography. Eur. J. Pharm. Sci. 2013, 50, 335–340. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, J.; Liu, H.; Liu, J.; Zhang, L.; Liu, K.; He, Z. Predicting skin permeability using liposome electrokinetic chromatography. Analyst 2009, 134, 267–272. [Google Scholar] [CrossRef]
- Seung Lim, J. EPI Suite: A Fascinate Predictive Tool for Estimating the Fates of Organic Contaminants. J. Bioremediation Biodegrad. 2016. [Google Scholar] [CrossRef]
- Bate-Smith, E.C.; Westall, R.G. Chromatographic behaviour and chemical structure I. Some naturally occurring phenolic substances. Biochim. et Biophys. Acta 1950, 4, 427–440. [Google Scholar] [CrossRef]
- Soczewiński, E.; Wachtmeister, C.A. The relation between the composition of certain ternary two- phase solvent systems and RM values. J. Chromatogr. A 1962, 7, 311–320. [Google Scholar] [CrossRef]
- Lipinski, C.A. Lead- and drug-like compounds: The rule-of-five revolution. Drug Discov. Today Technol. 2004, 1, 337–341. [Google Scholar] [CrossRef]
- Veber, D.F.; Johnson, S.R.; Cheng, H.-Y.; Smith, B.R.; Ward, K.W.; Kopple, K.D. Molecular Properties That Influence the Oral Bioavailability of Drug Candidates. J. Med. Chem. 2002, 45, 2615–2623. [Google Scholar] [CrossRef] [PubMed]
- Komsta, Ł.; Skibiński, R.; Berecka, A.; Gumieniczek, A.; Radkiewicz, B.; Radoń, M. Revisiting thin-layer chromatography as a lipophilicity determination tool—A comparative study on several techniques with a model solute set. J. Pharm. Biomed. Anal. 2010, 53, 911–918. [Google Scholar] [CrossRef]
- Sobańska, A.W.; Wójcicka, K.; Brzezińska, E. Evaluation of the lipophilicity of selected sunscreens- A chemometric analysis of thin-layer chromatographic retention data. J. Sep. Sci. 2014, 37, 3074–3081. [Google Scholar] [CrossRef]
- Sobańska, A.W.; Brzezińska, E. Application of RP-18 thin-layer chromatography and quantitative structure–activity relationship analysis for the prediction of the blood–brain barrier permeation. JPC J. Planar Chromatogr. Mod. TLC 2016, 29, 287–298. [Google Scholar] [CrossRef]
- Sobańska, A.W.; Wanat, K.; Brzezińska, E. Prediction of the Blood-Brain Barrier Permeability Using RP-18 Thin Layer Chromatography. Open Chem. 2019, 17, 43–56. [Google Scholar] [CrossRef]
- Pyzowski, J.; Brzezińska, E.; Sobańska, A.W. RP-18 chromatographic-based study of the blood—brain barrier permeability of selected sunscreens and preservatives. JPC J. Planar Chromatogr. Mod. TLC 2017, 30, 275–284. [Google Scholar] [CrossRef]
- Geldenhuys, W.J.; Mohammad, A.S.; Adkins, C.E.; Lockman, P.R. Molecular determinants of blood–brain barrier permeation. Ther. Deliv. 2015, 6, 961–971. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.C.; Wang, G.P.; Wang, Y.F.; Liang, W.Q.; Yu, Q.S.; Chow, M.S.S. Limitations of Potts and Guy model and a predictive algorithm for skin permeability including the effects of hydrogen-bond on diffusivity. Pharmazie 2004, 59, 282–285. [Google Scholar] [PubMed]
- Cronin, M.T.D.; Dearden, J.C.; Moss, G.P.; Murray-Dickson, G. Investigation of the mechanism of flux across human skin in vitro by quantitative structure-permeability relationships. Eur. J. Pharm. Sci. 1999, 7, 325–330. [Google Scholar] [CrossRef]

| Equation | n | R | Ref. |
|---|---|---|---|
| log kp = −1.36 Δlog Poct-hept− 3.38 | 21 | 0.90 | [4] |
| log Kp = −6.3 + 0.71 log Pow − 0.0061 Mw | 93 | 0.82 | [6] |
| log Kp = 0.82 log Pow − 0.0093 VM − 0.039 MPt − 2.36 | 60 | 0.95 | [8] |
| log Kp = 0.84 log Pow − 0.07 (log Pow)2 − 0.27 Hb − 1.84 log Mw + 4.39 | 22 | 0.98 | [23] |
| log Kp = 0.652 log Pow − 0.00603 Mw − 0.623 ABSQon − 0.313 SsssCH − 2.30 | 143 | 0.95 | [13] |
| log Kp = −5.426 − 0.106 E − 0.473 S − 0.473 A − 3.000 B + 2.296 V | 119 | 0.91 | [12] |
| log Kp = −3.05 − 0.0065 QXXp + 0.65 ALOGP − 1.75 Neoplastic-80 + 0.22 F06[C-N] | 158 | 0.91 | [14] |
| log Kp = −5.426 − 0.106 E − 0.473 S − 0.473 A − 3.000 B + 2.296 V | 119 | 0.91 | [12] |
| log Kp = −5.048 − 0.586 π2H − 0.633Σα2H − 3.481 Σβ2H + 1.787 V | 46 | 0.98 | [10] |
| Equation | n | R | Reference | |
|---|---|---|---|---|
| NP TLC | log Kp = −1.318 (RM0)2 − 7.529 RM0 − 9.142 (dioxane-cyclohexane) | 7 7 | 0.98 | [30] |
| log Kp = −0.762 (RM0)2 − 5.146 RM0 − 6.955 (THF-cyclohexane) | 0.97 | |||
| IAM HPLC | log Kp= −10.19 + 1.77 log kIAM | 10 | 0.94 | [31] |
| log Ksc= 0.40 + 0.64 log kIAM | 10 | 0.97 | ||
| log Kp= −6.16 − 0.46 (log kIAM)2 + 1.54 log kIAM | 14 | 0.80 | ||
| log Kp = −6.09 + 1.05 log kIAM | 14 | 0.88 | ||
| log Kp= −5.154 + 1.443 log kIAM | 32 | 0.51 | [33] | |
| log Ksc= 1.555 + 1.522 log kIAM | 15 | 0.92 | ||
| log Kp= −5.09 + 1.94 log kIAM | 32 | 0.55 | [34] | |
| log Kp= −3.58 + 2.56 log kIAM − 1.12 V | 32 | 0.86 | ||
| log Kp= −2.419 Δlog kwIAM − 2.206 | 10 | 0.95 | [32] | |
| log Kp= −2.136 Δlog kwIAM + 0.037 log Pow − 2.373 | 10 | 0.94 | ||
| log Kp= −2.182 Δlog kwIAM + 0.046 log kwIAM − 2.323 | 10 | 0.94 | ||
| RP-18 | log Kp = −4.76 + 1.44 log k − 1.16 V | 27 | 0.91 | [34] |
| log Kp = −5.728 + 1.636 log k (MSC18 column) | 32 | 0.75 | [33] | |
| log Kp = −5.865 + 1.849 log k(RP-18 column) | 32 | 0.73 | ||
| log Ksc = 1.131 + 0.855 log k (MSC18 column) | 15 | 0.87 | ||
| log Ksc = 1.099 + 0.95 log k (RP-18 column) | 15 | 0.85 | ||
| BMC | log Kp = −3.3 + 1.3 log kBMC − 0.008 MPt | 42 | 0.91 | [37] |
| log Kp = −2.24 + 1.83 log Pmw − 0.0123 Mw | 22 | 0.91 | [39] | |
| Keratin | log Kp = −6.558 + 1.920 log kIAM − 1.039 log kKERATIN | 17 | 0.93 | [36] |
| log KpEPI | log Kp(6) | log Kp(7) | log Kp(8) | log Kp(9) | log Kp(10) | log Kp(12) | log Kpexp | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | Diazepam | −2.53 | −1.99 | −1.99 | −1.94 | −1.95 | −2.02 | −2.01 | |
| 2 | Temazepam | −3.04 | −2.68 | −2.70 | −2.63 | −2.66 | −2.77 | −2.80 | |
| 3 | Alprazolam | −3.13 | −2.41 | −2.39 | −2.47 | −2.43 | −2.69 | −2.82 | |
| 4 | Medazepam | −1.39 | −1.41 | −1.41 | −1.53 | −1.54 | −1.68 | −1.67 | |
| 5 | Bromazepam | −3.22 | −2.71 | −2.73 | −2.64 | −2.65 | −3.17 | −3.25 | |
| 6 | Chlordiazepoxide | −2.87 | −2.66 | −2.68 | −2.69 | −2.73 | −2.83 | −2.84 | |
| 7 | Midazolam | −1.75 | −1.83 | −1.82 | −1.92 | −1.97 | −2.29 | −2.30 | |
| 8 | Oxazepam | −2.92 | −2.90 | −2.94 | −2.70 | −2.73 | −2.80 | −2.80 | |
| 9 | Lorazepam | −3.02 | −2.87 | −2.91 | −2.71 | −2.74 | −3.14 | −3.22 | |
| 10 | Lormetazepam | −3.20 | −2.66 | −2.68 | −2.48 | −2.53 | −2.87 | −2.87 | |
| 11 | Clorazepate | −3.21 | −3.16 | −3.15 | −2.95 | −2.94 | −2.94 | −2.96 | |
| 12 | Ibuprofen | −1.32 | −1.74 | −1.80 | −1.69 | −1.66 | −1.23 | −1.14 | −1.44 [9] |
| 13 | Zolpidem | −1.97 | −2.32 | −2.29 | −2.41 | −2.47 | −2.24 | −2.10 | |
| 14 | Tamoxifen | −0.70 | −0.87 | −0.80 | −0.89 | −0.89 | −0.61 | −0.51 | |
| 15 | Propranolol | −1.95 | −2.42 | −2.48 | −2.41 | −2.46 | −2.25 | −2.18 | |
| 16 | Ranitidine | −4.39 | −4.12 | −4.09 | −4.62 | −4.58 | −4.62 | −4.83 | −4.05 [9] |
| 17 | Methyldopa | −5.18 | −4.27 | −4.41 | −4.58 | −4.70 | −4.66 | −4.67 | |
| 18 | Amizepin | −2.50 | −2.49 | −2.56 | −2.29 | −2.29 | −2.36 | −2.38 | |
| 19 | Enalapril | −4.87 | −3.93 | −3.88 | −4.74 | −3.65 | −4.94 | −2.55 | |
| 20 | Paracetamol | −3.35 | −2.85 | −2.97 | −3.27 | −3.34 | −3.40 | −3.41 | |
| 21 | Aspirin | −3.03 | −2.84 | −2.88 | −3.17 | −3.21 | −3.07 | −3.00 | −2.14 [9] |
| 22 | Cefuroxime | −5.29 | −6.45 | −6.33 | −6.00 | −6.03 | −5.56 | −5.38 | |
| 23 | Theophylline | −3.84 | −3.76 | −3.77 | −3.86 | −3.84 | −3.69 | −3.63 | |
| 24 | Verapamil | −2.84 | −3.14 | −3.06 | −3.14 | −3.27 | −2.93 | −2.80 | |
| 25 | Clobazam | −3.08 | −2.55 | −2.56 | −2.58 | −2.64 | −2.81 | −2.79 | |
| 26 | Mitrazapin | −2.28 | −2.14 | −2.17 | −2.22 | −2.27 | −2.17 | −2.11 | |
| 27 | Promazine | −1.38 | −1.68 | −1.73 | −1.76 | −1.82 | −1.71 | −1.62 | |
| 28 | Phenytoin | −2.58 | −2.87 | −2.91 | −2.69 | −2.69 | −2.50 | −2.46 | |
| 29 | Hydroxyzine | −3.34 | −2.71 | −2.74 | −2.62 | −2.72 | −2.86 | −2.89 | |
| 30 | Mianserin | −1.47 | −1.66 | −1.71 | −1.74 | −1.80 | −1.73 | −1.67 | |
| 31 | Valproic acid | −1.79 | −2.30 | −2.43 | −2.27 | −2.30 | −1.90 | −1.83 | |
| 32 | Zopiclone | −3.97 | −4.10 | −4.00 | −4.13 | −4.21 | −4.25 | −4.14 | |
| 33 | Haloperidol | −2.06 | −2.35 | −2.40 | −2.08 | −2.24 | −2.28 | −2.19 | |
| 34 | Risperidone | −2.79 | −3.15 | −3.07 | −3.07 | −3.18 | −2.94 | −2.79 | |
| 35 | Loperamide | −2.06 | −2.48 | −2.47 | −2.14 | −2.29 | −2.21 | −2.11 | |
| 36 | Phenylbutazone | −2.44 | −2.78 | −2.82 | −2.73 | −2.84 | −2.66 | −2.57 | |
| 37 | Clonidine | −3.04 | −2.80 | −2.91 | −2.63 | −2.68 | −3.16 | −3.25 | |
| 38 | PABA | −3.02 | −3.38 | −3.57 | −3.22 | −3.26 | −3.09 | −3.11 | |
| 39 | Propylparaben | −1.80 | −2.23 | −2.27 | −2.35 | −2.31 | −2.06 | −2.05 | |
| 40 | Methylparaben | −2.36 | −2.39 | −2.45 | −2.61 | −2.57 | −2.44 | −2.47 | −2.04 [8] |
| 41 | Quetiap Quetiapine | −3.67 | −3.14 | −3.14 | −3.11 | −3.19 | −3.09 | −3.07 | |
| 42 | Chlorprotixen | −1.13 | −1.06 | −1.10 | −1.09 | −1.14 | −1.25 | −1.20 | |
| 43 | Perazine | −2.05 | −1.96 | −1.96 | −1.93 | −1.99 | −1.84 | −1.74 | |
| 44 | Trifluoperazine | −1.75 | −1.79 | −1.77 | −1.58 | −1.73 | −1.79 | −1.65 | |
| 45 | Thioridazine | −0.96 | −1.48 | −1.50 | −1.44 | −1.52 | −1.27 | −1.09 | |
| 46 | Fluconazole | −4.19 | −4.00 | −3.96 | −4.00 | −4.04 | −4.21 | −4.24 | |
| 47 | Tolperisone | −1.76 | −1.74 | −1.80 | −1.75 | −1.82 | −1.45 | −1.28 | |
| 48 | Fenspiride | −2.75 | −3.02 | −3.09 | −2.91 | −3.00 | −2.75 | −2.66 | |
| 49 | Pizotifen | −1.00 | −1.04 | −1.09 | −1.08 | −1.12 | −0.87 | −0.75 | |
| 50 | Cyproheptadine | −1.30 | −0.99 | −1.02 | −1.05 | −1.08 | −0.93 | −0.86 | |
| 51 | Clozapine | −2.52 | −2.91 | −2.96 | −2.69 | −2.79 | −2.99 | −2.97 | |
| 52 | Tiapride | −4.05 | −3.96 | −3.99 | −3.77 | −3.91 | −3.66 | −3.51 | |
| 53 | Olanzapine | −2.56 | −2.61 | −2.62 | −2.50 | −2.52 | −2.34 | −2.25 | |
| 54 | Betahistine | −3.12 | −2.66 | −2.84 | −2.68 | −2.75 | −2.66 | −2.66 | |
| 55 | Dexketoprofen | −2.16 | −2.71 | −2.82 | −2.61 | −2.70 | −2.45 | −2.37 | |
| 56 | Caffeine | −3.94 | −3.52 | −3.50 | −3.68 | −3.68 | −3.58 | −3.51 | −3.64 [34] |
| 57 | Hymecromone | −2.53 | −2.66 | −2.68 | −2.89 | −2.84 | −2.77 | −2.83 | |
| 58 | Ketotifen | −1.99 | −1.58 | −1.62 | −1.64 | −1.71 | −1.47 | −1.32 | |
| 59 | Clemastine | −1.09 | −1.62 | −1.66 | −1.52 | −1.63 | −1.64 | −1.57 | |
| 60 | Salicylic acid | −2.08 | −3.07 | −3.22 | −3.09 | −3.10 | −2.99 | −3.05 | −2.84 [9] |
| 61 | Indomethacin | −1.97 | −3.40 | −3.44 | −3.24 | −3.36 | −3.49 | −3.51 | −3.67 [9,13] |
| 62 | Piroxicam | −2.63 | −4.05 | −4.00 | −3.85 | −3.84 | −3.68 | −3.65 | −3.81 [9,13] |
| 63 | Naproxen | −1.98 | −2.60 | −2.69 | −2.63 | −2.68 | −2.52 | −2.54 | −2.54 [37] |
| Rf | Rf/PSA | RM | RM/MW | RM/VM | RM0 | S | ||
|---|---|---|---|---|---|---|---|---|
| 1 | Diazepam | 0.33 | 0.0101 | 0.308 | 0.00108 | 0.00123 | 3.578 | −4.176 |
| 2 | Temazepam | 0.50 | 0.0095 | 0.000 | 0.00000 | 0.00000 | 3.050 | −3.798 |
| 3 | Alprazolam | 0.22 | 0.0058 | 0.550 | 0.00178 | 0.00204 | 3.254 | −3.877 |
| 4 | Medazepam | 0.56 | 0.0359 | −0.105 | −0.00039 | −0.00042 | 2.528 | −3.035 |
| 5 | Bromazepam | 0.51 | 0.0094 | −0.017 | −0.00005 | −0.00007 | 2.496 | −3.269 |
| 6 | Chlordiazepoxide | 0.62 | 0.0117 | −0.213 | −0.00070 | −0.00079 | 2.131 | −2.551 |
| 7 | Midazolam | 0.58 | 0.0230 | −0.140 | −0.00043 | −0.00051 | 2.235 | −2.741 |
| 8 | Oxazepam | 0.60 | 0.0097 | −0.176 | −0.00061 | −0.00073 | 2.864 | −3.752 |
| 9 | Lorazepam | 0.61 | 0.0099 | −0.194 | −0.00060 | −0.00076 | 3.031 | −4.037 |
| 10 | Lormetazepam | 0.49 | 0.0093 | 0.017 | 0.00005 | 0.00006 | 3.303 | −4.207 |
| 11 | Clorazepate | 0.47 | 0.0060 | 0.052 | 0.00017 | 0.00020 | 3.117 | −3.840 |
| 12 | Ibuprofen | 0.46 | 0.0122 | 0.078 | 0.00038 | 0.00037 | 4.139 | −4.895 |
| 13 | Zolpidem | 0.68 | 0.0181 | −0.327 | −0.00106 | −0.00109 | 1.744 | −2.341 |
| 14 | Tamoxifen | 0.48 | 0.0381 | 0.043 | 0.00012 | 0.00015 | 5.041 | −5.908 |
| 15 | Propranolol | 0.82 | 0.0198 | −0.659 | −0.00254 | −0.00254 | 2.059 | −3.004 |
| 16 | Ranitidine | 0.82 | 0.0074 | −0.659 | −0.00208 | −0.00220 | 0.343 | −0.518 |
| 17 | Methyldopa | 0.98 | 0.0094 | −1.690 | −0.00800 | −0.00914 | 2.480 | −0.197 |
| 18 | Amizepin | 0.55 | 0.0119 | −0.087 | −0.00033 | −0.00040 | 2.484 | −3.221 |
| 19 | Enalapril | 0.82 | 0.0085 | −0.659 | −0.00175 | −0.00175 | 2.035 | −2.994 |
| 20 | Paracetamol | 0.85 | 0.0172 | −0.753 | −0.00498 | −0.00542 | 0.459 | −1.500 |
| 21 | Aspirin | 0.76 | 0.0119 | −0.501 | −0.00278 | −0.00328 | 1.301 | −2.204 |
| 22 | Cefuroxime | 0.77 | 0.0039 | −0.525 | −0.00124 | −0.00160 | 2.023 | −3.307 |
| 23 | Theophylline | 0.79 | 0.0114 | −0.575 | −0.00319 | −0.00110 | ||
| 24 | Verapamil | 0.77 | 0.0120 | −0.525 | −0.00115 | −0.00036 | ||
| 25 | Clobazam | 0.50 | 0.0124 | 0 | 0 | 0 | ||
| 26 | Mitrazapin | 0.71 | 0.0366 | −0.389 | −0.00147 | −0.00049 | ||
| 27 | Promazine | 0.71 | 0.0223 | −0.389 | −0.00137 | −0.00045 | ||
| 28 | Phenytoin | 0.70 | 0.0120 | −0.368 | −0.00146 | −0.00051 | ||
| 29 | Hydroxyzine | 0.76 | 0.0212 | −0.501 | −0.00134 | −0.00046 | ||
| 30 | Mianserin | 0.77 | 0.1185 | −0.525 | −0.00199 | −0.00065 | ||
| 31 | Valproic acid | 0.54 | 0.1185 | −0.070 | −0.00048 | −0.00013 | ||
| 32 | Zopiclone | 0.80 | 0.1185 | −0.602 | −0.00155 | −0.00059 | ||
| 33 | Haloperidol | 0.78 | 0.0192 | −0.550 | −0.00146 | −0.00053 | ||
| 34 | Risperidone | 0.55 | 0.0089 | −0.087 | −0.00021 | −0.00008 | ||
| 35 | Loperamide | 0.53 | 0.0121 | −0.052 | −0.00011 | −0.00004 | ||
| 36 | Phenylbutazone | 0.39 | 0.0096 | 0.194 | 0.00063 | 0.00021 | ||
| 37 | Clonidine | 0.83 | 0.0234 | −0.689 | −0.00299 | −0.00110 | ||
| 38 | PABA | 0.85 | 0.0134 | −0.753 | −0.00549 | −0.00170 | ||
| 39 | Propylparaben | 0.61 | 0.0131 | −0.194 | −0.00108 | −0.00032 | ||
| 40 | Methylparaben | 0.72 | 0.0155 | −0.410 | −0.00270 | −0.00084 | ||
| 41 | Quetiapine | 0.72 | 0.0098 | −0.410 | −0.00107 | −0.00037 | ||
| 42 | Chlorprotixen | 0.57 | 0.0200 | −0.122 | −0.00039 | −0.00013 | ||
| 43 | Perazine | 0.44 | 0.0126 | 0.105 | 0.00031 | 0.00011 | ||
| 44 | Trifluoperazine | 0.44 | 0.0126 | 0.105 | 0.00026 | 0.00010 | ||
| 45 | Thioridazine | 0.52 | 0.0091 | −0.035 | −0.00009 | −0.00003 | ||
| 46 | Fluconazole | 0.68 | 0.0095 | −0.327 | −0.00107 | −0.00042 | ||
| 47 | Tolperisone | 0.75 | 0.0369 | −0.477 | −0.00194 | −0.00059 | ||
| 48 | Fenspiride | 0.80 | 0.0178 | −0.602 | −0.00231 | −0.00076 | ||
| 49 | Pizotifen | 0.55 | 0.0175 | −0.087 | −0.00029 | −0.00010 | ||
| 50 | Cyproheptadine | 0.62 | 0.1914 | −0.213 | −0.00074 | −0.00024 | ||
| 51 | Clozapine | 0.68 | 0.0220 | −0.327 | −0.00100 | −0.00035 | ||
| 52 | Tiapride | 0.81 | 0.0096 | −0.630 | −0.00192 | −0.00064 | ||
| 53 | Olanzapine | 0.60 | 0.0102 | −0.176 | −0.00056 | −0.00020 | ||
| 54 | Betahistine | 0.72 | 0.0289 | −0.410 | −0.00301 | −0.00079 | ||
| 55 | Dexketoprofen | 0.61 | 0.0112 | −0.194 | −0.00076 | −0.00025 | ||
| 56 | Caffeine | 0.66 | 0.0123 | −0.288 | −0.00148 | −0.00050 | ||
| 57 | Hymecromone | 0.73 | 0.0157 | −0.432 | −0.00245 | −0.00083 | ||
| 58 | Ketotifen | 0.70 | 0.0144 | −0.368 | −0.00119 | −0.00042 | ||
| 59 | Clemastine | 0.45 | 0.0361 | 0.087 | 0.00025 | 0.00009 | ||
| 60 | Salicylic acid | 0.70 | 0.0122 | −0.368 | −0.00266 | −0.00088 | ||
| 61 | Indomethacin | 0.46 | 0.0066 | −0.069 | 0.000195 | 0.00007 | ||
| 62 | Piroxicam | 0.50 | 0.0046 | 0 | 0 | 0 | 2.598 | −3.193 |
| 63 | Naproxen | 0.59 | 0.0127 | −0.158 | −0.00069 | −0.00022 |
| PSA | HD | HA | log D | N+O | MW | ET | Eb | Ee | DM | EHOMO | ELUMO | Sa(a) | Sa(g) | VM | Eh | log P | R | α | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Diazepam | 32.7 | 0 | 3 | 2.96 | 3 | 284.7 | −69,868 | −3697 | −488,334 | 3.32 | −9.20 | −0.76 | 279.6 | 283.8 | 250.5 | −2.75 | 0.94 | 87.8 | 31.0 |
| 2 | Temazepam | 52.9 | 1 | 4 | 2.20 | 4 | 300.7 | −76,642 | −3799 | −541,464 | 3.98 | −9.27 | −0.87 | 289.2 | 291.9 | 257.1 | −7.84 | 1.08 | 89.0 | 31.6 |
| 3 | Alprazolam | 38.1 | 0 | 4 | 2.50 | 4 | 308.8 | −73,284 | −3950 | −550,378 | 6.48 | −9.65 | −1.23 | 293.7 | 299.4 | 269.4 | −9.24 | 2.13 | 95.4 | 33.8 |
| 4 | Medazepam | 15.6 | 0 | 2 | 4.43 | 2 | 270.8 | −63,807 | −3705 | −454,146 | 2.35 | −8.82 | −0.40 | 277.4 | 284.4 | 250.0 | −1.58 | 1.75 | 88.1 | 30.9 |
| 5 | Bromazepam | 54.4 | 1 | 4 | 2.06 | 4 | 316.2 | −67,922 | −3290 | −441,623 | 3.46 | −9.33 | −0.79 | 255.3 | 270.6 | 236.5 | −5.68 | −0.42 | 83.4 | 29.1 |
| 6 | Chlordiazepoxide | 53.1 | 1 | 4 | 2.36 | 4 | 301.8 | −74,644 | −3933 | −566,228 | 1.88 | −8.67 | −0.31 | 304.6 | 304.2 | 268.3 | −7.93 | 0.39 | 91.5 | 32.9 |
| 7 | Midazolam | 25.3 | 0 | 3 | 3.93 | 3 | 325.8 | −82,444 | −4091 | −609,612 | 4.38 | −9.17 | −0.96 | 300.0 | 309.6 | 277.3 | −3.37 | 0.13 | 98.4 | 34.4 |
| 8 | Oxazepam | 61.7 | 2 | 4 | 2.31 | 4 | 286.7 | −73,199 | −3524 | −494,470 | 2.74 | −9.13 | −0.73 | 266.5 | 274.9 | 240.7 | −7.92 | 0.84 | 84.1 | 29.8 |
| 9 | Lorazepam | 61.7 | 2 | 4 | 2.47 | 4 | 321.2 | −80,151 | −3508 | −544,373 | 4.02 | −9.28 | −0.87 | 283.6 | 291.3 | 254.6 | −9.96 | 0.61 | 88.8 | 31.7 |
| 10 | Lormetazepam | 52.9 | 1 | 4 | 2.36 | 4 | 335.2 | −83,588 | −3778 | −599,987 | 1.93 | −9.12 | −0.64 | 307.2 | 308.3 | 271.7 | −4.85 | 0.86 | 93.7 | 33.5 |
| 11 | Clorazepate | 78.8 | 2 | 5 | 2.90 | 5 | 314.7 | −82,710 | −3797 | −581,135 | 3.32 | −9.27 | −0.93 | 288.7 | 293.6 | 258.0 | −10.98 | 0.68 | 88.9 | 31.7 |
| 12 | Ibuprofen | 37.3 | 1 | 2 | 3.72 | 2 | 206.3 | −55,498 | −3380 | −344,748 | 1.86 | −9.51 | 0.06 | 262.5 | 251.3 | 210.1 | −4.81 | 2.75 | 64.1 | 24.0 |
| 13 | Zolpidem | 37.6 | 0 | 4 | 3.07 | 4 | 307.4 | −77,368 | −4724 | −613,528 | 4.07 | −8.56 | −0.55 | 355.6 | 351.1 | 300.7 | −1.03 | −0.22 | 99.6 | 35.9 |
| 14 | Tamoxifen | 12.5 | 0 | 2 | 7.88 | 2 | 371.5 | −91,827 | −6085 | −810,401 | 0.59 | −8.88 | 0.09 | 446.1 | 438.0 | 283.3 | −2.55 | 2.88 | 131.6 | 46.2 |
| 15 | Propranolol | 41.5 | 2 | 3 | 3.10 | 3 | 259.4 | −68,465 | −4113 | −472,868 | 1.26 | −8.62 | −0.43 | 311.9 | 307.7 | 259.4 | −7.41 | 0.68 | 83.4 | 30.3 |
| 16 | Ranitidine | 111.6 | 2 | 7 | 1.23 | 7 | 316.4 | −83,560 | −4192 | −562,535 | 3.41 | −7.96 | −0.21 | 403.6 | 378.1 | 299.3 | −28.08 | −4.02 | 89.1 | 33.6 |
| 17 | Methyldopa | 103.8 | 5 | 5 | 0.12 | 5 | 211.2 | −62,797 | −2902 | −363,522 | 2.59 | −9.03 | −0.01 | 225.9 | 224.7 | 185.0 | −21.50 | −1.46 | 57.2 | 21.1 |
| 18 | Amizepin | 46.3 | 2 | 3 | 2.67 | 3 | 263.3 | −59,477 | −3441 | −409,257 | 3.32 | −9.01 | −0.59 | 243.5 | 249.9 | 219.2 | −6.48 | −0.28 | 80.0 | 27.4 |
| 19 | Enalapril | 95.9 | 2 | 7 | 2.43 | 7 | 376.5 | −102,647 | −5843 | −879,009 | 2.57 | −8.94 | 0.28 | 421.3 | 441.2 | 376.5 | −2.24 | 2.57 | 111.0 | 42.3 |
| 20 | Paracetamol | 49.3 | 2 | 3 | 0.34 | 3 | 151.2 | −42,346 | −2132 | −207,000 | 4.31 | −8.43 | 0.21 | 174.8 | 172.1 | 139.0 | −10.61 | −1.32 | 45.6 | 16.2 |
| 21 | Aspirin | 63.6 | 1 | 4 | 1.19 | 4 | 180.2 | −54,523 | −2335 | −277,770 | 0.49 | −9.66 | −0.57 | 192.6 | 187.3 | 152.8 | −7.43 | −0.26 | 48.0 | 17.4 |
| 22 | Cefuroxime | 199.1 | 4 | 12 | 0.47 | 12 | 424.4 | −122,720 | −4706 | −1,017,047 | 3.74 | −9.47 | −1.61 | 222.3 | 377.3 | 328.4 | −18.43 | −2.18 | 99.7 | 38.1 |
| 23 | Theophylline | 69.3 | 1 | 6 | −0.20 | 6 | 180.2 | −50,484 | −2233 | −281,145 | 3.47 | −9.11 | −0.57 | 301.7 | 335.5 | 523.0 | −5.34 | −1.31 | 45.1 | 17.0 |
| 24 | Verapamil | 64.0 | 0 | 6 | 2.33 | 6 | 454.6 | −121,717 | −7044 | −1,150,691 | 3.64 | −8.78 | −0.95 | 705.7 | 817.4 | 1453.9 | −8.35 | 2.81 | 136.6 | 51.5 |
| 25 | Clobazam | 40.6 | 0 | 4 | 1.59 | 4 | 300.7 | −76,643 | −3800 | −546,998 | 0.55 | −8.68 | −0.23 | 402.3 | 486.0 | 813.3 | −3.41 | −1.40 | 89.7 | 31.5 |
| 26 | Mitrazapin | 19.4 | 0 | 3 | 1.97 | 3 | 265.4 | −64,413 | −4174 | −512,476 | 0.83 | −8.38 | 0.08 | 352.3 | 476.4 | 798.4 | −1.47 | 1.16 | 87.1 | 31.6 |
| 27 | Promazine | 31.8 | 0 | 2 | 2.63 | 2 | 284.4 | −65,321 | −4185 | 501,582 | 2.89 | −7.84 | −0.24 | 461.7 | 508.8 | 860.3 | −1.65 | 1.37 | 93.7 | 34.2 |
| 28 | Phenytoin | 58.2 | 2 | 4 | 2.48 | 4 | 252.3 | −66,250 | −3542 | −454,910 | 2.86 | −9.90 | −0.39 | 333.5 | 435.7 | 716.5 | −7.67 | 2.26 | 70.0 | 27.7 |
| 29 | Hydroxyzine | 35.9 | 1 | 4 | 2.00 | 4 | 374.9 | −95,297 | −5407 | 805,537 | 1.70 | −9.13 | −0.11 | 563.4 | 637.5 | 1092.8 | −8.90 | 3.49 | 107.1 | 41.7 |
| 30 | Mianserin | 6.5 | 0 | 2 | 2.76 | 2 | 264.4 | −63,761 | −4290 | −510,168 | 0.77 | −8.46 | 0.20 | 365.6 | 479.6 | 808.8 | −0.80 | 0.94 | 91.2 | 32.3 |
| 31 | Valproic acid | 37.3 | 1 | 2 | 0.16 | 2 | 144.2 | −41,139 | −2450 | −216,934 | 4.47 | −11.03 | 1.11 | 372.6 | 356.7 | 539.8 | −4.39 | 2.61 | 40.3 | 16.2 |
| 32 | Zopiclone | 91.8 | 0 | 9 | 0.65 | 8 | 388.8 | −102,536 | −4710 | −838,854 | 4.51 | −9.36 | −1.28 | 489.2 | 598.1 | 1025.2 | −5.05 | −1.83 | 101.9 | 37.9 |
| 33 | Haloperidol | 40.5 | 1 | 3 | 2.11 | 3 | 375.9 | −100,303 | −5164 | −774,341 | 1.14 | −9.12 | −0.70 | 526.5 | 605.2 | 1035.8 | −4.30 | 3.38 | 102.6 | 39.8 |
| 34 | Risperidone | 61.9 | 0 | 6 | 2.27 | 6 | 410.5 | −111,074 | −5964 | −985,849 | 5.49 | −8.87 | −0.88 | 489.7 | 640.6 | 1127.2 | −4.39 | 0.63 | 118.5 | 43.5 |
| 35 | Loperamide | 43.8 | 1 | 4 | 3.53 | 4 | 477.0 | −119,284 | −7065 | −1,205,052 | 3.73 | −8.93 | −0.09 | 588.1 | 713.8 | 1308.0 | −5.22 | 5.01 | 139.4 | 54.5 |
| 36 | Phenylbutazone | 40.6 | 0 | 4 | 0.10 | 4 | 308.4 | −80,026 | −4646 | −632,151 | 0.90 | −9.32 | −0.26 | 473.7 | 543.9 | 920.5 | −3.25 | 1.84 | 98.4 | 35.0 |
| 37 | Clonidine | 35.4 | 2 | 3 | 0.65 | 3 | 230.1 | −53,612 | −2372 | −304,330 | 1.17 | −8.96 | −0.19 | 321.3 | 401.1 | 624.9 | −5.73 | 0.28 | 62.2 | 22.7 |
| 38 | PABA | 63.3 | 3 | 3 | −1.61 | 3 | 137.1 | −38,905 | −1859 | −176,902 | 4.29 | −8.50 | −0.21 | 247.8 | 298.6 | 442.5 | −11.00 | 0.96 | 37.5 | 14.3 |
| 39 | Propylparaben | 46.5 | 1 | 3 | 2.87 | 3 | 180.2 | −51,913 | −2627 | −272,388 | 1.43 | −9.52 | −0.40 | 378.1 | 386.8 | 599.2 | −7.99 | 2.30 | 48.6 | 19.1 |
| 40 | Methylparaben | 46.5 | 1 | 3 | 1.81 | 3 | 152.2 | −45,017 | −2067 | −210,788 | 1.54 | −9.53 | −0.42 | 308.2 | 325.8 | 488.0 | −9.09 | 1.49 | 39.3 | 15.5 |
| 41 | Quetiapine | 73.6 | 1 | 5 | 1.55 | 5 | 383.5 | −95,297 | −5413 | −823,576 | 2.20 | −8.64 | −0.70 | 535.3 | 637.5 | 1098.9 | −11.29 | 2.84 | 111.6 | 43.0 |
| 42 | Chlorprotixen | 28.5 | 0 | 1 | 4.40 | 1 | 315.9 | −70,896 | −4164 | −520,729 | 1.94 | −8.35 | −0.56 | 510.5 | 545.8 | 912.1 | −1.47 | 4.33 | 95.5 | 36.4 |
| 43 | Perazine | 35.0 | 0 | 3 | 3.13 | 3 | 339.5 | −79,041 | −5068 | −693,691 | 2.18 | −7.81 | −0.17 | 453.1 | 550.9 | 986.5 | −1.37 | −0.76 | 114.4 | 40.3 |
| 44 | Trifluoperazine | 35.0 | 0 | 3 | 4.21 | 3 | 407.5 | −111,907 | −5402 | −911,148 | 3.51 | −8.19 | −0.79 | 534.0 | 599.0 | 1067.0 | −0.91 | −0.19 | 119.7 | 41.8 |
| 45 | Thioridazine | 57.1 | 0 | 2 | 3.94 | 2 | 370.6 | −82,689 | −5253 | −744,945 | 0.86 | −7.78 | −0.41 | 484.9 | 581.1 | 1039.3 | −1.39 | −0.42 | 123.0 | 43.8 |
| 46 | Fluconazole | 71.8 | 1 | 7 | 0.50 | 7 | 306.3 | −89,231 | −3607 | −625,777 | 0.86 | −10.43 | −1.03 | 345.7 | 469.7 | 783.0 | −10.28 | −1.41 | 79.5 | 28.6 |
| 47 | Tolperisone | 20.3 | 0 | 2 | 2.27 | 2 | 245.4 | −62,429 | −4147 | −464,977 | 2.97 | −9.05 | −0.15 | 436.5 | 486.1 | 815.0 | 1.41 | 3.01 | 79.6 | 29.5 |
| 48 | Fenspiride | 45.1 | 1 | 4 | 0.04 | 4 | 260.3 | −69,140 | −4020 | −499,628 | 5.09 | −9.28 | 0.16 | 401.1 | 475.0 | 791.6 | −4.01 | 1.40 | 73.7 | 28.8 |
| 49 | Pizotifen | 31.5 | 0 | 1 | 4.49 | 1 | 295.4 | −67,399 | −4466 | −549,282 | 1.15 | −8.89 | −0.32 | 379.1 | 505.1 | 869.1 | −0.98 | 1.58 | 95.7 | 35.7 |
| 50 | Cyproheptadine | 3.2 | 0 | 1 | 4.86 | 1 | 287.4 | −68,558 | −4726 | −566,080 | 1.04 | −8.73 | −0.36 | 378.9 | 516.5 | 887.5 | −1.13 | 1.77 | 102.8 | 36.0 |
| 51 | Closapine | 30.9 | 1 | 4 | 0.76 | 4 | 326.8 | −78,188 | −4481 | −629,966 | 3.11 | −8.45 | −0.61 | 433.0 | 545.3 | 926.1 | −2.78 | −0.73 | 103.5 | 36.5 |
| 52 | Tiapride | 84.1 | 1 | 6 | −1.48 | 6 | 328.4 | −88,376 | −4474 | −658,862 | 5.32 | −9.27 | −0.73 | 605.9 | 582.1 | 979.5 | −5.66 | −1.56 | 91.2 | 31.4 |
| 53 | Olanzapine | 59.1 | 1 | 4 | 2.68 | 4 | 312.4 | −72,794 | −4389 | −594,188 | 3.31 | −8.21 | −0.72 | 437.2 | 534.2 | 901.5 | −4.10 | 1.66 | 95.3 | 35.9 |
| 54 | Betahistine | 24.9 | 1 | 2 | −2.18 | 2 | 136.2 | −33,605 | −2197 | −176,624 | 2.59 | −9.19 | −0.05 | 328.2 | 351.2 | 521.3 | −4.27 | −0.52 | 46.0 | 16.6 |
| 55 | Dexketoprofen | 54.4 | 1 | 3 | −0.25 | 3 | 254.3 | −69,002 | −3723 | −449,051 | 1.60 | −9.97 | −0.57 | 402.6 | 470.1 | 768.0 | −6.46 | 2.56 | 79.9 | 28.2 |
| 56 | Caffeine | 53.5 | 0 | 6 | −0.13 | 6 | 194.2 | −53,927 | −2508 | −319,054 | 3.78 | −8.90 | −0.49 | 341.4 | 365.3 | 572.9 | −2.21 | −1.06 | 50.0 | 18.9 |
| 57 | Hymecromone | 46.5 | 1 | 3 | 2.36 | 4 | 176.2 | −50,477 | −2397 | −262,408 | 5.98 | −9.21 | −0.91 | 289.5 | 341.9 | 520.9 | −9.80 | −0.56 | 51.5 | 18.2 |
| 58 | Ketotifen | 48.6 | 0 | 2 | 3.28 | 2 | 309.4 | −73,450 | −4448 | −586,056 | 4.06 | −9.09 | −0.97 | 389.1 | 508.1 | 876.7 | −2.17 | 0.26 | 99.6 | 35.8 |
| 59 | Clemastine | 12.5 | 0 | 2 | 3.04 | 2 | 343.9 | −84,433 | −5152 | −711,749 | 1.96 | −8.95 | −0.15 | 501.2 | 584.3 | 1012.5 | −0.80 | 4.66 | 101.4 | 39.6 |
| 60 | Salicylic acid | 57.5 | 2 | 3 | −1.06 | 3 | 138.1 | −41,583 | −1801 | −184,688 | 0.99 | −9.45 | −0.60 | 236.5 | 284.1 | 420.5 | −11.88 | −0.04 | 38.6 | 13.7 |
| 61 | Indomethacin | 69.6 | 1 | 5 | −0.16 | 5 | 357.8 | −95,725 | −4971 | −704,963 | 2.36 | −8.56 | −0.61 | 509.6 | 562.9 | 961.3 | −9.47 | −1.43 | 103.3 | 36.7 |
| 62 | Piroxicam | 108.0 | 2 | 7 | 1.71 | 7 | 331.3 | −88,167 | −3947 | −657,874 | 5.06 | −8.99 | −1.21 | 320.8 | 308.3 | 268.4 | −11.67 | −2.25 | 91.6 | 30.3 |
| 63 | Naproxen | 46.5 | 1 | 3 | 0.47 | 3 | 230.3 | −63,546 | −3396 | −390,177 | 2.42 | −8.67 | −0.53 | 395.2 | 445.4 | 703.3 | −9.53 | 0.56 | 70.6 | 25.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sobańska, A.W.; Robertson, J.; Brzezińska, E. Application of RP-18 TLC Retention Data to the Prediction of the Transdermal Absorption of Drugs. Pharmaceuticals 2021, 14, 147. https://doi.org/10.3390/ph14020147
Sobańska AW, Robertson J, Brzezińska E. Application of RP-18 TLC Retention Data to the Prediction of the Transdermal Absorption of Drugs. Pharmaceuticals. 2021; 14(2):147. https://doi.org/10.3390/ph14020147
Chicago/Turabian StyleSobańska, Anna W., Jeremy Robertson, and Elżbieta Brzezińska. 2021. "Application of RP-18 TLC Retention Data to the Prediction of the Transdermal Absorption of Drugs" Pharmaceuticals 14, no. 2: 147. https://doi.org/10.3390/ph14020147
APA StyleSobańska, A. W., Robertson, J., & Brzezińska, E. (2021). Application of RP-18 TLC Retention Data to the Prediction of the Transdermal Absorption of Drugs. Pharmaceuticals, 14(2), 147. https://doi.org/10.3390/ph14020147






