Preclinical Drug Response Metric Based on Cellular Response Phenotype Provides Better Pharmacogenomic Variables with Phenotype Relevance
Abstract
:1. Introduction
2. Results
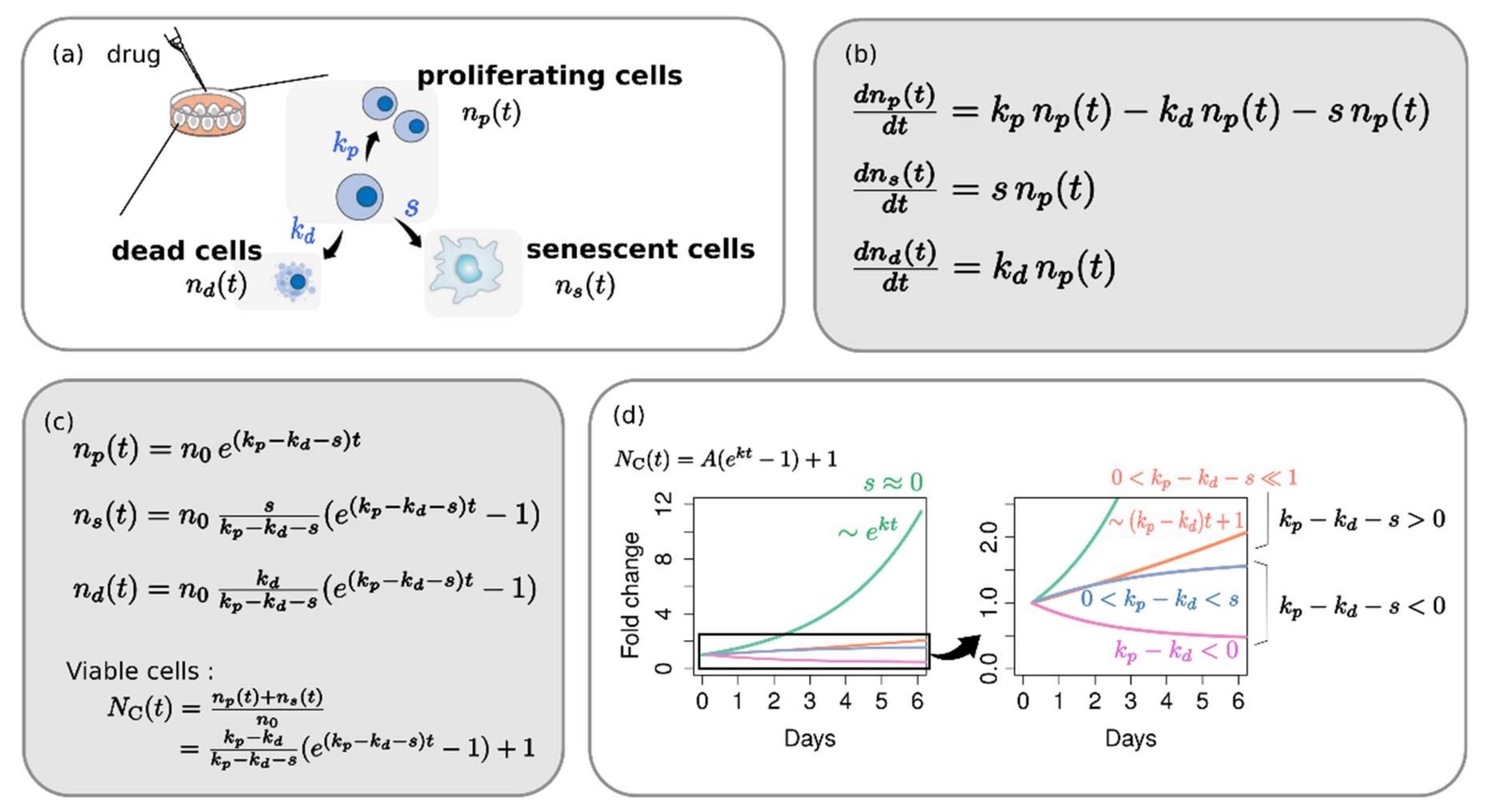
2.1. Phenotype Dynamics Model: Each Cellular Response Phenotype Contributes Differently to the Overall Growth Behavior
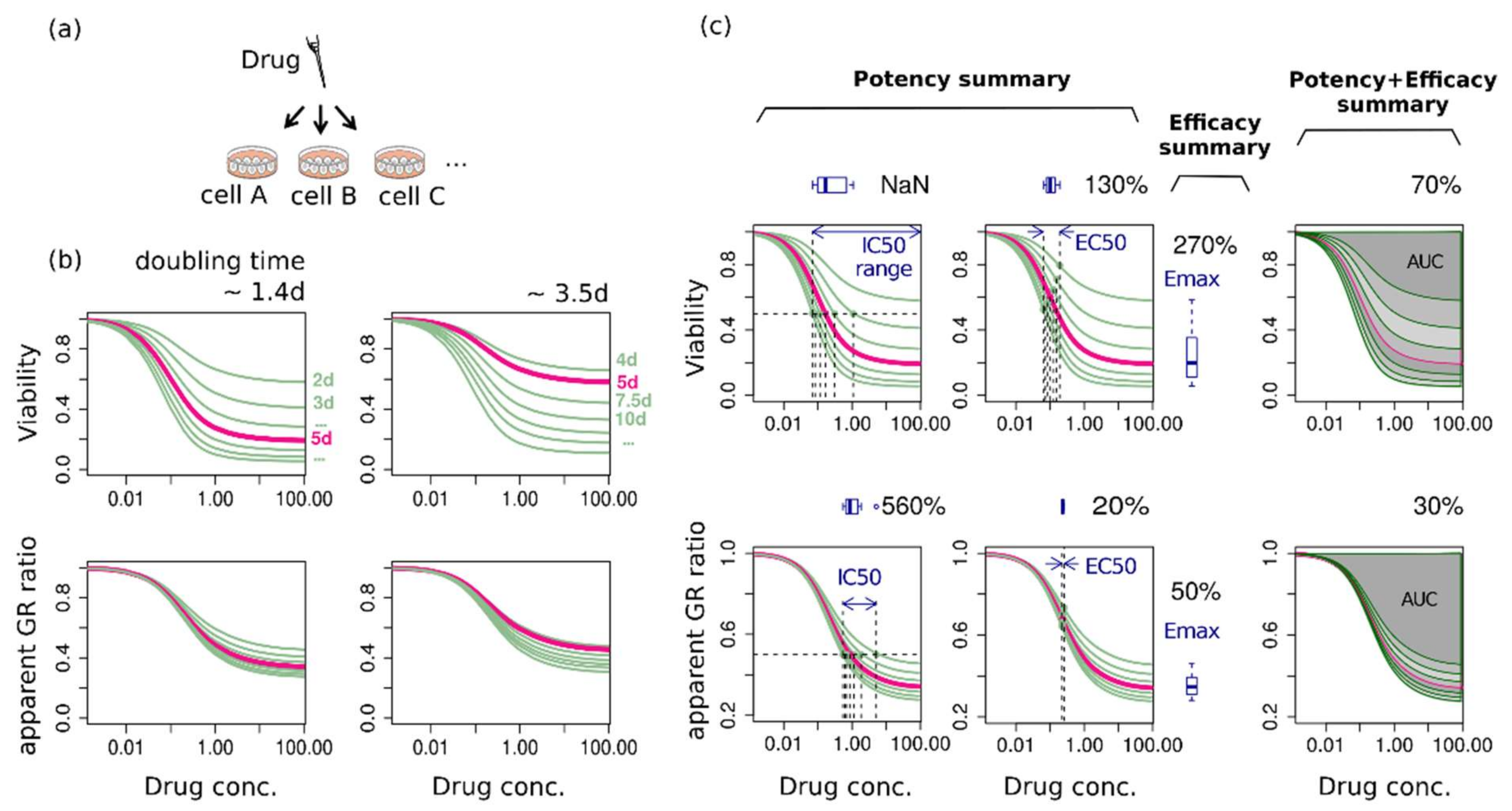
2.2. The Same Growth Curve Produces Different Dose-Response Curves Depending on the Assay Duration and the Metric
2.3. Assay-Duration-Dependency of Drug Response Causes Significant Uncertainties in Summary Factors
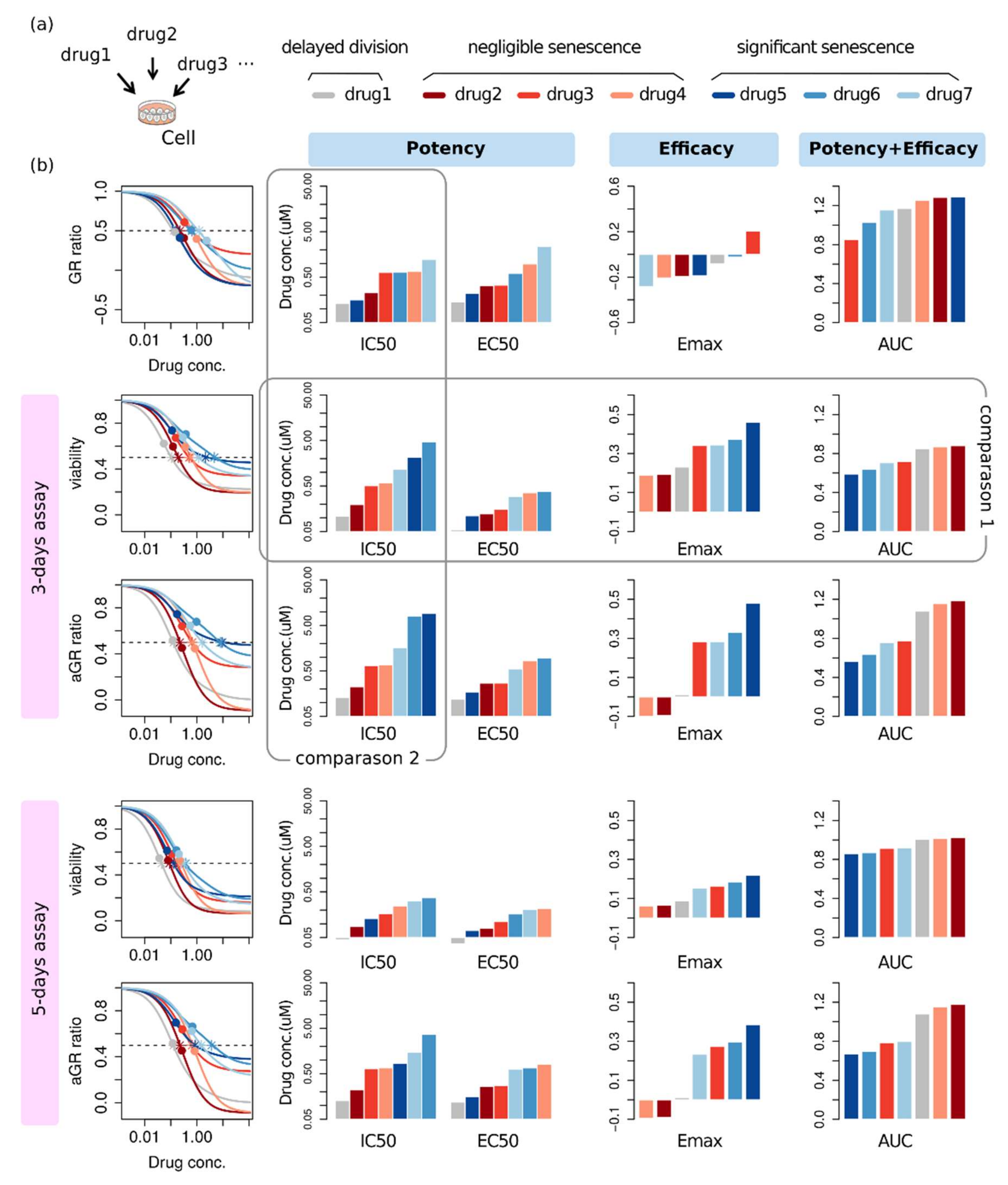
2.4. Effectiveness Ranking Based on a Dose-Response Curve Depends on the Assessment Method
2.5. Alternative Phenotype Metric Provides Time-Independent Characteristic Quantities of Drug Response
3. Discussion
4. Methods
4.1. Exploring the Conventional Evaluation Method of Drug Response
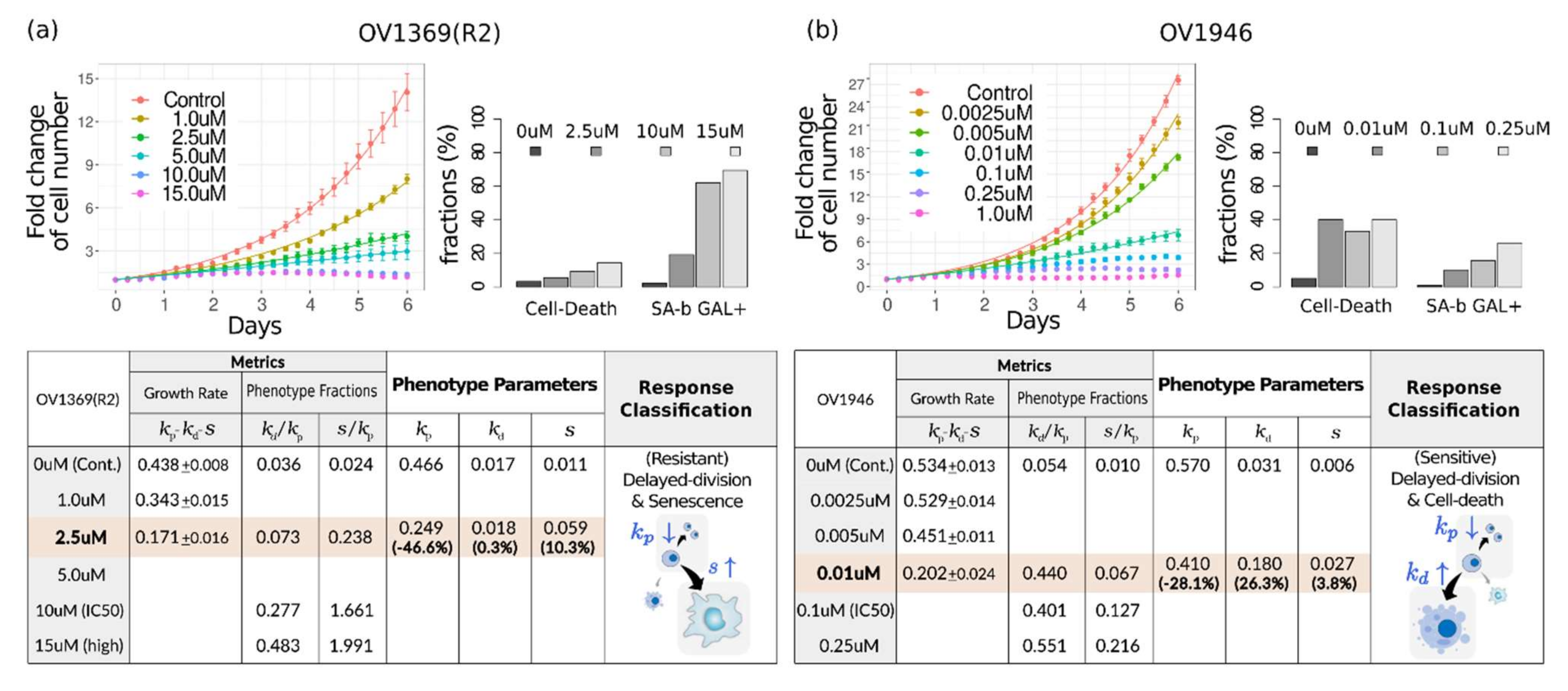
4.2. Drug Response Assessment of Public Data
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, L.; McLeod, H.L.; Weinshilboum, R.M. Genomics and Drug Response. N. Engl. J. Med. 2011, 364, 1144–1153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barretina, J.; Caponigro, G.; Stransky, N.; Venkatesan, K.; Margolin, A.A.; Kim, S.; Wilson, C.J.; Lehár, J.; Kryukov, G.V.; Sonkin, D.; et al. The Cancer Cell Line Encyclopedia Enables Predictive Modelling of Anticancer Drug Sensitivity. Nature 2012, 483, 603–607. [Google Scholar] [CrossRef] [PubMed]
- Garnett, M.J.; Edelman, E.J.; Heidorn, S.J.; Greenman, C.D.; Dastur, A.; Lau, K.W.; Greninger, P.; Thompson, I.R.; Luo, X.; Soares, J.; et al. Systematic Identification of Genomic Markers of Drug Sensitivity in Cancer Cells. Nature 2012, 483, 570–575. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Costello, J.C.; Heiser, L.M.; Georgii, E.; Gönen, M.; Menden, M.P.; Wang, N.J.; Bansal, M.; Ammad-Ud-Din, M.; Hintsanen, P.; Khan, S.A.; et al. A Community Effort to Assess and Improve Drug Sensitivity Prediction Algorithms. Nat. Biotechnol. 2014, 32, 1202–1212. [Google Scholar] [CrossRef]
- Iorio, F.; Knijnenburg, T.A.; Vis, D.J.; Bignell, G.R.; Menden, M.P.; Schubert, M.; Aben, N.; Gonçalves, E.; Barthorpe, S.; Lightfoot, H.; et al. A Landscape of Pharmacogenomic Interactions in Cancer. Cell 2016, 166, 740–754. [Google Scholar] [CrossRef] [Green Version]
- Rees, M.G.; Seashore-Ludlow, B.; Cheah, J.H.; Adams, D.J.; Price, E.V.; Gill, S.; Javaid, S.; Coletti, M.E.; Jones, V.L.; Bodycombe, N.E.; et al. Correlating Chemical Sensitivity and Basal Gene Expression Reveals Mechanism of Action. Nat. Chem. Biol. 2016, 12, 109–116. [Google Scholar] [CrossRef] [PubMed]
- Haibe-Kains, B.; El-Hachem, N.; Birkbak, N.J.; Jin, A.C.; Beck, A.H.; Aerts, H.J.W.L.; Quackenbush, J. Inconsistency in Large Pharmacogenomic Studies. Nature 2013, 504, 389–393. [Google Scholar] [CrossRef] [Green Version]
- Collins, F.S.; Tabak, L.A. Policy: NIH Plans to Enhance Reproducibility. Nat. News 2014, 505, 612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freedman, L.P.; Cockburn, I.M.; Simcoe, T.S. The Economics of Reproducibility in Preclinical Research. PLoS Biol. 2015, 13, e1002165. [Google Scholar] [CrossRef] [PubMed]
- Niepel, M.; Hafner, M.; Mills, C.E.; Subramanian, K.; Williams, E.H.; Chung, M.; Gaudio, B.; Barrette, A.M.; Stern, A.D.; Hu, B.; et al. A Multi-Center Study on the Reproducibility of Drug-Response Assays in Mammalian Cell Lines. Cell Syst. 2019, 9, 35–48.e5. [Google Scholar] [CrossRef] [Green Version]
- Hafner, M.; Niepel, M.; Chung, M.; Sorger, P.K. Growth Rate Inhibition Metrics Correct for Confounders in Measuring Sensitivity to Cancer Drugs. Nat. Methods 2016, 13, 521–527. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harris, L.A.; Frick, P.L.; Garbett, S.P.; Hardeman, K.N.; Paudel, B.B.; Lopez, C.F.; Quaranta, V.; Tyson, D.R. An Unbiased Metric of Antiproliferative Drug Effect In Vitro. Nat. Methods 2016, 13, 497–500. [Google Scholar] [CrossRef] [PubMed]
- Hafner, M.; Niepel, M.; Sorger, P.K. Alternative Drug Sensitivity Metrics Improve Preclinical Cancer Pharmacogenomics. Nat. Biotechnol. 2017, 35, 500–502. [Google Scholar] [CrossRef]
- Ewald, J.A.; Desotelle, J.A.; Wilding, G.; Jarrard, D.F. Therapy-Induced Senescence in Cancer. JNCI J. Natl. Cancer Inst. 2010, 102, 1536–1546. [Google Scholar] [CrossRef] [Green Version]
- Mikuła-Pietrasik, J.; Niklas, A.; Uruski, P.; Tykarski, A.; Książek, K. Mechanisms and Significance of Therapy-Induced and Spontaneous Senescence of Cancer Cells. Cell. Mol. Life Sci. 2020, 77, 213–229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, B.; Kohli, J.; Demaria, M. Senescent Cells in Cancer Therapy: Friends or Foes? Trends Cancer 2020, 6, 838–857. [Google Scholar] [CrossRef] [PubMed]
- Fleury, H.; Malaquin, N.; Tu, V.; Gilbert, S.; Martinez, A.; Olivier, M.-A.; Sauriol, A.; Communal, L.; Leclerc-Desaulniers, K.; Carmona, E.; et al. Exploiting Interconnected Synthetic Lethal Interactions between PARP Inhibition and Cancer Cell Reversible Senescence. Nat. Commun. 2019, 10, 2556. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gelles, J.D.; Mohammed, J.N.; Santos, L.C.; Legarda, D.; Ting, A.T.; Chipuk, J.E. Single-Cell and Population-Level Analyses Using Real-Time Kinetic Labeling Couples Proliferation and Cell Death Mechanisms. Dev. Cell 2019, 51, 277–291.e4. [Google Scholar] [CrossRef]
- Wang, D.; Hensman, J.; Kutkaite, G.; Toh, T.S.; Galhoz, A.; GDSC Screening Team; Dry, J.R.; Saez-Rodriguez, J.; Garnett, M.J.; Menden, M.P.; et al. A Statistical Framework for Assessing Pharmacological Responses and Biomarkers Using Uncertainty Estimates. eLife 2020, 9, e60352. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Soares, J.; Greninger, P.; Edelman, E.J.; Lightfoot, H.; Forbes, S.; Bindal, N.; Beare, D.; Smith, J.A.; Thompson, I.R.; et al. Genomics of Drug Sensitivity in Cancer (GDSC): A Resource for Therapeutic Biomarker Discovery in Cancer Cells. Nucleic Acids Res. 2013, 41, D955–D961. [Google Scholar] [CrossRef] [Green Version]
- Seashore-Ludlow, B.; Rees, M.G.; Cheah, J.H.; Cokol, M.; Price, E.V.; Coletti, M.E.; Jones, V.; Bodycombe, N.E.; Soule, C.K.; Gould, J.; et al. Harnessing Connectivity in a Large-Scale Small-Molecule Sensitivity Dataset. Cancer Discov. 2015, 5, 1210–1223. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fallahi-Sichani, M.; Honarnejad, S.; Heiser, L.M.; Gray, J.W.; Sorger, P.K. Metrics Other than Potency Reveal Systematic Variation in Responses to Cancer Drugs. Nat. Chem. Biol. 2013, 9, 708–714. [Google Scholar] [CrossRef] [PubMed] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Hwang, S. Preclinical Drug Response Metric Based on Cellular Response Phenotype Provides Better Pharmacogenomic Variables with Phenotype Relevance. Pharmaceuticals 2021, 14, 1324. https://doi.org/10.3390/ph14121324
Kim S, Hwang S. Preclinical Drug Response Metric Based on Cellular Response Phenotype Provides Better Pharmacogenomic Variables with Phenotype Relevance. Pharmaceuticals. 2021; 14(12):1324. https://doi.org/10.3390/ph14121324
Chicago/Turabian StyleKim, Sanghyun, and Sohyun Hwang. 2021. "Preclinical Drug Response Metric Based on Cellular Response Phenotype Provides Better Pharmacogenomic Variables with Phenotype Relevance" Pharmaceuticals 14, no. 12: 1324. https://doi.org/10.3390/ph14121324
APA StyleKim, S., & Hwang, S. (2021). Preclinical Drug Response Metric Based on Cellular Response Phenotype Provides Better Pharmacogenomic Variables with Phenotype Relevance. Pharmaceuticals, 14(12), 1324. https://doi.org/10.3390/ph14121324






