Binding Constants of Substituted Benzoic Acids with Bovine Serum Albumin
Abstract
1. Introduction
2. Methodology
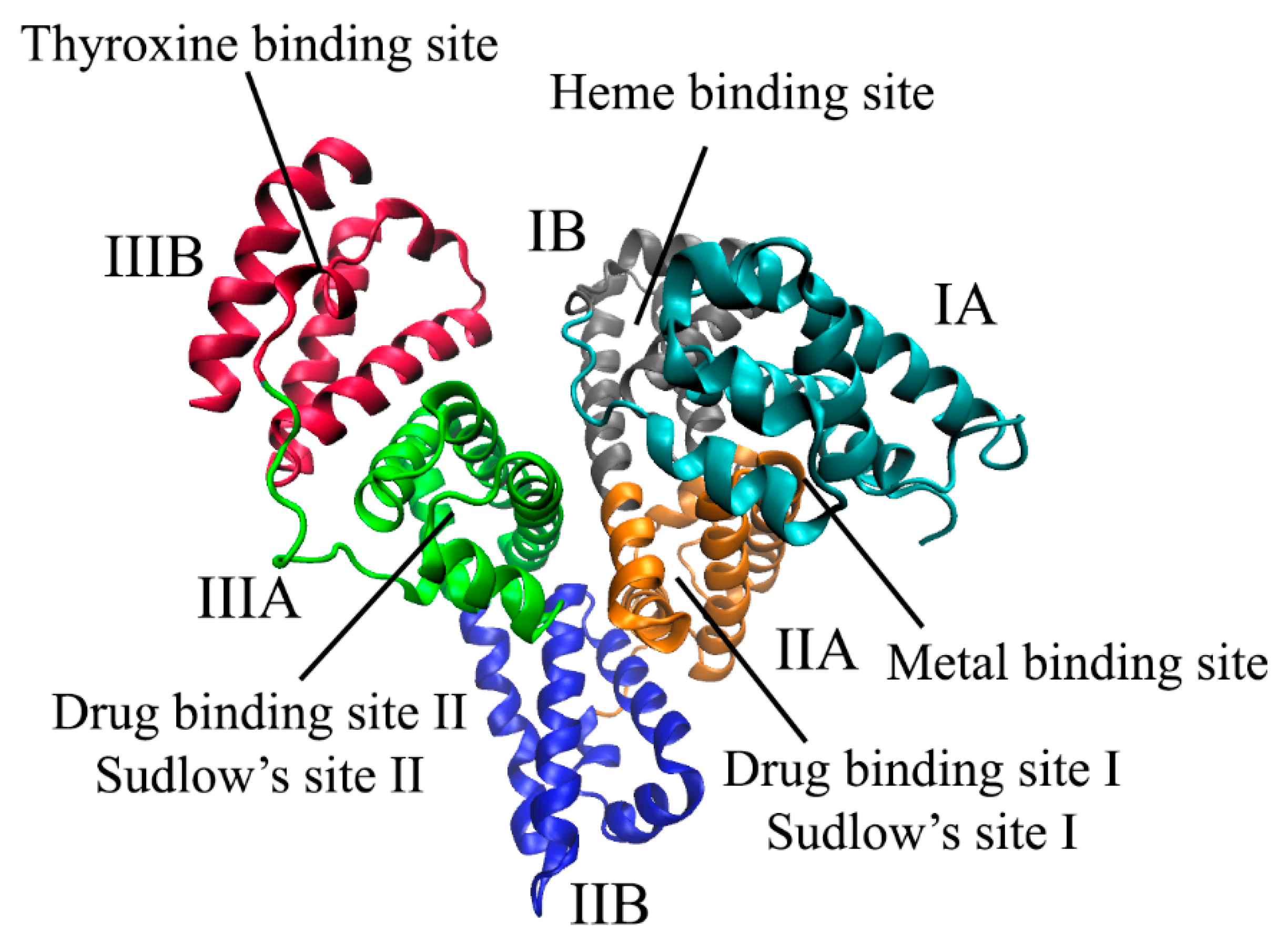
2.1. Binding Centers of Albumin
2.2. Spectrofluorimetric Method and Its Pitfalls
3. Experimental
3.1. Chemicals and Instruments
3.2. Spectrofluorimetric Titration Procedure
3.3. Evaluation of the Binding Constants
4. Discussion
4.1. Literature Albumin Binding Data for the Studied Compounds
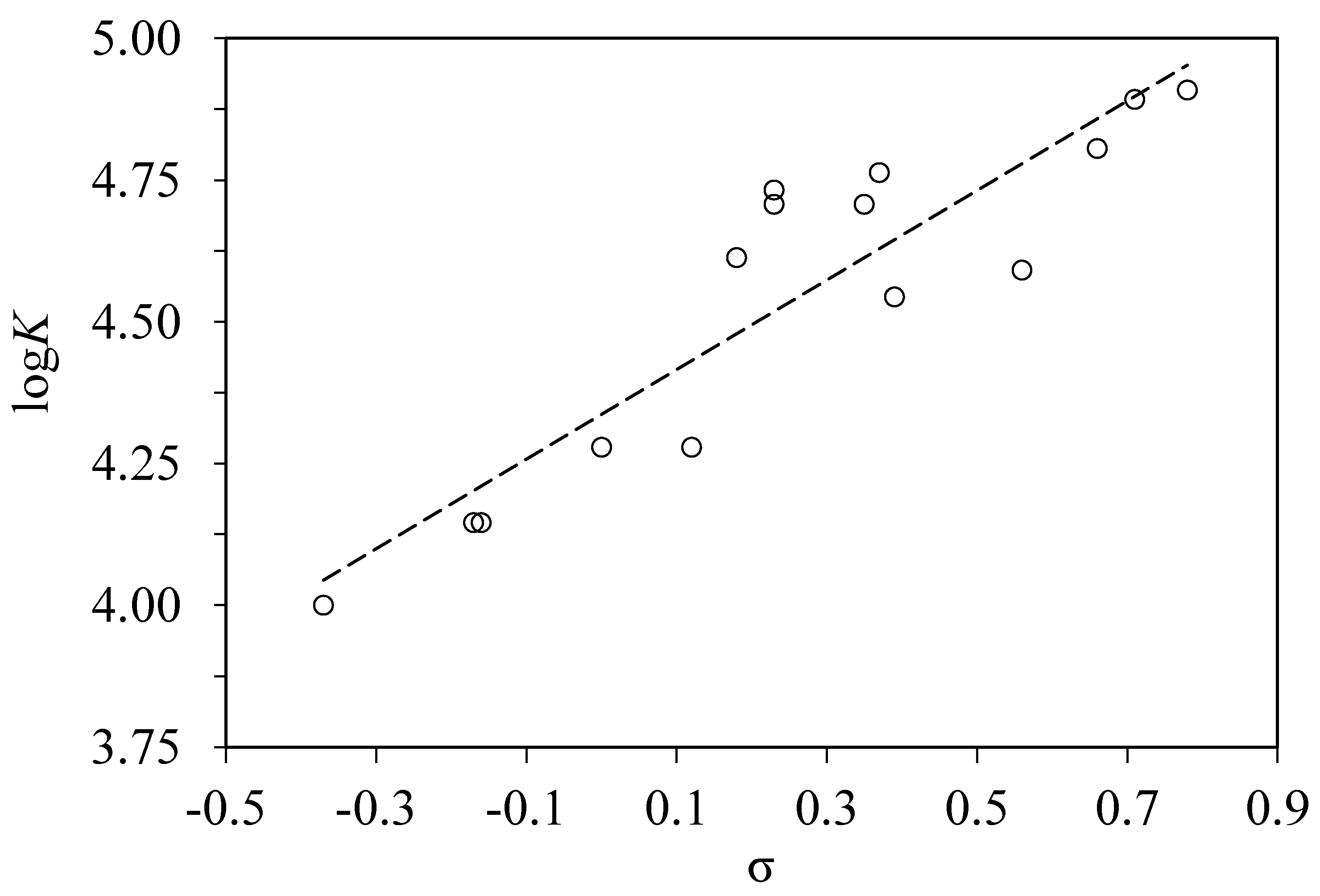
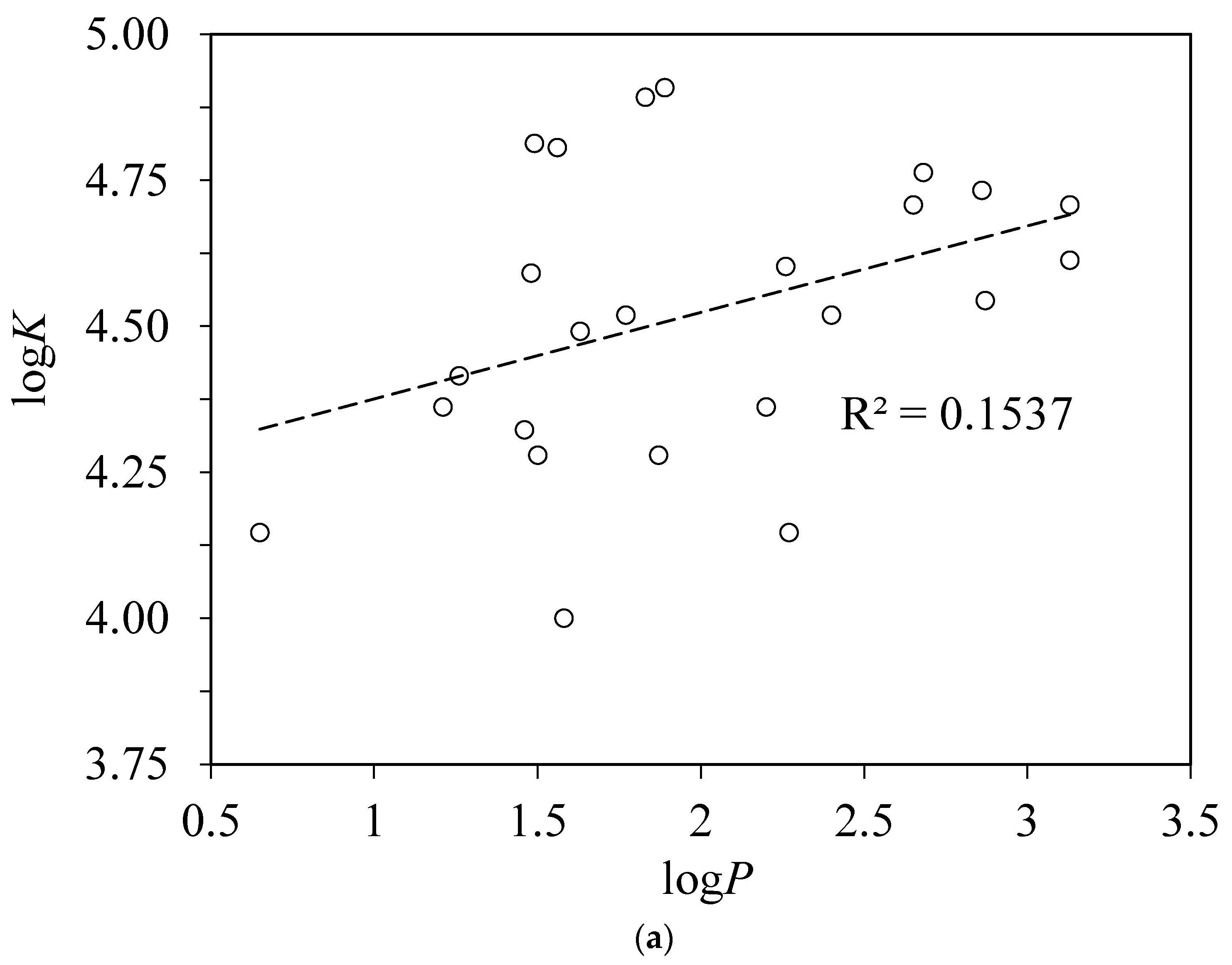
4.2. Correlation of the Binding Constants with Hammett Substituent Constants
RMS = 0.13, n = 15, r2 = 0.8257.
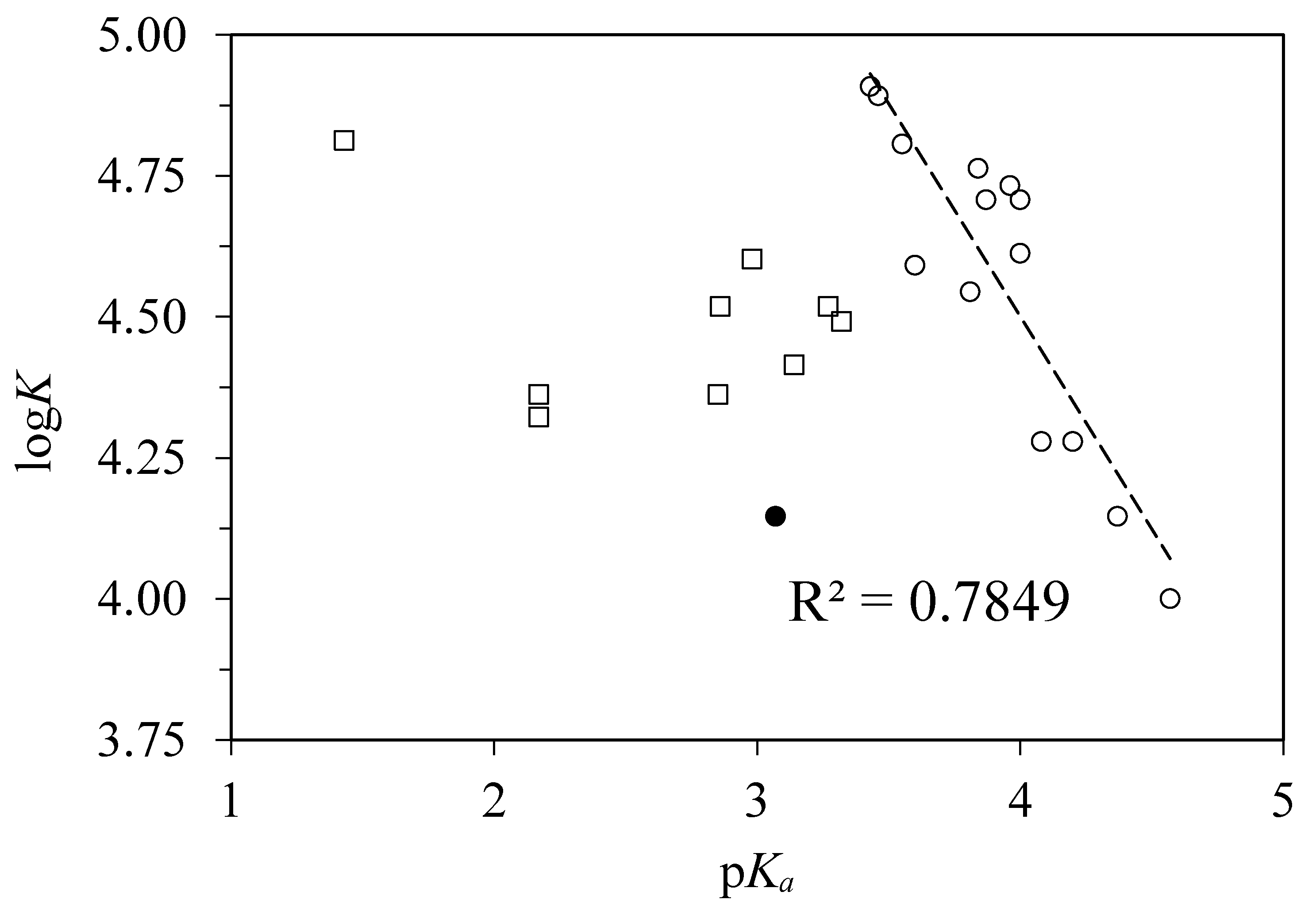
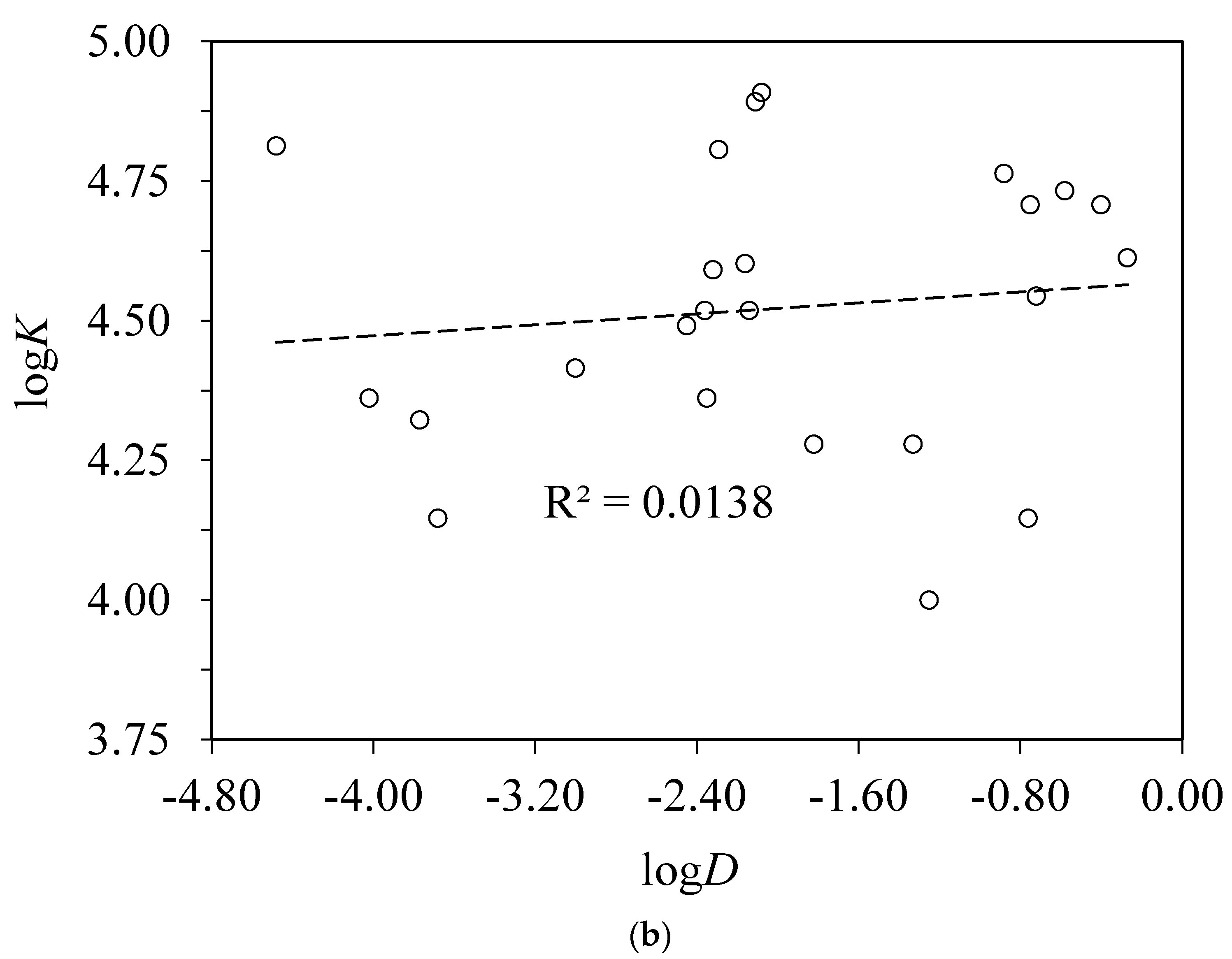
4.3. Correlations with Other Experimentally Derived Ligand Properties
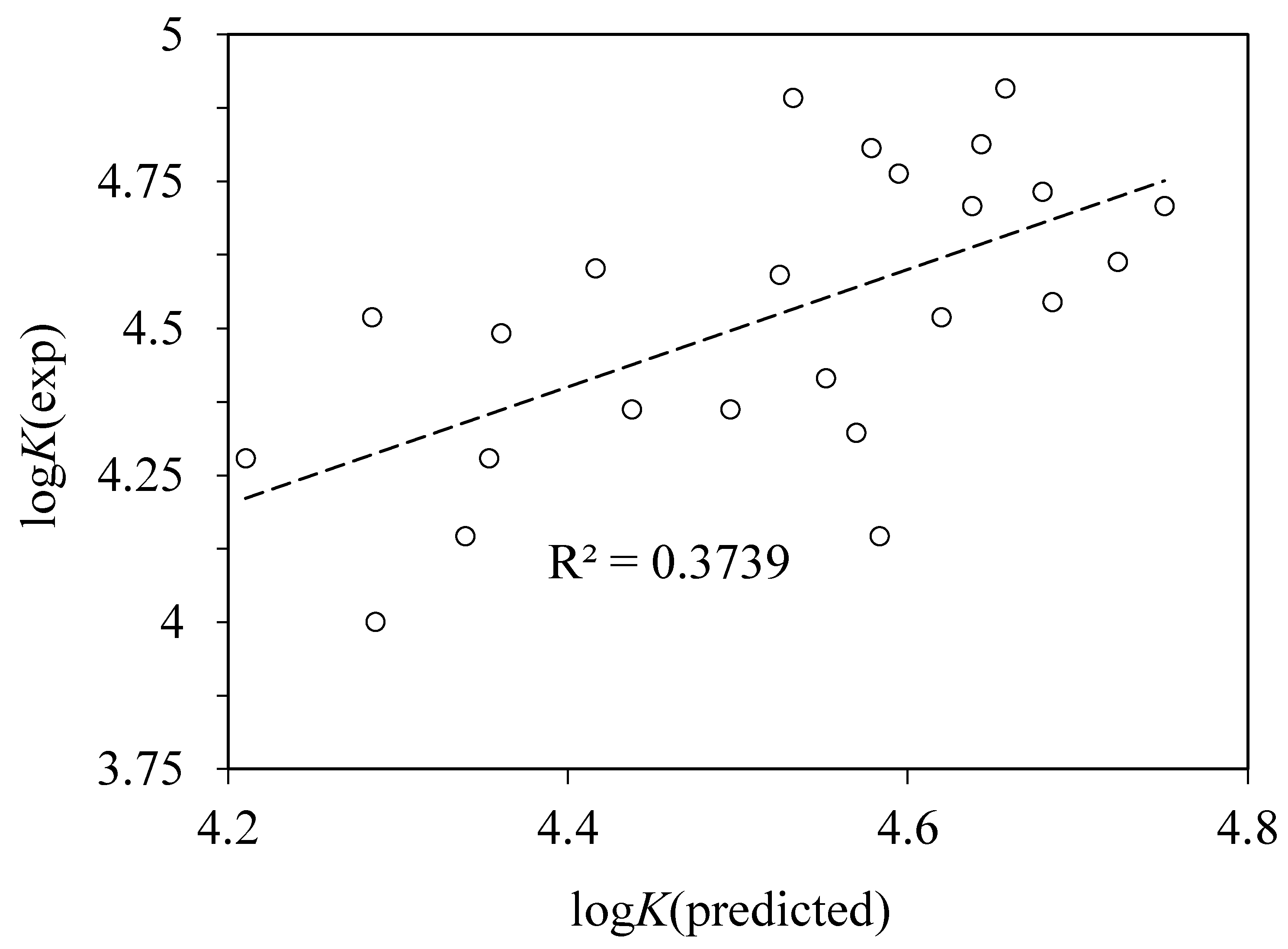
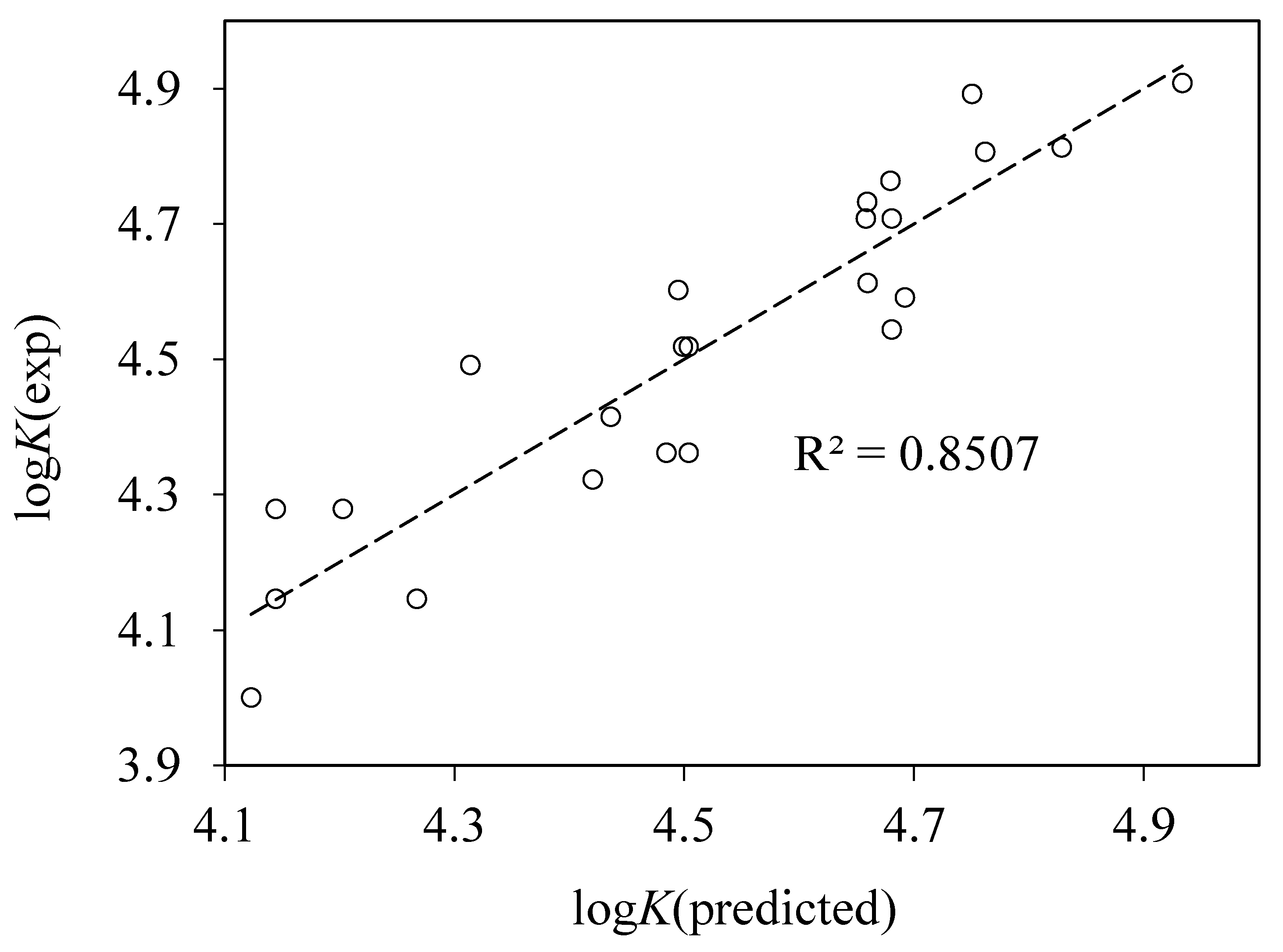
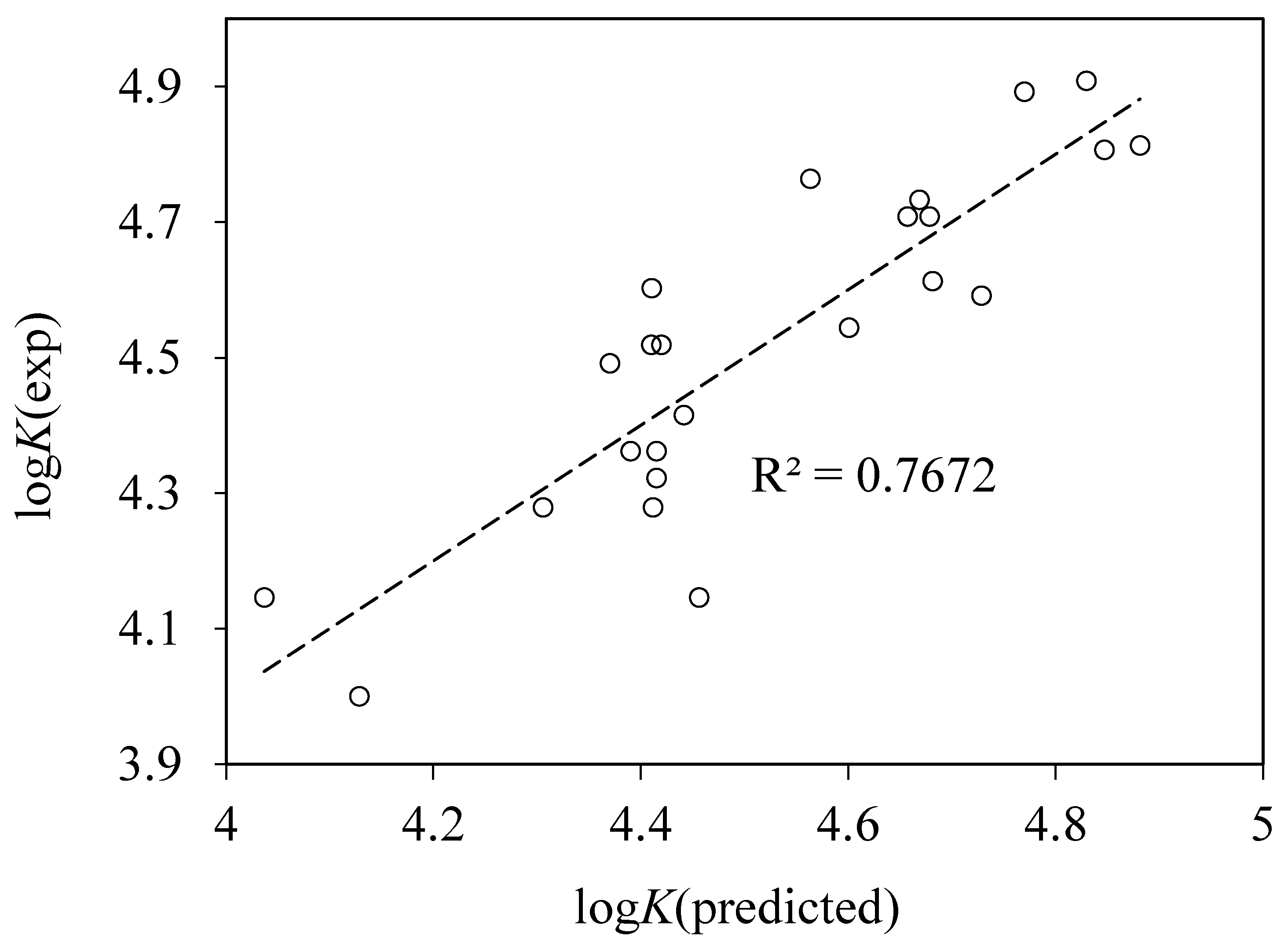
4.4. QSAR Modeling of Albumin Binding
RMS = 0.124, n = 24, r2 = 0.739
RMS = 0.094, n = 24, r2 = 0.851
RMS = 0.071, n = 24, r2 = 0.914
RMS = 0.117, n = 24, r2 = 0.767
RMS = 0.1, n = 24, r2 = 0.829
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Lexa, K.W.; Dolghih, E.; Jacobson, M.P. A Structure-Based Model for Predicting Serum Albumin Binding. PLoS ONE 2014, 9, e93323. [Google Scholar] [CrossRef] [PubMed]
- Valko, K.; Nunhuck, S.; Bevan, C.; Abraham, M.H.; Reynolds, D.P. Fast Gradient HPLC Method to Determine Compounds Binding to Human Serum Albumin. Relationships with Octanol/Water and Immobilized Artificial Membrane Lipophilicity. J. Pharm. Sci. 2003, 92, 2236–2248. [Google Scholar] [CrossRef] [PubMed]
- Kragh-Hansen, U. Molecular aspects of ligand binding to serum albumin. Pharmacol. Rev. 1981, 33, 17–53. [Google Scholar]
- Nakano, N.I.; Shimamori, Y.; Yamaguchi, S. Binding capacities of human serum albumin monomer and dimer by continuous frontal affinity chromatography. J. Chromatogr. A 1982, 237, 225–232. [Google Scholar] [CrossRef]
- Levi, V.; González Flecha, F.L. Reversible fast-dimerization of bovine serum albumin detected by fluorescence resonance energy transfer. Biochim. Biophys. Acta BBA Proteins Proteom. 2002, 1599, 141–148. [Google Scholar] [CrossRef]
- Lowry, T.H.; Richardson, K.S. Mechanism and Theory in Organic Chemistry, 3rd ed.; Harper & Row: New York, NY, USA, 1987; ISBN 978-0-06-044084-8. [Google Scholar]
- Kubinyi, H. QSAR: Hansch Analysis and Related Approaches. In Methods and Principles in Medicinal Chemistry; VCH: Weinheim, Germany; New York, NY, USA, 1993; ISBN 978-3-527-30035-8. [Google Scholar]
- Matsushita, Y.; Kijima (née Shimizu), Y.; Moriguchi, I. Comparison of binding characteristics of human and bovine serum albumins with benzoates over a wide range of concentration. Chem. Pharm. Bull. 1987, 35, 2589–2593. [Google Scholar] [CrossRef]
- Moriguchi, I. Protein Bindings. II. Binding of Aromatic Carboxylic Acids to Bovine Serum Albumin. Chem. Pharm. Bull. 1968, 16, 597–600. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, S.; Qin, Y.; Liu, J.; Liu, J.; Wang, Q.; Ren, F.; Zhang, H. Interaction of phenolic acids and their derivatives with human serum albumin: Structure–affinity relationships and effects on antioxidant activity. Food Chem. 2018, 240, 1072–1080. [Google Scholar] [CrossRef]
- Yuan, S.; Zhang, Y.; Liu, J.; Zhao, Y.; Tan, L.; Liu, J.; Wang, Q.; Zhang, H. Structure-affinity relationship of the binding of phenolic acids and their derivatives to bovine serum albumin. Food Chem. 2019, 278, 77–83. [Google Scholar] [CrossRef]
- Rosenoer, V.M.; Oratz, M.; Rothschild, M.A. (Eds.) Albumin Structure, Function and Uses, 1st ed.; Pergamon Press: Oxford, UK; New York, NY, USA, 1977; ISBN 978-0-08-019603-9. [Google Scholar]
- Kaneko, K.; Fukuda, H.; Chuang, V.T.G.; Yamasaki, K.; Kawahara, K.; Nakayama, H.; Suenaga, A.; Maruyama, T.; Otagiri, M. Subdomain IIIA of Dog Albumin Contains a Binding Site Similar to Site II of Human Albumin. Drug Metab. Dispos. 2008, 36, 81–86. [Google Scholar] [CrossRef]
- Majorek, K.A.; Porebski, P.J.; Dayal, A.; Zimmerman, M.D.; Jablonska, K.; Stewart, A.J.; Chruszcz, M.; Minor, W. Structural and immunologic characterization of bovine, horse, and rabbit serum albumins. Mol. Immunol. 2012, 52, 174–182. [Google Scholar] [CrossRef]
- Zhang, Y.-X.; Chen, C.-W.; Wang, M.; Wei, S.-S.; Guan, H.; Chi, T.-T.; Qi, X.-Z.; Hu, W.-T. Purification and Characterization of Albumin from Frog Skin of Duttaphrynus melanostictus. Protein J. 2011, 30, 464–470. [Google Scholar] [CrossRef] [PubMed]
- Sudlow, G.; Birkett, D.J.; Wade, D.N. The characterization of two specific drug binding sites on human serum albumin. Mol. Pharmacol. 1975, 11, 824–832. [Google Scholar] [PubMed]
- Wenskowsky, L.; Schreuder, H.; Derdau, V.; Matter, H.; Volkmar, J.; Nazaré, M.; Opatz, T.; Petry, S. Identification and Characterization of a Single High-Affinity Fatty Acid Binding Site in Human Serum Albumin. Angew. Chem. Int. Ed. 2018, 57, 1044–1048. [Google Scholar] [CrossRef] [PubMed]
- Goncharov, N.V.; Terpilovskii, M.A.; Shmurak, V.I.; Belinskaya, D.A.; Avdonin, P.V. Comparative analysis of esterase and paraoxonase activities of different serum albumin species. J. Evol. Biochem. Physiol. 2017, 53, 271–281. [Google Scholar] [CrossRef]
- Moriyama, Y.; Ohta, D.; Hachiya, K.; Mitsui, Y.; Takeda, K. Fluorescence behavior of tryptophan residues of bovine and human serum albumins in ionic surfactant solutions: A comparative study of the two and one tryptophan(s) of bovine and human albumins. J. Protein Chem. 1996, 15, 265–272. [Google Scholar] [CrossRef]
- Stella, L.; Van de Weert, M.; Burrows, H.D.; Fausto, R. Fluorescence spectroscopy and binding: Getting it right. J. Mol. Struct. 2014, 1077, 1–3. [Google Scholar] [CrossRef]
- Van de Weert, M.; Stella, L. Fluorescence quenching and ligand binding: A critical discussion of a popular methodology. J. Mol. Struct. 2011, 998, 144–150. [Google Scholar] [CrossRef]
- Li, Z.-M.; Wei, C.-W.; Zhang, Y.; Wang, D.-S.; Liu, Y.-N. Investigation of competitive binding of ibuprofen and salicylic acid with serum albumin by affinity capillary electrophoresis. J. Chromatogr. B 2011, 879, 1934–1938. [Google Scholar] [CrossRef]
- Matias, I.; Ceballos, A.; Gonzalez-Velasco, F.; Cachaza, J.M. Thermodynamics of the binding of salicylate to human serum albumin: Evidence of non-competition with imidazole. J. Pharm. Pharmacol. 1989, 41, 123–125. [Google Scholar] [CrossRef]
- Henneberger, L.; Goss, K.-U.; Endo, S. Equilibrium Sorption of Structurally Diverse Organic Ions to Bovine Serum Albumin. Environ. Sci. Technol. 2016, 50, 5119–5126. [Google Scholar] [CrossRef]
- Hansch, C.; Leo, A.; Taft, R.W. A survey of Hammett substituent constants and resonance and field parameters. Chem. Rev. 1991, 91, 165–195. [Google Scholar] [CrossRef]
- Hammett, L.P. Physical Organic Chemistry; Reaction Rates, Equilibria, and Mechanisms; McGraw-Hill: New York, NY, USA, 1970; ISBN 978-0-07-025905-8. [Google Scholar]
- Lewis, M.; Bagwill, C.; Hardebeck, L.K.E.; Wireduaah, S. The use of hammett constants to understand the non-covalent binding of aromatics. Comput. Struct. Biotechnol. J. 2012, 1, e201204004. [Google Scholar] [CrossRef] [PubMed]
- Talhout, R.; Engberts, J.B.F.N. Thermodynamic analysis of binding of p-substituted benzamidines to trypsin: Thermodynamics of binding of benzamidines to trypsin. Eur. J. Biochem. 2001, 268, 1554–1560. [Google Scholar] [CrossRef] [PubMed]
- Dearden, J.C.; Tomlinson, E. Physico-chemical studies of analgesics. The protein-binding of some p-substituted acetanilides. J. Pharm. Pharmacol. 1970, 22, 53S–59S. [Google Scholar] [CrossRef] [PubMed]
- McDaniel, D.H.; Brown, H.C. An Extended Table of Hammett Substitutent Constants Based on the Ionization of Substituted Benzoic Acids. J. Org. Chem. 1958, 23, 420–427. [Google Scholar] [CrossRef]
- Albert, A.; Serjeant, E.P. The Determination of Ionization Constants: A Laboratory Manual; Springer: Dordrecht, The Netherlands, 1984; ISBN 978-94-010-8948-7. [Google Scholar]
- Kamble, S.; Loadman, P.; Abraham, M.H.; Liu, X. Structural properties governing drug-plasma protein binding determined by high-performance liquid chromatography method. J. Pharm. Biomed. Anal. 2018, 149, 16–21. [Google Scholar] [CrossRef]
- Barbato, F.; di Martino, G.; Grumetto, L.; La Rotonda, M.I. Retention of quinolones on human serum albumin and α1-acid glycoprotein HPLC columns: Relationships with different scales of lipophilicity. Eur. J. Pharm. Sci. 2007, 30, 211–219. [Google Scholar] [CrossRef]
- Hansch, C.; Leo, A.; Hoekman, D.H. (Eds.) Exploring QSAR; ACS Professional Reference Book; American Chemical Society: Washington, DC, USA, 1995; ISBN 978-0-8412-2987-7. [Google Scholar]
- ACD/Absolv. The Absolv Prediction Module Calculates Abraham Solvation Parameters and Is the Result of Collaboration between ACD/Labs and Prof. MH Abraham. 2014. Available online: http://www.acdlabs.com/products/percepta/predictors/absolv/ (accessed on 15 February 2020).
- Colmenarejo, G.; Alvarez-Pedraglio, A.; Lavandera, J.-L. Cheminformatic Models to Predict Binding Affinities to Human Serum Albumin. J. Med. Chem. 2001, 44, 4370–4378. [Google Scholar] [CrossRef]
- Xue, C.X.; Zhang, R.S.; Liu, H.X.; Yao, X.J.; Liu, M.C.; Hu, Z.D.; Fan, B.T. QSAR Models for the Prediction of Binding Affinities to Human Serum Albumin Using the Heuristic Method and a Support Vector Machine. J. Chem. Inf. Comput. Sci. 2004, 44, 1693–1700. [Google Scholar] [CrossRef]
- Yap, C.W. PaDEL-descriptor: An open source software to calculate molecular descriptors and fingerprints. J. Comput. Chem. 2011, 32, 1466–1474. [Google Scholar] [CrossRef] [PubMed]
- Tetko, I.V.; Gasteiger, J.; Todeschini, R.; Mauri, A.; Livingstone, D.; Ertl, P.; Palyulin, V.A.; Radchenko, E.V.; Zefirov, N.S.; Makarenko, A.S.; et al. Virtual Computational Chemistry Laboratory-Design and Description. J. Comput. Aided Mol. Des. 2005, 19, 453–463. [Google Scholar] [CrossRef] [PubMed]
- Burden, F.R. Molecular identification number for substructure searches. J. Chem. Inf. Model. 1989, 29, 225–227. [Google Scholar] [CrossRef]
- Pearlman, R.S.; Smith, K.M. Metric Validation and the Receptor-Relevant Subspace Concept. J. Chem. Inf. Comput. Sci. 1999, 39, 28–35. [Google Scholar] [CrossRef]
- González, M.P.; Terán, C.; Teijeira, M.; Besada, P.; González-Moa, M.J. BCUT descriptors to predicting affinity toward A3 adenosine receptors. Bioorg. Med. Chem. Lett. 2005, 15, 3491–3495. [Google Scholar] [CrossRef]
- Pirard, B.; Pickett, S.D. Classification of Kinase Inhibitors Using BCUT Descriptors. J. Chem. Inf. Comput. Sci. 2000, 40, 1431–1440. [Google Scholar] [CrossRef]
- Hao, M.; Li, Y.; Wang, Y.; Zhang, S. A classification study of human β 3-adrenergic receptor agonists using BCUT descriptors. Mol. Divers. 2011, 15, 877–887. [Google Scholar] [CrossRef]
| Ligand | K∙10−4 |
|---|---|
| benzoic acid | 1.9 ± 0.1 |
| 2-hydroxybenzoic acid | 4.0 ± 0.2 |
| 3-hydroxybenzoic acid | 1.9 ± 0.1 |
| 4-hydroxybenzoic acid | 1.0 ± 0.1 |
| 2,4-dihydroxybenzoic acid | 3.1 ± 0.2 |
| 2-nitrobenzoic acid | 2.1 ± 0.2 |
| 3-nitrobenzoic acid | 7.8 ± 0.3 |
| 4-nitrobenzoic acid | 8.1 ± 0.2 |
| 2,4-dinitrobenzoic acid | 6.5 ± 0.2 |
| 2-aminobenzoic acid | 2.3 ± 0.2 |
| 3-aminobenzoic acid | 1.4 ± 0.2 |
| 2-fluorobenzoic acid | 3.3 ± 0.2 |
| 3-chlorobenzoic acid | 5.8 ± 0.3 |
| 4-chlorobenzoic acid | 5.1 ± 0.1 |
| 2-bromobenzoic acid | 2.3 ± 0.2 |
| 3-bromobenzoic acid | 3.5 ± 0.3 |
| 4-bromobenzoic acid | 5.4 ± 0.2 |
| 2-iodobenzoic acid | 3.3 ± 0.3 |
| 3-iodobenzoic acid | 5.1 ± 0.2 |
| 4-iodobenzoic acid | 4.1 ± 0.3 |
| 2-cyanobenzoic acid | 2.6 ± 0.1 |
| 3-cyanobenzoic acid | 3.9 ± 0.2 |
| 4-cyanobenzoic acid | 6.4 ± 0.2 |
| 4-methylbenzoic acid | 1.4 ± 0.1 |
| Acid | K·10−4 | |
|---|---|---|
| BSA | HSA | |
| 2-hydroxybenzoic acid | 3.92 (CE) [22], 7.38 (SF) [22], 10.0 (SP, 310 K) [9], 1.95 (SF) [11] | 5.99 (CE) [22], 1.89 (CS) [22], 190 (SF) [23], 1.95 (SF) [10] |
| 3-hydroxybenzoic acid | 5.01 (SP, 310 K) [9], 0.85(SF) [11] | 0.34 (SF) [10] |
| 4-hydroxybenzoic acid | 0.79 (SP, 310 K) [9], <0.1 (SF) [11], 0.68 (UC, 288 K) [8] | <0.1 (SF) [10], 0.45 (UC, 288 K) [8] |
| 2,4-dihydroxybenzoic acid | <0.1 (SF) [11] | 0.16 (SF) [10] |
| 4-nitrobenzoic acid | 6.03 (UC, 288 K) [8], 3.09 (ED, 310 K) [24] | 8.13 (UC, 288 K) [8] |
| 2-aminobenzoic acid | 0.63 (SP, 310 K) [9] | |
| 3-aminobenzoic acid | 0.32 (SP, 310 K) [9] | |
| 3-chlorobenzoic acid | 11.22 (ED, 310 K) [24] | |
| 4-chlorobenzoic acid | 14.13 (UC, 288 K) [8], 14.96 (ED, 310 K) [24] | 14.8 (UC, 288 K) [8] |
| 2-bromobenzoic acid | 3.98 (UC, 310 K) [9] | |
| 3-bromobenzoic acid | 63.1 (UC, 310 K) [9] | |
| 4-bromobenzoic acid | 20.0 (UC, 310 K) [9], 20.42 (ED, 310 K) [24] | |
| 4-cyanobenzoic acid | 1.66 (UC, 288 K) [8] | 2.75 (UC, 288 K) [8] |
| 4-methylbenzoic acid | 7.94 (SP, 310 K) [9], <0.1 (SF) [11], 6.76 (UC, 288 K) [8], 3.16 (ED, 310 K) [24] | 0.35 (SF) [10], 3.63 (UC, 288 K) [8] |
| benzoic acid | 5.01 (SP, 310 K) [9], 2.24 (UC, 288 K) [8], 1.15 (ED, 310 K) [24] | 2.29 (UC, 288 K) [8] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khaibrakhmanova, D.; Nikiforova, A.; Sedov, I. Binding Constants of Substituted Benzoic Acids with Bovine Serum Albumin. Pharmaceuticals 2020, 13, 30. https://doi.org/10.3390/ph13020030
Khaibrakhmanova D, Nikiforova A, Sedov I. Binding Constants of Substituted Benzoic Acids with Bovine Serum Albumin. Pharmaceuticals. 2020; 13(2):30. https://doi.org/10.3390/ph13020030
Chicago/Turabian StyleKhaibrakhmanova, Diliara, Alena Nikiforova, and Igor Sedov. 2020. "Binding Constants of Substituted Benzoic Acids with Bovine Serum Albumin" Pharmaceuticals 13, no. 2: 30. https://doi.org/10.3390/ph13020030
APA StyleKhaibrakhmanova, D., Nikiforova, A., & Sedov, I. (2020). Binding Constants of Substituted Benzoic Acids with Bovine Serum Albumin. Pharmaceuticals, 13(2), 30. https://doi.org/10.3390/ph13020030






