Abstract
Drug repurposing appears as an increasing popular tool in the search of new treatment options against bacteria. In this paper, a tree-based classification method using Linear Discriminant Analysis (LDA) and discrete indexes was used to create a QSAR (Quantitative Structure-Activity Relationship) model to predict antibacterial activity against Escherichia coli. The model consists on a hierarchical decision tree in which a discrete index is used to divide compounds into groups according to their values for said index in order to construct probability spaces. The second step consists in the calculation of a discriminant function which determines the prediction of the model. The model was used to screen the DrugBank database, identifying 134 drugs as possible antibacterial candidates. Out of these 134 drugs, 8 were antibacterial drugs, 67 were drugs approved for different pathologies and 55 were drugs in experimental stages. This methodology has proven to be a viable alternative to the traditional methods used to obtain prediction models based on LDA and its application provides interesting new drug candidates to be studied as repurposed antibacterial treatments. Furthermore, the topological indexes Nclass and Numhba have proven to have the ability to group active compounds effectively, which suggests a close relationship between them and the antibacterial activity of compounds against E. coli.
1. Introduction
Until the 1950s, drug development was a costly and time-consuming process based on experimental trial and error assays. The aim was to find a lead molecule by testing a group of compounds, both synthetic and natural, for a given pharmacological activity. Once the lead compound was identified, structural modifications were carried out to improve its properties [1]. In order to reduce the cost and time involved in drug discovery, QSAR (Quantitative Structure-Activity Relationship) methods were developed [2]. These methods marked a turning point in drug research, since they are able to predict the pharmacological activity of a molecule without having to synthesize or extract it. Thus, Computational Chemistry and Virtual Screening have become essential strategies for drug development [3].
In this context, machine learning (ML) has emerged as a key tool in pharmaceutical research, including bioactivity prediction, de novo molecular design, synthesis prediction and biological image analysis [4]. In fact, machine learning can aid several steps of the drug discovery process: prediction of target structure, construction of models to predict biological activity, discovery and optimization of lead compounds and prediction of pharmacokinetic and toxicological profiles [5,6]. Among the machine learning strategies available, tree-based methods or, CART (Classification and Regression Trees), appear as a powerful and popular option for the development of QSAR methods, seeing as they can be used for both classification and regression depending on the nature of the variable [7]. Variations of CART, including Random Forests (RF), have been used for the development of HIV [8], cancer [9] and Alzheimer’s disease [10] treatments. These models act by stratifying or segmenting the predictor space into a number of simpler regions. As a result, each observation belongs to the most commonly occurring class of training observations in the region to which it belongs [11]. These methods, combined with molecular topology, constitute a time- and cost-effective option to tackle drug discovery. In fact, molecular topology is especially interesting because the models built using molecular topology indices can be applied to databases with structural diversity, as the selection of active compounds is carried out taking only into account the mathematical-topological similarity [12]. As a consequence, the theoretically active compounds selected by these models will possess similar pharmacokinetic and pharmacodynamic properties, regardless of its structural family.
There are newer LBVS (ligand-based virtual screening) approaches, such as multitasking QSAR (mt-QSAR) [13,14] and multi-objective optimization QSAR (MOOP) [15,16] that aim to integrate multiple diverse chemical and biological data. In this sense, these models are capable of making predictions ranging from in vitro and in vivo activities to ADMET properties in order to obtain the drug candidate with not only the best activity but also the best pharmacokinetic and pharmacodynamic properties. These QSAR models are often built using ML techniques such as the one used in this paper [15]. However, mt-QSAR and MOOP QSAR were not considered for this paper as the goal was to obtain a highly precise predictive model capable of identifying candidates within a database of drugs that have already been characterized for these properties, to be repurposed as antibacterial agents against E. coli.
The main limiting factor in drug development and, especially in the development of antibacterial compounds, is its economic cost. This is an important deterrent for the pharmaceutical industry, seeing as investing said time and resources in an antibiotic which, besides being a short duration acute treatment, may have resistances appear withing a few years after implementing the treatment, does not appear as a profitable investment [17]. This is particularly important in the case of antibacterial drugs, for which the pharmaceutical industry has lost its interest [18]. Firstly, the increasing and apparently unstoppable appearance of antibiotic resistance results in a constant demand of new antibacterial agents. Furthermore, the identification of active compounds with structural diversity outside of the known antibacterial families could imply the discovery of new mechanisms of action, which could contribute to slow down the issue of antibiotic resistance [19].
Along these lines, drug repurposing offers an alternative method for the fast and cost-effective identification of new therapeutic agents [20,21]. The first examples of this approach date back to the 80s, when sildenafil, which was originally developed for chest angina, was finally marketed for erectile disfunction [22]. Another example is azidothymidine which, having failed as an antineoplastic drug, it was repurposed as a successful HIV treatment [23]. By using drug repurposing to discover new compounds with antibacterial activity, this paper aims to find a time- and cost-effective way to tackle the ever-growing issue of antibiotic resistance. Prior success stories such as those of sildenafil or azidothymidine encourage this work, since they prove the viability of this approach.
The main aim of this paper is to develop a tree-based QSAR model using Linear Discriminant Analysis (LDA) and discrete indexes for the screening of DrugBank [24] in order to identify drug candidates to be repurposed as antibacterial compounds against Escherichia coli infection.
2. Results
2.1. Tree-Based QSAR Model
2.1.1. Compound Selection and Index Calculation
A total of 82 molecules (Supplementary Material, Tables S1 and S2) belonging to the quinolone family of antibacterial compounds were selected and divided into two groups, 43 compounds with proven antibacterial activity and 39 compounds described as inactive against E. coli. In order to consider a compound as active, its minimum inhibitory concentration (MIC) had to be ≤ 1 mg/L. On the other hand, a compound was considered inactive when it had a MIC > 16 mg/L. The compounds with MIC values in the 1–16 mg/L range were not included in the study because the property studied is biological and the relationship with the chemical structure is a matter of probability. Therefore, we wanted to make a notable difference between groups in order to be able to identify relevant structural references among active and inactive compounds. Furthermore, in the case of molecules with chiral centers, we only included those where all the stereoisomers were described as active, seeing as all stereoisomers are represented by the same chemical graph.
2.1.2. Discrete Index Analysis
Firstly, we analyzed the probability distribution of 15 different discrete indexes calculated for our group of molecules in order to determine if any of them had good discriminant power (Supplementary Material, Figure S1)
When analyzing the distribution diagrams, two discrete indexes showed good discriminant power: Nclass and Numhba (Figure 1). However, Nclass was discarded because, when the compounds used to build the model were grouped according to their values for this index, it resulted in two groups for which DFs could not be calculated. This is due to the fact that the statistical program was chosen as the first step of the hierarchical decision tree, grouping the active compounds in the value range of 7–11 (Figure 1).
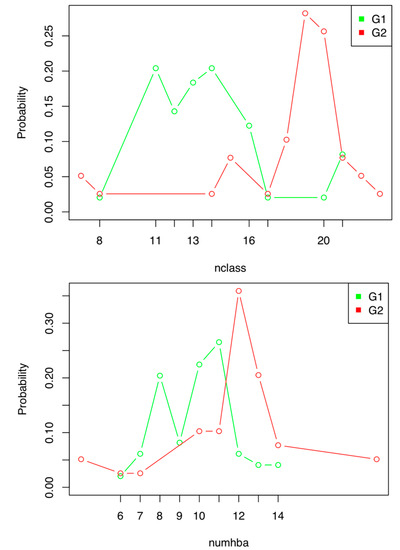
Figure 1.
Distribution diagram of the active (G1) and inactive (G2) compounds used to construct the antibiotic activity prediction model against E. coli according to their Nclass (up) and Numhba (down) values.
2.1.3. Probability Space Construction
After selecting the discrete index, we grouped the compounds used for the construction of the model according to their Numhba values, resulting in 2 groups:
- Numhba = 7–11
- Numhba 7–11
When analyzing the resulting groups, we observed that there were no active compounds among the molecules with values of Numhba 7–11, therefore, we decided that compounds with values of Numhba outside of the 7–11 range would be directly classified as inactive. Thus, only one discriminant function was calculated for the group of compounds with Numhba values within the 7–11 range.
2.1.4. Linear Discriminant Analysis
Once the probability spaces had been established, a DF, presented below along with its corresponding statistical parameters, was calculated for the maximum probability space using continuous indexes and LDA:
DF = −129.49658 − 16.29048Phia + 16.10739SHtCH + 3.57226S=N− − 5.11438S>N− − 25.958964CC
N = 48; λ = 0.1065407; F = 50.317
Analyzing the Pharmacological Distribution Diagram (PDD) for the calculated DF (Figure 2), it can be observed that active compounds lie in the 0–40 interval. On the other hand, compounds with DF values of < 0 and ≥ −50 are classified as inactive. Compounds with DF values < 40 and > −50 remain unclassifiable. As a consequence, the PDD defines the applicability domain of the model, which is limited to compounds with DF values between −50 and 40.
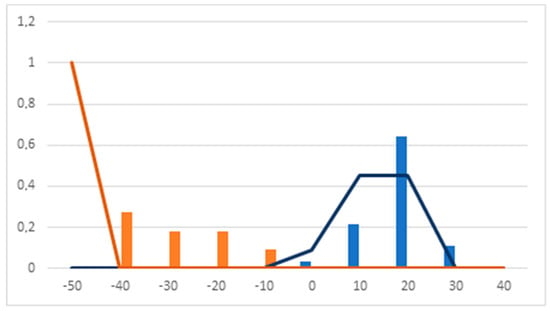
Figure 2.
Pharmacological distribution diagram of the discriminant function (DF). (Orange bars: inactive training. Blue bars: active training. Orange lines: inactive test. Blue lines: active test).
As it can be observed in Table 1, the model had a 100% accuracy classification rate using the training and test sets. Furthermore, due to the natural imbalance of the training and test sets, the Matthew’s Correlation Coefficient (MCC) was calculated, obtaining and MCC value of 1.

Table 1.
Classification matrix for DF.
Tables providing information regarding the value of each of the indexes present in the DF, the value of the DF for each compound, the classification probability for each compound and their final classification as active or inactive are provided as Supplementary Material (Tables S3–S6).
2.1.5. Hierarchical Tree Construction
Having established the maximum probability range for the discrete index Numhba and the corresponding DF, the hierarchical model was constructed (Figure 3).
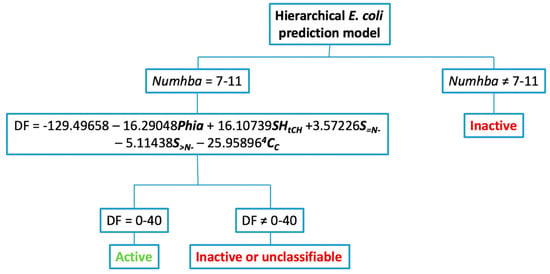
Figure 3.
Decision tree for the application of the hierarchical model to predict antibacterial activity against E. coli.
2.2. Virtual Screening of Adapted DrugBank Database
Once the DrugBank database had been adapted, the model described above was applied to identify drugs with theoretical antibacterial activity against E. coli. The model selected 134 drugs as theoretically active (Table 2 and Supplementary Material, Table S7). Of these, 8 were already described as antibacterial drugs against E. coli, which provides an initial success rate of 6.1%. The remaining drugs can be classified as 67 marketed drugs for different pathologies and 55 drugs in experimental stages.

Table 2.
Summary of theoretically active compounds against E. coli selected by the model.
3. Discussion
Regarding the methodology used to develop de tree-based QSAR model, LDA is a frequently used method for the development of QSAR models [25,26,27,28], however, it has a key limitation: variables with discrete values cannot be used for the development of the model since they cannot be analyzed using the same statistical methods [29]. This is an important issue in the development of QSAR models because discrete descriptors contain relevant information that could be useful in predicting pharmacological activity. The formalism for the development of QSAR/QSPR models using LDA is based on the hypothesis that there is a group of compounds, , where each compound shall be denoted by and the existence of a series of indexes we will design as , each element of this set is formed by the function , so that each compound has an assigned value for each index described [28]. If takes values in a discrete or numerable set, we face a discrete index. If, on the other hand, has at least an open interval of the real line, we face a continuous index. In this context, given any finite subset , we can consider the finite subset of indexes indexed by the subset and obtain the values for each compound as follows:
To construct a linear discriminant function associated to the set of indexes , we have to endow the set of compounds with a spatial probability structure . Thus, the linear discriminant function is constructed as:
where
For (active), 2 (inactive) is the conditioned probability of belonging to one of the two groups () when the index obtained using the set J ⊂ I is equal to . Given a compound ω, we will calculate its indexes and will say that
The usual hypotheses for the construction of are:
is a density function of multivariable normal distribution for .
As a consequence of condition II, we can only assure the construction of the function if the indexes for when are continuous variables. Consequently, we must exclude all discrete variables if we want to use this statistical technique.
A natural question that appears is, what happens when we want to use a discrete index I that we cannot include in our index collection for its use with LDA because it does not fulfill condition II. In order to solve this issue, we assume the following hypothesis:
We have an event and a natural number big enough in a way that
that is, the probability of belonging to the active compounds group () when the discrete index has values within a fixed interval (satisfying property A) is higher than the probability of belonging to the inactive group (). We will consider Ac the opposite event of A, that is, when the discrete index has values outside the interval of maximum probability. In this case .
In particular, this is equal to the condition
The consequence we can infer from the latter expression and the fact that
is
This means that the probability of belonging to the inactive group () when the discrete index does not have values within the desired interval (does not satisfy A) is higher than the probability of belonging to the active group () under the same condition. This allows for the creation of a hierarchical model. We first construct two probability spaces (, , ) and () where
This allows us to construct, under the appropriate hypothesis, the prediction model we have named hierarchical:
If the molecule , that is, it satisfies that , we construct a discriminant linear function
If the molecule , that is, it satisfies that or that , we construct the discriminant linear function
In conclusion, this model provides a hyperplane which separates two regions, allowing the discrimination between active and inactive compounds [30]. By incorporating the decision tree, a high probability sub-space is created which, implicitly, aims towards increasing the precision of the model as the molecules used to calculate de DF already belong to this space of higher probability of activity.
The model was constructed using a combined CART + LDA approach for several reasons. Firstly, the methodology used in the present paper was developed after identifying the impossibility of using discrete indexes with LDA. Additionally, the data available for many of the molecules used in the development of the model was limited to in vitro activity against E. coli. This means that there was no information regarding in vivo activity or ADMET properties, which immediately discarded the option of a mt-QSAR or MOOP-based QSAR model. Furthermore, the software that was available for the development of the model was limited to R and BMDP. Lastly, as it was mentioned in the introduction, this model was developed to identify drug candidates for repurposing, which implies that, for most cases, ADMET and other properties of the theoretically active compounds selected by the model are already known.
Focusing on the indexes selected by the model, the discrete index Numhba, which takes into account the number of hydrogen bond acceptors in the molecule, is interesting because the presence of a certain number of hydrogen bond acceptors in a molecule results in a better pharmacological profile when administered orally, which is especially interesting for quinolones [30]. This is one of the properties used in Lipinski’s “Rule of 5” in which Numhba, considering nitrogen and oxygen, must be ≤ 10, seeing as molecules with a higher number have many interactions with water and hinders transport through the lipid bilayer [31]. In this case, Numhba considers nitrogen, oxygen and fluorine as hydrogen bond acceptors.
As for the indexes selected for the DF, the electrotopological index for hydrogen atoms bonded to tertiary carbons (SHtCH) and the electrotopological index for imines (S=N−) have a positive effect on the DF value. On the other hand, the number of rotational bonds, represented by the Phia (ϕ) index, which refers to the flexibility of the molecule [32], the electrotopological index for tertiary nitrogens (S>N−) and the quotient between non-valence and valence order 4 cluster index (4CC) have a negative effect on the value of the DF.
The negative sign associated to the electrotopological index for tertiary nitrogens (S>N−), which indicated an unfavorable influence, is especially interesting. However, as the structure-activity relationship of quinolones states, this group in position 1 is an essential part of the pharmacophore [33]. Thus, we can deduce that it is an excess of this group what would affect activity negatively. Moreover, the value of this index is also influenced by the electronegative groups surrounding the tertiary nitrogen atoms [34].
The authors decided to use this model for the virtual screening of DrugBank because it is an open access database with information about more than 11,200 drugs which can be used for drug discovery and repurposing [24].
Many research [35,36,37,38,39,40,41,42,43,44,45,46] groups are taking similar approaches to repurpose drugs for which safety and toxicity data have been already collected from clinical assays in order to use them as antibiotic compounds with new pharmacological activity. (Table 3).

Table 3.
Drug candidates to be repurposed with in vitro antibacterial activity.
Regarding the drug candidates selected by the prediction model, besides the 8 antibacterial drugs mentioned previously, there were 10 antiviral and 12 antineoplastic compounds. These are especially interesting because both types of drugs are destined towards the destruction of undesired cells, which could include bacteria. In the same way that quinolones have both, antibacterial and cytotoxic activities [47], the mechanisms of action by which these 22 drugs inhibit or destroy viruses and tumor cells could also affect bacterial cells. In fact, recent studies suggest the possibility of reusing antineoplastic drugs for the treatment of bacterial infections [48,49]. Along these lines, Shah et al. have already described the antibacterial activity of antineoplastic drugs against drug-resistant Escherichia coli among other bacteria [50].
On the other hand, the model also selected 12 glucocorticoids. Any compound in this therapeutic group is not an interesting candidate when it comes to repositioning it as an antibacterial drug because they suppress the immune response by blocking antimicrobial autophagy and nitric oxide production [51,52]. This, in turn, could worsen symptoms and extend the duration of the bacterial infection. However, these molecules could be used as lead compounds and, via pharmacomodulation, reduce their immunosuppressive effect while improving their antibacterial activity [53].
4. Materials and Methods
4.1. Tree-Based QSAR Model Construction
The procedure to use the hierarchical methodology presented in the discussion was used to obtain a tree-based prediction method following the steps presented below.
- 1.
- Compound selection and index calculation: the compounds selected to build the prediction model must belong to the same structural family. These compounds were divided into two groups, active and inactive. Once the group of compounds had been selected, the molecular descriptors or indexes of each of the molecules were calculated using MOLCONN-Z [54] and DESMOL13 [55] software.
- 2.
- Discrete index analysis: the discrete indexes were analyzed to determine if there were any with a value range that grouped the active compounds. The condition of a compound having the value of that discrete index within the range of maximum probability acted as the first step in the decision tree. Furthermore, this analysis could also act as a fast way to determine new structure activity relationships. It must be noted that, for indexes in which not enough inactive compounds are found in the higher probability space, this methodology cannot be applied for two reasons. Firstly, the lack of inactive compounds makes it impossible to obtain a discriminant function. Moreover, this type of index would lead to overfitting.
- 3.
- Probability space construction: the compounds used for the construction of the model were separated in groups according to their value for the chosen discrete indexes.
- 4.
- Linear Discriminant Analysis: a discriminant function was calculated for the selected group of molecules using only continuous indexes. This DF was calculated using the BMDP (BioMedicine Department Program) module 7M [56]. Compounds used to calculate the DF were randomly split into training and test groups by the BMDP software.
- 5.
- Hierarchical decision tree construction: once the probability spaces of the discrete indexes had been determined and the corresponding discriminant functions (DFs) calculated, a hierarchical tree was built. In the first level of this decision tree, compounds were grouped according to their value for the selected discrete index. Those that lie outside of the maximum probability space were directly classified as inactive. The remaining compounds went on to the second level of the tree. In this level, the DF is applied. Compounds within the established highest activity expectancy range are classified as active, while the rest are classified as inactive or unclassifiable.
4.2. DrugBank Database Construction
In order to build the database from DrugBank, the structures were retrieved from ChemSpider, an open access database that allows easy access to more than 67 million chemical structures, properties and associated information. This database integrates compounds from hundreds of high quality databases among which is DrugBank. Moreover, ChemSpider allows the selection of one or several databases and the individual download of structures in “mol” format, numbered by default with the identification number from ChemSpider, which allows us to know which structures are included in our database.
Once the structures were downloaded, a series of modifications had to be carried out to transform them into chemical graphs that our index calculation softwares, MOLCONN-Z and DESMOL11, could use. All the modifications explained below were made using the drawing software ChemDraw Professional 17.0 from the ChemOffice 2017 software package.
Firstly, the stereochemistry had to be removed from all molecules, seeing as the index calculation softwares only work with the 2D graph. This had to be done one molecule at a time, changing the bonds that indicated chirality for flat bonds. Furthermore, these softwares do not accept molecules with more than 99 bonds from end to end of the molecule thus, compounds exceeding 99 bonds had to be removed. Moreover, we were only able to calculate the indexes of molecules containing C, F, Cl, Br, I, O, N, S, P, B, Si, Ge, Sn and Pb, as well as hydrogen, thus, each molecule had to be analyzed to detect any other atoms and delete them. Having taken all these considerations, we were able to build our own DrugBank subset with 7031 chemical graphs of approved and experimental drugs.
5. Conclusions
The prediction QSAR model constructed using a hierarchical tree-based methodology has selected 134 drugs with theoretical antibacterial activity against E. coli. Of these, 22 could be interesting candidates to be further studied due to their proven pharmacological activity, which could provide new mechanisms of action, further contributing to combat emerging antibiotic resistance. As a result, drug repurposing appears as a cost- and time-effective alternative for the development of new antibacterial drugs, broadening the existing pipeline. Furthermore, the topological indexes Nclass and Numhba have proven to have the ability to group active compounds effectively, which suggests a close relationship between them and the antibacterial activity of compounds against E. coli.
Supplementary Materials
The following are available online at https://www.mdpi.com/1424-8247/13/12/431/s1, Table S1: Active compounds against E. coli, Table S2: Inactive compounds against E. coli, Table S3: Results obtained in the LDA and compounds classification according to the DF, active training group, Table S4: Results obtained in the LDA and compound classification according to the DF, inactive training group, Table S5: Results obtained in the LDA and compounds classification according to the DF, active test group, Table S6: Results obtained in the LDA and compound classification according to the DF, inactive test group, Table S7: Theoretically active compounds against E. coli selected by the model, Figure S1: Probability distribution diagrams of the analyzed discrete indexes.
Author Contributions
Conceptualization, B.S.-G., A.F. and P.A.A.L.; methodology, B.S.-G., J.I.B.-B. and A.F. validation, M.T.P.-G., G.M.A.-F., P.A.A.-L. and A.F.; formal analysis, A.F.; investigation, B.S.-G.; data curation, B.S.-G. and J.I.B.-B.; writing—original draft preparation, B.S.-G. and P.A.A.-L.; writing—review and editing, M.T.P.G and A.F.; visualization, G.M.A.-F.; supervision, M.T.P.-G., P.A.A.-L. and A.F.; funding acquisition, A.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Li, J.W.; Vederas, J.C. Drug discovery and natural products: End of an era or endless frontier? Science 2009, 325, 161–165. [Google Scholar] [CrossRef] [PubMed]
- Karelson, M. Molcular Descriptors in QSAR/QSPR; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- López-Vallejo, F.; Caulfield, T.; Martínez-Mayorga, K.; Giulianotti, M.A.; Nefzi, A.; Houghten, R.A.; Medina-Franco, J.L. Integrating virtual screening and combinatorial chemistry for accelerated drug discovery. Comb. Chem. High Throughput Screen. 2011, 14, 475–487. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Engkvist, O.; Wang, Y.; Olivecrona, M.; Blaschke, T. The rise of deep learning in drug discovery. Drug Discov. Today 2018, 23, 1241–1250. [Google Scholar] [CrossRef] [PubMed]
- Fox, T.; Kriegl, J.M. Machine learning techniques for in silico modeling of drug metabolism. Curr. Top. Med. Chem. 2006, 6, 1579–1591. [Google Scholar] [CrossRef]
- Maltarrollo, V.G.; Gertrudes, J.C.; Oliveira, P.R.; Honorio, K.M. Applying machine learning techniques for ADME-Tox prediction: A review. Expert Opin. Drug Metab. Toxicol. 2015, 11, 259–271. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.; Stone, C. Classification and Regression Trees (Wadsworth Statistics/Probability); Chapman and Hall/CRC: New York, NY, USA, 1984. [Google Scholar]
- Hdoufane, I.; Bjij, I.; Soliman, M.; Tadjer, A.; Villemin, D.; Bogdanov, J.; Cherqaoui, D. In Silico SAR Studies of HIV-1 Inhibitors. Pharmaceuticals 2018, 11, 69. [Google Scholar] [CrossRef]
- Hu, Y.; Lu, Y.; Wang, S.; Zhang, M.; Qu, X.; Niu, B. Application of Machine Learning Approaches for the design and study of anticancer drugs. Curr. Drug Targets 2019, 20, 488–500. [Google Scholar] [CrossRef]
- Carpenter, K.A.; Huang, X. Machine Learning-based Virtual Screening and Its Applications to Alzheimer’s Drug Discovery: A Review. Curr. Pharm. Des. 2018, 24, 3347–3358. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning with Applications in R; Springer: New York, NY, USA, 2013. [Google Scholar]
- Bueso-Bordils, J.I.; Alemán-López, P.A.; Suay-Garcia, B.; Martín-Algarra, R.; Duart, M.J.; Falcó, A.; Antón-Fos, G.M. Molecular Topology for the Discovery of New Broad-Spectrum Antibacterial Drugs. Biomolecules 2020, 10, 1343. [Google Scholar] [CrossRef]
- Speck-Planche, A.; Kleandrova, V.V.; Cordeiro, M.N.D.S. Chemoinformatics for rational discovery of safe antibacterial drugs: Simultaneous predictions of biological activity against streptococci and toxicological profiles in laboratory animals. Bioorganic Med. Chem. 2013, 21, 2727–2732. [Google Scholar] [CrossRef]
- Ambure, P.; Halder, A.K.; González-Diaz, H.; Cordeiro, M.N.D.S. QSAR-Co: An Open Source Software for Developing Robust Multitasking or Multitarget Classification-Based QSAR Models. J. Chem. Inf. Model. 2019, 59, 2538–2544. [Google Scholar] [CrossRef] [PubMed]
- Cruz-Monteagudo, M.; Borges, F.; Cordeiro, M.N.D.S. Jointly handling potency and toxicity of antimicrobial peptidomimetics by sumple rules from desirability theory and chemoinformatics. J. Chem. Inf. Model. 2011, 51, 3060–3077. [Google Scholar] [CrossRef] [PubMed]
- Nicolaou, C.A.; Brown, N. Multi-objective optimization methods in drug design. Drug Discov. Today Technol. 2013, 10, e427–e435. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Sun, W.; Simeonov, A. Drug repurposing screens and synergistic drug- combinations for infectious diseases. Br. J. Pharmacol. 2017, 175, 181–191. [Google Scholar] [CrossRef] [PubMed]
- Aubé, J. Drug Repurposing and the Medicinal Chemist. ACS Med. Chem. Lett. 2012, 3, 442–444. [Google Scholar] [CrossRef]
- Ghofrani, H.A.; Osterloh, I.H.; Grimminger, F. Sildenafil: From angina to erectile dysfunction to pulmonary hypertension and beyon. Nat. Rev. Drug Discov. 2006, 5, 689–702. [Google Scholar] [CrossRef]
- Broder, S. The development of antiretroviral therapy and its impact on the HIV-1/AIDS pandemic. Antivir. Res. 2010, 85, 1. [Google Scholar] [CrossRef]
- Scannell, J.W.; Blanckley, A.; Boldon, H.; Warrington, B. Diagnosing the decline in pharmaceutical R&D efficiency. Nat. Rev. Drug Discov. 2012, 11, 191–200. [Google Scholar] [CrossRef]
- Piddock, L.J. The crisis of no new antibiotics—What is the way forward? Lancet Infect. Dis. 2012, 12, 249–253. [Google Scholar] [CrossRef]
- Ashburn, T.T.; Thor, K.B. Drug repositioning: Identifying and developing new uses for existing drugs. Nat. Rev. Drug Discov. 2004, 3, 673–683. [Google Scholar] [CrossRef]
- DrugBank. Available online: https://www.drugbank.ca (accessed on 1 August 2020).
- Amin, S.A.; Adhikari, N.; Bhargava, S.; Jha, T.; Gayen, S. Designing Potential Antitrypanosomal Thiazol-2-ethylamines through Predictive Regression Based and Classification Based QSAR Analyses. Curr. Drug Discov. Technol. 2017, 14, 39–52. [Google Scholar] [CrossRef] [PubMed]
- Jha, T.; Adhikari, N.; Saha, A.; Amin, S.A. Multiple molecular modelling studies on some derivatives and analogues of glutamic acid as matrix metalloproteinase-2 inhibitors. SAR QSAR Environ. Res. 2018, 29, 43–68. [Google Scholar] [CrossRef] [PubMed]
- Bueso-Bordils, J.I.; Pérez-Gracia, M.T.; Suay-Garcia, B.; Duart, M.J.; Algarra, R.V.M.; Lahuerta-Zamora, L.; Antón-Fos, G.M.; Alemán-López, P.A. Topological pattern for the search of new active drugs against methicillin resistant Staphylococcus aureus. Eur. J. Med. Chem. 2017, 138, 807–815. [Google Scholar] [CrossRef] [PubMed]
- Santana, K.D.; Rivera-Borroto, O.M.; Puris, A.; Pham-The, H.; Le-Thi-Thu, H.; Rasulev, B.; Casañola-Martin, G.M. Beyond model interpretability using LDA and decisión tres for a-amylase and a-glucosidase inhibitor classification studies. Chem. Biol. Drug Des. 2019, 94, 1414–1421. [Google Scholar] [CrossRef]
- Roy, K.; Kar, S.; Das, R.N. “QSAR/QSPR Modeling: Introduction”. A Primer on QSAR/QSPR Modeling—Fundamental Concepts; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Webb, A.R. “Introduction to Statistical Pattern Recognition”. Statistical Pattern Recognition; Wiley-Blackwell: Oxford, UK, 2011. [Google Scholar]
- Lipinski, C.A. Lead- and drug-like compounds: The rule-of-five revolution. Drug Discov. Today Technol. 2004, 1, 337–341. [Google Scholar] [CrossRef]
- Kier, L.B. An index of molecular flexibility from kappa shape attributes. Quant. Struct.-Act. Relat. 1989, 8, 221–224. [Google Scholar] [CrossRef]
- Gund, P. Three-dimensional pharmacophoric pattern searching. Prog. Mol. Subcell. Biol. 1977, 5, 117–143. [Google Scholar]
- Kier, L.B.; Hall, L.H. The E-state as an extended free valence. J. Chem. Inf. Comput. Sci. 1997, 37, 548–552. [Google Scholar] [CrossRef]
- Ejim, L.; A Farha, M.; Falconer, S.B.; Wildenhain, J.; Coombes, B.K.; Tyers, M.; Brown, E.D.; Wright, G.D. Combinations of antibiotics and nonantibiotic drugs enhance antimicrobial efficacy. Nat. Chem. Biol. 2011, 6, 348–350. [Google Scholar] [CrossRef]
- Thangamani, S.; Mohammad, H.; Abushahba, M.F.N.; Sobreira, T.J.P.; Seleem, M.N. Repurposing auranofin for the treatment of cutaneous staphylococcal infections. Int. J. Antimicrob. Agents 2016, 47, 195–201. [Google Scholar] [CrossRef]
- Thangamani, S.; Younis, W.; Seleem, M.N. Repurposing Clinical Molecule Ebselen to Combat Drug Resistant Pathogens. PLoS ONE 2015, 10, e0133877. [Google Scholar] [CrossRef] [PubMed]
- Lim, L.E.; Vilcheze, C.; Jacobs, W.R., Jr.; Ramon-García, S.; Thompson, C.J. Anthelmintic avermectins kill Mycobacterium tuberculosis, including multidrug-resistant clinical strains. Antimicrob. Agents Chemother. 2013, 57, 1040–1046. [Google Scholar] [CrossRef] [PubMed]
- Kinnings, S.L.; Liu, N.; Buchmeier, N.; Tonge, P.J.; Xie, L.; Bourne, P.E. Drug discovery using chemical system biology: Repositioning the safe medicine comtan to treat multi- drug and extensively drug resistant tuberculosis. PLoS Comput. Biol. 2009, 5, e1000423. [Google Scholar] [CrossRef] [PubMed]
- Ordway, D.J.; Viveiros, M.; Leandro, C.; Bettencourt, R.; Almeida, J.; Martins, M.; Kristiansen, J.E.; Molnar, J.; Amaral, L. Clinical concentrations of thioridazine kill intracellular multidrug-resistant Mycobacterium tuberculosis. Antimicrob. Agents Chemother. 2003, 47, 917–922. [Google Scholar] [CrossRef] [PubMed]
- Walz, J.M.; Avelar, R.L.; Longtine, K.J.; Carter, K.L.; Mermel, L.A.; Heard, S.O. Anti-infective external coating of central venous catheters: A randomized, noninferiority trial comparing 5-fluorouracil with chlorhexidine/silver sulfadiazine in preventing catheter colonization. Crit. Care Med. 2010, 38, 2095–2102. [Google Scholar] [CrossRef] [PubMed]
- Carlson-Banning, K.M.; Chou, A.; Liu, Z.; Hamill, R.J.; Song, Y.; Zechiedrich, L. Toward repurposing ciclopirox as an antibiotic against drug-resistant Acinetobacter baumannii, Escherichia coli, and Klebsiella pneumoniae. PLoS ONE 2013, 8, e69646. [Google Scholar] [CrossRef]
- Khodaverdian, V.; Pesho, M.; Truitt, B.; Bollinger, L.; Patel, P.; Nithianantham, S.; Yu, G.; Delaney, E.; Jankowsky, E.; Shoham, M. Discovery of antivirulence agents against methicillin-resistant Staphylococcus aureus. Antimicrob. Agents Chemother. 2013, 57, 3645–3652. [Google Scholar] [CrossRef]
- Rosch, J.W.; Boyd, A.R.; Hinojosa, E.; Pestina, T.; Hu, Y.; Persons, D.A.; Orihuela, C.J.; Tuomanen, E.I. Statins protect against fulminant pneumococcal infection and cytolysin toxicity in a mouse model of sickle cell disease. J. Clin. Investig. 2010, 120, 627–635. [Google Scholar] [CrossRef]
- Perlmutter, J.I.; Forbes, L.T.; Krysan, D.J.; Ebsworth-Mojica, K.; Colquhoun, J.M.; Wang, J.L.; Dunman, P.M.; Flaherty, D.P. Repurposing the antihistamine terfandine for antimicrobial activity against Staphylococcus aureus. J. Med. Chem. 2014, 57, 8540–8562. [Google Scholar] [CrossRef]
- Pinault, L.; Han, J.S.; Kang, C.M.; Franco, J.; Ronning, D.R. Zafirlukast inhibits complexation of Lsr2 with DNA and growth of Mycobacterium tuberculosis. Antimicrob. Agents Chemother. 2013, 57, 2134–2140. [Google Scholar] [CrossRef]
- Bisacchi, G.S.; Hale, M.R. A “Double-Edged” Scaffold: Antitumor Power within the Antibacterial Quinolone. Curr. Med. Chem. 2016, 23, 520–577. [Google Scholar] [CrossRef] [PubMed]
- Soo, V.W.C.; Kwan, B.W.; Quezada, H.; Castillo-Juárez, I.; Pérez-Eretza, B.; García-Contreras, S.J.; Martínez-Vázquez, M.; Wood, T.K.; García-Contreras, R. Repurposing of Anticancer Drugs for the Treatment of Bacterial Infections. Curr. Top. Med. Chem. 2017, 17, 1157–1176. [Google Scholar] [CrossRef] [PubMed]
- Boder, C.A.; Jorgensen, J.H.; Drutz, D.J. Antibacterial activities of antineoplastic agents. Antimicrob. Agents Chemother. 1985, 28, 437–439. [Google Scholar] [CrossRef]
- Shah, Z.; Mahbuba, R.; Turcotte, B. The anticancer drug tirapazamine has antimicrobial activity against Escherichia coli, Staphylococcus aureus and Clostridium difficile. FEMS Microbiol. Lett. 2013, 347, 61–69. [Google Scholar] [CrossRef]
- Schleimer, R.P. Glucocorticoids Supress Inflammation but Spare Innate Immune Responses in Airway Epithelium. Proc. Am. Thorac. Soc. 2004, 1, 222–230. [Google Scholar] [CrossRef]
- Wang, J.; Wang, R.; Wang, H.; Yang, X.; Yang, J.; Xiong, W.; Wen, Q.; Ma, L. Glucocorticoids Supress Antimicrobial Autophagy and Nitric Oxide Production and Facilitate Mycobacterial Survival in Macrophages. Sci. Rep. 2017, 7, 982. [Google Scholar] [CrossRef]
- Lalut, J.; Santoni, G.; Karila, D.; Lecoutey, C.; Davis, A.; Nachon, F.; Silman, I.; Sussman, J.; Weik, M.; Maurice, T.; et al. Novel multitarget-directed ligands targeting acetylcholinesterase and σ1 receptors as lead compounds for treatment of Alzheimer’s disease: Synthesis, evaluation, and structural characterization of their complexes with acetylcholinesterase. Eur. J. Med. Chem. 2018, 162, 234–248. [Google Scholar] [CrossRef]
- Hall, L.H. MOLCONN-Z Software; Eastern Nazarene College: Quincy, MA, USA, 1995. [Google Scholar]
- DESMOL13 Software. Unidad de Investigación de Diseño de Fármacos y Conectividad Molecular; Facultad de Farmacia, Universidad de Valencia: Valencia, Spain, 2000. [Google Scholar]
- Dixon, W.J.; Brown, M.B.; Engelman, L.; Jenrich, R.I. BMDP Statistical Software Manual; University of California Press: Berkeley, CA, USA, 1990. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).