A High Resolution Color Image Restoration Algorithm for Thin TOMBO Imaging Systems
Abstract
:1. Introduction
2. Image Restoration Method for TOMBO Color Imaging Systems
2.1. System Model
- gi,j(x,y,ϑ),ϑ ∈ {R, G, B} represents the blurred, LR and noisy color component for the ith,jth captured unit image with resolution (M × N) pixels per color
- hi,j(x,y,ϑ) is an (l × l) PSF that represents the overall channel blur affecting gi,j(x,y,ϑ) unit image for the color component ϑ, also called the intrachannel. We assume here that the blur is different for each color of each unit image
- hi,j(x, y, GR),hi,j(x, y, BR),hi,j(x, y, BG) are (l × l) PSFs representing the overall mutual relation between red-green, red-blue and green-blue respectively.
- “* *” represents the 2-D convolution operator w.r.t x, y
- f(x, y, ϑ) is the ϑ color component of the original scene with resolution (M × N) > (M × N) per color component
- vi,j(x, y, ϑ) is the additive 2-D, zero mean white Gaussian noise per color component that affect the unit image gi,j(x,y,ϑ)
- ↓ D is the down-sampling operator representing the LR process
2.2. Formulation of the Restoration Method
- represents the image of interest plus the noise term (defined in-frequency band useful terms),
- , are the aliasing out of frequency band image terms,
- , are the aliasing out-of-frequency band noise terms.
- , are the GR overall cross-talk terms.
- , are the BR overall cross-talk terms.
2.3. Restoration Process
3. Color Image Restoration Algorithm
- For restoring the imagewhere, FM is the mean value of a mesh of pixels in the region < x, y > ∈ [LM, LN] surrounding symmetrically the pixel index (x, y), F∞ is a threshold of a large value pre-defined for the case when the summation of the PSF spectra in Equation 13 is close to zero.
- For estimating the PSFs
- Pixel amplitudes that reach values greater than 255 are scaled using the following histogram normalization,where a and b are usually 255 and 0 respectively (but other values can be also used to adjust contrast and brightness), fmax, R and fmin, R are the maximum and minimum pixel values of the color component R. For improved performance, fmm,R and fmax,R are usually chosen as the 5% and 95% levels in the histogram distribution respectively (confidence interval).
- The mean value of the input image(s) and the output image is to be maintained (note that there are twice as many green pixels as red/blue pixel for the Bayer filter)
- To resolve the problem of having zeros or nulls in the spectra, the following equation for the interpolated f(x,y, R) is used:followed by:where α1,α2 are two positive numbers representing the extent of additive noise in the residual terms, β is a recursive stability factor controls the amount of information needed from posterior image estimates (0 < β < 1 ), n + 1 is the current iteration number. Typical values of β range between 0.5 to 0.9. Like in adaptive systems, the value of β can be adjusted to avoid such that impulsive-like outputs.
- For initialization, one of the images is used as an initial estimate of the HR image. The up-sampling and interpolation process is done by zero-padding in the spatial domain between the image samples. Afterwards the FFT is applied. In the Fourier domain, a single spectrum is then taken out of the repetitive spectra using a low pass filter with cut-off frequency and zeroing the rest of the spectrum. Finally, inverse fast Fourier transform (IFFT) is applied to inverse back to the image domain. It is essential that the zero-padding be done such that the zero frequency components remain the same. In addition, zero-padding should be applied to both positive and negative frequencies. Unlike existing techniques that use lower order functions for interpolation (cubic interpolation used in [2]), our method uses the more efficient sinc function.
- We use the 2-D fast fourier transform (FFT) to estimate spectra and cross spectra needed for the algorithm
3.1. Convergence Analysis
4. Results and Discussion
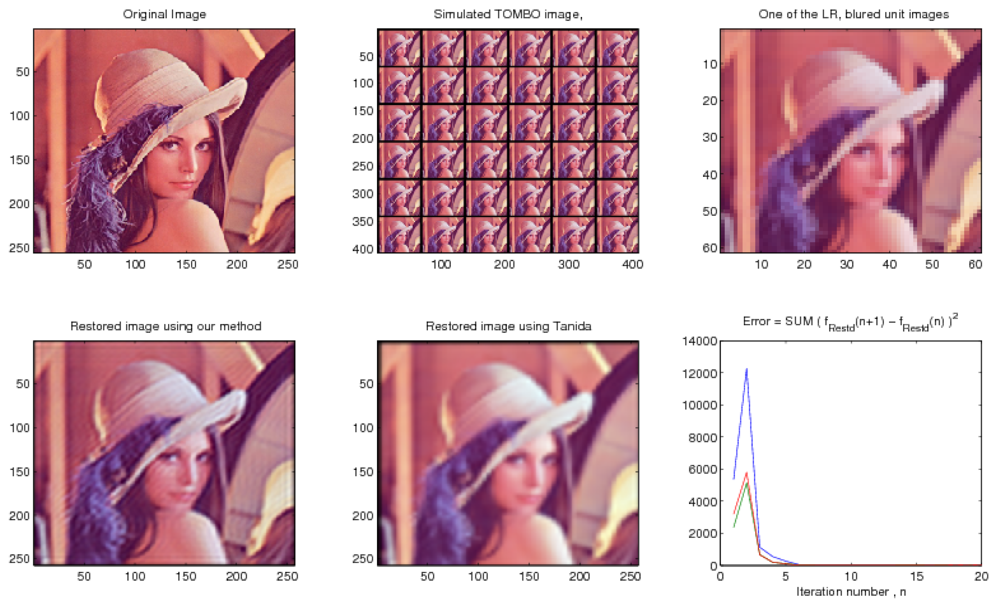
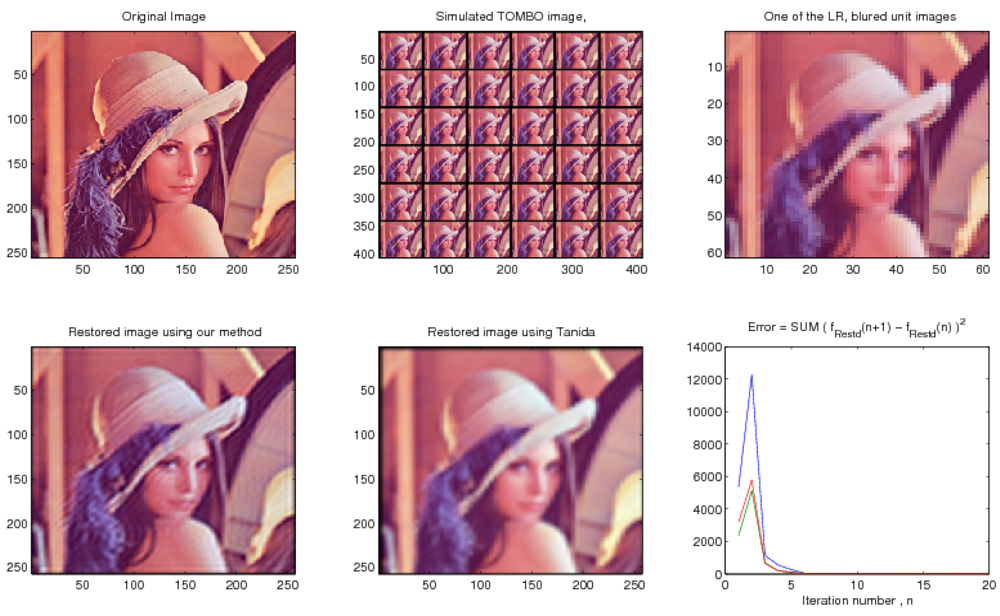
- Restore a HR image from multiple blurred, LR and noisy “simulated” TOMBO color images.
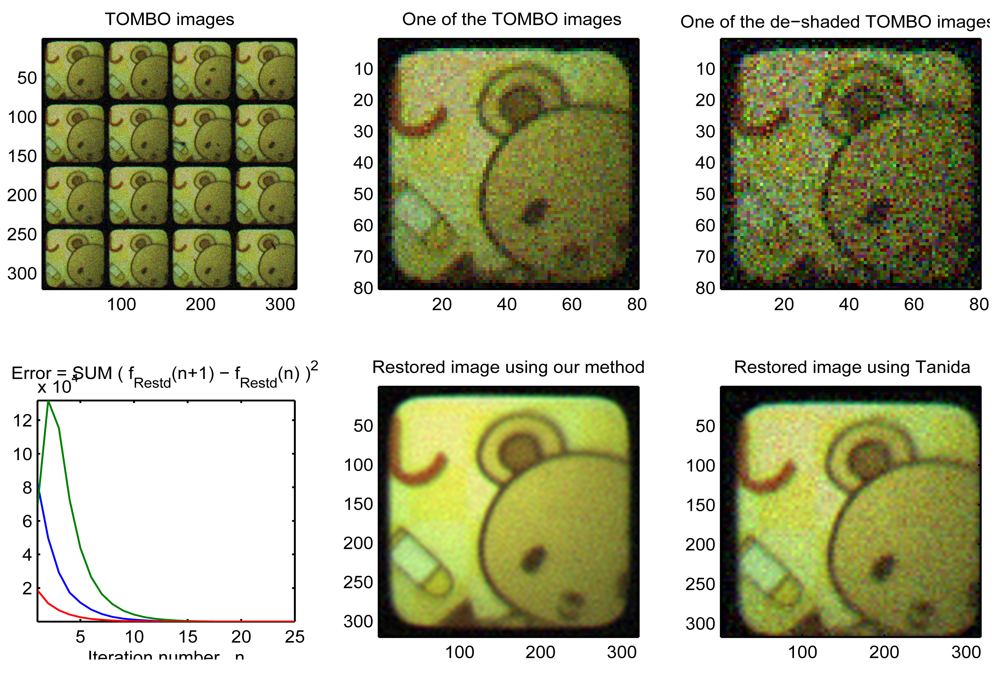
- Restore a HR image from multiple blurred, noisy “real” TOMBO color images.
4.1. Examples of Simulated Images
4.2. Comparison with Existing Image Restoration Methods
4.3. Examples of Real Images
5. Conclusions
Acknowledgments
References and Notes
- El-Sallam, A.; Boussaid, F. Spectral-based blind image restoration method for thin TOMBO imagers. Sensors 2008, 8, 6108–6124. [Google Scholar]
- Tanida, J.; Kumagai, T.; Yamada, K.; Miyatake, S.; Ishida, K.; Morimoto, T.; Kondou, N.; Miyazaki, D.; Ichioka, Y. Thin observation module by bound optics (TOMBO): Concept and experimental verification. Appl. Opt. 2001, 40, 1806–1813. [Google Scholar]
- Yamada, K.; Tanida, J.; Yu, W.; Miyatake, S.; Ishida, K.; Miyazaki, D. Fabrication of diffractive microlens array for opto-electronic hybrid information system. Proc. Diffract. Opt. 1999, 22, 52–53. [Google Scholar]
- Tanida, J.; Kumagai, T.; Yamada, K.; Miyatake, S.; Ishida, K.; Morimoto, T.; Kondou, N.; Miyazaki, D.; Ichioka, Y. Thin observation module by bound optics-TOMBO: an optoelectronic image capturing system. Proc. SPIE Opt. Comput. 2000, 4086, 1030–1036. [Google Scholar]
- Tanida, J.; Yamada, K. TOMBO: thin observation module by bound optics. Proceedings of the 15th Annual Meeting of the IEEE in Lasers and Electro-Optics, Glasgow, Scotland, November 10-14, 2002; 1, pp. 233–234.
- Kitamura, Y.; Shogenji, R.; Yamada, K.; Miyatake, S.; Miyamoto, M.; Morimoto, T.; Masaki, Y.; Kondou, N.; Miyazaki, D.; Tanida, J.; Ichioka, Y. Reconstruction of a high-resolution image on a compound-eye image-capturing system. Appl. Opt. 2004, 43, 1719–1727. [Google Scholar]
- Nitta, K.; Shogenji, R.; Miyatake, S.; Tanida, J. Image reconstruction for thin observation module by bound optics by using the iterative backprojection method. Appl. Opt. 2006, 45, 2893–2900. [Google Scholar]
- Yamada, K.; Ishida, K.; Shougenji, R.; Tanida, J. Development of three dimensional endoscope by Thin Observation by Bound Optics (TOMBO). Proceedings of World Automation Congress WAC'06, Budapest, Hungary, July 24-26, 2006; pp. 1–4.
- Farsiu, S.; Elad, M.; Milanfar, P. Multiframe demosaicing and super-resolution of color images. IEEE Trans. Image Process. 2006, 15, 141–159. [Google Scholar]
- Filip, S.; Flusser, J. Multichannel blind deconvolution of spatially misaligned images. IEEE Trans. Image Process. 2005, 14, 874–883. [Google Scholar]
- Yu, H.; Yap, K.; Li, C; Chau, L. A new color image regularization scheme for blind image decon-volution. Proceedings of the IEEE ICASSP'08, Las Vegas, Nevada, USA, March 30 - April 4, 2008.
- He, Y.; Yap, K.H.; Chen, L.; Chau, L.P. A novel hybrid model framework to blind color image deconvolution. IEEE Trans. Syst. Man Cybern. Part A: Syst. Humans 2008, 38, 862–880. [Google Scholar]
- Vega, M.; Molina, R.; Katsaggelos, A.K. A Bayesian super-resolution approach to demosaicing of blurred images. EURASIP 2006, 25072:1–25072:12. [Google Scholar]
- Ohta, Y.I.; Kanade, T.; Sakai, T. Color information for region segmentation. J. Comput. Graph. Image Process. 1980, 13, 222–241. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, August 2007. [Google Scholar]
- Pratt, W.K. Digital Image Processing, 4th ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Lagendijk, R.L.; Biemond, J. Iterative Identification and Restoration of Images; Springer-Verlag Inc.: New York, NY, USA, 2007. [Google Scholar]
- Jain, A.K. Fundamentals of Digital Image Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Banham, M.R.; Katsaggelos, A.K. Digital image restoration. IEEE Signal Process. Mag. 1997, 14, 24–41. [Google Scholar]
- Zhao, W.; Pope, A. Image restoration under significant additive noise. IEEE Signal Process. Lett. 2007, 14, 401–404. [Google Scholar]
- Ohyama, N.; Yachida, M.; Badique, E.; Tsujiuchi, J.; Honda, T. Least squares filter for color image restoration. J. Opt. Soc. Am. A 1988, 5, 19–24. [Google Scholar]
- Zing, X.Y.; Chen, Y.W.; Nakao, Z. Classification of remedy sensed images using independent component analysis and spatial consistency. J. Adv. Comput. Intell. Intell. Inform. 2004, 8, 216–217. [Google Scholar]
- Boo, K.J.; Bose, N.K. Multispectral image restoration with multisensors. Proceedings of International Conference on Image Processing, Lausanne, Switzerland, September 16-19, 1996; 3, pp. 995–998.
- Brillinger, D.R. Time Series: Data Analysis and Theory; Holden-Day, Inc.: San Francisco, CA, USA, 1981. [Google Scholar]
- Kay, S.M. Modern Spectral Estimation: Theory and Application; Prentice Hall: Englewood Cliffs, NJ, USA, 1988. [Google Scholar]
- Choi, K.; Schulz, T.J. Signal-processing approaches for image-resolution restoration for TOMBO imagery. Appl. Opt. 2008, 47, B104–B116. [Google Scholar]
- Kundur, D.; Hatzinakos, D. Blind image deconvolution revisited. IEEE Signal Process. Mag. 1996, 13, 61–63. [Google Scholar]
- Chen, L.; Yap, K.; He, Y. Efficient recursive multichannel blind image restoration. EURASIP J. Adv. Signal Process. 2007, 2007, 1–10. [Google Scholar]
- Munson, D.C. A note on lena. IEEE Trans. Image Process. 1996, 5, 1–2. [Google Scholar]
- Huynh-Thu, Q.; Ghanbari, M. Scope of validity of PSNR in image/video quality assessment. Electron. Lett. 2008, 44, 800–801. [Google Scholar]
- Girod, A. What's wrong with mean-squared error? In Digital images and human vision; MIT Press: Cambridge, MA, USA, 1993; pp. 207–220. [Google Scholar]
- Shogenji, R.; Kitamura, Y.; Yamada, K.; Miyatake, S.; Tanida, J. Color imaging with an integrated compound imaging system. Opt. Expr. Opt. Soc. Am. 2003, 11, 2109–2117. [Google Scholar]
- Tanida, J.; Shogenji, R.; Kitamura, Y.; Yamada, K.; Miyamoto, M.; Miyatake, S. Multispectral imaging using compact compound optics. Opt. Expr. Opt. Soc. Am. 2004, 12, 1643–1655. [Google Scholar]
- Kanaev, A.V.; Ackerman, J.R.; Fleet, E.F.; Scibner, D.A. TOMBO sensors with scene-independent superresolution processing. Opt. lett. 2007, 32, 2855–2857. [Google Scholar]




| Step 1: Set the values of L, ℓ, α1, α2,β, FM, F∞ |
| Step 2: Select the color to be restored ϑ ε {R, G, B} |
| Step 3: Iteration n = 1, initialize f̂ (x, y, ϑ), hence F̂(f1, f2,ϑ) = FFT {(x, y, ϑ)} |
| Step4:For i,j = 1,2, …, μ estimate |
| Step 5: Impose PSF constraints to get the accurate estimates |
| Step 6: Estimate the biased image spectra |
| Step 7: Impose the image constraints |
| then estimate the original image by updating the estimates using |
| Step 8: Scale the estimated images pixels or use histogram normalization to find a and b, then adjust the image using |
| Step 9: Repeat from Step 4 until convergence, then repeat for another color ϑ |
| μ × μ | M × N | SNER | ℓ | LM ×LN | α1 | α2 | β | # Iterations | |
|---|---|---|---|---|---|---|---|---|---|
| Figure 4 | 6 × 6 | 60 × 60 | - | 7 | 240 × 240 | 0.1 | 10 | 0.1 | 20 |
| Figure 5 | 6 × 6 | 60 × 60 | 4.968 dB | 7 | 240 × 240 | 0.1 | 10 | 0.1 | 20 |
| Sina [9] | Sroubek [10] | This Work | |
|---|---|---|---|
| Noiseless | 21.986 | 18.250 | 16.348 |
| Noisy | 14.13 | 13.78 | 10.89 |
| μ × μ | M × N | SNER | ℓ | ↑L | LM | × LN | α11 | α2 | β | # of Iterations | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Figure 7 | 4 ×4 | 60 × 0 | 15.774 dB | 5 | 4 | 240 | 40 | 0.001 | 0.001 | 0.9 | 25 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
El-Sallam, A.A.; Boussaid, F. A High Resolution Color Image Restoration Algorithm for Thin TOMBO Imaging Systems. Sensors 2009, 9, 4649-4668. https://doi.org/10.3390/s90604649
El-Sallam AA, Boussaid F. A High Resolution Color Image Restoration Algorithm for Thin TOMBO Imaging Systems. Sensors. 2009; 9(6):4649-4668. https://doi.org/10.3390/s90604649
Chicago/Turabian StyleEl-Sallam, Amar A., and Farid Boussaid. 2009. "A High Resolution Color Image Restoration Algorithm for Thin TOMBO Imaging Systems" Sensors 9, no. 6: 4649-4668. https://doi.org/10.3390/s90604649
APA StyleEl-Sallam, A. A., & Boussaid, F. (2009). A High Resolution Color Image Restoration Algorithm for Thin TOMBO Imaging Systems. Sensors, 9(6), 4649-4668. https://doi.org/10.3390/s90604649





