Noise Reduction for CFA Image Sensors Exploiting HVS Behaviour
Abstract
:1. Introduction
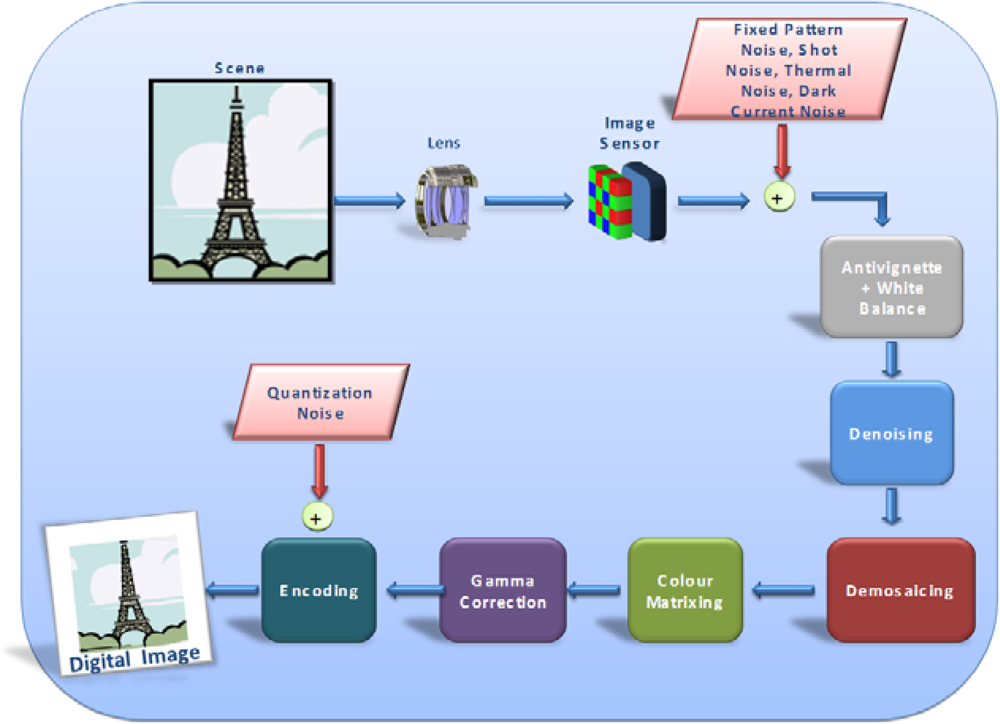
2. Background
2.1. Bayer Data
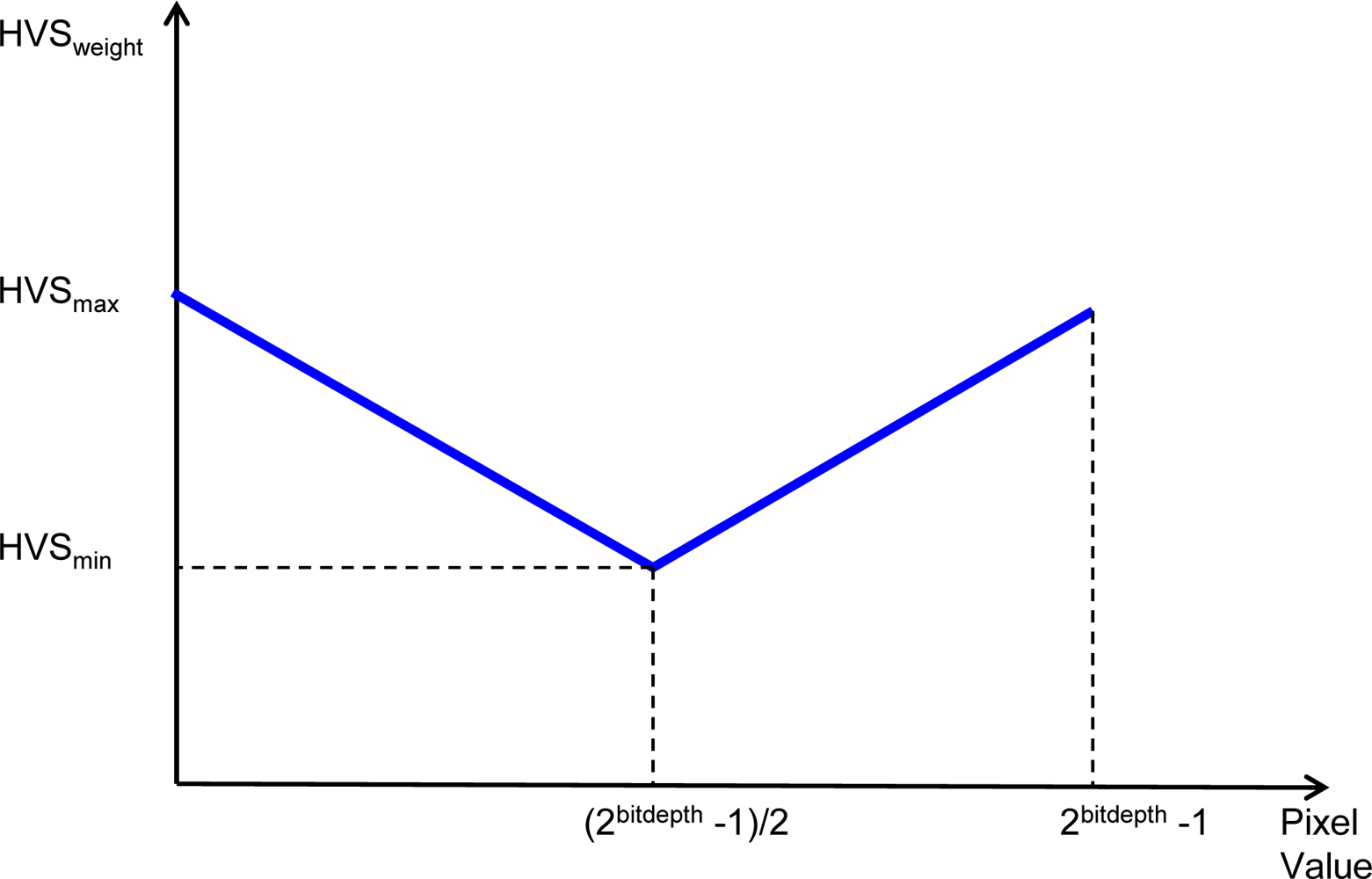
2.2. Basic Concepts about the Human Visual System
- - if the local area is homogeneous, then it can be heavily filtered because pixel variations are basically caused by random noise.
- - if the local area is textured, then it must be lightly filtered because pixel variations are mainly caused by texture and by noise to a lesser extent; hence only the little differences can be safely filtered, as they are masked by the local texture.
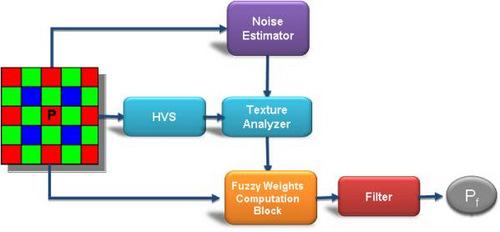
3. The Proposed Technique
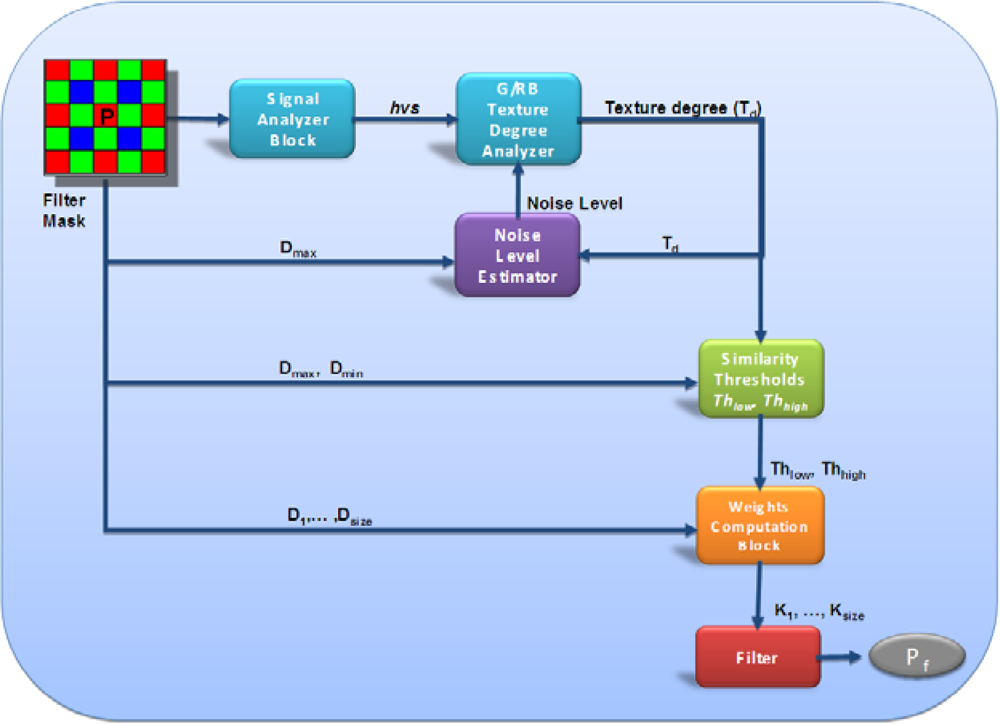
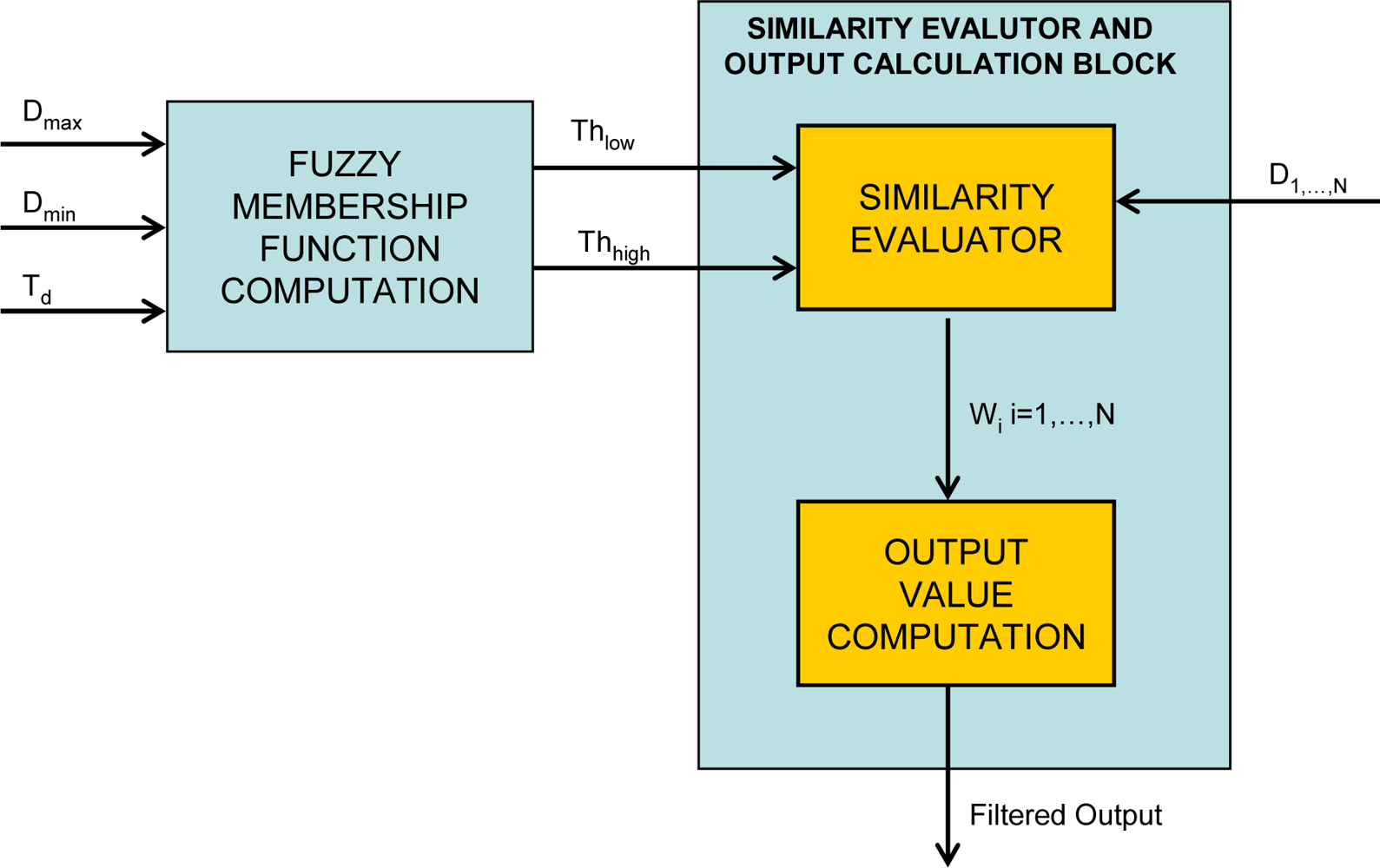
3.1. Overall filter block diagram
- Signal Analyzer Block: computes a filter parameter incorporating the effects of human visual system response and signal intensity in the filter mask.
- Texture Degree Analyzer: determines the amount of texture in the filter mask using information from the Signal Analyzer Block.
- Noise Level Estimator: estimates the noise level in the filter mask taking into account the texture degree.
- Similarity Thresholds Block: computes the fuzzy thresholds that are used to determine the weighting coefficients for the neighborhood of the central pixel.
- Weights Computation Block: uses the coefficients computed by the Similarity Thresholds Block and assigns a weight to each neighborhood pixel, representing the degree of similarity between pixel pairs.
- Filter Block: actually computes the filter output.
3.2. Signal Analyzer Block
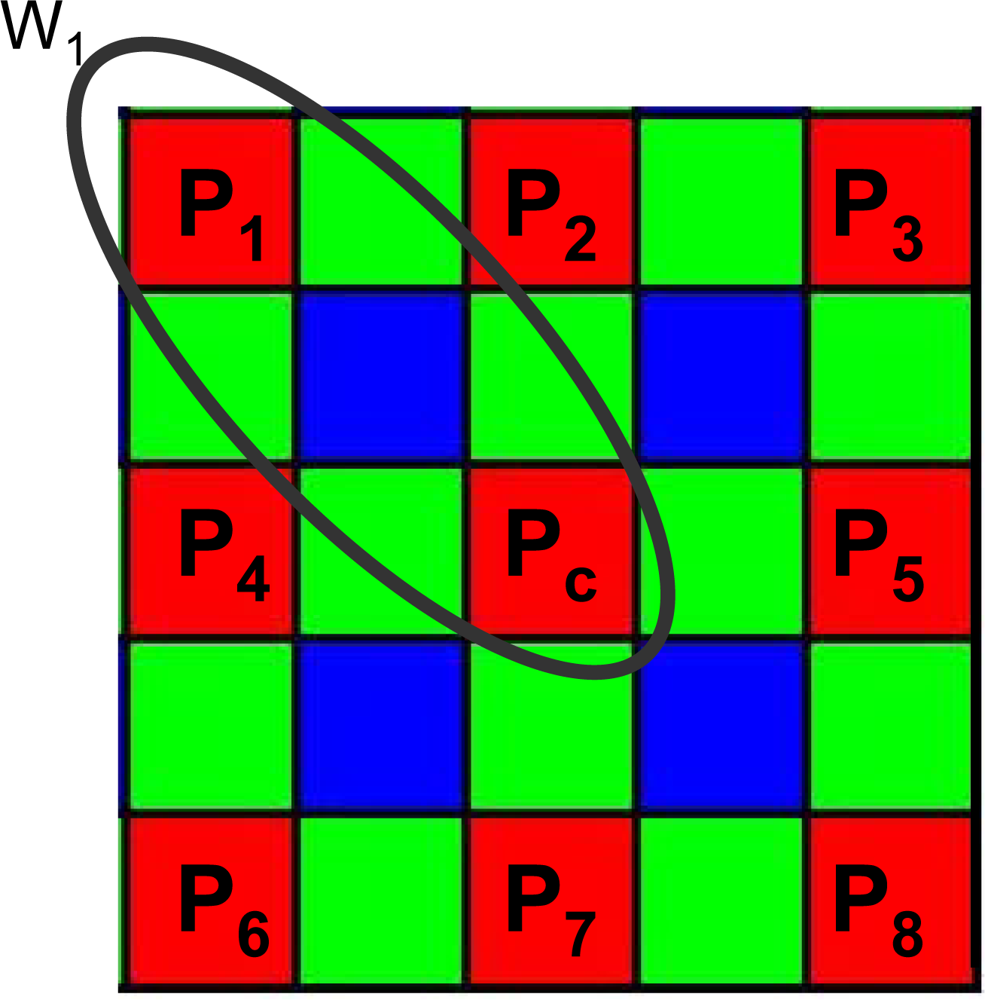
3.3. Filter Masks
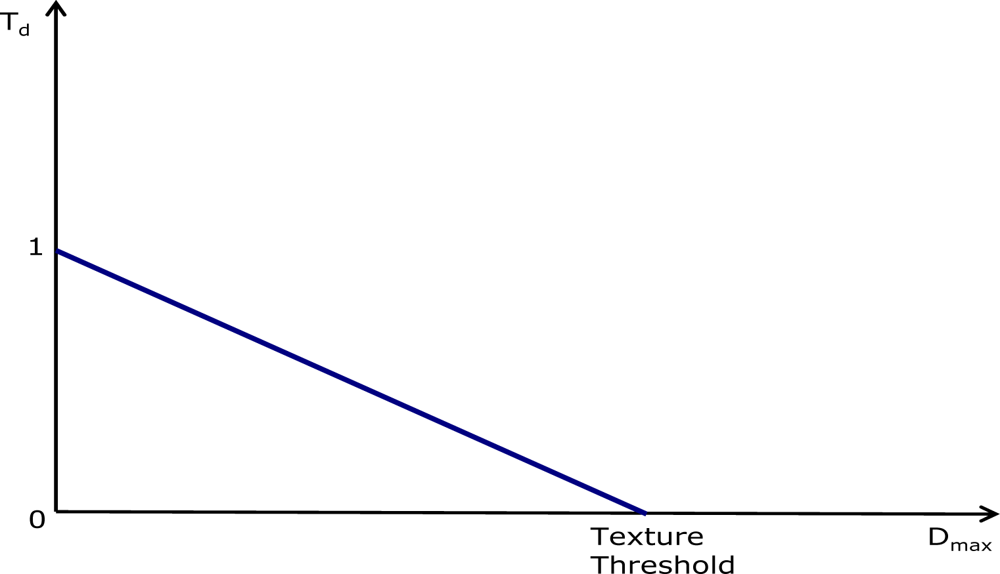
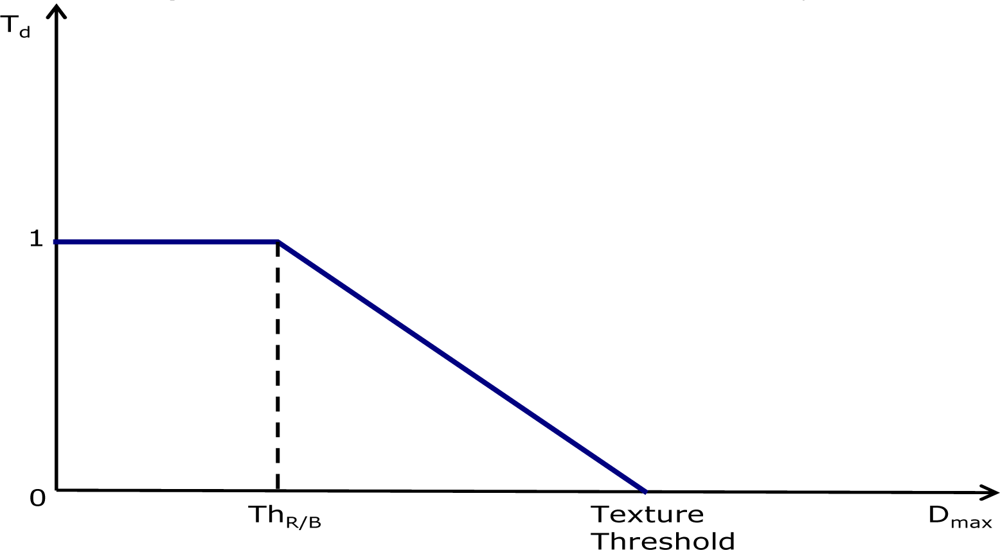
3.4. Texture Degree Analyzer
- - if Td = 1 the area is assumed to be completely flat;
- - if 0 < Td < 1 the area contains a variable amount of texture;
- - if Td = 0, the area is considered to be highly textured.
3.5. Noise Level Estimator
- if the local area is completely flat (Td = 1), then the noise level is set to Dmax;
- if the local area is highly textured (Td = 0), the noise estimation is kept equal to the previous region (i.e., pixel);
- otherwise a new value is estimated.
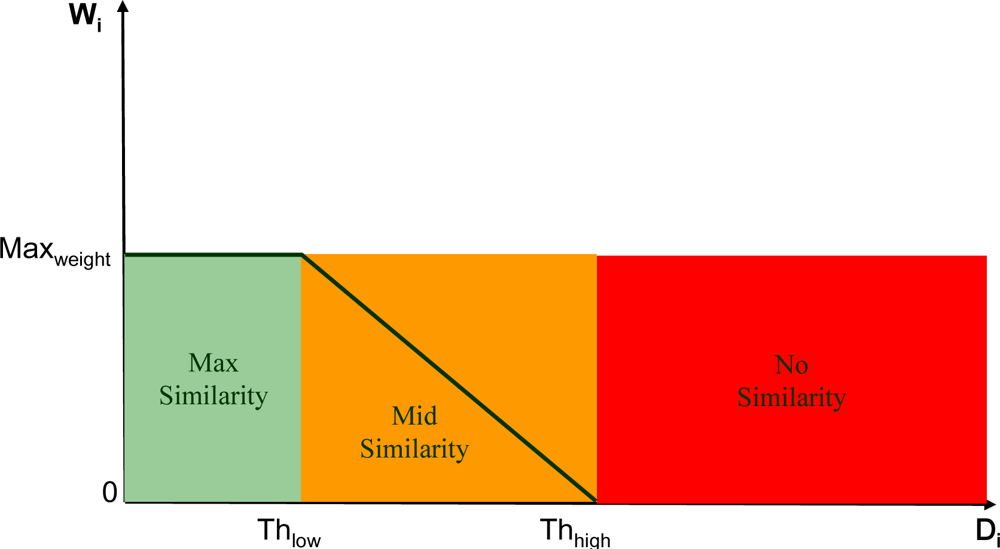
3.6. Similarity Thresholds and Weighting Coefficients computation
- - Pc be the central pixel of the working window;
- - Pi, i = 1,…,7, be the neighborhood pixels;
- - Di = abs(Pc − Pi), i=1,…,7 the set of absolute differences between the central pixel and its neighborhood;
- small enough to be heavily filtered,
- big enough to remain untouched,
- an intermediate value to be properly filtered.
3.7. Final Weighted Average
4. Experimental Results
4.1. Noise Power Test
- INOISY: Noisy CFA Pattern
- IFILTERED: Filtered CFA Pattern
- IORIGINAL: Original noiseless CFA Pattern
- INOISY − IORIGINAL = IADDED_NOISE
- IFILTERED − IORIGINAL = IRESIDUAL_NOISE
4.2. Visual Quality Test
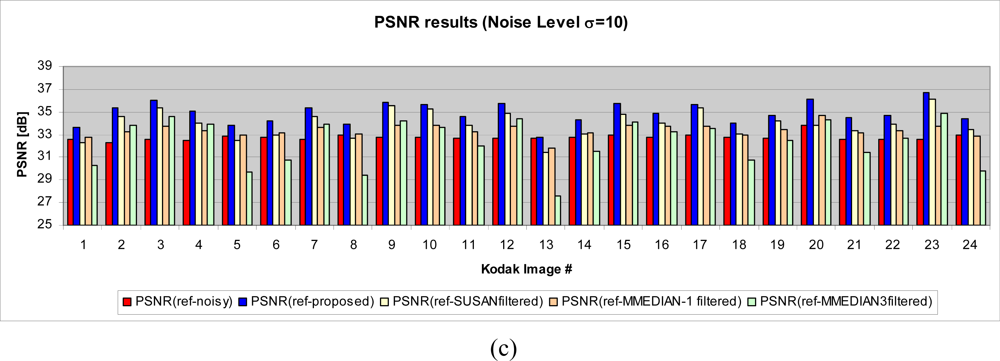
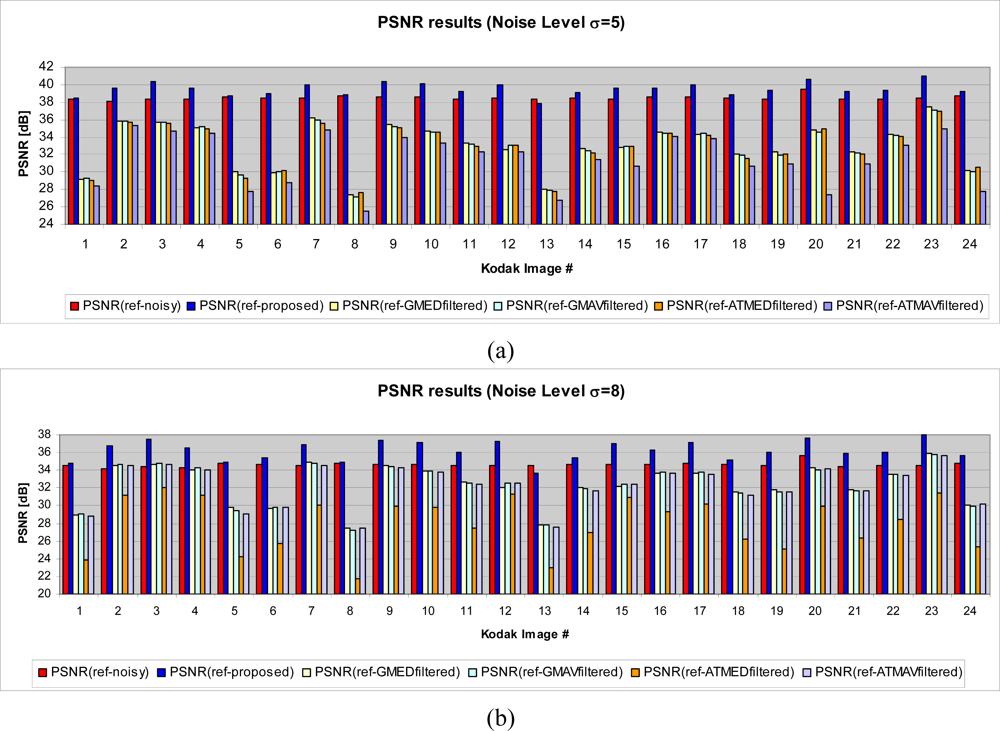
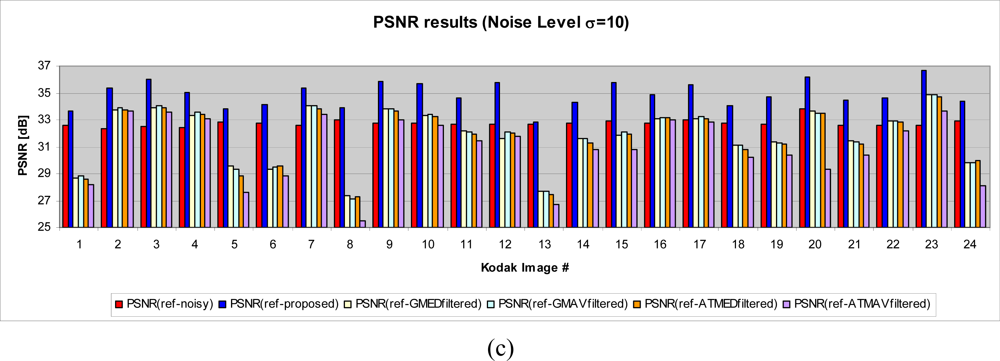
4.3. PSNR test
- - GMED: Gaussian Fuzzy Filter with Median Center
- - GMAV: Gaussian Fuzzy Filter with Moving Average Center
- - ATMED: Asymmetrical Triangular Fuzzy Filter with Median Center
- - ATMAV: Asymmetrical Triangular Fuzzy Filter with Moving Average Center
Conclusions and Future Work
Acknowledgments
References and Notes
- Lukac, R. Single-sensor imaging in consumer digital cameras: a survey of recent advances and future directions. J. Real-Time Image Process 2006, 1, 45–52. [Google Scholar]
- Battiato, S.; Castorina, A.; Mancuso, M. High Dynamic Range Imaging for Digital Still Camera: an Overview. SPIE J. Electron. Imaging 2003, 12, 459–469. [Google Scholar]
- Messina, G.; Battiato, S.; Mancuso, M.; Buemi, A. Improving Image Resolution by Adaptive Back-Projection Correction Techniques. IEEE Trans. Consum. Electron 2002, 48, 409–416. [Google Scholar]
- Battiato, S.; Bosco, A.; Castorina, A.; Messina, G. Automatic Image Enhancement by Content Dependent Exposure Correction. EURASIP J. Appl. Signal Process 2004, 2004, 1849–1860. [Google Scholar]
- Battiato, S.; Castorina, A.; Guarnera, M.; Vivirito, P. A Global Enhancement Pipeline for Low-cost Imaging Devices. IEEE Trans. Consum. Electron 2003, 49, 670–675. [Google Scholar]
- Bayer, B.E. Color Imaging Array. US. Pat. 3,971,965 1976. [Google Scholar]
- Hirakawa, K.; Parks, TW. Joint demosaicing and denoising. Proceedings of the IEEE International Conference on Image Processing (ICIP 2005), Genova, Italy, Sept. 2005; pp. 309–312.
- Hirakawa, K.; Parks, T.W. Joint demosaicing and denoising. IEEE Trans. Image Process 2006, 15, 2146–2157. [Google Scholar]
- Lu, W.; Tan, Y.P. Color Filter Array Demosaicking: New Method and Performance Measures. IEEE Trans. Image Process 2003, 12, 1194–1210. [Google Scholar]
- Trussel, H.; Hartwig, R. Mathematics for Demosaicking. IEEE Trans. Image Process 2002, 11, 485–492. [Google Scholar]
- Battiato, S.; Mancuso, M. An Introduction to the Digital Still Camera Technology. ST J. Syst. Res. — Special Issue on Image. Process. Digital Still Camera 2001, 2, 2–9. [Google Scholar]
- Jayantn, N.; Johnston, J.; Safranek, R. Signal Compression Based On Models Of Human Perception. Proceedings of the IEEE 1993, 81, 1385–1422. [Google Scholar]
- Nadenau, M.J.; Winkler, S.; Alleysson, D.; Kunt, M. Human Vision Models for Perceptually Optimized Image Processing - a Review. IEEE Trans. Image Process 2003, 12, 58–70. [Google Scholar]
- Pappas, T.N.; Safranek, R.J. Perceptual Criteria for Image Quality Evaluation. In Handbook of Image and Video Processing; Bovik, A.C., Ed.; Publisher: Academic Press: San Diego, CA, USA, 2000; pp. 669–684. [Google Scholar]
- Wang, Z.; Lu, L.; Bovik, A. Why Is Image Quality Assessment so difficult? Presented at the IEEE International Conference on Acoustics, Speech, & Signal Processing, Orlando, FL, USA, May 2002; pp. 3313–3316.
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process 2004, 13, 600–612. [Google Scholar]
- Longere, P.; Xuemei, Z.; Delahunt, P.B.; Brainard, D.H. Perceptual Assessment of Demosaicing Algorithm Performance. Proceedings of the IEEE, Jan 2002; pp. 123–132.
- Pizurica, A.; Zlokolica, V.; Philips, W. Combined wavelet domain and temporal denoising. Proceedings of the IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Miami, FL., USA, July 2003; pp. 334–341.
- Portilla, J.; Strela, V.; Wainwright, M.J.; Simoncelli, E.P. Image Denoising Using Scale Mixtures of Gaussians in the Wavelet Domain. IEEE Trans. Image Process 2003, 12, 1338–1351. [Google Scholar]
- Scharcanski, J.; Jung, C.R.; Clarke, R.T. Adaptive Image Denoising Using Scale and Space Consistency. IEEE Trans. Image Process 2002, 11, 1092–1101. [Google Scholar]
- Barcelos, C.A.Z.; Boaventura, M.; Silva, E.C. A Well-Balanced Flow Equation for Noise Removal and Edge Detection. IEEE Trans. Image Process 2003, 12, 751–763. [Google Scholar]
- Amer, A.; Dubois, E. Fast and reliable structure-oriented video noise estimation. IEEE Trans. Circuits Syst. Video Technol 2005, 15, 113–118. [Google Scholar]
- Kim, Y.-H.; Lee, J. Image feature and noise detection based on statistical hypothesis tests and their applications in noise reduction. IEEE Trans. Consum. Electron 2005, 51, 1367–1378. [Google Scholar]
- Russo, F. Technique for Image Denoising Based on Adaptive Piecewise Linear Filters and Automatic Parameter Tuning. IEEE Trans. Instrum. Meas 2006, 55, 1362–1367. [Google Scholar]
- Kwan, H.K.; Cai, Y. Fuzzy filters for image filtering. Proceedings of the International Symposium on Circuits and Systems, Aug. 2003; pp. 161–164.
- Schulte, S.; De Witte, V.; Kerre, E.E. A fuzzy noise reduction method for colour images. IEEE Trans. Image Process 2007, 16, 1425–1436. [Google Scholar]
- Bosco, A.; Findlater, K.; Battiato, S.; Castorina, A. Noise Reduction Filter for Full-Frame Imaging Devices. IEEE Trans. Consum. Electron 2003, 49, 676–682. [Google Scholar]
- Wandell, B. Foundations of Vision, 1st Edition ed; Sinauer Associates: Sunderland, Massachusetts, USA, 1995. [Google Scholar]
- Gonzales, R.; Woods, R. Digital Image Processing, 3rd Edition ed; Addison-Wesley: Reading, MA, 1992. [Google Scholar]
- Lian, N.; Chang, L.; Tan, Y.-P. Improved color filter array demosaicking by accurate luminance estimation. Proceedings of the IEEE International Conference on Image Processing (ICIP 2005), Genova, Italy, Sept. 2005; pp. 41–44.
- Chou, C-H.; Li, Y.-C. A perceptually tuned subband image coder based on the measure of just-noticeable-distortion profile. IEEE Trans. Circuits Syst. Video Technol 1995, 5, 467–476. [Google Scholar]
- Hontsch, I.; Karam, L.J. Locally adaptive perceptual image coding. IEEE Trans. Image Process 2000, 9, 1472–1483. [Google Scholar]
- Zhang, X.H.; Lin, W.S.; Xue, P. Improved estimation for just-noticeable visual distortion. Signal Process 2005, 85, 795–808. [Google Scholar]
- Foi, A.; Alenius, S.; Katkovnik, V.; Egiazarian, K. Noise measurement for raw-data of digital imaging sensors by automatic segmentation of non-uniform targets. IEEE Sensors J 2007, 7, 1456–1461. [Google Scholar]
- Foi, A.; Trimeche, M.; Katkovnik, V.; Egiazarian, K. Practical Poissonian-Gaussian Noise Modeling and Fitting for Single-Image Raw-Data. IEEE Trans. Image Process 2008, 17, 1737–1754. [Google Scholar]
- Kalevo, O.; Rantanen, H. Noise Reduction Techniques for Bayer-Matrix Images. Proceedings of SPIE Electronic Imaging, Sensors and Cameras Systems for Scientific, Industrial and Digital Photography Applications III, San Jose, CA, USA, Jan 2002; 4669.
- Smith, S.M.; Brady, J.M. SUSAN - A New Approach to Low Level Image Processing. Int. J. Comput. Vision 1997, 23, 45–78. [Google Scholar]
- Zhang, L.; Wu, X.; Zhang, D. Color Reproduction from Noisy CFA Data of Single Sensor Digital Cameras. IEEE Trans. Image Process 2007, 16, 2184–2197. [Google Scholar]
- Standard Kodak test images. http://r0k.us/graphics/kodak/.













© 2009 by the authors; licensee MDPI, Basel, Switzerland This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bosco, A.; Battiato, S.; Bruna, A.; Rizzo, R. Noise Reduction for CFA Image Sensors Exploiting HVS Behaviour. Sensors 2009, 9, 1692-1713. https://doi.org/10.3390/s90301692
Bosco A, Battiato S, Bruna A, Rizzo R. Noise Reduction for CFA Image Sensors Exploiting HVS Behaviour. Sensors. 2009; 9(3):1692-1713. https://doi.org/10.3390/s90301692
Chicago/Turabian StyleBosco, Angelo, Sebastiano Battiato, Arcangelo Bruna, and Rosetta Rizzo. 2009. "Noise Reduction for CFA Image Sensors Exploiting HVS Behaviour" Sensors 9, no. 3: 1692-1713. https://doi.org/10.3390/s90301692
APA StyleBosco, A., Battiato, S., Bruna, A., & Rizzo, R. (2009). Noise Reduction for CFA Image Sensors Exploiting HVS Behaviour. Sensors, 9(3), 1692-1713. https://doi.org/10.3390/s90301692