Intercomparison of Evapotranspiration Over the Savannah Volta Basin in West Africa Using Remote Sensing Data
Abstract
:1. Introduction
2. Materials and Methods
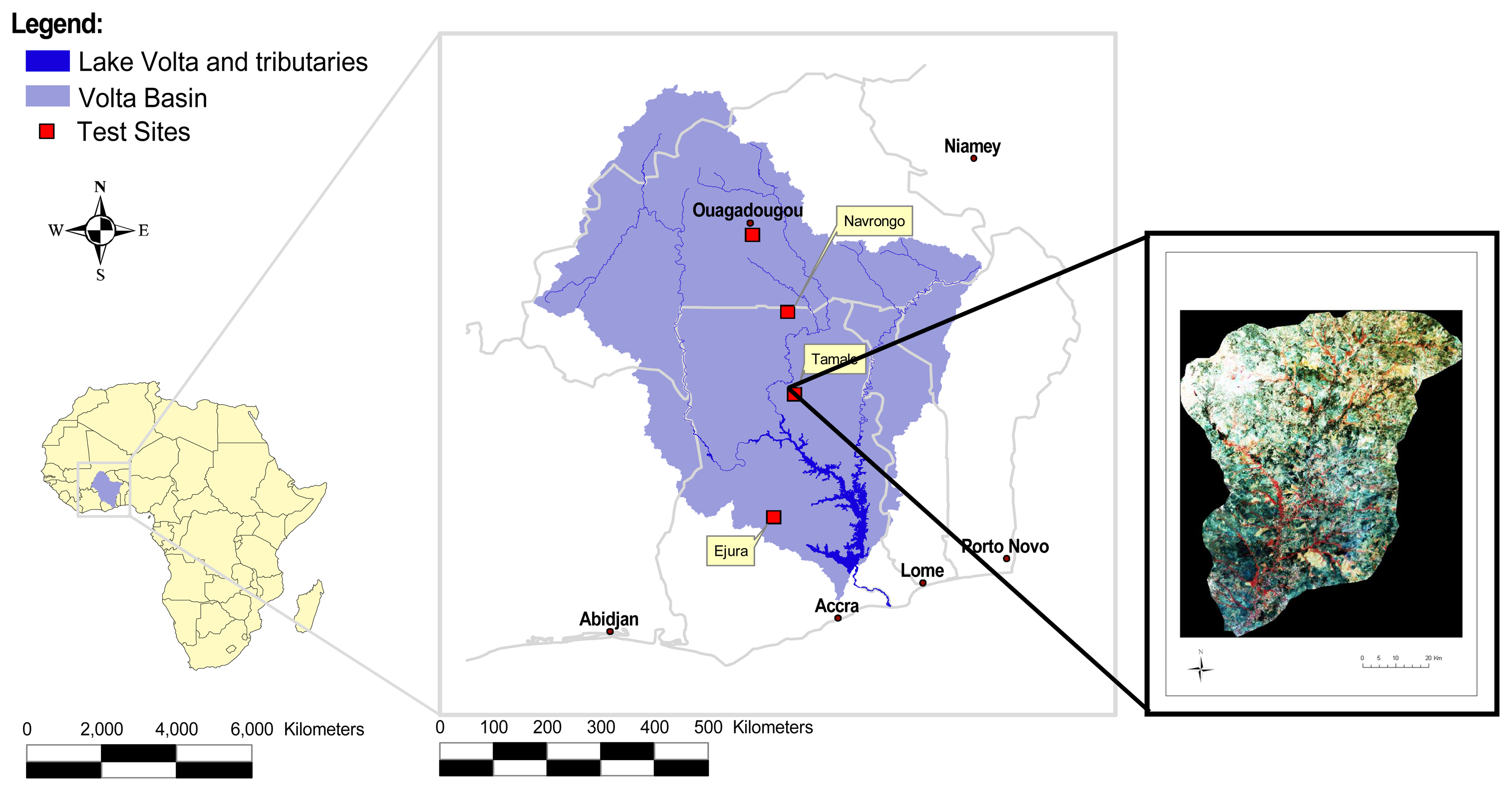
2.1. The Study Area
2.2. Data Sources
2.3. Study Methods
2.3.1. Image Processing
- The raw Level 1B AATSR images (Table 2) were first read using the Windows version of the European Space Agency (ESA) Basic ERS & ENVISAT AATSR and MERIS software (BEAM) ( http://www.brockmann-consult.de/beam/). The BEAM is a collection of executable tools and an application programming interface which have been developed to facilitate the utilisation, viewing and processing of ENVISAT data products. It is particularly useful for importing image data, visual interpretation, image geo-referencing, band arithmetic and image statistics.
- Brightness temperatures at the top of atmosphere (TB) were directly retrieved after running the BEAM software; the software automatically implements an inverted version of the Planck's equation where image radiances are converted to TB (see equation 1). The TB files were then exported and stored as GeoTIFF for further use.
- The raw Level 1B MODIS data (Table 2) were also read using NASA's HDF-EOS to GIS (HEG) conversion toolbox ( http://eosweb.1arc.nasa.gov/PRODOCS/misr/geotiff_tool.html). The HEG software is useful for image viewing, geo-referencing to standard projections such as UTM and data conversion to GeoTIFF.
- Examination of the MODIS header files enabled the retrieval of calibration constants from the reflectance (Bands 1 and 2) and radiance (Bands 31 and 32) files of the composite product. The reflectance and radiance values were then used as appropriate to calculate calibrated versions of time series data following NASA's re-calibration procedures described in the MODIS L1B Product User's Guide [16]. The inverted Planck's equation was then applied to convert the image radiances (L) of each of the thermal infrared bands (TIR) to TB following the approach of [20] (equation 1) and later used as model inputs for calculating Ts.
- To solve for equation 1 an ERDAS-Imagine based algorithm was applied for both the Landsat ETM+ scene (5th January 2004) and the MODIS time series data (Table 2).
- Further, ERDAS spatial modelling tools were used to calculate NDVI (normalized difference vegetation index) for the Landsat ETM+, MODIS and AATSR imagery using the equation below [21]:where NIR and R are light reflectance in the near infrared band and the red bands of the electromagnetic spectrum, respectively.
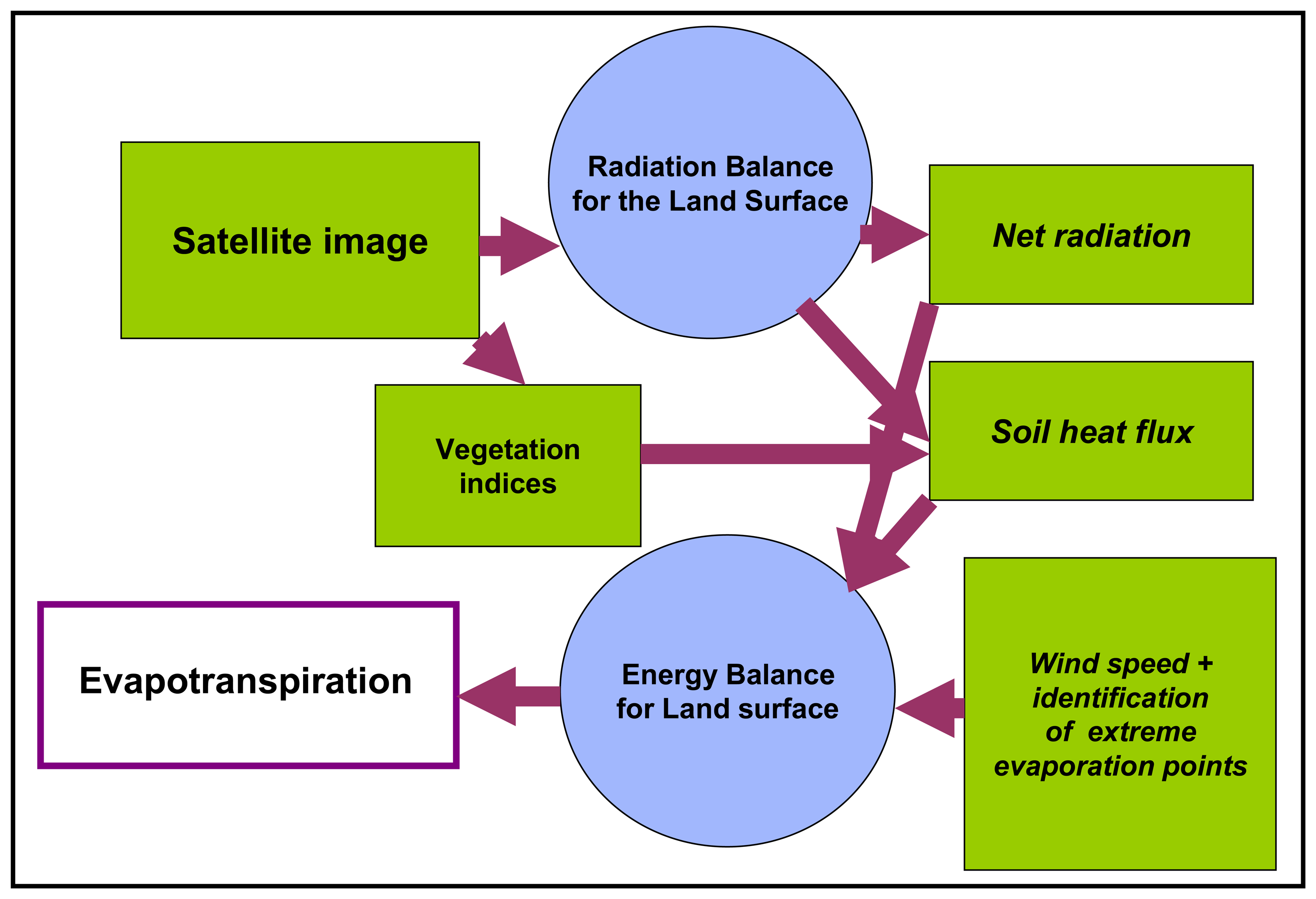
2.3.2 SEBAL Processing in MATLAB
Net Radiation (Rn)
Soil Heat Flux (G0)
Sensible Heat Flux (H)
Evapotranspiration (ET) Up-scaling Methods
Derivation of Land Surface Temperature (Ts)
3. Results and Discussion
3.1. Results
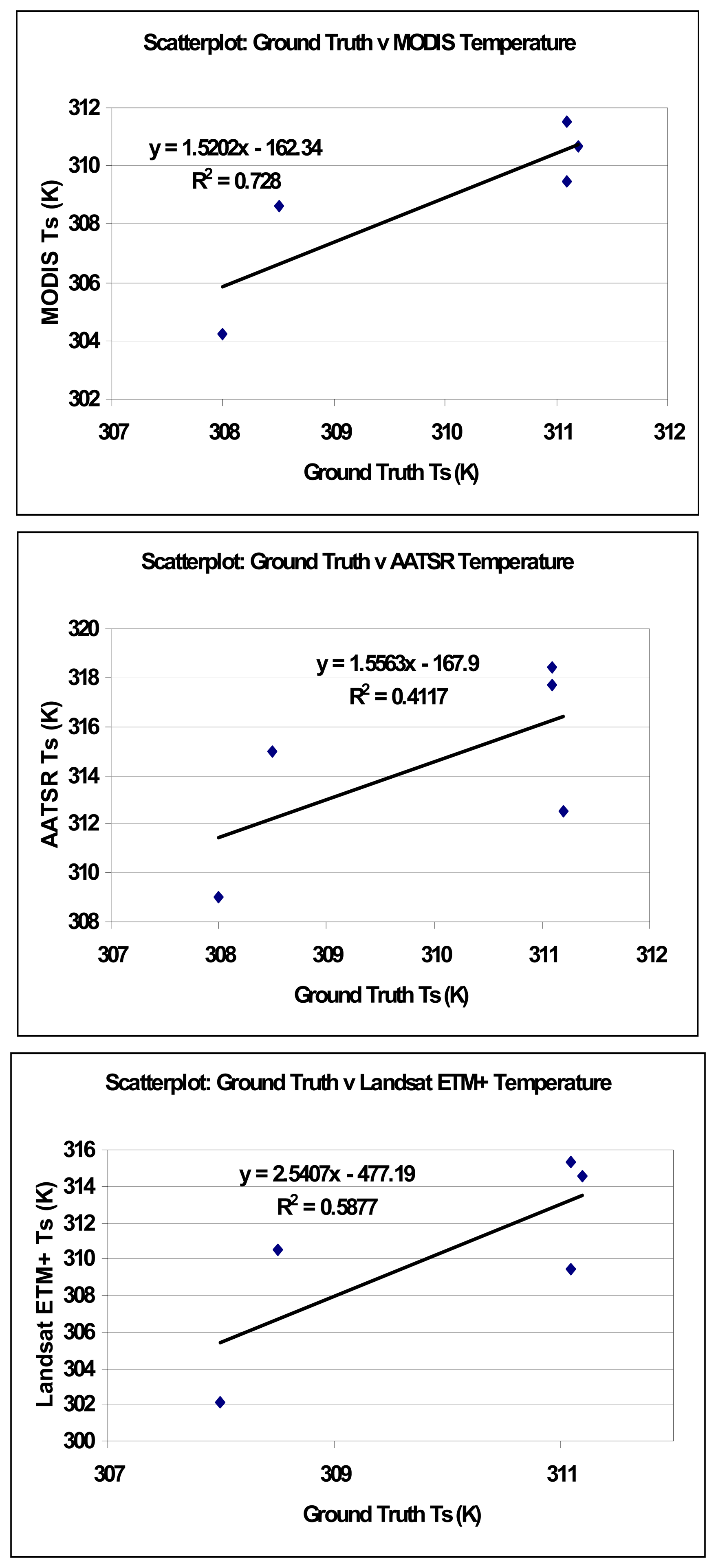
3.1.1. Sensor Intercomparison of Ts
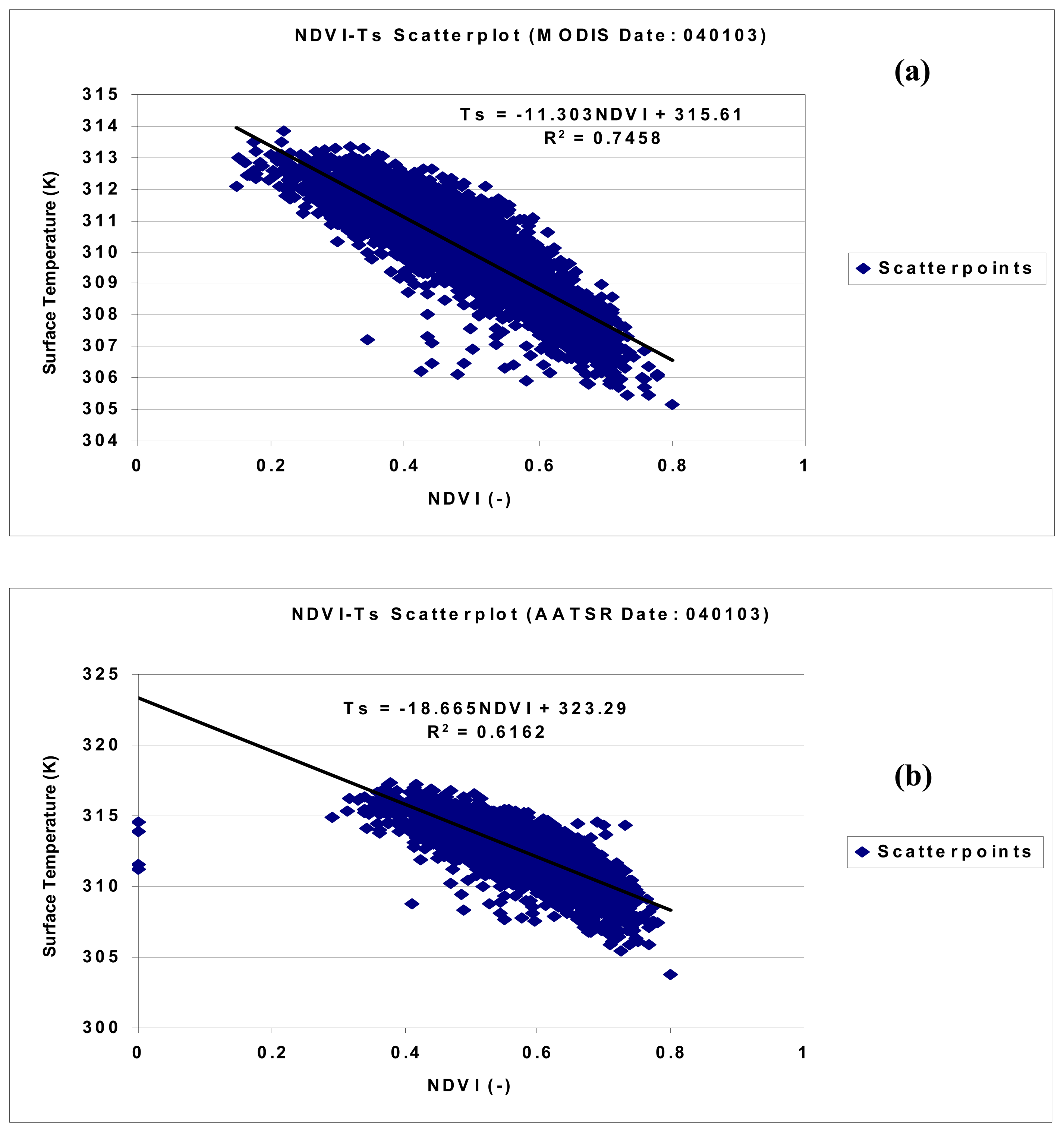
Sensor Intercomparison of NDVI
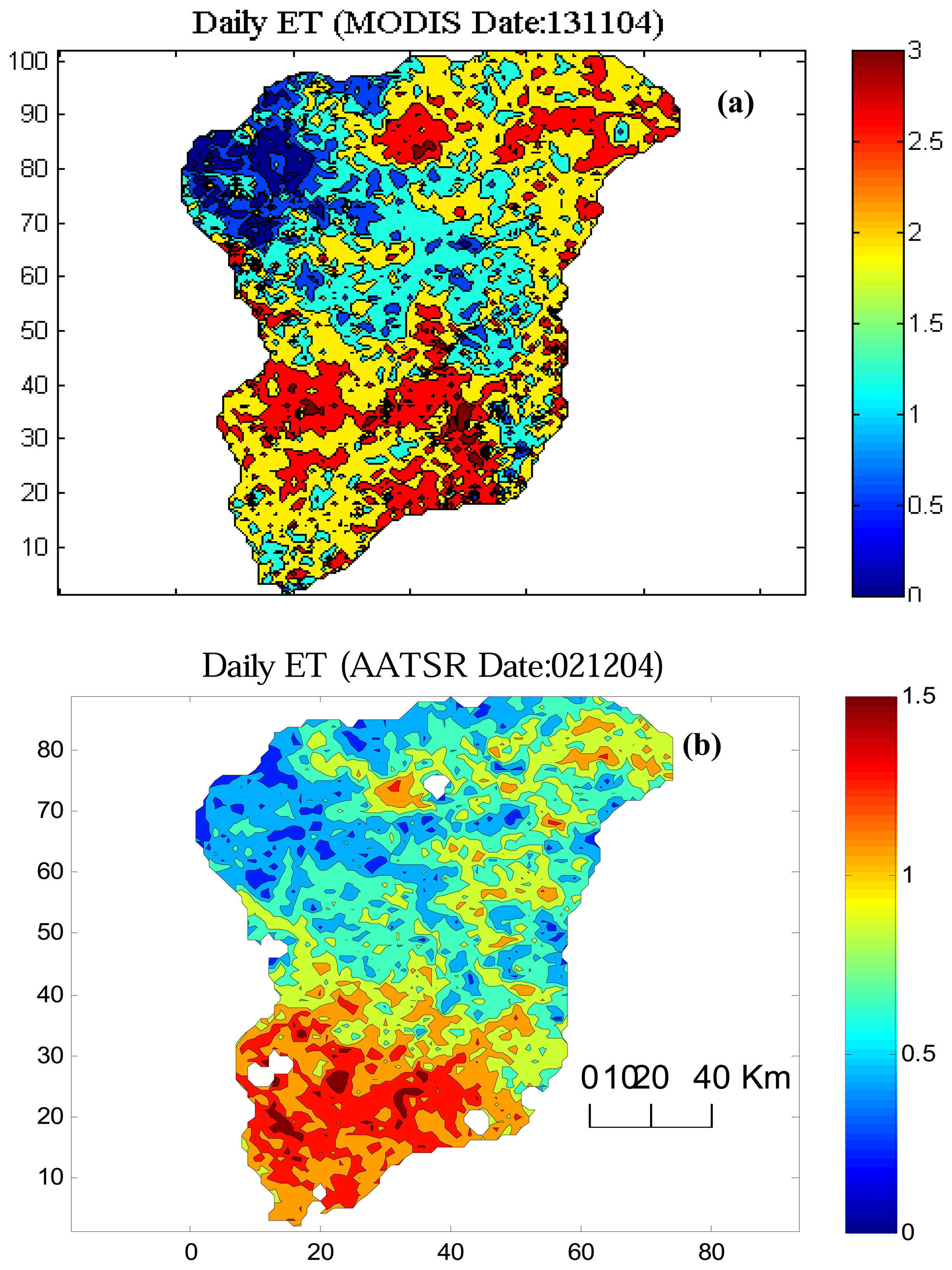
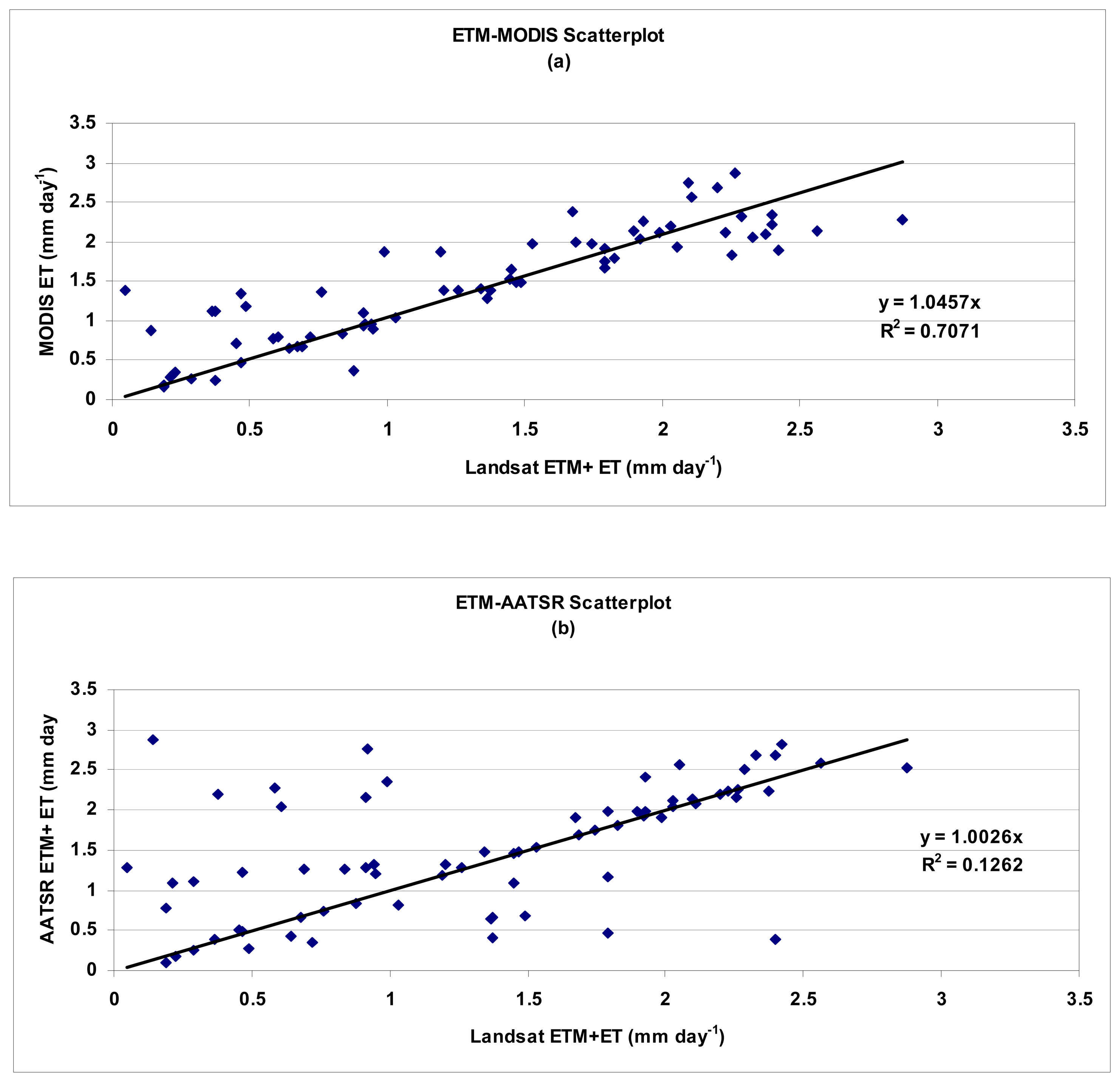
Sensor Intercomparison of ET
3.2. Discussion
4. Conclusion
Acknowledgments
References
- Washington, R.; Harrison, M.; Conway, D.; Black, E.; Challinor, A.; Grimes, D.; Jones, R.; Morse, A.; Kay, G.; Todd, M. African climate change: Taking the shorter route. BAMS 2006, 10, 1355–1365. [Google Scholar]
- Gyau-Boakye, P.; Timbulto, J.W. The Volta Lake and declining rainfall and streamflows in the Volta river basin. Environ. Dev. Sustainability 2000, 2, 1–10. [Google Scholar]
- Oguntunde, P.G. Evapotranspiration and complimentary relations in the water balance of the Volta basin: Field measurements and GIS-based regional estimates; Ecology and Development Series; Denich, M., Martius, C., van de Giesen, N., Eds.; Cuvillier Verlag: Göttingen, 2004; pp. 103–155. [Google Scholar]
- Bisht, G.; Venturini, V.; Jiang, L.; Islam, S. Estimation of the net radiation using MODIS data for clear-sky dates. Rem. Sens. Environ. 2005, 97, 52–97. [Google Scholar]
- Brata, N.; Islam, S.; Venturini, V.; Bisht, G.; Jiang, L. Estimation and comparison of evapotranspiration from MODIS and AVHRR sensors for clear sky days over the Southern Great Plains. Rem. Sens. Environ. 2006, 103, 1–15. [Google Scholar]
- Parks, S.; Feddema, J.J.; Egbert, S.L. MODIS land surface temperature composite data their relationships with climate water budget factors in the Central Great Plains. Int. J. Rem. Sens. 2005, 26(6), 1127–1144. [Google Scholar]
- Prata, F. Land surface temperature measurement from space: AATSR algorithm – Theoretical basis document.; Technical Report: 2002; CSIRO, Canberra: Australia.
- Sòria, G.; Sobrino, J.A. AATSR derived land surface temperature from heterogeneous areas. Proc. ESA's ENVISAT MERIS-AATSR workshop; Frascati, Italy, 2005; pp. 1–6. http://envisat.esa.int.
- Jiang, L.; Islam, S. An intercomparison of regional heat flux estimation using remote sensing data. Int. J. Rem. Sens. 2003, 24(11), 2221–2236. [Google Scholar]
- Günther, K.P.; Maier, S.W. AVHRR compatible vegetation index derived from MERIS data. Int. J. Rem. Sens. 2007, 24(3-4), 693–708. [Google Scholar]
- ZEF (Centre for Development Research). Ecology and Development Series: GLOWA-Volta Project, 1999-2005; Cuvelier Verlag: Göttingen, 2004. [Google Scholar]
- Nicholson, S.E.; Grist, J.P. A conceptual model for understanding rainfall variability in the West African Sahel interannual and interdecadal timescales. Int. J. Climatol. 2001, 21, 1733–1757. [Google Scholar]
- Ayibotele, N.B. Regional hydrology and water resources in the African humid tropics. In Hydrology and water management in the humid tropics.; Bonnel, M., Hufschmidt, M.M., Gladwell, J.S., Eds.; University Press: Cambridge, 1993; pp. 112–134. [Google Scholar]
- Ghana Meteorological Services Department (MSD). Daily rainfall and temperature records over the Volta basin in Ghana, 1961- 2000; July 2004; pp. 22–134. [Google Scholar]
- Prince, S.D.; Kerr, Y.H.; Goutorbe, T.; Lebel, J-P.; Tinga, A.; Bessemoulin, P.; Brouwer, J.; Dolman, A.J.; Engman, E.T.; Gash, J.C.H. Geographical, biological and remote sensing aspects of the Hydrological Atmospheric Pilot Experiment in the Sahel (HAPEX-Sahel). Rem. Sens. Environ. 1995, 51, 215–234. [Google Scholar]
- MODIS Characterization Support Team (MCST). MODIS LUT Information Guide For Level 1B; MCST Internal Memorandum # M1036, 1 December 2003. The latest release is available on-line at http://www.mcst.ssai.biz/mcstweb/L1B/product.html.
- Wan, Z. MODIS land surface temperature validation. The Earth Obs. 1999, 11(3), 29–31. [Google Scholar]
- Opoku-Duah, S. Remote Sensing of Energy and Water Fluxes over Volta Savannah Catchments in West Africa. Unpublished Ph.D. Thesis, Durham University, UK, 2007; pp. 123–222. [Google Scholar]
- Donoghue, D.N.M. Remote Sensing: sensors and applications. Prog. Phys. Geogr. 2000, 24(3), 407–414. [Google Scholar]
- Price, J.C. Land surface temperature measurements from split window channels of the NOAA-7 Advanced Very High Resolution Radiometer. J. Geophys. Res. 1984, D5(89), 7231–7237. [Google Scholar]
- Goetz, S.J. Multi-sensor analysis of NDVI, surface temperature and biophysical variables at a mixed grassland site. Int. J. Rem. Sens. 1987, 18(1), 71–94. [Google Scholar]
- Bastiannssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL) – Part 1: Formulation. J. Hydrol. 1998, 228, 198–212. [Google Scholar]
- Bastiaanssen, W.G.M.; Pelgrum, H.; Wang, J.; Ma, J.; Moreno, J.; Roerink, G.J.; Van Der Wal, T. (1998) The Surface Energy Balance Algorithm for Land (SEBAL): Part 2 validation. J. Hydrol. 1998, 228, 213–229. [Google Scholar]
- Morse, A.; Tasumi, M.; Allen, R.G.; Kramber, W.J. Application of the SEBAL Methodology for Estimating Consumptive Use of Water and Streamflow Depletion in the Bear River Basin of Idaho through Remote Sensing. In Final Project Report; 2000; The Raytheon Systems Company: Idaho, USA; pp. 1–107. [Google Scholar]
- FAO. Evapotranspiration Guidelines for computing crop water requirements. In UN-FAO, Irrigation & Drainage Paper No. 56; Land and Water Division, FAO Press: Rome, 1998; pp. 107–288. [Google Scholar]
- Chen, T.S.; Ohring, G. On the relationship between clear-sky planetary and surface albedos: a parameterization for simple energy balance climate models. Adv. Space Res. 1985, 5(6), 41–144. [Google Scholar]
- Mekonnen, S.C. Assessment of catchment water balance using GIS and Remote Sensing: Roxo Portugal. Unpublished MSc. Thesis, ITC-Enschede, The Netherlands, 2005; pp. 1–39. [Google Scholar]
- van de Griend, A.A.; Owe, M. On the relationship between thermal emissivity and the normalized difference vegetation index for natural surfaces. Int. J. Rem. Sens. 1993, 14(6), 1119–1131. [Google Scholar]
- Prata, F. Land surface temperatures derived from the Advanced Very High Resolution Radiometer and the Along-Track Scanning Radiometer. J. Geophys. Res. 1994, 99, 13–25. [Google Scholar]
- Sellers, P.J. Canopy reflectance, photosynthesis and transpiration. Int. J. Rem. Sens. 1985, 6(8), 1335–1372. [Google Scholar]
- Sobrino, J.A.; Jiménez-Muńoz, J.C. Land surface temperature retrieval from thermal infrared data: An assessment in the context of the surface processes and ecosystem changes through response analysis (SPECTRA) mission. J. Geophy. Res. 2005, 110, D16103, doi: 1029/2004JD005588. [Google Scholar]
- Salomonson, V.V.; Barnes, W. L.; Xiong, X.; Kempler, S.; Masuoka, E. An Overview of the Earth Observing System MODIS Instrument and Associated Data Systems Performance. In Proceedings of IGARSS; Barnes, T.G., Ed.; Chicago, 2002; pp. 23–31. [Google Scholar]
- El Maayar, M.; Chen, J.M. Spatial scaling of evapotranspiration as affected by heterogeneities in vegetation, topography and soil texture. Rem. Sens. Environ. 2006, 102, 33–51. [Google Scholar]

| Data Monitoring Station | Geographical location | Country | Ecological zone | Mean annual rainfall (mm) | Mean annual evapotran-spiration (mm) | Mean annual temp. (0C) | Period of climate records | |
|---|---|---|---|---|---|---|---|---|
| Lat. | Lon. | |||||||
| Niamey | 130 48′N | 20 16′ W | Niger | Sahel savannah | 560 | 2000 | 36.0 | 1905-1989 |
| Koro | 120 46′N | 70 49′ W | Mali | Sahel savannah | 522 | 2041 | 36.8 | 1971-1990 |
| Bobo Dioulasso | 110 16′N | 40 31′ W | Burkina Faso | Sudan savannah | 759 | 1958 | 31.5 | 1971-2000 |
| Tamale | 9025′N | 0050′W | Ghana | Guinea savannah | 1087 | 1650 | 28.2 | 1961-2000 |
| Axim | 50 09′N | 20 57′ W | Ghana | Forest | 2148 | 1315 | 25.8 | 1961-2000 |
| Image Date | Satellite overpass (UTC) | Orbit | Track | Frame | Central coordinates | |
|---|---|---|---|---|---|---|
| Lat | Lon | |||||
| AATSR Sensor | ||||||
| 040103 | 10:13:07 - 10:14:43 | 4441 | 380 | 3500 | 90 51′N | 10 58′W |
| 131104 | 10:04:47 - 10:06:23 | 14146 | 65 | 3500 | 90 18′N | 00 04E |
| 021204 | 10:07:35 - 10:09:11 | 14418 | 337 | 3500 | 90 36′N | 00 35′W |
| 181204 | 10:04:44 - 10:06:20 | 14647 | 65 | 3500 | 90 19′N | 00 04′E |
| 250105 | 10:10:25 - 10:12:01 | 15191 | 108 | 3500 | 90 37′N | 10 18′W |
| MODIS Sensor | ||||||
| 040103 | 10:25:00 - 10:30:00 | 16209 | - | - | 90 51′N | 010 58′W |
| 131104 | 10:30:00 - 10:35:00 | 26097 | - | - | 30 54′N | 000 530E |
| 021204 | 11:00:00 - 11:05:00 | 26374 | - | - | 60 83′N | 070 510E |
| 181204 | 11:00:00 - 11:00:00 | 26607 | - | - | 70 91′N | 070 320E |
| 250105 | 10:25:00 - 10:30:00 | 27160 | - | - | 90 37′N | 010 18′W |
| Landsat ETM+ | ||||||
| 050104 | 10:40:00 - 10:41:00 | - | 194 | 53 | 100 06′N | 000 36′W |
| Logger A | Logger B | Logger C | Logger D | Logger E | |
|---|---|---|---|---|---|
| Date: 131104 | |||||
| Time 10:12 | 309.19 | 310.21 | 309.19 | 308.72 | 307.58 |
| 10.32 | 309.27 | 310.32 | 309.97 | 308.86 | 307.97 |
| 11:12 | 309.27 | 310.29 | 309.92 | 308.45 | 308.49 |
| Av. Temp (K) | 309.24 | 310.29 | 309.69 | 308.68 | 307.95 |
| Date: 021204 | |||||
| Time 10:12 | 312.67 | 312.08 | 312.39 | 308.11 | 307.88 |
| 10.32 | 312.98 | 312.21 | 312.33 | 308.07 | 307.70 |
| 11:12 | 312.98 | 312.29 | 312.38 | 308.64 | 308.66 |
| Av. Temp (K) | 312.88 | 312.19 | 312.37 | 308.27 | 308.08 |
| Table 3b. Geographical locations of the thermal loggers. | ||||
|---|---|---|---|---|
| Geographical description (see Fig 2) | Latitude (0N) | Longitude (0W) | Land cover class | |
| Logger A | North-west | 090 26′ | 000 51′ | Urban |
| Logger B | North-east | 090 28′ | 000 26′ | Grassland-bush |
| Logger C | Central | 090 14′ | 000 37′ | Agriculture |
| Logger D | East | 090 04′ | 000 28′ | Open Woodland |
| Logger E | South | 080 56′ | 000 50′ | Closed Woodland |
| Data source | Spatial resolution (m) | Spectral range (μm) | |||
|---|---|---|---|---|---|
| *VIS | NIR band | MIR band | TIR band | ||
| Landsat ETM+ | 30 (15m for panchromatic and 60m for thermal band) | Band1 (0.45-0.52) | Band4 (0.76-0.90) | Band5 (1.55- 1.75) | Band6 (10.4-12.50) |
| Band2 (0.52-0.60) | |||||
| Band3 (0.63-0.69) | Band7 (2.08- 2.35) | ||||
| Pan (0.5-0.90) | |||||
| ENVISAT AATSR Level 1B | 1km | Band1 (0.545-0.565) | Band3 (0.855-0.875) | Band4 (1.580-1.640) | Band5 (3.50-3.89) |
| Band2 (0.649-0.669) | Band6 (10.40-11.30) | ||||
| Band7 (11.50-12.50) | |||||
| MODIS Level 1B | 250 (500m for bands 3-7) and 1000m for bands 8-36) | Band1 (0.62-0.670) | Band2 (0.84-0.87) | Band6 (1.628-1.652) | Band20 (3.66-3.84) |
| Band3 (0.46-0.48) | Band5 (1.23-2.50) | Band21 (3.92-3.98) | |||
| Band4 (0.55-0.57) | Band15(0.74-0.75) | Band7 (2.105-2.155) | Band22 (3.92-3.98) | ||
| Band8 (0.41-0.42) | Band16(0.86-0.87) | Band23 (4.02-4.08) | |||
| Band9 (0.44-0.45) | Band17(0.89-0.92) | Band26 (1.36-1.39) | Band24 (4.43-4.49) | ||
| Band10 (0.44-0.49) | Band18(0.93-0.94) | Band25 (4.48-4.54) | |||
| Band11 (0.53-0.54) | Band19(0.91-0.96) | Band31 (10.78-11.28) | |||
| Band12 (0.55-0.56) | Band32 (11.77-12.27) | ||||
| Band13(0.66-0.67) | |||||
| Band14 (0.67-0.68) | |||||
| Data Type | Use of the Data | |
|---|---|---|
| Satellite data | MODIS/AATSR time series | The MODIS and AATSR provided the key instantaneous data needed for energy and water balance modelling (net radiation, NDVI, BT) |
| imagery A Landsat ETM+ scene acquired on 5th January 2004 | The Landsat image also provided energy balance modelling data. In addition, it was used for a detailed land use/cover classification and ET maps for other purposes: (1) a guide for fieldwork; (2) to map wet and evaporation points to guide SEBAL-based energy balance modelling; and (3) as a source of validation for MODIS & AATSR ET estimates | |
| Satellite- based intermediate parameters | Brightness temperatures (TB) | TB was derived from satellite data. It served as the main intermediate data for deriving Ts using the split-window algorithm [8] |
| Local and global climate records | Radiation data and constants (e.g. US Navy website) | Radiation constants e.g. sunshine duration (n=12-14) were used as input data to: (1) validate satellite radiation measurements; and (2) up-scale instantaneous to daily net radiation (see equation 20). |
| Local wind speed (u) | Wind speed was used as a source of momentum data for SEBAL-based energy balance modelling | |
| Local air temperature (Ta) | Ta was used as a data source for the prediction of pixel-based Ta in equation 18. | |
| Data from fieldwork | HOBO logger temperatures | Field temperatures were used as a source of SEBAL initialization and validation data for satellite-based temperature estimates |
| ET validation data | GLOWA-Volta field data | The GLOWA data was used as one of the main sources validation for satellite-derived net radiation and energy fluxes (e.g. ET) |
| Penman-Monteith estimates (Tamale district) | The Penman-Monteith estimates were used as additional source of validation data for satellite-based ET | |
| Date of image acquisition [Julian day] | Landsat ETM+ | MODIS | AATSR | ||||
|---|---|---|---|---|---|---|---|
| 050104 [05] | 131104 [318] | 021204 [337] | 250105 [25] | 131104 [318] | 021204 [337] | 250105 [25] | |
| Land Surface Temperature (Ts) | |||||||
| Maximum | 312.451 | 309.476 | 309.650 | 310.390 | 317.037 | 323.089 | 322.356 |
| Minimum | 286.318 | 302.078 | 302.616 | 306.691 | 308.623 | 308.750 | 312.347 |
| Mean | 301.869 | 304.383 | 306.217 | 308.586 | 312.463 | 318.970 | 319.050 |
| Std. Deviation | 7.091 | 1.594 | 1.999 | 0.965 | 1.871 | 2.890 | 1.882 |
| NDVI | |||||||
| Maximum | 0.809 | 0.727 | 0.720 | 0.661 | 0.751 | 0.701 | 0.693 |
| Minimum | 0.025 | 0.387 | 0.326 | 0.312 | 0.519 | 0.461 | 0.488 |
| Mean | 0.521 | 0.620 | 0.566 | 0.489 | 0.639 | 0.587 | 0.582 |
| Std. Deviation | 0.083 | 0.066 | 0.079 | 0.068 | 0.045 | 0.074 | 0.046 |
| Daily Evapotrans piration (ET 24) | |||||||
| Maximum | 8.510 | 2.297 | 3.082 | 2.831 | 0.987 | 1.471 | 0.706 |
| Minimum | 0.000 | 0.020 | 0.025 | 0.904 | 0.000 | 0.300 | 0.000 |
| Mean | 3.102 | 0.918 | 1.469 | 2.052 | 0.283 | 0.965 | 0.170 |
| Std. Deviation | 1.424 | 0.609 | 0.840 | 0.400 | 0.213 | 0.282 | 0.140 |
| Date of image acquisition [Julian day] | MODIS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 131104 [318] | 021204 [337] | 250105 [25] | ||||||||
| 11μm | 12μm | 11μm | 12μm | 11μm | 12μm | |||||
| Maximum | 301.8 | 299.3 | 303.2 | 301.6 | 309.1 | 306.3 | ||||
| Minimum | 281.4 | 289.8 | 291.6 | 294.3 | 298.0 | 299.9 | ||||
| Mean | 296.0 | 292.0 | 299.3 | 292.7 | 302.2 | 300.8 | ||||
| Std. Deviation | 1.231 | 1.032 | 0.853 | 1.110 | 1.543 | 1.276 | ||||
| AATSR | ||||||||||
| 131104 [318] | 021204 [337] | 250105 [25] | ||||||||
| 11μm | 12μm | 11μm | 12μm | 11μm | 12μm | |||||
| Maximum | 303.2 | 297.6 | 314.8 | 312.2 | 317.7 | 313.3 | ||||
| Minimum | 292.6 | 289.2 | 299.6 | 298.4 | 307.7 | 302.8 | ||||
| Mean | 298.9 | 294.8 | 305.0 | 303.3 | 309.1 | 304.7 | ||||
| Std. Deviation | 1.055 | 0.807 | 2.276 | 2.078 | 1.441 | 1.511 | ||||
| Landsat ETM+(10.4-12.5 μm) | ||||||||||
| 050104 [05] | ||||||||||
| Maximum | 309.990 | |||||||||
| Minimum | 283.720 | |||||||||
| Mean | 293.719 | |||||||||
| Std. Deviation | 7.691 | |||||||||
| Method | Scale | Range | Mean | Standard deviation |
|---|---|---|---|---|
| Penman-Monteith | Local (Tamale) | 1.53 – 4.87 | 3.90 | 0.66 |
| Scintillometer | Local (Tamale) | - | 1.79 | - |
| Landsat ETM+ | Regional | 0.15 – 2.93 | 2.10 | 0.42 |
| MODIS | Regional | 0.05 – 2.83 | 2.07 | 0.37 |
| AATSR | Regional | 0.01 – 2.09 | 1.21 | 0.86 |
© 2008 by MDPI (http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Opoku-Duah, S.; Donoghue, D.N.M.; Burt, T.P. Intercomparison of Evapotranspiration Over the Savannah Volta Basin in West Africa Using Remote Sensing Data. Sensors 2008, 8, 2736-2761. https://doi.org/10.3390/s8042736
Opoku-Duah S, Donoghue DNM, Burt TP. Intercomparison of Evapotranspiration Over the Savannah Volta Basin in West Africa Using Remote Sensing Data. Sensors. 2008; 8(4):2736-2761. https://doi.org/10.3390/s8042736
Chicago/Turabian StyleOpoku-Duah, S., D. N.M. Donoghue, and T. P. Burt. 2008. "Intercomparison of Evapotranspiration Over the Savannah Volta Basin in West Africa Using Remote Sensing Data" Sensors 8, no. 4: 2736-2761. https://doi.org/10.3390/s8042736
APA StyleOpoku-Duah, S., Donoghue, D. N. M., & Burt, T. P. (2008). Intercomparison of Evapotranspiration Over the Savannah Volta Basin in West Africa Using Remote Sensing Data. Sensors, 8(4), 2736-2761. https://doi.org/10.3390/s8042736





