Improving Distributed Runoff Prediction in Urbanized Catchments with Remote Sensing based Estimates of Impervious Surface Cover
Abstract
:1. Introduction
2. Study area and data
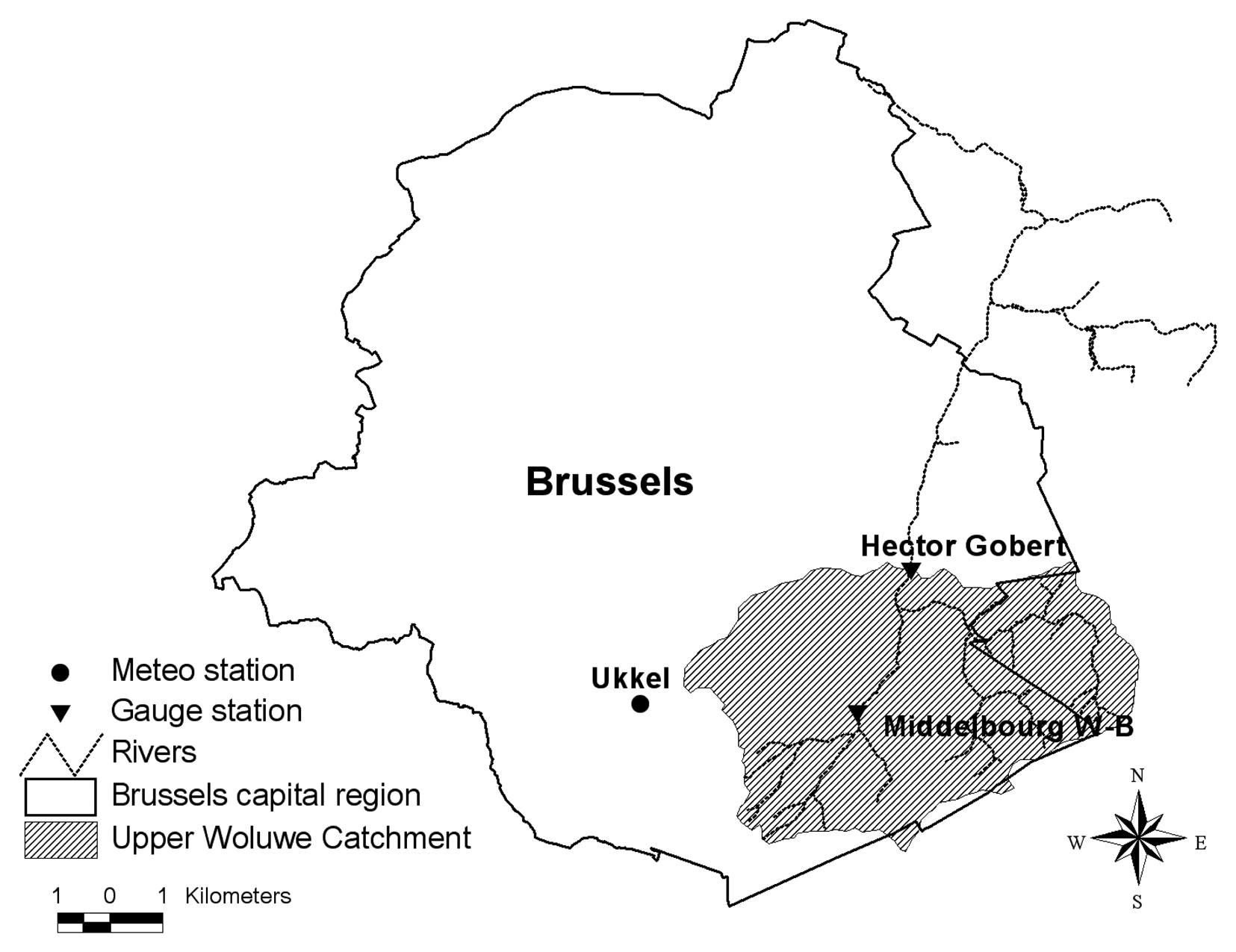
2.1. Study area
2.2. Remote sensing data
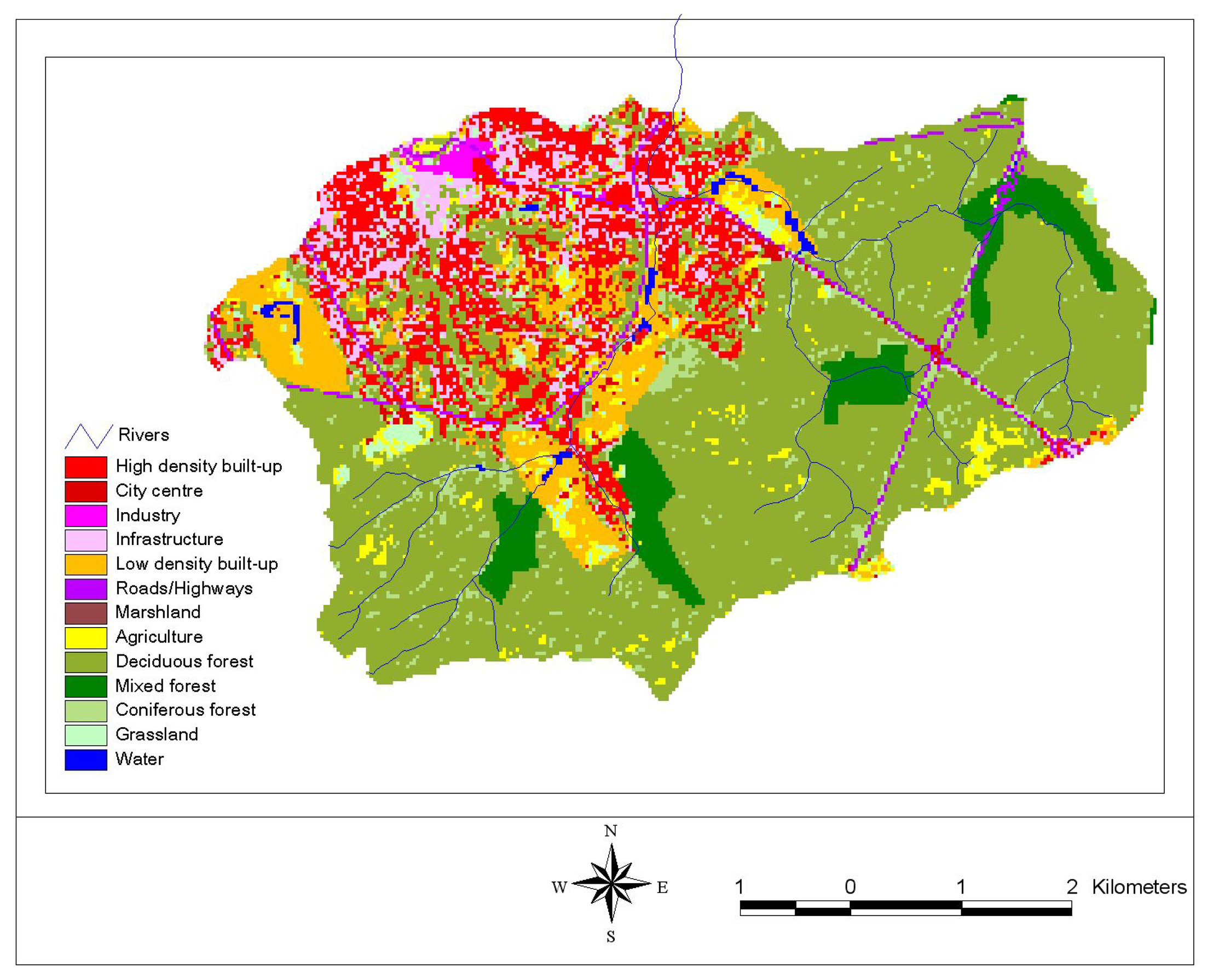
2.3. Land-use, DEM and soil data
2.4. Hydrometeorological data
3. Methods
3.1. Hydrological modelling
3.2. Estimation of impervious surface cover
3.2.1. High-resolution land-cover mapping
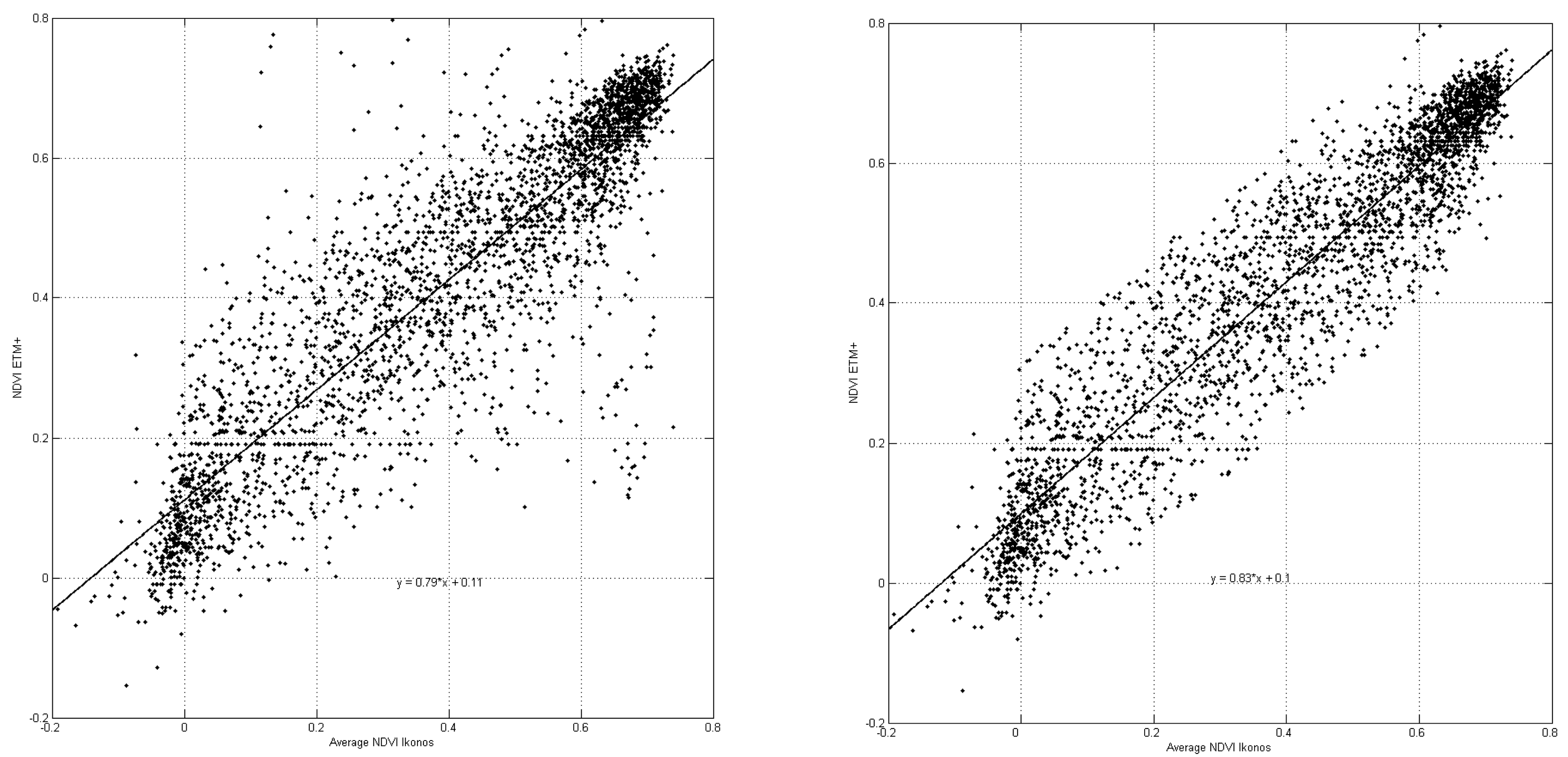
3.2.2. Subpixel classification of Landsat ETM+ imagery
- N: the total number of pixels in the validation sample
- Cj: target class j
- Pij: the proportion of class j inside validation pixel i, derived from the high-resolution land-cover map (ground truth)
- P′ij: the proportion of class j inside validation pixel i, estimated by the sub-pixel classifier
3.3. Formulation of scenarios
3.3.1. Scenario 1: Homogeneous distribution of impervious surfaces (non-distributed approach)
3.3.2. Scenario 2: Land-use specific distribution of impervious surfaces (semi-distributed approach)
3.3.3. Scenario 3: Cell-specific distribution of impervious surfaces (fully-distributed approach)
4. Results and discussion
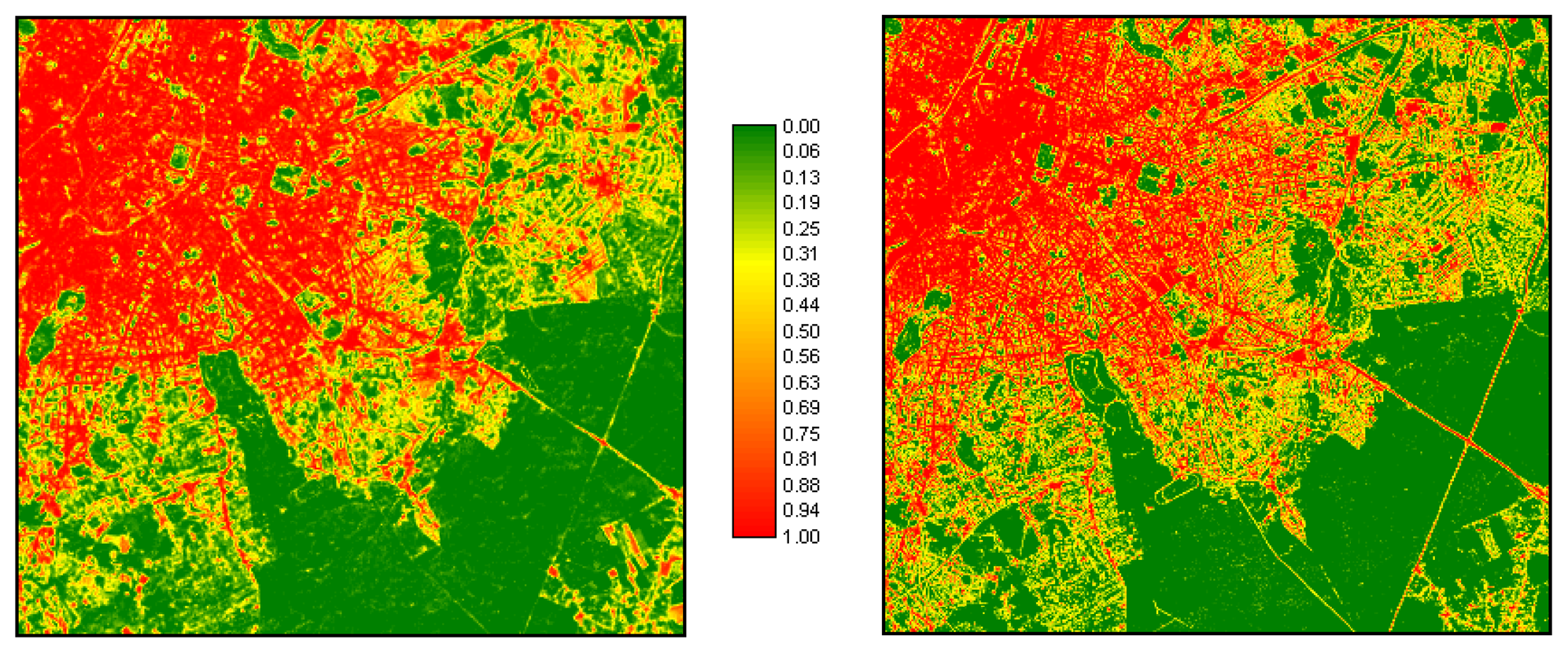
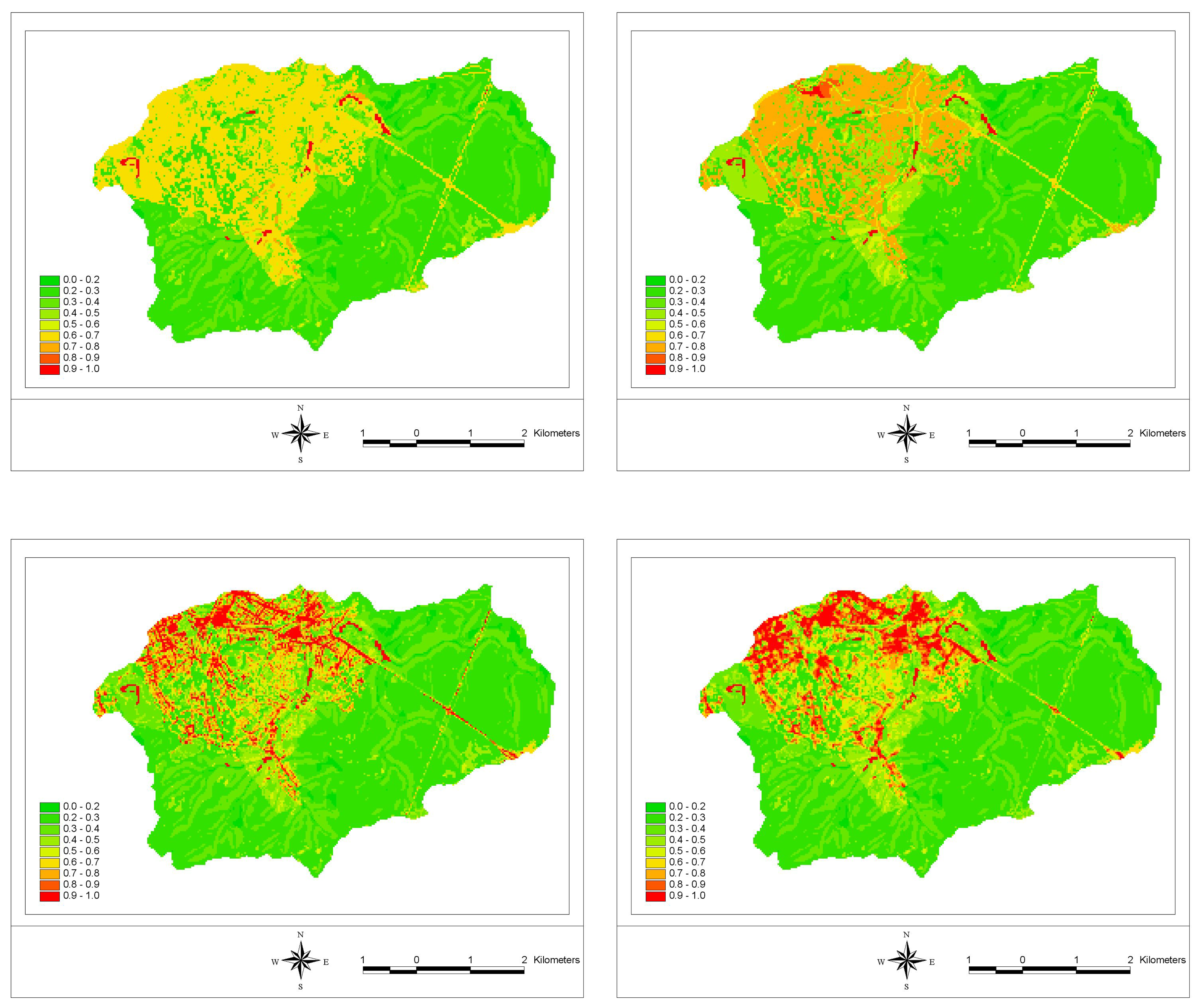
4.1. Estimation of impervious surface cover
4.1.1. High-resolution land-cover mapping
4.1.2. Temporal filtering
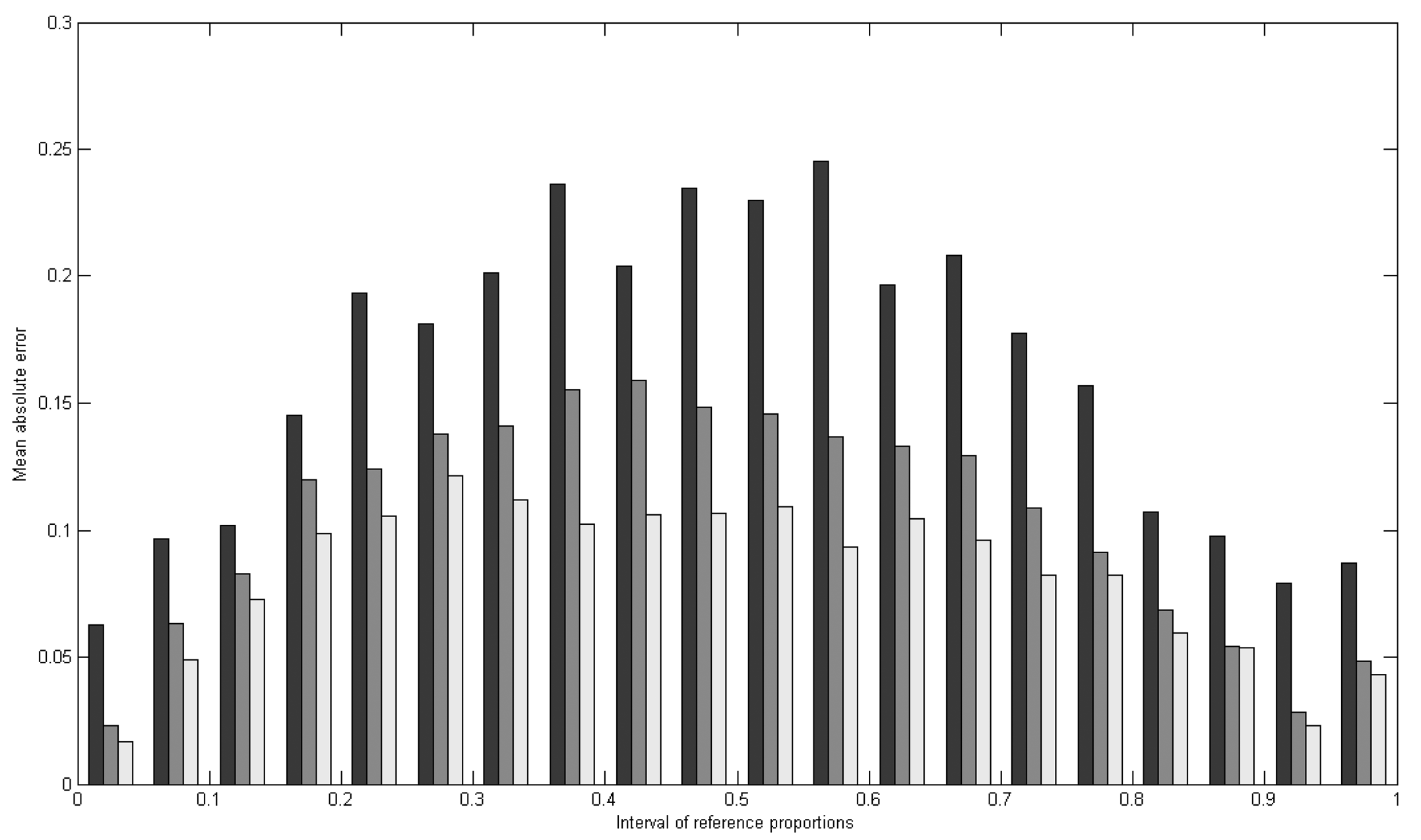
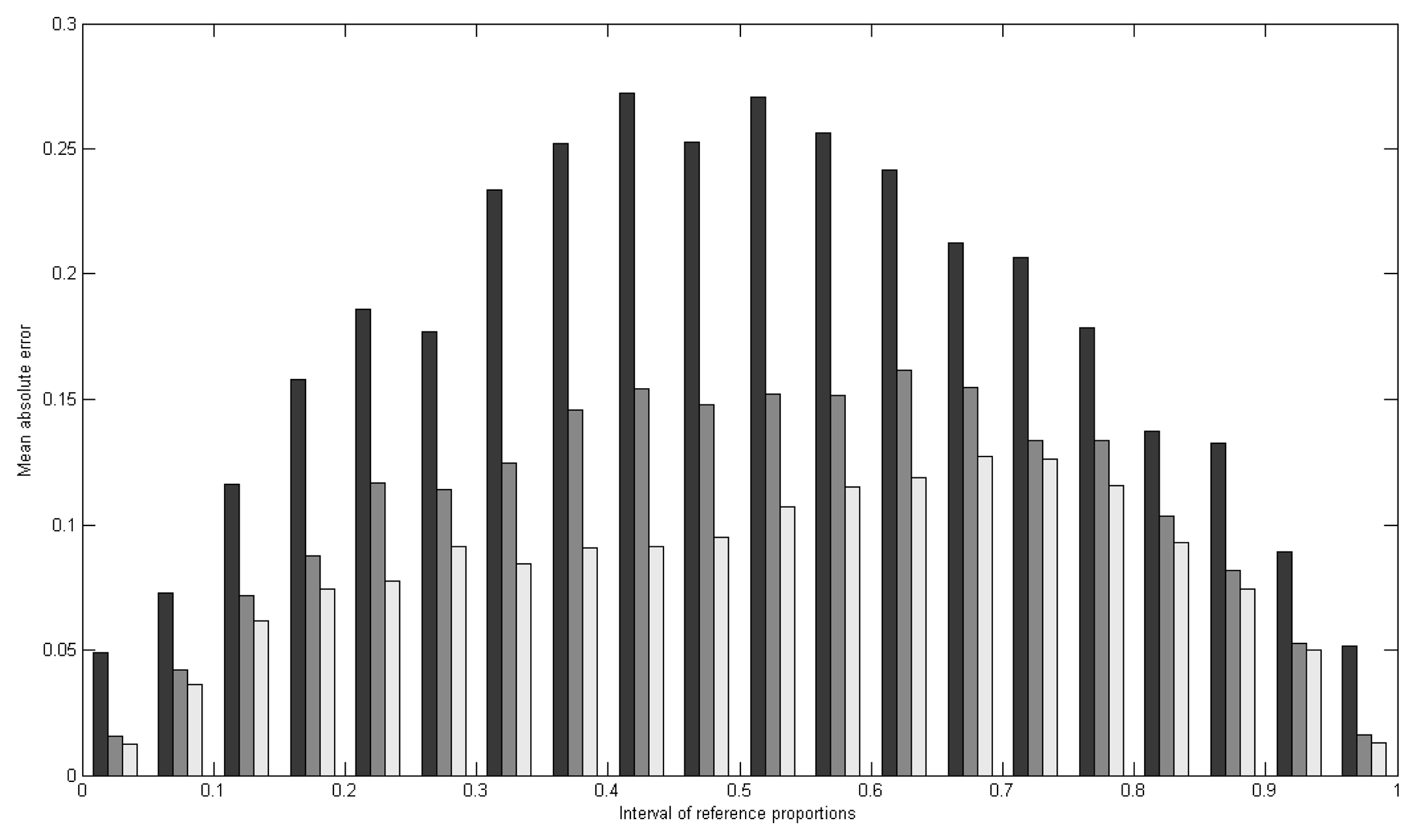
4.1.3. Sub-pixel classification
4.2 Hydrological modelling
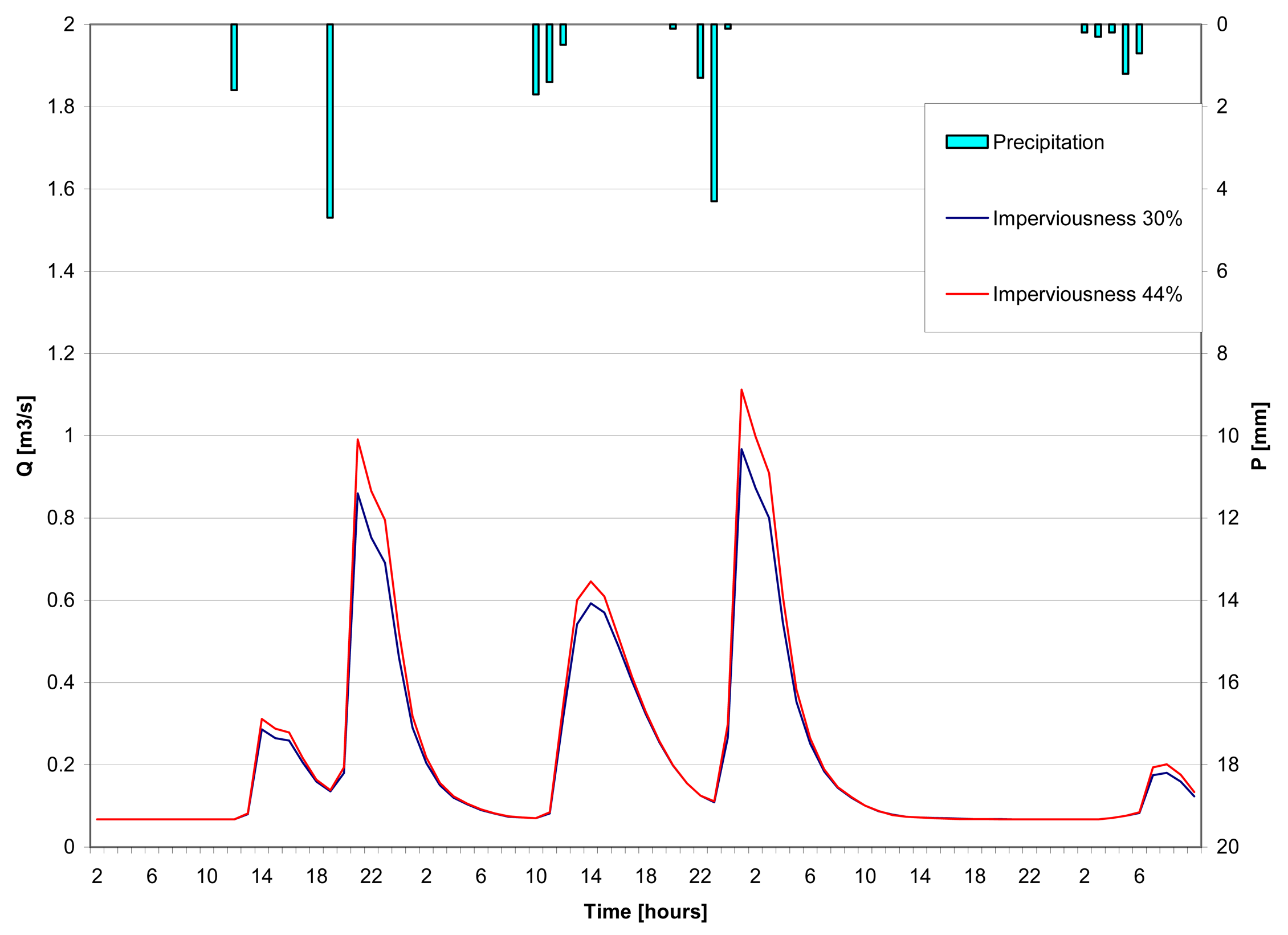
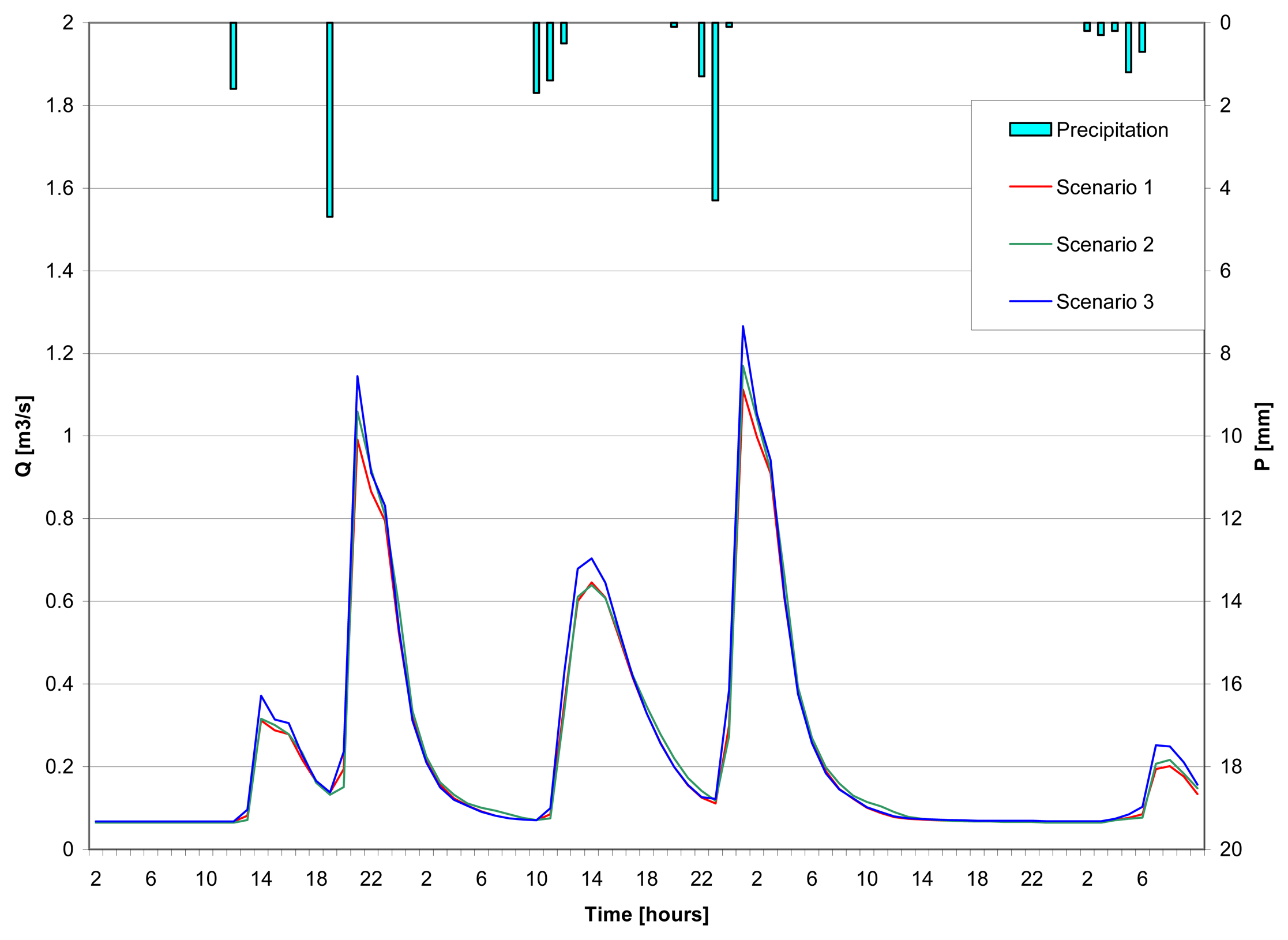
4.2.1 Scenario 1: non-distributed approach
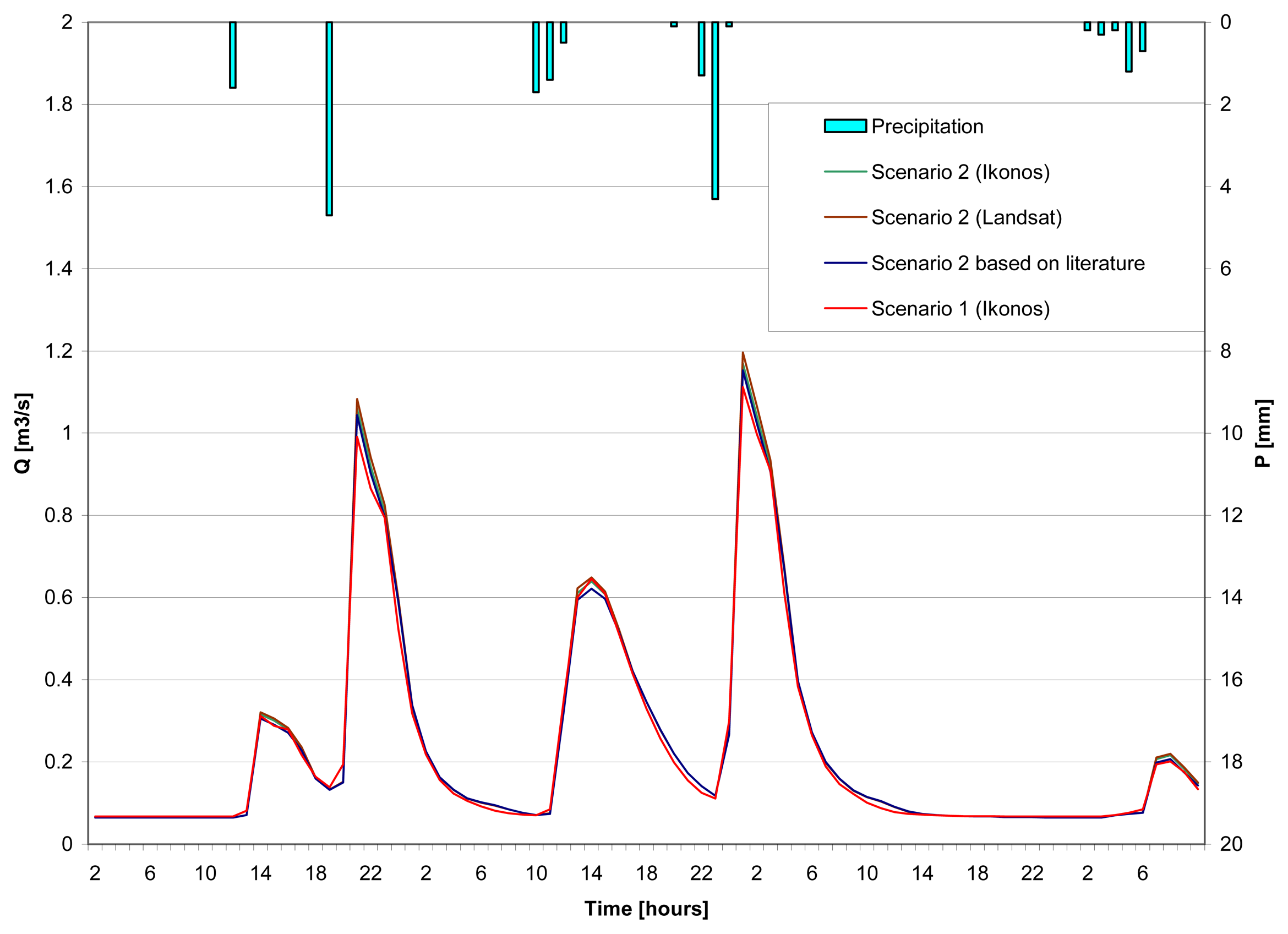
4.2.2 Scenario 2: semi-distributed approach
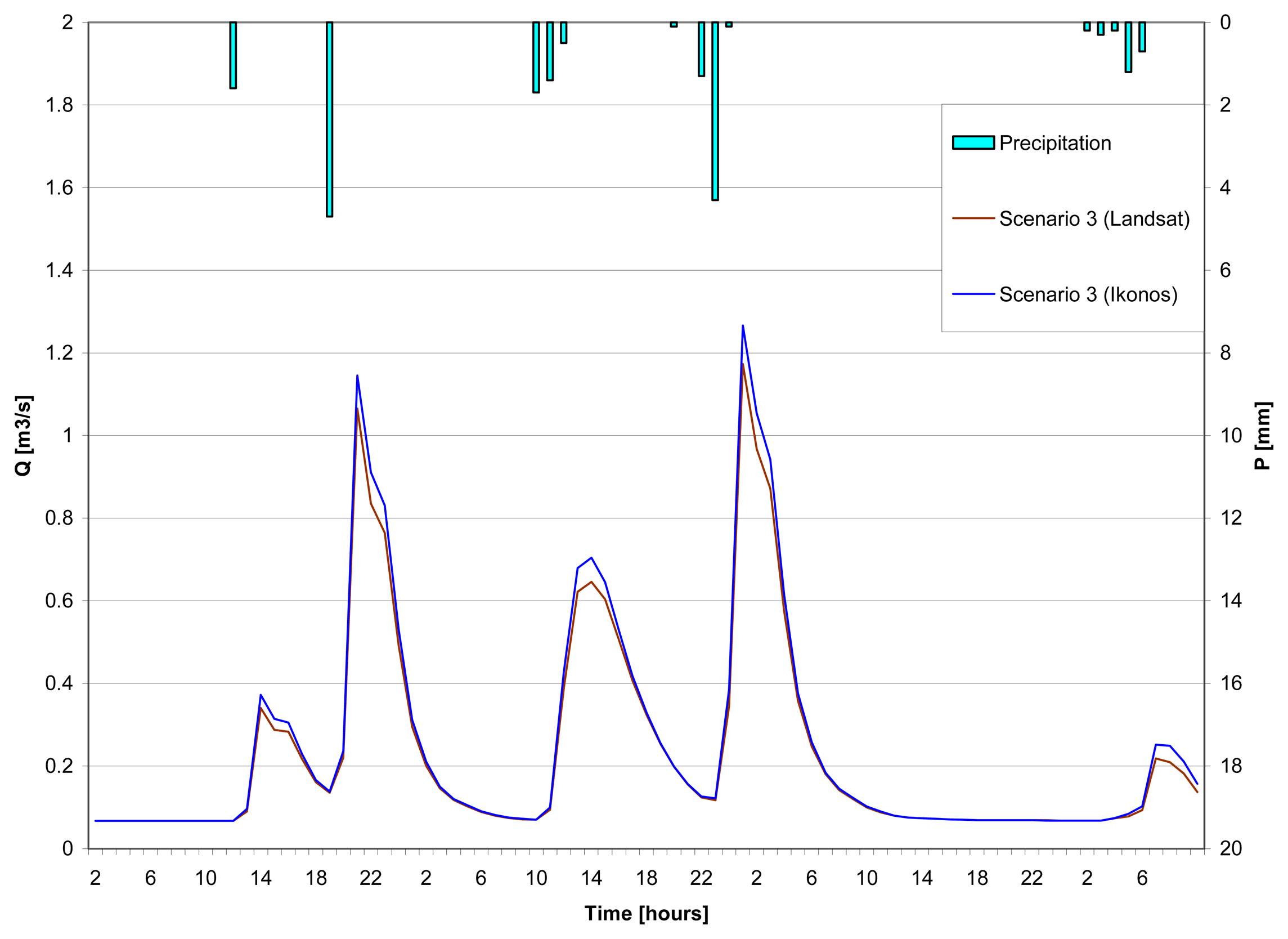
4.2.3 Scenario 3: fully-distributed approach
5. Conclusions
Acknowledgments
References
- Arnold, J.G.; Srinivasan, S.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment. Part I: Model development. Journal of the American Water Resources Association. 1998, 34, 73–87. [Google Scholar]
- Downer, C.W.; Ogden, F.L.; Martin, W.; Harmon, R.S. Theory, development, and applicability of the surface water hydrologic model CASC2D. Hydrol. Process. 2002, 16, 255–275. [Google Scholar]
- Borah, D.K.; Xia, R.; Bera, M. DWSM - A dynamic watershed simulation model. In Mathematical Models of Small Watershed Hydrology and Applications; Singh, V.P., Freyert, D.K., Eds.; Water Resources Publications, LLC: Highlands Ranch, Colorado, 2002; pp. 113–166. [Google Scholar]
- Fortin, J.P.; Turcotte, R.; Massicotte, S.; Moussa, R.; Fitzback, J.; Villeneuve, J.P. A distributed watershed model compatible with remote sensing and GIS data, I: Description of the model. J. Hydrological Eng. ASCE. 2001, 6, 91–99. [Google Scholar]
- Quinn, P.; Beven, K.; Chevallier, P.; Planchon, O. The prediction of hillslope flow paths for distributed hydrological modeling using digital terrain models. Hydrol. Process. 1991, 5, 59–79. [Google Scholar]
- Ewen, J.; Parkin, G.; O'Connell, P.E. SHETRAN: distributed river basin flow and transport modeling system. J. Hydrologic Eng. ASCE. 2000, 5, 250–258. [Google Scholar]
- Behera, S.; Panda, R.K. Evaluation of management alternatives for an agricultural watershed in a sub-humid subtropical region using a physical process based model. Agriculture, Ecosystems and Environment. 2006, 113, 62–72. [Google Scholar]
- Van Der Sande, C.J.; de Jong, S.M.; de Roo, A.P.J. A segmentation and classification approach of IKONOS-2 imagery for land cover mapping to assist flood risk and flood damage assessment. Int. Journal of Applied Earth Observation and Geoinformation. 2003, 4, 217–229. [Google Scholar]
- King, C.; Lecomte, V.; Le Bissonnais, Y.; Baghdadi, N.; Souchère, V.; Cerdan, O. Remote-sensing data as an alternative input for the dSTREAMT runoff model. Catena. 2005, 62, 125–135. [Google Scholar]
- Brivio, P.A.; Colombo, R.; Maggi, M.; Tomasoni, R. Integration of remote sensing data and GIS for accurate mapping of flooded areas. International Journal of Remote Sensing. 2002, 23, 429–441. [Google Scholar]
- Islam, M.; Sado, K. Development priority map for flood countermeasures by remote sensing data with geographic information system. Journal of Hydrologic Engineering. 2002, 7, 346–355. [Google Scholar]
- Chormański, J.; Mirosław-Świątek, D.; Okruszko, T. Remote sensing limitation in flood modeling verification in wetlands. In Model Application for Wetlands Hydrology and Hydraulics; Kubrak, J., Okruszko, T., Ignar, S., Eds.; Warsaw Agricultural Press: Warsaw, 2004; pp. 51–72. [Google Scholar]
- Baumgartner, M.F.; Apfl, G. Towards an integrated geographic analysis system with remote sensing, GIS and consecutive modeling for snow cover monitoring. International Journal of Remote Sensing. 1994, 15, 1507–1518. [Google Scholar]
- Tait, A.B.; Hall, D.K.; Foster, J.L.; Armstring, R.L. Utilizing multiple datasets for snow-cover mapping. Remote Sensing of Environment. 2000, 72, 111–126. [Google Scholar]
- Biftu, G.F.; Gan, T.Y. Semi-distributed, physically based, hydrologic modeling of the Paddle River Basin, Alberta, using remotely sensed data. Journal of Hydrology. 2001, 244, 137–156. [Google Scholar]
- Kim, G.; Barros, A.P. Space-time characterization of soil moisture from passive microwave remotely sensed imagery and ancillary data. Remote Sensing of Environment. 2002, 81, 393–403. [Google Scholar]
- Boegh, E.; Thorsen, M.; Butts, M.B.; Hansen, S.; Christiansen, J.S.; Abrahamsen, P.; Hasager, C.B.; Jensen, N.O.; van der Keura, P.; Refsgaard, J.C.; Schelde, K.; Soegaard, H.; Thomsen, A. Incorporating remote sensing data in physically based distributed agro-hydrological modelling. Journal of Hydrology. 2004, 287, 279–299. [Google Scholar]
- Chen, J.M.; Chen, X.; Ju, W.; Geng, X. Distributed hydrologic model for mapping evapotranspiration using remote sensing inputs. Journal of Hydrology. 2005, 305, 15–39. [Google Scholar]
- Schueler, T.R. The importance of imperviousness. Watershed Protection Techniques. 1994, 1, 100–110. [Google Scholar]
- Arnold, C.A., Jr; Gibbons, C.J. Impervious surface coverage: the emergence of a key urban environmental indicator. Journal of the American Planning Association. 1996, 62, 243–258. [Google Scholar]
- Sleavin, W.J.; Civco, D.L.; Prisloe, S.; Gianotti, L. Measuring impervious surfaces for nonpoint source pollution modeling. Proceedings of the ASPRS 2000 Annual Conference, Washington, Dc, 22-26 April; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, 2000. unpaginated CD-ROM. [Google Scholar]
- Prisloe, M.; Gianotti, L.; Sleavin, W. Determining impervious surfaces for watershed modeling applications. Proceedings of the 8th National Nonpoint Source Monitoring Workshop, Hartford, Connecticut, 10-14 September; 2000. [Google Scholar]
- Cain, A. The usefulness of impervious cover mapping and analysis based on pre-existing classified land use datasets. Proceedings of the 2004 IMAGIN Annual Conference, East Lansing, Michigan; 2004. Available online at: http://www.imagin.org/awards/sp2004/Cain.pdf.
- Yang, X.; Liu, Z. Use of satellite-derived landscape imperviousness index to characterize urban spatial growth. Computers, Environment and Urban Systems. 2005, 29, 524–540. [Google Scholar]
- Ji, M.; Jensen, J.R. Effectiveness of subpixel analysis in detecting and quantifying urban imperviousness from Landsat Thematic Mapper imagery. Geocarto International. 1999, 14, 33–41. [Google Scholar]
- Phinn, S.; Stanford, M.; Scarth, P.; Murray, A.T.; Shyy, T. Monitoring the composition and form of urban environments based on the vegetation–impervious surface–soil (VIS) model by sub-pixel analysis techniques. International Journal of Remote Sensing. 2002, 23, 4131–4153. [Google Scholar]
- Wu, C.; Murray, A.T. Estimating impervious surface distribution by spectral mixture analysis. Remote Sensing of Environment. 2003, 84, 493–505. [Google Scholar]
- Lu, D.; Weng, Q. Spectral mixture analysis of the urban landscapes in Indianapolis with Landsat ETM+ imagery. Photogrammetric Engineering and Remote Sensing. 2004, 70, 1053–1062. [Google Scholar]
- Flanagan, M.; Civco, D.L. Subpixel impervious surface mapping. Proceedings of the ASPRS 2001 Annual Conference, St. Louis, MO, 23-27 April; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, 2001. unpaginated CD-ROM. [Google Scholar]
- Wang, Y.; Zhang, X. A SPLIT model for extraction of subpixel impervious surface information. Photogrammetric Engineering and Remote Sensing 2004, 70, 821–828. [Google Scholar]
- Huang, C.; Townshend, J.R.G. A stepwise regression tree for nonlinear approximation: applications to estimating subpixel land cover. International Journal of Remote Sensing. 2003, 24, 75–90. [Google Scholar]
- Yang, L.; Huang, C.; Homer, C.G.; Wylie, B.K.; Coan, M.J. An approach for mapping large-area impervious surfaces: synergistic use of Landsat-7 ETM+ and high spatial resolution imagery. Canadian Journal of Remote Sensing. 2003, 29, 230–240. [Google Scholar]
- Xian, G. Assessing urban growth with sub-pixel impervious surface coverage. In Urban Remote Sensing; Weng, Q., Quattrochi, D.A., Eds.; Taylor & Francis Group: Boca Raton, FL, 2006; p. 179. [Google Scholar]
- Hutchinson, M.F. A new procedure for gridding elevation and stream linear data with automatic removal of spurious sinks. Journal of Hydrology. 1989, 106, 211–232. [Google Scholar]
- Wang, Z.; Batelaan, O.; De Smedt, F. A distributed model for Water and Energy Transfer between Soil, Plants and Atmosphere. Phys. Chem. Earth. 1996, 21, 189–193. [Google Scholar]
- De Smedt, F.; Liu, Y.B.; Gebremeskel, S. Hydrologic modeling on a catchment scale using GIS and remote sensed land use information. In Risk Analysis II; Brebbia, C.A., Ed.; WTI press: Southampton, Boston, 2000; pp. 295–304. [Google Scholar]
- Liu, Y.B.; De Smedt, F.; Pfister, L. Flood prediction with the WetSpa model on catchment scale. In Flood Defence ‘2002; Wu, et al., Eds.; Science Press: New York, 2002; pp. 499–507. [Google Scholar]
- Linsley, R.K.J.; Kohler, M.A.; Paulhus, J.L.H. Hydrology for Engineers, 3rd Ed. ed; McGraw-Hill: New York, 1982; p. 237. [Google Scholar]
- Thornthwaite, C. W.; Mather, J. R. The water balance. In Laboratory of Climatology Publ; No 8, Centerton, NJ, 1955. [Google Scholar]
- Wittenberg, H; Sivapalan, M. Watershed groundwater balance estimation using streamflow recession analysis and baseflow separation. Journal of Hydrology. 1999, 219, 20–33. [Google Scholar]
- Murphy, D.L. Estimating neighborhood variability with a binary comparison matrix. Photogrammetric Engineering and Remote Sensing. 1985, 51, 667–674. [Google Scholar]
- Van de Voorde, T.; De Genst, W.; Canters, F. Improving pixel-based VHR land-cover classifications of urban areas with post-classification techniques. Photogrammetric Engineering and Remote Sensing. 2007, 73, 1017–1027. [Google Scholar]
- Taylor, M. Ikonos Planetary Reflectance and Mean Solar Exoatmospheric Irradiance; Space Imaging Inc.: Thornton, Colorado, 2005. URL: http://www.spaceimaging.com/whitepapers_pdfs/Esun1.pdf.
- Irish, R.R. Landsat 7 Science Data Users Handbook. Report 430-15-01-003-0; National Aeronautics and Space Administration, Goddard Space Flight Center: Maryland, 2000. URL: http://ltpwww.gsfc.nasa.gov/IAS/handbook/handbook_toc.html.
- Liu, Y.B.; De Smedt, F. Flood modeling for complex terrain using GIS and remote sensed information. Water Resources Management. 2005, 19, 605–624. [Google Scholar]
- Liu, Y.B. Development and Application of a GIS-based Hydrological Model for Flood Prediction. PhD. Thesis, Vrije Universiteit Brussel, Belgium, Brussel, 2004; p. 315. [Google Scholar]
- Van de Voorde, T.; Chormanski, J.; Batelaan, O.; Canters, F. Multi-resolution impervious surface mapping for improved runoff estimation at catchment level. Proceedings of the 1st Workshop of the EARSeL Special Interest Group on Urban Remote Sensing: Urban remote sensing, challenges and solutions, Berlin, Germany, March 2-3; 2006. [Google Scholar]
- NeuralWare. NeuralWorks Predict: The Complete Solution for Neural Data Modeling - User Guide; NeuralWare: Carnegie, PA, 2007. [Google Scholar]
- Van de Voorde, T.; De Roeck, T.; Canters, F. A comparison of two spectral mixture modelling approaches for impervious surface mapping in urban areas. International Journal of Remote Sensing. accepted.
| Ground truth | Sum | User's accuracy | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Red | Bare | Water | Grass | Crops | Trees | Grey | ||||
| Classification | Red | 87 | 87 | 1.000 | ||||||
| Bare | 1 | 146 | 1 | 1 | 149 | 0.980 | ||||
| Water | 1 | 59 | 5 | 65 | 0.908 | |||||
| Grass | 1 | 278 | 51 | 7 | 337 | 0.825 | ||||
| Crops | 172 | 172 | 1.000 | |||||||
| Trees | 6 | 2 | 346 | 354 | 0.977 | |||||
| Grey | 2 | 1 | 797 | 800 | 0.996 | |||||
| Sum | 88 | 154 | 60 | 285 | 225 | 354 | 803 | |||
| Producer's accuracy | 0.987 | 0.980 | 0.983 | 0.975 | 0.764 | 0.978 | 0.993 | kappa = 0.947 | ||
| Mean error (MECj) | Mean absolute error (MAECj) | |||||||
|---|---|---|---|---|---|---|---|---|
| Cell size | Impervious | Vegetation | Bare soil | Water | Impervious | Vegetation | Bare soil | Water |
| 30m | -0.018 | 0.015 | -0.049 | 0.011 | 0.1030 | 0.1017 | 0.0593 | 0.0166 |
| 60m | -0.017 | 0.014 | -0.048 | 0.011 | 0.0752 | 0.0720 | 0.0514 | 0.0152 |
| 90m | -0.019 | 0.015 | -0.045 | 0.011 | 0.0611 | 0.0590 | 0.0467 | 0.0153 |
| Land-use class | Default degree of imperviousness | Ikonos-derived value | Landsat-derived value |
|---|---|---|---|
| Low density built-up | 0.30 | 0.12 | 0.12 |
| High density built-up | 0.50 | 0.57 | 0.61 |
| City centre | 0.70 | 0.45 | 0.38 |
| Infrastructure | 0.50 | 0.58 | 0.60 |
| Roads/Highways | 0.50 | 0.36 | 0.31 |
| Industry | 0.70 | 0.84 | 0.86 |
© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Chormanski, J.; Van de Voorde, T.; De Roeck, T.; Batelaan, O.; Canters, F. Improving Distributed Runoff Prediction in Urbanized Catchments with Remote Sensing based Estimates of Impervious Surface Cover. Sensors 2008, 8, 910-932. https://doi.org/10.3390/s8020910
Chormanski J, Van de Voorde T, De Roeck T, Batelaan O, Canters F. Improving Distributed Runoff Prediction in Urbanized Catchments with Remote Sensing based Estimates of Impervious Surface Cover. Sensors. 2008; 8(2):910-932. https://doi.org/10.3390/s8020910
Chicago/Turabian StyleChormanski, Jaroslaw, Tim Van de Voorde, Tim De Roeck, Okke Batelaan, and Frank Canters. 2008. "Improving Distributed Runoff Prediction in Urbanized Catchments with Remote Sensing based Estimates of Impervious Surface Cover" Sensors 8, no. 2: 910-932. https://doi.org/10.3390/s8020910
APA StyleChormanski, J., Van de Voorde, T., De Roeck, T., Batelaan, O., & Canters, F. (2008). Improving Distributed Runoff Prediction in Urbanized Catchments with Remote Sensing based Estimates of Impervious Surface Cover. Sensors, 8(2), 910-932. https://doi.org/10.3390/s8020910




