Study of the origin of bending induced by bimetallic effect on microcantilever
Abstract
:1. Introduction
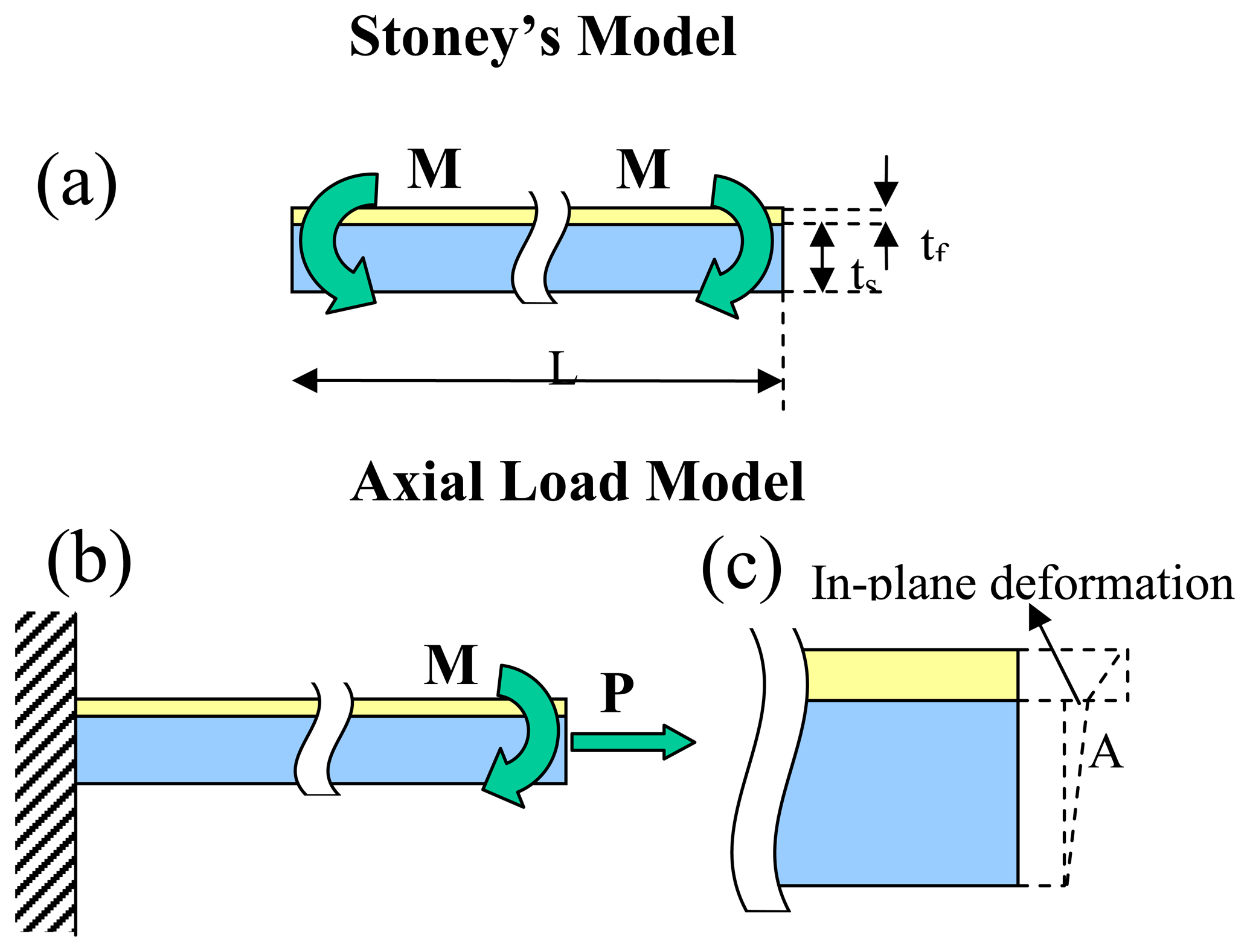
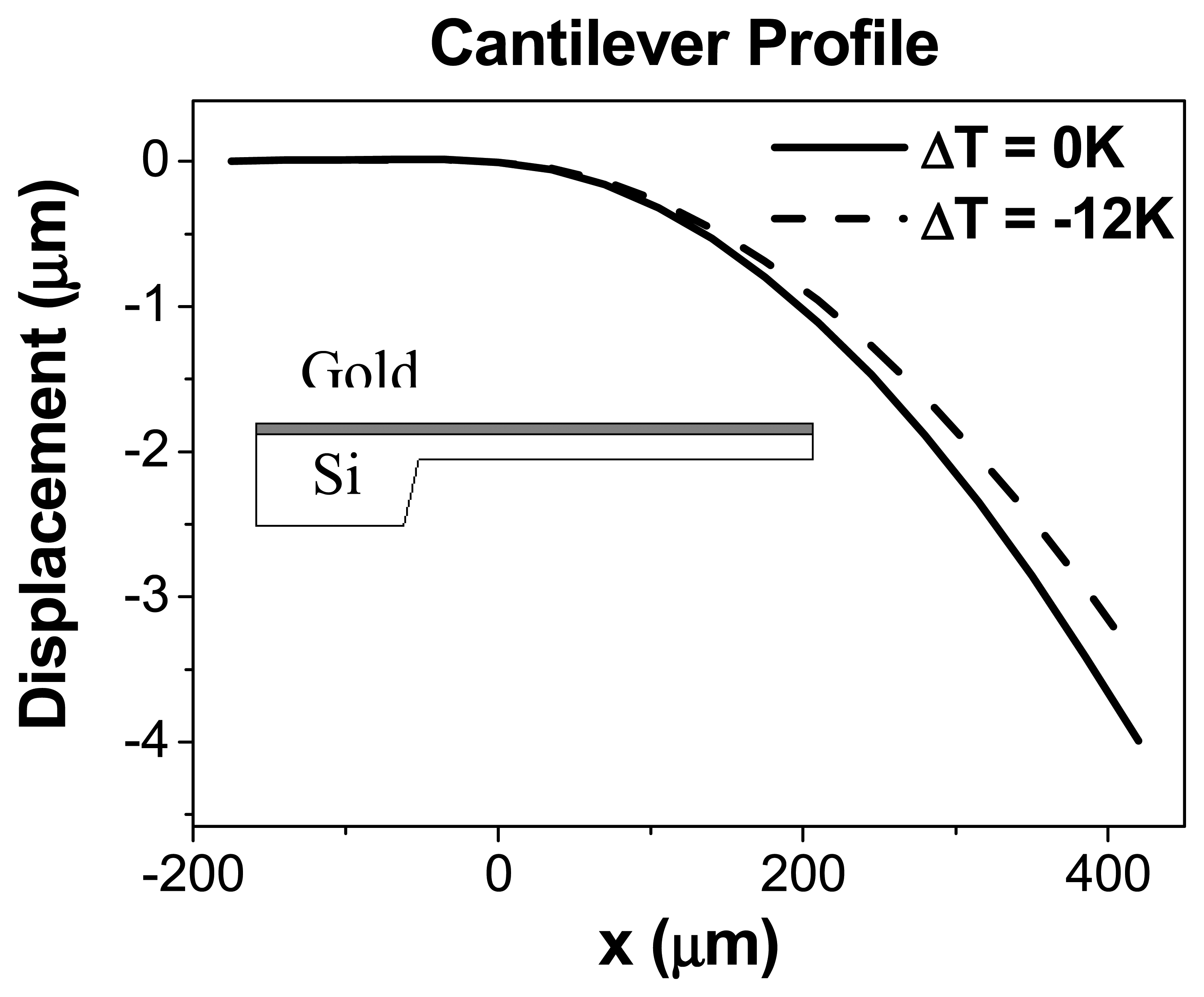
2. Theory
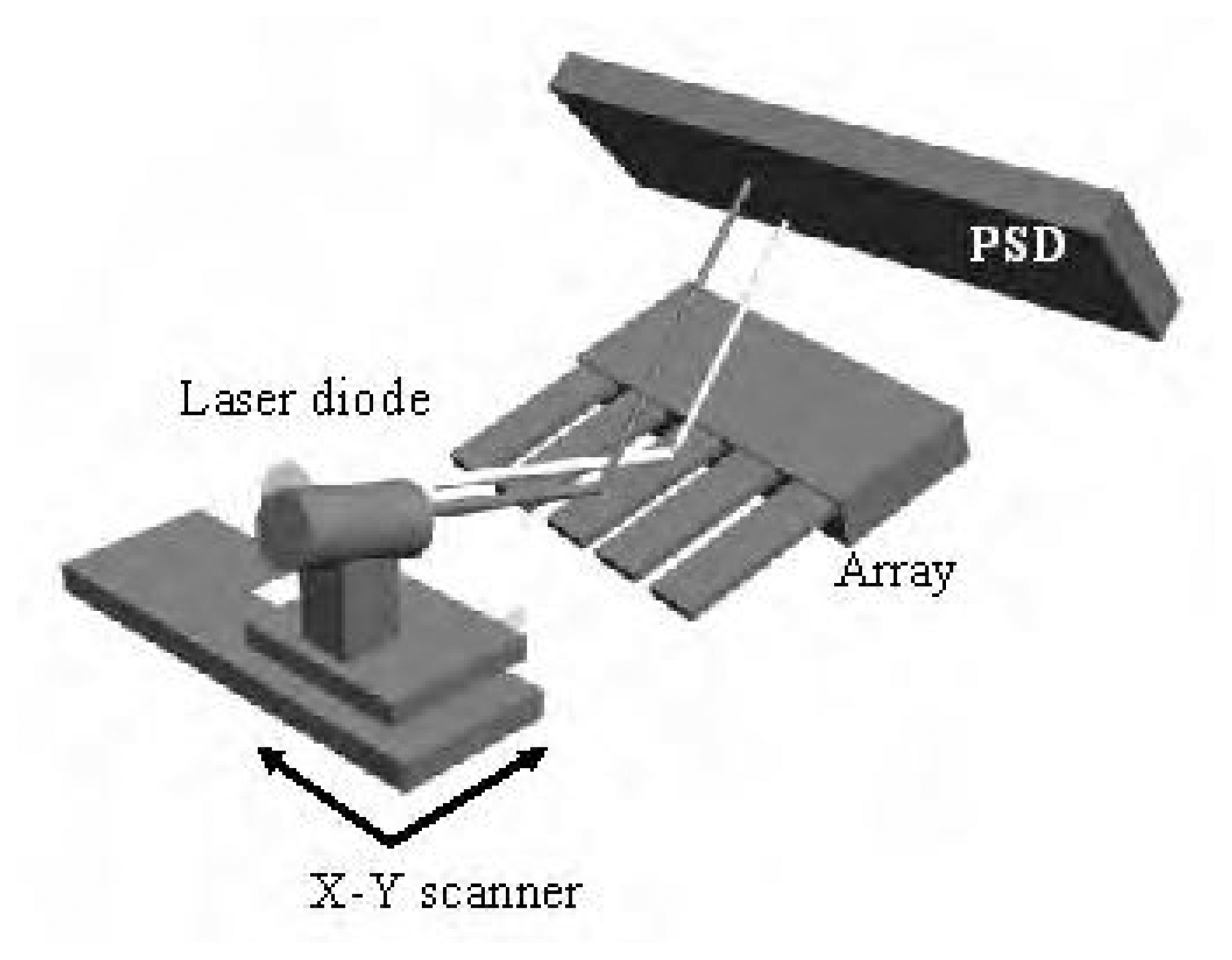
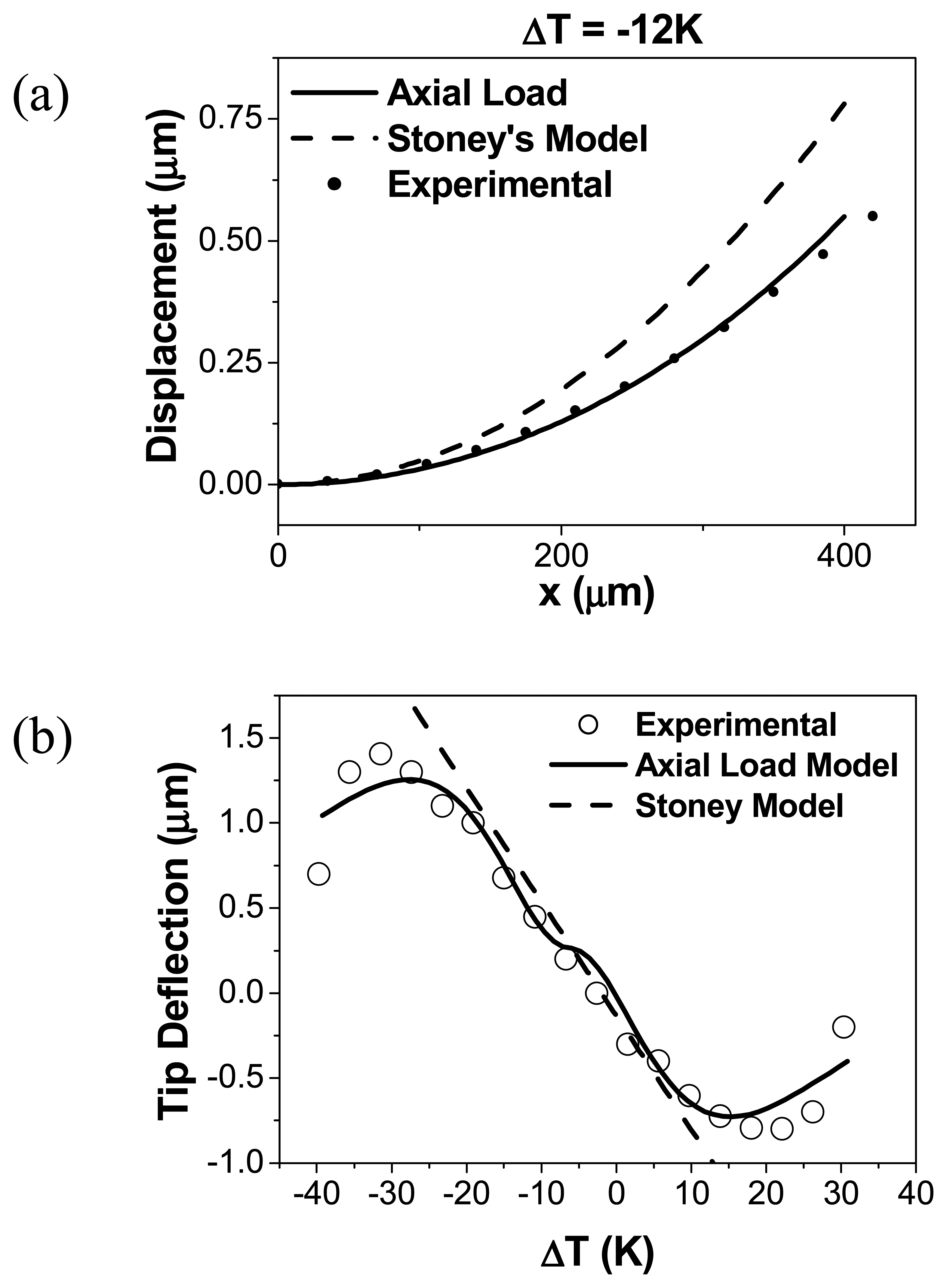
3. Experimental Section
Conclusions
Acknowledgments
References and Notes
- Mertens, J.; Finot, E.; Thundat, T.; Fabre, A.; Nadal, M.-H.; Eyraud, V.; Bourillot, E. Effects of temperature and pressure on microcantilever resonance response. Ultramicroscopy 2003, 97, 119. [Google Scholar]
- King, W.P.; Saxena, S.; Nelson, B.A. Nanoscale thermal analysis of an energetic material. Nano Letters 2006, 6, 2145. [Google Scholar]
- Nonnenmacher, M.; Wickramasinghe, H. K. Scanning probe microscopy of thermal conductivity and subsurface properties. Applied Physics Letters 1992, 61, 168. [Google Scholar]
- Abedinov, N.; Grabiec, P.; Gotszalk, T.; Ivanov, Tz.; Voigt, J.; Rangelow, I.W. Micromachined piezoresistive cantilever array with integrated resistive microheater for calorimetry and mass detection. Journal of Vacuum Science and Technology A 2001, 19, 2884. [Google Scholar]
- Gotsmann, B.; Durig, U. Thermally activated nanowear modes of a polymer surface induced by a heated tip. Langmuir 2004, 20, 1495. [Google Scholar]
- Berger, R.; Lang, H.; Gerber, C.; Gimzewski, J.; Fabian, J.; Scandella, L.; Meyer, E.; Guntherodt, H. Micromechanical thermogravimetry. Chemical Physics Letter 1998, 294, 363. [Google Scholar]
- Pinnaduwage, L.A.; Wig, A.; Hedden, D.L.; Gehl, A.; Yi, D.; Thundat, T.; Lareau, R.T. Detection of trinitrotoluene via deflagration on a microcantilever. Journal of Applied Physics 2004, 95, 5871. [Google Scholar]
- Wallis, T.M.; Moreland, J.; Riddle, B.; Kabos, P. Microwave power imaging with ferromagnetic calorimeter probes on bimaterial cantilevers. Journal of Magnetism and Magnetic Material 2005, 286, 320. [Google Scholar]
- King, W.P.; Kenny, T.W.; Goodson, K.E.; G. Cross, G.; Despont, M.; Durig, U.; H. Rothuizen, H.; Binnig, G.K.; Vettiger, P. Atomic force microscope cantilevers for combined thermomechanical data writing and reading. Applied Physics Letters 2001, 78, 1300. [Google Scholar]
- Mamin, H. J.; Fan, L.S.; Rugar, D.; Hoen, S. Tip-based data storage using micromechanical cantilevers. Sensors and Actuators A: Physical 1995, 48, 215–219. [Google Scholar]
- Wang, D. A.; Bullen, J.; Zou, C.; Liu, J.; Mirkin, C. Thermally actuated probe array for parallel dip-pen nanolithography. Journal of Vacuum Science and Technology B 2004, 22, 2563. [Google Scholar]
- Gotsmann, B.; Duerig, U.; Frommer, J.; Hawker, C. J. Exploiting chemical switching in a Diels-Alder polymer for nanoscale probe lithography and data storage. Advanced Functional Materials 2006, 16, 1499. [Google Scholar]
- Sheehan, P. E.; Whitman, L.J.; King, W.P.; Nelson, B. A. Nanoscale deposition of solid inks via thermal dip pen nanolithography. Applied Physics Letter 2004, 85, 1589. [Google Scholar]
- Nishimura, S.; Takemura, Y.; Shirakashi, J. SPM local oxidation nanolithography with active control of cantilever dynamics. Journal of Physics: Conference Series 2007, 61, 1066. [Google Scholar]
- Lalinský, T.; Burian, E.; Drzृk, M.; Hascृk, S.; Mozolová, Z.; Kuzmृk, J. Thermal actuation of a GaAs cantilever beam. Journal of Micromechanics and Microengineering 2000, 10, 293. [Google Scholar]
- Grigorov, A.V.; Davis, Z.J.; Rasmussen, P.; Boisen, A. A longitudinal thermal actuation principle for mass detection using a resonant micro-cantilever in a fluid medium. Microelectronic Engineering 2004, 73, 881. [Google Scholar]
- Sulchek, T.; Minne, S. C.; Adams, J.D.; Fletcher, D. A.; Atalar, A.; Quate, C.F.; Adderton, D.M. Dual integrated actuators for extended range high speed atomic force microscopy. Applied Physics Letters 1999, 75, 1637. [Google Scholar]
- Barnes, J.R.; Stephenson, R.J.; Welland, M.E.; Gerber, C.; Gimzewski, J.K. Photothermal spectroscopy with femtojoule sensitivity using a micromechanical device. Nature 1994, 372, 79. [Google Scholar]
- Chu, W.-H.; Mehregany, M.; Mullen, R. L. Analysis of tip deflection and cantilever force of a bimetallic cantilever microactuator. J. Micromech. Microeng. 1993, 3, 4–7. [Google Scholar]
- Shuir, E. Stresses in bi-metal thermostats. J. Appl. Mech. 1986, 53, 657–660. [Google Scholar]
- Stoney, G. G. The Tension of metallic films deposited by electrolysis. Proc. R. Soc. London, Ser. A 1909, 82, 172–175. [Google Scholar]
- Timoshenko, S. Analysis of bi-metal thermostats. J. Opt. Soc. Am. 1925, 11, 233–255. [Google Scholar]
- Yi, J. W.; Shih, W. Y.; Shih, W.-H. Effect of length, width, and mode on the mass detection sensitivity of piezoelectric unimorph cantilevers. J. Appl. Phys. 2002, 91, 1680–1686. [Google Scholar]
- Hsueh, C. H. Modeling of elastic deformation of multilayers due to residual stresses and external bending. J. Appl. Phys. 2002, 91, 9652–9656. [Google Scholar]
- MacFarland, A. W.; Poggi, M. A.; Doyle, M. J.; Bottomley, L. A.; Colton, J. S. Influence of surface stress on the resonance behavior of microcantilevers. Appl. Phys. Letts. 2005, 87, 053505. [Google Scholar]
- Zhang, Y.; Zhao, Y.-P. Applicability range of Stoney's formula and modified formulas for a film/substrate bilayer. J. Appl. Phys. 2006, 99, 053513. [Google Scholar]
- Mertens, J.; Álvarez, M.; Tamayo, J. Real-time profile of microcantilevers for sensing applications. Appl. Phys. Lett. 2005, 87, 2344102. [Google Scholar]
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Ramos, D.; Mertens, J.; Calleja, M.; Tamayo, J. Study of the origin of bending induced by bimetallic effect on microcantilever. Sensors 2007, 7, 1757-1765. https://doi.org/10.3390/s7091757
Ramos D, Mertens J, Calleja M, Tamayo J. Study of the origin of bending induced by bimetallic effect on microcantilever. Sensors. 2007; 7(9):1757-1765. https://doi.org/10.3390/s7091757
Chicago/Turabian StyleRamos, Daniel, Johann Mertens, Montserrat Calleja, and Javier Tamayo. 2007. "Study of the origin of bending induced by bimetallic effect on microcantilever" Sensors 7, no. 9: 1757-1765. https://doi.org/10.3390/s7091757
APA StyleRamos, D., Mertens, J., Calleja, M., & Tamayo, J. (2007). Study of the origin of bending induced by bimetallic effect on microcantilever. Sensors, 7(9), 1757-1765. https://doi.org/10.3390/s7091757



