A Wetness Index Using Terrain-Corrected Surface Temperature and Normalized Difference Vegetation Index Derived from Standard MODIS Products: An Evaluation of Its Use in a Humid Forest-Dominated Region of Eastern Canada
Abstract
:1. Introduction
2. Study Area and Data Used
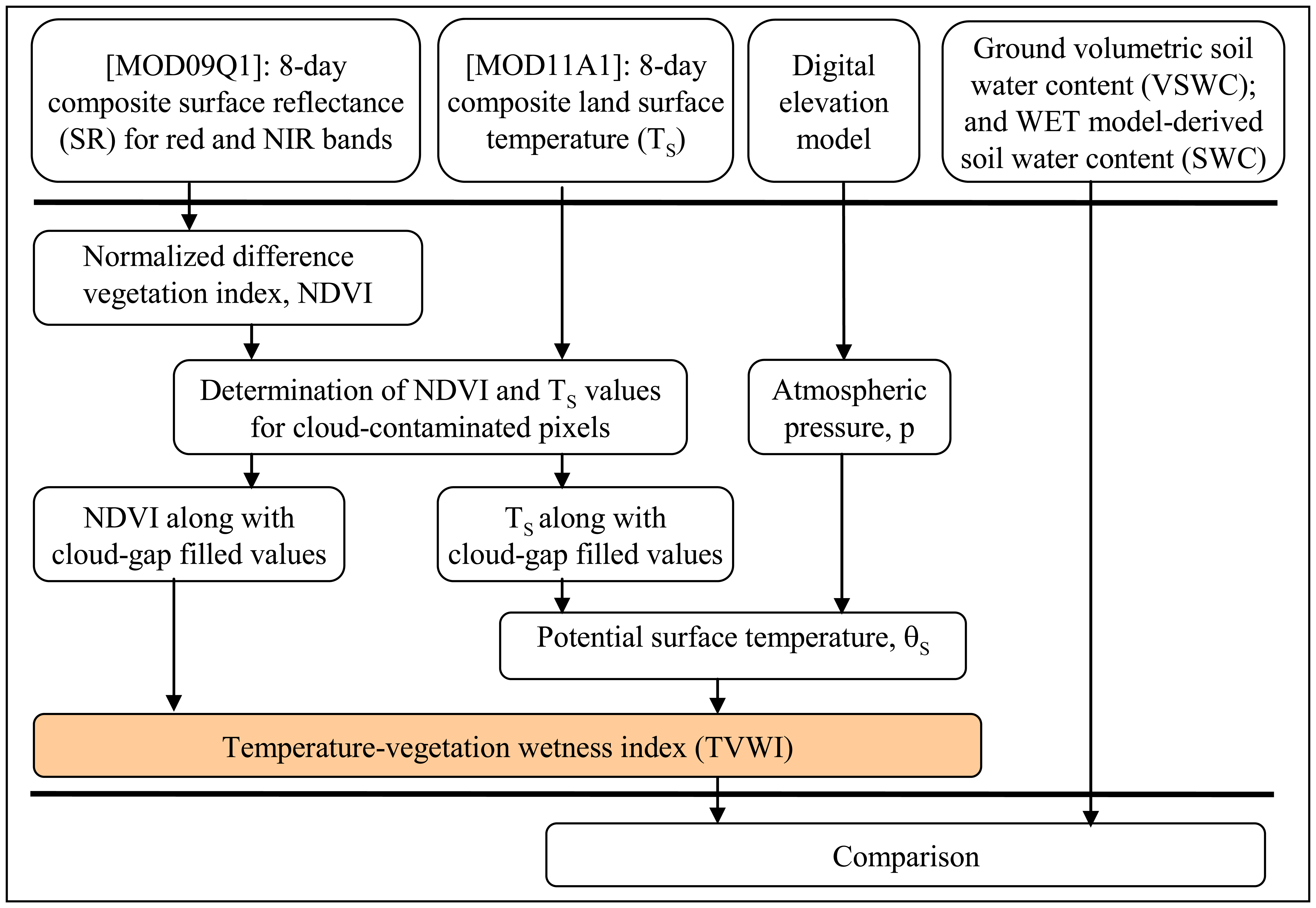
3. Methods
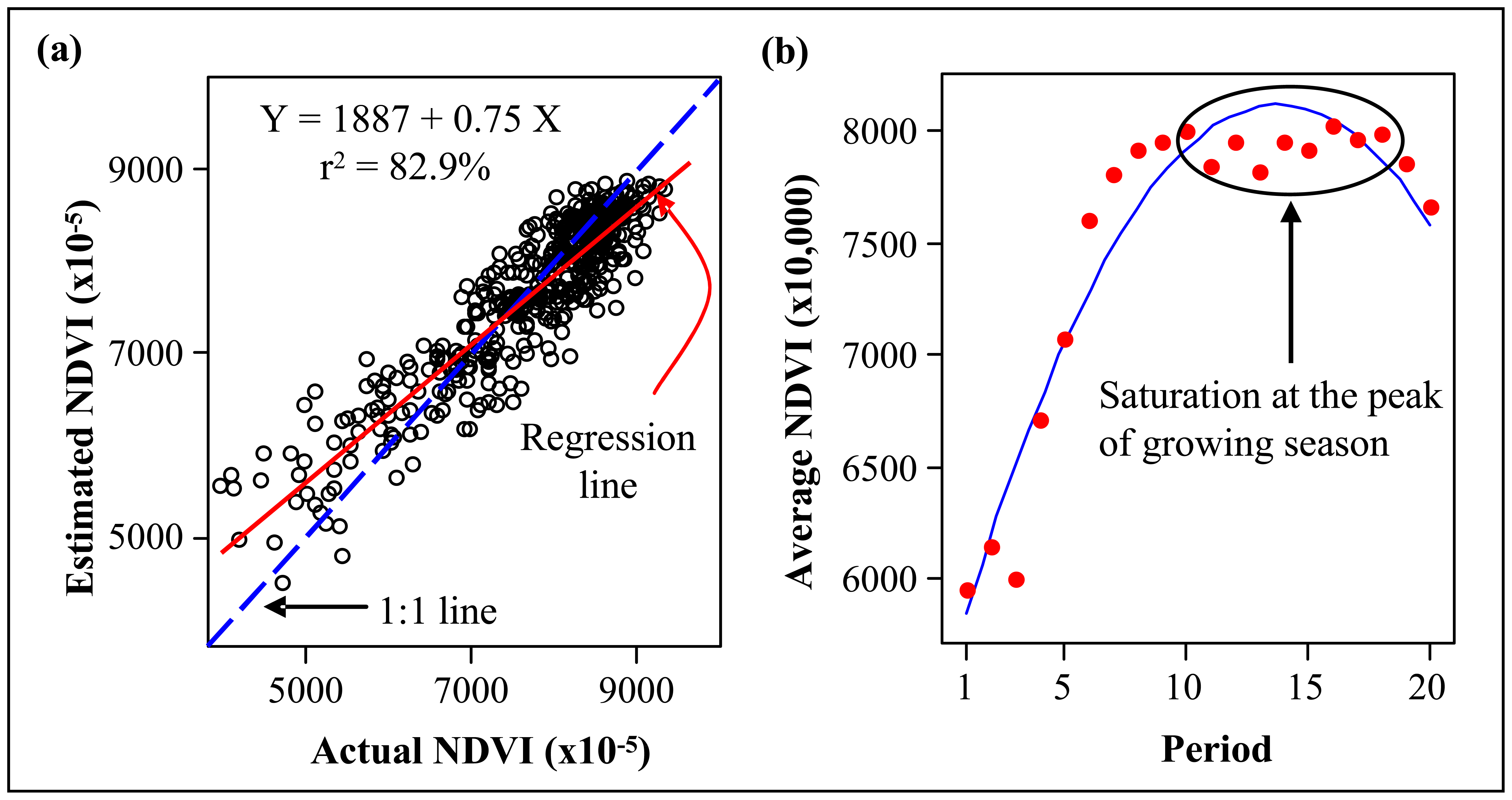
3.1. Pre-processing of the MODIS Images
3.2. Calculating θS and TVWI
3.3. TVWI and SWC comparisons
4. Results and Discussion
- (i)
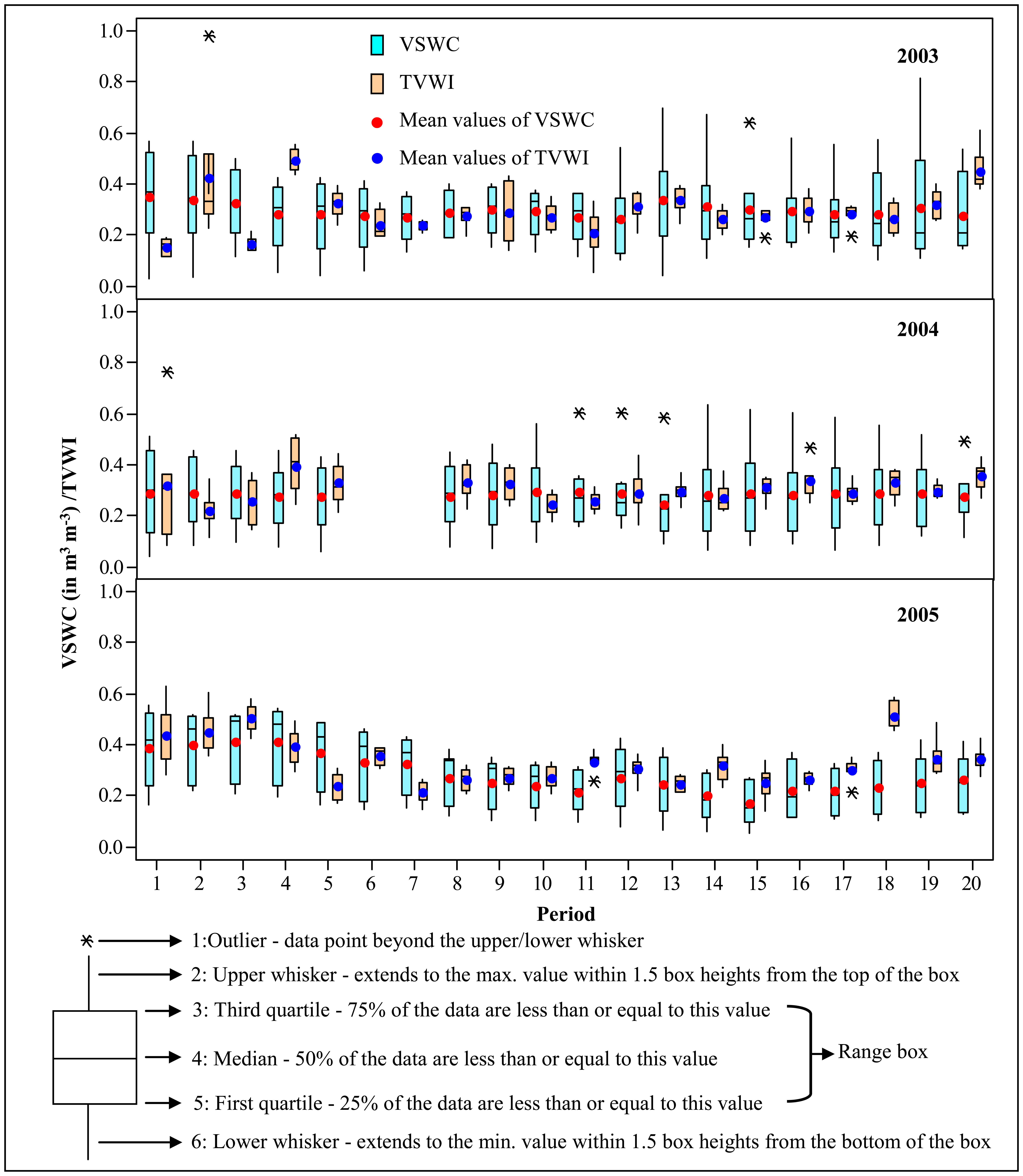
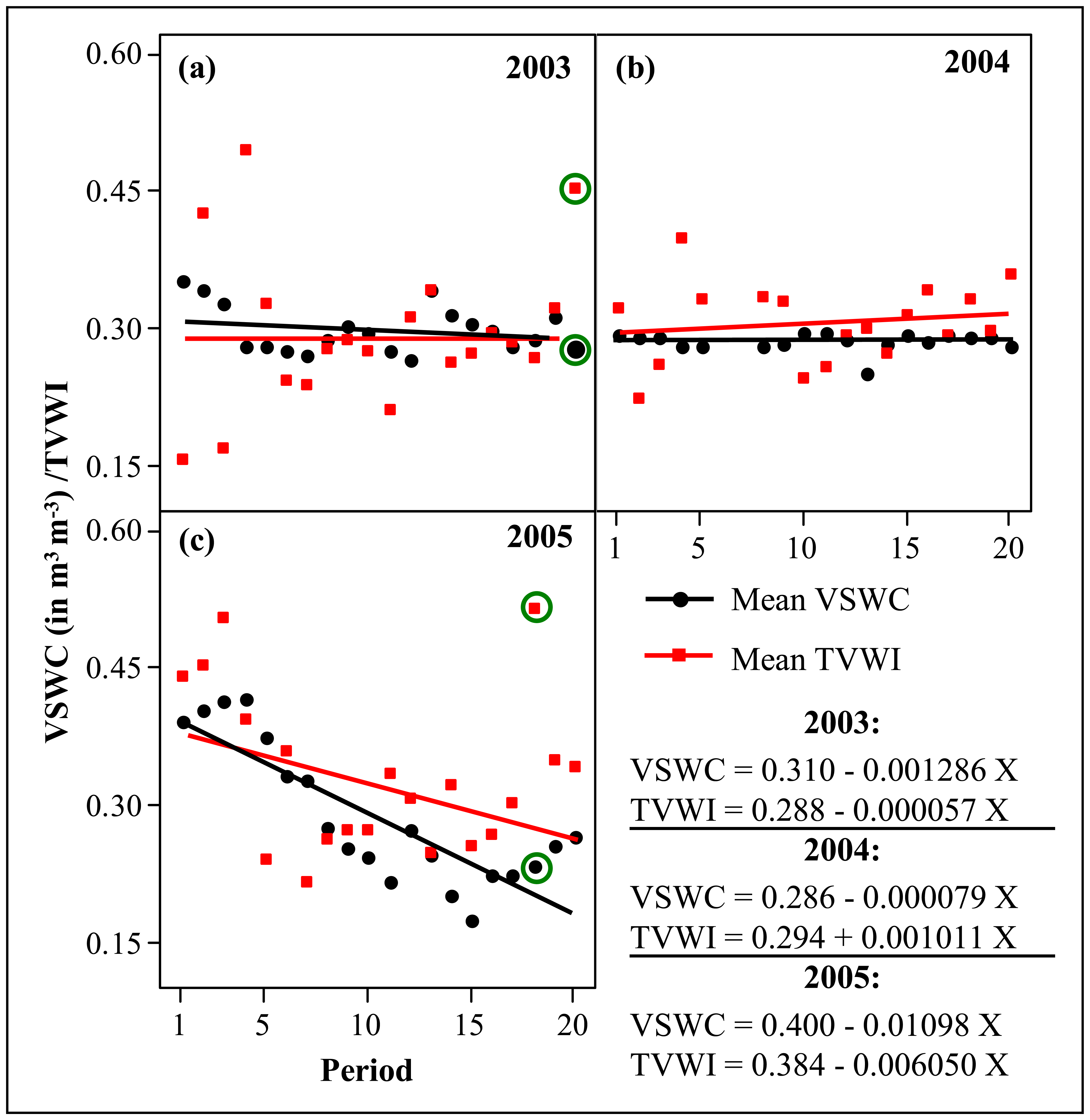
- The TVWI values were extremely close to VSWC values in terms of their magnitudes, even in heavily-forested areas (see Figure 7).
- (ii)
- As TVWI is based on the measure of surface properties, TVWI could be viewed as an indirect indicator of canopy (overstory foliage) WC. Canopy foliage WC in normal conditions is in equilibrium with SWC due to the relation between the water balance and total leaf area index [26]. This equilibrium could proceed uninterrupted if plant growth is unaffected by disturbance agents such as disease, insect infestation, physiological drought caused by soil-water logging or disruption of root to shoot ratios by air pollutant deposition [27-28] or winter conditions such as prolonged winter thaws [29]. Moreover, plant water potential (a measure of in-canopy WC) and soil water potential (an indirect measure of SWC) were shown to be strongly correlated [30-31]. In humid, water surplus conditions it is expected that ET would proceed at sufficiently elevated rates to cause measurable cooling of the immediate environment; on average, ∼ 2/3 of available net radiation goes to ET in water surplus areas of the world [32].Figure 9a provides a map of long-term averages of TVWI produced by averaging the 58 TVWI images. TVWI values fell mostly in the range of 20-60% with an average of 40%. In summary:
- (i)
- The areas along the coastlines and wider river channels showed higher TVWI, > 50%, due to their proximity to water and low elevation relative to exposed water.
- (ii)
- Some high relief areas, such as in northwestern NB and in the eastern part of NS, had comparatively lower TVWI values than other regions in the Maritime Provinces (20-32%). A similar pattern was observed with “% of saturation” values generated with the WET model for the Province of NB, despite some minor differences in low-lying areas of the Province (Figure 9c).
- (iii)
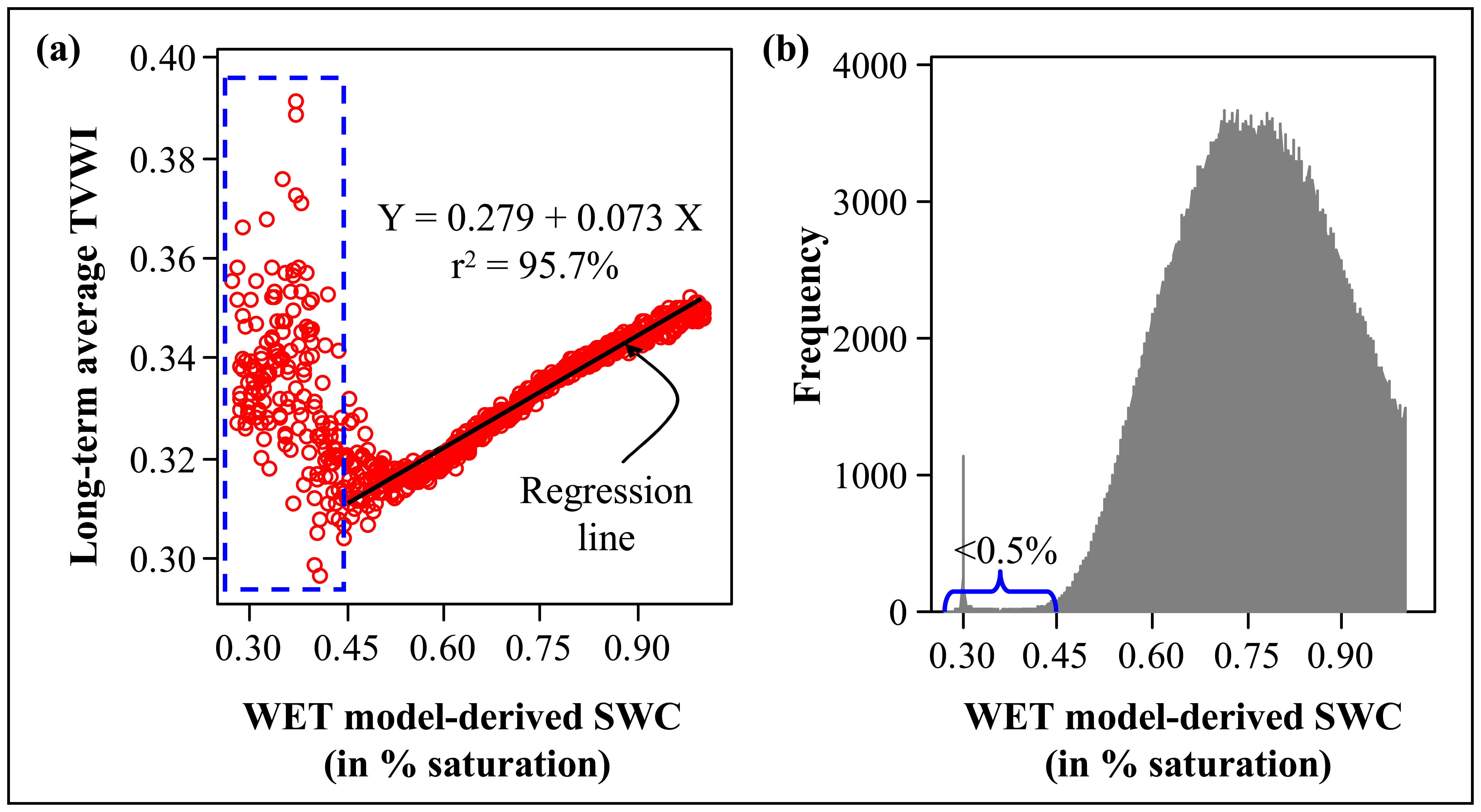
- A comparison of mean values of TVWI with values of “% of saturation” for the same pixels and region provided reasonable agreement (r2=95.7%; Figure 10a); indicating that for the most part (for > 99.5% of the values) the wetness distributions in Figures 9a and 9c for the Province of NB, despite having different wetness units (Figures 9b and 10b), were mostly the same. Values of “% of saturation” < 0.45 were not included in the comparison as (i) the mean TVWI values did not show any clear pattern with modelled wetness values (Figure 10a), and (ii) the amount of data involved was fairly small, comprising < 0.5% of total available data points (Figure 10b). Reasons for divergence in the low “% of saturation” range (Figure 10a) remain unknown to us.
5. Concluding Remarks
Acknowledgments
References and Notes
- Moran, M.S.; Peters-Lidard, C.D.; Watts, J.M.; McElroy, J. Estimating soil moisture at the watershed scale with satellite-based radar and land surface models. Can. J. Remote Sens. 2004, 30, 805–826. [Google Scholar]
- Nemani, R.; Running, S. Estimation of regional surface resistance to evapotranspiration from NDVI and thermal-IR AVHRR data. J. Appl. Meteor. 1989, 28, 276–284. [Google Scholar]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar]
- Moran, M.S.; Clarke, T.R.; Inoue, Y.; Vidal, A. Estimating crop water-deficit using the relation between surface-air Temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar]
- Lambin, E.F.; Ehrlich, D. The surface temperature -vegetation index space for land cover and land-cover change analysis. Int. J. Remote Sens. 1996, 17, 463–487. [Google Scholar]
- Nemani, R.; Pierce, L.; Running, S.; Goward, S. Developing satellite-derived estimates of surface moisture status. J. Appl. Meteor. 1993, 32, 548–557. [Google Scholar]
- Carlson, T.N.; Gillies, R.R.; Schmugge, T.J. An interpretation of methodologies for indirect measurement of soil water content. Agric. and For. Meteor. 1995, 77, 191–205. [Google Scholar]
- Dupigny-Giroux, L.; Lewis, J.E. A moisture index for surface characterization over a semiarid area. Photo. Eng. & Remote Sens. 1999, 65, 937–946. [Google Scholar]
- Goward, S.N.; Xue, Y.; Czajkowski, K.P. Evaluating land surface moisture conditions from the remotely sensed temperature/vegetation index measurements: an exploration with the simplified simple biosphere model. Remote Sens. Environ. 2002, 79, 225–242. [Google Scholar]
- Jiang, L.; Islam, S. Estimation of surface evaporation map over southern Great Plains using remote sensing data. Water Resour. Res. 2001, 37, 329–340. [Google Scholar]
- Nishida, K.; Nemani, R.R.; Glassy, J.M.; Running, S.W. Development of an evapotranspiration index from Aqua/MODIS for monitoring surface moisture status. IEEE Trans. Geosci. and Remote Sens. 2003, 41, 493–501. [Google Scholar]
- Hassan, Q.K.; Bourque, C.P.-A. Estimating daily evapotranspiration for forests in Atlantic Maritime Canada: application of MODIS imagery. Proc. ASPRS 2006, 11p, CD-ROM unpaginated. [Google Scholar]
- Vidal, A.; Devaux-Ros, C. Evaluating forest fire hazard with a Landsat TM derived water stress index. Agric. and For. Meteor. 1995, 77, 207–224. [Google Scholar]
- Wang, C.; Qi, S.; Niu, Z.; Wang, J. Evaluating soil moisture status in China using the temperature–vegetation dryness index (TVDI). Can. J. Remote Sens. 2004, 30, 671–679. [Google Scholar]
- Gilles, R.R.; Carlson, T.N.; Cui, J.; Kustas, W.P.; Humes, K.P. Verification of the triangle method for obtaining surface soil water content and energy fluxes from remote measurements of Normalized Difference Vegetation Index (NDVI) and surface radiant temperature. Int. J. Remote Sens. 1997, 18, 3145–3166. [Google Scholar]
- Vicente-Serrano, S.M.; Pons-Fernández, X.; Cuadrat-Prats, J.M. Mapping soil moisture in the central Ebro river valley (northeast Spain) with Landsat and NOAA satellite imagery: a comparison with meteorological data. Int. J. of Remote Sens. 2004, 25, 4325–4350. [Google Scholar]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar]
- Rogers, R.R.; Yau, M.K. A short course in cloud physicsButterworth-Heinemann: Woburn, MA, USA, 3rd edition; 1989; p. 304p. [Google Scholar]
- Ecological Stratification Working Group. A National Ecological Framework for Canada.; Agriculture and Agri-Food Canada, Research Branch, Centre for Land and Biological Resources Research and Environment Canada, State of Environment Directorate: Ottawa/Hull, 1996; p. 125p. [Google Scholar]
- Coursolle, C.; Margolis, H.A.; Barr, A.G.; Black, T.A.; Amiro, B.D.; McCaughey, J.H.; Flanagan, L.B.; Lafleur, P.M.; Roulet, N.T.; Bourque, C.P-A.; Arain, M.A.; Wofsy, S.C.; Dunn, A.; Morgenstern, K.; Orchansky, A.L.; Bernier, P.Y.; Chen, J.M.; Kidston, J.; Saigusa, N.; Hedstrom, N. Late-summer carbon fluxes from Canadian forests and peatlands along an east–west continental transect. Can. J. For. Res. 2006, 36, 783–800. [Google Scholar]
- Moore, I.D.; Norton, T.W.; Williams, J.E. Modelling environmental heterogeneity in forested landscapes. J. Hydrology 1993, 150, 717–747. [Google Scholar]
- Gallant, J. Complex wetness index calculations, WET documentation version 2.0.; Centre for Resource and Environmental Studies, Australian National University: Canberra, 1996. [Google Scholar]
- Bourque, C.P.-A.; Meng, F.R.; Gullison, J.J.; Bridgland, J. Biophysical and potential vegetation growth surfaces for a small watershed in northern Cape Breton Island, Nova Scotia, Canada. Can. J. For. Res. 2000, 30, 1179–1195. [Google Scholar]
- Hassan, Q.K.; Bourque, C.P.-A.; Meng, F.-R.; Richards, W. Spatial mapping of growing degree days: an application of MODIS-based surface temperatures and enhanced vegetation index. J. Appl. Remote Sens. 2007, 1, 013511 (12p.). [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration: guide-lines for computing crop water requirements.; Food and Agriculture Organizations of the United Nations: Rome, Italy, 1998; ISBN 92-5-104219-5; p. 290p. [Google Scholar]
- Grier, C.C.; Running, S.W. Leaf area of mature northwestern coniferous forests: relation to site water balance. Ecology 1977, 58, 893–899. [Google Scholar]
- Rennenberg, H.; Herschbach, C.; Polle, A. Consequences of air pollution on shoot-root interactions. J. Plant Physiology 1996, 148, 296–301. [Google Scholar]
- Persson, H.; Majdi, H. Effects of acid deposition on tree roots in Swedish forest stands. Water Air Soil Pollution 1995, 85, 1287–1292. [Google Scholar]
- Bourque, C.P.-A.; Cox, R.M.; Allen, D.J.; Arp, P.A.; Meng, F.-R. Spatial extent of winter thaw events in eastern North America: historical weather records in relation to yellow birch decline. Global Change Biology 2005, 11, 1477–1492. [Google Scholar]
- Pabst, R.J.; Tappeiner II, J.C.; Newton, M. Varying densities of Pacific madrone in a young stand in Oregon alter soil water-potential, plant moisture stress, and growth of Douglas fir,”. For. Ecology & Management 1990, 37, 267–283. [Google Scholar]
- Fotelli, M.N.; Geßler, A.; Peuke, A.D.; Rennenberg, H. Drought affects the competitive interactions between Fagus sylvatica seedlings and an early successional species, Rubus fruticosus: responses of growth, water status and δ13C composition. New Phytologist 2001, 151, 427–435. [Google Scholar]
- Oke, T.R. Boundary layer climatesRoutledge: London, UK, 2nd edition; 1987; p. 464p. [Google Scholar]


| Ref. | TS-VI approaches used in the past* |
|---|---|
| [3] |
|
| [5] |
|
| [6] |
|
| [7, 15] |
|
| [8] |
|
| [9] |
|
| [16] |
|
| Period no. | Day of year | Dates in 2003 and 2005 | Dates in 2004 | Period no. | Day of year | Dates in 2003 and 2005 | Dates in 2004 |
|---|---|---|---|---|---|---|---|
| 1 | 121-128 | 01 May-08 May | 30 Apr.-07 May | 11 | 201-208 | 20 Jul.-27 Jul. | 19 Jul.-26 Jul. |
| 2 | 129-136 | 09 May-16 May | 08 May-15 May | 12 | 209-216 | 28 Jul.-04 Aug. | 27 Jul.-03 Aug. |
| 3 | 137-144 | 17 May-24 May | 16 May-23 May | 13 | 217-224 | 05 Aug.-12 Aug. | 04 Aug.-11Aug. |
| 4 | 145-152 | 25 May-01 Jun. | 24 May-30 May | 14 | 225-232 | 13 Aug.-20 Aug. | 12 Aug.-19 Aug. |
| 5 | 153-160 | 02 Jun.-09 Jun. | 01 Jun.-08 Jun. | 15 | 233-240 | 21 Aug.-28 Aug. | 20 Aug.-27 Aug. |
| 6 | 161-168 | 10 Jun.-17 Jun. | 09 Jun.-16 Jun. | 16 | 241-248 | 29 Aug.-05 Sep. | 28 Aug.-04 Sep. |
| 7 | 169-176 | 18 Jun.-25 Jun. | 17 Jun.-24 Jun. | 17 | 249-256 | 06 Sep.-13 Sep. | 05 Sep.-12 Sep. |
| 8 | 177-184 | 26 Jun.-03 Jul. | 25 Jun.-02 Jul. | 18 | 257-264 | 14 Sep.-21 Sep. | 13 Sep.-20 Sep. |
| 9 | 185-192 | 04 Jul.-11 Jul. | 03 Jul.-10 Jul. | 19 | 265-272 | 22 Sep.-29 Sep. | 21 Sep.-28 Sep. |
| 10 | 193-200 | 12 Jul.-19 Jul. | 11 Jul.-18 Jul. | 20 | 273-280 | 30 Sep.-07 Oct. | 29 Sep.-06 Oct. |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Hassan, Q.K.; Bourque, C.P.-A.; Meng, F.-R.; Cox, R.M. A Wetness Index Using Terrain-Corrected Surface Temperature and Normalized Difference Vegetation Index Derived from Standard MODIS Products: An Evaluation of Its Use in a Humid Forest-Dominated Region of Eastern Canada. Sensors 2007, 7, 2028-2048. https://doi.org/10.3390/s7102028
Hassan QK, Bourque CP-A, Meng F-R, Cox RM. A Wetness Index Using Terrain-Corrected Surface Temperature and Normalized Difference Vegetation Index Derived from Standard MODIS Products: An Evaluation of Its Use in a Humid Forest-Dominated Region of Eastern Canada. Sensors. 2007; 7(10):2028-2048. https://doi.org/10.3390/s7102028
Chicago/Turabian StyleHassan, Quazi K., Charles P.-A. Bourque, Fan-Rui Meng, and Roger M. Cox. 2007. "A Wetness Index Using Terrain-Corrected Surface Temperature and Normalized Difference Vegetation Index Derived from Standard MODIS Products: An Evaluation of Its Use in a Humid Forest-Dominated Region of Eastern Canada" Sensors 7, no. 10: 2028-2048. https://doi.org/10.3390/s7102028
APA StyleHassan, Q. K., Bourque, C. P.-A., Meng, F.-R., & Cox, R. M. (2007). A Wetness Index Using Terrain-Corrected Surface Temperature and Normalized Difference Vegetation Index Derived from Standard MODIS Products: An Evaluation of Its Use in a Humid Forest-Dominated Region of Eastern Canada. Sensors, 7(10), 2028-2048. https://doi.org/10.3390/s7102028






