Simulation Study on Anti-Interference Performance Degradation of GIS UHF Sensors Based on Substation White Noise Reconstruction
Abstract
1. Introduction
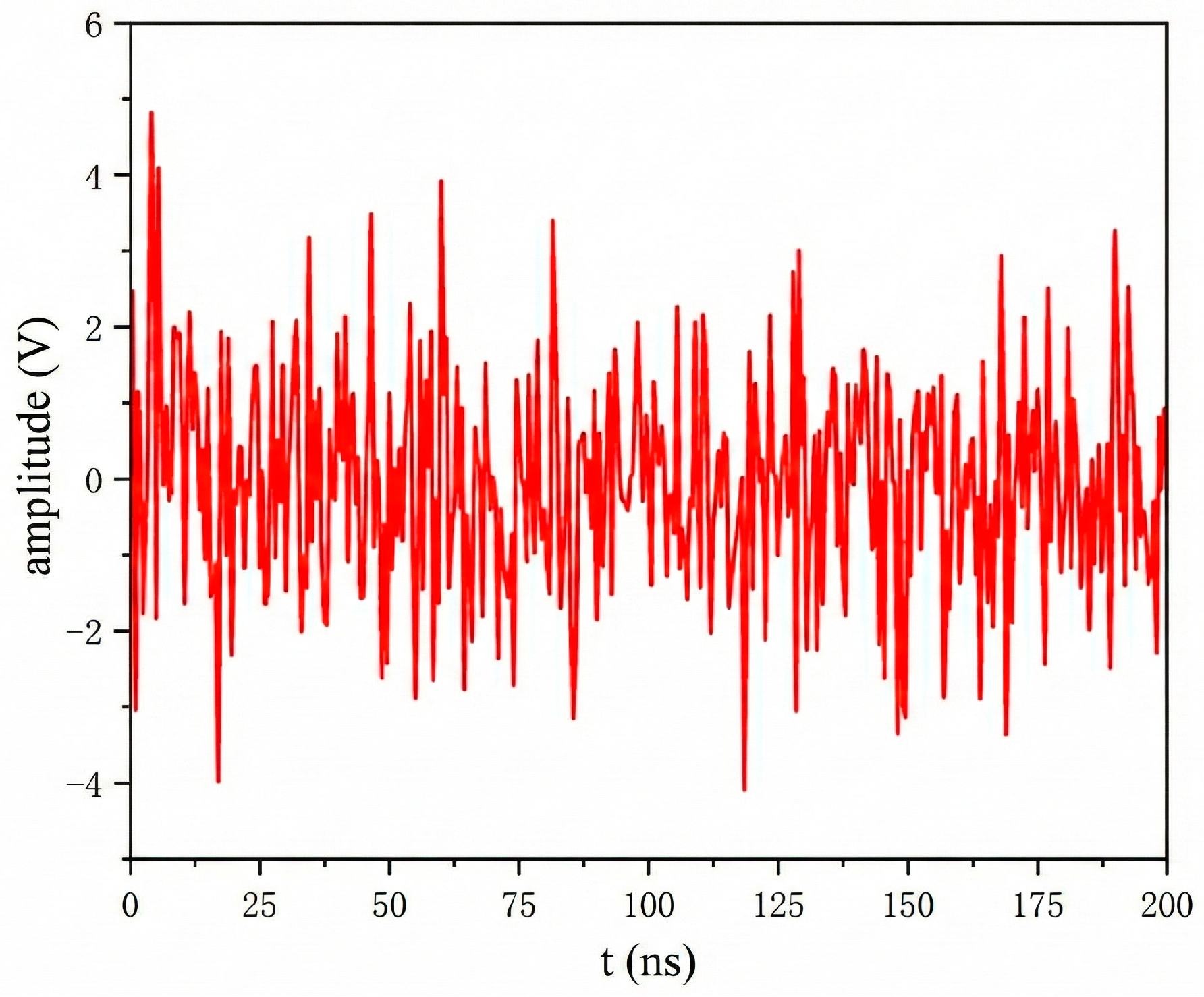
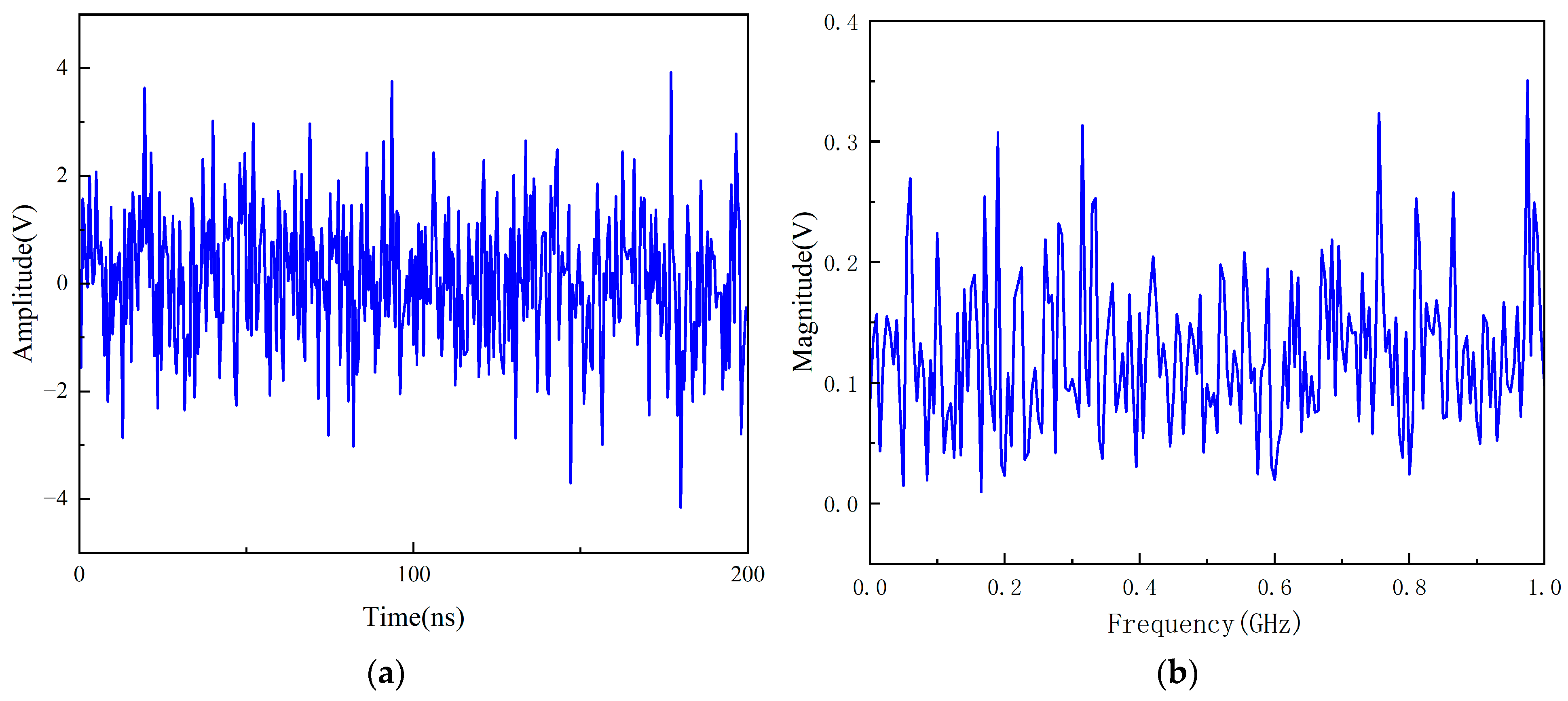
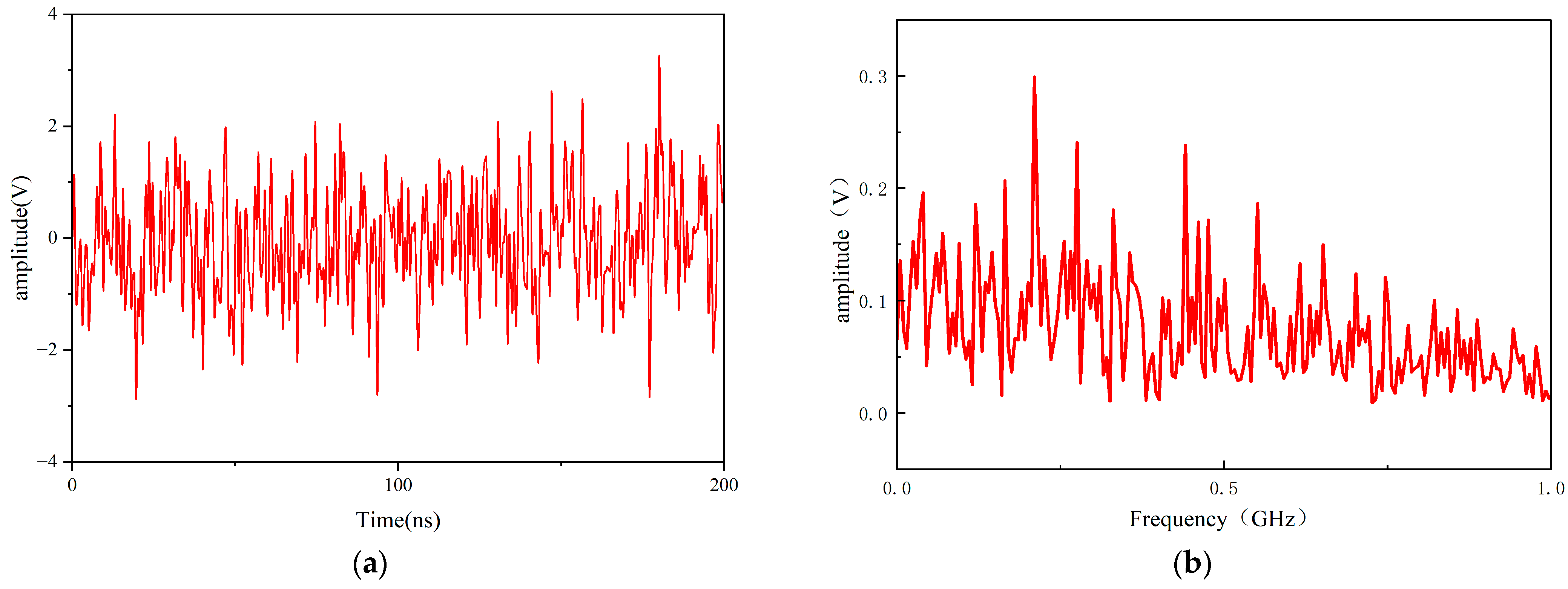
2. UHF White Noise Characteristics Analysis and Reconstruction
2.1. White Noise Characteristics and Simulation Reconstruction
2.2. Equivalence Validation of Reconstructed Signals
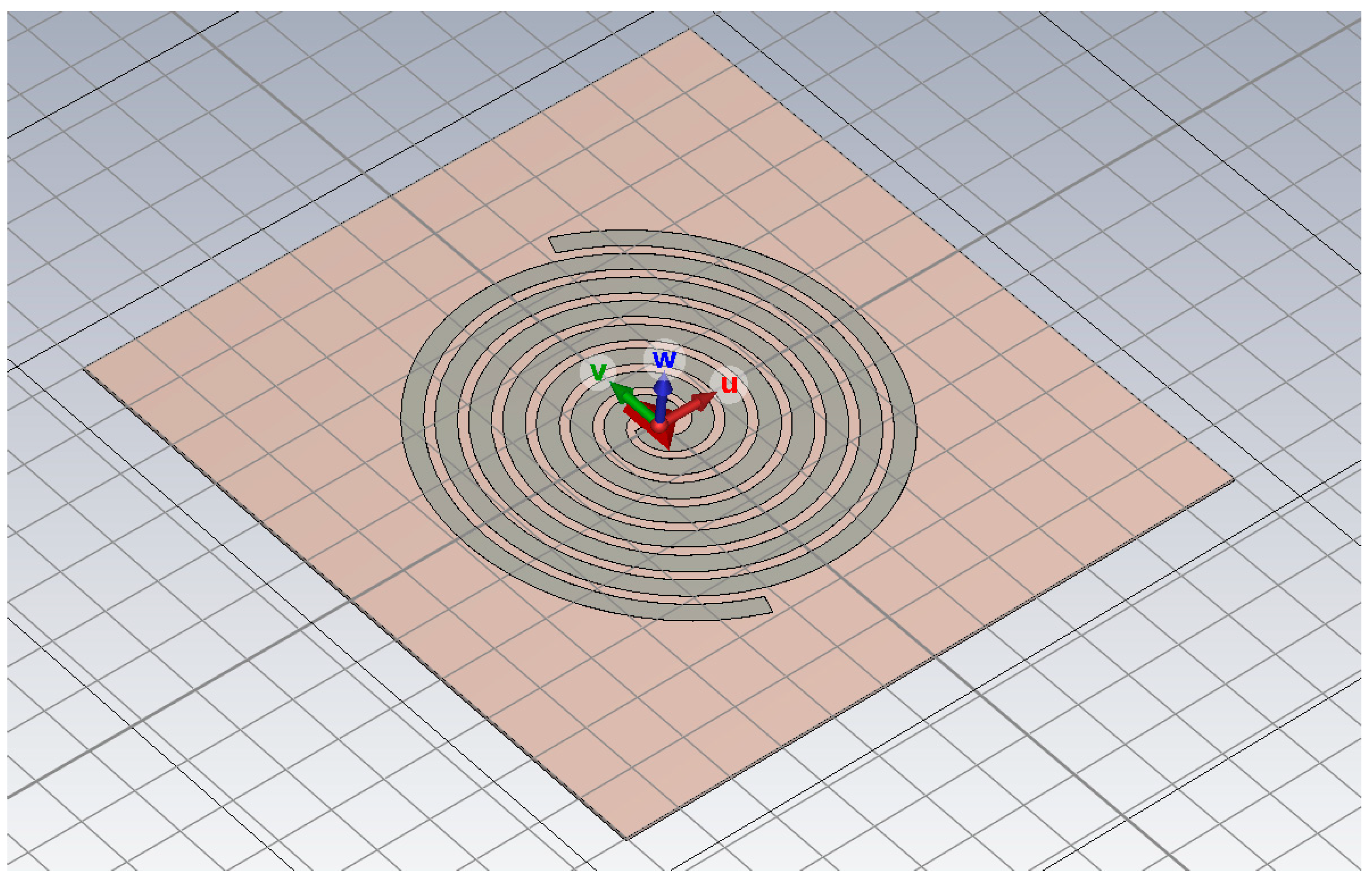
3. UHF Sensor Modeling and Performance Degradation Analysis
3.1. Standard Ultra-High-Frequency Sensor Simulation
3.2. Simulation of Oxidation and Corrosion on Antenna Rotating Arms
4. Simulation and Calibration of Sensor Performance in White Noise Environment
5. Conclusions
- The Gaussian white noise simulation model constructed by measured noise ANOVA, its craggy value and autocorrelation characteristics are highly consistent with the measured noise, and it can reproduce the white noise interference in the 0–1 GHz band in CST.
- Antenna corrosion causes the VSWR to deteriorate from 1.94 (normal) to 4.18 (severe corrosion), the S11 parameter deterioration reaches 4.78 dB, and the gain of the directional map is attenuated by 39%. The mapping relationship of “corrosion line width—resonance point offset—receiver characteristic degradation” is established.
- In the superposition of white noise and local amplifier pulse, the power of the local amplifier signal received by the sensor decreases by 55.27%, the power of the noise signal increases by 64.11%, and the signal-to-noise ratio decreases from −9.70 dB to −15.34 dB. The simulation results prove that the aging of the sensor material greatly reduces the signal-to-noise ratio of the sensor signal and provides theoretical references for the on-site calibration of the degraded sensors.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UHF | Ultrahigh Frequency |
| PD | Partial Discharge |
| GIS | Gas-Insulated Switchgear |
| VSWR | Voltage Standing Wave Ratio |
| SNR | Signal-to-Noise Ratio |
References
- Zhang, X.; Shi, M.; Cai, J.; Li, J. A Novel Partial Discharge Detection Method for Power Transformers On Site Adopting Its Component as Ultra-High Frequency Sensor. IEEE Trans. Power Deliv. 2019, 34, 2269–2271. [Google Scholar] [CrossRef]
- Chen, X.; Qian, Y.; Sheng, G.; Jiang, X. A time-domain characterization method for UHF partial discharge sensors. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 110–119. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Zhang, K.; Yang, X.; Ji, S.; Zhu, L. Research on Ultrasonic Detection Method for Partial Discharge of Dry Type Transformer. In Proceedings of the 2023 IEEE 4th International Conference on Electrical Materials and Power Equipment (ICEMPE), Shanghai, China, 7–10 May 2023; pp. 1–4. [Google Scholar]
- Su, Q.; Sack, K. New techniques for on-line partial discharge measurements. In Proceedings of the IEEE International Multi Topic Conference, 2001. IEEE INMIC 2001. Technology for the 21st Century, Lahore, Pakistan, 30 December 2001; pp. 49–53. [Google Scholar]
- Liška, J.; Jakl, J.; Künkel, S.; Šťastný, L.; Mego, R. Partial discharge detection in modern power grid. In Proceedings of the 2022 International Conference on Diagnostics in Electrical Engineering (Diagnostika), Pilsen, Czech Republic, 6–8 September 2022; pp. 1–4. [Google Scholar]
- Zhang, M.; Hu, J.; Guo, H. Partial Discharge Detection Method of Ring Main Unit Based on Filtered UHF Signal. In Proceedings of the 2023 10th International Forum on Electrical Engineering and Automation (IFEEA), Nanjing, China, 3–5 November 2023; pp. 1059–1063. [Google Scholar]
- Feng, X.; Xing, H.; Sun, Y.; Zhang, M.; Wang, K. Research on RF Sensor for Partial Discharge Detection Based on Microstrip Antenna. In Proceedings of the 2022 IEEE International Conference on Power Systems and Electrical Technology (PSET), Aalborg, Denmark, 13–15 October 2022; pp. 101–104. [Google Scholar]
- Wan, Y.L.; Zhang, Y.Z. The application of UHF detection & positioning method into the process of partial discharge detection of switch cabinet. In Proceedings of the 2016 China International Conference on Electricity Distribution (CICED), Xi’an, China, 10–13 August 2016; pp. 1–4. [Google Scholar]
- Lu, Y.; Qiu, Z.; Liao, C.; Li, T.; Wu, Z.; Hu, Y. The Application of High Frequency and Ultra High Frequency Partial Discharge Detection to Gas Insulated Switchgear. In Proceedings of the 2022 4th Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 25–28 March 2022; pp. 712–716. [Google Scholar]
- Xu, B.; Duan, C.; Wang, J.; Zhang, L.; Zhang, G.; Zhang, G.; Li, G. Research on Miniaturized UHF Sensing Technology for PD Detection in Power Equipment Based on Symmetric Cut Theory. Sensors 2024, 24, 3313. [Google Scholar] [CrossRef] [PubMed]
- Hu, X.; Zhang, G.; Liu, X.; Chen, K.; Zhang, X. Design of High-Sensitivity Flexible Low-Profile Spiral Antenna Sensor for GIS Built-in PD Detection. Sensors 2023, 23, 4722. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhang, G.; Lu, C.; Tian, H.; Liu, J.; Zhang, X. Flexible Planar Monopole Built-in GIS PD Sensor Based on Meandering Technology. Sensors 2022, 22, 4134. [Google Scholar] [CrossRef] [PubMed]
- Liao, C.; Zhang, L.; Zhang, G.; Lu, C.; Zhang, X. Partial Discharge Wideband Full-Band High-Gain Resonant Cavity UHF Sensor Research. Sensors 2023, 23, 6847. [Google Scholar] [CrossRef] [PubMed]
- Jing, W. Research and Application of GIS Partial Discharge Signal Positioning Based on UHF Intelligent Sensors. In Proceedings of the 2022 IEEE International Conference on Electrical Engineering, Big Data and Algorithms (EEBDA), Changchun, China, 25–27 February 2022; pp. 1163–1167. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, S.; Wei, L. Ultrasonic Detection of Partial Discharge on Typical Defects of Basin Insulator in GIS. In Proceedings of the 2019 8th International Conference on Power Science and Engineering (ICPSE), Dublin, Ireland, 2–4 December 2019; pp. 40–43. [Google Scholar] [CrossRef]
- Lopez-Roldan, J.; Tang, T.; Gaskin, M. Optimisation of a sensor for onsite detection of partial discharges in power transformers by the UHF method. IEEE Trans. Dielectr. Electr. Insul. 2008, 15, 1634–1639. [Google Scholar] [CrossRef]
- Qi, B.; Li, C.; Hao, Z.; Geng, B.; Xu, D.; Liu, S. Partial discharge detection for GIS: A comparison between UHF and acoustic methods. In Proceedings of the 2010 IEEE International Symposium on Electrical Insulation, San Diego, CA, USA, 6–9 June 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Kornhuber, S.; Jani, K.; Boltze, M.; Valtin, G. Partial discharge (PD) detection on medium voltage switchgears using non-invasive sensing methods. In Proceedings of the 2012 IEEE International Conference on Condition Monitoring and Diagnosis, Bali, Indonesia, 23–27 September 2012; pp. 392–395. [Google Scholar] [CrossRef]
- Thungsook, K.; Pattanadech, N.; Nimsanong, P.; Srinangyam, C. The Bandwidth Verification of VHF Antenna and Apply for Partial Discharge Measurement. In Proceedings of the 2022 9th International Conference on Condition Monitoring and Diagnosis (CMD), Kitakyushu, Japan, 13–18 November 2022; pp. 559–562. [Google Scholar] [CrossRef]
- Hoshino, T.; Maruyama, S.; Ohtsuka, S.; Hikita, M.; Wada, J.; Okabe, S. Sensitivity comparison of disc- and loop-type sensors using the UHF method to detect partial discharges in GIS. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 910–916. [Google Scholar] [CrossRef]
- Ishak, A.M.; Ishak, M.T.; Jusoh, M.T.; Syed Dardin, S.F.; Judd, M.D. Design and Optimization of UHF Partial Discharge Sensors Using FDTD Modeling. IEEE Sens. J. 2017, 17, 127–133. [Google Scholar] [CrossRef]
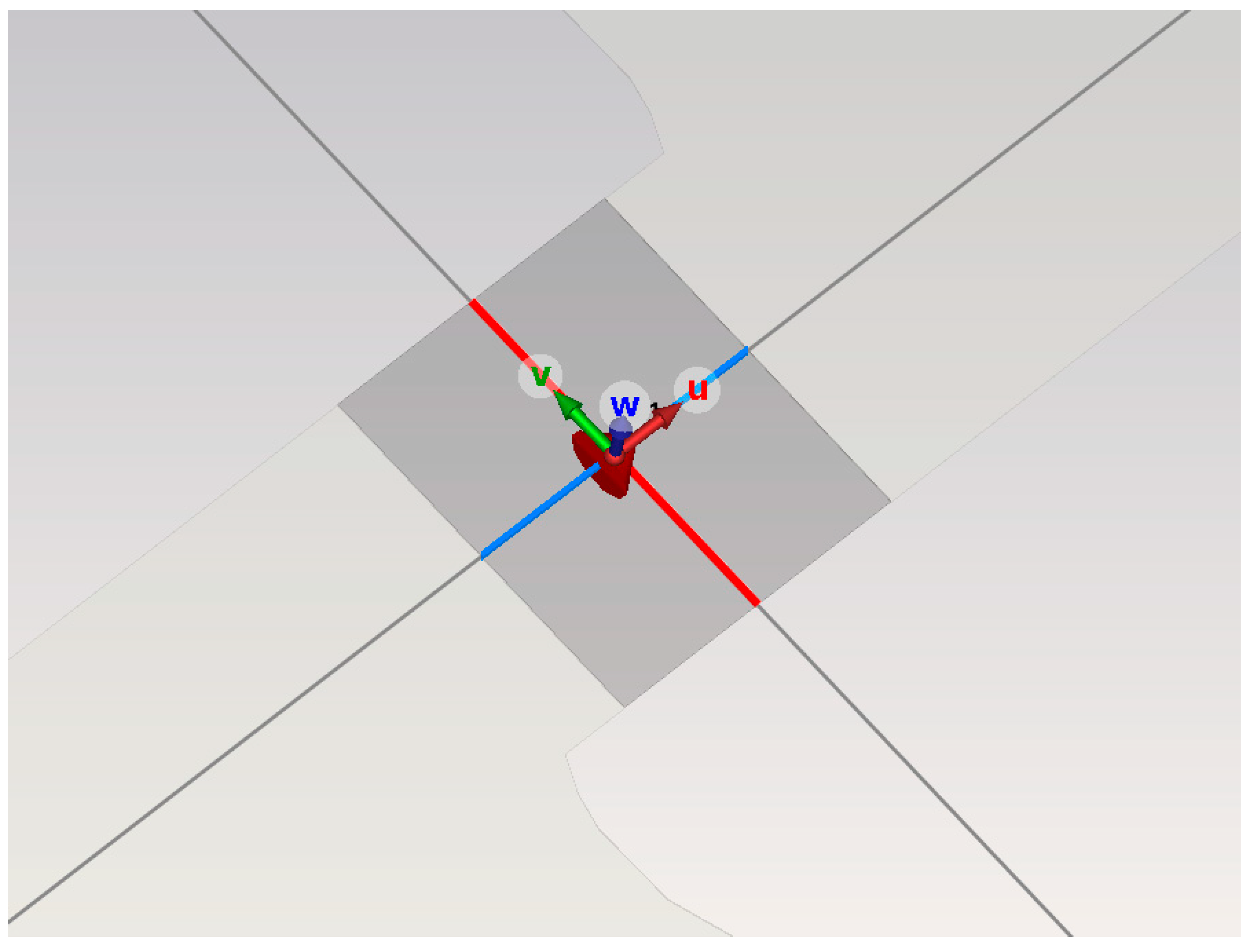
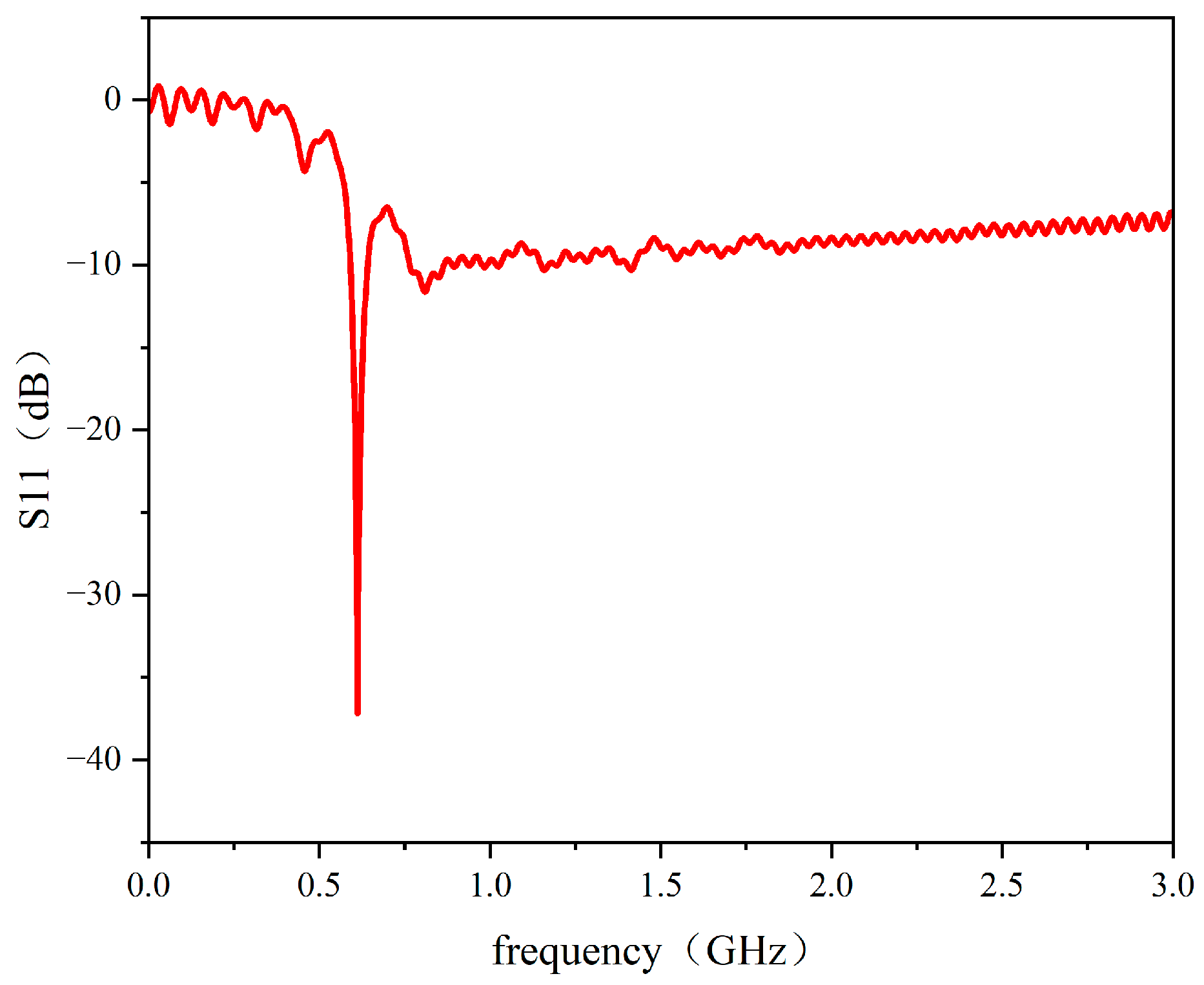
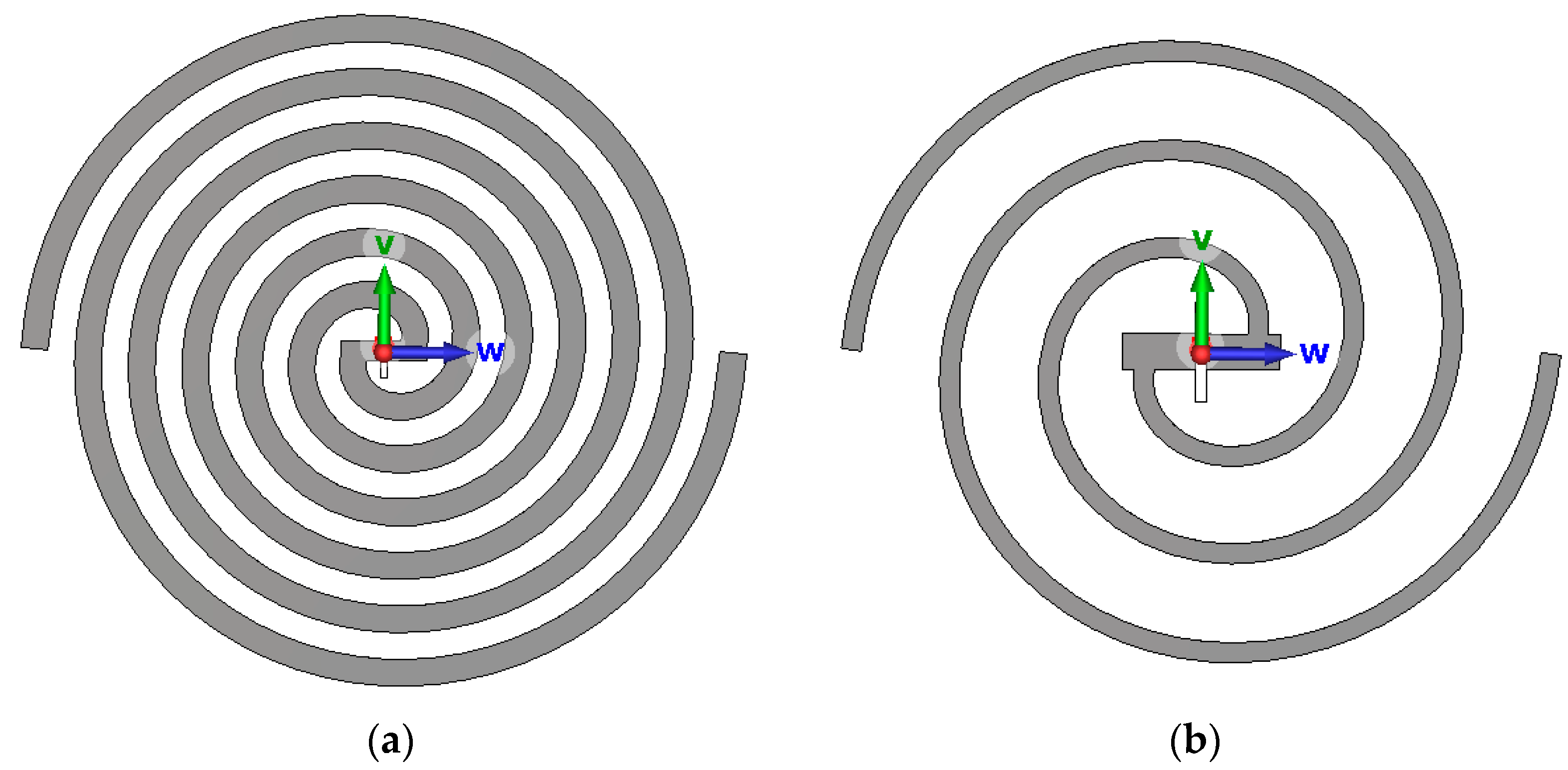
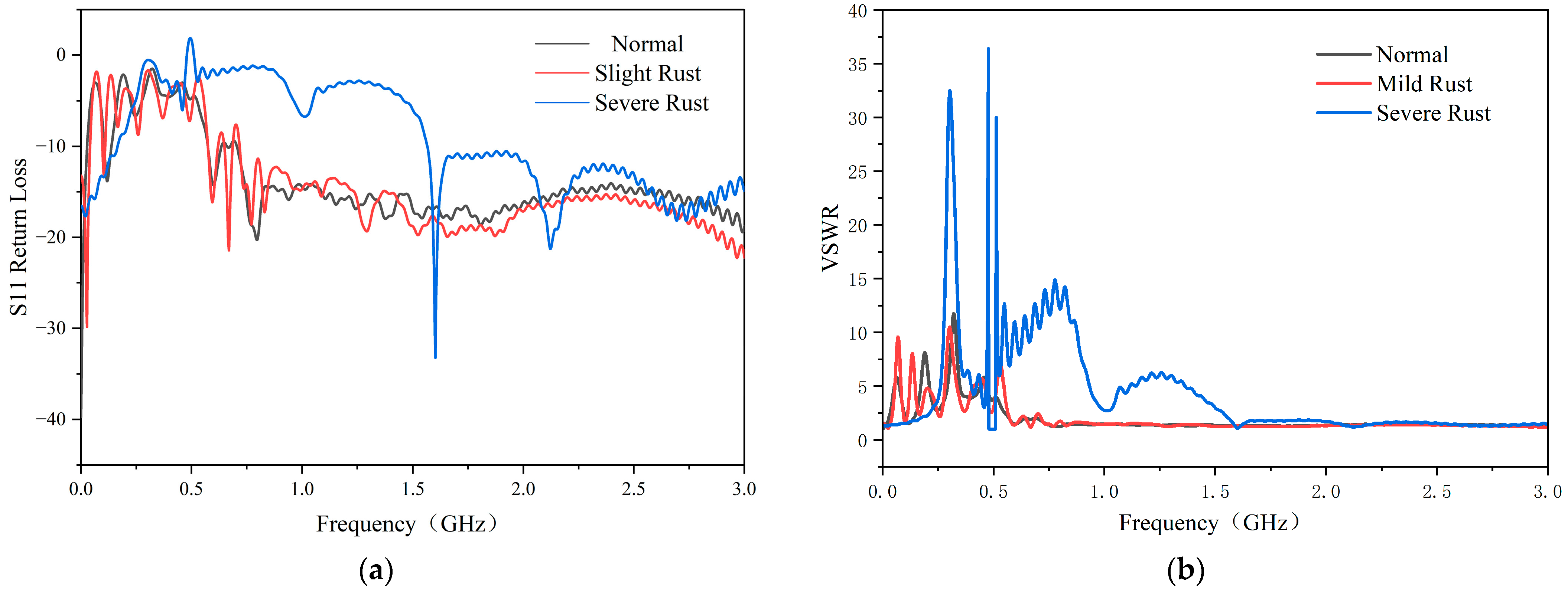
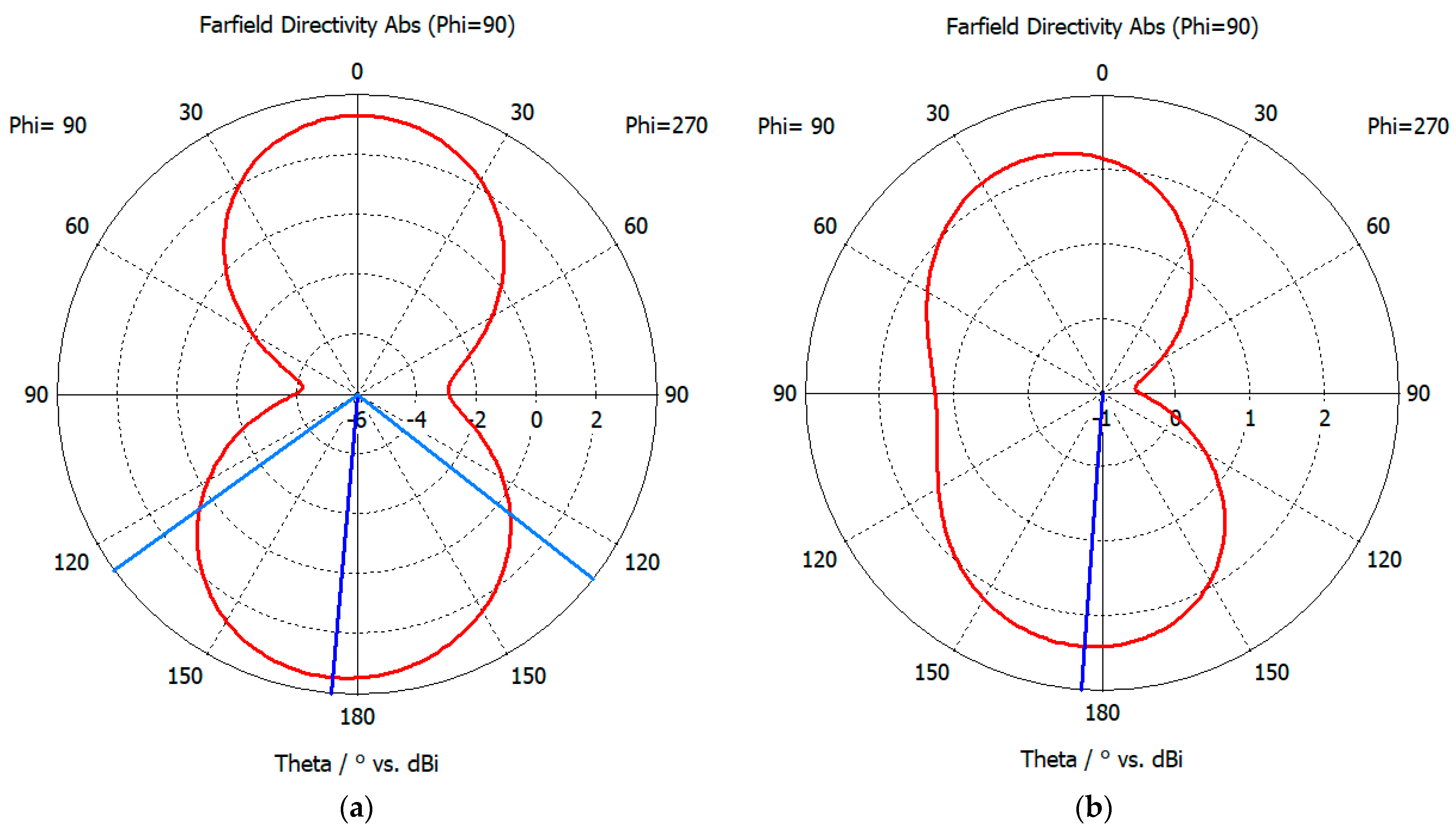

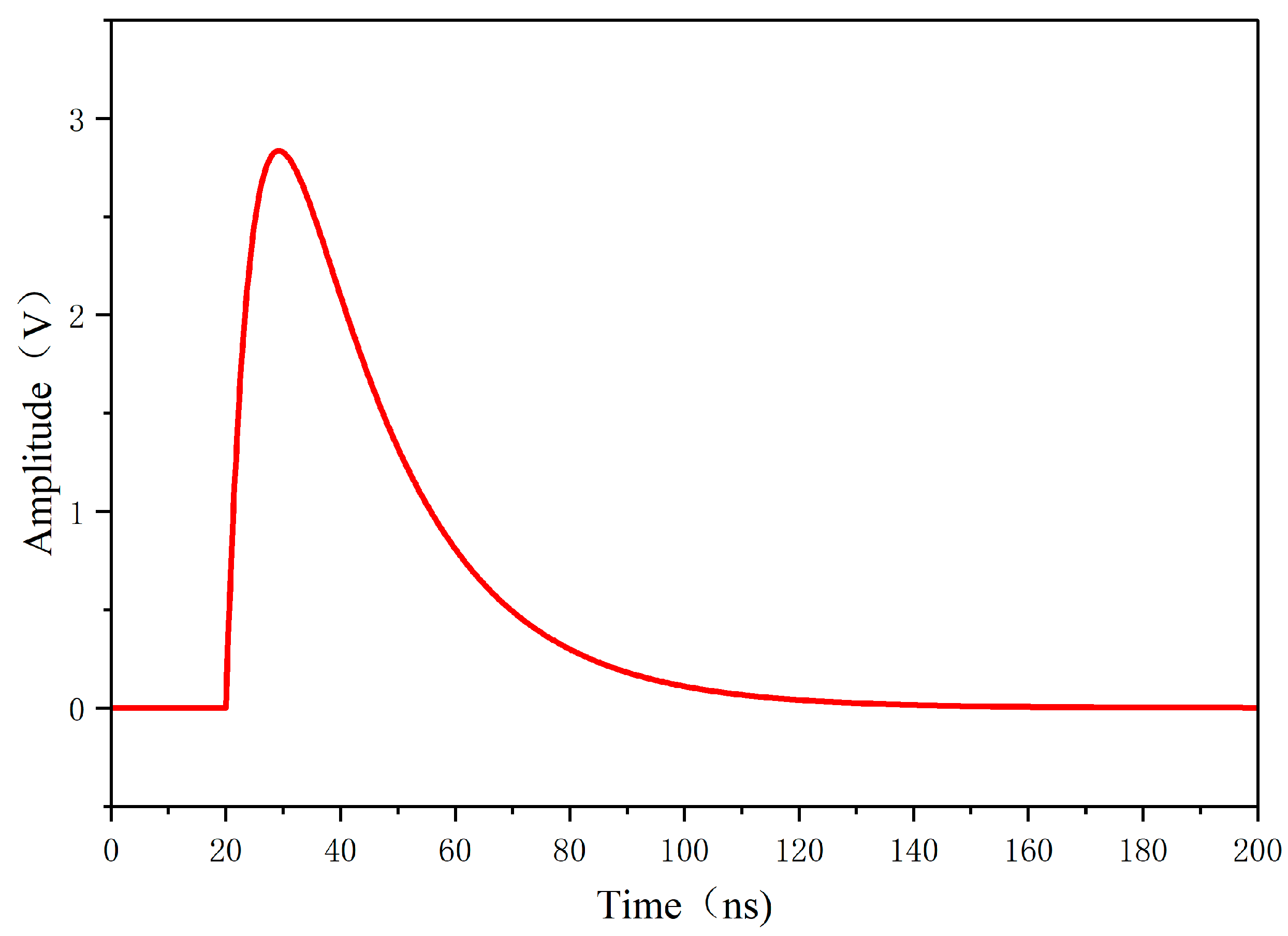
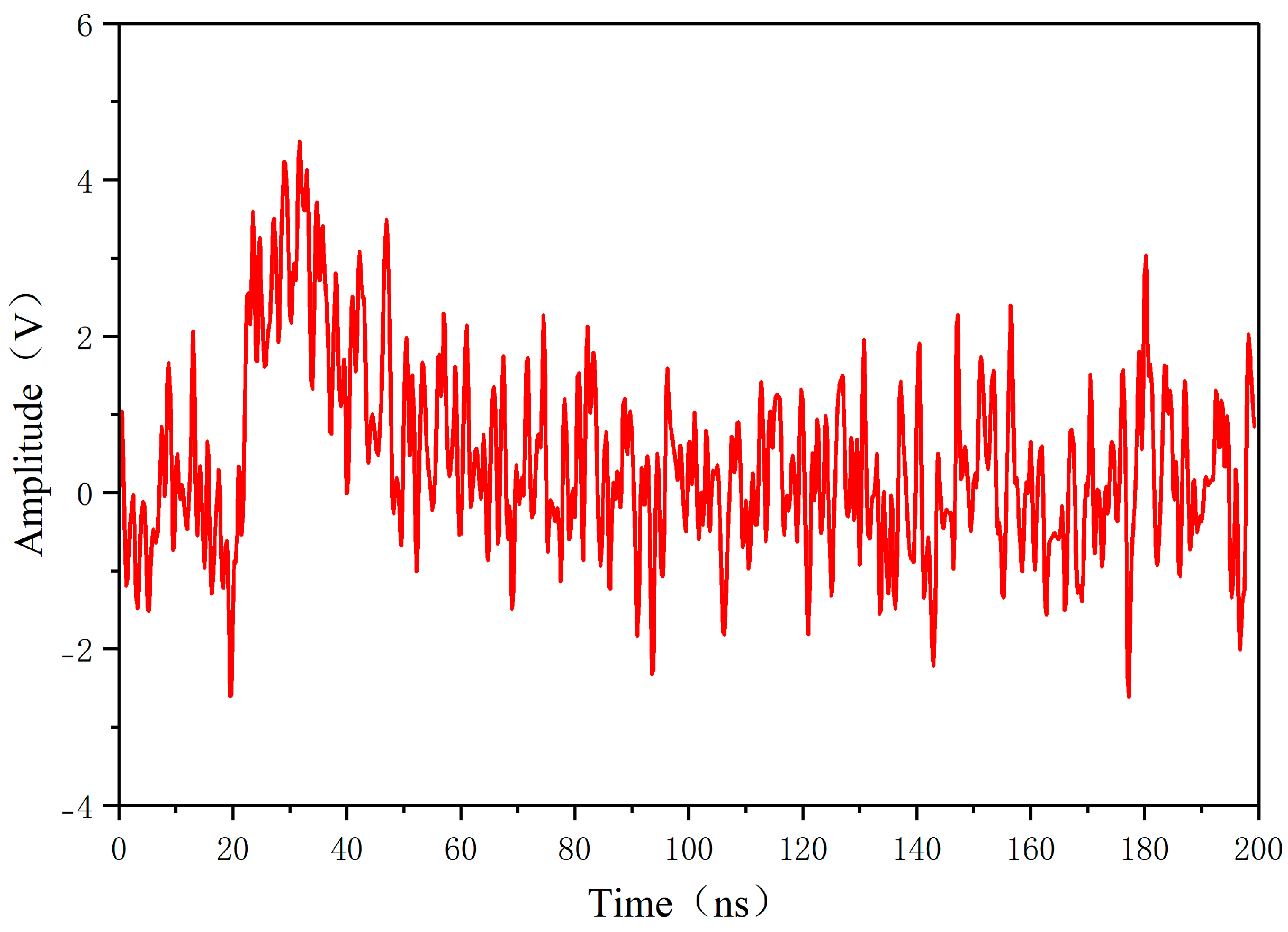
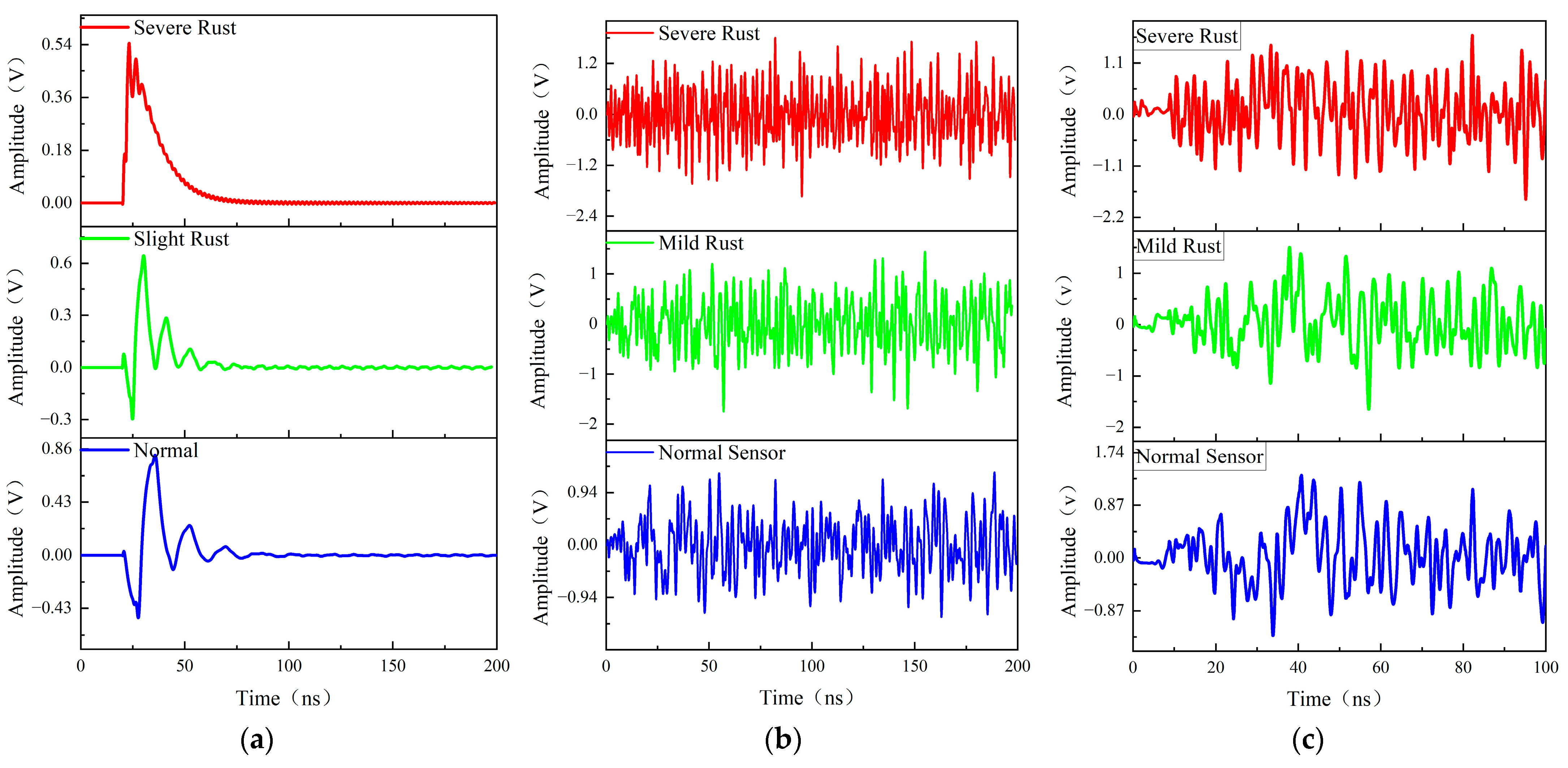
| Sensor Degradation | VSWR | S11 (Return Loss) |
|---|---|---|
| Normal | 1.94 | −13.85 dB |
| Slight corrosion | 2.19 | −14.23 dB |
| Heavy corrosion | 4.18 | −9.07 dB |
| Component | Dimensions | |
|---|---|---|
| GIS pipe body | 4.5 m | |
| GIS tube radius | Inner wall 0.26 m | Outer wall 0.27 m |
| Inner conductor | radius 0.25 m | |
| Handhole radius | Inner wall 0.14 m | Outer wall 0.15 m |
| Handhole spacing | 2.5 m | |
| Basin insulator | Radius 0.3 m | Width 0.1 m |
| Sensor Degradation | Signal Power (V2) | Noise Signal Power (V2) | SNR |
|---|---|---|---|
| Normal | 0.0237 | 0.2207 | −9.70 dB |
| Slight Corrosion | 0.0096 | 0.2541 | −14.24 dB |
| Heavy corrosion | 0.0106 | 0.3622 | −15.34 dB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Wang, L.; Yang, Y.; Zhu, Z.; Yang, H.; Wu, J.; Wu, X.; Xie, Y. Simulation Study on Anti-Interference Performance Degradation of GIS UHF Sensors Based on Substation White Noise Reconstruction. Sensors 2026, 26, 303. https://doi.org/10.3390/s26010303
Wang L, Yang Y, Zhu Z, Yang H, Wu J, Wu X, Xie Y. Simulation Study on Anti-Interference Performance Degradation of GIS UHF Sensors Based on Substation White Noise Reconstruction. Sensors. 2026; 26(1):303. https://doi.org/10.3390/s26010303
Chicago/Turabian StyleWang, Lujia, Yongze Yang, Zixi Zhu, Haitao Yang, Jie Wu, Xingwang Wu, and Yiming Xie. 2026. "Simulation Study on Anti-Interference Performance Degradation of GIS UHF Sensors Based on Substation White Noise Reconstruction" Sensors 26, no. 1: 303. https://doi.org/10.3390/s26010303
APA StyleWang, L., Yang, Y., Zhu, Z., Yang, H., Wu, J., Wu, X., & Xie, Y. (2026). Simulation Study on Anti-Interference Performance Degradation of GIS UHF Sensors Based on Substation White Noise Reconstruction. Sensors, 26(1), 303. https://doi.org/10.3390/s26010303






