Magnetic Circuit Design and Optimization of Tension–Compression Giant Magnetostrictive Force Sensor
Abstract
1. Introduction
2. Structure Design of Giant Magnetostrictive Force Sensor
3. Theoretical Model
4. Based on COMSOL Multiphysics Finite Element Simulation Analysis
4.1. Finite Element Model of Giant Magnetostrictive Force Sensor
- (1)
- Establish a two-dimensional axisymmetric model in geometry, as shown in Figure 3.
- (2)
- Define the material properties of the relevant material, as shown in Table 1. Select the domain corresponding to the material.
- (3)
- The boundary conditions, magnetic circuit and air domain are set and meshed. The results are shown in Figure 4.
- (4)
- The simulation process uses the orthogonal method to analyze the magnetic circuit and output the simulation results through the drawing group.
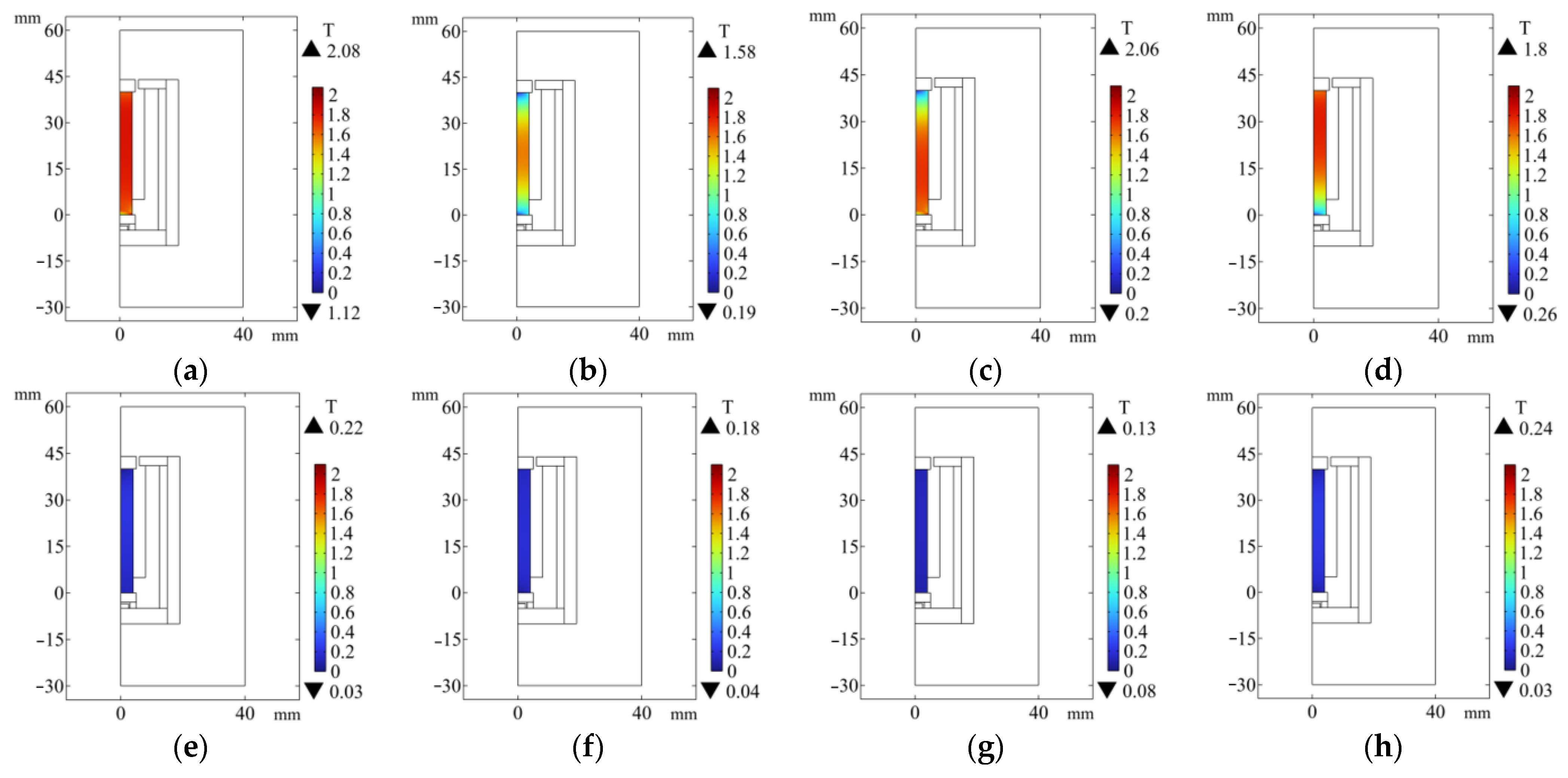
4.2. Effect of Magnetic Circuit Mode on GMM Flux
4.3. Effect of Relative Permeability of Magnetic Material on Magnetic Flux of Magnetic Circuit
4.4. The Influence of Structural Parameters of Magnetic Materials on the Magnetic Flux of Magnetic Circuit
4.5. The Influence of Air Gap on the Magnetic Flux of Magnetic Circuit
4.6. Optimized Combination of Magnetic Circuit Structure
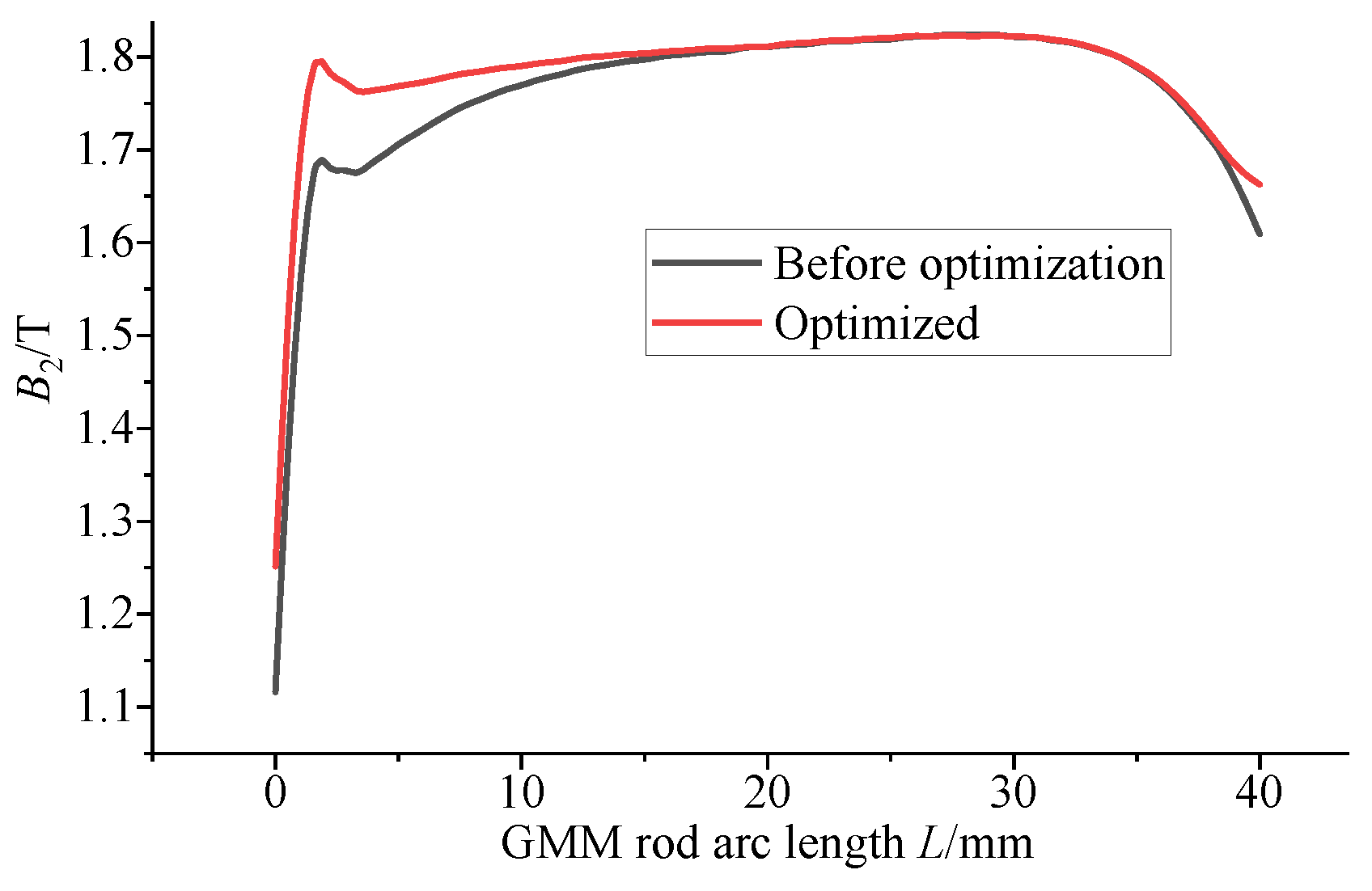
4.7. Optimization of Giant Magnetostrictive Force Sensor
5. Conclusions
- (1)
- When the permanent magnet is used to provide the bias magnetic field, the uniformity and flux of the GMM rod can be improved by using the non-magnetic side wall. The increase in the relative permeability of the magnetic material can improve the magnetic flux density and magnetic flux uniformity through the GMM rod and reduce the degree of magnetic flux leakage. With the increase in the relative permeability, the magnetic flux density and magnetic flux uniformity through the GMM rod tend to be stable.
- (2)
- The increase in the thickness of the lower conducting magnetic sheet will reduce the magnetic flux density and uniformity through the GMM rod. The increase in the thickness of the upper and lower conducting magnetic block can improve the magnetic flux density and uniformity through the GMM rod. The radius of the upper conducting magnetic block should be slightly larger than the diameter of the GMM rod. The existence of air gap will affect the magnetic flux density intensity and magnetic flux density uniformity through the GMM rod, and the air gap should be set at about 0.8 mm.
- (3)
- The flux density of the optimized giant magnetostrictive force sensor is 13.9 mT higher than that of the GMM rod before optimization, and the uniformity is increased by 7.44%. At this time, the Hall output voltage increases linearly by 1.125%, directly enhancing the output signal amplitude and effectively improving the signal-to-noise ratio of the system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, H.L.; Wang, Z.F.; Teng, F.; Xia, P.Q. Dynamic Strain Measurement of Rotor Blades in Helicopter Flight Using Fiber Bragg Grating Sensor. Sensors 2023, 23, 6692. [Google Scholar] [CrossRef] [PubMed]
- Hong, L.; Shang, L.L.; Qiu, Z.C.; Li, Y.N.; Han, Z.M. Study on Stress Detection Method of Ferromagnetic Member Based on Inverse Magneto-strictive Effect. Instrum. Tech. Sens. 2020, 6, 4. [Google Scholar]
- Jiang, S.Q. Vehicle application and research status of giant magnetostrictive materials. Times Automot. 2021, 20, 6–7. [Google Scholar]
- Chen, Y.K.; Yang, X.; Yang, M.Z. Characterization of Giant Magnetostrictive Materials Using Three Complex Material Parameters by Particle Swarm Optimization. Micromachines 2021, 12, 1416. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Zhang, J.; Feng, P.; Yu, D.; Wang, J. On the optimum resonance of giant magnetostrictive ultrasonic transducer with capacitance-based impedance compensation. Smart Mater. Struct. 2020, 29, 105002. [Google Scholar] [CrossRef]
- Yan, R.; Yang, Q. Research on giant magnetostrictive force sensor. In Proceedings of the 2009 National Electrical Theory and New Technology Annual Conference (CTATEE’09), Harbin, China, 10–13 August 2009; pp. 220–223. [Google Scholar]
- Liu, H.; Jia, Z. Research on key technologies of giant magnetostrictive material force sensing actuator. J. Mech. Eng. 2014, 50, 1. [Google Scholar] [CrossRef]
- Talebian, S. Theoretical and experimental study on optimum operational conditions of a magnetostrictive force sensor. J. Magn. Magn. Mater. 2022, 562, 169847. [Google Scholar] [CrossRef]
- Bian, L.X.; Peng, W.M.; Huang, Z.J. Modeling and Design of Resonant Magnetic Field Sensors in the Scheme of Differential Magnetostrictive Actuation with Compact Bias Magnetic Circuit. IEEE Sens. J. 2022, 22, 9361–9370. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, J.; Lu, G. Magnetic circuit optimization design and analysis of giant magnetostrictive force sensing actuator. Sens. Microsyst. 2024, 43, 115–119. [Google Scholar]
- Liu, Y.; Meng, J.; Tang, R. Magnetic circuit simulation and optimization of giant magnetostrictive actuator based on COMSOL. J. Lanzhou Jiaotong Univ. 2023, 42, 79–84+131. [Google Scholar]
- Tu, J.W.; Liu, Z.F.; Li, Z. Magnetic circuit optimization design and finite element analysis of giant magnetostrictive actuator. J. Chongqing Univ. 2021, 44, 52–63. [Google Scholar] [CrossRef]
- Deng, J. Study on giant magnetostrictive material with transducer finite element analysis. Adv. Mater. Res. 2013, 700, 3–6. [Google Scholar]
- Xue, G.M.; Zhang, P.L.; Li, X.Y. A review of giant magnetostrictive injector (GMI). Sens. Actuators A Phys. 2018, 273, 159–181. [Google Scholar] [CrossRef]
- Huang, W.M.; Li, Y.F.; Weng, L. Multifield Coupling Model with Dynamic Losses for Giant Magnetostrictive Transducer. IEEE Trans. Appl. Supercond. 2016, 26, 4900805. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, X.; Li, S. Dynamic modeling of stack giant magnetostrictive actuator with magnetic equivalent network considering eddy current effect. J. Appl. Phys. 2022, 131, 224503. [Google Scholar] [CrossRef]
- Engdahl, G. Handbook of Giant Magnetostrictive Materials; Elsevier: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Shi, R. Research on the Design of Force Sensor Based on GMM Magnetic Theory and Its Accuracy Guarantee Strategy. Master’s Thesis, Anhui University of Science and Technology, Hefei, China, 2022. [Google Scholar]
- Shi, J. Study on the Characteristics of Several Proportional Solenoid Valve Actuators. Master’s Thesis, Taiyuan University of Technology, Taiyuan, China, 2005. [Google Scholar]
- Chen, J.; Fu, J.; Jiang, J. Study on magnetic characteristics of four-redundancy linear force motor for direct drive servo valve. Mach. Tool Hydraul. 2024, 52, 167–172. [Google Scholar]
- Yu, Z.; Zhao, H.; Zhang, C. Simulation analysis of axial non-uniform magnetic field of giant magnetostrictive actuator. Magn. Mater. Devices 2019, 50, 10–16. [Google Scholar]
- Yang, X.L.; Zhu, Y.C.; Fei, S.S. Magnetic field analysis and optimization of giant magnetostrictive electro-hydrostatic actuator. J. Aeronaut. Dyn. 2016, 31, 2210–2217. [Google Scholar]
- Yu, C.; Wang, C.; Deng, H. Analysis and optimization of magnetic field performance of giant magnetostrictive actuator. Mod. Manuf. Eng. 2015, 8, 136–140. [Google Scholar]
- Cui, L. Design and Research of Pressure Sensor Based on Inverse Magnetostrictive Effect. Master’s Thesis, Anhui University of Science and Technology, Hefei, China, 2020. [Google Scholar]
- Yan, H.; Cao, R.; Wang, J. Performance simulation analysis of vibration isolation and energy harvesting dual-function giant magnetostrictive actuator. Magn. Mater. Devices 2021, 52, 73–77. [Google Scholar]
- Lu, Y.; Yu, H.; Li, G. Experimental Design and Data Processing; Chemical Industry Press: Beijing, China, 2021; p. 197. [Google Scholar]






















| GMM | Stainless Steel | Soft Iron | Air | Permanent Magnet | |
|---|---|---|---|---|---|
| Young’s modulus (Pa) | 6 × 1010 | ||||
| Poisson ratio (1) | 0.45 | ||||
| Density (kg/m3) | 9250 | 7900 | |||
| Electric conductivity (S/m) | 5.96 × 106 | 1.73913 × 106 | 0 | 0 | |
| Relative dielectric constant (1) | 1 | 1 | 1 | 1 | 1 |
| Saturation magnetization (A/m) | 1.5 × 106 | ||||
| Saturation magnetostriction (ppm) | 1500 | ||||
| Relative permeability (1) | B–H curve | 1 | B–H curve | 1 | |
| Recoverable permeability (1) | 1.05 | ||||
| Remanence (T) | 1.2 | ||||
| Relative permeability (1) | 1.05 |
| Level | Factor | ||||
|---|---|---|---|---|---|
| Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | |
| 1 | 1 | 2 | 2 | 1 | 0.2 |
| 2 | 3 | 4 | 4 | 3 | 0.4 |
| 3 | 5 | 6 | 6 | 5 | 0.6 |
| 4 | 9 | 9 | 9 | 6 | 0.8 |
| Numbering | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Result |
|---|---|---|---|---|---|---|
| 1 | 1(1) | 1(2) | 1(2) | 1(1) | 1(0.2) | 42.42% |
| 2 | 1(1) | 2(4) | 2(4) | 2(3) | 2(0.4) | 64.97% |
| 3 | 1(1) | 3(6) | 3(6) | 3(5) | 3(0.6) | 68.81% |
| 4 | 1(1) | 4(9) | 4(9) | 4(6) | 4(0.8) | 70.12% |
| 5 | 2(3) | 1(2) | 2(4) | 3(5) | 4(0.8) | 64.85% |
| 6 | 2(3) | 2(4) | 1(2) | 4(6) | 3(0.6) | 55.47% |
| 7 | 2(3) | 3(6) | 4(9) | 1(1) | 2(0.4) | 50.01% |
| 8 | 2(3) | 4(9) | 3(6) | 2(3) | 1(0.2) | 63.82% |
| 9 | 3(5) | 1(2) | 3(6) | 4(6) | 2(0.4) | 66.97% |
| 10 | 3(5) | 2(4) | 4(9) | 3(5) | 1(0.2) | 70.73% |
| 11 | 3(5) | 3(6) | 1(2) | 2(3) | 4(0.8) | 58.25% |
| 12 | 3(5) | 4(9) | 2(4) | 1(1) | 3(0.6) | 43.70% |
| 13 | 4(8) | 1(2) | 4(9) | 2(3) | 3(0.6) | 54.30% |
| 14 | 4(8) | 2(4) | 3(6) | 1(1) | 4(0.8) | 54.28% |
| 15 | 4(8) | 3(6) | 2(4) | 4(6) | 1(0.2) | 60.77% |
| 16 | 4(8) | 4(9) | 1(2) | 3(5) | 2(0.4) | 56.20% |
| K1 | 246.32% | 228.55% | 212.34% | 189.75% | 237.74% | |
| K2 | 234.15% | 244.78% | 234.29% | 241.34% | 238.15% | |
| K3 | 239.66% | 237.85% | 253.22% | 260.58% | 222.29% | |
| K4 | 224.88% | 233.83% | 245.16% | 253.33% | 246.83% | |
| N1 | 61.58% | 57.14% | 53.09% | 47.44% | 59.44% | |
| N2 | 58.54% | 61.20% | 58.57% | 60.34% | 59.54% | |
| N3 | 59.91% | 59.46% | 63.30% | 65.15% | 55.57% | |
| N4 | 56.22% | 58.46% | 61.29% | 63.33% | 61.71% | |
| R | 5.36% | 4.06% | 10.22% | 17.71% | 6.14% | |
| Secondary factors | Ⅳ, Ⅲ, Ⅴ, Ⅰ, Ⅱ | |||||
| Superior level | Ⅳ3, Ⅲ3, Ⅴ4, Ⅰ1, Ⅱ2 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Li, L.; Sun, H.; Wei, Y.; Li, B.; Cui, H.; Liu, R. Magnetic Circuit Design and Optimization of Tension–Compression Giant Magnetostrictive Force Sensor. Sensors 2026, 26, 295. https://doi.org/10.3390/s26010295
Li L, Sun H, Wei Y, Li B, Cui H, Liu R. Magnetic Circuit Design and Optimization of Tension–Compression Giant Magnetostrictive Force Sensor. Sensors. 2026; 26(1):295. https://doi.org/10.3390/s26010295
Chicago/Turabian StyleLi, Long, Hailong Sun, Yingling Wei, Boda Li, Hongwei Cui, and Ruifeng Liu. 2026. "Magnetic Circuit Design and Optimization of Tension–Compression Giant Magnetostrictive Force Sensor" Sensors 26, no. 1: 295. https://doi.org/10.3390/s26010295
APA StyleLi, L., Sun, H., Wei, Y., Li, B., Cui, H., & Liu, R. (2026). Magnetic Circuit Design and Optimization of Tension–Compression Giant Magnetostrictive Force Sensor. Sensors, 26(1), 295. https://doi.org/10.3390/s26010295





