Efficient Deep Learning Model Compression for Sensor-Based Vision Systems via Outlier-Aware Quantization
Abstract
1. Introduction
- We introduce a novel perspective that perceptually approximating the trained weight distribution is critical for minimizing quantization error in post-training settings. To the best of our knowledge, this is the first work to apply the structural similarity (SSIM) index to weight distribution evaluation in quantization.
- We propose outlier-aware quantization (OAQ), a lightweight post-training method that adaptively rescales weight outliers to reduce dynamic range distortion and improve quantization resolution, without requiring retraining or data access.
- The proposed OAQ method is model-agnostic and compatible with a wide range of quantization schemes, including both uniform and non-uniform strategies. It can be seamlessly integrated into existing pipelines with negligible computational overhead.
- Extensive experiments on multiple architectures and bit widths demonstrated that OAQ significantly improved performance, particularly under 4-bit quantization, compared with prior PTQ baselines.
2. Related Work
2.1. Outlier-Handling Techniques
2.2. Uniform/Non-Uniform Quantization
2.3. Quantization-Aware Training and Post-Training Quantization
3. Outlier-Aware Quantization
3.1. Motivation
3.2. PTQ-Friendly Weight Distribution Reshaping
3.3. Handling Outliers with Scaling Factor
| Algorithm 1: A Modified Weight Normalization-based PTQ Method Exploiting OAQ | ||
| Input: – The full-precision trained weights | ||
| Output: – The quantized weights | ||
| 1: | Procedure FINE-TUNING | |
| 2: | Initialize weights to | |
| 3: | for do | |
| 4: | ||
| 5: | ||
| 6: | Compute the loss | |
| 7: | Compute the gradient w.r.t. the output | |
| 8: | for do | |
| 9: | Given | |
| 10: | Compute the gradient of the | |
| 11: | Update the | |
| 12: | Compute | |
| 13: | Procedure INFERENCE | |
| 14: | Initialize weights to | |
| 15: | for do | |
| 16: | ||
| 17: | ||
| 18: | Deploy the quantized weights | |
| 19: | End | |
3.4. Fine-Tuning of Scaling Factor
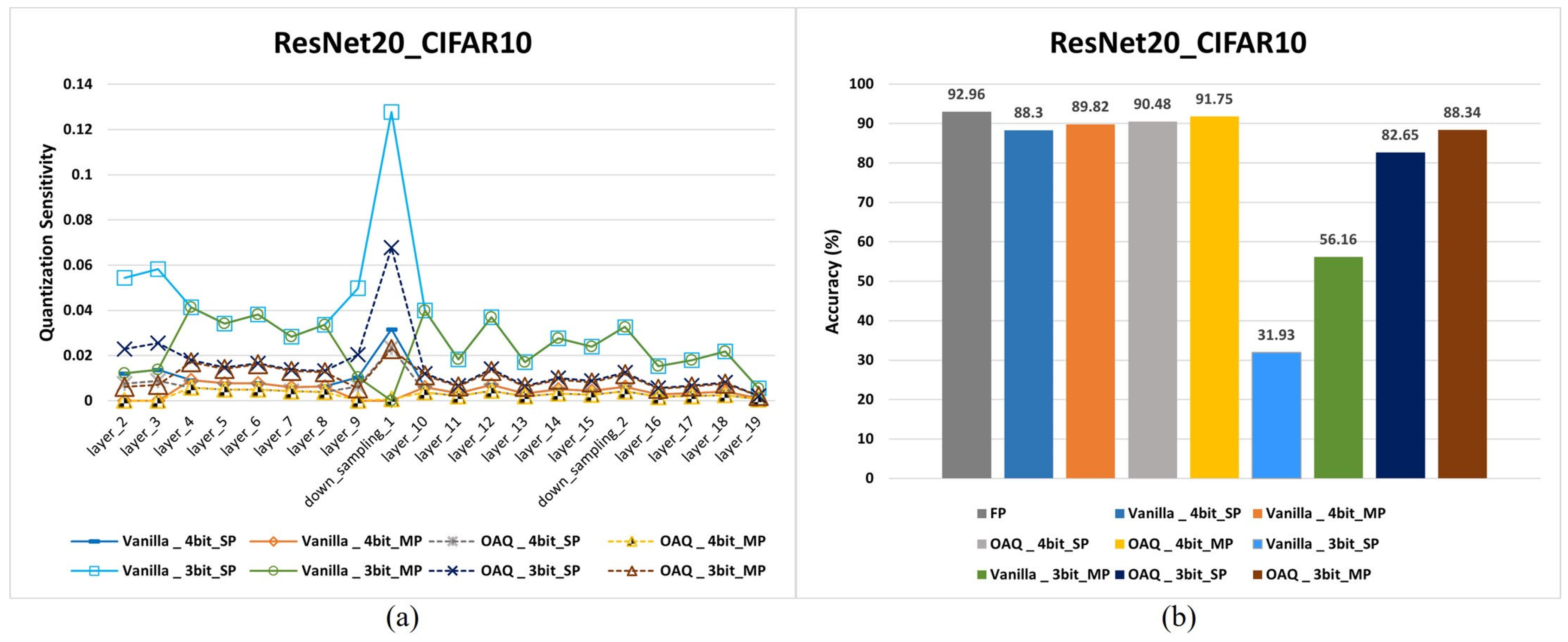
3.5. Measuring Quantization Sensitivity
4. Experiments
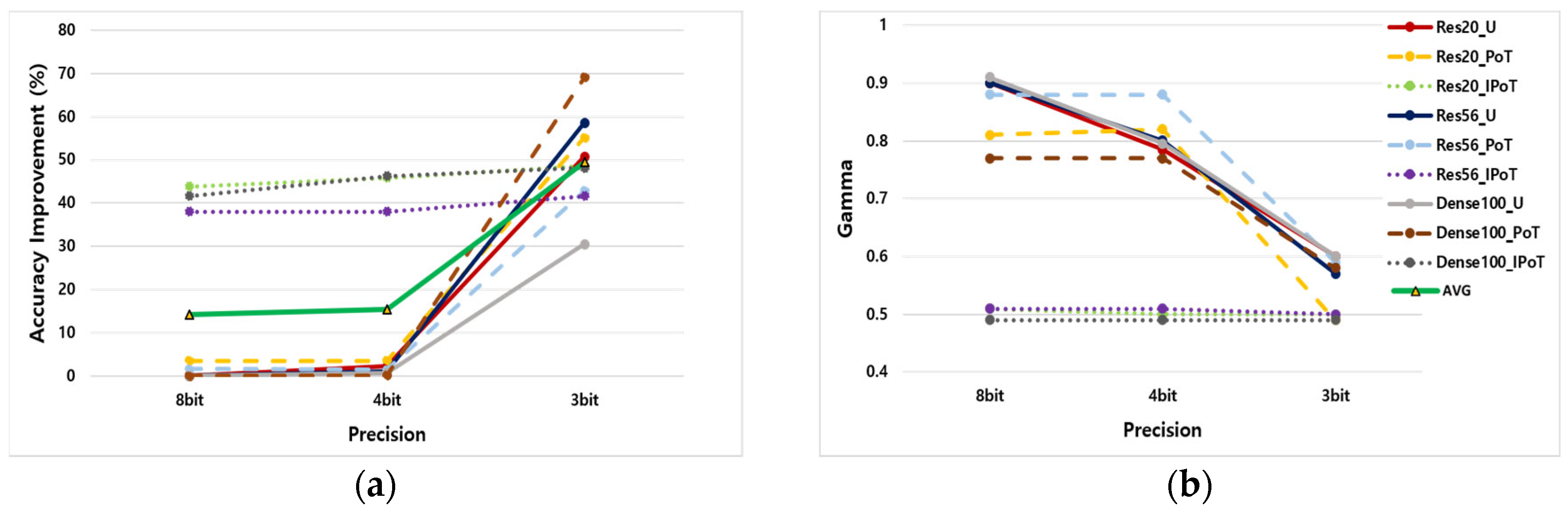
4.1. Fixed Scaling Factor in Uniform and Non-Uniform OAQ
4.2. Fine-Tuning the Scaling Factor for Optimization
4.3. OAQ with Mixed-Precision Quantization
4.4. Integrating OAQ with Quantization-Aware Training
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DNN | Deep neural network |
| CNN | Convolutional neural network |
| QAT | Structural similarity |
| OAQ | Outlier-aware quantization |
| PTQ | Post-training quantization |
| QAT | Quantization-aware training |
| QIL | Quantization interval learning |
| OCS | Outlier channel splitting |
| DFQ | Data free quantization |
| PoT | Power-of-two |
| IPoT | Inverse power-of-two |
| GDPR | General data protection regulation |
| ACIQ | Analytical clipping for integer quantization |
| STE | Straight-through estimator |
| KLD | Kullback–Leibler divergence |
| SP | Single precision |
| MP | Mixed precision |
| FP | Full precision |
| FT | Fine-tuning |
References
- Fabre, W.; Haroun, K.; Lorrain, V.; Lepecq, M.; Sicard, G. From near-sensor to in-sensor: A state-of-the-art review of embedded AI vision systems. Sensors 2024, 24, 5446. [Google Scholar] [CrossRef] [PubMed]
- Ju, Z.; Zhang, H.; Li, X.; Chen, X.; Han, J.; Yang, M. A survey on attack detection and resilience for connected and automated vehicles: From vehicle dynamics and control perspective. IEEE Trans. Intell. Veh. 2022, 7, 815–837. [Google Scholar] [CrossRef]
- Khan, S.; Adnan, A.; Iqbal, N. Applications of artificial intelligence in transportation. In Proceedings of the 2022 International Conference on Electrical, Computer and Energy Technologies (ICECET), Prague, Czech Republic, 20–22 July 2022. [Google Scholar] [CrossRef]
- Hwang, G.; Park, M.; Lee, S. Lightweight deep learning model for heart rate estimation form facial videos. IEMEK J. Embed. Syst. Appl. 2023, 18, 51–58. [Google Scholar] [CrossRef]
- Hwang, S. Performance analysis of lightweight AI frameworks for on-device vision inspection. IEMEK J. Embed. Syst. Appl. 2024, 19, 275–281. [Google Scholar] [CrossRef]
- Lee, M.; Lee, S.; Kim, T. Performance evaluation of efficient vision transformers on embedded edge platforms. IEMEK J. Embed. Syst. Appl. 2023, 18, 89–100. [Google Scholar] [CrossRef]
- Sze, V.; Chen, Y.H.; Yang, T.J.; Emer, J.S. Efficient processing of deep neural networks: A tutorial and survey. Proc. IEEE 2017, 42, 513–520. [Google Scholar] [CrossRef]
- Kuzmin, A.; Van Baalen, M.; Ren, Y.; Nagel, M.; Peters, J.; Blankevoort, T. FP8 quantization: The power of the exponent. arXiv 2022, arXiv:2208.09225. [Google Scholar]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. XNOR-Net: ImageNet Classification Using Binary Convolutional Neural Networks. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016; Springer: Cham, Switzerland, 2016; pp. 525–542. [Google Scholar] [CrossRef]
- Rusci, M.; Capotondi, A.; Benini, L. Memory-driven mixed low precision quantization for enabling deep network inference on microcontrollers. arXiv 2019, arXiv:1905.13082. [Google Scholar]
- Vandersteegen, M.; Van Beeck, K.; Goedemé, T. Integer-only CNNs with 4 bit weights and bit-shift quantization scales at full-precision accuracy. Electronics 2021, 10, 2823. [Google Scholar] [CrossRef]
- Zhang, Y.; Matinez-Rau, L.S.; Vu, Q.N.P.; Oelmann, B.; Bader, S. Survey of quantization techniques for on-device vision-based crack detection. arXiv 2025, arXiv:2502.02269. [Google Scholar]
- Lee, D.; Kim, J.; Moon, W.; Ye, J. CollaGAN: Collaborative GAN for missing image data imputation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 2487–2496. [Google Scholar]
- Nie, X.; Ding, H.; Qi, M.; Wang, Y.; Wong, E.K. URCA-GAN: UpSample residual channel-wise attention generative adversarial network for image-to-image translation. Neurocomputing 2021, 443, 75–84. [Google Scholar] [CrossRef]
- Przeqlocka-Rus, D.; Kryjak, T. Power-of-Two quantized YOLO network for pedestrian detection with dynamic vision sensor. In Proceedings of the 26th Euromicro Conference on Digital System Design, Golem, Albania, 6–8 September 2023. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, Y.; Sheng, H. Residual networks for light field image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11046–11055. [Google Scholar] [CrossRef]
- Courbariaux, M.; Hubara, I.; Soudry, D.; El-Yaniv, R.; Bengio, Y. Binarized neural networks. Adv. Neural Inf. Process. Syst. (NeurIPS) 2016, 29, 4114–4122. [Google Scholar]
- Li, F.; Liu, B. Ternary Weight Networks. arXiv 2016, arXiv:1605.04711. [Google Scholar]
- Zhou, S.; Wu, Y.; Ni, Z.; Zhou, X.; Wen, H.; Zou, Y. Dorefa-net: Training low bitwidth convolutional neural networks with low bitwidth gradients. arXiv 2016, arXiv:1606.06160. [Google Scholar]
- Banner, R.; Nahshan, Y.; Hoffer, E.; Soudry, D. ACIQ: Analytical Clipping for Integer Quantization of Neural Networks. OpenReview. Available online: https://openreview.net/forum?id=B1x33sC9KQ (accessed on 28 September 2018).
- Banner, R.; Nahshan, Y.; Soudry, D. Post-training 4-bit quantization of convolutional networks for rapid deployment. Adv. Neural Inf. Process. Syst. 2019, 32, 7950–7958. [Google Scholar]
- Choi, J.; Wang, Z.; Venkataramani, S.; Chuang, P.; Srinivasan, V.; Gopalakrishnan, K. Pact: Parameterized clipping activation for quantized neural networks. arXiv 2018, arXiv:1805.06085. [Google Scholar]
- Hong, C.; Kim, H.; Baik, S.; Oh, J.; Lee, K. DAQ: Channel-wise distribution-aware quantization for deep image super-resolution networks. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 2675–2684. [Google Scholar]
- Ryu, H.; Park, N.; Shim, H. DGQ: Distribution-aware group quantization for text-to-image diffusion models. arXiv 2025, arXiv:2501.04304. [Google Scholar]
- Shen, X.; Kong, Z.; Yang, C.; Han, Z.; Lu, L.; Dong, P.; Lyu, C.; Li, C.; Guo, X.; Shu, Z.; et al. EdgeQAT: Entropy and distribution guided quantization-aware training for the acceleration of lightweight LLMs on the edge. arXiv 2024, arXiv:2402.10787. [Google Scholar]
- Cai, W.; Li, W. Weight normalization based quantization for deep neural network compression. arXiv 2019, arXiv:1907.00593. [Google Scholar]
- Jung, S.; Son, C.; Lee, S.; Son, J.; Han, J.; Kwak, Y.; Choi, C. Learning to quantize deep networks by optimizing quantization intervals with task loss. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 4350–4359. [Google Scholar]
- Zhao, R.; Hu, Y.; Dotzel, J.; De Sa, C.; Zhang, Z. Improving neural network quantization without retraining using outlier channel splitting. arXiv 2019, arXiv:1901.09504. [Google Scholar]
- Nagel, M.; Baalen, M.V.; Blankevoort, T.; Welling, M. Data-free quantization through weight equalization and bias correction. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 1325–1334. [Google Scholar]
- Baskin, C.; Schwartz, E.; Zheltonozhskii, E.; Liss, N.; Giryes, R.; Bronstein, A.; Mendelson, A. UNIQ: Uniform noise injection for non-uniform quantization of neural networks. arXiv 2018, arXiv:1804.10969. [Google Scholar] [CrossRef]
- Wess, M.; Dinakarrao, S.M.P.; Jantsch, A. Weighted quantization-regularization in DNNs for weight memory minimization toward HW implementation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 2929–2939. [Google Scholar] [CrossRef]
- Choi, J.; Yoo, J. Performance evaluation of stochastic quantization methods for compressing the deep neural network model. J. Inst. Control Robot. Syst. 2019, 25, 775–781. [Google Scholar] [CrossRef]
- Li, Y.; Dong, X.; Wang, W. Additive powers-of-two quantization: An efficient non-uniform discretization for neural networks. arXiv 2019, arXiv:1909.13144. [Google Scholar]
- Liu, Z.; Cheng, K.T.; Huang, D.; Xing, E.P.; Shen, Z. Nonuniform-to-uniform quantization: Towards accurate quantization via generalized straight-through estimation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 4942–4952. [Google Scholar]
- Zhang, D.; Yang, J.; Ye, D.; Hua, G. LQ-nets: Learned quantization for highly accurate and compact deep neural networks. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 373–390. [Google Scholar]
- Gong, R.; Liu, X.; Jiang, S.; Li, T.; Hu, P.; Lin, J.; Yu, F.; Yan, J. Differentiable soft quantization: Bridging full-precision and low-bit neural networks. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 4852–4861. [Google Scholar]
- Dong, Z.; Yao, Z.; Gholami, A.; Mahoney, M.W.; Keutzer, K. HAWQ: Hessian-aware quantization of neural networks with mixed-precision. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 293–302. [Google Scholar]
- Cai, Y.; Yao, Z.; Dong, Z. Zeroq: A novel zero shot quantization framework. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Yang, Z.; Lin, T.; Li, C.; Qian, B.; Yang, X.; Wei, X. Adaptive knowledge transfer for data-free low-bit quantization via tiered collaborative learning. Neurocomputing 2025, 638, 130097. [Google Scholar] [CrossRef]
- Sun, X.; Panda, R.; Chen, C.; Wang, N.; Pan, B.; Oliva, A.; Feris, R.; Saenko, K. Improved techniques for quantizing deep networks with adaptive bit-widths. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 1–6 January 2024; pp. 957–967. [Google Scholar]
- Azizi, S.; Nazemi, M.; Fayyazi, A.; Pedram, M. Sensitivity-aware mixed-precision quantization and width optimization of deep neural networks through cluster-based tree-structured parzan estimation. arXiv 2024, arXiv:2308.06422. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Horé, A.; Ziou, D. Image quality metrics: PSNR vs. SSIM. In Proceedings of the 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Yu, H.; Wen, T.; Cheng, G.; Sun, J.; Han, Q.; Shi, J. Low-bit quantization needs good distribution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 680–681. [Google Scholar] [CrossRef]
- Bengio, Y.; Léonard, N.; Courville, A. Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv 2013, arXiv:1308.3432. [Google Scholar]
- Le, H.; Høier, R.K.; Lin, C.T.; Zach, C. AdaSTE: An adaptive straight-through estimator to train binary neural networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 460–469. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar] [CrossRef]
- Ban, G.; Yoo, J. SWNQ: Scaled weight normalization based post-training quantization method. J. Korean Inst. Commun. Inf. Sci. 2021, 46, 583–590. [Google Scholar] [CrossRef]
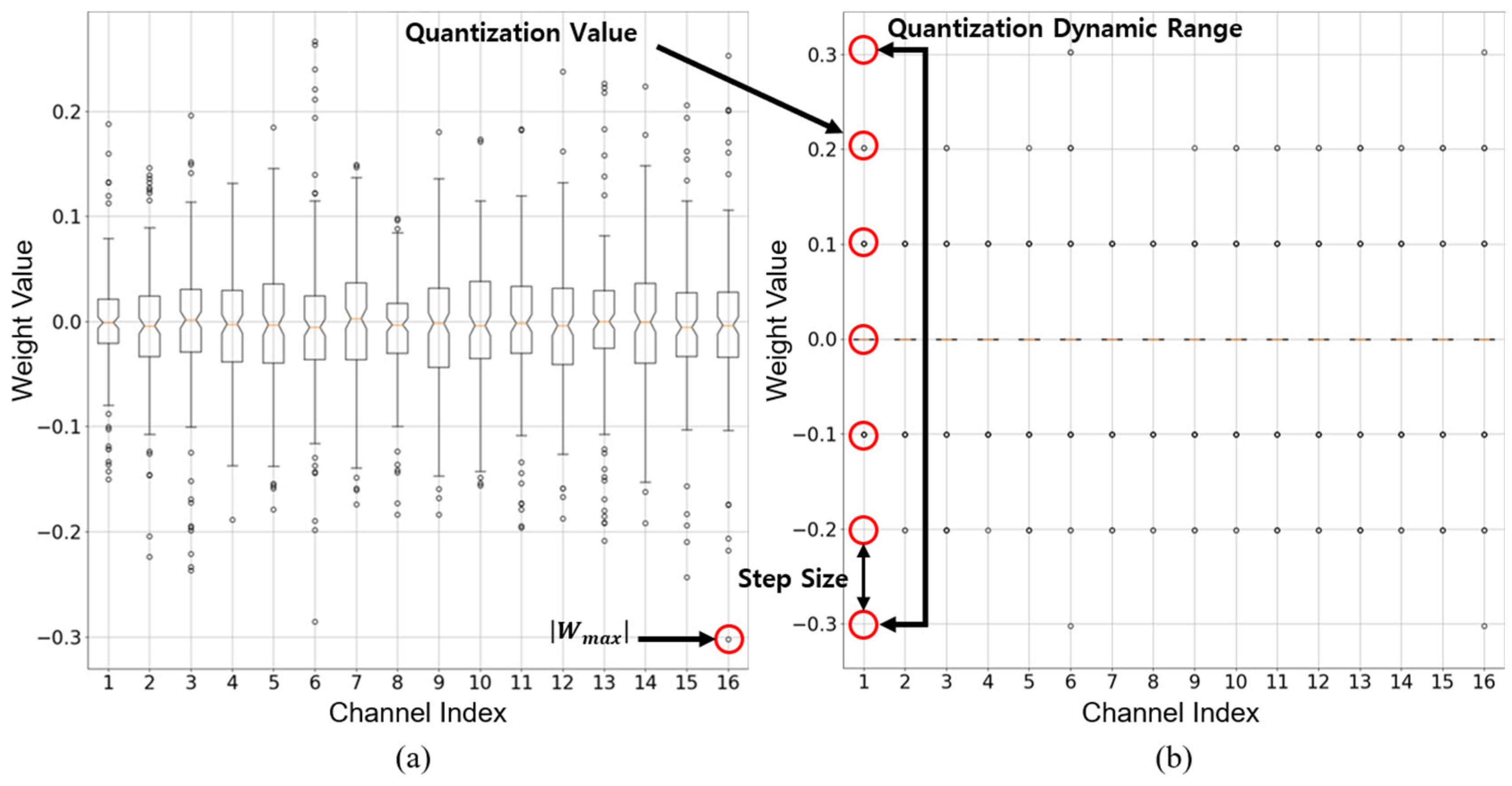
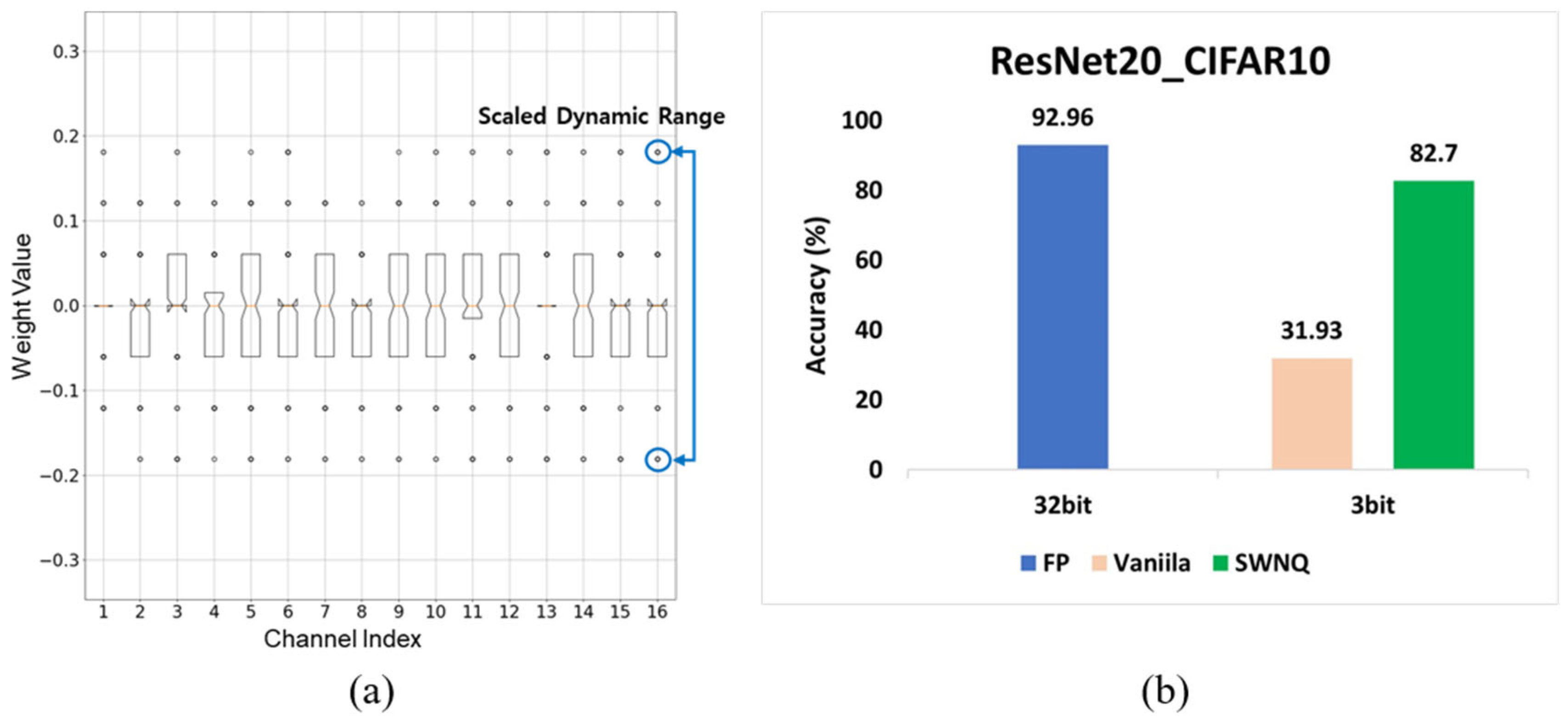

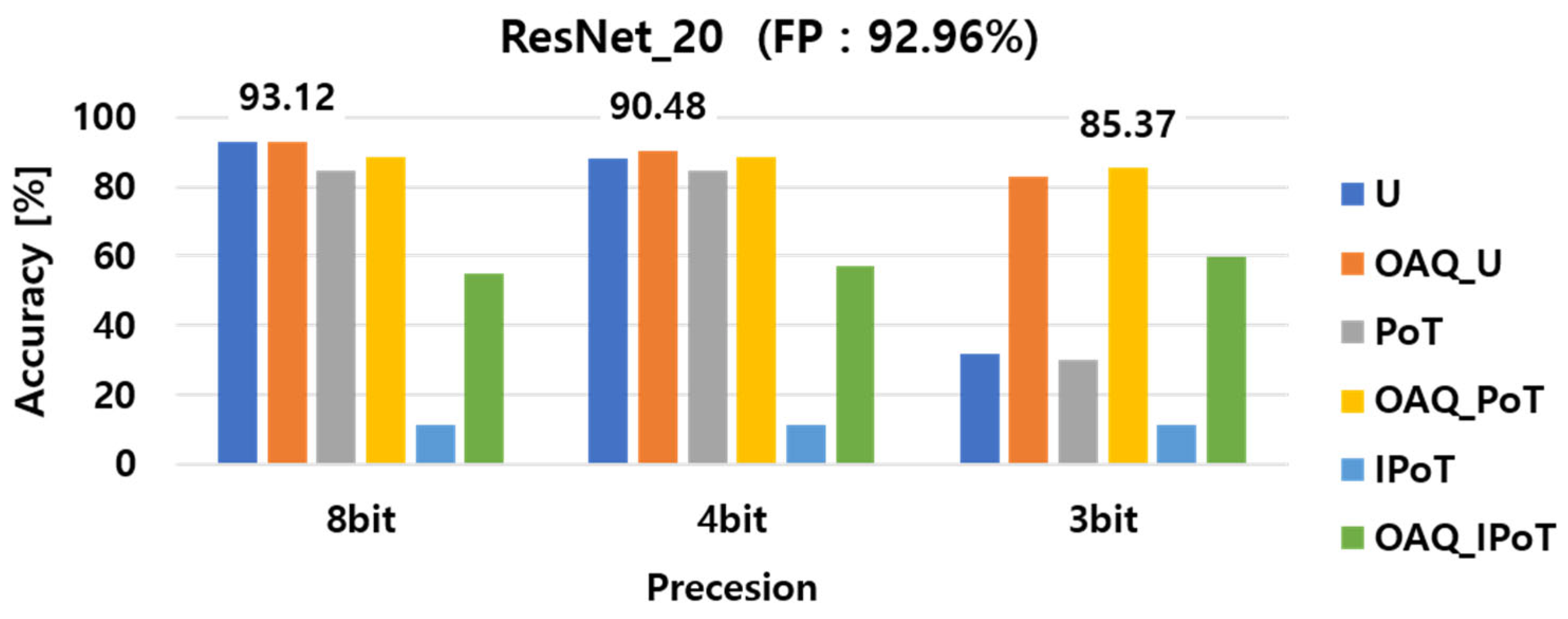
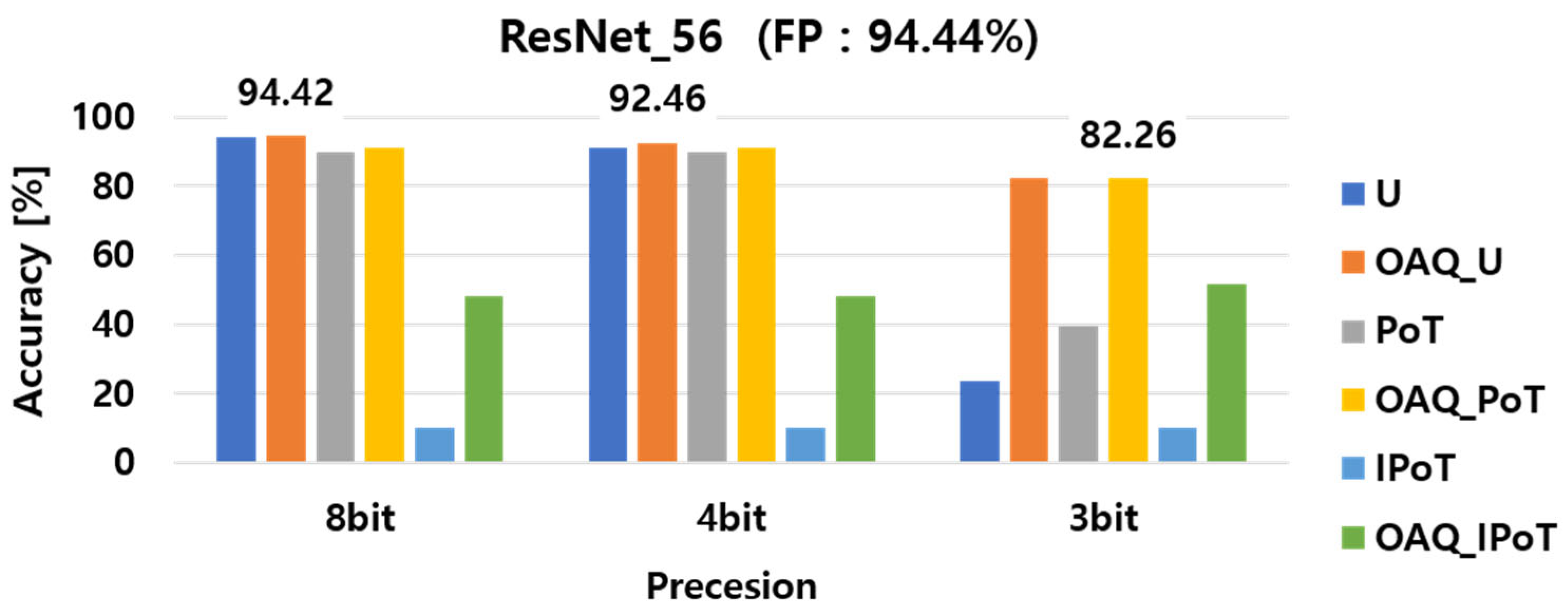

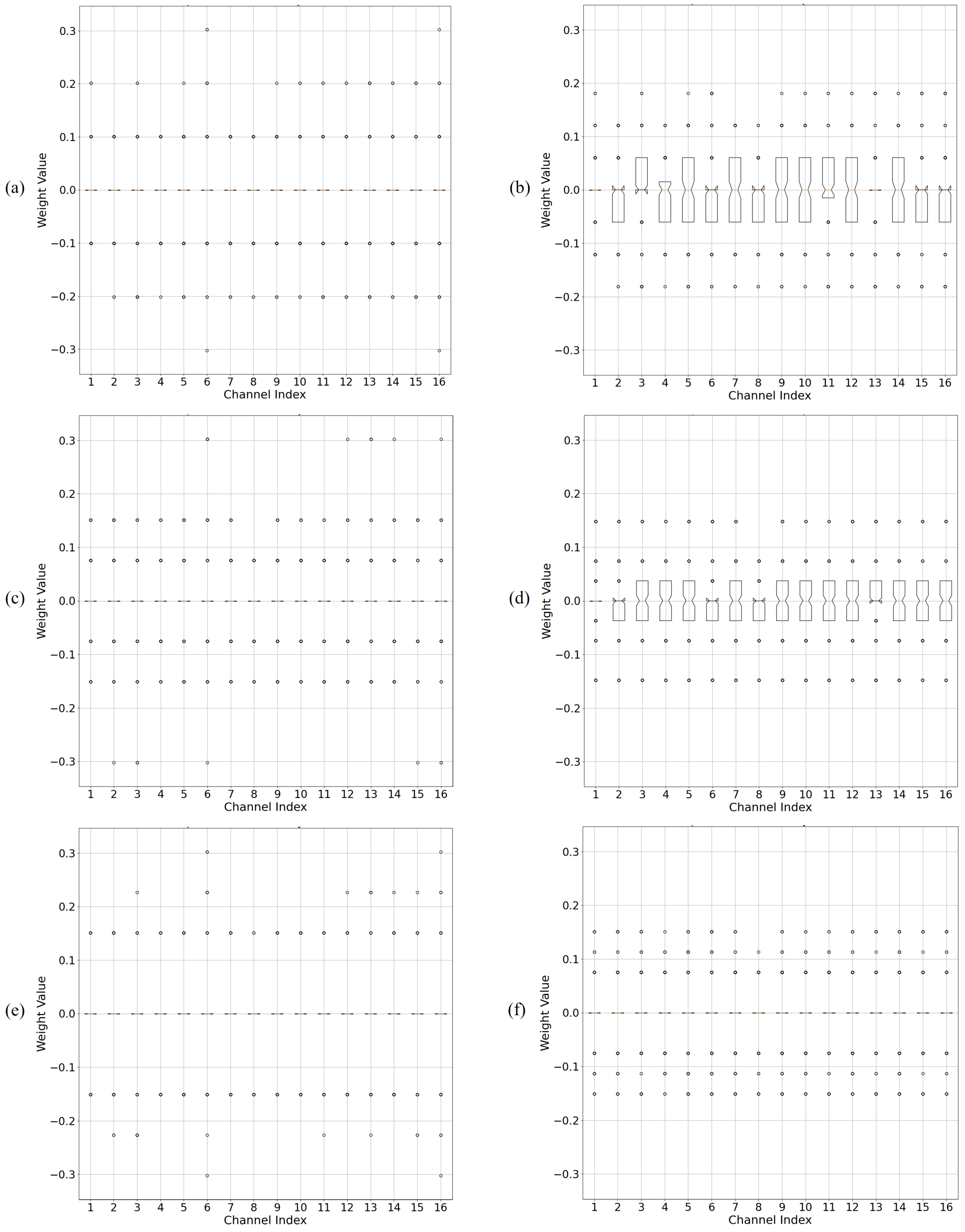
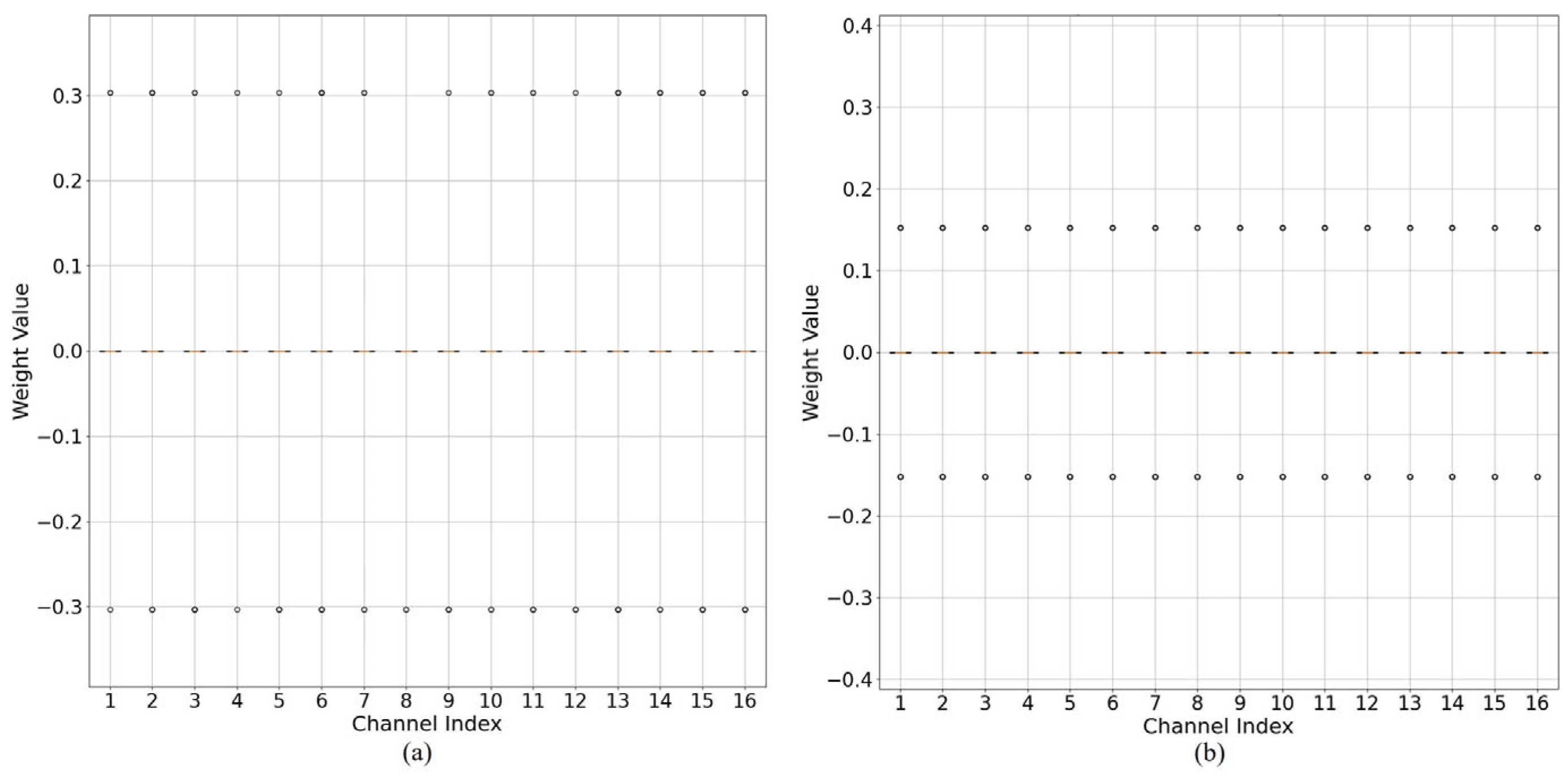
| Methods | SSIM Index Between Distributions [%] ↑ | SSIM Index Between Weights [sum] ↓ |
|---|---|---|
| Trained weight distribution | 100 | 1.5942 |
| Equalization (DFQ/GDRQ) | 80.85 | 0.0765 |
| Clipping (ACIQ) | 99.99 | 1.5951 |
| Proposed OAQ | 96.13 | 0.9976 |
| Model | Method | 8-bit | 4-bit | 3-bit |
|---|---|---|---|---|
| ResNet20 | Vanilla | 92.9 | 88.0 | 36.5 |
| ResNet20 | OAQ | 93.1 | 90.5 | 85.4 |
| ResNet56 | Vanilla | 94.1 | 90.6 | 23.7 |
| ResNet56 | OAQ | 94.4 | 92.5 | 82.3 |
| DenseNet100 | Vanilla | 94.6 | 92.3 | 55.3 |
| DenseNet100 | OAQ | 94.7 | 93.2 | 86.7 |
| Methods | Precision (Bit Widths of Weights/Activations) | Accuracy (%) (FP-32/Quantized) | Relative Performance Change Before and After Applying Quantization (%) |
|---|---|---|---|
| ZeroQ [38] | 8-bit/8-bit | 94.03/93.94 | −0.09 |
| OAQ (w/o FT) | 92.60/93.12 | +0.52 | |
| OAQ (w/FT) | 92.60/93.10 | +0.55 | |
| APoT [33] | 4-bit/8-bit | 91.60/92.30 | +0.70 |
| OAQ (w/o FT) | 92.60/90.51 | −2.09 | |
| OAQ (w/FT) | 92.60/92.66 | +0.06 | |
| OCS [28] | 4-bit/4-bit | 92.96/89.10 | −3.86 |
| DoReFa-Net [19] | 91.60/90.50 | −1.10 | |
| PACT [20] | 91.60/91.70 | +0.10 | |
| OAQ (w/o FT) | 92.60/89.66 | −2.94 | |
| OAQ (w/FT) | 92.60/92.61 | +0.01 |
| Methods | Precision (Weights) | Accuracy (%) [FP: 92.60%] |
|---|---|---|
| Vanilla | 4-bit | 92.64 |
| 3-bit | 90.91 | |
| 2-bit | 46.59 | |
| OAQ | 4-bit | 92.79 |
| 3-bit | 92.12 | |
| 2-bit | 90.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, J.; Ban, G. Efficient Deep Learning Model Compression for Sensor-Based Vision Systems via Outlier-Aware Quantization. Sensors 2025, 25, 2918. https://doi.org/10.3390/s25092918
Yoo J, Ban G. Efficient Deep Learning Model Compression for Sensor-Based Vision Systems via Outlier-Aware Quantization. Sensors. 2025; 25(9):2918. https://doi.org/10.3390/s25092918
Chicago/Turabian StyleYoo, Joonhyuk, and Guenwoo Ban. 2025. "Efficient Deep Learning Model Compression for Sensor-Based Vision Systems via Outlier-Aware Quantization" Sensors 25, no. 9: 2918. https://doi.org/10.3390/s25092918
APA StyleYoo, J., & Ban, G. (2025). Efficient Deep Learning Model Compression for Sensor-Based Vision Systems via Outlier-Aware Quantization. Sensors, 25(9), 2918. https://doi.org/10.3390/s25092918






