Online ECG Biometrics for Streaming Data with Prototypes Learning and Memory Enhancement
Abstract
1. Introduction
- We propose a novel ECG biometrics method, which is designed to be in the online mode, with three well-designed modules, i.e., bidirectional regressions, prototypes learning, and memory enhancement.
- For streaming data, our online method is capable of learning discriminative representations while effectively mitigating the catastrophic forgetting problem and addressing the class-incremental problem.
- Experimental results from two datasets demonstrate that the proposed method performs better than all baselines, demonstrating the effectiveness of our method.
2. Related Works
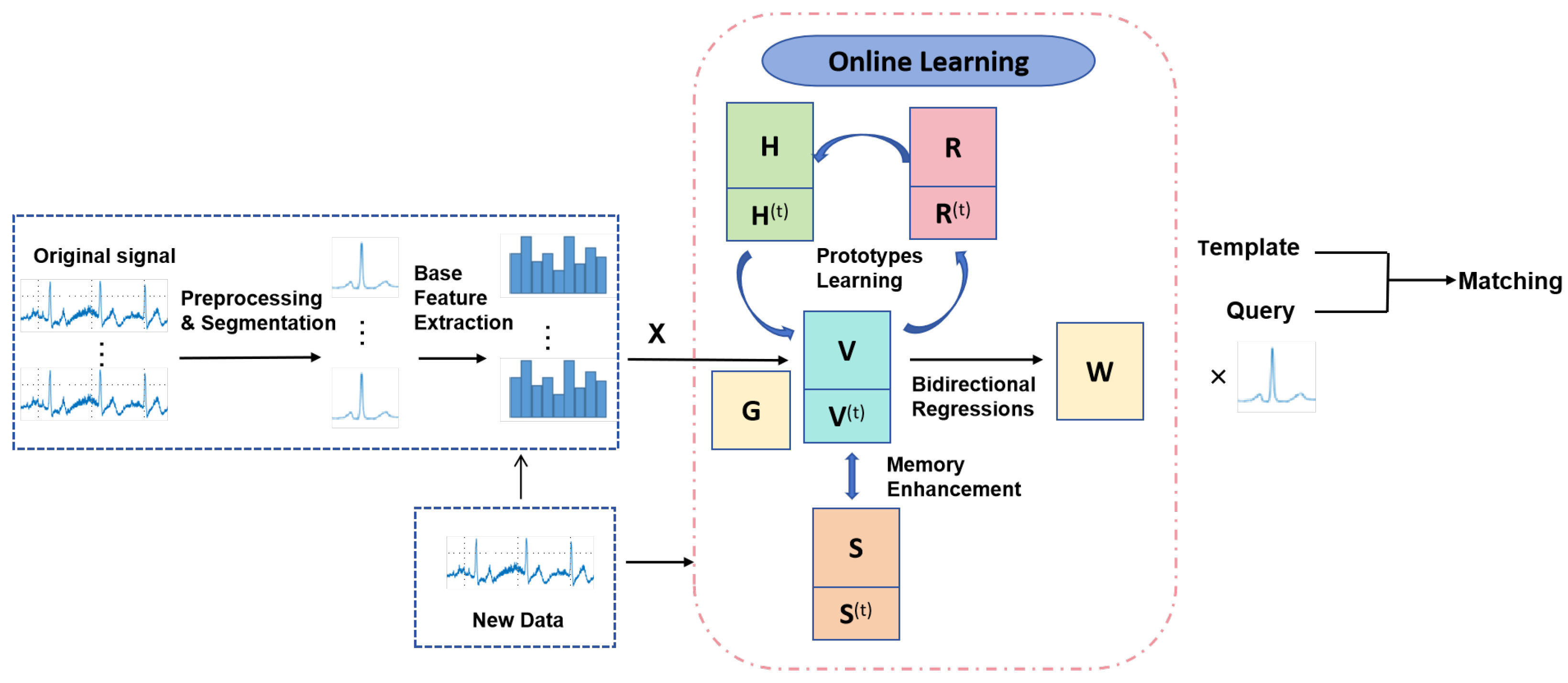
3. Proposed Method
3.1. Notations and Problem Definition
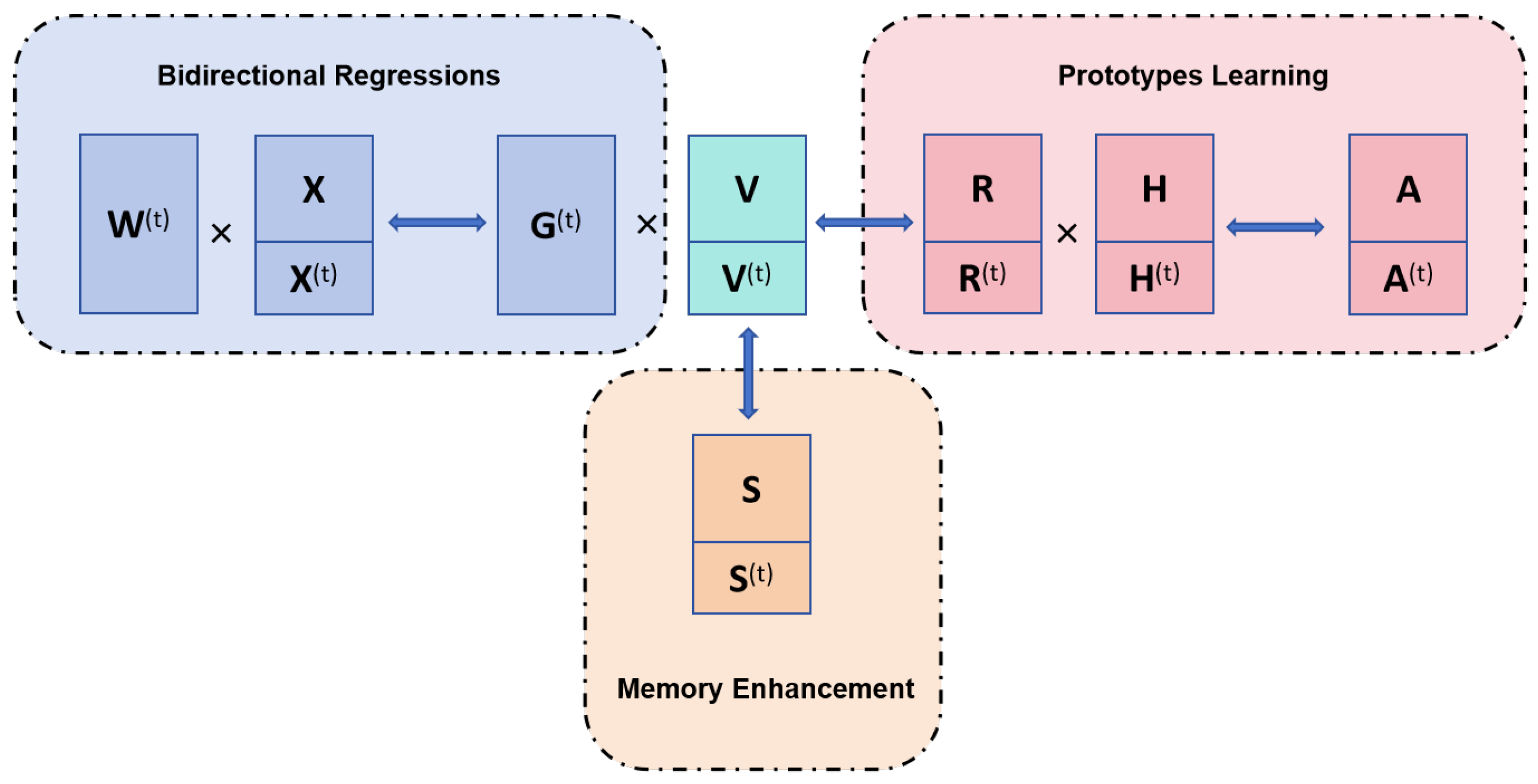
3.2. Bidirectional Regressions
3.3. Prototypes Learning for Individuals
3.4. Memory Enhancement
3.5. Overall Objective Function
3.6. Online Optimization
| Algorithm 1: The online optimization of our method at round t. |
| Input: the t-th data chunk with features ; information stored in our memory ; auxiliary variables , , and ; trade-off parameters; iteration number T. |
| Output: Projection matrix . |
| Procedure: |
| Randomly initialize all variables , , , and ; |
| for iter = do |
| Updating with (6); |
| Updating with (8); |
| Updating with (10); |
| Updating with (12); |
| end for |
| Return: auxiliary variables , , and ; variables , , , and . |
3.7. Convergence Proof
3.8. Matching
4. Experiments
4.1. Experimental Settings
4.1.1. Datasets
4.1.2. Evaluation Metrics
4.1.3. Extracting Features from ECG Signals
4.1.4. Online Setting and Implementation Details
4.2. Comparison with the State-of-the-Art Method
4.3. Further Analysis
4.3.1. Ablation Study
4.3.2. Parameters Sensitive and Convergence Analysis
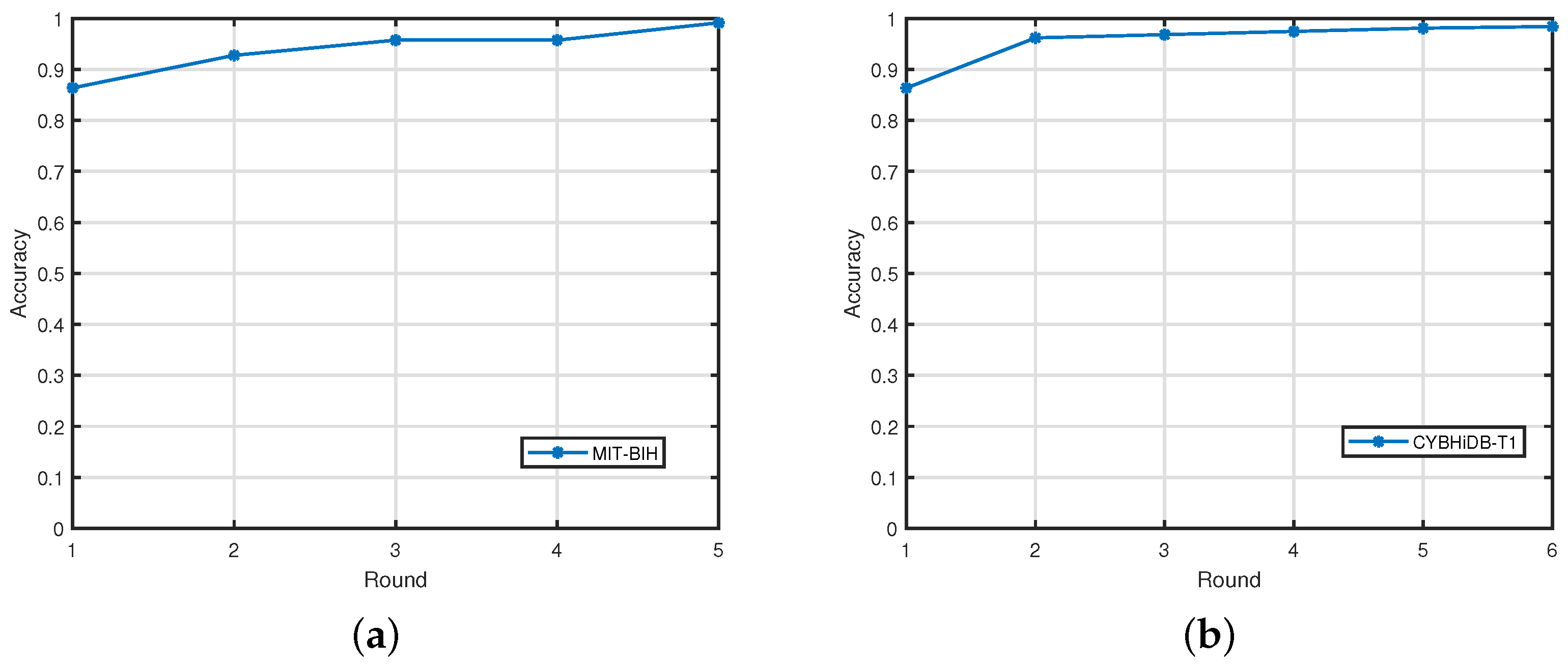
4.3.3. Streaming Data Handling Performance
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karimian, N.; Tehranipoor, S.; Lyp, T. Trustworthy of implantable medical devices using ecg biometric. In Proceedings of the 2023 Silicon Valley Cybersecurity Conference (SVCC), San Jose, CA, USA, 17–19 May 2023; pp. 1–6. [Google Scholar]
- Tuerxunwaili, R.; Nor, M.; Rahman, A.W.B.A.; Sidek, K.A.; Ibrahim, A.A. Electrocardiogram identification: Use a simple set of features in qrs complex to identify individuals. In Proceedings of the 12th International Conference on Computing and Information Technology (IC2IT), Bangkok, Thailand, 8–9 July 2016; Springer: Cham, Switzerland, 2016; pp. 139–148. [Google Scholar]
- Wang, J.; She, M.; Nahavandi, S.; Kouzani, A. Human identification from ecg signals via sparse representation of local segments. IEEE Signal Process. Lett. 2013, 20, 937–940. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, G.; Wang, K.; Liu, H.; Yin, Y. Learning joint and specific patterns: A unified sparse representation for off-the-person ECG biometric recognition. IEEE Trans. Inf. Forensics Secur. 2021, 16, 147–160. [Google Scholar] [CrossRef]
- Chan, A.D.C.; Hamdy, M.M.; Badre, A.; Badee, V. Wavelet distance measure for person identification using electrocardiograms. IEEE Trans. Instrum. Meas 2008, 57, 248–253. [Google Scholar] [CrossRef]
- Odinaka, I.; Lai, P.; Kaplan, A.D.; O’Sullivan, J.A.; Sirevaag, E.J.; Kristjansson, S.D.; Sheffield, A.K.; Rohrbaugh, J.W. ECG biometrics: A robust short-time frequency analysis. In Proceedings of the 2010 IEEE International Workshop on Information Forensics and Security, Seattle, WA, USA, 12–15 December 2010; pp. 1–6. [Google Scholar]
- Hejazi, M.; Al-Haddad, S.; Hashim, S.J.; Aziz, A.F.A.; Singh, Y.P. Feature level fusion for biometric verification with two-lead ecg signals. In Proceedings of the 2016 IEEE 12th International Colloquium on Signal Processing & Its Applications (CSPA), Melaka, Malaysia, 4–6 March 2016; pp. 54–59. [Google Scholar]
- Plataniotis, K.N.; Hatzinakos, D.; Lee, J.K. ECG biometric recognition without fiducial detection. In Proceedings of the 2006 Biometrics Symposium: Special Session on Research at the Biometric Consortium Conference, Baltimore, MD, USA, 19 September–21 August 2006; pp. 1–6. [Google Scholar]
- Raj, S.; Ray, K.C. ECG signal analysis using dct-based dost and pso optimized svm. IEEE Trans. Instrum. Meas. 2017, 66, 470–478. [Google Scholar] [CrossRef]
- Wang, K.; Yang, G.; Huang, Y.; Yang, L.; Yin, Y. Joint dual-domain matrix factorization for ecg biometric recognition. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 3134–3138. [Google Scholar]
- Wang, G.; Shanker, S.; Nag, A.; Lian, Y.; John, D. ECG biometric authentication using self-supervised learning for iot edge sensors. IEEE J. Biomed. Health Inform. 2024, 28, 6606–6618. [Google Scholar] [CrossRef]
- Zehir, H.; Hafs, T.; Daas, S. Empirical mode decomposition-based biometric identification using gru and lstm deep neural networks on ecg signals. Evol. Syst. 2024, 15, 2193–2209. [Google Scholar] [CrossRef]
- Li, Y.; Pang, Y.; Wang, K.; Li, X. Toward improving ecg biometric identification using cascaded convolutional neural networks. Neurocomputing 2020, 391, 83–95. [Google Scholar] [CrossRef]
- Ihsanto, E.; Ramli, K.; Sudiana, D.; Gunawan, T.S. Fast and accurate algorithm for ecg authentication using residual depthwise separable convolutional neural networks. Appl. Sci. 2020, 10, 3304. [Google Scholar] [CrossRef]
- Jyotishi, D.; Dandapat, S. An ecg biometric system using hierarchical lstm with attention mechanism. IEEE Sensors J. 2021, 22, 6052–6061. [Google Scholar] [CrossRef]
- Hazratifard, M.; Agrawal, V.; Gebali, F.; Elmiligi, H.; Mamun, M. Ensemble siamese network (esn) using ecg signals for human authentication in smart healthcare system. Sensors 2023, 23, 4727. [Google Scholar] [CrossRef]
- Wang, K.; Yang, G.; Huang, Y.; Yang, L.; Yin, Y. Online ecg biometrics via hadamard code. In Proceedings of the ICASSP 2022—2022 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Singapore, 23–27 May 2022; pp. 2924–2928. [Google Scholar]
- D’angelis, O.; Bacco, L.; Vollero, L.; Merone, M. Advancing ecg biometrics through vision transformers: A confidence-driven approach. IEEE Access 2023, 11, 140710–140721. [Google Scholar] [CrossRef]
- Biel, L.; Pettersson, O.; Philipson, L.; Wide, P. Ecg analysis: A new approach in human identification. IEEE Trans. Instrum. Meas 2001, 50, 808–812. [Google Scholar] [CrossRef]
- Arteaga-Falconi, J.; Osman, H.A.; El Saddik, A. Ecg authentication for mobile devices. IEEE Trans. Instrum. Meas 2015, 65, 591–600. [Google Scholar] [CrossRef]
- Barros, A.; do Rosário, D.; Resque, P.; Cerqueira, E. Heart of iot: ECG as biometric sign for authentication and identification. In Proceedings of the 2019 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 307–312. [Google Scholar]
- Fatimah, B.; Singh, P.; Singhal, A.; Pachori, R.B. Biometric identification from ecg signals using fourier decomposition and machine learning. IEEE Trans. Instrum. Meas. 2022, 71, 4008209. [Google Scholar] [CrossRef]
- Galli, A.; Giorgi, G.; Narduzzi, C. Individual recognition by gaussian ecg features. In Proceedings of the 2020 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Dubrovnik, Croatia, 25–28 May 2020; pp. 1–5. [Google Scholar]
- Hejazi, M.; Al-Haddad, S.; Singh, Y.P.; Hashim, S.J.; Aziz, A.F.A. ECG biometric authentication based on non-fiducial approach using kernel methods. Digit. Signal Process. 2016, 52, 72–86. [Google Scholar] [CrossRef]
- Balasubramanian, R.; Chaspari, T.; Narayanan, S.S. A knowledge-driven framework for ECG representation and interpretation for wearable applications. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 1018–1022. [Google Scholar]
- Xu, J.; Yang, G.; Wang, K.; Huang, Y.; Liu, H.; Yin, Y. Structural sparse representation with class-specific dictionary for ECG biometric recognition. Pattern Recognit. Lett. 2020, 135, 44–49. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, G.; Wang, K.; Liu, H.; Yin, Y. Robust multi-feature collective non-negative matrix factorization for ecg biometrics. Pattern Recognit. 2022, 123, 108376. [Google Scholar] [CrossRef]
- Wang, K.; Yang, G.; Huang, Y.; Yin, Y. Multi-scale differential feature for ECG biometrics with collective matrix factorization. Pattern Recognit. 2020, 102, 107211. [Google Scholar] [CrossRef]
- Li, R.; Yang, G.; Wang, K.; Huang, Y.; Yuan, F.; Yin, Y. Robust ECG biometrics using GNMF and sparse representation. Pattern Recognit. Lett. 2020, 129, 70–76. [Google Scholar] [CrossRef]
- Martis, R.J.; Acharya, U.R.; Min, L.C. Ecg beat classification using pca, lda, ica and discrete wavelet transform. Biomed. Signal Process. Control 2013, 8, 437–448. [Google Scholar] [CrossRef]
- Kanaan, L.; Merheb, D.; Kallas, M.; Francis, C.; Amoud, H.; Honeine, P. Pca and kpca of ecg signals with binary svm classification. In Proceedings of the 2011 IEEE Workshop on Signal Processing Systems (SiPS), Beirut, Lebanon, 4–7 October 2011; pp. 344–348. [Google Scholar]
- Wu, S.-C.; Chen, P.-T.; Swindlehurst, A.L.; Hung, P.-L. Cancelable biometric recognition with ecgs: Subspace-based approaches. IEEE Trans. Inf. Forensics Secur. 2018, 14, 1323–1336. [Google Scholar] [CrossRef]
- Chen, J.; Fang, B.; Li, H.; Zhang, L.-B.; Teng, Y.; Fortino, G. Emcnet: Ensemble multiscale convolutional neural network for single-lead ecg classification in wearable devices. IEEE Sensors J. 2024, 24, 8754–8762. [Google Scholar] [CrossRef]
- Byeon, Y.-H.; Pan, S.-B.; Kwak, K.-C. Intelligent deep models based on scalograms of electrocardiogram signals for biometrics. Sensors 2019, 19, 935. [Google Scholar] [CrossRef]
- Rincon-Melchor, V.; Nakano-Miyatake, M.; Juarez-Sandoval, O.; Olivares-Mercado, J.; Moreno-Saenz, J.; Benitez-Garcia, G. Deep learning algorithm for the people identification using their ecg signals as a biometric parameter. In Proceedings of the 46th International Conference on Telecommunications and Signal Processing (TSP), Prague, Czech Republic, 12–14 July 2023; pp. 154–159. [Google Scholar]
- Srivastva, R.; Singh, A.; Singh, Y.N. Plexnet: A fast and robust ecg biometric system for human recognition. Inf. Sci. 2021, 558, 208–228. [Google Scholar] [CrossRef]
- Rudin, W. Principles of Mathematical Analysis; McGraw-Hill: New York, NY, USA, 1976; Volume 3. [Google Scholar]
- Moody, G.; Mark, R. The impact of the mit-bih arrhythmia database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- da Silva, H.P.; Lourenço, A.; Fred, A.; Raposo, N.; Aires-de-Sousa, M. Check your biosignals here: A new dataset for off-the-person ECG biometrics. Comput. Methods Programs Biomed. 2014, 113, 503–514. [Google Scholar] [CrossRef]
- Pereira, T.M.C.; Conceição, R.C.; Sencadas, V.; Sebastião, R. Biometric recognition: A systematic review on electrocardiogram data acquisition methods. Sensors 2023, 23, 1507. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Tompkins, W.J. A real-time qrs detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef]
- Louis, W.; Hatzinakos, D. Enhanced binary patterns for electrocardiogram (ECG) biometrics. In Proceedings of the 2016 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), Vancouver, BC, Canada, 15–18 May 2016; pp. 1–4. [Google Scholar]
- Abdeldayem, S.S.; Bourlai, T. A novel approach for ecg-based human identification using spectral correlation and deep learning. IEEE Trans. Biom. Behav. Identity Sci. 2020, 2, 1–14. [Google Scholar] [CrossRef]
- Salloum, R.; Kuo, C.J. Ecg-based biometrics using recurrent neural networks. In Proceedings of the 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2062–2066. [Google Scholar]
- Wang, X.; Cai, W.; Wang, M. A novel approach for biometric recognition based on ECG feature vectors. Biomed. Signal Process. Control 2023, 86 Pt A, 104922. [Google Scholar] [CrossRef]
- Wang, K.; Yang, G.; Yang, L.; Huang, Y.; Yin, Y. Ecg biometrics via enhanced correlation and semantic-rich embedding. Mach. Intell. Res. 2023, 20, 697–706. [Google Scholar] [CrossRef]
- da Silva Luz, E.J.; Moreira, G.J.; Oliveira, L.S.; Schwartz, W.R.; Menotti, D. Learning deep off-the-person heart biometrics representations. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1258–1270. [Google Scholar] [CrossRef]
- ur Rehman, U.; Kamal, K.; Iqbal, J.; Sheikh, M.F. Biometric identification through ECG signal using a hybridized approach. In Proceedings of the 2019 5th International Conference on Computing and Artificial Intelligence, Bali, Indonesia, 19–22 April 2019; pp. 226–230. [Google Scholar]
- Islam, M.S.; Alajlan, N. Biometric template extraction from a heartbeat signal captured from fingers. Multim. Tools Appl. 2017, 76, 12709–12733. [Google Scholar] [CrossRef]


| Dataset | Method | Mode | EER (%) | Accuracy (%) |
|---|---|---|---|---|
| MIT-BIH | [11] | Batch | - | 97.96 |
| [12] | Batch | - | 98.57 | |
| [28] | Batch | 2.73 | 94.68 | |
| [43] | Batch | - | 96.5 | |
| [44] | Batch | 1.37 | 99.08 | |
| [45] | Batch | - | 97.66 | |
| [46] | Batch | 1.06 | 99.1 | |
| [35] | Batch | - | 98.0 | |
| [17] | Online | 0.64 | 99.15 | |
| OURS | Online | 0.62 | 99.25 |
| Dataset | Method | Mode | EER (%) | Accuracy (%) | ||
|---|---|---|---|---|---|---|
| T1 | T2 | T1 | T2 | |||
| CYBHiDB | [4] | Batch | 1.26 | 2.28 | 97.43 | 95.32 |
| [47] | Batch | 1.85 | 3.35 | 97.12 | 94.95 | |
| [48] | Batch | 2.52 | 3.89 | 96.07 | 94.23 | |
| [49] | Batch | 5.45 | 6.53 | 93.52 | 91.41 | |
| [46] | Batch | 3.17 | 3.70 | 98.4 | 96.8 | |
| [17] | Online | 1.58 | 1.71 | 98.73 | 97.78 | |
| Ours | Online | 1.31 | 1.65 | 98.89 | 97.92 | |
| Method | Mode | Training | Testing | EER (%) | Accuracy (%) |
|---|---|---|---|---|---|
| [4] | Batch | T1 | T2 | 10.26 | 87.75 |
| T2 | T1 | 11.14 | 86.24 | ||
| [47] | Batch | T1 | T2 | 12.78 | 85.46 |
| T2 | T1 | 12.83 | 84.46 | ||
| [48] | Batch | T1 | T2 | 13.87 | 84.35 |
| T2 | T1 | 14.56 | 83.92 | ||
| [49] | Batch | T1 | T2 | 15.23 | 82.49 |
| T2 | T1 | 14.78 | 83.83 | ||
| [46] | Batch | T1 | T2 | 6.17 | 92.86 |
| T2 | T1 | 5.86 | 96.03 | ||
| [17] | Online | T1 | T2 | 3.17 | 96.51 |
| T2 | T1 | 2.70 | 96.19 | ||
| Ours | Online | T1 | T2 | 2.77 | 95.56 |
| T2 | T1 | 2.56 | 96.67 |
| Variant | BR | PL | ME | MIT-BIH | CYBHiDB-T1 | CYBHiDB-T2 |
|---|---|---|---|---|---|---|
| OURS_BR | ✓ | ✓ | 87.23 | 86.35 | 85.40 | |
| OURS_PL | ✓ | ✓ | 86.38 | 85.71 | 85.08 | |
| OURS_ME | ✓ | ✓ | 91.49 | 87.94 | 84.13 | |
| OURS | ✓ | ✓ | ✓ | 99.25 | 98.89 | 97.92 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Wang, N. Online ECG Biometrics for Streaming Data with Prototypes Learning and Memory Enhancement. Sensors 2025, 25, 2908. https://doi.org/10.3390/s25092908
Wang K, Wang N. Online ECG Biometrics for Streaming Data with Prototypes Learning and Memory Enhancement. Sensors. 2025; 25(9):2908. https://doi.org/10.3390/s25092908
Chicago/Turabian StyleWang, Kuikui, and Na Wang. 2025. "Online ECG Biometrics for Streaming Data with Prototypes Learning and Memory Enhancement" Sensors 25, no. 9: 2908. https://doi.org/10.3390/s25092908
APA StyleWang, K., & Wang, N. (2025). Online ECG Biometrics for Streaming Data with Prototypes Learning and Memory Enhancement. Sensors, 25(9), 2908. https://doi.org/10.3390/s25092908






