Interruption-Aware Computation Offloading in the Industrial Internet of Things
Abstract
1. Introduction
- We investigate a case in IIoT edge computing where edge service can be interrupted during operation. We use a load-based exponential function to simulate the interruption probability of edge servers based on their total load. By using this formulation, we can simulate the situation where offloading decisions can lead to interruption, which is more realistic compared to the random-based model.
- We propose a novel task offloading strategy that utilizes a multi-agent deep reinforcement learning-based Advantage Actor–Critic architecture. This approach enables devices to select the optimal computation node by considering factors such as channel status and edge node availability, ensuring an optimal tradeoff between service latency and the consistent operation of the system under interruptions.
- We conduct comparative experiments to assess the effectiveness of the proposed task offloading strategy, and the results demonstrate that our method surpasses its counterparts in terms of total average delay.
- We conduct further experiments to analyze how system parameters impact performance in an interruptible edge task offloading scenario, providing insights into the tradeoffs between service latency, availability, and system stability.
2. Related Work
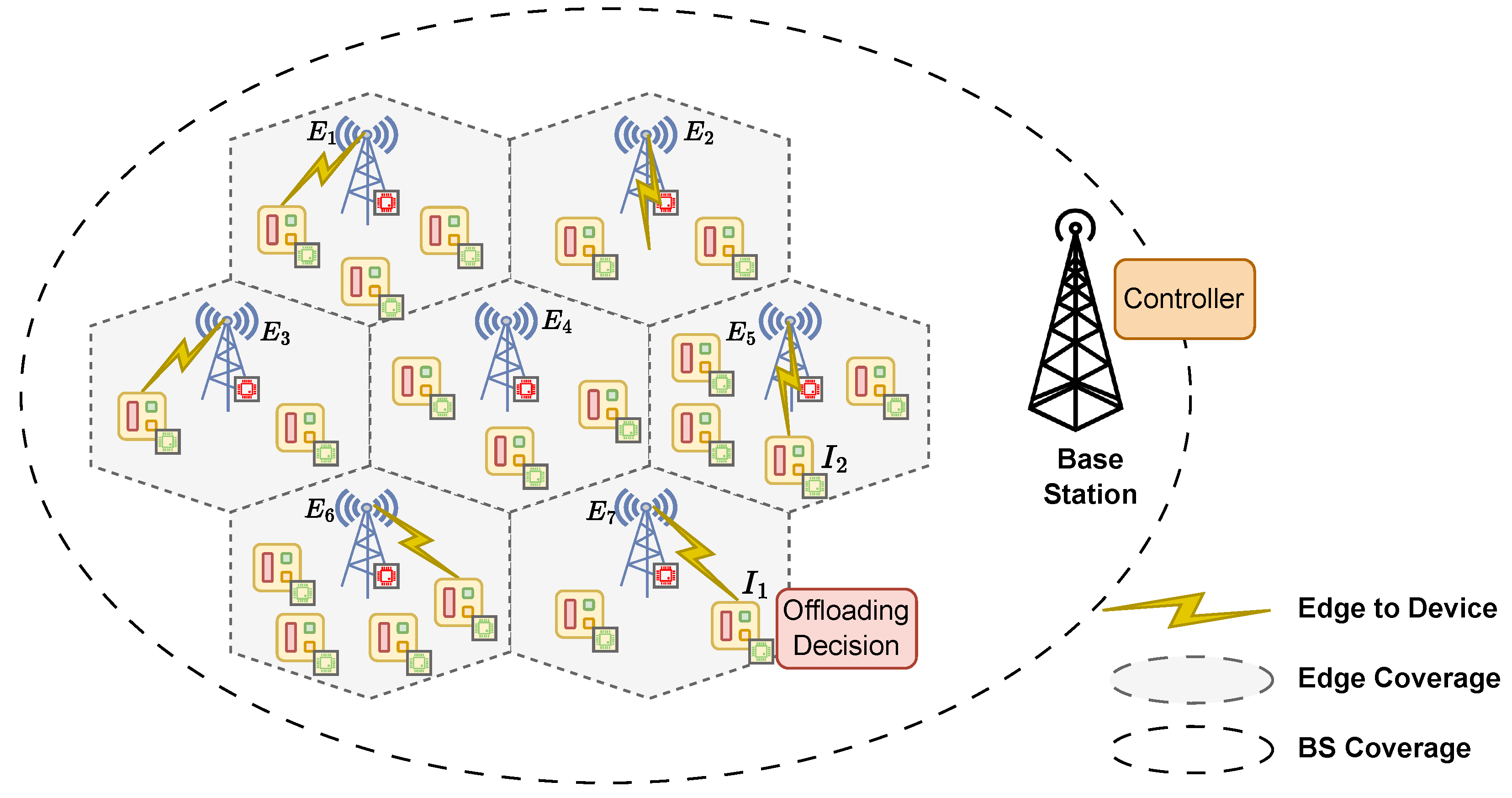
3. System Model
3.1. Task Offloading and Computation Delay Model
3.2. Transmission Delay Model
3.3. Load-Based Interruption Model and Interruption Delay
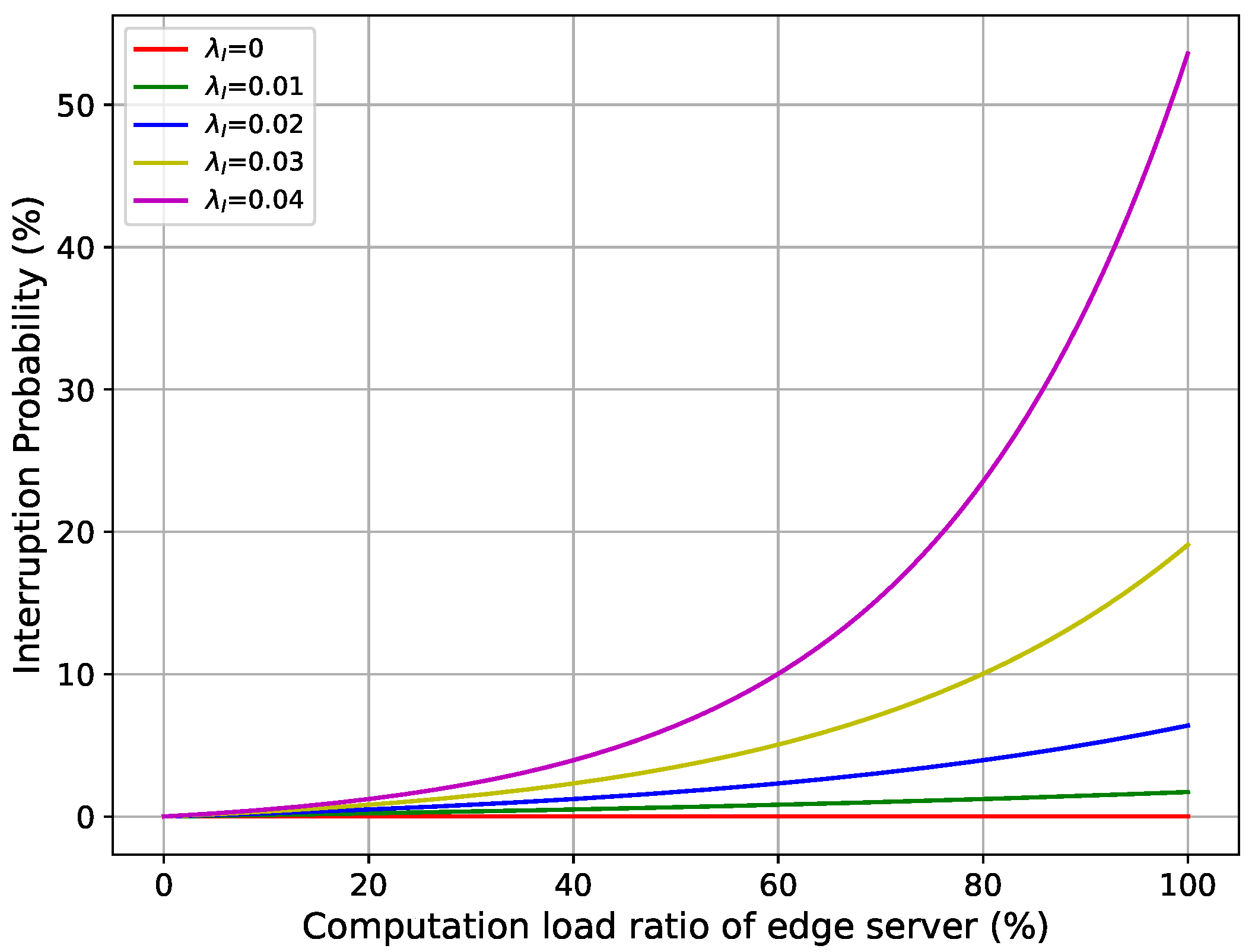
3.3.1. Interruption Probability
3.3.2. Interruption Delay Model
- If the triggering task comes from a device within the coverage area of edge server (), the interruption delay is
- If the task was offloaded from a remote device (), the interruption delay includes both wireless and wired transmission delays:where represents the index of the device whose task arrival updated the server’s load and triggered the interruption, and is the index of the local edge server of device .
- If is interrupted when Task 2 arrives, the interruption delay can be computed using Equation (13) with and Task 1, and Task 2 must be recomputed at local devices with the same additional delay .
- If is interrupted when Task 3 arrives (from ), the interruption delay is computed using Equation (14) with . Task 2 and Task 3 must fallback to the local device computation. However, in this case, Task 1 is already finished before the interruption, so it is not affected by the interruption.
3.4. Total Delay Model
3.4.1. Total Delay Model with No Interruption
- When , device processes the task using its hardware. In this case, the total delay can be computed as the processing time on the local device:
- When , device offloads the task to its local edge server. In this case, the total delay can be computed as the sum of the wireless transmission delay and the computation delay at the local edge:
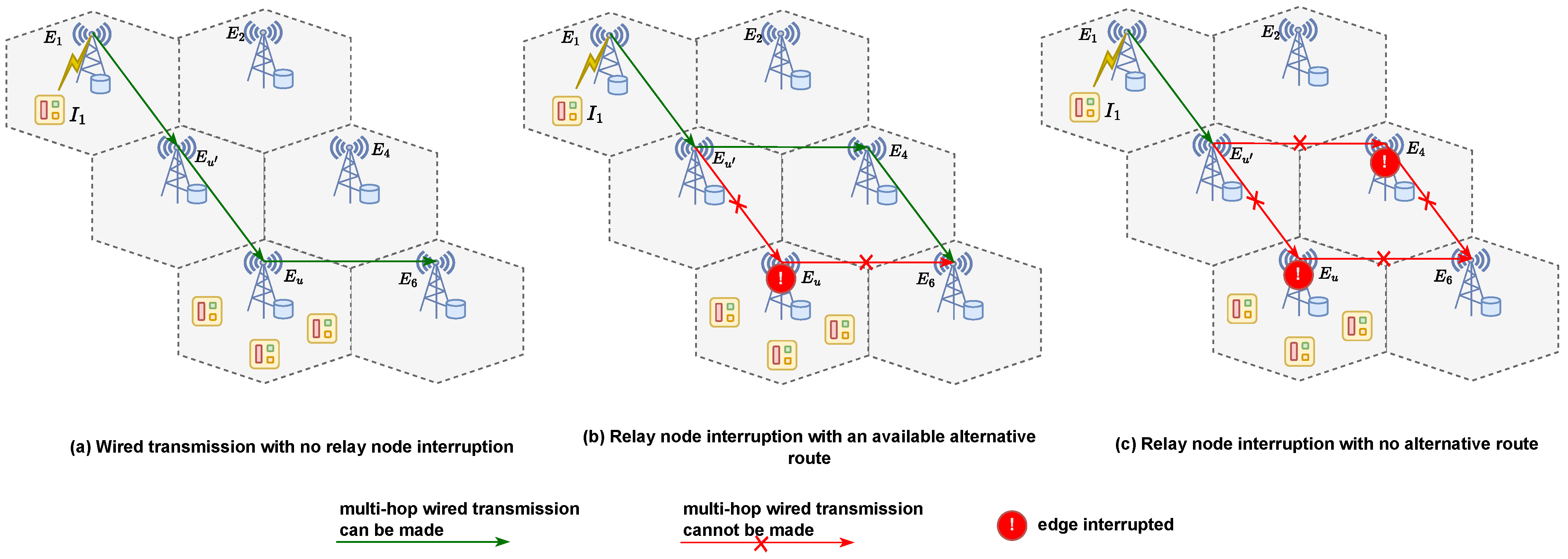
- When , and , device offloads the task to remote edge server . In this case, the device experiences wireless transmission delay, multi-hop wired transmission delay, and remote edge computation delay.
3.4.2. Total Delay Model with Computation Node Interruption
3.4.3. Total Delay Model with Relay Node Interruption
3.5. Problem Formulation
4. Multi-Agent Deep Reinforcement Learning for Task Offloading
4.1. Partially Observable Markov Decision Process
4.1.1. Observation Space
4.1.2. Action Space
4.1.3. State Transition Probability
4.1.4. Reward Function
4.2. Agent Training and Execution
5. Experiment
5.1. Experimental Setup
5.1.1. Comparison Counterpart Setup
- MAA2C-based (#1—ours): This is our proposed task offloading strategy that uses a MAA2C-based approach to solve the offloading optimization problem to minimize the total delay with the proposed load-based interruption model.
- MAD2QN (#2): A multi-agent version of the Double Deep Q-Network (D2QN), where each agent independently learns a Q-function while using double Q-learning techniques to stabilize training. This approach addresses the same optimization problem as #1 but uses value-based learning instead of Actor–Critic methods.
- A2C (#3): A single-agent Advantage Actor–Critic (A2C) method where a centralized controller is responsible for offloading decisions for all devices. This baseline highlights the difference between centralized and decentralized decision-making in multi-agent environments.
- Greedy (#4): A heuristic-based offloading strategy where tasks are prioritized based on their required computational cycles per second (). Devices first attempt to offload to the least-loaded, nearby available servers. If no servers are suitable, tasks are processed locally.
- Random (#5): Within this approach, offloading decisions are randomly made.
- LocalEdge (#6): This strategy restricts the IIoT device to offload its task to the local edge server.
- OnDevice (#7): The IIoT device only uses its hardware to compute the tasks.
5.1.2. Evaluation Metrics
- Average total delay (Avg. Delay) in milliseconds. This is the value of the objective function, which can be computed using Equation (21).
- Availability score (Avail.) in percentage, which monitors the availability status of an edge server:
5.2. Experiment Results and Analysis
5.2.1. Impact of Interruption on Simulation Results
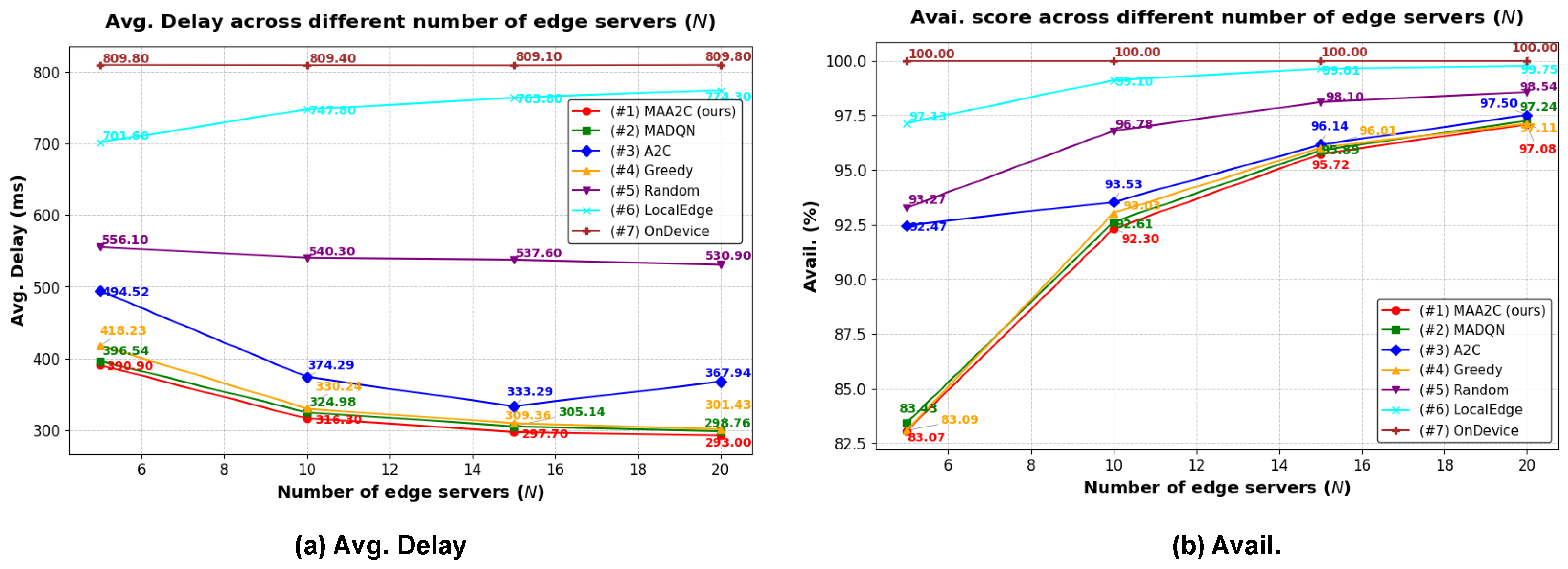
5.2.2. Simulation Results Using Different Numbers of Edge Servers
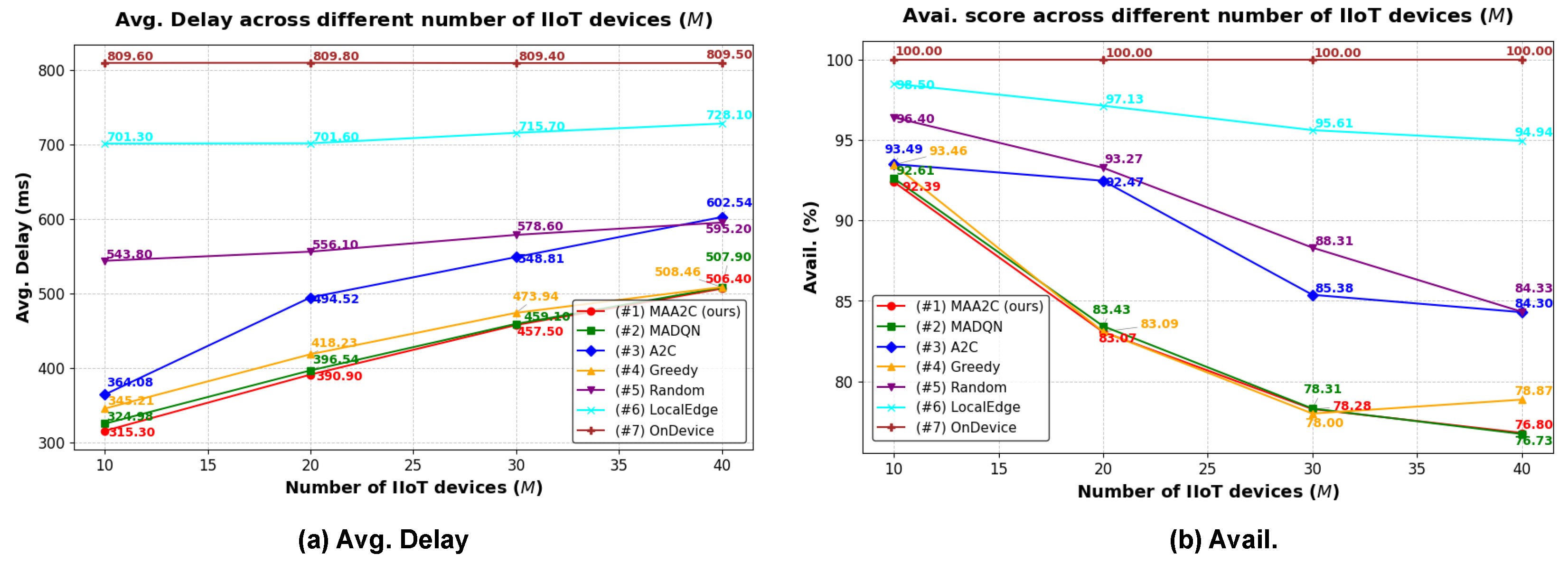
5.2.3. Simulation Results Using Different Numbers of IIoT Devices
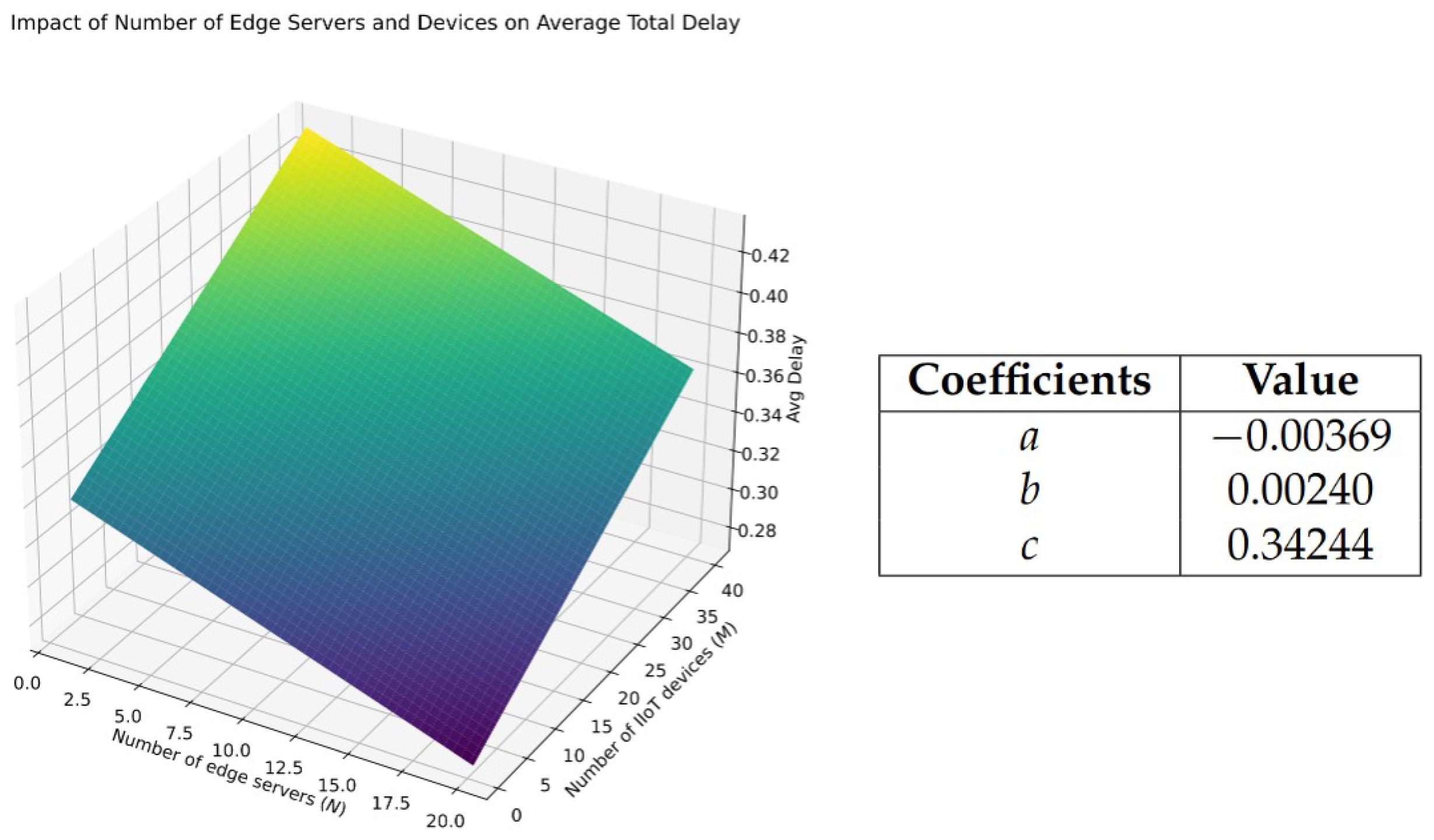
5.2.4. Analysis of the Impact of Edge Server and Device Density on Average Total Delay via Linear Regression
5.2.5. Simulation Results Using Different Interruption Sensitivity Values
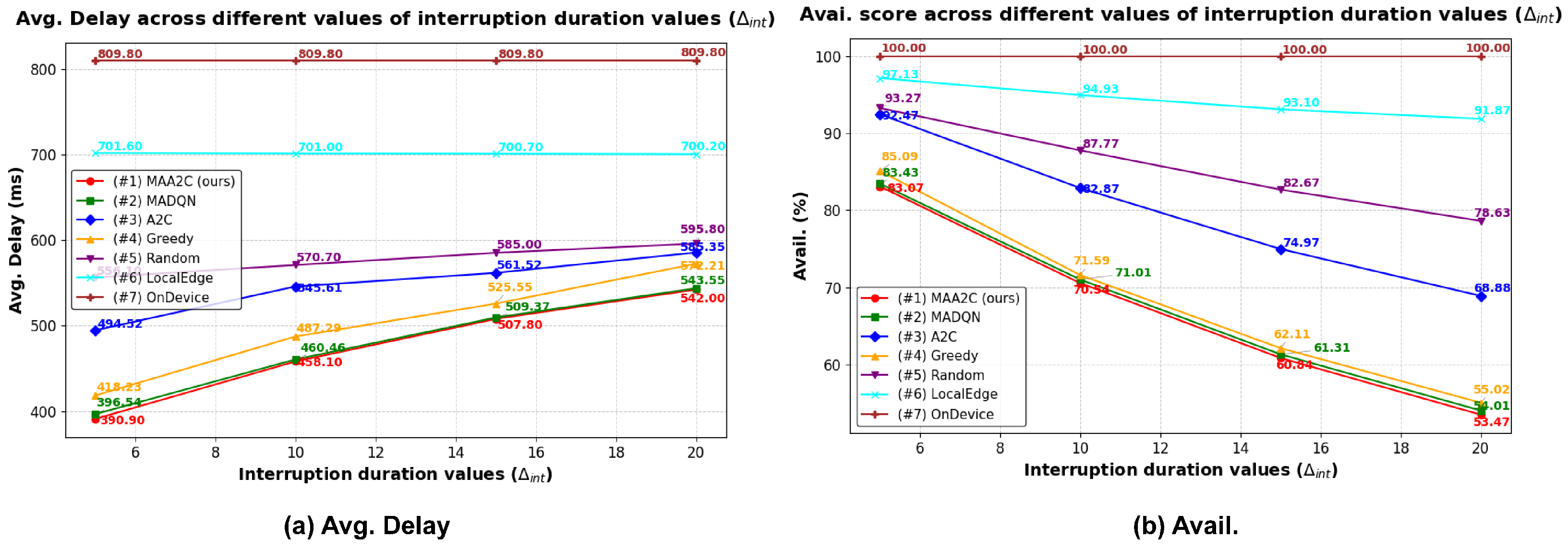
5.2.6. Simulation Results Using Different Interruption Durations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kong, L.; Tan, J.; Huang, J.; Chen, G.; Wang, S.; Jin, X.; Zeng, P.; Khan, M.; Das, S.K. Edge-computing-driven internet of things: A survey. ACM Comput. Surv. 2022, 55, 174. [Google Scholar] [CrossRef]
- Qadri, Y.A.; Nauman, A.; Zikria, Y.B.; Vasilakos, A.V.; Kim, S.W. The future of healthcare internet of things: A survey of emerging technologies. IEEE Commun. Surv. Tutor. 2020, 22, 1121–1167. [Google Scholar] [CrossRef]
- Badreldin, N.; Cheng, X.; Youssef, A. An Overview of Software Sensor Applications in Biosystem Monitoring and Control. Sensors 2024, 24, 6738. [Google Scholar] [CrossRef] [PubMed]
- Al-Turjman, F.; Lemayian, J.P. Intelligence, security, and vehicular sensor networks in internet of things (IoT)-enabled smart-cities: An overview. Comput. Electr. Eng. 2020, 87, 106776. [Google Scholar] [CrossRef]
- Fernández, H.; Rubio, L.; Rodrigo Peñarrocha, V.M.; Reig, J. Dual-Slope Path Loss Model for Integrating Vehicular Sensing Applications in Urban and Suburban Environments. Sensors 2024, 24, 4334. [Google Scholar] [CrossRef]
- Latif, S.; Mahfooz, S.; Ahmad, N.; Jan, B.; Farman, H.; Khan, M.; Han, K. Industrial internet of things based efficient and reliable data dissemination solution for vehicular ad hoc networks. Wirel. Commun. Mob. Comput. 2018, 2018, 1857202. [Google Scholar] [CrossRef]
- Tariq, U.; Ahmed, I.; Bashir, A.K.; Shaukat, K. A critical cybersecurity analysis and future research directions for the internet of things: A comprehensive review. Sensors 2023, 23, 4117. [Google Scholar] [CrossRef]
- Akhlaqi, M.Y.; Hanapi, Z.B.M. Task offloading paradigm in mobile edge computing-current issues, adopted approaches, and future directions. J. Netw. Comput. Appl. 2023, 212, 103568. [Google Scholar] [CrossRef]
- Chen, B.; Wan, J.; Celesti, A.; Li, D.; Abbas, H.; Zhang, Q. Edge computing in IoT-based manufacturing. IEEE Commun. Mag. 2018, 56, 103–109. [Google Scholar] [CrossRef]
- Saeik, F.; Avgeris, M.; Spatharakis, D.; Santi, N.; Dechouniotis, D.; Violos, J.; Leivadeas, A.; Athanasopoulos, N.; Mitton, N.; Papavassiliou, S. Task offloading in Edge and Cloud Computing: A survey on mathematical, artificial intelligence and control theory solutions. Comput. Netw. 2021, 195, 108177. [Google Scholar] [CrossRef]
- Elbamby, M.S.; Bennis, M.; Saad, W. Proactive edge computing in latency-constrained fog networks. In Proceedings of the 2017 European Conference on Networks and Communications (EuCNC), Oulu, Finland, 12–15 June 2017; pp. 1–6. [Google Scholar]
- Cai, L.; Wei, X.; Xing, C.; Zou, X.; Zhang, G.; Wang, X. Failure-resilient DAG task scheduling in edge computing. Comput. Netw. 2021, 198, 108361. [Google Scholar] [CrossRef]
- Feng, M.; Krunz, M.; Zhang, W. Joint task partitioning and user association for latency minimization in mobile edge computing networks. IEEE Trans. Veh. Technol. 2021, 70, 8108–8121. [Google Scholar] [CrossRef]
- Do-Duy, T.; Van Huynh, D.; Dobre, O.A.; Canberk, B.; Duong, T.Q. Digital twin-aided intelligent offloading with edge selection in mobile edge computing. IEEE Wirel. Commun. Lett. 2022, 11, 806–810. [Google Scholar] [CrossRef]
- Fan, W.; Li, S.; Liu, J.; Su, Y.; Wu, F.; Liu, Y. Joint task offloading and resource allocation for accuracy-aware machine-learning-based IIoT applications. IEEE Internet Things J. 2022, 10, 3305–3321. [Google Scholar] [CrossRef]
- Tolba, B.; Abo-Zahhad, M.; Elsabrouty, M.; Uchiyama, A.; Abd El-Malek, A.H. Joint user association, service caching, and task offloading in multi-tier communication/multi-tier edge computing heterogeneous networks. Ad. Hoc. Netw. 2024, 160, 103500. [Google Scholar] [CrossRef]
- Fang, C.; Liu, C.; Xu, H.; Wang, Z.; Chen, H.; Sun, Y.; Hu, X.; Zeng, D.; Dong, M. Q-learning based delay-aware content delivery in cloud-edge cooperation networks. In Proceedings of the 2021 7th International Conference on Computer and Communications (ICCC), Chengdu, China, 10–13 December 2021; pp. 1458–1462. [Google Scholar]
- Du, Y.; Zhang, K.; Peng, Y. Interruption-Aware Task Offloading for Vehicular Edge Computing of Parking Lots. In Proceedings of the 2023 IEEE Smart World Congress (SWC), Portsmouth, UK, 28–31 August 2023; pp. 1–6. [Google Scholar]
- Wu, H.; Geng, J.; Bai, X.; Jin, S. Deep reinforcement learning-based online task offloading in mobile edge computing networks. Inf. Sci. 2024, 654, 119849. [Google Scholar] [CrossRef]
- Li, T.; Liu, Y.; Ouyang, T.; Zhang, H.; Yang, K.; Zhang, X. Multi-Hop Task Offloading and Relay Selection for IoT Devices in Mobile Edge Computing. IEEE Trans. Mob. Comput. 2024, 24, 466–481. [Google Scholar] [CrossRef]
- Zhao, H.; Lu, G.; Liu, Y.; Chang, Z.; Wang, L.; Hämäläinen, T. Safe DQN-based AoI-minimal task offloading for UAV-aided edge computing system. IEEE Internet Things J. 2024, 11, 32012–32024. [Google Scholar] [CrossRef]
- Xu, Y.; Lv, Z.; Zhao, J. A Study on Task Offloading Based on Multi-Agent Advantage Actor Critic Algorithms in IIoT. In Proceedings of the 2024 5th International Conference on Computers and Artificial Intelligence Technology (CAIT), Hangzhou, China, 20–22 December 2024; pp. 297–302. [Google Scholar]
- Liu, X.; Chen, A.; Zheng, K.; Chi, K.; Yang, B.; Taleb, T. Distributed Computation Offloading for Energy Provision Minimization in WP-MEC Networks with Multiple HAPs. IEEE Trans. Mob. Comput. 2024, 24, 2673–2689. [Google Scholar] [CrossRef]
- Yin, L.; Luo, J.; Qiu, C.; Wang, C.; Qiao, Y. Joint task offloading and resources allocation for hybrid vehicle edge computing systems. IEEE Trans. Intell. Transp. Syst. 2024, 25, 10355–10368. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Long, K.; Nallanathan, A.; Leung, V.C. Energy efficient user association, resource allocation and caching deployment in fog radio access networks. IEEE Trans. Veh. Technol. 2021, 71, 1846–1856. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, A.; Liu, C.; Zhang, T.; Qi, L.; Wang, S.; Buyya, R. Reliability-enhanced task offloading in mobile edge computing environments. IEEE Internet Things J. 2021, 9, 10382–10396. [Google Scholar] [CrossRef]
- Fu, Q.; Li, Z.; Ding, Z.; Chen, J.; Luo, J.; Wang, Y.; Lu, Y. ED-DQN: An event-driven deep reinforcement learning control method for multi-zone residential buildings. Build. Environ. 2023, 242, 110546. [Google Scholar] [CrossRef]
- Ling, C.; Peng, K.; Wang, S.; Xu, X.; Leung, V.C. A Multi-Agent DRL-Based Computation Offloading and Resource Allocation Method with Attention Mechanism in MEC-Enabled IIoT. IEEE Trans. Serv. Comput. 2024, 17, 3037–3051. [Google Scholar] [CrossRef]
- Prakash, S.; Vyas, V. Proactive Fault Detection in Weather Forecast Control Systems Through Heartbeat Monitoring and Cloud-Based Analytics. In Quantum Computing Models for Cybersecurity and Wireless Communications; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2025; Chapter 5; pp. 73–97. [Google Scholar] [CrossRef]
- Bian, H.; Zhang, Q.; Zhao, J.; Zhang, H. RAT selection for IoT devices in HetNets: Reinforcement learning with hybrid SMDP algorithm. Phys. Commun. 2022, 54, 101833. [Google Scholar] [CrossRef]
- Do, H.M.; Tran, T.P.; Yoo, M. Deep reinforcement learning-based task offloading and resource allocation for industrial IoT in MEC federation system. IEEE Access 2023, 11, 83150–83170. [Google Scholar]
- Shi, W.; Chen, L.; Zhu, X. Task offloading decision-making algorithm for vehicular edge computing: A deep-reinforcement-learning-based approach. Sensors 2023, 23, 7595. [Google Scholar] [CrossRef]
- Huang, L.; Bi, S.; Zhang, Y.J.A. Deep reinforcement learning for online computation offloading in wireless powered mobile-edge computing networks. IEEE Trans. Mob. Comput. 2019, 19, 2581–2593. [Google Scholar] [CrossRef]
- Dong, L.; He, W.; Yao, H. Task offloading and resource allocation for tasks with varied requirements in mobile edge computing networks. Electronics 2023, 12, 366. [Google Scholar] [CrossRef]
- Nieto, G.; de la Iglesia, I.; Lopez-Novoa, U.; Perfecto, C. Deep Reinforcement Learning techniques for dynamic task offloading in the 5G edge-cloud continuum. J. Cloud Comput. 2024, 13, 94. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Y.; Pan, D.; Yuan, D. QoS-aware task offloading and resource allocation optimization in vehicular edge computing networks via MADDPG. Comput. Netw. 2024, 242, 110282. [Google Scholar] [CrossRef]
- Cai, J.; Zhu, X.; Ackah, A.E. Mobility-Aware Task Offloading Scheme for 6G Networks With Temporal Graph and Graph Matching. IEEE Internet Things J. 2024, 11, 20840–20852. [Google Scholar] [CrossRef]
- Satria, D.; Park, D.; Jo, M. Recovery for overloaded mobile edge computing. Future Gener. Comput. Syst. 2017, 70, 138–147. [Google Scholar] [CrossRef]
- Du, W.; He, Q.; Ji, Y.; Cai, C.; Zhao, X. Optimal user migration upon server failures in edge computing environment. In Proceedings of the 2021 IEEE International Conference on Web Services (ICWS), Virtual, 5–10 September 2021; pp. 272–281. [Google Scholar]
- Ma, Y.; Liu, L.; Liu, Z.; Li, F.; Xie, Q.; Chen, K.; Lv, C.; He, Y.; Li, F. A survey of ddos attack and defense technologies in multi-access edge computing. IEEE Internet Things J. 2024, 12, 1428–1452. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, F.; Cao, M.; Feng, C.; Chen, D. Enhancing UAV-assisted vehicle edge computing networks through a digital twin-driven task offloading framework. Wirel. Netw. 2024, 31, 965–981. [Google Scholar] [CrossRef]
- Schroeder, B.; Gibson, G.A. A large-scale study of failures in high-performance computing systems. IEEE Trans. Dependable Secur. Comput. 2009, 7, 337–350. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Pieter Abbeel, O.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–7 December 2017; pp. 6382–6393. [Google Scholar]
- Chu, X.; Ye, H. Parameter sharing deep deterministic policy gradient for cooperative multi-agent reinforcement learning. arXiv 2017, arXiv:1710.00336. [Google Scholar]
- Li, D.; Lou, N.; Zhang, B.; Xu, Z.; Fan, G. Adaptive parameter sharing for multi-agent reinforcement learning. In Proceedings of the ICASSP 2024—2024 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Seoul, Republic of Korea, 14–19 April 2024; pp. 6035–6039. [Google Scholar]
- Chen, Z.; Liao, G.; Ma, Q.; Chen, X. Adaptive Privacy Budget Allocation in Federated Learning: A Multi-Agent Reinforcement Learning Approach. In Proceedings of the ICC 2024-IEEE International Conference on Communications, Denver, CO, USA, 9–13 June 2024; pp. 5166–5171. [Google Scholar]
- Oroojlooy, A.; Hajinezhad, D. A review of cooperative multi-agent deep reinforcement learning. Appl. Intell. 2023, 53, 13677–13722. [Google Scholar] [CrossRef]


| Paper | Year | Decisions | Approach | Objectives | Interruption Awared | Interruption Model |
|---|---|---|---|---|---|---|
| [13] | 2021 | - task offloading - delivery | heuristic | delay | ||
| [14] | 2022 | - task offloading - delivery - resource allocation | heuristic | delay | ||
| [17] | 2022 | - caching - task offloading - resource allocation | DRL-based | delay | ||
| [15] | 2022 | - task offloading - resource allocation | heuristic | delay | ||
| [19] | 2024 | - task offloading | DRL-based | delay | ||
| [24] | 2024 | - task offloading - resource allocation | game theory | delay | ||
| [20] | 2024 | - task offloading - relay selection | DRL-based | delay | ||
| [21] | 2024 | - task offloading | DRL-based | age of information | ||
| [16] | 2024 | - caching - task offloading - delivery | heuristic | delay | ||
| [23] | 2024 | - task offloading - resource allocation | MADRL-based | energy | ||
| [22] | 2024 | - task offloading | MADRL-based | delay | ||
| [28] | 2024 | - task offloading - resource allocation | MADRL-based | delay, energy | ||
| [12] | 2021 | - task offloading | greedy | delay | ✓ | Fixed value |
| [26] | 2022 | - task offloading | heuristic | delay, bandwidth | ✓ | Random-based |
| [18] | 2023 | - task offloading | DRL-based | delay | ✓ | |
| Ours | - task offloading | DRL-based | delay | ✓ | Load-based | |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| System Parameters | |||
| Number of IIoT devices M | Edge server total channel bandwidth | 20 MHz | |
| Number of edge servers N | Edge server sub-channel bandwidth | 2 MHz | |
| Task size | MB | RSU transmission power | 30 |
| Required CPU cycles | cycles | Noise power | −174 dBm/Hz |
| Task deadline | s | Edge-to-edge data rate | 150 Mbps |
| Computation capacity of edge server | 25 GHz | Interruption sensitivity | |
| Maximun computation capacity for each task | 5 GHz | Interruption duration | time slots |
| Computation capacity of IIoT device | 1 GHz | - | - |
| Parameters for MAA2C | |||
| Training step | steps | Replay memory size | 10,000 |
| Model hidden dimension | 128 | Batch size | 32 |
| Discount factor | 0.99 | Reward scaling factor , | |
| Actor learning rate | Critic learning rate | ||
| No | Model | Interruption | |||
|---|---|---|---|---|---|
| No () | Yes () | ||||
| Avg. Delay (ms) | Avail. (%) | Avg. Delay (ms) | Avail. (%) | ||
| #1 | MAA2C | 273.43 ± 20.84 | 100 | 390.95 ± 112.63 | 83.07 |
| #2 | MAD2QN | 323.56 ± 18.18 | 396.54 ± 110.47 | 83.43 | |
| #3 | A2C | 297.91 ± 11.79 | 494.52 ± 81.81 | 92.47 | |
| #4 | Greedy | 298.75 ± 11.87 | 418.23 ± 111.84 | 83.09 | |
| #5 | Random | 392.39 ± 48.55 | 556.09 ± 66.28 | 93.27 | |
| #6 | LocalEdge | 272.70 ± 26.57 | 701.59 ± 200.21 | 97.13 | |
| #7 | OnDevice | 809.84 ± 41.30 | 809.84± 41.30 | 100.00 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bui, K.A.; Yoo, M. Interruption-Aware Computation Offloading in the Industrial Internet of Things. Sensors 2025, 25, 2904. https://doi.org/10.3390/s25092904
Bui KA, Yoo M. Interruption-Aware Computation Offloading in the Industrial Internet of Things. Sensors. 2025; 25(9):2904. https://doi.org/10.3390/s25092904
Chicago/Turabian StyleBui, Khoi Anh, and Myungsik Yoo. 2025. "Interruption-Aware Computation Offloading in the Industrial Internet of Things" Sensors 25, no. 9: 2904. https://doi.org/10.3390/s25092904
APA StyleBui, K. A., & Yoo, M. (2025). Interruption-Aware Computation Offloading in the Industrial Internet of Things. Sensors, 25(9), 2904. https://doi.org/10.3390/s25092904








