Privacy-Preserving Federated Learning for Space–Air–Ground Integrated Networks: A Bi-Level Reinforcement Learning and Adaptive Transfer Learning Optimization Framework
Abstract
1. Introduction
1.1. Background
1.2. Motivation and Contributions
2. Related Work
2.1. Space–Air–Ground Integrated Network
2.2. Federated Learning
Federated Learning Applications in Satellite Networks
2.3. Privacy Protection
3. Federated Learning for Space–Air–Ground Integrated Networks
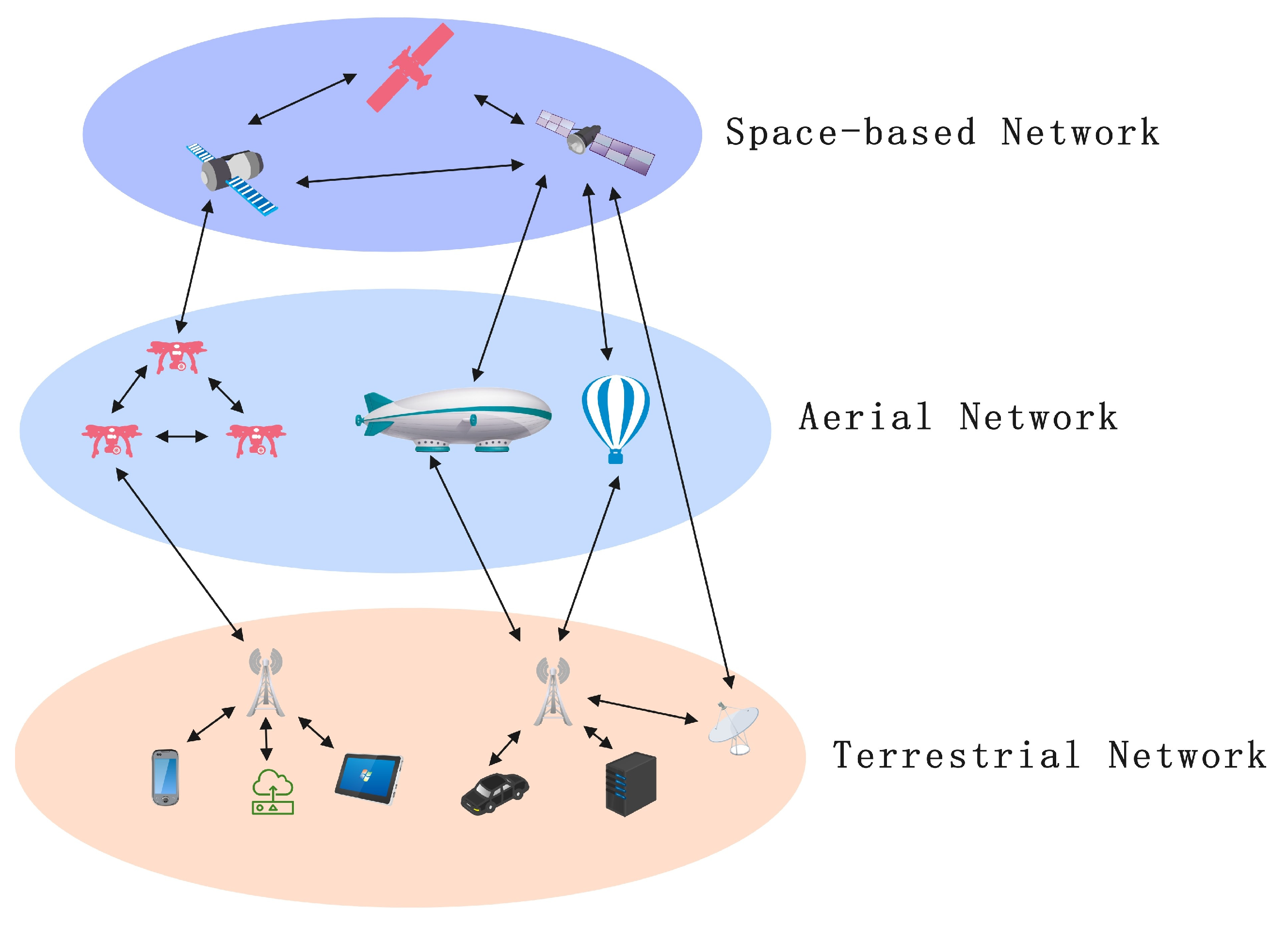
3.1. Space–Air–Ground Integrated Network Architecture
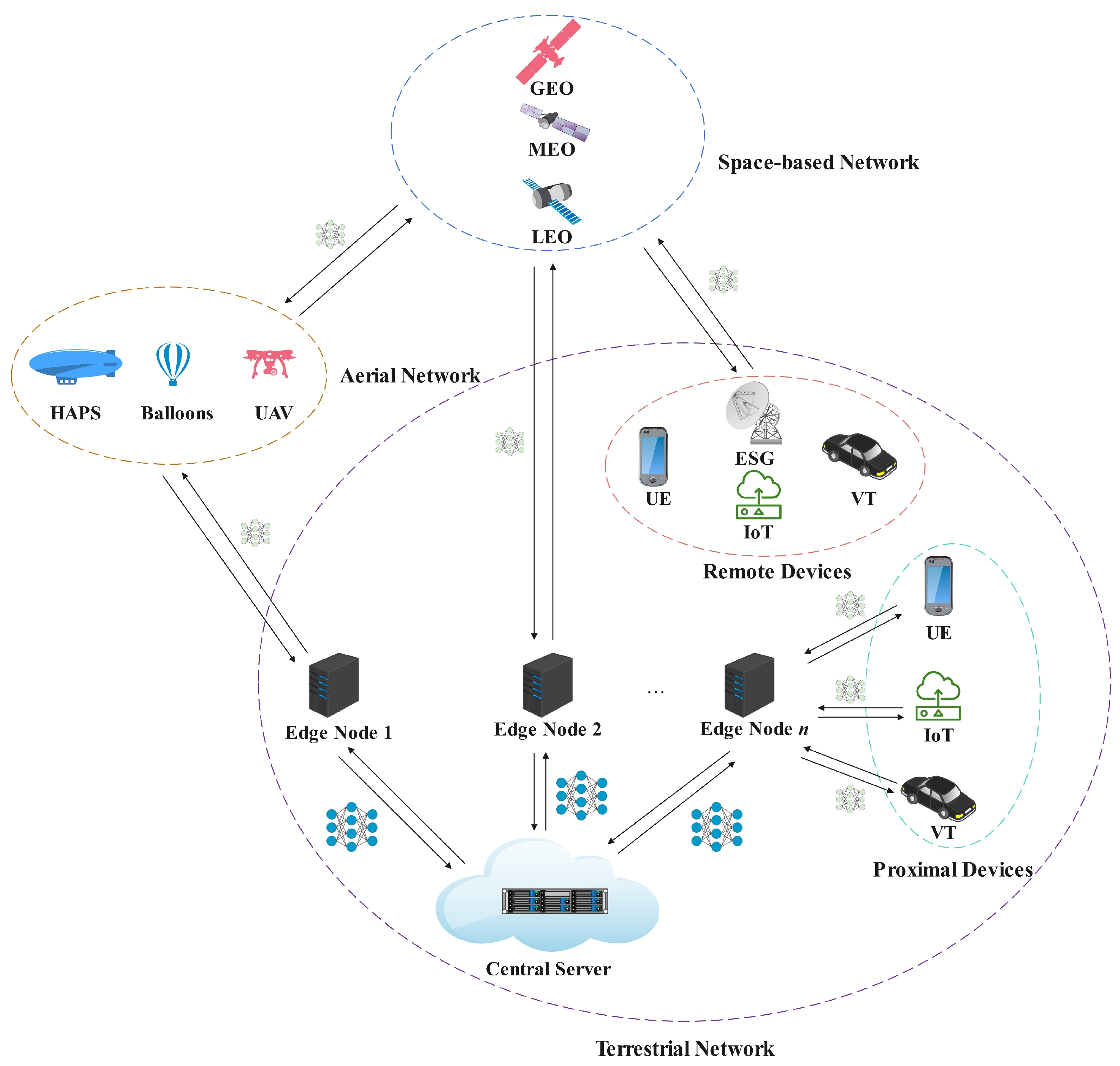
3.2. Federated Learning Framework for Space–Air–Ground Integrated Networks
3.3. Adaptive Transfer Learning Strategy
3.4. Device Selection Optimization Strategy Based on Hierarchical Reinforcement Learning
3.4.1. Hierarchical Reinforcement Learning Strategy
3.4.2. Hierarchical Attention Mechanism
3.4.3. Meta-Learning-Based Strategy Optimization
3.5. Privacy-Preserving Federated Learning
3.5.1. Local Training at Terminal Nodes
3.5.2. Local Aggregation at Edge Nodes
3.5.3. Global Model Aggregation at the Central Server
4. Experimental Evaluation
4.1. Experimental Setup
4.1.1. Experimental Environment
4.1.2. Datasets
4.2. Experimental Results and Analysis
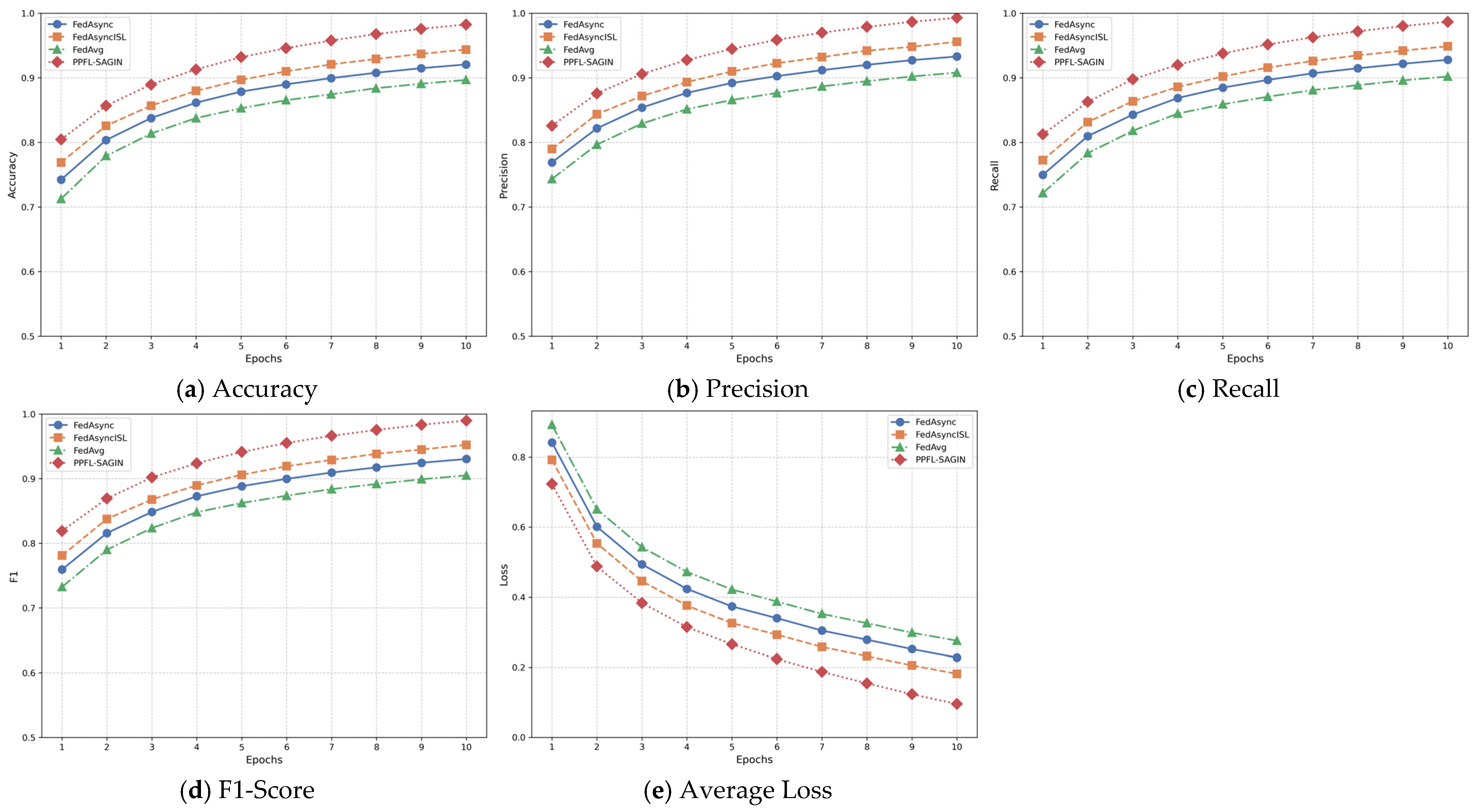
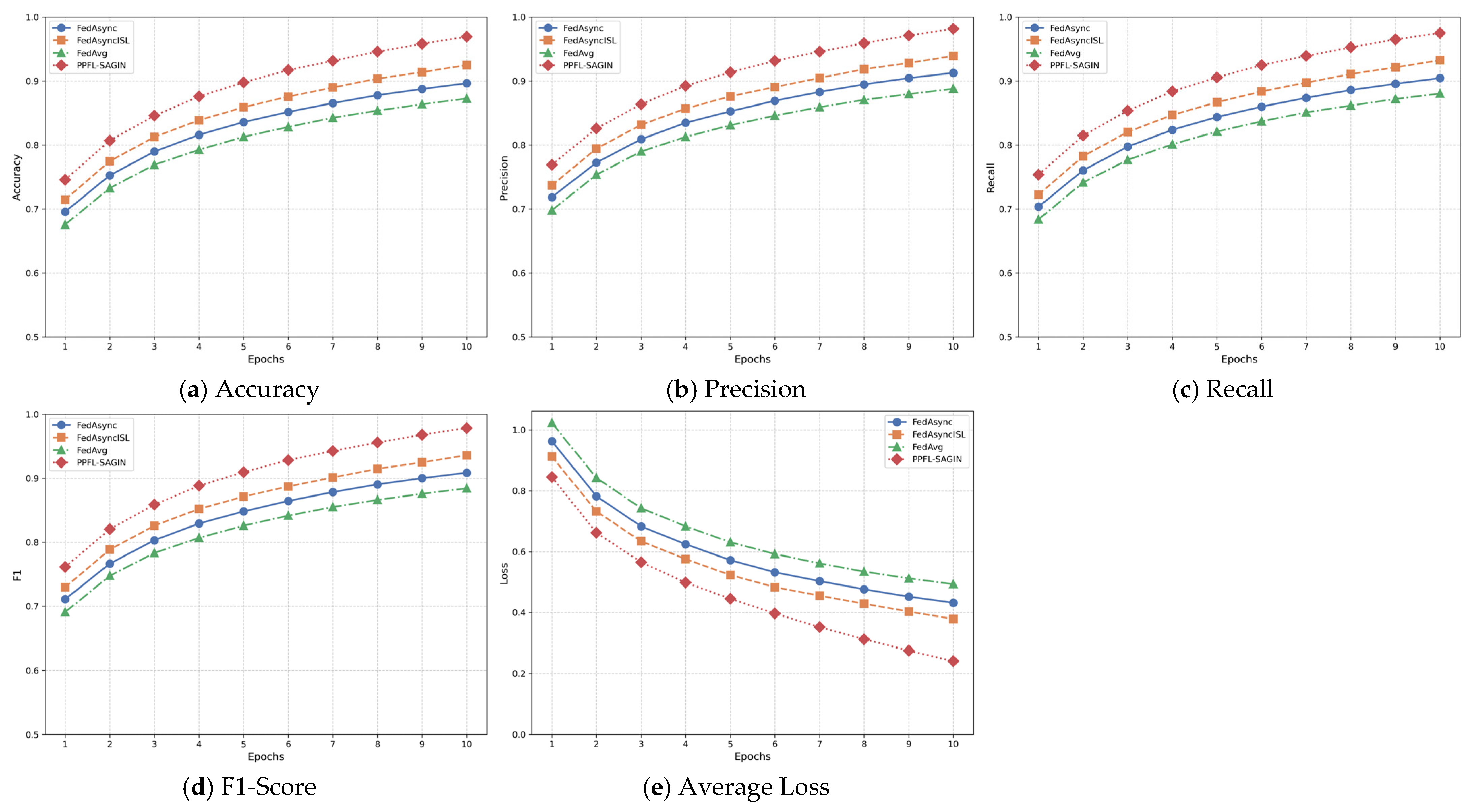
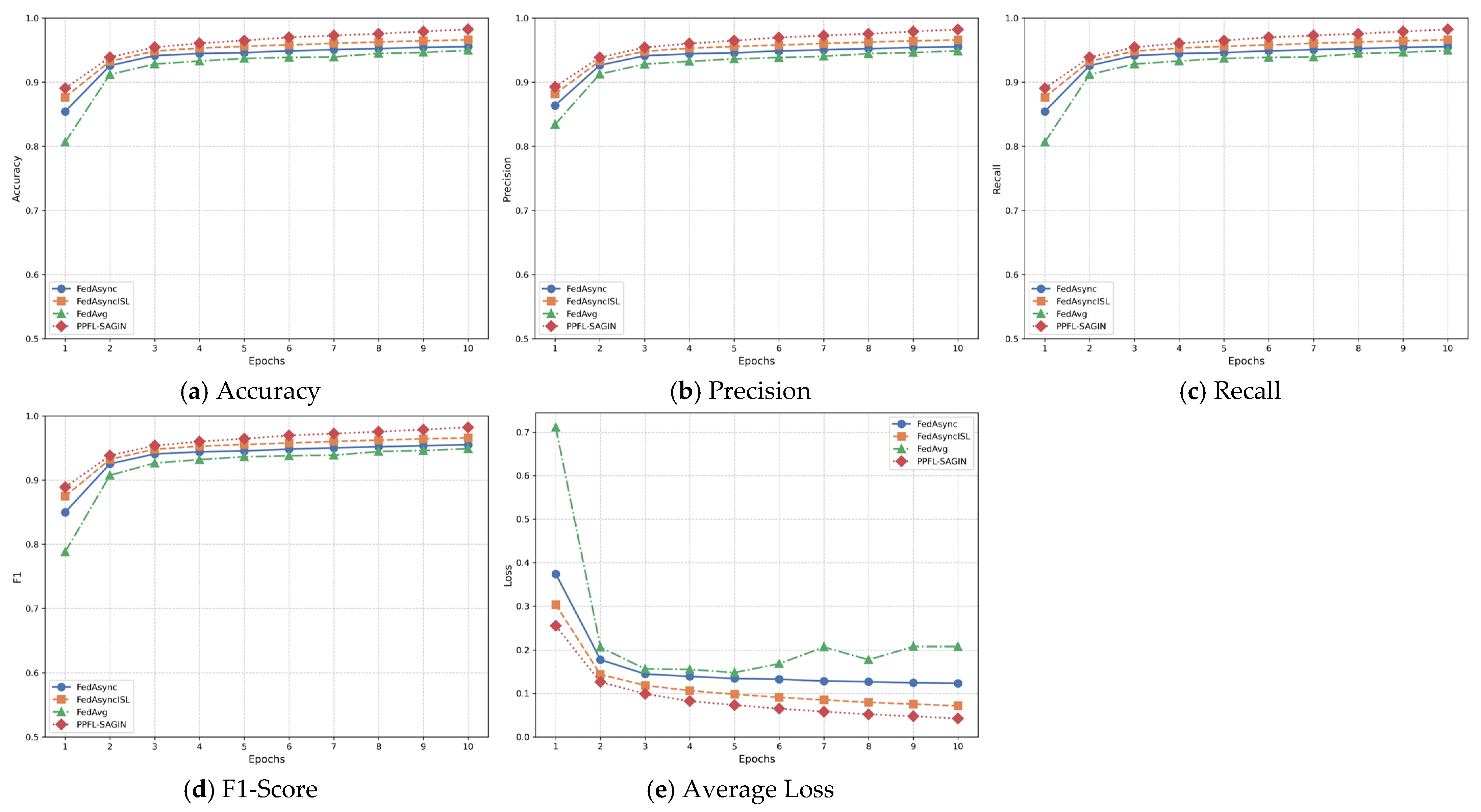
4.2.1. Performance Metric Evaluation Based on Four Datasets
4.2.2. Time Overhead Evaluation
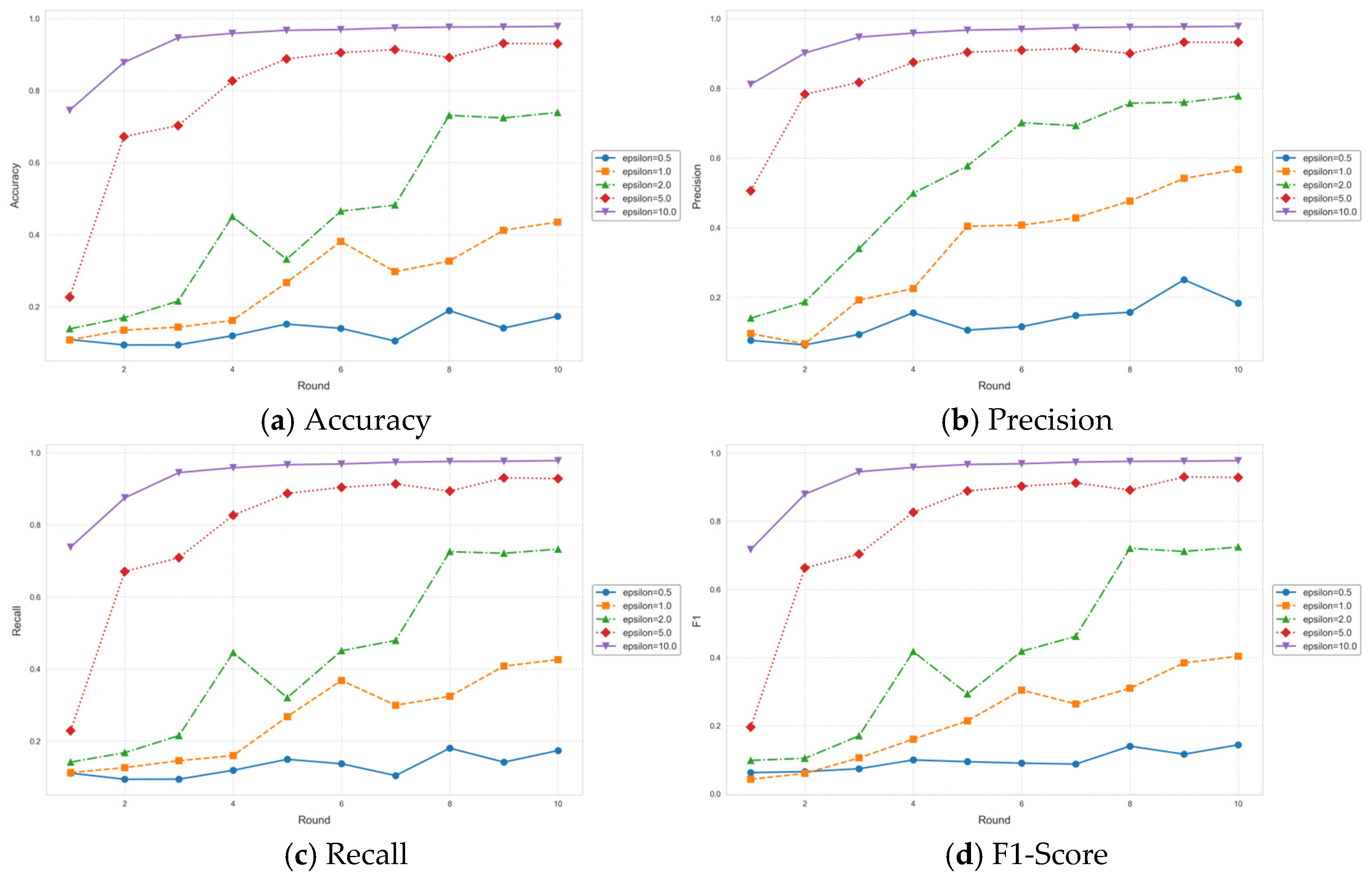
4.2.3. Privacy Protection Evaluation
4.2.4. Ablation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- ├── main.py # Main entry point for experiments
- ├── config/
- │ └── config.yaml # Configuration parameters
- ├── models/
- │ ├── neural_networks.py # Neural network model definitions
- │ └── federated_models.py # Federated learning model implementations
- ├── algorithms/
- │ ├── adaptive_transfer.py # Adaptive transfer learning implementation
- │ ├── hierarchical_rl.py # Hierarchical reinforcement learning
- │ ├── privacy_budget.py # Privacy budget allocation
- │ └── robust_aggregation.py # Robust aggregation methods
- ├── utils/
- │ ├── data_loader.py # Dataset loading and preprocessing
- │ ├── metrics.py # Evaluation metrics
- │ └── visualization.py # Results visualization
- └── simulation/
- ├── network_topology.py # SAGIN network topology simulator
- ├── device_manager.py # Device status and capability simulator
- Detailed Code Structure Introduction
References
- Liu, J.; Shi, Y.; Fadlullah, Z.M.; Kato, N. Space-air-ground integrated network: A Survey. IEEE Commun. Surv. Tutor. 2018, 20, 2714–2741. [Google Scholar] [CrossRef]
- Shen, Z.; Jin, J.; Tan, C.; Tagami, A.; Wang, S.; Li, Q.; Zheng, Q.; Yuan, J. A survey of next-generation computing technologies in space-air-ground integrated networks. ACM Comput. Surv. 2023, 56, 1–40. [Google Scholar] [CrossRef]
- Shang, B.; Yi, Y.; Liu, L. Computing over space-air-ground integrated networks: Challenges and Opportunities. IEEE Netw. 2021, 35, 302–309. [Google Scholar] [CrossRef]
- Zhang, L.; Abderrahim, W.; Shihada, B. Heterogeneous traffic offloading in space-air-ground integrated networks. IEEE Access 2021, 9, 165462–165475. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Meng, Y.; Li, S.; Ma, L.; Liu, Z.; Zhu, H. Secure and efficient uav tracking in space-air-ground integrated network. IEEE Trans. Veh. Technol. 2023, 72, 10682–10695. [Google Scholar] [CrossRef]
- Siddiqa, A.; Hashem, I.A.T.; Yaqoob, I.; Marjani, M.; Shamshirband, S.; Gani, A.; Nasaruddin, F. A survey of big data management: Taxonomy and State-of-the-Art. J. Netw. Comput. Appl. 2016, 71, 151–166. [Google Scholar] [CrossRef]
- Chen, X.; Feng, W.; Chen, Y.; Ge, N.; He, Y. Access-Side DDoS Defense for Space-Air-Ground Integrated 6G V2X Networks. IEEE Open J. Commun. Soc. 2024, 5, 2847–2868. [Google Scholar] [CrossRef]
- Banabilah, S.; Aloqaily, M.; Alsayed, E.; Malik, N.; Jararweh, Y. Federated learning review: Fundamentals, enabling technologies, and future applications. Inf. Process. Manag. 2022, 59, 103061. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, J. A survey on differential privacy for unstructured data content. ACM Comput. Surv. (CSUR) 2022, 54, 1–28. [Google Scholar] [CrossRef]
- Munjal, K.; Bhatia, R. A systematic review of homomorphic encryption and its contributions in healthcare industry. Complex Intell. Syst. 2023, 9, 3759–3786. [Google Scholar] [CrossRef]
- Cui, H.; Zhang, J.; Geng, Y.; Xiao, Z.; Sun, T.; Zhang, N.; Liu, J.; Wu, Q.; Cao, X. Space-air-ground integrated network (SAGIN) for 6G: Requirements, Architecture and Challenges. China Commun. 2022, 19, 90–108. [Google Scholar] [CrossRef]
- Li, H.; Ota, K.; Dong, M. AI in SAGIN: Building Deep Learning Service-Oriented Space-Air-Ground Integrated Networks. IEEE Netw. 2023, 37, 154–159. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Y.; Kumar, N.; Guizani, M. Dynamic SFC embedding algorithm assisted by federated learning in space–air–ground-integrated network resource allocation scenario. IEEE Internet Things J. 2022, 10, 9308–9318. [Google Scholar] [CrossRef]
- Xu, M.; Niyato, D.; Xiong, Z.; Kang, J.; Cao, X.; Shen, X.; Miao, C. Quantum-secured space-air-ground integrated networks: Concept, Framework, and Case Study. IEEE Wirel. Commun. 2022, 30, 136–143. [Google Scholar] [CrossRef]
- Zhang, C.; Xie, Y.; Bai, H.; Yu, B.; Li, W.; Gao, Y. A survey on federated learning. Knowl.-Based Syst. 2021, 216, 106775. [Google Scholar] [CrossRef]
- McMahan, B.; Moore, E.; Ramage, D.; Hampson, S.; Arcas, B. Communication-efficient learning of deep networks from decentralized data. In Proceedings of the 20th International Conference on Artificial Intelligence and Statistics (AISTATS), Lauderdale, FL, USA, 20–22 April 2017; pp. 1273–1282. [Google Scholar]
- Geyer, R.C.; Klein, T.; Nabi, M. Differentially private federated learning: A Client Level Perspective. arXiv 2017, arXiv:1712.07557. [Google Scholar]
- Shah, S.M.; Lau, V.K.N. Model compression for communication efficient federated learning. IEEE Trans. Neural Netw. Learn. Syst. 2021, 34, 5937–5951. [Google Scholar] [CrossRef]
- Sattler, F.; Wiedemann, S.; Müller, K.R.; Samek, W. Robust and communication-efficient federated learning from non-iid data. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 3400–3413. [Google Scholar] [CrossRef]
- Zhou, Y.; Pang, X.; Wang, Z.; Hu, J.; Sun, P.; Ren, K. Towards Efficient Asynchronous Federated Learning in Heterogeneous Edge Environments. In Proceedings of the IEEE INFOCOM 2024—IEEE Conference on Computer Communications, Vancouver, BC, Canada, 20–23 May 2024; pp. 2448–2457. [Google Scholar]
- Wang, F.; Hugh, E.; Li, B. More Than Enough is Too Much: Adaptive Defenses Against Gradient Leakage in Production Federated Learning. IEEE/ACM Trans. Netw. 2024, 32, 3061–3075. [Google Scholar] [CrossRef]
- Nasr, M.; Shokri, R.; Houmansadr, A. Comprehensive privacy analysis of deep learning: Passive and Active White-Box Inference Attacks Against Centralized and Federated Learning. In Proceedings of the IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 19–23 May 2019; pp. 739–753. [Google Scholar]
- Zhu, L.; Liu, Z.; Han, S. Deep leakage from gradients. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; pp. 14774–14784. [Google Scholar]
- Bagdasaryan, E.; Veit, A.; Hua, Y.; Estrin, D.; Shmatikov, V. How to backdoor federated learning. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Online, 26–28 August 2020; pp. 2938–2948. [Google Scholar]
- Anzalchi, J.; Couchman, A.; Gabellini, P.; Gallinaro, G.; D’Agristina, L.; Alagha, N.; Angeletti, P. Beam hopping in multi-beam broadband satellite systems: System Simulation and Performance Comparison with Non-Hopped Systems. In Proceedings of the 2010 5th Advanced Satellite Multimedia Systems Conference and the 11th Signal Processing for Space Communications Workshop, Cagliari, Italy, 13–15 September 2010; IEEE: Piscataway, NJ, USA; pp. 248–255. [Google Scholar]
- Dabiri, M.T.; Khankalantary, S.; Piran, M.J.; Ansari, I.S.; Uysal, M.; Saad, W. UAV-assisted free space optical communication system with amplify-and-forward relaying. IEEE Trans. Veh. Technol. 2021, 70, 8926–8936. [Google Scholar] [CrossRef]
- Dwork, C.; McSherry, F.; Nissim, K.; Smith, A. Calibrating noise to sensitivity in private data analysis. In Theory of Cryptography, Proceedings of the Third Theory of Cryptography Conference, TCC 2006, New York, NY, USA, 4–7 March 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 265–284. [Google Scholar]
- Ogburn, M.; Turner, C.; Dahal, P. Homomorphic encryption. Procedia Comput. Sci. 2013, 20, 502–509. [Google Scholar] [CrossRef]
- Zhang, C.; Li, S.; Xia, J.; Wang, W.; Yan, F.; Liu, Y. BatchCrypt: Efficient Homomorphic Encryption for Cross-Silo Federated Learning. In Proceedings of the 2020 USENIX Annual Technical Conference (USENIX ATC 20), 15–17 July 2020; pp. 493–506. [Google Scholar]
- Knott, B.; Venkataraman, S.; Hannun, A.; Sengupta, S.; Ibrahim, M.; Maaten, L. Crypten: Secure Multi-Party Computation Meets Machine Learning. Adv. Neural Inf. Process. Syst. 2021, 34, 4961–4973. [Google Scholar]
- Kanagavelu, R.; Li, Z.; Samsudin, J.; Yang, Y.; Yang, F.; Goh, R.S.M.; Cheah, M.; Praewpiraya, W.; Khajonpong, A.; Wang, S. Two-phase multi-party computation enabled privacy-preserving federated learning. In Proceedings of the 2020 20th IEEE/ACM International Symposium on Cluster, Cloud and Internet Computing (CCGRID), Melbourne, VIC, Australia, 11–14 May 2020; IEEE: Piscataway, NJ, USA; pp. 410–419. [Google Scholar]
- Li, L.; Zhu, L.; Li, W. Cloud–Edge–End Collaborative Federated Learning: Enhancing Model Accuracy and Privacy in Non-IID Environments. Sensors 2024, 24, 8028. [Google Scholar] [CrossRef] [PubMed]
- Puterman, M.L. Markov decision processes. Handb. Oper. Res. Manag. Sci. 1990, 2, 331–434. [Google Scholar]
- Hospedales, T.; Antoniou, A.; Micaelli, P.; Storkey, A. Meta-learning in neural networks: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5149–5169. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, X.; Tang, W.; Lai, J.; Cao, L. Meta weight learning via model-agnostic meta-learning. Neurocomputing 2021, 432, 124–132. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-visual-words and spatial extensions for land-use classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 270–279. [Google Scholar]
- Li, H.; Dou, X.; Tao, C.; Wu, Z.; Chen, J.; Peng, J.; Deng, M.; Zhao, L. RSI-CB: A Large-Scale Remote Sensing Image Classification Benchmark Using Crowdsourced Data. Sensors 2020, 20, 1594. [Google Scholar] [CrossRef]
- Xu, C.; Qu, Y.; Xiang, Y.; Gao, L. Asynchronous federated learning on heterogeneous devices: A Survey. Comput. Sci. Rev. 2023, 50, 100595. [Google Scholar] [CrossRef]
- Zhou, A.; Wang, Y.; Zhang, Q. A Two-layer Federated Learning for LEO Constellation in IoT. In Proceedings of the 2024 IEEE International Workshop on Radio Frequency and Antenna Technologies (iWRF&AT), Shenzhen, China, 31 May 2024; IEEE: Piscataway, NJ, USA; pp. 499–503. [Google Scholar]




| Parameter | Value/Range | Description |
|---|---|---|
| LEO: Circular orbit with 90-min period | ||
| MEO: Circular orbit with 6-h period | ||
| Node Mobility Pattern | Varied | GEO: Fixed relative to Earth |
| UAV: Random waypoint model at 100–300 m | ||
| HAPS: Fixed position at 20 km altitude | ||
| LEO–Ground: 5–15 min | ||
| MEO–Ground: 20–40 min | ||
| Connection Duration(min) | 5—Continuous | GEO–Ground: Continuous |
| UAV–Ground: 10–30 min | ||
| HAPS–Ground: Continuous | ||
| LEO visibility changes: Every 5–15 min | ||
| Topology Change Frequency | Varied | UAV connectivity changes: Every 10–30 min |
| Ground device mobility: Every 30–60 min | ||
| Space nodes: 10–50% | ||
| Disconnection Probability | 0–50% | Air nodes: 5–30% |
| (per hour) | Ground nodes: 0–10% |
| Method | Accuracy | Precision | Recall | F1-Score | Average Loss |
|---|---|---|---|---|---|
| PPFL-SAGIN (dynamic weighting) | 0.9502 | 0.9534 | 0.9502 | 0.9512 | 0.1204 |
| Static weighting strategy | 0.8512 | 0.8567 | 0.8512 | 0.8525 | 0.2695 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Zhu, L.; Li, W. Privacy-Preserving Federated Learning for Space–Air–Ground Integrated Networks: A Bi-Level Reinforcement Learning and Adaptive Transfer Learning Optimization Framework. Sensors 2025, 25, 2828. https://doi.org/10.3390/s25092828
Li L, Zhu L, Li W. Privacy-Preserving Federated Learning for Space–Air–Ground Integrated Networks: A Bi-Level Reinforcement Learning and Adaptive Transfer Learning Optimization Framework. Sensors. 2025; 25(9):2828. https://doi.org/10.3390/s25092828
Chicago/Turabian StyleLi, Ling, Lidong Zhu, and Weibang Li. 2025. "Privacy-Preserving Federated Learning for Space–Air–Ground Integrated Networks: A Bi-Level Reinforcement Learning and Adaptive Transfer Learning Optimization Framework" Sensors 25, no. 9: 2828. https://doi.org/10.3390/s25092828
APA StyleLi, L., Zhu, L., & Li, W. (2025). Privacy-Preserving Federated Learning for Space–Air–Ground Integrated Networks: A Bi-Level Reinforcement Learning and Adaptive Transfer Learning Optimization Framework. Sensors, 25(9), 2828. https://doi.org/10.3390/s25092828







