Multiple Sclerosis Classification Using the Local Divergence Exponent: Parameters Selection for State-Space Reconstruction
Abstract
1. Introduction
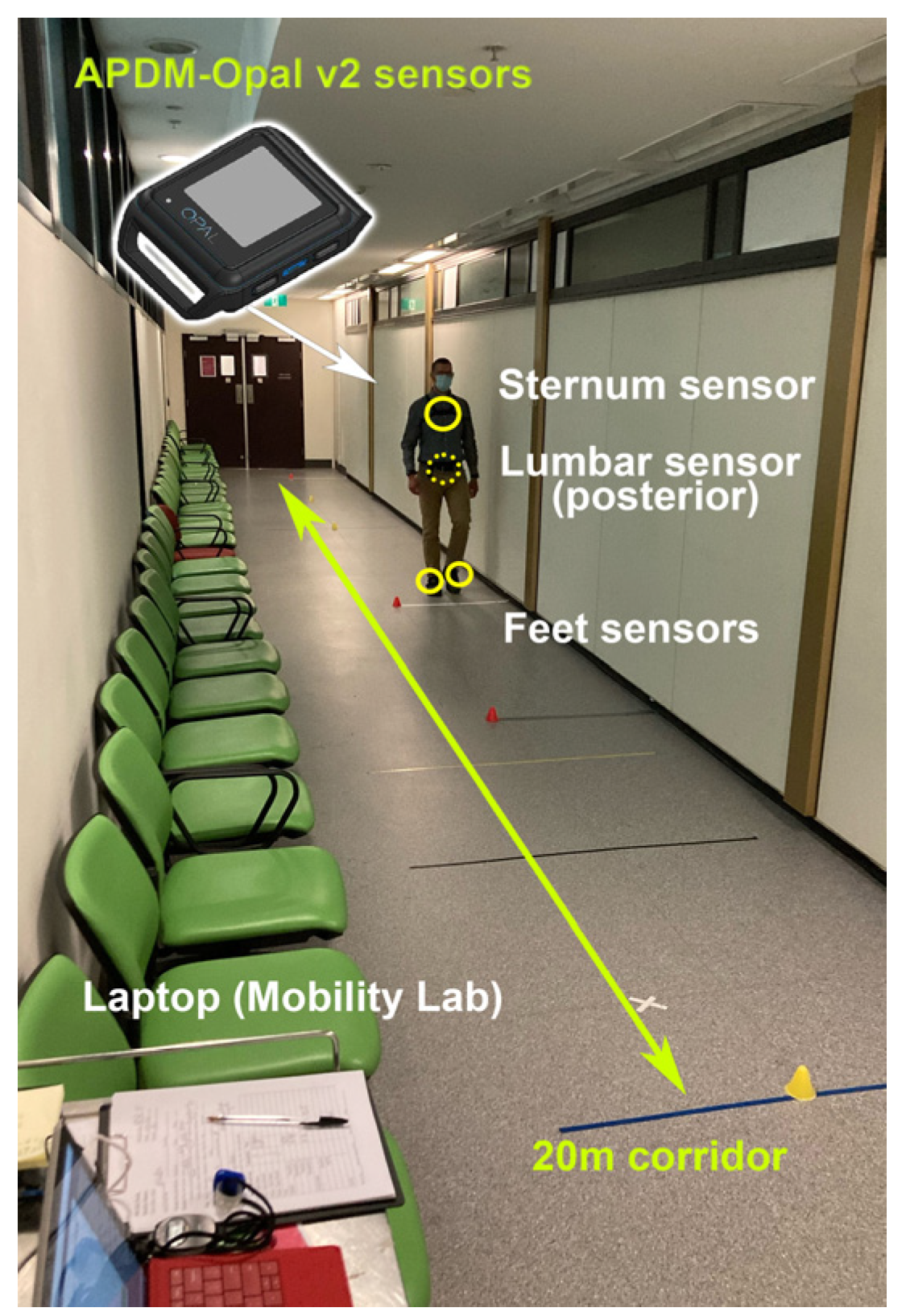
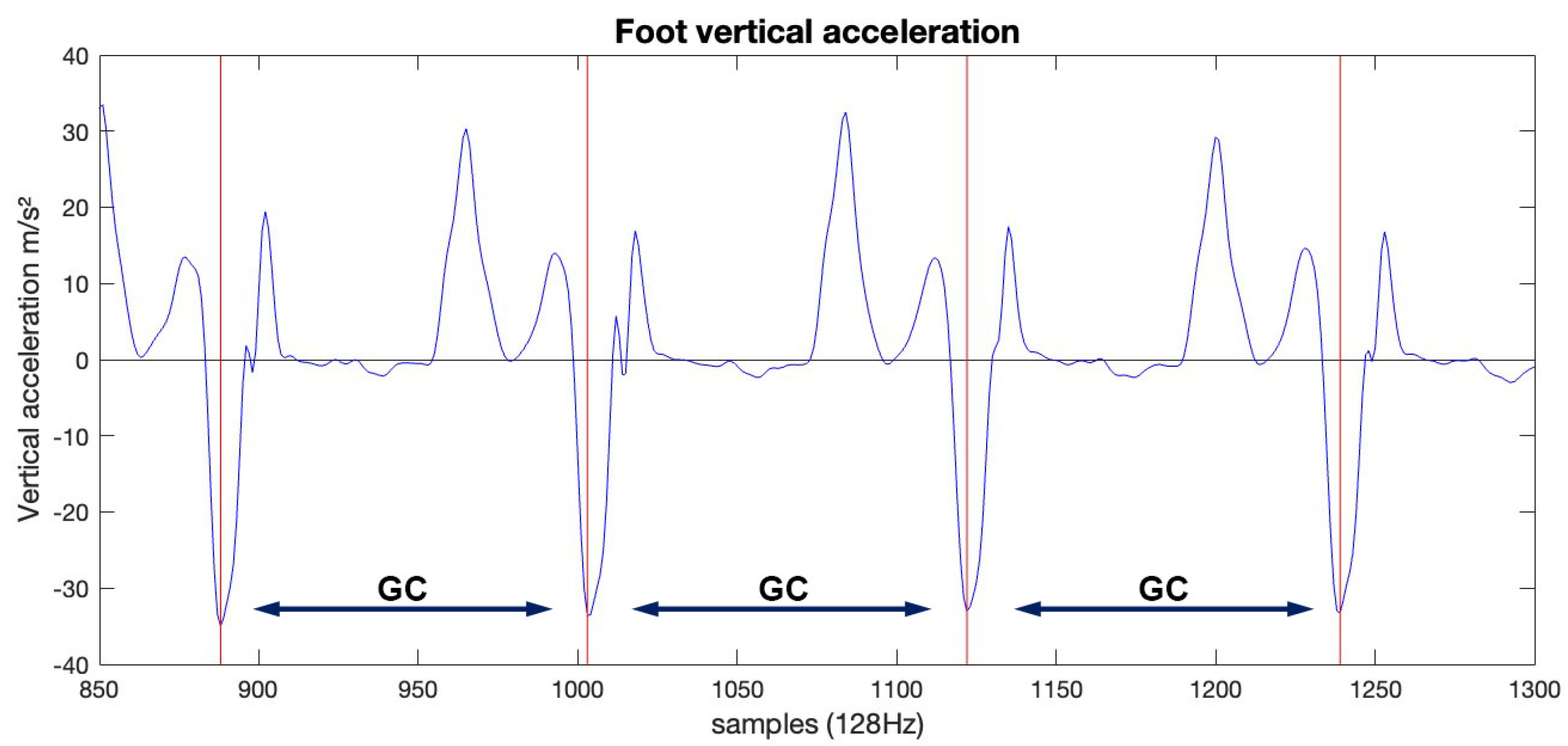
2. Materials and Methods
3. Results
3.1. Participant Demographics
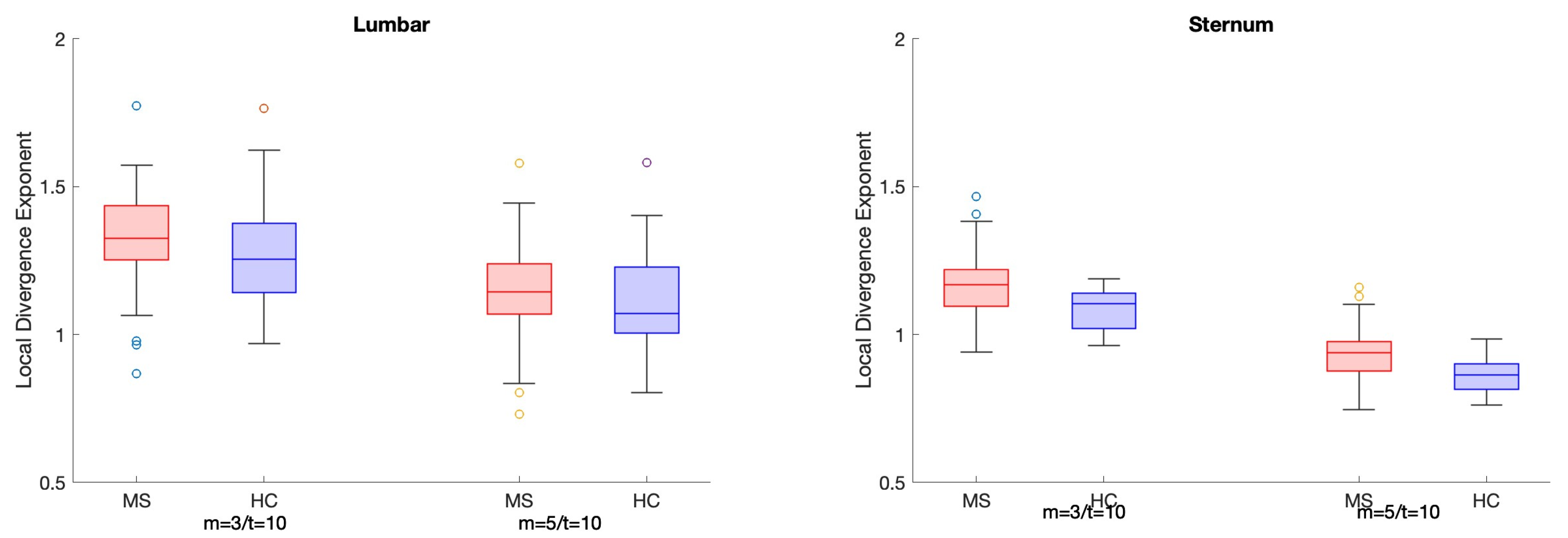
3.2. Classification Analysis
4. Discussion
Limitations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gervasoni, E.; Anastasi, D.; Di Giovanni, R.; Solaro, C.; Rovaris, M.; Brichetto, G.; Confalonieri, P.; Tacchino, A.; Carpinella, I.; Cattaneo, D. Uncovering Subtle Gait Deterioration in People with Early-Stage Multiple Sclerosis Using Inertial Sensors: A 2-Year Multicenter Longitudinal Study. Sensors 2023, 23, 9249. [Google Scholar] [CrossRef] [PubMed]
- Cofré Lizama, L.E.; Bruijn, S.M.; Galea, M.P. Gait stability at early stages of multiple sclerosis using different data sources. Gait Posture 2020, 77, 214–217. [Google Scholar] [CrossRef]
- Cofré Lizama, L.E.; Panisset, M.G.; Peng, L.; Tan, Y.; Kalincik, T.; Galea, M.P. Optimal sensor location and direction to accurately classify people with early-stage MS using gait stability. Gait Posture 2023, 102, 39–42. [Google Scholar] [CrossRef] [PubMed]
- Müller, R.; Schreff, L.; Koch, L.-E.; Oschmann, P.; Hamacher, D. Measuring Gait Stability in People with Multiple Sclerosis Using Different Sensor Locations and Time Scales. Sensors 2021, 21, 4001. [Google Scholar] [CrossRef]
- Peebles, A.T.; Bruetsch, A.P.; Lynch, S.G.; Huisinga, J.M. Dynamic Balance Is Related to Physiological Impairments in Persons With Multiple Sclerosis. Arch. Phys. Med. Rehabil. 2018, 99, 2030–2037. [Google Scholar] [CrossRef]
- Cofré Lizama, L.E.; Strik, M.; Van der Walt, A.; Kilpatrick, T.J.; Kolbe, S.C.; Galea, M.P. Gait stability reflects motor tracts damage at early stages of multiple sclerosis. Mult. Scler. J. 2022, 28, 1773–1782. [Google Scholar] [CrossRef]
- Mehdizadeh, S. The largest Lyapunov exponent of gait in young and elderly individuals: A systematic review. Gait Posture 2018, 60, 241–250. [Google Scholar] [CrossRef] [PubMed]
- Bruijn, S.M.; Meijer, O.G.; Beek, P.J.; van Dieen, J.H. Assessing the stability of human locomotion: A review of current measures. J. R. Soc. Interface 2013, 10, 20120999. [Google Scholar] [CrossRef]
- Hussain, V.S.; Spano, M.L.; Lockhart, T.E. Effect of data length on time delay and embedding dimension for calculating the Lyapunov exponent in walking. J. R. Soc. Interface 2020, 17, 20200311. [Google Scholar] [CrossRef]
- Park, I.; Lee, J.H.; Ahn, J. Effects of the kinematic variable, time delay and data length on test–retest reliability of the maximal Lyapunov exponent of human walking. R. Soc. Open Sci. 2024, 11, 240333. [Google Scholar] [CrossRef]
- Raffalt, P.C.; Kent, J.A.; Wurdeman, S.R.; Stergiou, N. Selection Procedures for the Largest Lyapunov Exponent in Gait Biomechanics. Ann. Biomed. Eng. 2019, 47, 913–923. [Google Scholar] [CrossRef] [PubMed]
- Tajali, S.; Mehravar, M.; Negahban, H.; van Dieen, J.H.; Shaterzadeh-Yazdi, M.J.; Mofateh, R. Impaired local dynamic stability during treadmill walking predicts future falls in patients with multiple sclerosis: A prospective cohort study. Clin. Biomech. 2019, 67, 197–201. [Google Scholar] [CrossRef] [PubMed]
- Janshen, L.; Santuz, A.; Ekizos, A.; Arampatzis, A. Fuzziness of muscle synergies in patients with multiple sclerosis indicates increased robustness of motor control during walking. Sci. Rep. 2020, 10, 7249. [Google Scholar] [CrossRef] [PubMed]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Rispens, S.M.; Pijnappels, M.; van Dieën, J.H.; van Schooten, K.S.; Beek, P.J.; Daffertshofer, A. A benchmark test of accuracy and precision in estimating dynamical systems characteristics from a time series. J. Biomech. 2014, 47, 470–475. [Google Scholar] [CrossRef]
- Gates, D.H.; Dingwell, J.B. Comparison of different state space definitions for local dynamic stability analyses. J. Biomech. 2009, 42, 1345–1349. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef]
- van Schooten, K.S.; Rispens, S.M.; Pijnappels, M.; Daffertshofer, A.; van Dieen, J.H. Assessing gait stability: The influence of state space reconstruction on inter- and intra-day reliability of local dynamic stability during over-ground walking. J. Biomech. 2013, 46, 137–141. [Google Scholar] [CrossRef]
- Caronni, A.; Gervasoni, E.; Ferrarin, M.; Anastasi, D.; Brichetto, G.; Confalonieri, P.; Di Giovanni, R.; Prosperini, L.; Tacchino, A.; Solaro, C.; et al. Local Dynamic Stability of Gait in People With Early Multiple Sclerosis and No-to-Mild Neurological Impairment. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 1389–1396. [Google Scholar] [CrossRef]
- Carpinella, I.; Gervasoni, E.; Anastasi, D.; Di Giovanni, R.; Tacchino, A.; Brichetto, G.; Confalonieri, P.; Rovaris, M.; Solaro, C.; Ferrarin, M.; et al. Instrumentally assessed gait quality is more relevant than gait endurance and velocity to explain patient-reported walking ability in early-stage multiple sclerosis. Eur. J. Neurol. 2021, 28, 2259–2268. [Google Scholar] [CrossRef]
- Abarbanel, H.D.I.; Brown, R.; Sidorowich, J.J.; Tsimring, L.S. The analysis of observed chaotic data in physical systems. Rev. Mod. Phys. 1993, 65, 1331–1392. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. Classification. In An Introduction to Statistical Learning: With Applications in R; James, G., Witten, D., Hastie, T., Tibshirani, R., Eds.; Springer US: New York, NY, USA, 2021; pp. 129–195. [Google Scholar] [CrossRef]
- Tan, E.; Algar, S.; Corrêa, D.; Small, M.; Stemler, T.; Walker, D. Selecting embedding delays: An overview of embedding techniques and a new method using persistent homology. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 032101. [Google Scholar] [CrossRef]
- Carpinella, I.; Bertoni, R.; Anastasi, D.; Cardini, R.; Lencioni, T.; Ferrarin, M.; Cattaneo, D.; Gervasoni, E. Walk Longer! Using Wearable Inertial Sensors to Uncover Which Gait Aspects Should Be Treated to Increase Walking Endurance in People with Multiple Sclerosis. Sensors 2024, 24, 7284. [Google Scholar] [CrossRef] [PubMed]
- Arpan, I.; Fino, P.C.; Fling, B.W.; Horak, F. Local dynamic stability during long-fatiguing walks in people with multiple sclerosis. Gait Posture 2020, 76, 122–127. [Google Scholar] [CrossRef]
- Hilfiker, R.; Vaney, C.; Gattlen, B.; Meichtry, A.; Deriaz, O.; Lugon-Moulin, V.; Anchisi-Bellwald, A.-M.; Palaci, C.; Foinant, D.; Terrier, P. Local dynamic stability as a responsive index for the evaluation of rehabilitation effect on fall risk in patients with multiple sclerosis: A longitudinal study. BMC Res. Notes 2013, 6, 260. [Google Scholar] [CrossRef]
- Peebles, A.T.; Bruetsch, A.P.; Lynch, S.G.; Huisinga, J.M. Dynamic balance in persons with multiple sclerosis who have a falls history is altered compared to non-fallers and to healthy controls. J. Biomech. 2017, 63, 158–163. [Google Scholar] [CrossRef]
- Rispens, S.M.; Van Dieen, J.H.; Van Schooten, K.S.; Cofre Lizama, L.E.; Daffertshofer, A.; Beek, P.J.; Pijnappels, M. Fall-related gait characteristics on the treadmill and in daily life. J. Neuroeng. Rehabil. 2016, 13, 12. [Google Scholar]
- Dingwell, J.B.; Cusumano, J.P.; Cavanagh, P.R.; Sternad, D. Local Dynamic Stability Versus Kinematic Variability of Continuous Overground and Treadmill Walking. J. Biomech. Eng. 2000, 123, 27–32. [Google Scholar] [CrossRef]
- Craig, J.J.; Bruetsch, A.P.; Lynch, S.G.; Huisinga, J.M. Trunk and foot acceleration variability during walking relates to fall history and clinical disability in persons with multiple sclerosis. Clin. Biomech. 2020, 80, 105100. [Google Scholar] [CrossRef]
- Bruijn, S.M.; van Dieën, J.H.; Meijer, O.G.; Beek, P.J. Statistical precision and sensitivity of measures of dynamic gait stability. J. Neurosci. Methods 2009, 178, 327–333. [Google Scholar] [CrossRef]
- Cofré Lizama, L.E.; He, X.; Kalincik, T.; Galea, M.P.; Panisset, M.G. Sample Entropy Improves Assessment of Postural Control in Early-Stage Multiple Sclerosis. Sensors 2024, 24, 872. [Google Scholar] [CrossRef] [PubMed]
- Cofré Lizama, L.E.; Panisset, M.G.; Peng, L.; Tan, Y.; Kalincik, T.; Galea, M.P. Postural behaviour in people with multiple sclerosis: A complexity paradox. Gait Posture 2024, 111, 14–21. [Google Scholar] [CrossRef] [PubMed]
- Ihlen, E.A.F.; Weiss, A.; Beck, Y.; Helbostad, J.L.; Hausdorff, J.M. A comparison study of local dynamic stability measures of daily life walking in older adult community-dwelling fallers and non-fallers. J. Biomech. 2016, 49, 1498–1503. [Google Scholar] [CrossRef] [PubMed]


| Sensor | Direction | Median dE | Range dE | Median τ | Range τ |
|---|---|---|---|---|---|
| Sternum (STR) | VT | 7 | [6, 8] | 10 | [6, 14] |
| ML | 7 | [6, 9] | 10 | [4, 16] | |
| AP | 7 | [6, 10] | 9 | [4, 18] | |
| N | 7 | [6, 8] | 10 | [4, 14] | |
| Lumbar (LUM) | VT | 7 | [5, 9] | 7 | [3, 13] |
| ML | 7 | [6, 10] | 5 | [3, 10] | |
| AP | 7 | [6, 10] | 5 | [3, 13] | |
| N | 7 | [6, 9] | 8 | [3, 14] |
| Variable | HC (n = 23) | PwMS (n = 55) | p |
|---|---|---|---|
| EDSS (median) [IQR] | - | 2.0 [1–2.5] | |
| Age (mean ± SD) | 44.52 ± 12.13 | 41.69 ± 10.65 | 0.31 |
| Sex ratio (m/f, % female) | 8/15, (65%) | 18/37, (67%) | 0.86 |
| Height (cm) (mean ± SD) | 171.48 ± 29.03 | 170.54 ± 8.98 | 0.67 |
| Body mass index (kg/m2) (mean ± SD) | 23.96 ± 5.75 | 27.64 ± 4.98 | <0.01 |
| Input | VT | ML | AP | N | 3D * | |
|---|---|---|---|---|---|---|
| Lumbar | Individual (I) | 0.690 | 0.684 | 0.685 | 0.685 | 0.690 |
| Median (M) | 0.701 | 0.703 | 0.694 | 0.721 | 0.679 | |
| Fixed (F) | 0.717 | 0.689 | 0.692 | 0.715 | ||
| Sternum | Individual (I) | 0.685 | 0.678 | 0.704 | 0.705 | 0.770 |
| Median (M) | 0.707 | 0.694 | 0.692 | 0.716 | 0.761 | |
| Fixed (F) | 0.775 | 0.779 | 0.771 | 0.826 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cofré Lizama, L.E.; Peng, L.; Kalincik, T.; Galea, M.P.; Panisset, M.G. Multiple Sclerosis Classification Using the Local Divergence Exponent: Parameters Selection for State-Space Reconstruction. Sensors 2025, 25, 2819. https://doi.org/10.3390/s25092819
Cofré Lizama LE, Peng L, Kalincik T, Galea MP, Panisset MG. Multiple Sclerosis Classification Using the Local Divergence Exponent: Parameters Selection for State-Space Reconstruction. Sensors. 2025; 25(9):2819. https://doi.org/10.3390/s25092819
Chicago/Turabian StyleCofré Lizama, L. Eduardo, Liuhua Peng, Tomas Kalincik, Mary P. Galea, and Maya G. Panisset. 2025. "Multiple Sclerosis Classification Using the Local Divergence Exponent: Parameters Selection for State-Space Reconstruction" Sensors 25, no. 9: 2819. https://doi.org/10.3390/s25092819
APA StyleCofré Lizama, L. E., Peng, L., Kalincik, T., Galea, M. P., & Panisset, M. G. (2025). Multiple Sclerosis Classification Using the Local Divergence Exponent: Parameters Selection for State-Space Reconstruction. Sensors, 25(9), 2819. https://doi.org/10.3390/s25092819






