Transmission Raman Spectroscopy for Inner Layers Chemical Analysis of Fresh Produce
Abstract
Highlights
- Optimal design aspects and optical parameters for Inner Layers Chemical Analysis of Fresh Produce with transmission Raman spectroscopy
- Non-destructive chemical analysis of fresh produce inner layers;
- Technology for detecting internal properties and problems in agricultural produce.
Abstract
1. Introduction
2. Methods and Results
3. Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jijakli, M.H.; Lepoivre, P. State of the Art and Challenges of Post-Harvest Disease Management in Apples. In Fruit and Vegetable Diseases; Mukerji, K.G., Ed.; Disease Management of Fruits and Vegetables; Springer: Dordrecht, The Netherlands, 2004; pp. 59–94. ISBN 978-0-306-48575-6. [Google Scholar]
- Sharma, I.M.; Negi, H.S.; Khosla, K. Prevalence, Diagnosis and Management of Core Rot in Apple Fruits. J. Mycol. Plant Pathol. 2013, 43, 261–270. [Google Scholar]
- Niem, J.; Miyara, I.; Ettedgui, Y.; Reuveni, M.; Flaishman, M.; Prusky, D. Core Rot Development in Red Delicious Apples Is Affected by Susceptibility of the Seed Locule to Alternaria Alternata Colonization. Phytopathology 2007, 97, 1415–1421. [Google Scholar] [CrossRef]
- Sever, Z.; Ivić, D.; Kos, T.; Miličević, T. Identification of Fusarium Species Isolated from Stored Apple Fruit in Croatia. Arh. Hig. Rada Toksikol. 2012, 63, 463–469. [Google Scholar] [CrossRef] [PubMed]
- Ntasiou, P.; Myresiotis, C.; Konstantinou, S.; Papadopoulou-Mourkidou, E.; Karaoglanidis, G.S. Identification, Characterization and Mycotoxigenic Ability of Alternaria Spp. Causing Core Rot of Apple Fruit in Greece. Int. J. Food Microbiol. 2015, 197, 22–29. [Google Scholar] [CrossRef]
- Troncoso-Rojas, R.; Tiznado-Hernández, M.E. Chapter 5—Alternaria Alternata (Black Rot, Black Spot). In Postharvest Decay; Bautista-Baños, S., Ed.; Academic Press: San Diego, CA, USA, 2014; pp. 147–187. ISBN 978-0-12-411552-1. [Google Scholar]
- Logrieco, A.; Moretti, A.; Solfrizzo, M. Alternaria Toxins and Plant Diseases: An Overview of Origin, Occurrence and Risks. World Mycotoxin J. 2009, 2, 129–140. [Google Scholar] [CrossRef]
- Chironi, S.; Sortino, G.; Allegra, A.; Saletta, F.; Caviglia, V.; Ingrassia, M. Consumer Assessment on Sensory Attributes of Fresh Table Grapes Cv “Italia” and “Red Globe” after Long Cold Storage Treatment. Chem. Eng. Trans. 2017, 58, 421–426. [Google Scholar] [CrossRef]
- Jackman, R.L.; Yada, R.Y.; Marangoni, A.; Parkin, K.L.; Stanley, D.W. Chilling Injury. a Review of Quality Aspects. J. Food Qual. 1988, 11, 253–278. [Google Scholar] [CrossRef]
- Keijbets, M.J.H.; Ebbenhorst-Seller, G. Loss of Vitamin C (L-Ascorbic Acid) during Long-Term Cold Storage of Dutch Table Potatoes. Potato Res. 1990, 33, 125–130. [Google Scholar] [CrossRef]
- Wang, C.Y. Chilling Injury of Fruits and Vegetables. Food Rev. Int. 1989, 5, 209–236. [Google Scholar] [CrossRef]
- Fan, Z.; Hasing, T.; Johnson, T.S.; Garner, D.M.; Schwieterman, M.L.; Barbey, C.R.; Colquhoun, T.A.; Sims, C.A.; Resende, M.F.R.; Whitaker, V.M. Strawberry Sweetness and Consumer Preference Are Enhanced by Specific Volatile Compounds. Hortic. Res. 2021, 8, 66. [Google Scholar] [CrossRef]
- Grubb, E.H.; Guilford, W.S. Botany, Physical And Chemical Composition Potato. Part 2. In The Potato: A Compilation of Information from Every Available Source; Doubleday, Page & Company: New York, NY, USA, 1912. [Google Scholar]
- Maldonado-Celis, M.E.; Yahia, E.M.; Bedoya, R.; Landázuri, P.; Loango, N.; Aguillón, J.; Restrepo, B.; Guerrero Ospina, J.C. Chemical Composition of Mango (Mangifera indica L.) Fruit: Nutritional and Phytochemical Compounds. Front. Plant Sci. 2019, 10, 1073. [Google Scholar] [CrossRef]
- Wierzchnicki, R. Stable Isotopes Methods For Juice Authenticity Control. In Institute of Nuclear Chemistry And Technology Annual Report; Institute of Nuclear Chemistry and Technology: Warsaw, Poland, 2011. [Google Scholar]
- Adiani, V.; Gupta, S.; Variyar, P.S. Microbial Quality Assessment of Minimally Processed Pineapple Using GCMS and FTIR in Tandem with Chemometrics. Sci. Rep. 2020, 10, 6203. [Google Scholar] [CrossRef] [PubMed]
- Fischböck, G.; Pfannhauser, W.; Kellner, R. Characterization of Citrus and Kiwi Flavors and Their Degradation Processes by Combination of GC/FTIR and GC/MS. Microchim. Acta 1988, 94, 27–30. [Google Scholar] [CrossRef]
- Zheng, Q.; Song, J.; Doncaster, K.; Rowland, E.; Byers, D.M. Qualitative and Quantitative Evaluation of Protein Extraction Protocols for Apple and Strawberry Fruit Suitable for Two-Dimensional Electrophoresis and Mass Spectrometry Analysis. J. Agric. Food Chem. 2007, 55, 1663–1673. [Google Scholar] [CrossRef]
- Blasco, C.; Picó, Y.; Mañes, J.; Font, G. Determination of Fungicide Residues in Fruits and Vegetables by Liquid Chromatography–Atmospheric Pressure Chemical Ionization Mass Spectrometry. J. Chromatogr. A 2002, 947, 227–235. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, I.; Morales, A.; Barba, A.; Oliva, J. Determination of Natural Pesticides in Fresh Fruits Using Liquid Chromatography/Mass Spectrometry. J. AOAC Int. 2012, 95, 238–243. [Google Scholar] [CrossRef]
- Wilkes, J.G.; Conte, E.D.; Kim, Y.; Holcomb, M.; Sutherland, J.B.; Miller, D.W. Sample Preparation for the Analysis of Flavors and Off-Flavors in Foods. J. Chromatogr. A 2000, 880, 3–33. [Google Scholar] [CrossRef] [PubMed]
- Fischböck, G.; Pfannhauser, W.; Kellner, R. GC-FTIR as a Powerful Tool for the Characterization of Flavor Components in Kiwi. Mikrochim. Acta 1988, 96, 249–257. [Google Scholar] [CrossRef]
- Segelstein, D.J. The Complex Refractive Index of Water. Master’s Thesis, University of Missouri-Kansas City, Kansas, MO, USA, 1981. [Google Scholar]
- Ben-Zvi, R.; Ignat, T.; Alchanatis, V.; Hoffman, A.; Borochov-Neori, H.; Immerman, A.; Schmilovitch, Z. New Post-Harvest Aproach for High Quality Fresh ‘Medjhool’ Date. Postharvest Biol. Technol. 2017, 124, 35–44. [Google Scholar] [CrossRef]
- Alm, E.; Bro, R.; Engelsen, S.B.; Karlberg, B.; Torgrip, R.J.O. Vibrational Overtone Combination Spectroscopy (VOCSY)—A New Way of Using IR and NIR Data. Anal. Bioanal. Chem. 2007, 388, 179–188. [Google Scholar] [CrossRef]
- Rotbart, N.; Schmilovitch, Z.; Cohen, Y.; Alchanatis, V.; Erel, R.; Ignat, T.; Shenderey, C.; Dag, A.; Yermiyahu, U. Estimating Olive Leaf Nitrogen Concentration Using Visible and Near-Infrared Spectral Reflectance. Biosyst. Eng. 2013, 114, 426–434. [Google Scholar] [CrossRef]
- Shenderey, C.; Shmulevich, I.; Alchanatis, V.; Egozi, H.; Hoffman, A.; Ostrovsky, V.; Lurie, S.; Ben Arie, R.; Schmilovitch, Z. NIRS Detection of Moldy Core in Apples. Food Bioprocess Technol. 2010, 3, 79–86. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, W.; Cui, C.; Zhang, Z.; He, L.; Zheng, J.; Hou, R. Development of a Method to Evaluate the Tenderness of Fresh Tea Leaves Based on Rapid, in-Situ Raman Spectroscopy Scanning for Carotenoids. Food Chem. 2020, 308, 125648. [Google Scholar] [CrossRef] [PubMed]
- Raj, T.; Hashim, F.H.; Huddin, A.B.; Hussain, A.; Ibrahim, M.F.; Abdul, P.M. Classification of Oil Palm Fresh Fruit Maturity Based on Carotene Content from Raman Spectra. Sci. Rep. 2021, 11, 18315. [Google Scholar] [CrossRef]
- Yang, D.; Ying, Y. Applications of Raman Spectroscopy in Agricultural Products and Food Analysis: A Review. Appl. Spectrosc. Rev. 2011, 46, 539–560. [Google Scholar] [CrossRef]
- Guo, Z.; Huang, W.; Chen, Q.; Wang, Q.; Zhang, C.; Zhao, J. Design and Test of On-Line Detection System for Apple Core Rot Disease Based on Transmitted Spectrum. Trans. Chin. Soc. Agric. Eng. 2016, 32, 283–288. [Google Scholar]
- Tian, S.; Zhang, J.; Zhang, Z.; Zhao, J.; Zhang, Z.; Zhang, H. Effective Modification through Transmission Vis/NIR Spectra Affected by Fruit Size to Improve the Prediction of Moldy Apple Core. Infrared Phys. Technol. 2019, 100, 117–124. [Google Scholar] [CrossRef]
- Zhaoyong, Z.; Yu, L.; Dong, S.; Haihui, Z.; Dongjian, H.; Yang, C. Detection of Moldy Core in Apples and Its Symptom Types Using Transmittance Spectroscopy. Int. J. Agric. Biol. Eng. 2016, 9, 148–155. [Google Scholar] [CrossRef]
- Tian, X.; Wang, Q.; Huang, W.; Fan, S.; Li, J. Online Detection of Apples with Moldy Core Using the Vis/NIR Full-Transmittance Spectra. Postharvest Biol. Technol. 2020, 168, 111269. [Google Scholar] [CrossRef]
- Georgiou, R.; Sahle, C.J.; Sokaras, D.; Bernard, S.; Bergmann, U.; Rueff, J.-P.; Bertrand, L. X-Ray Raman Scattering: A Hard X-Ray Probe of Complex Organic Systems. Chem. Rev. 2022, 122, 12977–13005. [Google Scholar] [CrossRef]
- Tuschel, D. Selecting an Excitation Wavelength for Raman Spectroscopy. Spectroscopy 2016, 31, 14–23. [Google Scholar]
- Eliasson, C.; Macleod, N.A.; Jayes, L.C.; Clarke, F.C.; Hammond, S.V.; Smith, M.R.; Matousek, P. Non-Invasive Quantitative Assessment of the Content of Pharmaceutical Capsules Using Transmission Raman Spectroscopy. J. Pharm. Biomed. Anal. 2008, 47, 221–229. [Google Scholar] [CrossRef]
- Guo, N.; Niu, S.; Geng, Y.; Shan, G.; Wei, N.; Chen, H. Non-Destructive Quantification of Low Colchicine Concentrations in Commercially Available Tablets Using Transmission Raman Spectroscopy with Partial Least Squares. Int. J. Pharm. X 2025, 9, 100321. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Zhao, X.; Wang, J.; Cheng, M.; Jiang, Y.; Lian, X.; Zhao, T.; Shan, G. A Nondestructive and Rapid Method for the Determination of Triamterene Content by Transmission Raman Spectroscopy Combined with Chemometrics. Curr. Pharm. Anal. 2024, 20, 898–906. [Google Scholar] [CrossRef]
- Ghita, A.; Matousek, P.; Stone, N. High Sensitivity Non-Invasive Detection of Calcifications Deep inside Biological Tissue Using Transmission Raman Spectroscopy. J. Biophotonics 2018, 11, e201600260. [Google Scholar] [CrossRef]
- Kim, Y.; Hilderbrand, S.A.; Weissleder, R.; Tung, C.-H. Sugar Sensing Based on Induced pH Changes. Chem. Commun. 2007, 2299–2301. [Google Scholar] [CrossRef]
- Bos, A. The UV Spectra of Cellulose and Some Model Compounds. J. Appl. Polym. Sci. 1972, 16, 2567–2576. [Google Scholar] [CrossRef]
- Krauss, P.; Markstädter, C.; Riederer, M. Attenuation of UV Radiation by Plant Cuticles from Woody Species. Plant Cell Environ. 1997, 20, 1079–1085. [Google Scholar] [CrossRef]
- Hennemeyer, M.; Burghardt, S.; Stark, R.W. Cantilever Micro-Rheometer for the Characterization of Sugar Solutions. Sensors 2008, 8, 10–22. [Google Scholar] [CrossRef]
- Gunasekaran, S.; Devi, M.K. UV-Vis Spectroscopic Investigation on Hydrolysis of Starch and Starch-Drug Interaction. Asian J. Chem. 2007, 19, 3363–3374. [Google Scholar]
- Arielly, R. Transmission Raman Spectroscopy for Inner Layers Chemical Analysis of Fresh Produce—Raw Spectroscopic Data. Mendeley Data. 2024. [Google Scholar] [CrossRef]
- Pretsch, E.; Bühlmann, P.; Badertscher, M. Structure Determination of Organic Compounds Tables of Spectral Data; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-93810-1. [Google Scholar]
- Princeton Instruments Spectroscopy Group. SpectraPro HRS Series, Imaging Spectrographs & Scanning Monochromators, Datasheet; Princeton Instruments Spectroscopy Group: Trenton, NJ, USA, 2022. [Google Scholar]
- SynapsePlus BIVS, High Speed Scientific CCD Camera; Horiba Scientific: Palaiseau, France, 2017.
- Princeton Instruments Spectroscopy Group. Pixis: 2K eXcelon; Princeton Instruments Spectroscopy Group: Trenton, NJ, USA, 2014. [Google Scholar]
- Lurie, S. Postharvest Heat Treatments. Postharvest Biol. Technol. 1998, 14, 257–269. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, Z.; Wu, J. Dual-Wavelength External Cavity Laser Device for Fluorescence Suppression in Raman Spectroscopy. In Proceedings of the AOPC 2017: Laser Components, Systems, and Applications, Beijing, China, 24 October 2017; SPIE: Washington, DC, USA, 2017; Volume 10457, pp. 137–142. [Google Scholar]
- Maiwald, M.; Erbert, G.; Klehr, A.; Kronfeldt, H.-D.; Schmidt, H.; Sumpf, B.; Tränkle, G. Rapid Shifted Excitation Raman Difference Spectroscopy with a Distributed Feedback Diode Laser Emitting at 785 Nm. Appl. Phys. B 2006, 85, 509–512. [Google Scholar] [CrossRef]
- Maiwald, M.; Schmidt, H.; Sumpf, B.; Erbert, G.; Kronfeldt, H.-D.; Tränkle, G. Microsystem 671 Nm Light Source for Shifted Excitation Raman Difference Spectroscopy. Appl. Opt. 2009, 48, 2789–2792. [Google Scholar] [CrossRef]
- Grüber, K.; Kiefer, J. Advanced Instantaneous Shifted-Excitation Raman Difference Spectroscopy (iSERDS) Using a Laser Pointer. J. Raman Spectrosc. 2016, 47, 1049–1055. [Google Scholar] [CrossRef]
- HÜBNER. Photonics Cobolt 06-01 Series. Available online: https://hubner-photonics.com/products/lasers/diode-lasers/06-01-series/ (accessed on 15 December 2023).
- Laserglow 690 Nm Low-Noise Collimated Diode Laser System. Available online: https://www.laserglow.com/product/J69-R-690-nm-Low-Noise-Collimated-Diode-Laser-Syst (accessed on 15 December 2023).
- Roithner Lasertechnik. LASER DIODES—STANDARD DEVICES. Available online: https://www.roithner-laser.com/ld_standard.html (accessed on 15 December 2023).
- Ushio Red Laser (630 Nm–690 Nm). Available online: https://www.ushio.eu/product/red-laser-630nm-690nm/ (accessed on 15 December 2023).
- Thorlabs. HL6738MG Specifications Sheet; Thorlabs: Newton, NJ, USA, 2023. [Google Scholar]
- Ushio. HL6738MG Data Sheet; Ushio: Tokoy, Japan, 2019. [Google Scholar]
- Yerolatsitis, S.; Kufcsák, A.; Ehrlich, K.; Wood, H.A.C.; Fernandes, S.; Quinn, T.; Young, V.; Young, I.; Hamilton, K.; Akram, A.R.; et al. Sub Millimetre Flexible Fibre Probe for Background and Fluorescence Free Raman Spectroscopy. J. Biophotonics 2021, 14, e202000488. [Google Scholar] [CrossRef]
- Bonati, C.; Fay, V.; Dornier, R.; Loterie, D.; Moser, C. Lock-in Raman Difference Spectroscopy. Opt. Express OE 2022, 30, 28601–28613. [Google Scholar] [CrossRef] [PubMed]
- Korinth, F.; Mondol, A.S.; Stiebing, C.; Schie, I.W.; Krafft, C.; Popp, J. New Methodology to Process Shifted Excitation Raman Difference Spectroscopy Data: A Case Study of Pollen Classification. Sci. Rep. 2020, 10, 11215. [Google Scholar] [CrossRef]
- Agiltron Dual Spectrum Stabilized Fiber-Coupled Raman Laser Source; Agiltron: San Francisco, CA, USA, 2023.
- SK Advanced Group. LS-2—Raman Spectroscopy—Stabilized Dual Laser Source; SK Advanced Group: Kadima, Israel, 2023. [Google Scholar]
- Fu, X.; Ying, Y.; Zhou, Y.; Xie, L.; Xu, H. Application of NIR Spectroscopy for Firmness Evaluation of Peaches. J. Zhejiang Univ. Sci. B 2008, 9, 552–557. [Google Scholar] [CrossRef]
- Iqbal, Z.; Herodian, S.; Widodo, S. Development of Partial Least Square (PLS) Prediction Model to Measure the Ripeness of Oil Palm Fresh Fruit Bunch (FFB) by Using NIR Spectroscopy. IOP Conf. Ser. Earth Environ. Sci. 2019, 347, 012079. [Google Scholar] [CrossRef]


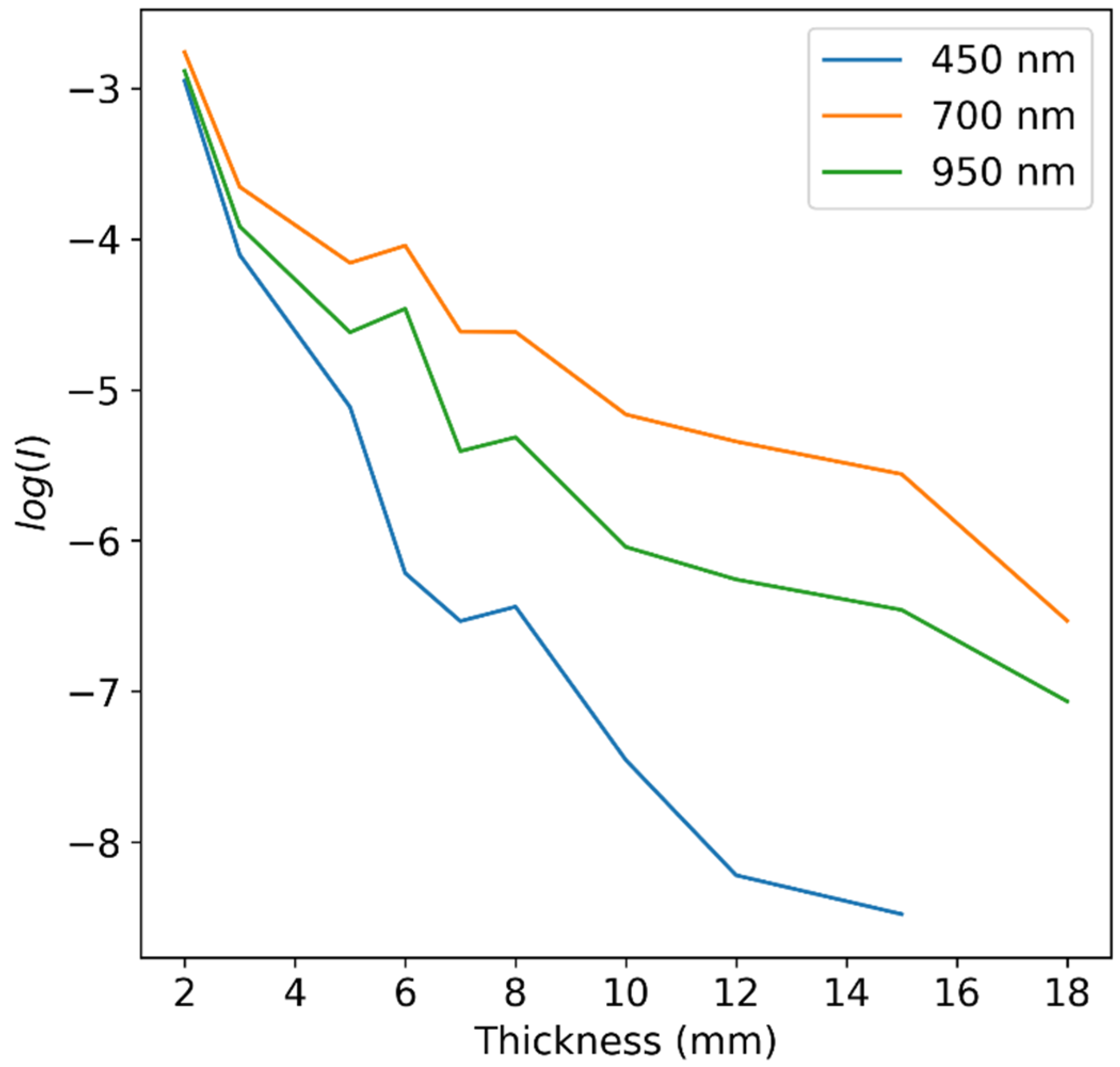

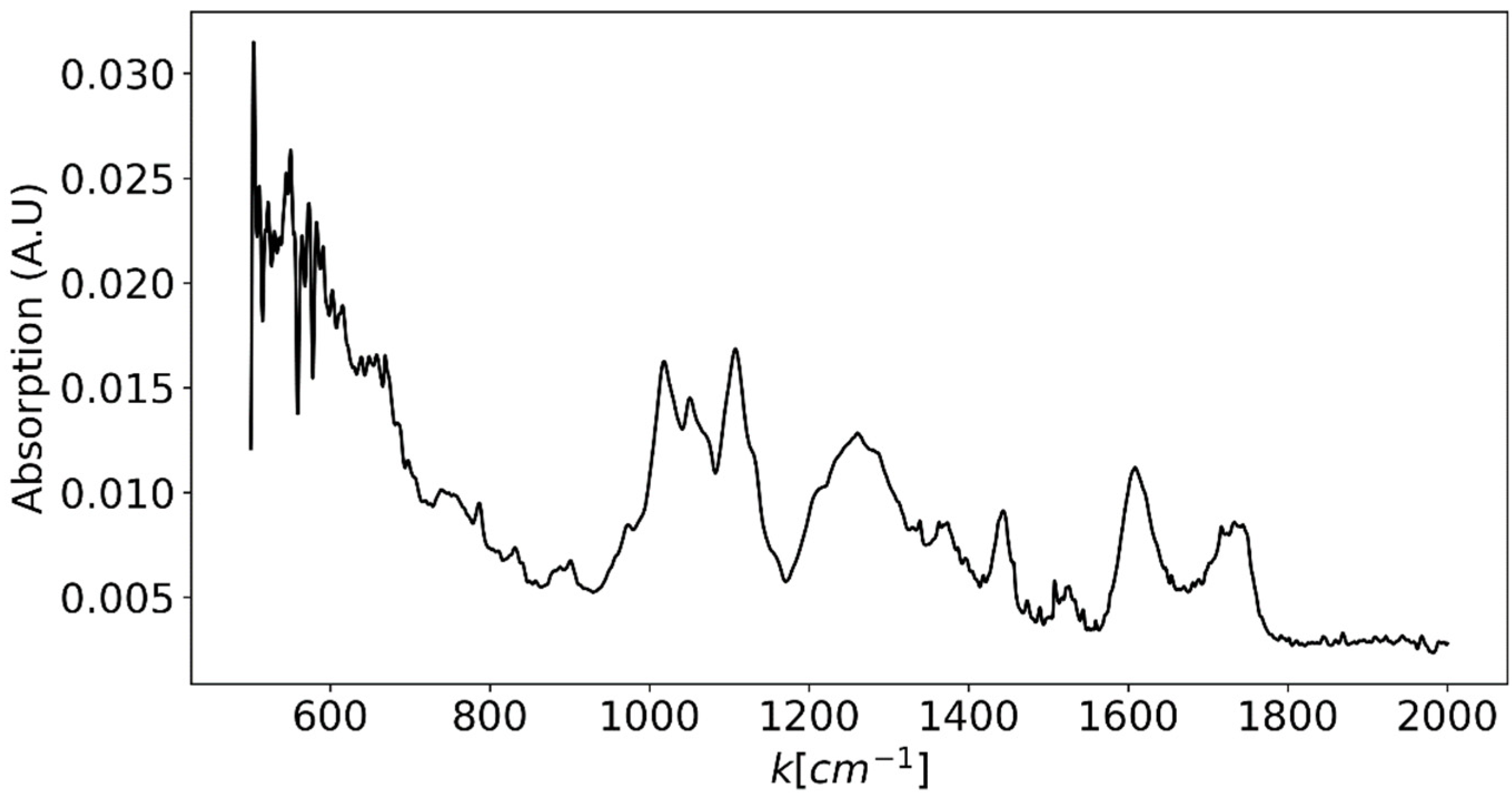

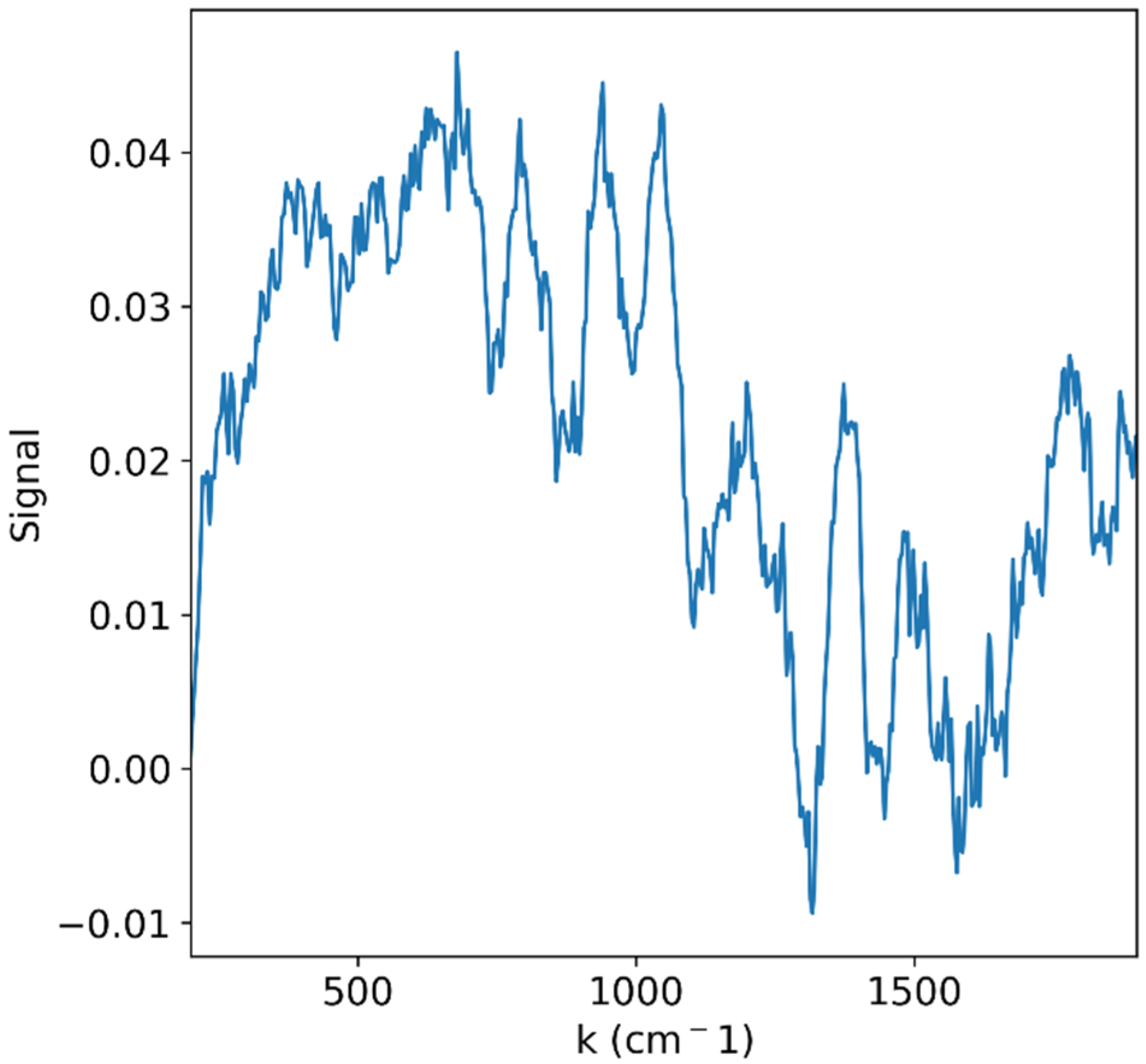

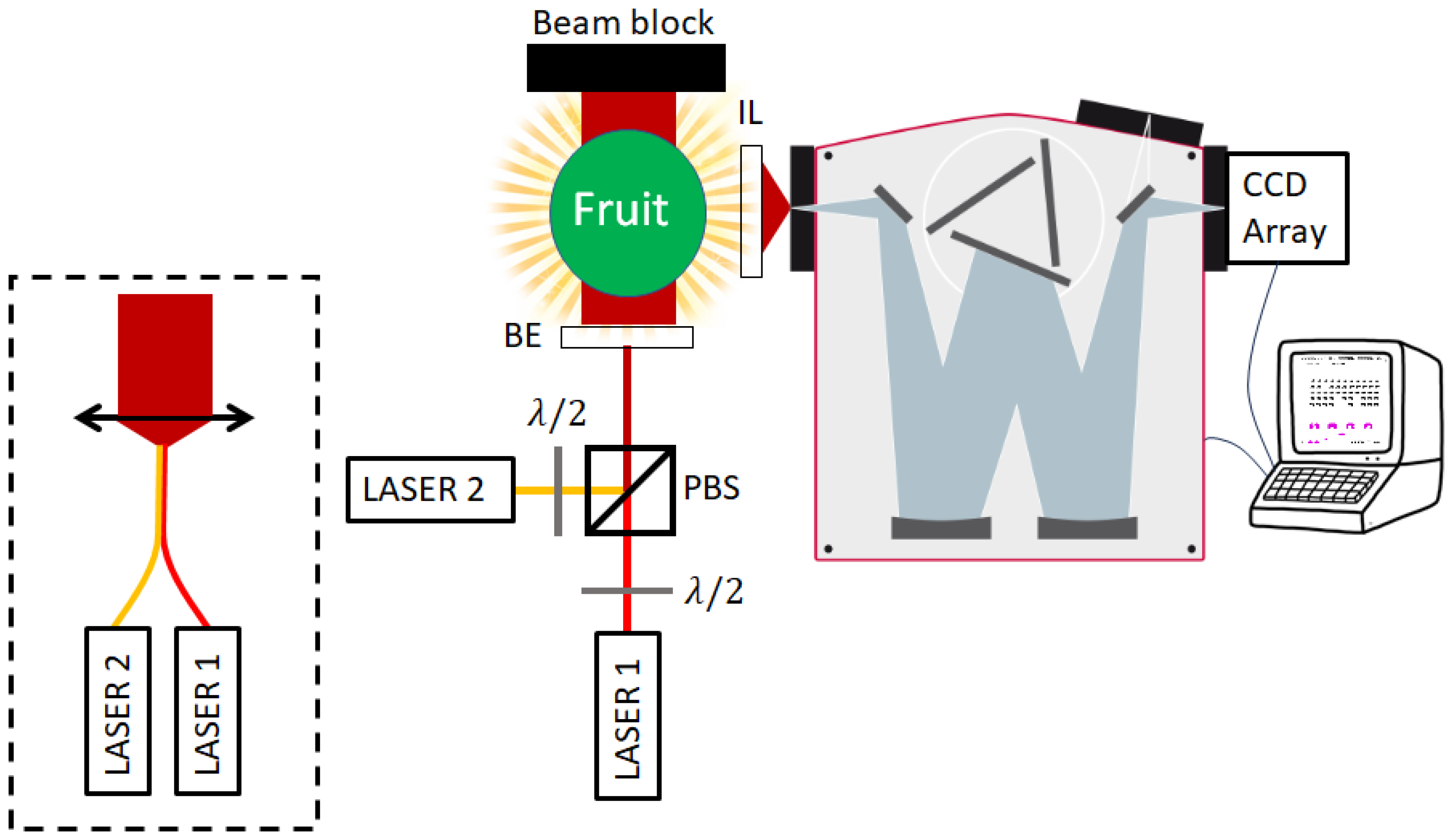
| Excitation Wavelength [nm] | Wavelength Range [nm] | Dispersion [nm/pixel] | Number of Pixels | ||
|---|---|---|---|---|---|
| Highest Wavenumber | 600 | 774 | 0.108 | 1613 | |
| 620 | 808 | 0.115 | 1629 | ||
| 640 | 842 | 0.123 | 1645 | ||
| 660 | 877 | 0.131 | 1661 | ||
| 680 | 913 | 0.139 | 1678 | ||
| 700 | 949 | 0.147 | 1695 | ||
| 725 | 820 | 0.158 | 603 | ||
| 750 | 852 | 0.169 | 606 | ||
| 775 | 885 | 0.180 | 609 | ||
| 800 | 917 | 0.192 | 612 | ||
| 825 | 950 | 0.204 | 615 | ||
| Blaze | Efficiency | |||||
|---|---|---|---|---|---|---|
| 300 | 300 | 700 | 985 | 0.139 | >60% | |
| 300 | 600 | 800 | 933 | 0.065 | >70% | |
| 500 | 300 | 772 | 950 | 0.086 | >75% | |
| 150 | 600 | 800 | 1027 | 0.111 | >70% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arielly, R. Transmission Raman Spectroscopy for Inner Layers Chemical Analysis of Fresh Produce. Sensors 2025, 25, 2805. https://doi.org/10.3390/s25092805
Arielly R. Transmission Raman Spectroscopy for Inner Layers Chemical Analysis of Fresh Produce. Sensors. 2025; 25(9):2805. https://doi.org/10.3390/s25092805
Chicago/Turabian StyleArielly, Rani. 2025. "Transmission Raman Spectroscopy for Inner Layers Chemical Analysis of Fresh Produce" Sensors 25, no. 9: 2805. https://doi.org/10.3390/s25092805
APA StyleArielly, R. (2025). Transmission Raman Spectroscopy for Inner Layers Chemical Analysis of Fresh Produce. Sensors, 25(9), 2805. https://doi.org/10.3390/s25092805






