A Novel Low-Rank Embedded Latent Multi-View Subspace Clustering Approach
Abstract
1. Introduction
- (1)
- By leveraging low-rank embedding to model the shared subspace structure of multi-view data, our approach effectively suppresses noise and redundant information that allows us to enhance the robustness in handling outliers and noisy environments;
- (2)
- We can map information from different views into a unified semantic space through a latent multi-view learning fusion mechanism. This process preserves the unique characteristics of each view while strengthening inter-view consistency;
- (3)
- We have designed a cross-view projection mapping mechanism that transforms the original high-dimensional heterogeneous data into a low-rank latent space. This allows the separation of shared subspace and view-specific information, enabling a more precise capture of the consistent structure across multiple views.
2. Related Works
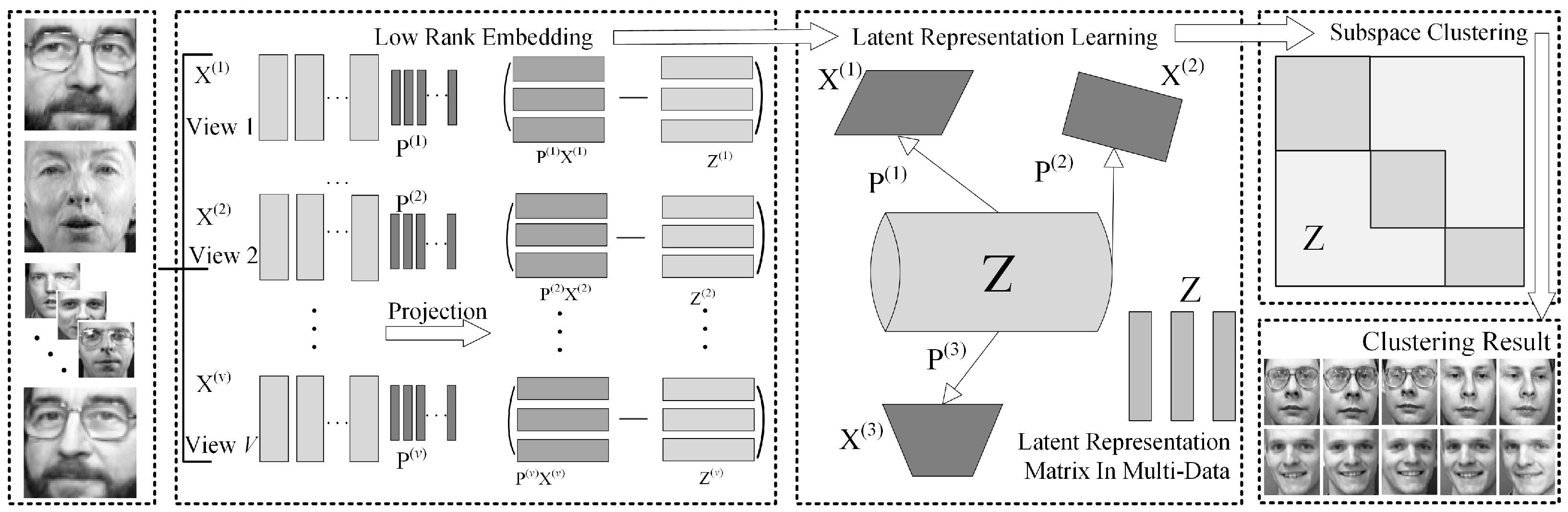
3. Proposed Approach
3.1. Low-Rank Embedding
3.2. The Latent Multi-View Representation Based on Low-Rank Embedding
3.3. ALM-ADM Optimization
| Algorithm 1: Optimization for the LRE-LAMVSC. |
Set Repeat: update according to Problem (9) update according to Problem (11) update according to Problem (14) update according to Problem (18) update , and according to Problems (22–25) Until: Output: |
4. Results and Discussion
4.1. Parameter Settings and Evaluation Indicators
4.2. Datasets and Comparative Algorithms
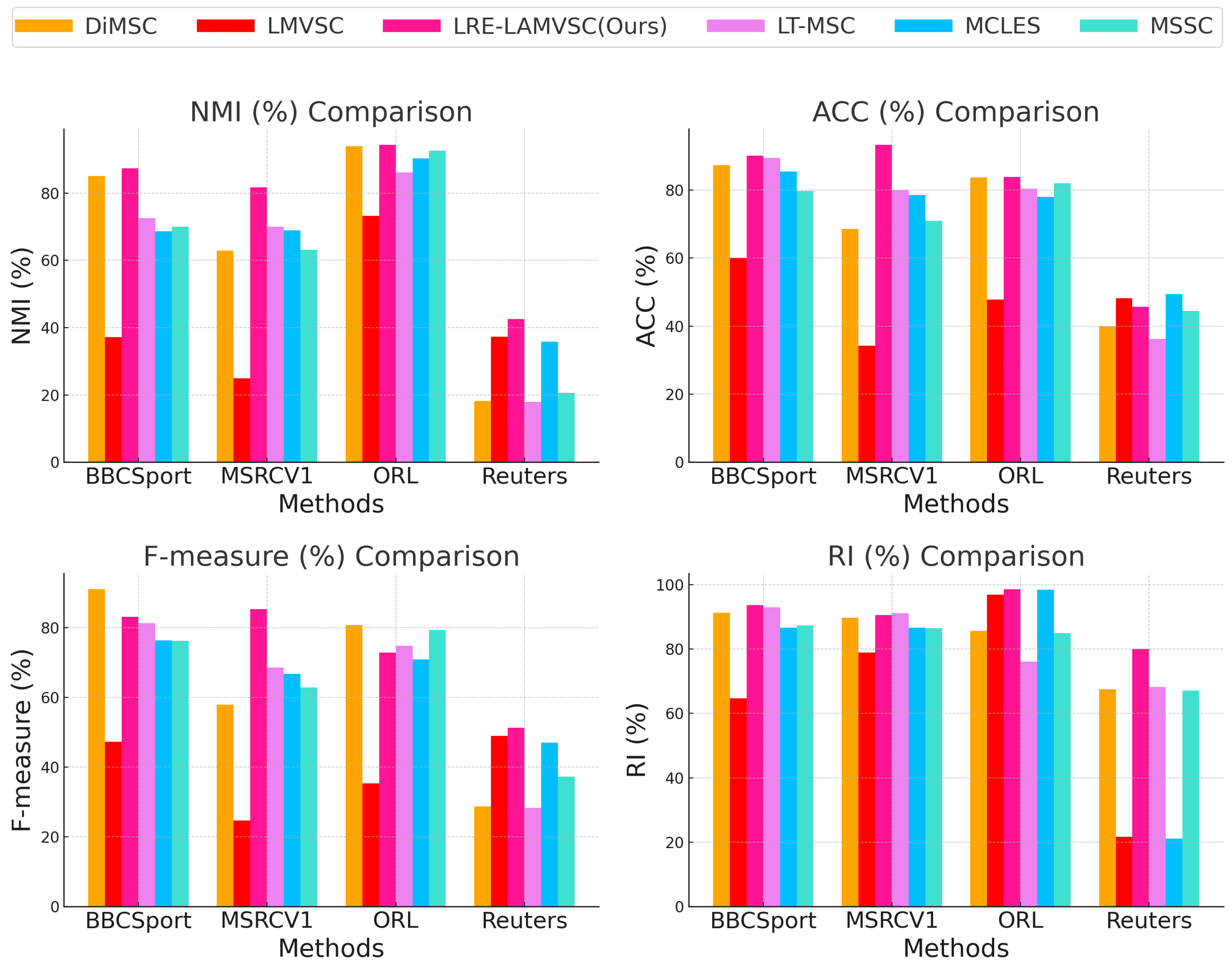
4.3. Comparative Studies
4.4. Discussions on the Comparisons with the Existing Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Devagiri, V.M.; Boeva, V.; Abghari, S.; Basiri, F.; Lavesson, N. Multi-View Data Analysis Techniques for Monitoring Smart Building Systems. Sensors 2021, 21, 6775. [Google Scholar] [CrossRef]
- Hao, C.-Y.; Chen, Y.-C.; Ning, F.-S.; Chou, T.-Y.; Chen, M.-H. Using Sparse Parts in Fused Information to Enhance Performance in Latent Low-Rank Representation-Based Fusion of Visible and Infrared Images. Sensors 2024, 24, 1514. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, Q.; Zhang, B.; He, S.; Dan, T.; Peng, H. Deep Multiview Clustering via Iteratively Self-Supervised Universal and Specific Space Learning. IEEE Trans. Cybern. 2021, 52, 11734–11746. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Zhou, J.T.; Zhu, H.; Zhang, C.; Lv, J.; Peng, X. Deep Spectral Representation Learning from Multi-view Data. IEEE Trans. Image Process. 2021, 30, 5352–5362. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Chen, Z.; Du, S.; Lin, Z. Learning deep sparse regularizers with applications to multi-view clustering and semi-supervised classification. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5042–5055. [Google Scholar] [CrossRef]
- Li, Z.; Tang, C.; Liu, X.; Zheng, X.; Zhang, W.; Zhu, E. Consensus Graph Learning for Multi-view Clustering. IEEE Trans. Multimed. 2021, 24, 2461–2472. [Google Scholar] [CrossRef]
- Fang, U.; Li, M.; Li, J.; Gao, L.; Jia, T.; Zhang, Y. A comprehensive survey on multi-view clustering. IEEE Trans. Knowl. Data Eng. 2023, 35, 12350–12368. [Google Scholar] [CrossRef]
- Meng, X.; Feng, L.; Wang, H. Multi-view low-rank preserving embedding: A novel method for multi-view representation. Eng. Appl. Artif. Intell. 2021, 99, 104140. [Google Scholar] [CrossRef]
- Chen, J. Multiview subspace clustering using low-rank representation. IEEE Trans. Cybern. 2021, 52, 12364–12378. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhu, J.; Li, Z. Collaborative unsupervised multi-view representation learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 4202–4210. [Google Scholar] [CrossRef]
- He, C.; Wei, Y.; Guo, K.; Han, H. Removal of Mixed Noise in Hyperspectral Images Based on Subspace Representation and Nonlocal Low-Rank Tensor Decomposition. Sensors 2024, 24, 327. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Dong, W.; Liu, Q. Multi-view representation learning with deep Gaussian processes. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 43, 4453–4468. [Google Scholar] [CrossRef]
- Dang, P.; Zhu, H.; Guo, T.; Wan, C.; Zhao, T.; Salama, P.; Wang, Y.; Cao, S.; Zhang, C. Generalized Matrix Local Low Rank Representation by Random Projection and Submatrix Propagation. In Proceedings of the 29th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Long Beach, CA, USA, 6–10 August 2023; pp. 390–401. [Google Scholar] [CrossRef]
- Xie, D.; Zhang, X.; Gao, Q.; Han, J.; Xiao, S.; Gao, X. Multiview clustering by joint latent represcnta-tion and similarity lcarning. IEEE Trans. Cybcrnctics 2019, 50, 4848–4854. [Google Scholar] [CrossRef]
- Fu, Z.; Zhao, Y.; Chang, D.; Wang, Y.; Wen, J. Latent low-rank representation with weighted distance penalty for clustering. IEEE Trans. Cybern. 2022, 53, 6870–6882. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wang, S.; Peng, C.; Hua, Z.; Zhou, Y. Generalized Nonconvex Low-Rank Tensor Approximation for Multi-View Subspace Clustering. IEEE Trans. Image Process. 2021, 30, 4022–4035. [Google Scholar] [CrossRef]
- Chen, M.; Lin, J.; Li, X.; Liu, B.; Wang, C.; Huang, D.; Lai, J. Representation learning in multi-view clustering: A literature review. Data Sci. Eng. 2022, 7, 225–241. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiang, M.; Yang, B. Low-rank preserving embedding. Pattern Recognit. 2017, 70, 112–125. [Google Scholar] [CrossRef]
- Cai, B.; Wang, H.; Yao, M.; Fu, X. Focus More on What? Guiding Multi-Task Training for End-to-End Person Search. IEEE Trans. Circuits Syst. Video Technol. 2025. [Google Scholar] [CrossRef]
- Fu, Y.; Luo, C.; Bi, Z. Low-rank joint embedding and its application for robust process monitoring. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Li, S.; Li, X. Fully Incomplete Information for Multiview Clustering in Postoperative Liver Tumor Diagnoses. Sensors 2025, 25, 1215. [Google Scholar] [CrossRef]
- Sakovich, N.; Aksenov, D.; Pleshakova, E.; Gataullin, S. MAMGD: Gradient-based optimization method using exponential decay. Technologies 2024, 12, 154. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhu, J.; Li, Z.; Pang, S.; Wang, J.; Li, Y. Feature concatenation multi-view subspace clustering. Neurocomputing 2020, 379, 89–102. [Google Scholar] [CrossRef]
- Zhang, G.; Huang, D.; Wang, C. Facilitated low-rank multi-view subspace clustering. Knowl.-Based Syst. 2023, 260, 110141. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 171–184. [Google Scholar] [CrossRef]
- Wang, H.; Yao, M.; Chen, Y.; Xu, Y.; Liu, H.; Jia, W.; Fu, X.; Wang, Y. Manifold-based incomplete multi-view clustering via bi-consistency guidance. IEEE Trans. Multimed. 2024, 26, 10001–10014. [Google Scholar] [CrossRef]
- Xu, C.; Tao, D.; Xu, C. Multi-view intact space learning. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 2531–2544. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, L.; Shen, F.; Shen, H.T.; Shao, L. Binary Multi-View Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 1774–1782. [Google Scholar] [CrossRef]
- Zhang, C.; Fu, H.; Hu, Q.; Cao, X.; Xie, Y.; Tao, D. Generalized Latent Multi-View Subspace Clustering. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 86–99. [Google Scholar] [CrossRef]
- Xue, Z.; Li, G.; Wang, S.; Zhang, W.; Huang, Q. Bilevel multiview latent space learning. IEEE Trans. Circuits Syst. Video Technol. 2016, 28, 327–341. [Google Scholar] [CrossRef]
- Yao, M.; Wang, H.; Chen, Y.; Fu, X. Between/within view information completing for tensorial incomplete multi-view clustering. IEEE Trans. Multimed. 2024, 27, 1538–1550. [Google Scholar] [CrossRef]
- Huang, A.; Chen, W.; Zhao, T.; Chen, C. Joint learning of latent similarity and local embedding for multi-view clustering. IEEE Trans. Image Process. 2021, 30, 6772–6784. [Google Scholar] [CrossRef]
- Xia, R.; Pan, Y.; Du, L.; Yin, J. Robust multi-view spectral clustering via low-rank and sparse decomposition. In Proceedings of the AAAI Conference on Artificial Intelligence, Québec City, QC, Canada, 27–31 July 2014; Volume 28. [Google Scholar] [CrossRef]
- Cao, X.; Zhang, C.; Fu, H.; Liu, S.; Zhang, H. Diversity-induced multi-view subspace clustering. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 586–594. Available online: https://openaccess.thecvf.com/content_cvpr_2015/papers/Cao_Diversity-Induced_Multi-View_Subspace_2015_CVPR_paper.pdf (accessed on 6 March 2025).
- Zhao, H.-h.; Ji, T.-l.; Rosin, P.L.; Lai, Y.-K.; Meng, W.-l.; Wang, Y.-n. Cross-lingual font style transfer with full-domain convolutional attention. Pattern Recognit. 2024, 155, 110709. [Google Scholar] [CrossRef]
- Zhou, J.; Pedrycz, W.; Wan, J.; Gao, C.; Lai, Z.; Yue, X. Low-rank linear embedding for robust clustering. IEEE Trans. Knowl. Data Eng. 2022, 35, 5060–5075. [Google Scholar] [CrossRef]
- Li, L.; Cai, M. Drug target prediction by multi-view low rank embedding. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 16, 1712–1721. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Fu, H.; Liu, S.; Liu, G.; Cao, X. Low-rank tensor constrained multiview subspace clustering. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1582–1590. Available online: https://openaccess.thecvf.com/content_iccv_2015/papers/Zhang_Low-Rank_Tensor_Constrained_ICCV_2015_paper.pdf (accessed on 6 March 2025).
- Abavisani, M.; Patel, V. Multimodal sparse and low-rank subspace clustering. Inf. Fusion 2018, 39, 168–177. [Google Scholar] [CrossRef]
- Wong, W.; Lai, Z.; Wen, J.; Fang, X.; Lu, Y. Low-rank embedding for robust image feature extraction. IEEE Trans. Image Process. 2017, 26, 2905–2917. [Google Scholar] [CrossRef]
- Kuhn, H.W. The Hungarian method for the assignment problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
- Samaria, F.S.; Harter, A.C. Parameterisation of a stochastic model for human face identification. In Proceedings of the 1994 IEEE Workshop on Applications of Computer Vision, Sarasota, FL, USA, 5–7 December 1994; pp. 138–142. [Google Scholar] [CrossRef]
- Amini, M.R.; Usunier, N.; Goutte, C. Learning from multiple partially observed views—An application to multilingual text categorization. Adv. Neural Inf. Process. Syst. 2009, 22, 28–36. Available online: https://proceedings.neurips.cc/paper/2009/hash/f79921bbae40a577928b76d2fc3edc2a-Abstract.html (accessed on 6 March 2025).
- Greene, D.; Cunningham, P. Practical solutions to the problem of diagonal dominance in kernel document clustering. In Proceedings of the 23rd International Conference on Machine Learning (ICML’06), Pittsburgh, PA, USA, 25–29 June 2006; pp. 377–384. [Google Scholar] [CrossRef]
- He, X.; Yan, S.; Hu, Y.; Niyogi, P.; Zhang, H.-J. Face recognition using Laplacianfaces. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 328–340. [Google Scholar] [CrossRef]
- Estévez, P.A.; Tesmer, M.; Perez, C.A.; Zurada, J.M. Normalized mutual information feature selection. IEEE Trans. Neural Netw. 2009, 20, 189–201. [Google Scholar] [CrossRef]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. Morgan Kaufman Publishing. 1995. Available online: https://www.researchgate.net/profile/Ron-Kohavi/publication/2352264_A_Study_of_Cross-Validation_and_Bootstrap_for_Accuracy_Estimation_and_Model_Selection/links/02e7e51bcc14c5e91c000000/A-Study-of-Cross-Validation-and-Bootstrap-for-Accuracy-Estimation-and-Model-Selection.pdf (accessed on 6 March 2025).
- Sokolova, M.; Lapalme, G. A systematic analysis of performance measures for classification tasks. Inf. Process. Manag. 2009, 45, 427–437. [Google Scholar] [CrossRef]
- Sundqvist, M.; Chiquet, J.; Rigaill, G. Adjusting the adjusted Rand Index—A multinomial story. arXiv 2020, arXiv:2011.08708. [Google Scholar] [CrossRef]
- Brbić, M.; Kopriva, I. Multi-view low-rank sparse subspace clustering. Pattern Recognit. 2018, 73, 247–258. [Google Scholar] [CrossRef]
- Kang, Z.; Zhou, W.; Zhao, Z.; Shao, J.; Han, M.; Xu, Z. Large-scale multi-view subspace clustering in linear time. AAAI Conf. Artif. Intell. 2020, 34, 4412–4419. [Google Scholar] [CrossRef]
- Chen, M.-S.; Huang, L.; Wang, C.-D.; Huang, D. Multi-view clustering in latent embedding space. AAAI Conf. Artif. Intell. 2020, 34, 3513–3520. [Google Scholar] [CrossRef]


| Notation | Explanation |
|---|---|
| the feature matrix of the v-th view | |
| the projection matrix of the v-th view | |
| low-dimensional embedding across different views | |
| error matrix | |
| regularization parameter | |
| penalty parameter | |
| lagrange multiplier |
| Datasets | Samples | Classes | Views |
|---|---|---|---|
| ORL [42] | 400 | 40 | 3 |
| Reuters [43] | 2000 | 5 | 2 |
| MSRCV1 [44] | 210 | 7 | 5 |
| BBCSport [45] | 282 | 4 | 3 |
| Datasets | Methods | NMI (%) | ACC (%) | F-Measure (%) | RI (%) |
|---|---|---|---|---|---|
| ORL | MSSC | 92.63 | 82.00 | 79.35 | 84.94 |
| DiMSC | 94.00 | 83.80 | 80.70 | 85.60 | |
| LT-MSC | 86.20 | 80.40 | 74.80 | 76.10 | |
| LMVSC | 73.30 | 47.75 | 35.36 | 96.85 | |
| MCLES | 90.33 | 78.00 | 70.91 | 98.46 | |
| LRE-LAMVSC (Ours) | 94.40 | 83.90 | 72.80 | 98.60 | |
| Reuters | MSSC | 20.56 | 44.50 | 37.23 | 67.09 |
| DiMSC | 18.21 | 40.00 | 28.68 | 67.49 | |
| LT-MSC | 17.93 | 36.20 | 28.29 | 68.16 | |
| LMVSC | 37.28 | 48.17 | 48.89 | 21.73 | |
| MCLES | 35.79 | 49.47 | 47.04 | 21.07 | |
| LRE-LAMVSC (Ours) | 42.50 | 45.70 | 51.30 | 80.05 | |
| MSRCV1 | MSSC | 63.10 | 70.99 | 62.87 | 86.54 |
| DiMSC | 62.87 | 68.57 | 57.92 | 89.72 | |
| LT-MSC | 70.04 | 80.00 | 68.48 | 91.12 | |
| LMVSC | 24.95 | 34.28 | 24.74 | 78.93 | |
| MCLES | 68.89 | 78.57 | 66.77 | 86.68 | |
| LRE-LAMVSC (Ours) | 81.70 | 93.38 | 85.29 | 90.60 | |
| BBCSport | MSSC | 69.96 | 79.78 | 76.13 | 87.27 |
| DiMSC | 85.11 | 87.32 | 91.02 | 91.32 | |
| LT-MSC | 72.56 | 89.43 | 81.19 | 92.91 | |
| LMVSC | 37.18 | 60.11 | 47.27 | 64.73 | |
| MCLES | 68.70 | 85.48 | 76.32 | 86.68 | |
| LRE-LAMVSC (Ours) | 87.31 | 90.17 | 83.09 | 93.70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Chen, L.; Liang, Z.; Liu, Q. A Novel Low-Rank Embedded Latent Multi-View Subspace Clustering Approach. Sensors 2025, 25, 2778. https://doi.org/10.3390/s25092778
Wang S, Chen L, Liang Z, Liu Q. A Novel Low-Rank Embedded Latent Multi-View Subspace Clustering Approach. Sensors. 2025; 25(9):2778. https://doi.org/10.3390/s25092778
Chicago/Turabian StyleWang, Sen, Lian Chen, Zhijian Liang, and Qingyang Liu. 2025. "A Novel Low-Rank Embedded Latent Multi-View Subspace Clustering Approach" Sensors 25, no. 9: 2778. https://doi.org/10.3390/s25092778
APA StyleWang, S., Chen, L., Liang, Z., & Liu, Q. (2025). A Novel Low-Rank Embedded Latent Multi-View Subspace Clustering Approach. Sensors, 25(9), 2778. https://doi.org/10.3390/s25092778






