Optimized Design of the Basic Structure of Dry-Coupled Shear Wave Probe for Ultrasonic Testing of Rock and Concrete
Abstract
1. Introduction
2. Materials and Methods
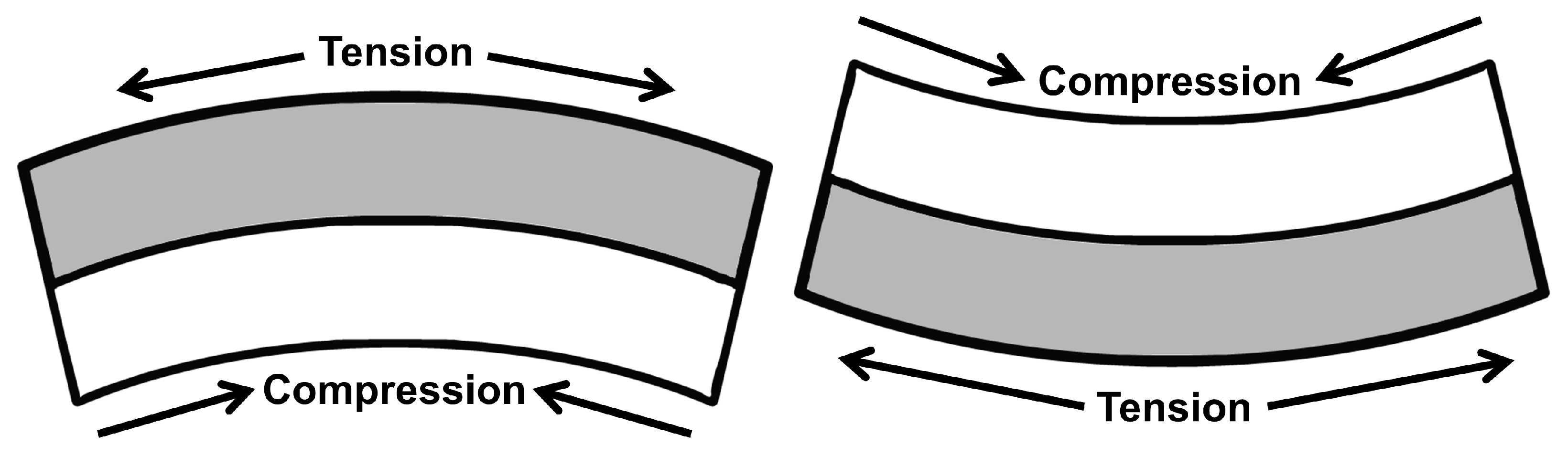
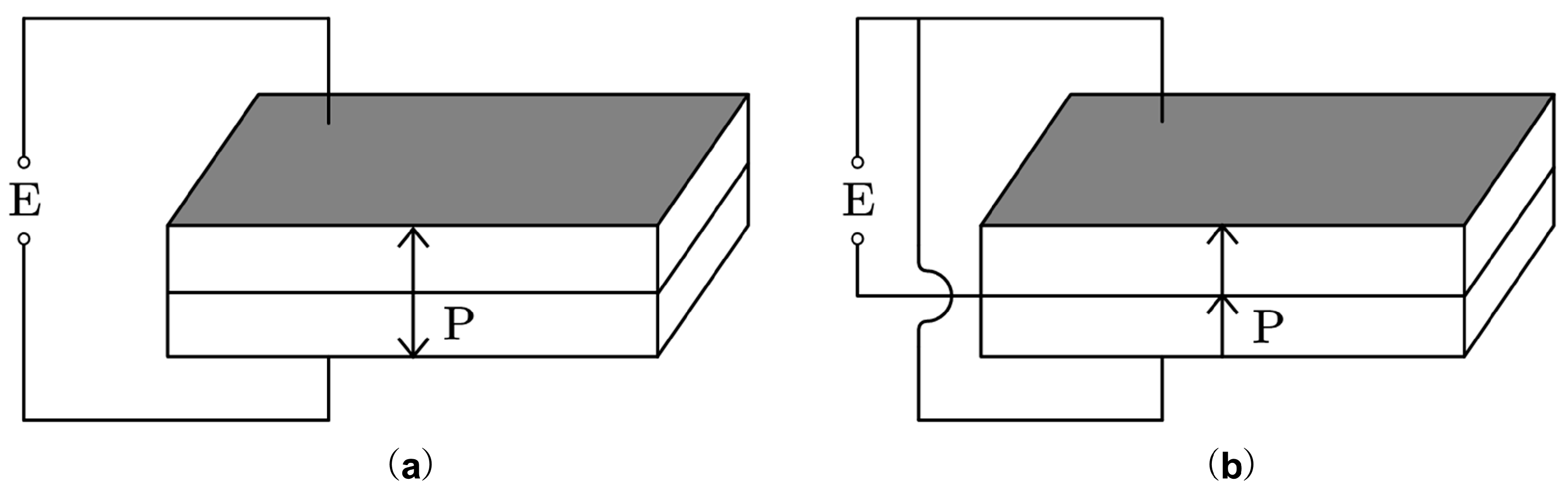
2.1. Flexural Vibration of a Long Strip Rectangular Double-Laminated Piezoelectric Ceramic Vibrator
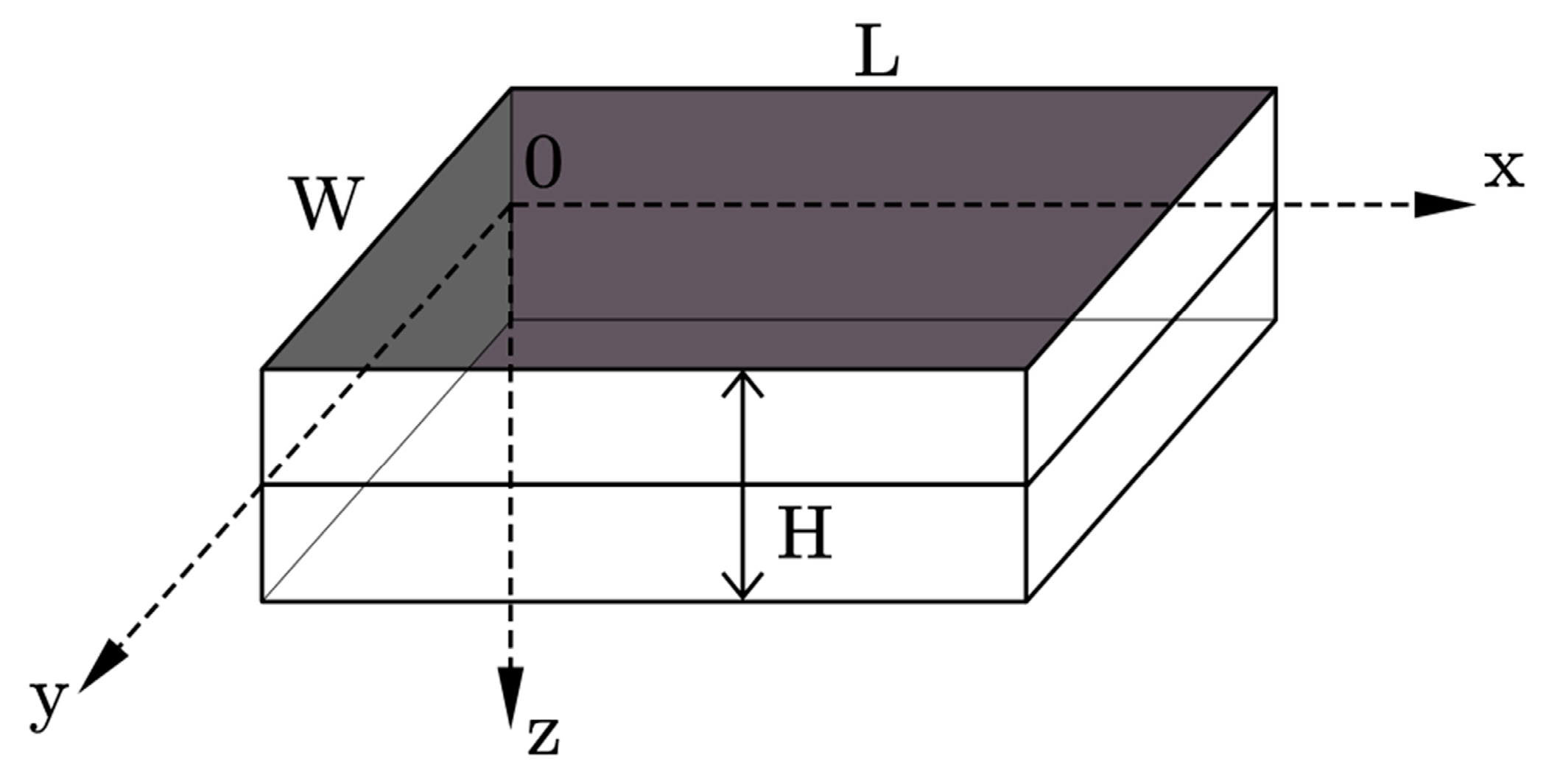
2.2. Flexural Vibration of a Finite-Width Rectangular Double-Laminated Piezoelectric Ceramic Vibrator
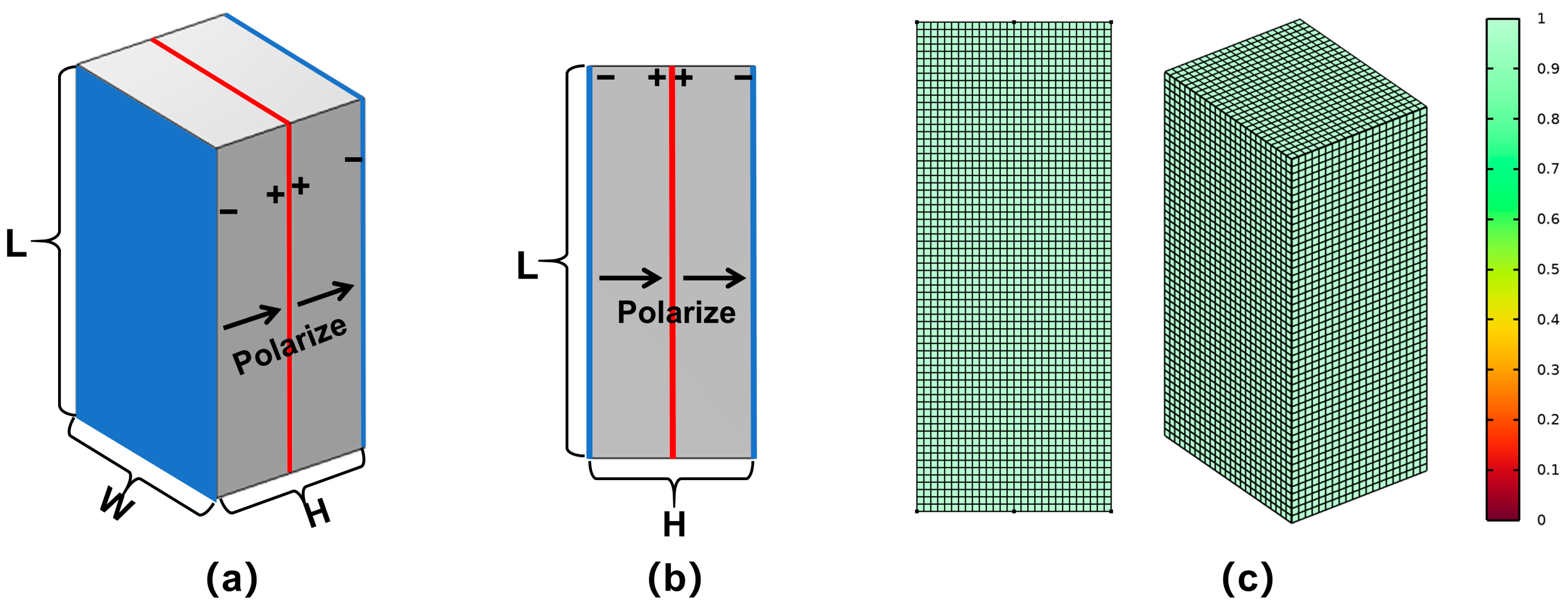
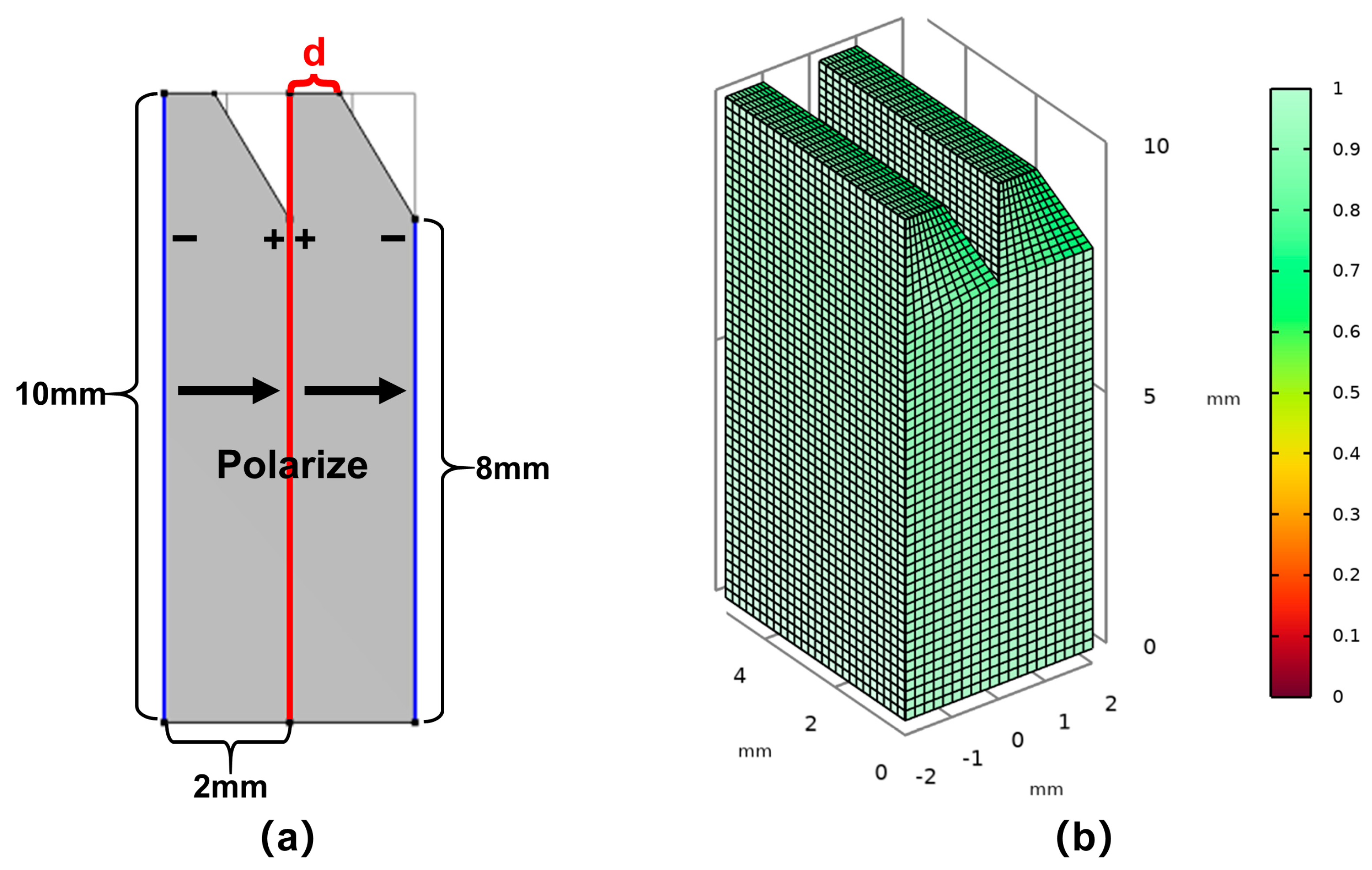
2.3. Numerical Calculation Based on the Finite Element Method
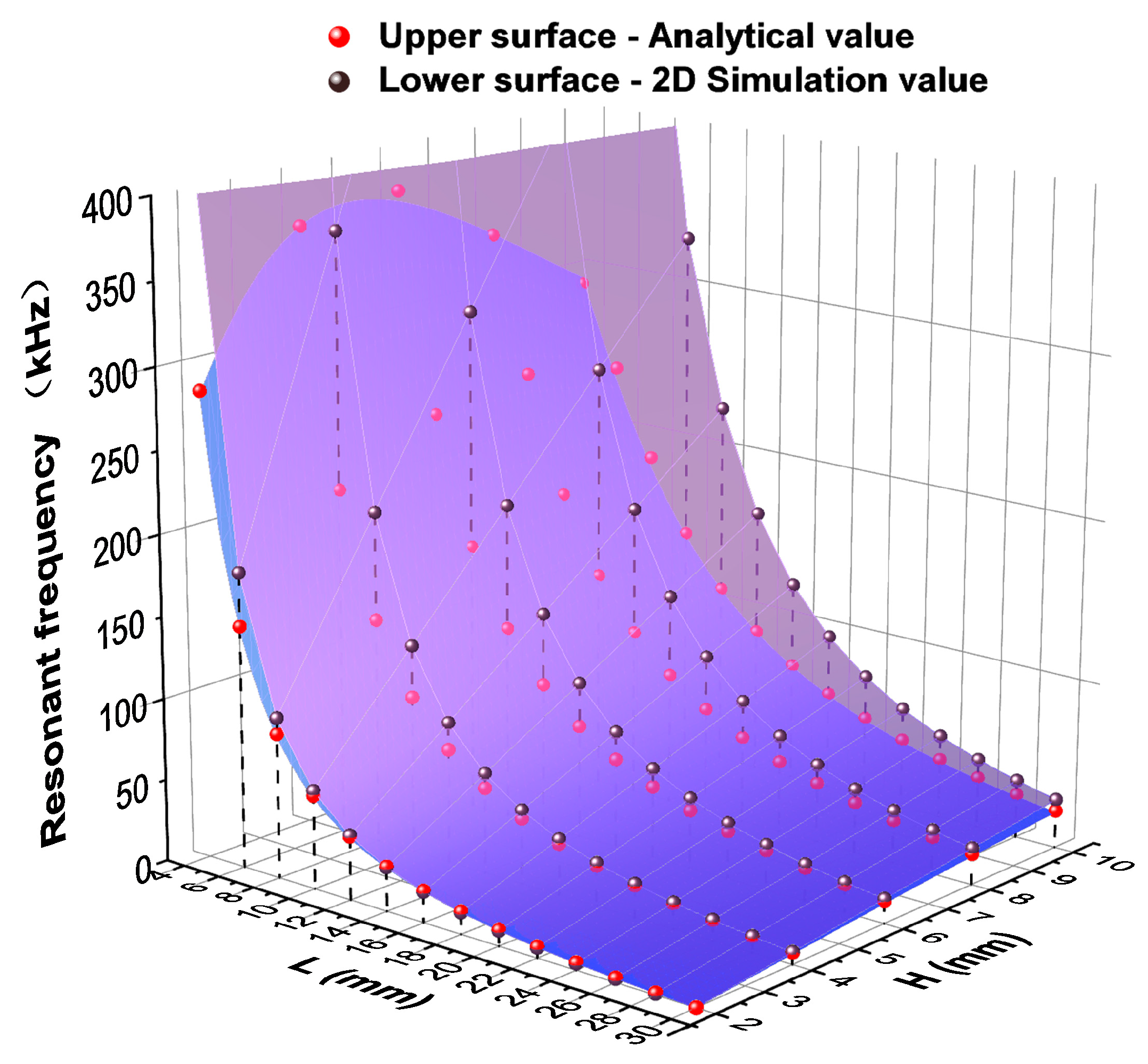
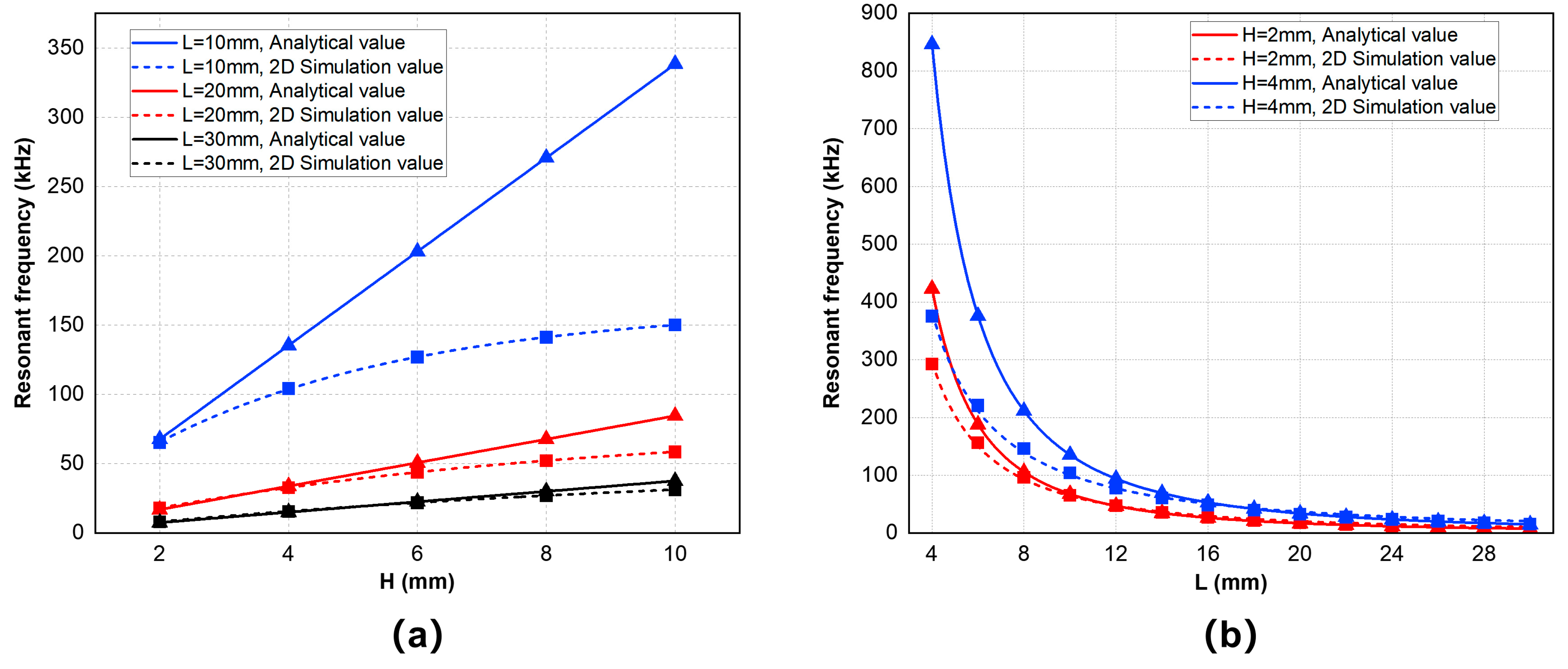
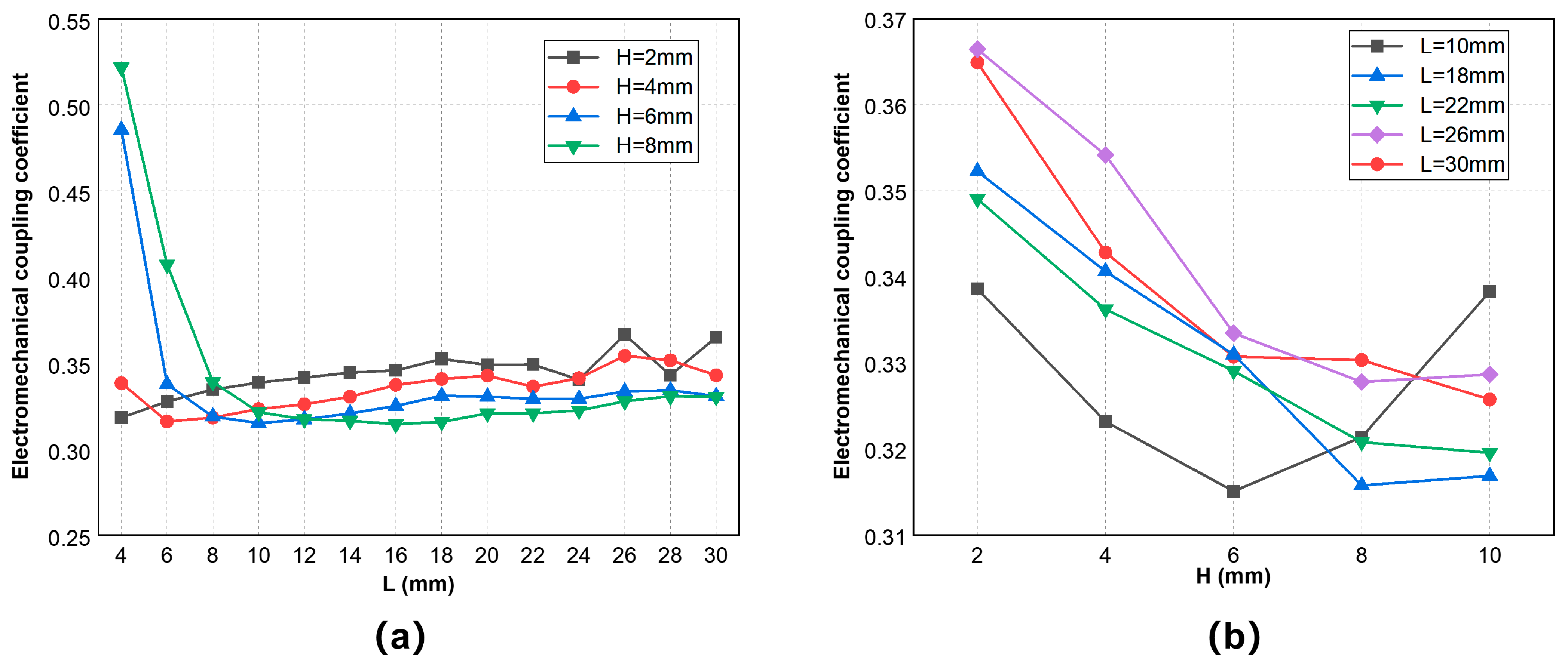
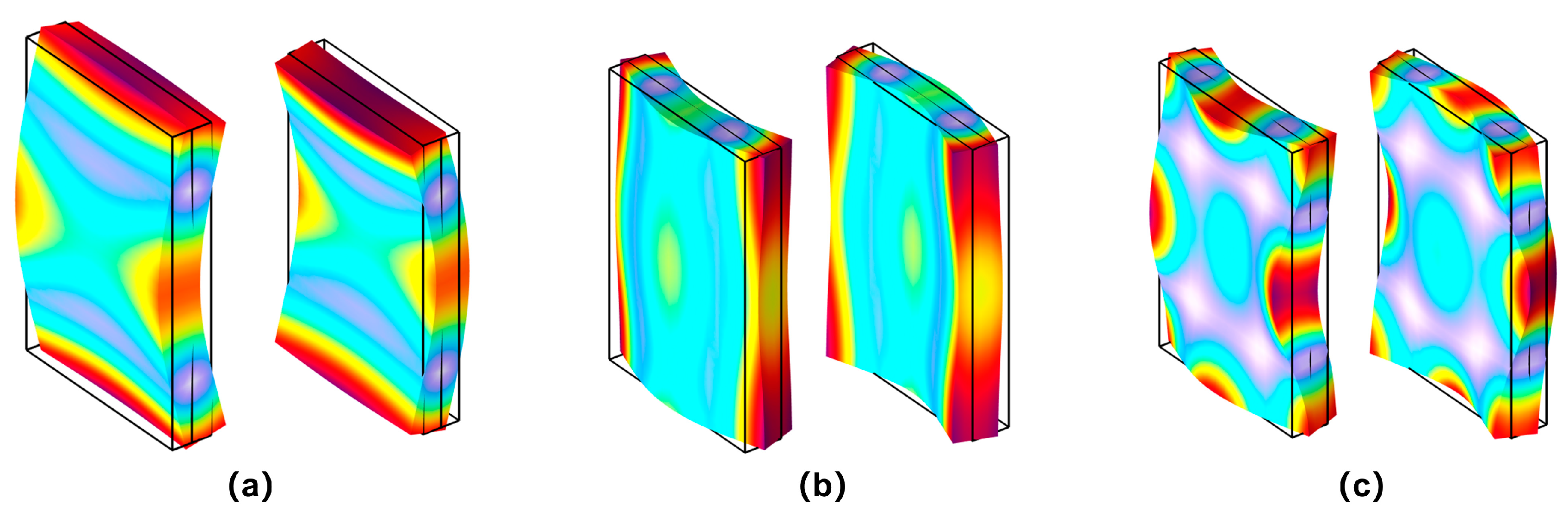
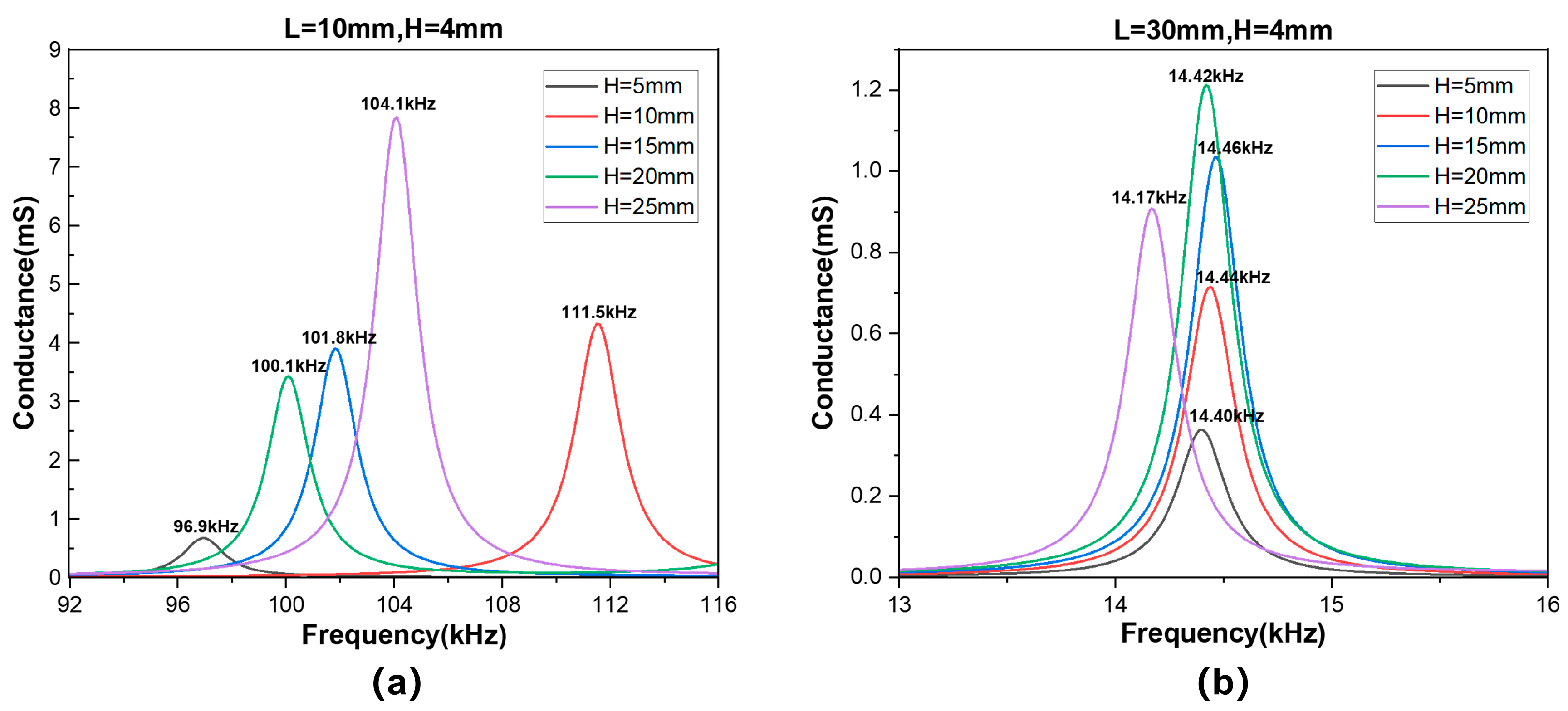
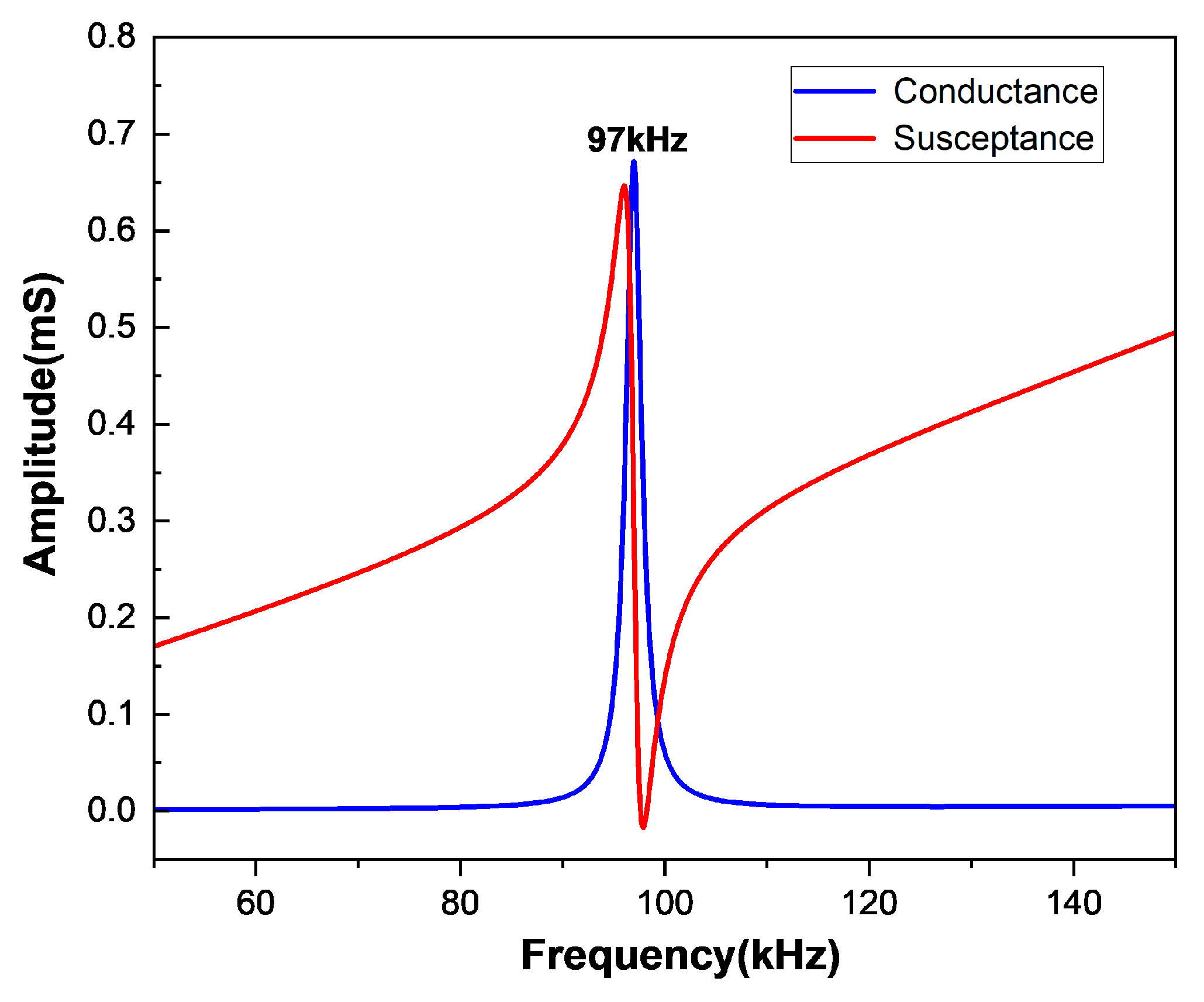
3. Finite Element Simulation Results
3.1. Finite Element Analysis of Flexural Vibration of Rectangular Double-Laminated Vibrator
3.1.1. Two-Dimensional Model
3.1.2. Three-Dimensional Model
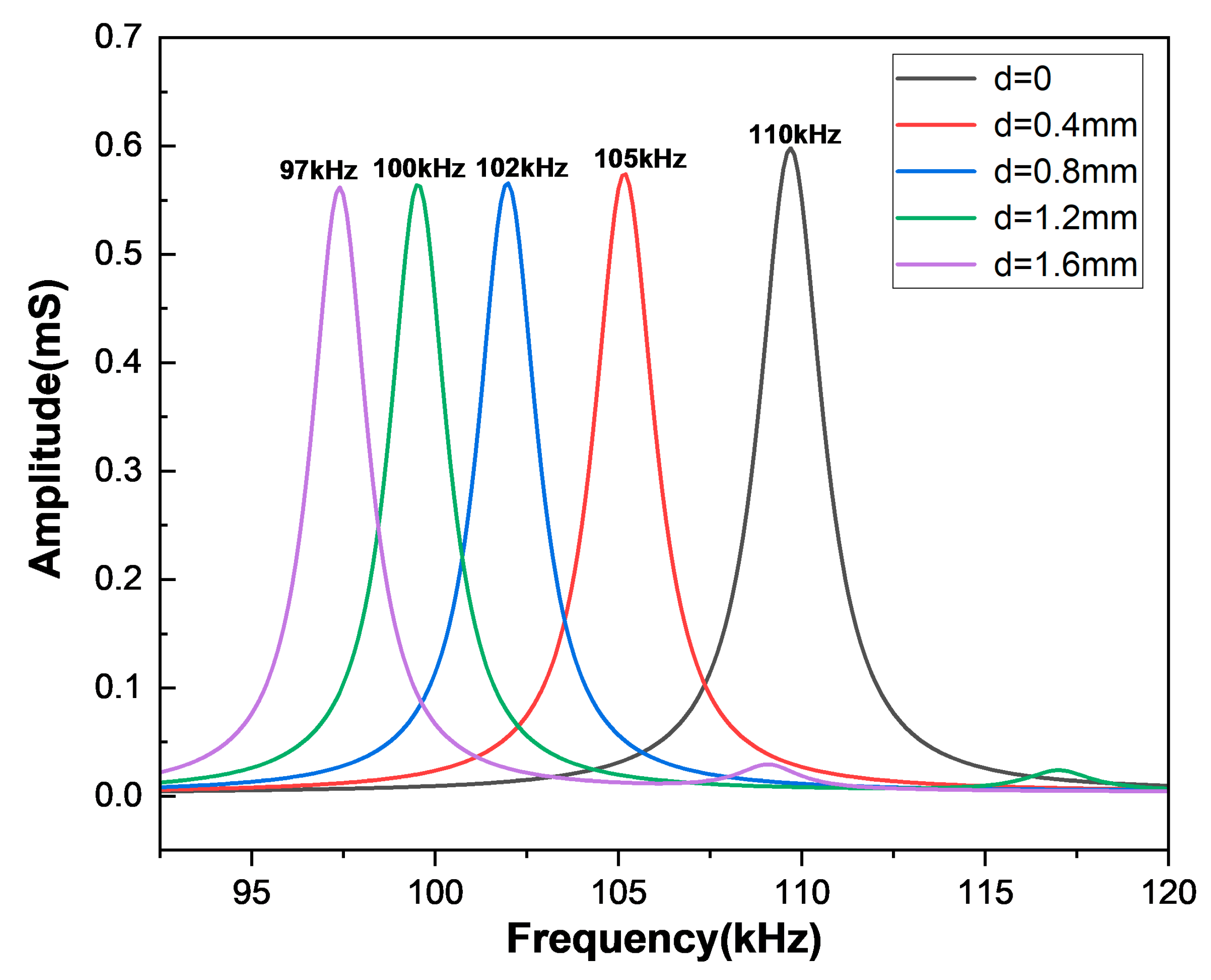
3.1.3. Double-Laminated Vibrator with the Wedge Structure
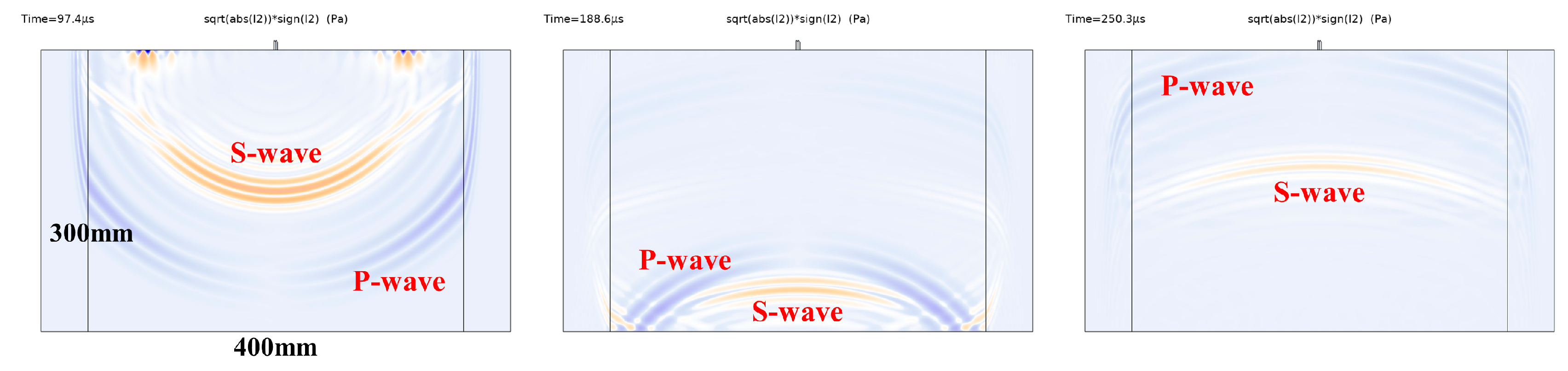
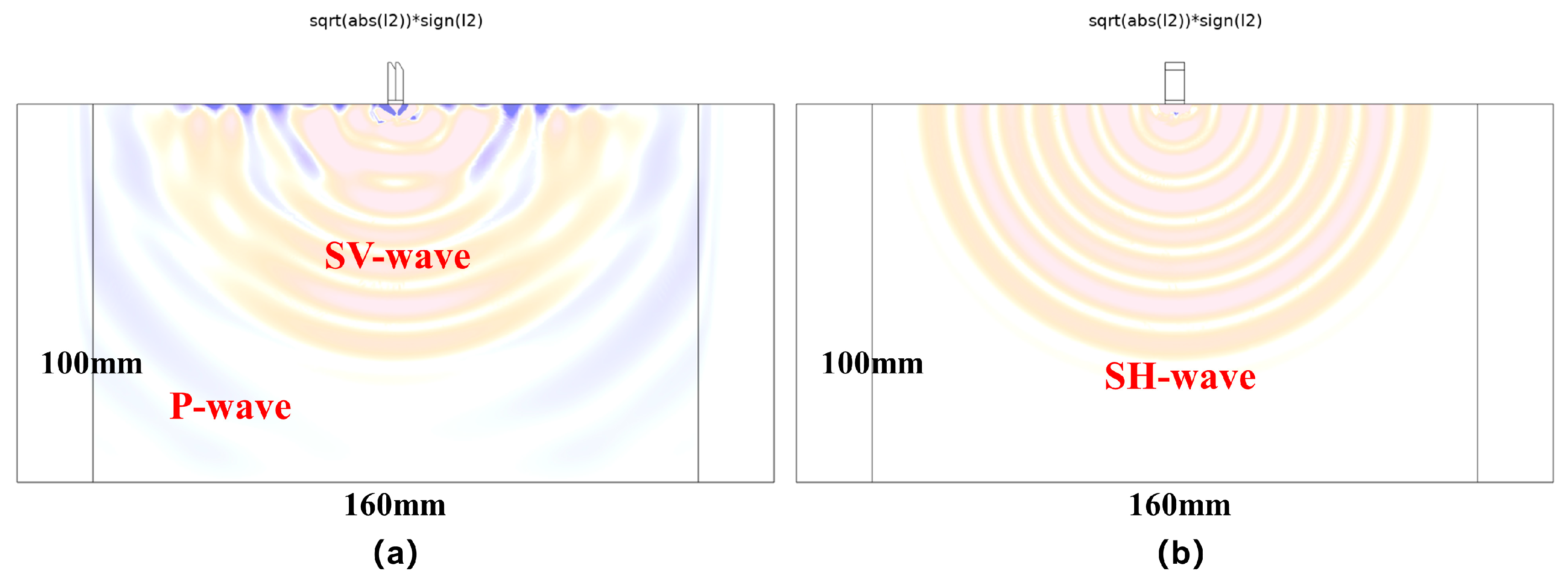
3.2. Wavefield in Time Domain Based on Finite Element Analysis
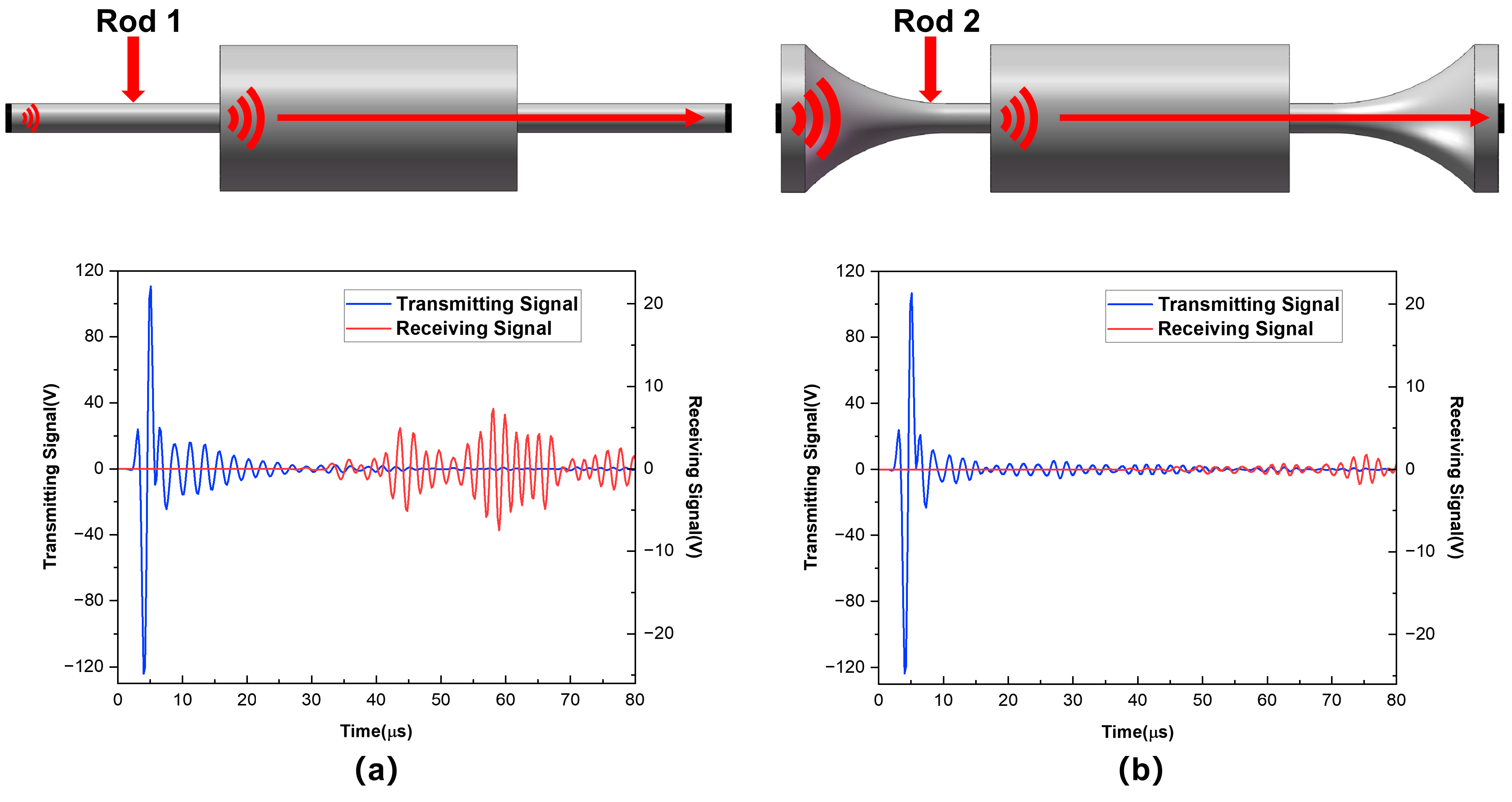
3.3. Discussion of Transducer Coupling Methods
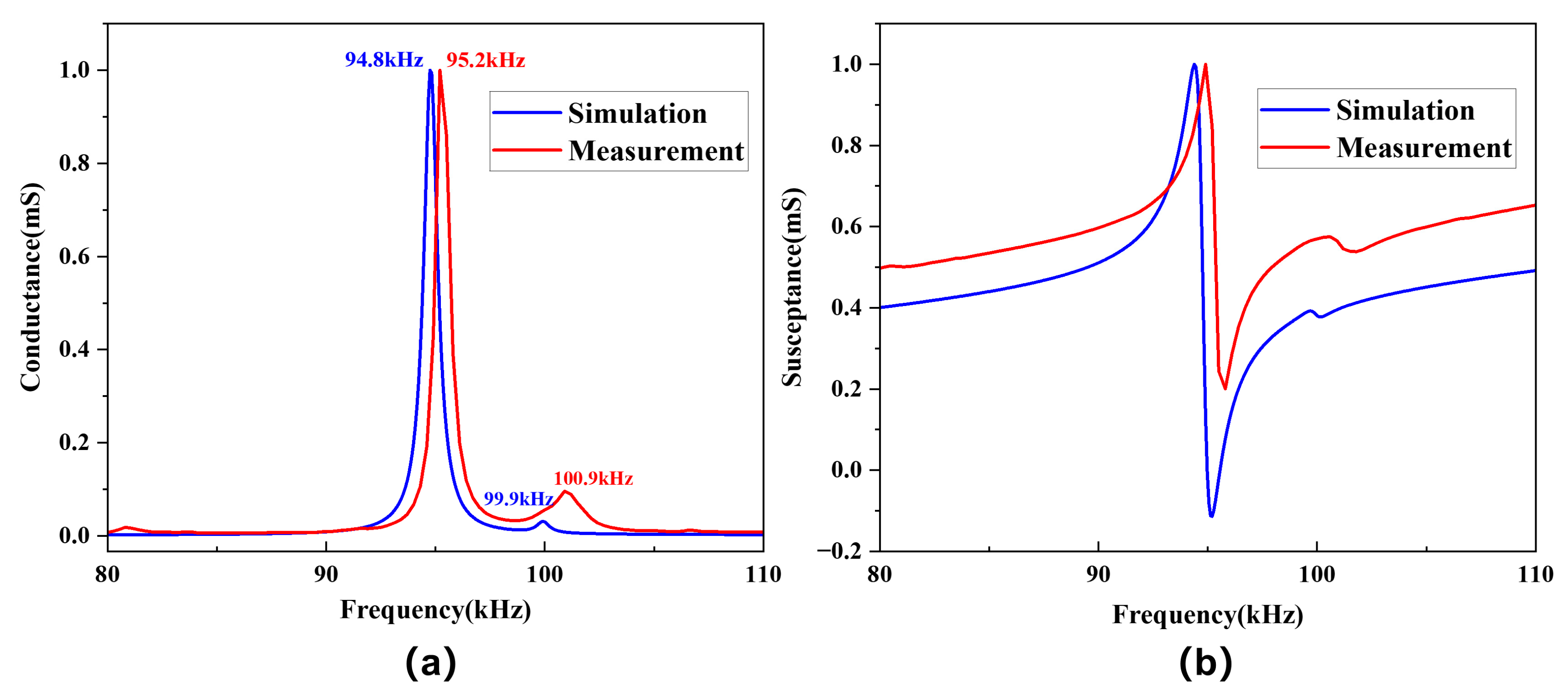
4. Measurement Results
5. Discussions and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zheng, C.; Kizil, M.S.; Chen, Z.; Aminossadati, S.M. Role of multi-seam interaction on gas drainage engineering design for mining safety and environmental benefits: Linking coal damage to permeability variation. Process Saf. Environ. Protect. 2018, 114, 310–322. [Google Scholar] [CrossRef]
- Shah, A.A.; Ribakov, Y. Non-destructive measurements of crack assessment and defect detection in concrete structures. Mater. Des. 2008, 29, 61–69. [Google Scholar] [CrossRef]
- Jia, Y.; Wen, J.; Zhao, B.; Yang, C. Concrete Structure Ultrasonic Testing Technology Research Latest Progress and Development Trend. E3S Web Conf. 2023, 372, 02020. [Google Scholar] [CrossRef]
- Janků, M.; Cikrle, P.; Grošek, J.; Anton, O.; Stryk, J. Comparison of infrared thermography, ground-penetrating radar and ultrasonic pulse echo for detecting delaminations in concrete bridges. Constr. Build. Mater. 2019, 225, 1098–1111. [Google Scholar] [CrossRef]
- Azari, H.; Yuan, D.; Nazarian, S.; Gucunski, N. Sonic Methods to Detect Delamination in Concrete Bridge Decks. Transp. Res. Rec. J. Transp. Res. Board 2012, 2292, 113–124. [Google Scholar] [CrossRef]
- Capozzoli, L.; Rizzo, E. Combined NDT techniques in civil engineering applications: Laboratory and real test. Constr. Build. Mater. 2017, 154, 1139–1150. [Google Scholar] [CrossRef]
- Cheng, C.-C.; Cheng, T.-M.; Chiang, C.-H. Defect detection of concrete structures using both infrared thermography and elastic waves. Autom. Constr. 2008, 18, 87–92. [Google Scholar] [CrossRef]
- Yehia, S.; Abudayyeh, O.; Nabulsi, S.; Abdelqader, I. Detection of Common Defects in Concrete Bridge Decks Using Nondestructive Evaluation Techniques. J. Bridge Eng. 2007, 12, 215–225. [Google Scholar] [CrossRef]
- Nilsson, M.; Ulriksen, P.; Rydén, N. Ultrasonic imaging of concrete-embedded corroded steel liners using linear and nonlinear evaluation. Nondestruct. Test. Eval. 2024, 1–29. [Google Scholar] [CrossRef]
- Godinho, L.; Dias-da-Costa, D.; Areias, P.; Júlio, E.; Soares, D. Numerical study towards the use of a SH wave ultrasonic-based strategy for crack detection in concrete structures. Eng. Struct. 2013, 49, 782–791. [Google Scholar] [CrossRef]
- Komsky, I.N. Transmission of Longitudinal and Transverse Ultrasonic Waves Using Dry-Coupled Transducer Modules. AIP Conference Proceedings 2005, 760, 1010–1017. [Google Scholar]
- Si, W.; Yang, Q.; Wang, H.; Liu, D.; Xue, S. Experimental analysis of the influence of coupling methods on rock samples acoustic velocity measurement. Prog. Geophys. 2018, 33, 1951–1955. [Google Scholar]
- Waag, G.; Hoff, L.; Norli, P. Air-coupled ultrasonic through-transmission thickness measurements of steel plates. Ultrasonics 2015, 56, 332–339. [Google Scholar] [CrossRef] [PubMed]
- Jayakumar, A.; Balachandran, A.; Mani, A.; Balasubramaniam, K. Falling film thickness measurement using air-coupled ultrasonic transducer. Exp. Therm. Fluid Sci. 2019, 109, 109906. [Google Scholar] [CrossRef]
- Zhang, K.; Li, S.; Zhou, Z. Detection of disbonds in multi-layer bonded structures using the laser ultrasonic pulse-echo mode. Ultrasonics 2019, 94, 411–418. [Google Scholar] [CrossRef]
- Matsumoto, T.; Nose, T.; Nagata, Y.; Kawashima, K.; Yamada, T.; Nakano, H.; Nagai, S. Measurement of High-Temperature Elastic Properties of Ceramics Using a Laser Ultrasonic Method. J. Am. Ceram. Soc. 2004, 84, 1521–1525. [Google Scholar] [CrossRef]
- Ding, X.; Wu, X.; Wang, Y. Bolt axial stress measurement based on a mode-converted ultrasound method using an electromagnetic acoustic transducer. Ultrasonics 2014, 54, 914–920. [Google Scholar] [CrossRef]
- Xie, S.; Tian, M.; Xiao, P.; Pei, C.; Chen, Z.; Takagi, T. A hybrid nondestructive testing method of pulsed eddy current testing and electromagnetic acoustic transducer techniques for simultaneous surface and volumetric defects inspection. NDT E Int. 2017, 86, 153–163. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, E.; Chen, Y.; Wang, X.; Sun, C.; Tan, J. Measurement of fastening force using dry-coupled ultrasonic waves. Ultrasonics 2020, 108, 106178. [Google Scholar] [CrossRef]
- Krautkraemer, J.; Krautkraemer, H. Ultrasonic Testing of Materials, 4th ed.; Springer: Berlin, Germany, 1990; pp. 266–278. [Google Scholar]
- Edwards, C.; Dixon, S.; Palmer, S.B. Improvements to dry coupled ultrasound for wall thickness and weld inspection. AIP Conf. Proc. 2000, 509, 1779–1786. [Google Scholar]
- Ravindran, V.K.; Bhaumik, B. Dry-coupled Pulse Echo Ultrasonic Inspection Methodology for Solid Graphite Products of Rocket Boosters. Def. Sci. J. 2002, 52, 27–32. [Google Scholar] [CrossRef]
- Robinson, A.; Drinkwater, B.W.; Allin, J. Dry-coupled low-frequency ultrasonic wheel probes: Application to adhesive bond inspection. NDT E Int. 2003, 36, 27–36. [Google Scholar] [CrossRef]
- Augereau, F.; Laux, D.; Allais, L.; Mottot, M.; Caes, C. Ultrasonic measurement of anisotropy and temperature dependence of elastic parameters by a dry coupling method applied to a 6061-T6 alloy. Ultrasonics 2007, 46, 34–41. [Google Scholar] [CrossRef] [PubMed]
- Shevaldykin, V.G.; Samokrutov, A.A.; Kozlov, V.N. Ultrasonic low-frequency transducers with dry dot contact and their applications for evaluation of concrete structures. In Proceedings of the 2002 IEEE Ultrasonics Symposium Proceedings, Munich, Germany, 8–11 October 2002; Volumes 1–2, pp. 793–798. [Google Scholar]
- Woollett, R.S.; Finch, R.D. The Flexural Bar Transducer. J. Acoust. Soc. Am. 1990, 87, 1378. [Google Scholar] [CrossRef]
- Shuyu, L. Piezoelectric ceramic rectangular transducers in flexural vibration. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004, 51, 865–870. [Google Scholar] [CrossRef]




| Parameters | PZT-4 | Parameters | PZT-4 |
|---|---|---|---|
| 13.9 | 7500 | ||
| 7.78 | −123 | ||
| 7.43 | 289 | ||
| 11.5 | 496 | ||
| 2.56 | −5.2 | ||
| 12.3 | 15.1 | ||
| −4.05 | 12.7 | ||
| −5.31 | 730 | ||
| 15.5 | 635 | ||
| 39.0 |
| L (mm) | H (mm) | Analytical Values (Hz) | Simulation Values (Hz) | Relative Error (%) |
|---|---|---|---|---|
| 10 | 2 | 67,694 | 65,300 | 3.54% |
| 4 | 135,389 | 104,200 | 23.04% | |
| 6 | 203,083 | 126,900 | 37.51% | |
| 8 | 270,778 | 141,200 | 47.85% | |
| 10 | 338,472 | 150,200 | 55.62% | |
| 20 | 2 | 16,924 | 17,900 | 5.45% |
| 4 | 33,847 | 32,700 | 3.39% | |
| 6 | 50,771 | 43,800 | 13.73% | |
| 8 | 67,694 | 52,100 | 23.04% | |
| 10 | 84,618 | 58,500 | 30.87% | |
| 30 | 2 | 7522 | 8100 | 7.14% |
| 4 | 15,043 | 15,500 | 2.95% | |
| 6 | 22,565 | 21,800 | 3.39% | |
| 8 | 30,086 | 27,000 | 10.26% | |
| 10 | 37,608 | 31,200 | 17.04% |
| H (mm) | L (mm) | Analytical Values (Hz) | Simulation Values (Hz) | Relative Error (%) |
|---|---|---|---|---|
| 2 | 6 | 188,040 | 156,100 | 16.99% |
| 12 | 47,010 | 47,000 | 0.02% | |
| 18 | 20,893 | 21,900 | 4.60% | |
| 24 | 11,753 | 12,600 | 6.72% | |
| 30 | 7522 | 8100 | 7.14% | |
| 4 | 6 | 376,080 | 220,600 | 41.34% |
| 12 | 94,020 | 78,000 | 17.04% | |
| 18 | 41,787 | 39,400 | 5.71% | |
| 24 | 23,505 | 23,500 | 0.02% | |
| 30 | 15,043 | 15,500 | 2.95% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Zhou, Y.; Zhu, C.; Cao, X.; Chen, H. Optimized Design of the Basic Structure of Dry-Coupled Shear Wave Probe for Ultrasonic Testing of Rock and Concrete. Sensors 2025, 25, 2660. https://doi.org/10.3390/s25092660
Lu Y, Zhou Y, Zhu C, Cao X, Chen H. Optimized Design of the Basic Structure of Dry-Coupled Shear Wave Probe for Ultrasonic Testing of Rock and Concrete. Sensors. 2025; 25(9):2660. https://doi.org/10.3390/s25092660
Chicago/Turabian StyleLu, Yonghao, Yinqiu Zhou, Chenhui Zhu, Xueshen Cao, and Hao Chen. 2025. "Optimized Design of the Basic Structure of Dry-Coupled Shear Wave Probe for Ultrasonic Testing of Rock and Concrete" Sensors 25, no. 9: 2660. https://doi.org/10.3390/s25092660
APA StyleLu, Y., Zhou, Y., Zhu, C., Cao, X., & Chen, H. (2025). Optimized Design of the Basic Structure of Dry-Coupled Shear Wave Probe for Ultrasonic Testing of Rock and Concrete. Sensors, 25(9), 2660. https://doi.org/10.3390/s25092660








