A Fading Suppression Method for Φ-OTDR Systems Based on Multi-Domain Multiplexing
Abstract
1. Introduction
2. Multi-Domain Multiplexing Principle
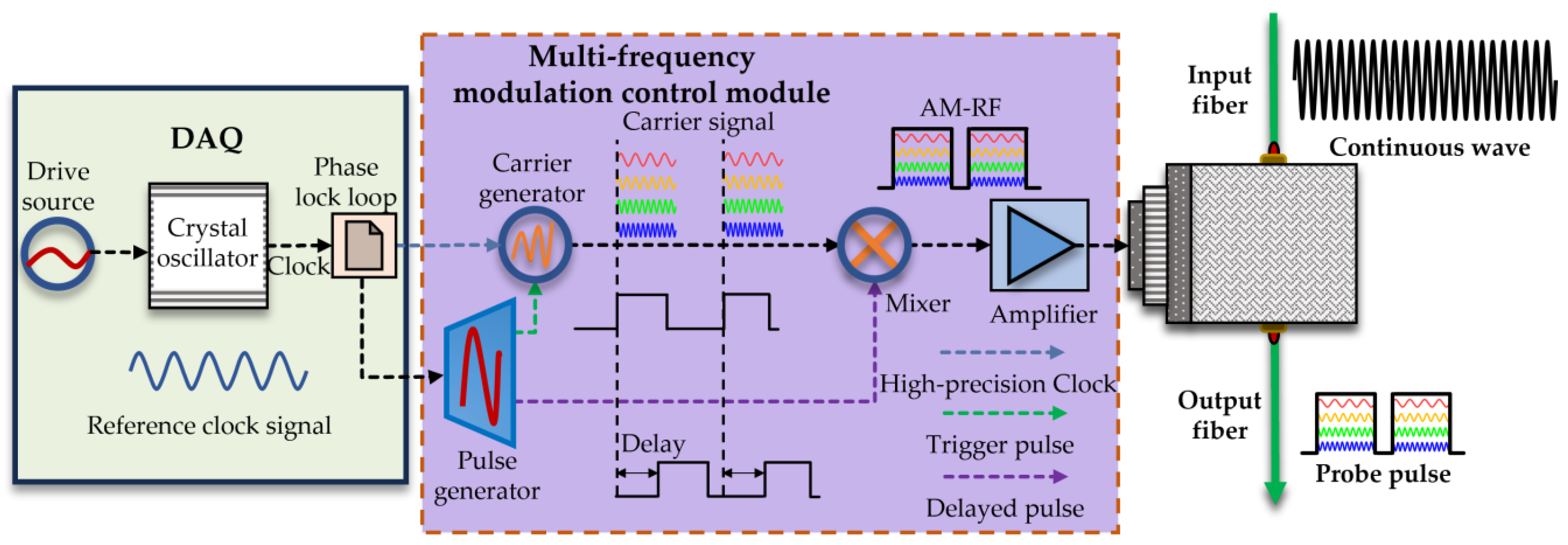
3. Schematic of the Proposed Multi-Domain Multiplexing System
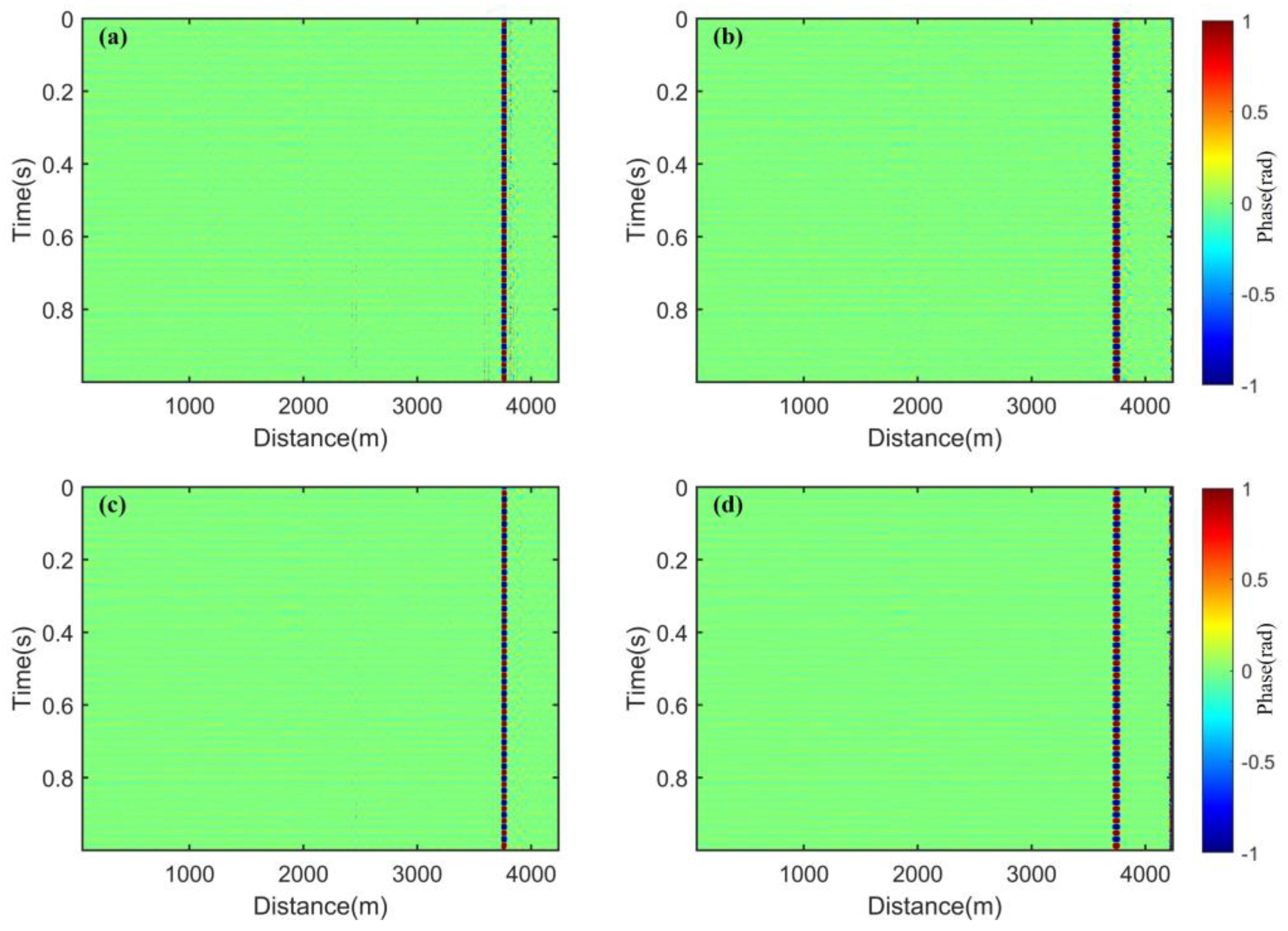
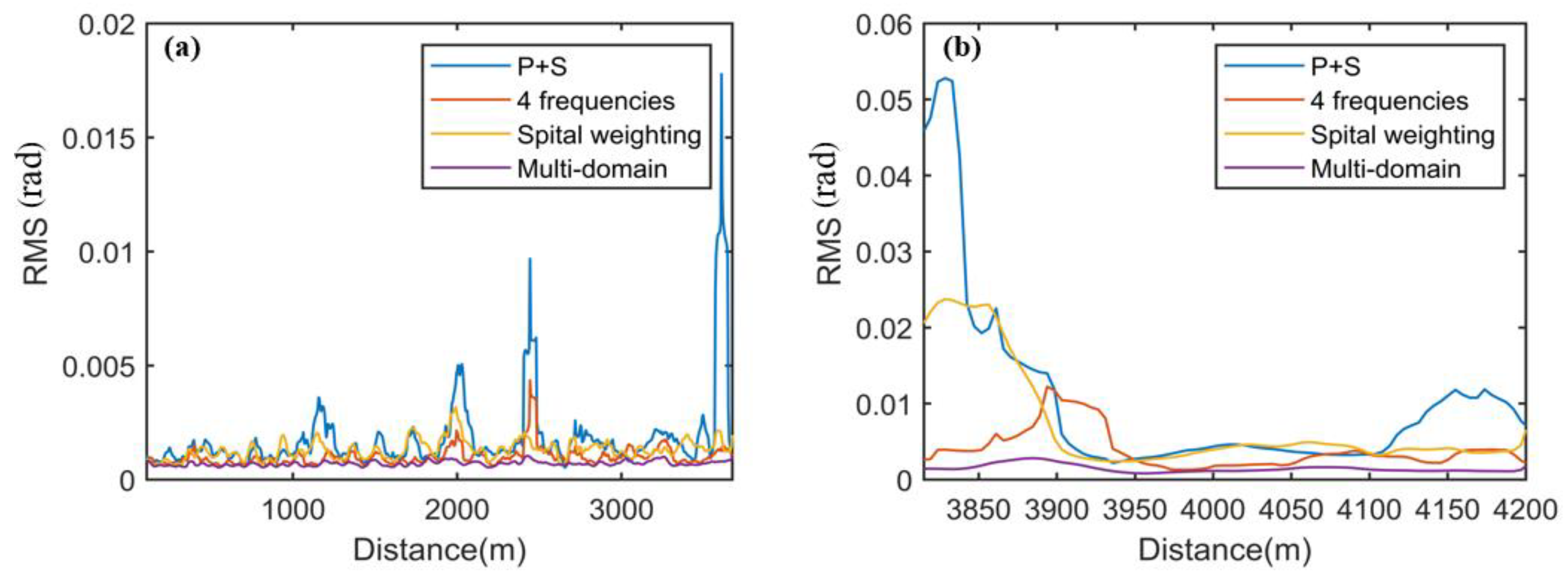
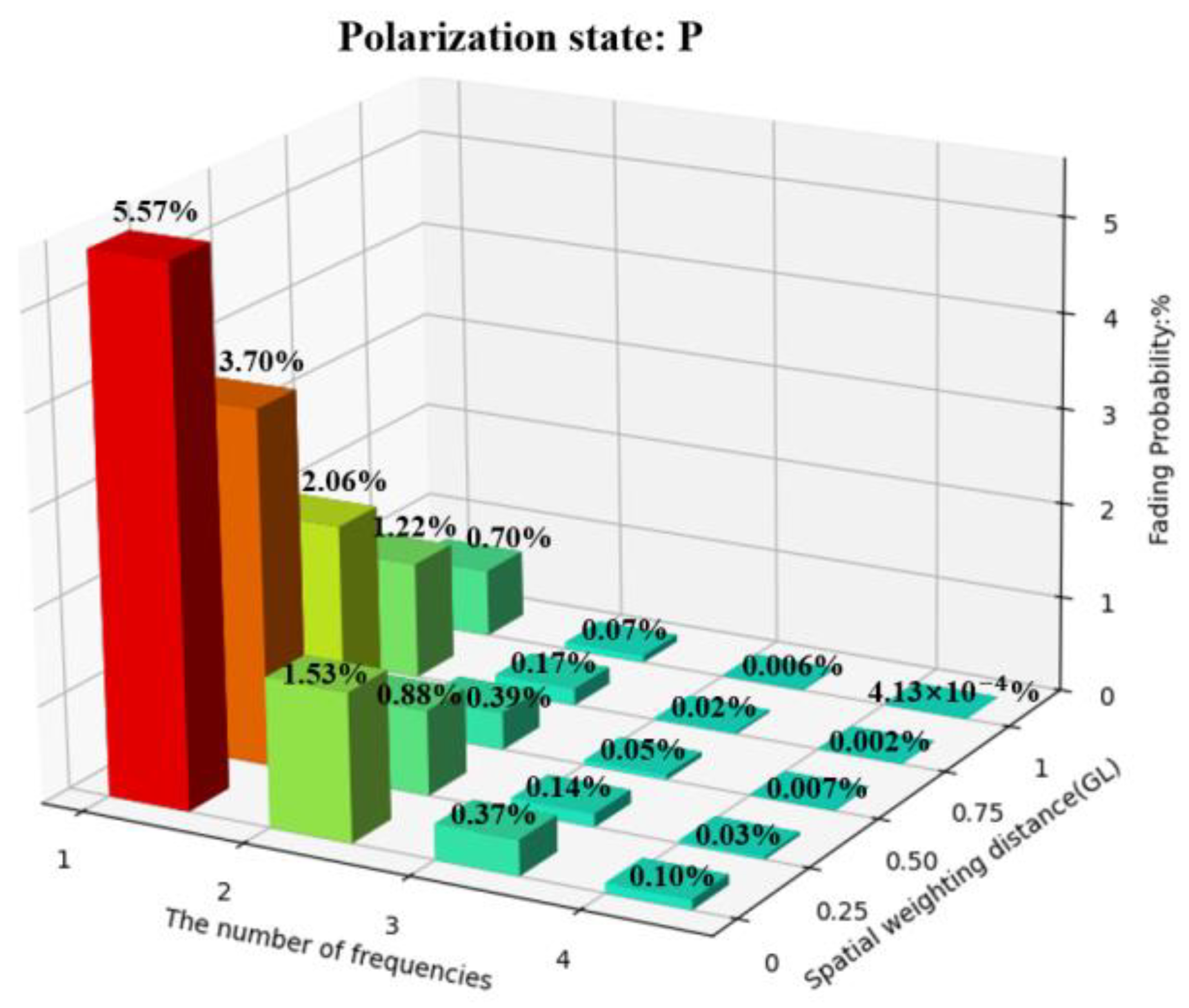
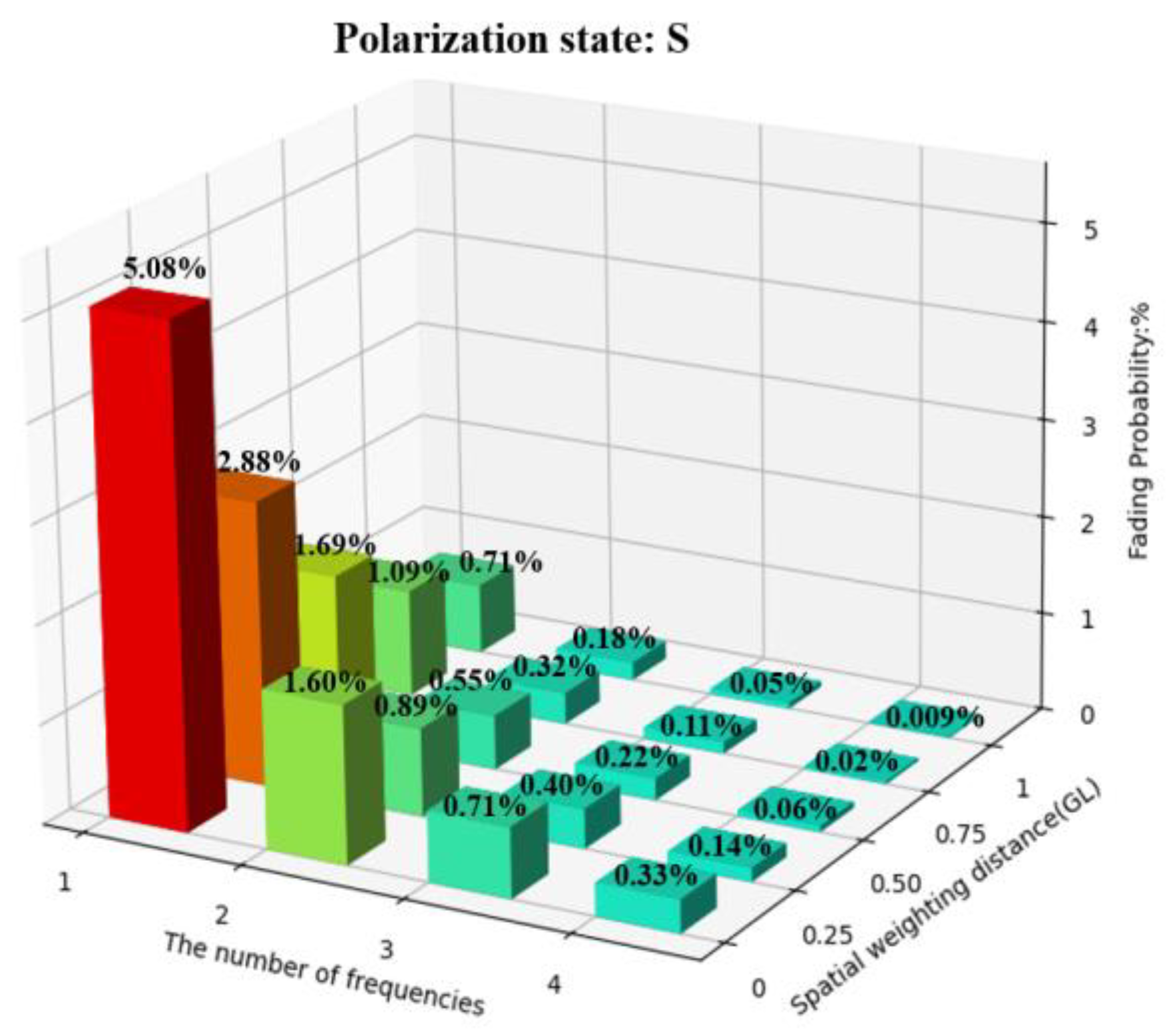
4. Experimental Results and Analysis
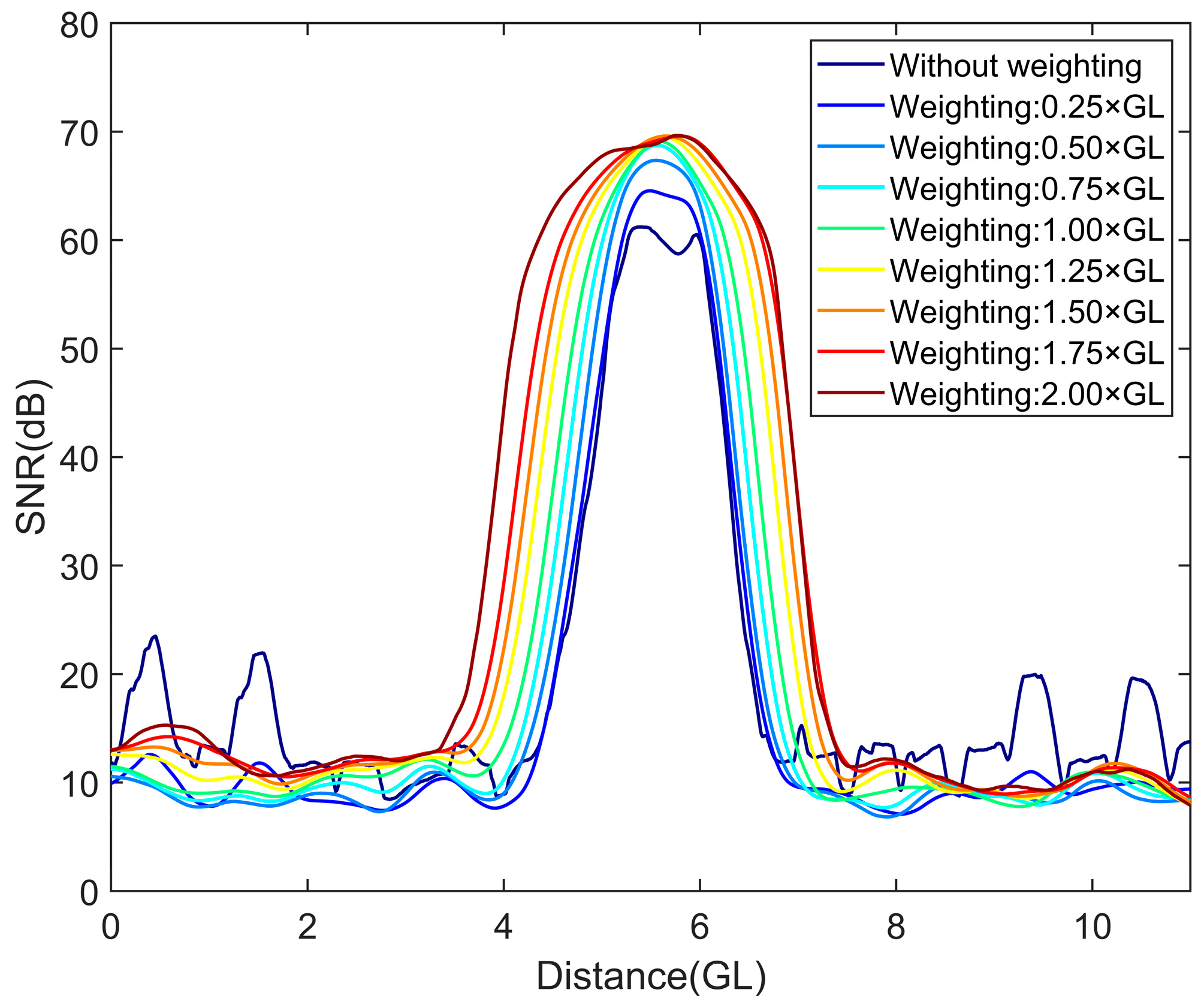
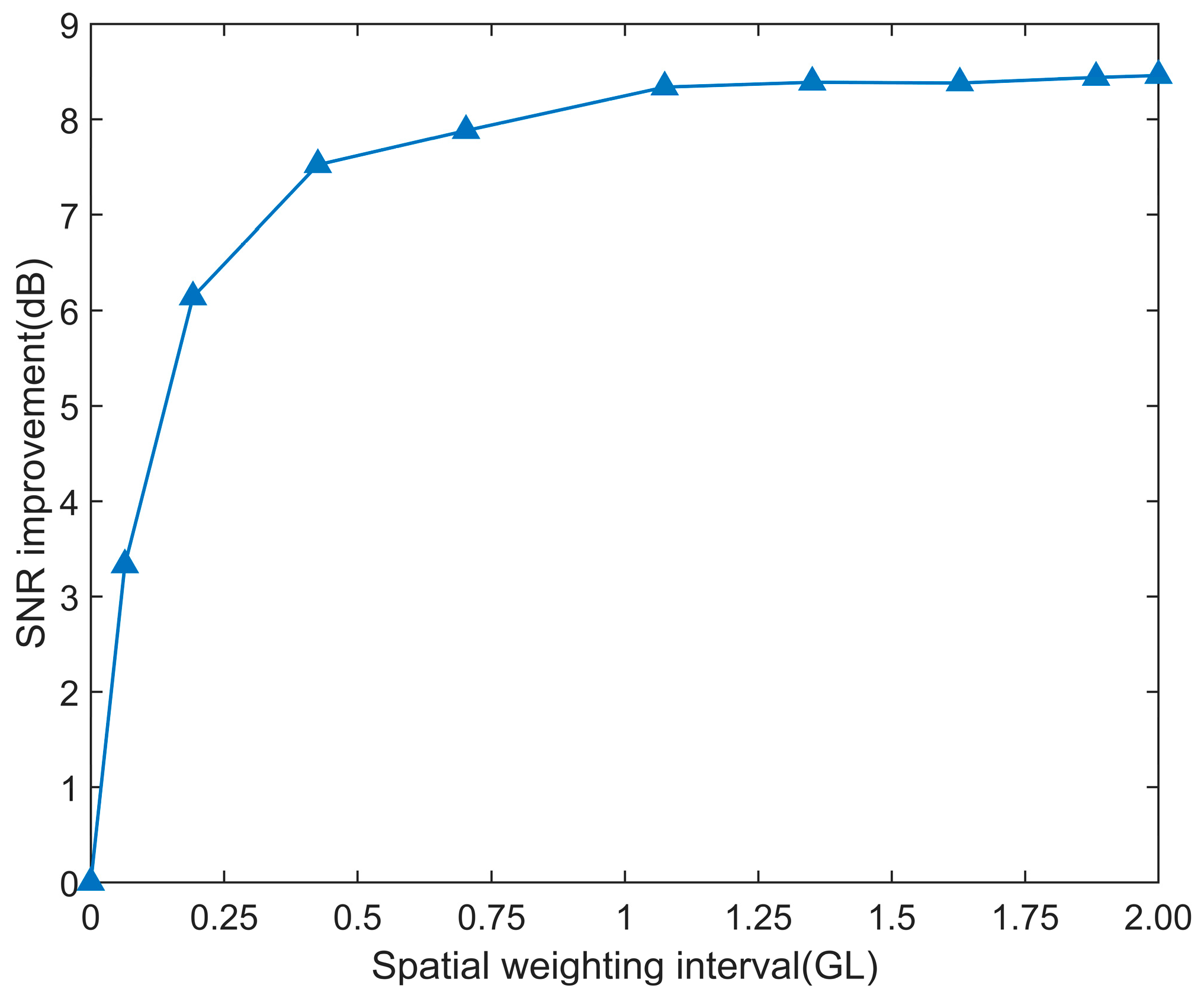
4.1. Spatial Weighting
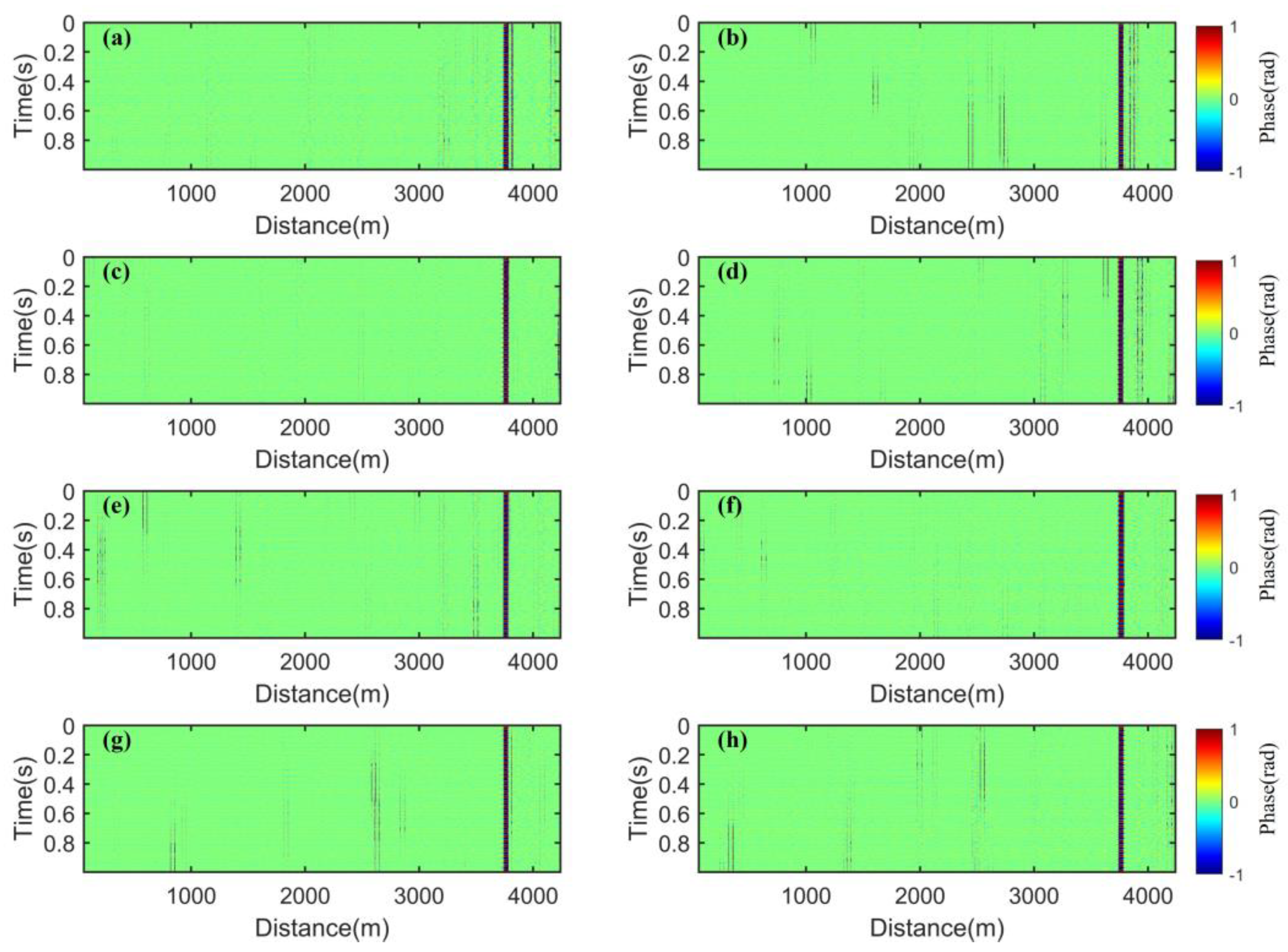
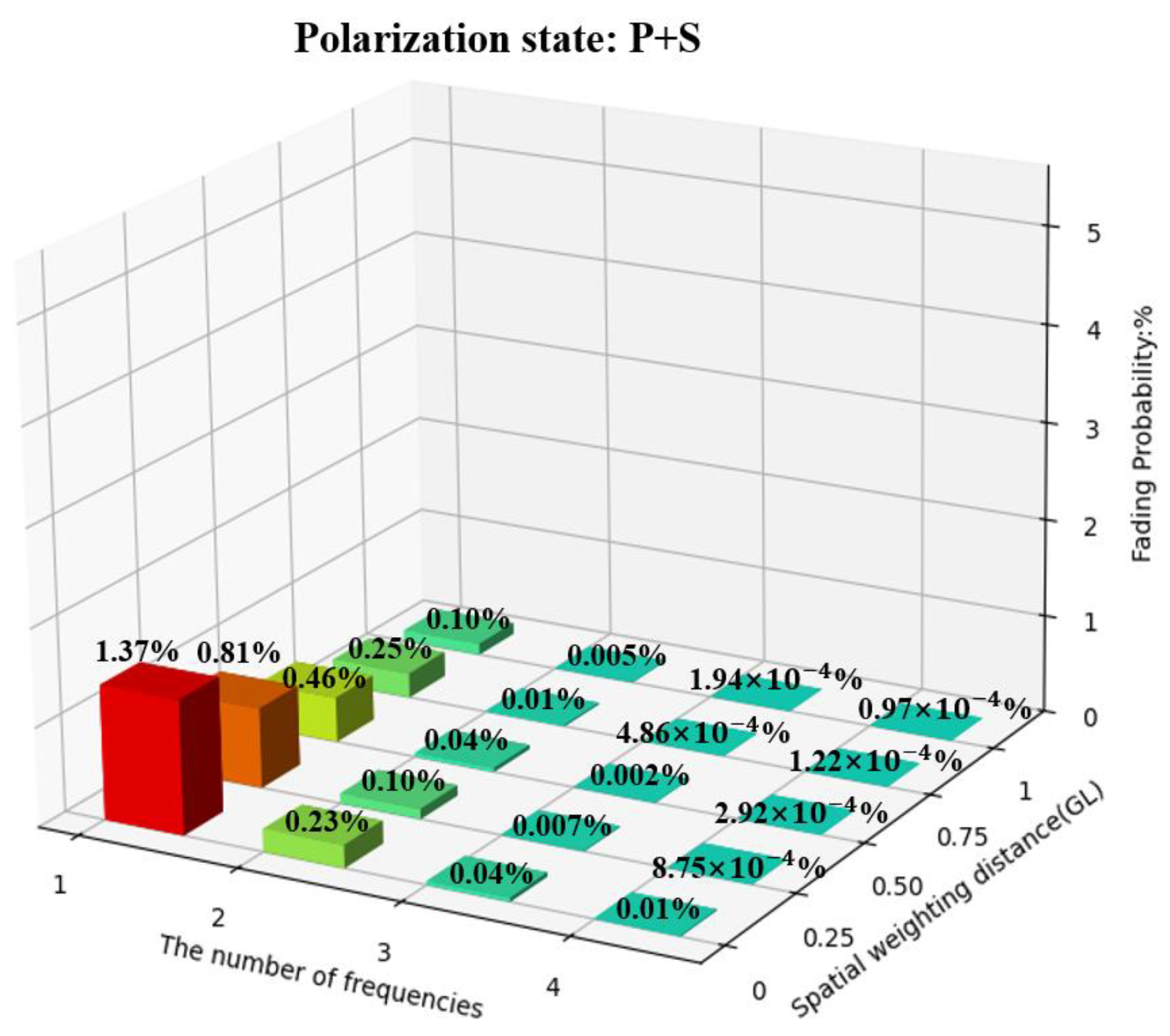
4.2. PDM, FDM, and Spatial Weighting
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Φ-OTDR | Phase-sensitive optical time domain reflectometry |
| RBS | Rayleigh backscattered signal |
| IF | Intermediate frequency |
| SNR | Signal-to-noise ratio |
| SDM | Spatial domain multiplexing |
| PDM | Polarization domain multiplexing |
| FDM | Frequency domain multiplexing |
| CNR | Carrier-to-noise ratio |
| OSPP | Orthogonal SOP pulse pair |
| MDM | Multi-domain multiplexing |
| NLL | Narrow linewidth laser |
| CW | Continuous wave |
| OC | Optical coupler |
| AOM | Acousto-optic modulator |
| PDR | Polarization diversity receiver |
| DAQ | Data acquisition card |
| EDFA | Erbium-doped fiber amplifier |
| CIR | Circulator |
| FUT | Fiber under test |
| PZT | Piezoelectric ceramic transducer |
| AWG | Arbitrary waveform generator |
| STFT | Short-time Fourier transform |
| GL | Gauge length |
| RMS | Root mean square |
References
- Bao, X.; Chen, L. Recent progress in distributed fiber optic sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Zhu, T.; Chen, L.; Bao, X. Distributed vibration sensor based on coherent detection of phase-OTDR. J. Light. Technol. 2010, 28, 3243–3249. [Google Scholar]
- Madan, A.; Zhao, C.; Han, C.; Dong, Y.; Yang, Y. Monitoring rail track bolt loosening using fiber-optic distributed acoustic sensing. Sens. Actuators A Phys. 2025, 382, 116176. [Google Scholar] [CrossRef]
- Zahoor, R.; Cerri, E.; Vallifuoco, R.; Zeni, L.; De Luca, A.; Caputo, F.; Minardo, A. Lamb wave detection for structural health monitoring using a Φ-OTDR system. Sensors 2022, 22, 5962. [Google Scholar] [CrossRef]
- Chen, Y.; Zong, J.; Liu, C.; Cao, Z.; Duan, P.; Li, J.; Hu, G. Offshore subsurface characterization enabled by fiber-optic distributed acoustic sensing (DAS): An East China Sea 3D VSP survey example. Front. Earth Sci. 2023, 11, 1033456. [Google Scholar] [CrossRef]
- Verma, S.; Kumari, J.; Mondal, A.; Santhanakrishnan, T.; Mathew, J.; Gupta, S. Modeling and simulation of Φ-OTDR system suitable for underwater intrusion detection and classification. Optik 2024, 311, 171876. [Google Scholar] [CrossRef]
- Strumia, C.; Trabattoni, A.; Supino, M.; Baillet, M.; Rivet, D.; Festa, G. Sensing optical fibers for earthquake source characterization using raw DAS records. J. Geophys. Res. Solid Earth 2024, 129, e2023JB027860. [Google Scholar] [CrossRef]
- Baba, S.; Araki, E.; Yamamoto, Y.; Hori, T.; Fujie, G.; Nakamura, Y.; Yokobiki, T.; Matsumoto, H. Observation of shallow slow earthquakes by distributed acoustic sensing using offshore fiber-optic cable in the Nankai Trough, Southwest Japan. Geophys. Res. Lett. 2023, 50, e2022GL102678. [Google Scholar] [CrossRef]
- Healey, P. Fading in heterodyne OTDR. Electron. Lett. 1984, 20, 30–32. [Google Scholar] [CrossRef]
- Juarez, J.C.; Taylor, H.F. Polarization discrimination in a phase-sensitive optical time-domain reflectometer intrusion-sensor system. Opt. Lett. 2005, 30, 3284–3286. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, J.; Xiong, F.; Zhang, X.; Chen, X.; Ding, Z.; Zheng, Y.; Wang, F.; Chen, M. A space-division multiplexing method for fading noise suppression in the Φ-OTDR system. Sensors 2021, 21, 1694. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhou, T.; Ding, Z.; Lu, Y.; Zhang, X.; Wang, F.; Zou, N. Classification of interference-fading tolerant Φ-OTDR signal using optimal peak-seeking and machine learning [Invited]. Chin. Opt. Lett. 2021, 19, 030601. [Google Scholar] [CrossRef]
- Ding, Z.; Wang, S.; Kang, J.; Zhao, C.; Zhang, Y. Distributed Acoustic Sensing-Based Weight Measurement Method. J. Light. Technol. 2024, 42, 3454–3460. [Google Scholar] [CrossRef]
- Tong, S.; Zhao, X.; Zhang, C.; Ding, C.; Ding, H.; Awan, I.N.; Zou, N.; Liu, H.; Xiong, F.; Zhang, Y.; et al. Research on PFN suppression methods in φ-OTDR systems based on the MSI-VPFN algorithm. Opt. Express 2024, 32, 47123–47136. [Google Scholar] [CrossRef]
- Ren, M.; Lu, P.; Chen, L.; Bao, X. Theoretical and Experimental Analysis of Φ-OTDR Based on Polarization Diversity Detection. IEEE Photonics Technol. Lett. 2015, 28, 697–700. [Google Scholar] [CrossRef]
- Xu-Ping, Z.; Yi-Xin, Z.; Feng, W.; Yuan-Yuan, S.; Zhen-Hong, S.; Yan-Zhu, H. The mechanism and suppression methods of optical background noise in phase-sensitive optical time domain reflectometry. Acta Phys. Sin. 2017, 66, 070707. [Google Scholar] [CrossRef]
- Zabihi, M.; Chen, Y.; Zhou, T.; Liu, J.; Shan, Y.; Meng, Z.; Wang, F.; Zhang, Y.; Zhang, X.; Chen, M. Continuous fading suppression method for Φ-OTDR systems using optimum tracking over multiple probe frequencies. J. Light. Technol. 2019, 37, 3602–3610. [Google Scholar] [CrossRef]
- Hu, Y.; Meng, Z.; Zabihi, M.; Shan, Y.; Fu, S.; Wang, F.; Zhang, X.; Zhang, Y.; Zeng, B. Performance Enhancement Methods for the Distributed Acoustic Sensors Based on Frequency Division Multiplexing. Electronics 2019, 8, 617. [Google Scholar] [CrossRef]
- Hartog, A.; Liokumovich, L.; Ushakov, N.; Kotov, O.; Dean, T.; Cuny, T.; Constantinou, A. The use of multi-frequency acquisition to significantly improve the quality of fibre-optic-distributed vibration sensing. Geophys. Prospect. 2018, 66, 192–202. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tong, S.; Tang, S.; Lu, Y.; Yuan, N.; Zhang, C.; Liu, H.; Zhang, D.; Zou, N.; Zhang, X.; Zhang, Y. A Fading Suppression Method for Φ-OTDR Systems Based on Multi-Domain Multiplexing. Sensors 2025, 25, 2629. https://doi.org/10.3390/s25082629
Tong S, Tang S, Lu Y, Yuan N, Zhang C, Liu H, Zhang D, Zou N, Zhang X, Zhang Y. A Fading Suppression Method for Φ-OTDR Systems Based on Multi-Domain Multiplexing. Sensors. 2025; 25(8):2629. https://doi.org/10.3390/s25082629
Chicago/Turabian StyleTong, Shuai, Shaoxiong Tang, Yifan Lu, Nuo Yuan, Chi Zhang, Huanhuan Liu, Dao Zhang, Ningmu Zou, Xuping Zhang, and Yixin Zhang. 2025. "A Fading Suppression Method for Φ-OTDR Systems Based on Multi-Domain Multiplexing" Sensors 25, no. 8: 2629. https://doi.org/10.3390/s25082629
APA StyleTong, S., Tang, S., Lu, Y., Yuan, N., Zhang, C., Liu, H., Zhang, D., Zou, N., Zhang, X., & Zhang, Y. (2025). A Fading Suppression Method for Φ-OTDR Systems Based on Multi-Domain Multiplexing. Sensors, 25(8), 2629. https://doi.org/10.3390/s25082629






