Stereo Online Self-Calibration Through the Combination of Hybrid Cost Functions with Shared Characteristics Considering Cost Uncertainty
Abstract
1. Introduction
- We propose a hybrid approach that combines cost functions with similar properties to play complementary roles, ensuring a consistent optimization direction. Specifically, we integrate cost functions with shared characteristics to achieve the y-axis alignment of corresponding points and enforce the epipolar constraints of the essential matrix in stereo rectification, considering cost uncertainty. This helps reduce the risk of overfitting and enhances generalization performance.
- For global optimization for multi-pair cases, particularly to minimize the spatiotemporal noise of corresponding points in stereo cameras, we propose a method that enhances generalized stability through a probabilistic spatial and temporal approach. This involves zero-shot-based semantic segmentation for a spatial probabilistic approach and Bayesian filtering to accumulate relationships between the current and previous frames for a temporal probabilistic approach.
- The weight of the corresponding points is based not only on the robustness of the feature characteristics but also on the geometry of the camera, using stereo disparity information. This approach is grounded in the fact that, in the perspective view, the area occupied by distant data is significantly smaller than that of nearby data. Therefore, it is proposed that as the pseudo-depth error in stereo geometry increases, the weight of the corresponding points decreases.
2. Related Works
3. Methodology
3.1. Prerequisites
3.2. Cost Functions with Shared Characteristics
3.3. Hybrid Nonlinear Optimization
3.4. Spatiotemporal Filtering for Multi-Pair Cases
4. Experimental Results
4.1. Theoretical Feasibility
| Algorithm 1 Hybrid nonlinear optimization. |
- We fixed the right camera as a reference and conducted quantitative performance tests by adjusting the left camera at different angles while increasing the outlier ratio.
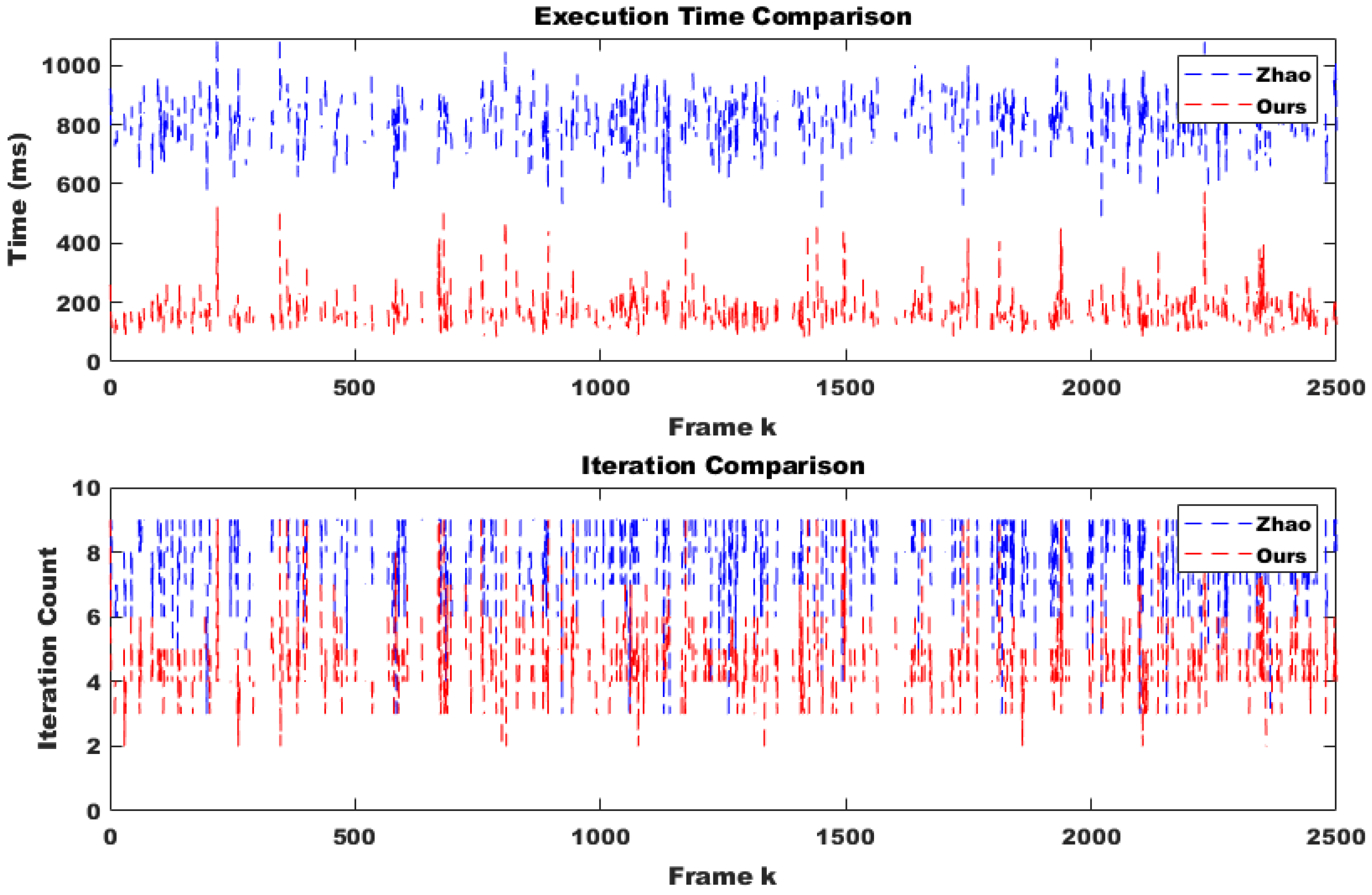
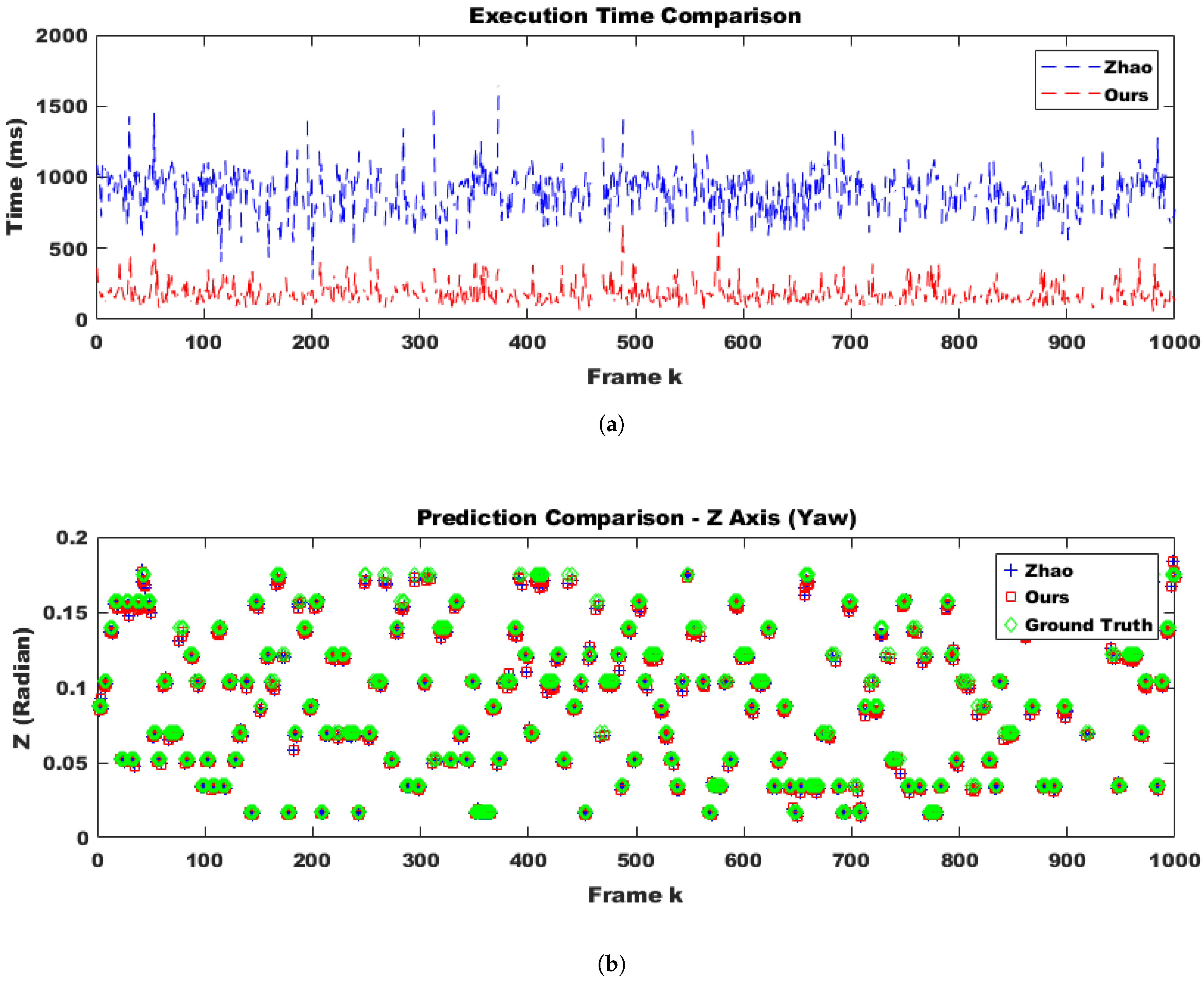
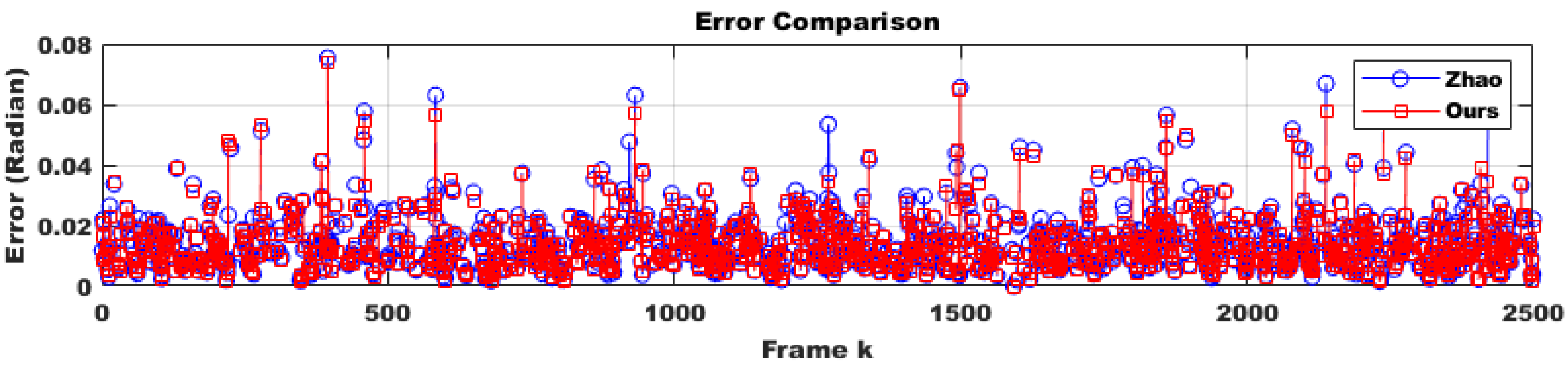
- The number of optimization iterations was quantitatively analyzed compared to Hongbo Zhao’s algorithm, and the appropriateness of cost reduction was verified.
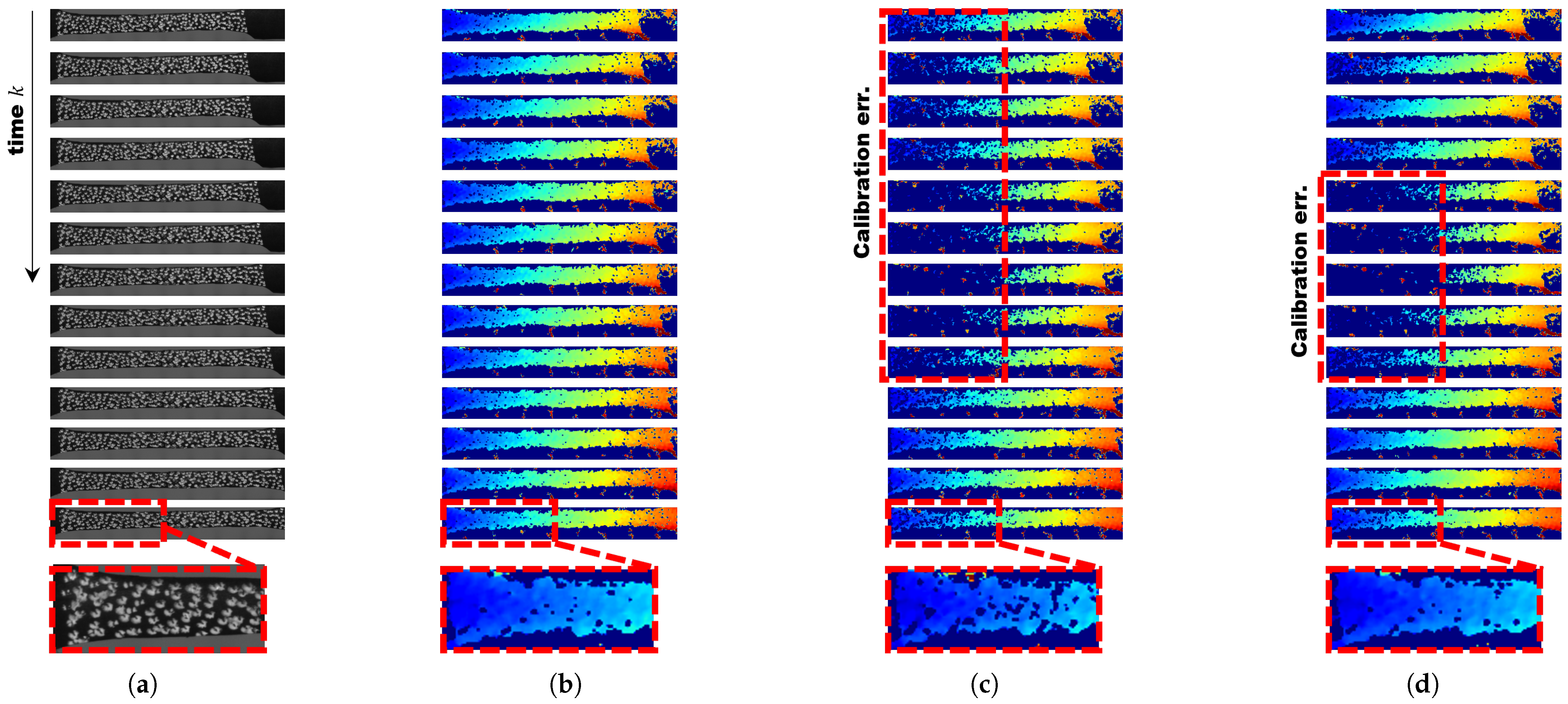
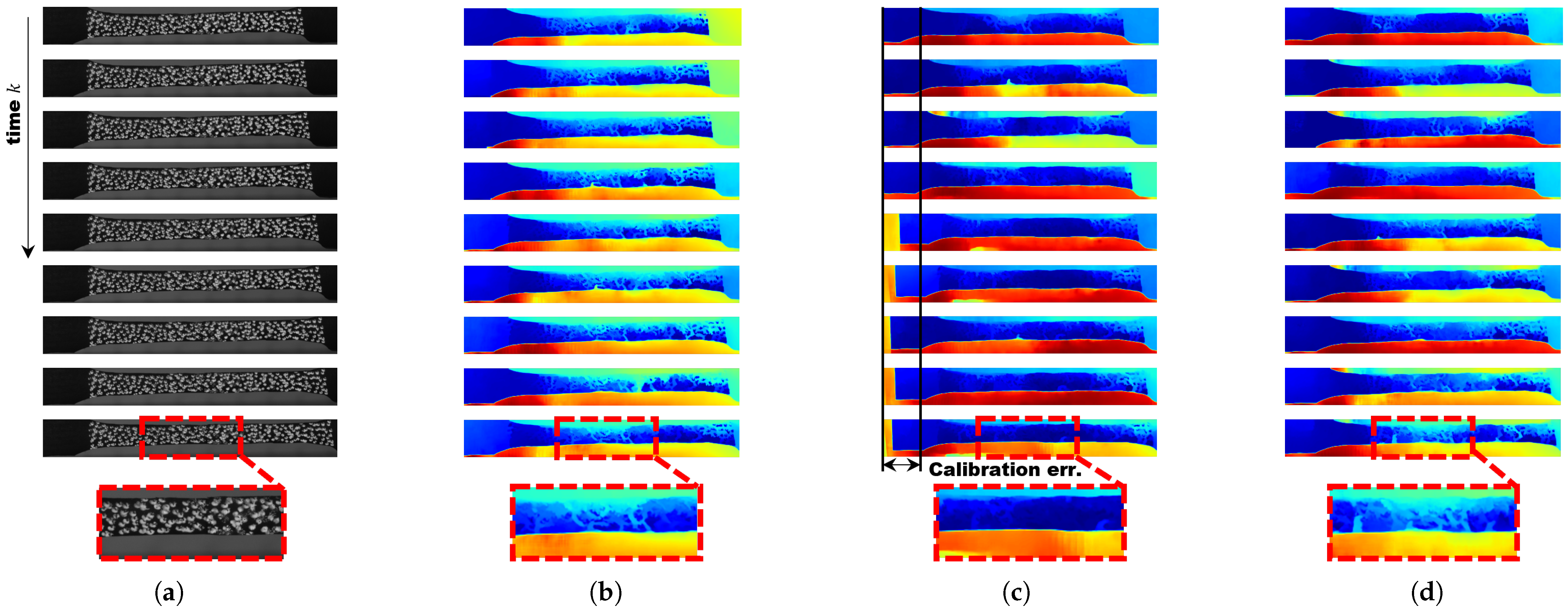
- To evaluate the performance of spatiotemporal filtering, qualitative measurements of temporal variations were conducted using fragmentation simulations.
- Using stress–strain analysis data, a qualitative evaluation of disparity estimation was performed in comparison with Hongbo Zhao’s algorithm.
4.1.1. Quantitative Evaluation of Extrinsic Parameter Estimation
4.1.2. Convergence Speed Evaluation
- One-tailed p-value: 0.2722 → This meant that under the null hypothesis, the probability of obtaining the observed value or a more extreme one was 27.22%. Since this value was greater than 0.05, there was insufficient evidence to reject the null hypothesis.
- Two-tailed p-value: 0.5445 → This meant that the probability of obtaining an equally extreme value in either direction was 54.45%, which was much higher than 0.05. This further confirmed that the result was not statistically significant.
- One-tailed p-value: 0.0031 → This meant that the probability of obtaining a more extreme value under the null hypothesis was 0.31%, which was much smaller than 0.05. Thus, the result was statistically significant, providing strong evidence to reject the null hypothesis and accept the alternative hypothesis.
- Two-tailed p-value: 0.0061 → This meant that the probability of obtaining an equally extreme value in either direction was 0.61%, which was also much smaller than 0.05. Again, this confirmed statistical significance and supported rejecting the null hypothesis.
4.1.3. Qualitative Experimental Results
4.2. Deployment Considerations
4.2.1. Problem Simplification for Low Complexity
- Number of addition operators (+): (vs. Hongbo Zhao: 2).
- Number of subtraction operators (−): (vs. Hongbo Zhao: 22).
- Number of multiplication operators (∗): (vs. Hongbo Zhao: 52).
- Number of division operators (/): (vs. Hongbo Zhao: 7).
- Number of matrix multiplication operators (@): (vs. Hongbo Zhao: 31).
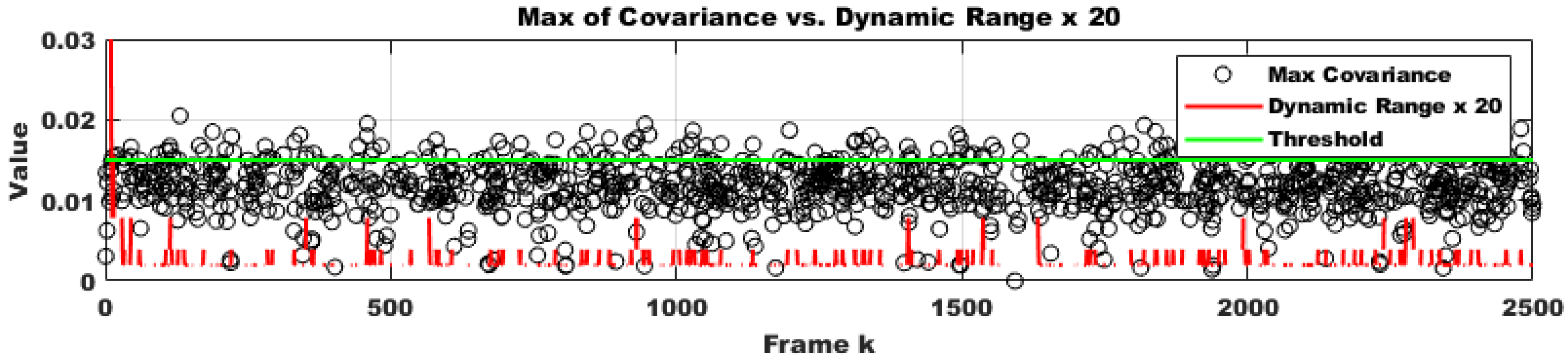
4.2.2. Covariance-Based Search Space Reduction for Initial Guesses
- Compute the Jacobian of the error from the previous frame’s optimization result.
- Approximate the parameter covariance as the Jacobian of the error to define the confidence interval.
- Define rules for the dynamic adjustment of the range for the current initial value.
- Iteratively reduce the range using dynamic updates.
| Algorithm 2 Covariance-based search space reduction for initial guesses. |
|
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 22, 1330–1334. [Google Scholar] [CrossRef]
- Kannala, J.; Brandt, S.S. A generic camera model and calibration method for conventional, wide-angle, and fish-eye lenses. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1335–1340. [Google Scholar] [CrossRef] [PubMed]
- Nakano, G. Camera calibration using parallel line segments. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 1505–1512. [Google Scholar]
- Fu, W.; Wu, L. Camera calibration based on improved differential evolution particle swarm. Meas. Control 2023, 56, 27–33. [Google Scholar] [CrossRef]
- Hao, Y.; Tai, V.C.; Tan, Y.C. A systematic stereo camera calibration strategy: Leveraging latin hypercube sampling and 2k full-factorial design of experiment methods. Sensors 2023, 23, 8240. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Zheng, H.; Zhang, X. A robust checkerboard corner detection method for camera calibration based on improved YOLOX. Front. Phys. 2022, 9, 819019. [Google Scholar] [CrossRef]
- Jeon, M.; Park, J.; Kim, J.W.; Woo, S. Triple-Camera Rectification for Depth Estimation Sensor. Sensors 2024, 24, 6100. [Google Scholar] [CrossRef] [PubMed]
- Wong, E.; Humphrey, I.; Switzer, S.; Crutchfield, C.; Hui, N.; Schurgers, C.; Kastner, R. Underwater depth calibration using a commercial depth camera. In Proceedings of the 16th International Conference on Underwater Networks & Systems, Boston, MA, USA, 14–16 November 2022; pp. 1–5. [Google Scholar]
- Yang, M. Research on depth measurement calibration of light field camera based on Gaussian fitting. Sci. Rep. 2024, 14, 8774. [Google Scholar] [CrossRef] [PubMed]
- Lopez, M.; Mari, R.; Gargallo, P.; Kuang, Y.; Gonzalez-Jimenez, J.; Haro, G. Deep single image camera calibration with radial distortion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11817–11825. [Google Scholar]
- Zhang, C.; Rameau, F.; Kim, J.; Argaw, D.M.; Bazin, J.C.; Kweon, I.S. Deepptz: Deep self-calibration for ptz cameras. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Village, CO, USA, 1–5 March 2020; pp. 1041–1049. [Google Scholar]
- Fang, J.; Vasiljevic, I.; Guizilini, V.; Ambrus, R.; Shakhnarovich, G.; Gaidon, A.; Walter, M.R. Self-supervised camera self-calibration from video. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 8468–8475. [Google Scholar]
- Hagemann, A.; Knorr, M.; Stiller, C. Deep geometry-aware camera self-calibration from video. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 3438–3448. [Google Scholar]
- Dexheimer, E.; Peluse, P.; Chen, J.; Pritts, J.; Kaess, M. Information-theoretic online multi-camera extrinsic calibration. IEEE Robot. Autom. Lett. 2022, 7, 4757–4764. [Google Scholar] [CrossRef]
- Tsaregorodtsev, A.; Muller, J.; Strohbeck, J.; Herrmann, M.; Buchholz, M.; Belagiannis, V. Extrinsic camera calibration with semantic segmentation. In Proceedings of the 2022 IEEE 25th International Conference on Intelligent Transportation Systems (ITSC), Macau, China, 8–12 October 2022; pp. 3781–3787. [Google Scholar]
- Kanai, T.; Vasiljevic, I.; Guizilini, V.; Gaidon, A.; Ambrus, R. Robust self-supervised extrinsic self-calibration. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 1932–1939. [Google Scholar]
- Luo, Z.; Yan, G.; Cai, X.; Shi, B. Zero-training lidar-camera extrinsic calibration method using segment anything model. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 14472–14478. [Google Scholar]
- Kirillov, A.; Mintun, E.; Ravi, N.; Mao, H.; Rolland, C.; Gustafson, L.; Xiao, T.; Whitehead, S.; Berg, A.C.; Lo, W.Y.; et al. Segment anything. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 4015–4026. [Google Scholar]
- Song, J.G.; Lee, J.W. A CNN-based online self-calibration of binocular stereo cameras for pose change. IEEE Trans. Intell. Veh. 2023, 9, 2542–2552. [Google Scholar] [CrossRef]
- D’Amicantonio, G.; Bondarev, E. Automated camera calibration via homography estimation with gnns. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 4–8 January 2024; pp. 5876–5883. [Google Scholar]
- Zhao, H.; Zhang, Y.; Chen, Q.; Fan, R. Dive deeper into rectifying homography for stereo camera online self-calibration. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 14479–14485. [Google Scholar]
- Ling, Y.; Shen, S. High-precision online markerless stereo extrinsic calibration. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Republic of Korea, 9–14 October 2016; pp. 1771–1778. [Google Scholar]
- Kendall, A.; Gal, Y.; Cipolla, R. Multi-task learning using uncertainty to weigh losses for scene geometry and semantics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7482–7491. [Google Scholar]
- Solav, D.; Silverstein, A. Duodic: 3d digital image correlation in Matlab. J. Open Source Softw. 2022, 7, 4279. [Google Scholar] [CrossRef]
- Menze, M.; Heipke, C.; Geiger, A. Joint 3D Estimation of Vehicles and Scene Flow. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 427–434. [Google Scholar] [CrossRef]
- Menze, M.; Heipke, C.; Geiger, A. Object Scene Flow. ISPRS J. Photogramm. Remote Sens. (JPRS) 2018, 140, 60–76. [Google Scholar] [CrossRef]
- Schöps, T.; Schönberger, J.L.; Galliani, S.; Sattler, T.; Schindler, K.; Pollefeys, M.; Geiger, A. A Multi-View Stereo Benchmark with High-Resolution Images and Multi-Camera Videos. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Scharstein, D.; Hirschmüller, H.; Kitajima, Y.; Krathwohl, G.; Nešić, N.; Wang, X.; Westling, P. High-resolution stereo datasets with subpixel-accurate ground truth. In Proceedings of the Pattern Recognition: 36th German Conference, GCPR 2014, Münster, Germany, 2–5 September 2014; Proceedings 36. Springer: Cham, Switzerland, 2014; pp. 31–42. [Google Scholar]
- Hirschmuller, H. Accurate and efficient stereo processing by semi-global matching and mutual information. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 807–814. [Google Scholar]
- Lipson, L.; Teed, Z.; Deng, J. Raft-stereo: Multilevel recurrent field transforms for stereo matching. In Proceedings of the 2021 International Conference on 3D Vision (3DV), London, UK, 1–3 December 2021; pp. 218–227. [Google Scholar]
- Wen, B.; Trepte, M.; Aribido, J.; Kautz, J.; Gallo, O.; Birchfield, S. FoundationStereo: Zero-Shot Stereo Matching. arXiv 2025, arXiv:2501.09898. [Google Scholar]





| Scenario | Outlier Ratio | Algorithm | 0 deg. | 1 deg. | 2 deg. | 3 deg. | 4 deg. | 5 deg. | 6 deg. | 7 deg. | 8 deg. | 9 deg. | Mean ↓ | Std. ↓ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Indoor | 0% | [21] | 0.1532 | 0.0722 | 0.1596 | 0.1105 | 0.1282 | 0.1421 | 0.1356 | 0.1222 | 0.1369 | 0.1531 | 0.1314 | 0.0257 |
| Ours | 0.0373 | 0.0251 | 0.0400 | 0.0301 | 0.0339 | 0.0409 | 0.0377 | 0.0351 | 0.0375 | 0.0436 | 0.0361 | 0.0054 | ||
| 10% | [21] | 0.1998 | 0.0881 | 0.2031 | 0.1373 | 0.1170 | 0.1730 | 0.1282 | 0.1087 | 0.1286 | 0.1295 | 0.1413 | 0.0383 | |
| Ours | 0.0511 | 0.0294 | 0.0451 | 0.0384 | 0.0444 | 0.0649 | 0.0446 | 0.0393 | 0.0426 | 0.0434 | 0.0443 | 0.0091 | ||
| 20% | [21] | 0.2266 | 0.0903 | 0.1889 | 0.1448 | 0.1536 | 0.2245 | 0.0976 | 0.1719 | 0.1378 | 0.1317 | 0.1568 | 0.0468 | |
| Ours | 0.0494 | 0.0309 | 0.0436 | 0.0487 | 0.0531 | 0.0707 | 0.0488 | 0.0457 | 0.0468 | 0.0472 | 0.0485 | 0.0097 | ||
| 30% | [21] | 0.2474 | 0.1562 | 0.1943 | 0.1641 | 0.1702 | 0.2441 | 0.1110 | 0.1315 | 0.1467 | 0.1250 | 0.1690 | 0.0469 | |
| Ours | 0.0469 | 0.0335 | 0.0440 | 0.0517 | 0.0558 | 0.0746 | 0.0544 | 0.0494 | 0.0509 | 0.0526 | 0.0514 | 0.0103 | ||
| 40% | [21] | 0.2696 | 0.1709 | 0.2418 | 0.1593 | 0.1849 | 0.2751 | 0.2733 | 0.1574 | 0.1609 | 0.1383 | 0.2031 | 0.0551 | |
| Ours | 0.0492 | 0.0353 | 0.0454 | 0.0539 | 0.0578 | 0.0777 | 0.0587 | 0.0524 | 0.0565 | 0.0572 | 0.0544 | 0.0108 | ||
| 50% | [21] | 0.2060 | 0.1738 | 0.2653 | 0.1709 | 0.1946 | 0.2341 | 0.3000 | 0.1617 | 0.1749 | 0.1699 | 0.2051 | 0.0468 | |
| Ours | 0.0506 | 0.0372 | 0.0469 | 0.0571 | 0.0566 | 0.0816 | 0.0624 | 0.0575 | 0.0601 | 0.0604 | 0.0570 | 0.0115 | ||
| Outdoor | 0% | [21] | 0.0016 | 0.0030 | 0.0037 | 0.0024 | 0.0026 | 0.0019 | 0.0030 | 0.0022 | 0.0030 | 0.0036 | 0.0027 | 0.0006 |
| Ours | 0.0014 | 0.0031 | 0.0036 | 0.0025 | 0.0028 | 0.0018 | 0.0030 | 0.0020 | 0.0029 | 0.0034 | 0.0026 | 0.0007 | ||
| 10% | [21] | 0.0060 | 0.0033 | 0.0035 | 0.0025 | 0.0031 | 0.0125 | 0.0122 | 0.0089 | 0.0140 | 0.0127 | 0.0079 | 0.0046 | |
| Ours | 0.0066 | 0.0029 | 0.0036 | 0.0025 | 0.0033 | 0.0127 | 0.0128 | 0.0096 | 0.0148 | 0.0142 | 0.0083 | 0.0050 | ||
| 20% | [21] | 0.0085 | 0.0068 | 0.0059 | 0.0072 | 0.0044 | 0.0105 | 0.0109 | 0.0113 | 0.0195 | 0.0209 | 0.0106 | 0.0055 | |
| Ours | 0.0082 | 0.0057 | 0.0056 | 0.0064 | 0.0038 | 0.0105 | 0.0111 | 0.0113 | 0.0184 | 0.0190 | 0.0100 | 0.0052 | ||
| 30% | [21] | 0.0190 | 0.0127 | 0.0093 | 0.0115 | 0.0078 | 0.0088 | 0.0080 | 0.0119 | 0.0227 | 0.0187 | 0.0130 | 0.0052 | |
| Ours | 0.0178 | 0.0112 | 0.0083 | 0.0101 | 0.0070 | 0.0086 | 0.0075 | 0.0116 | 0.0203 | 0.0179 | 0.0120 | 0.0048 | ||
| 40% | [21] | 0.0347 | 0.0251 | 0.0167 | 0.0176 | 0.0107 | 0.0075 | 0.0071 | 0.0092 | 0.0207 | 0.0164 | 0.0166 | 0.0086 | |
| Ours | 0.0354 | 0.0237 | 0.0150 | 0.0152 | 0.0096 | 0.0073 | 0.0068 | 0.0094 | 0.0186 | 0.0167 | 0.0158 | 0.0087 | ||
| 50% | [21] | 0.0448 | 0.0361 | 0.0230 | 0.0215 | 0.0137 | 0.0074 | 0.0077 | 0.0074 | 0.0182 | 0.0139 | 0.0194 | 0.0126 | |
| Ours | 0.0459 | 0.0354 | 0.0210 | 0.0195 | 0.0124 | 0.0070 | 0.0074 | 0.0075 | 0.0171 | 0.0147 | 0.0188 | 0.0127 |
| Scenario | Outlier Ratio | Algorithm | 0∼1 deg. | 2∼3 deg. | 4∼5 deg. | 6∼7 deg. | 8∼9 deg. | Mean ↓ | Std. ↓ | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| # of iter. | Cost | # of iter. | Cost | # of iter. | Cost | # of iter. | Cost | # of iter. | Cost | # of iter. | Cost | # of iter. | Cost | |||
| Indoor | 0∼10% | [21] | 14.8 | 0.0008 | 17.1 | 0.0009 | 15.1 | 0.0009 | 14.8 | 0.0010 | 15.0 | 0.0010 | 15.3 | 0.0009 | 0.9836 | |
| ours | 16.1 | 0.0004 | 15.5 | 0.0005 | 16.1 | 0.0006 | 16.2 | 0.0005 | 16.7 | 0.0005 | 16.1 | 0.0005 | 0.4454 | |||
| 20∼30% | [21] | 19.1 | 0.0015 | 18.4 | 0.0017 | 13.5 | 0.0018 | 16.3 | 0.0019 | 14.6 | 0.0018 | 16.4 | 0.0017 | 2.4045 | 0.0001 | |
| ours | 15.5 | 0.0007 | 15.2 | 0.0010 | 15.8 | 0.0012 | 16.1 | 0.0011 | 16.3 | 0.0009 | 15.8 | 0.0010 | 0.4668 | 0.0001 | ||
| 40∼50% | [21] | 21.7 | 0.0017 | 13.5 | 0.0019 | 14.1 | 0.0021 | 17.1 | 0.0022 | 13.8 | 0.0021 | 16.1 | 0.0020 | 3.4648 | 0.0001 | |
| ours | 15.5 | 0.0008 | 15.4 | 0.0010 | 15.3 | 0.0013 | 16.3 | 0.0013 | 16.7 | 0.0011 | 15.8 | 0.0011 | 0.6364 | 0.0002 | ||
| Outdoor | 0∼10% | [21] | 14.7 | 0.0030 | 14.3 | 0.0040 | 14.7 | 0.0039 | 14.3 | 0.0043 | 13.5 | 0.0046 | 14.3 | 0.0040 | 0.4853 | 0.0006 |
| ours | 16.4 | 0.0023 | 15.0 | 0.0032 | 15.4 | 0.0031 | 16.0 | 0.0034 | 19.4 | 0.0036 | 16.5 | 0.0031 | 1.7508 | 0.0005 | ||
| 20∼30% | [21] | 12.6 | 0.0054 | 12.6 | 0.0071 | 12.8 | 0.0072 | 11.5 | 0.0076 | 11.3 | 0.0080 | 12.2 | 0.0071 | 0.6855 | 0.0010 | |
| ours | 14.3 | 0.0042 | 10.9 | 0.0057 | 11.2 | 0.0058 | 11.2 | 0.0062 | 12.4 | 0.0065 | 12.0 | 0.0057 | 1.4131 | 0.0009 | ||
| 40∼50% | [21] | 10.4 | 0.0072 | 12.5 | 0.0084 | 12.7 | 0.0079 | 11.8 | 0.0082 | 11.7 | 0.0084 | 11.8 | 0.0080 | 0.9115 | 0.0005 | |
| ours | 12.4 | 0.0058 | 11.4 | 0.0067 | 11.4 | 0.0062 | 11.8 | 0.0066 | 12.4 | 0.0067 | 11.9 | 0.0064 | 0.5184 | 0.0004 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, W. Stereo Online Self-Calibration Through the Combination of Hybrid Cost Functions with Shared Characteristics Considering Cost Uncertainty. Sensors 2025, 25, 2565. https://doi.org/10.3390/s25082565
Lee W. Stereo Online Self-Calibration Through the Combination of Hybrid Cost Functions with Shared Characteristics Considering Cost Uncertainty. Sensors. 2025; 25(8):2565. https://doi.org/10.3390/s25082565
Chicago/Turabian StyleLee, Wonju. 2025. "Stereo Online Self-Calibration Through the Combination of Hybrid Cost Functions with Shared Characteristics Considering Cost Uncertainty" Sensors 25, no. 8: 2565. https://doi.org/10.3390/s25082565
APA StyleLee, W. (2025). Stereo Online Self-Calibration Through the Combination of Hybrid Cost Functions with Shared Characteristics Considering Cost Uncertainty. Sensors, 25(8), 2565. https://doi.org/10.3390/s25082565





