Distributed Secure Economic Dispatch Strategy Based on Robust Graph Theory and W-MSR Algorithm
Abstract
1. Introduction
- (1)
- Attack detection and isolation methods are widely adopted in the research on information security for distributed economic dispatch. Although these methods are effective to some extent, the isolation of nodes may lead to the infringement of individual rights or impair the system’s power generation capability. Therefore, it is necessary to develop an algorithm that can resist attacks without isolating nodes, ensuring both the information security and system stability of distributed economic dispatch.
- (2)
- In distributed systems, traditional methods typically rely on network connectivity to measure system convergence. However, in scenarios where network topology dynamically switches, the implementation of such methods faces significant challenges. Additionally, in distributed modes, it is difficult to provide the global network information required for calculating connectivity. Therefore, it is essential to explore new analytical methods to more effectively analyze the communication network topology of distributed systems.
2. Attack Modes and Their Impacts on a Distributed Dispatch System
2.1. Structure of the Distributed Economic Dispatch System
2.2. Node Attack Models
2.3. Influences of the Attacks
3. Secure Dispatch Strategy Based on W-MSR Algorithm
3.1. Consensus Algorithm
3.2. W-MSR Algorithm
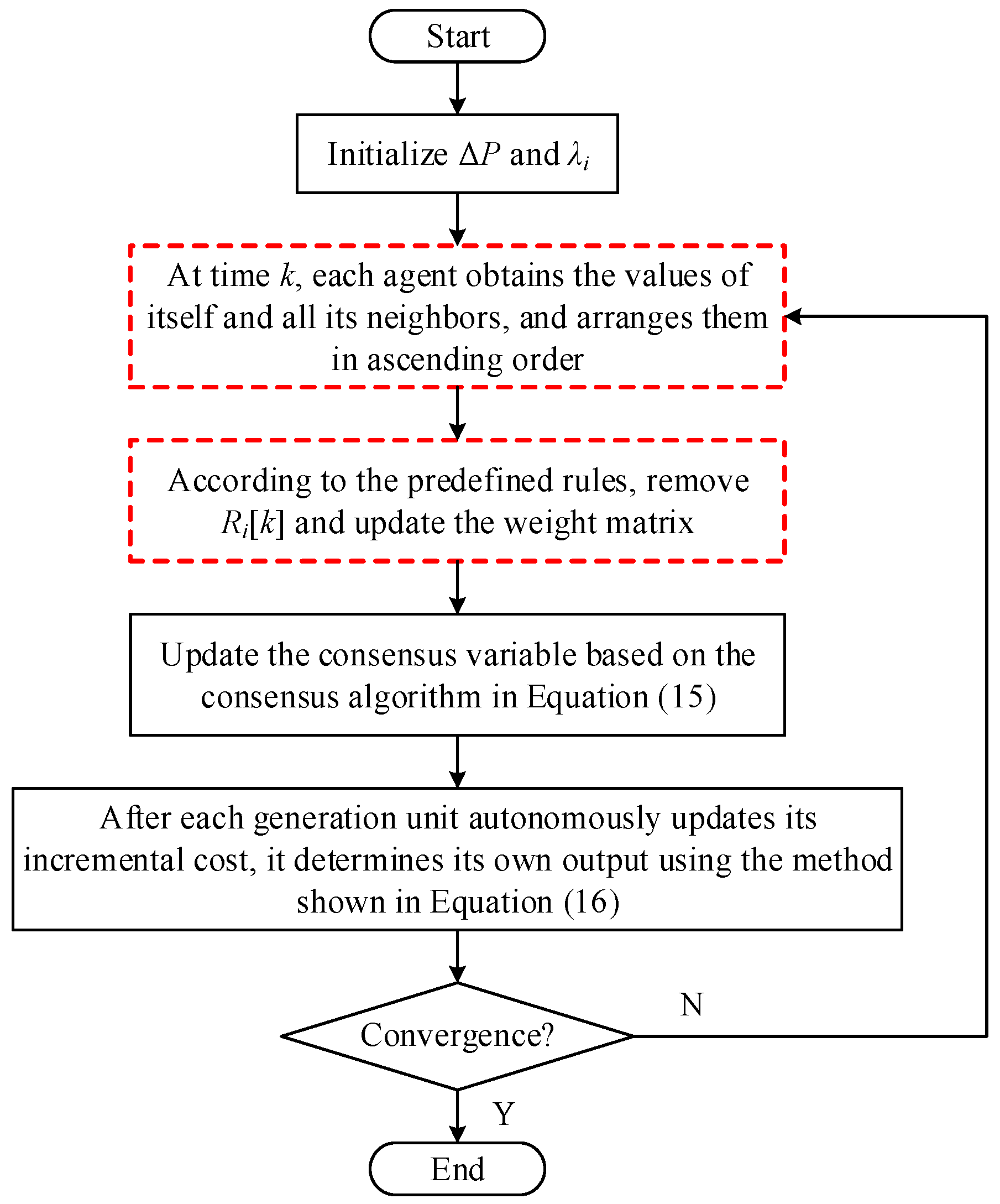
- Node i obtains the data for itself and all of its neighbors at cycle k and arranges them by size.
- If there are less than F neighbors strictly greater than its own value xi[k], then all values strictly greater than itself must be removed. Otherwise, the first F maximum values shall be removed. Similarly, if there are less than F neighbors strictly less than its own value xi[k], then all values strictly less than itself must be removed. Otherwise, F minimums must be ignored.
- Let Ri[k] represent the set of neighbors removed by node i in Step 2, and the state update role of node i is modified to the following:
3.3. Distributed Secure and Economic Dispatch Strategy
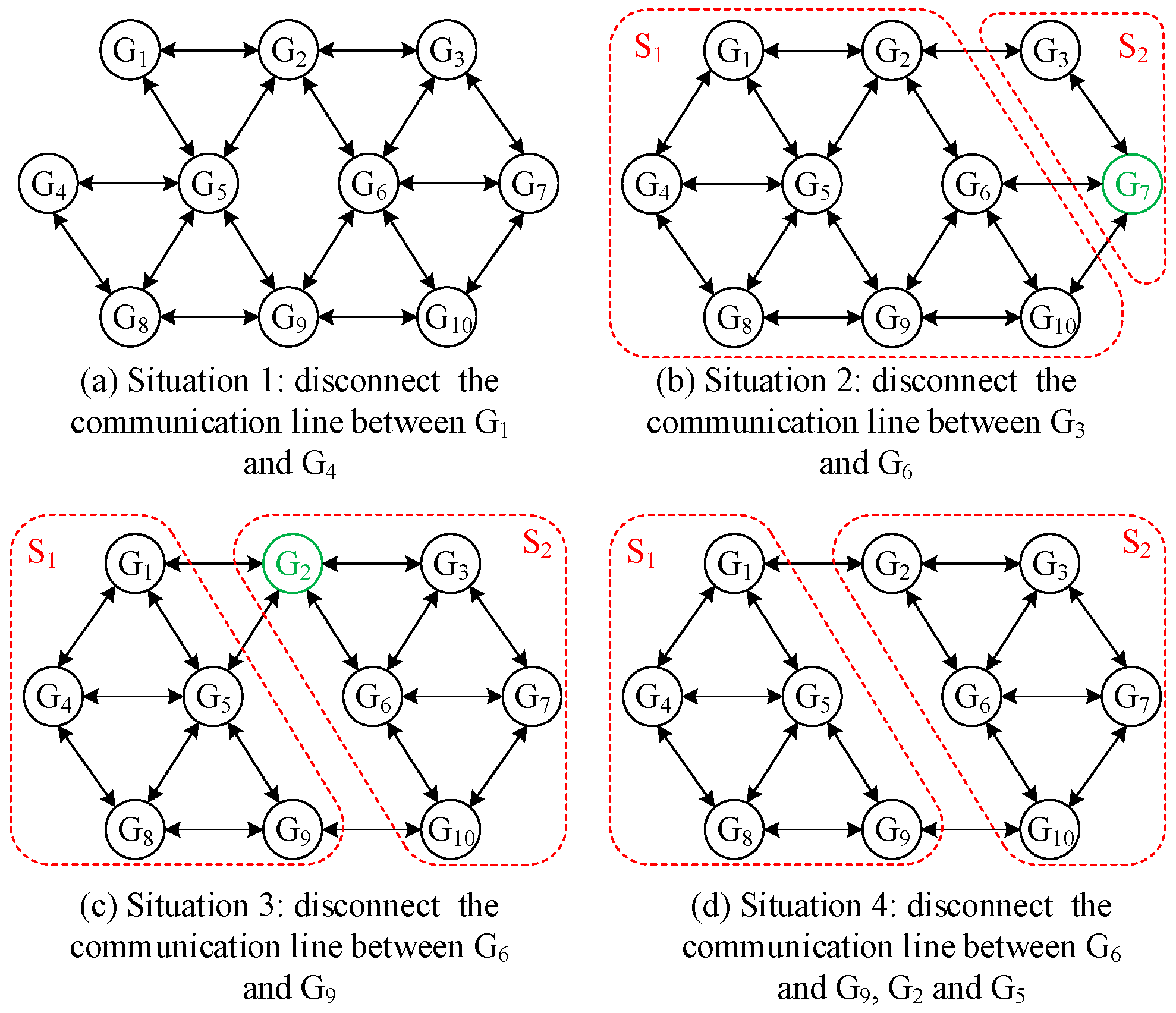
4. Topology Analysis of Communication Network Based on a Robust Graph
5. Simulation Verification
5.1. Configuration of the Dispatch System
5.2. Analysis of the System with 10 Distributed Generation Units
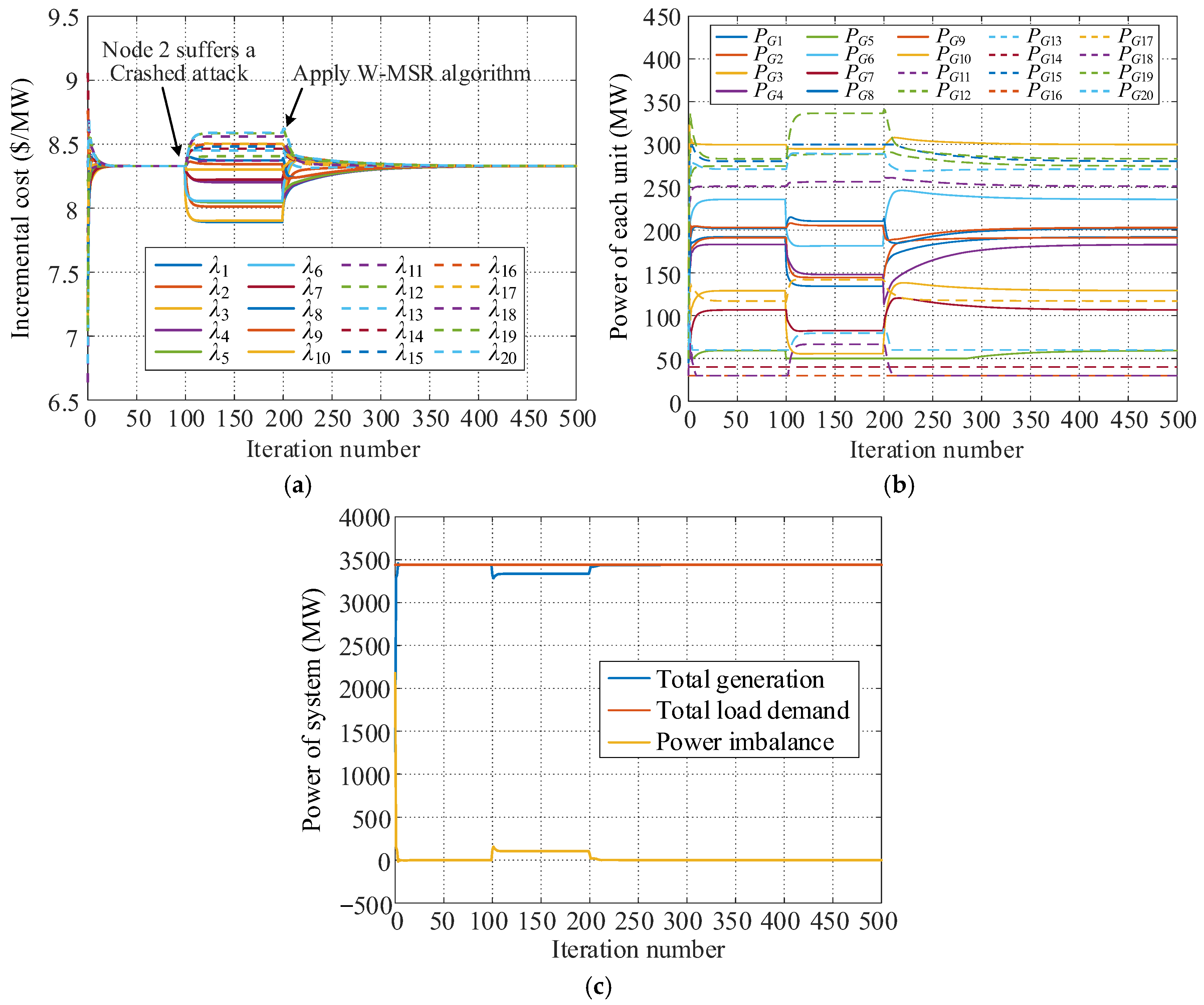
5.2.1. Simulation for Crashed Attack
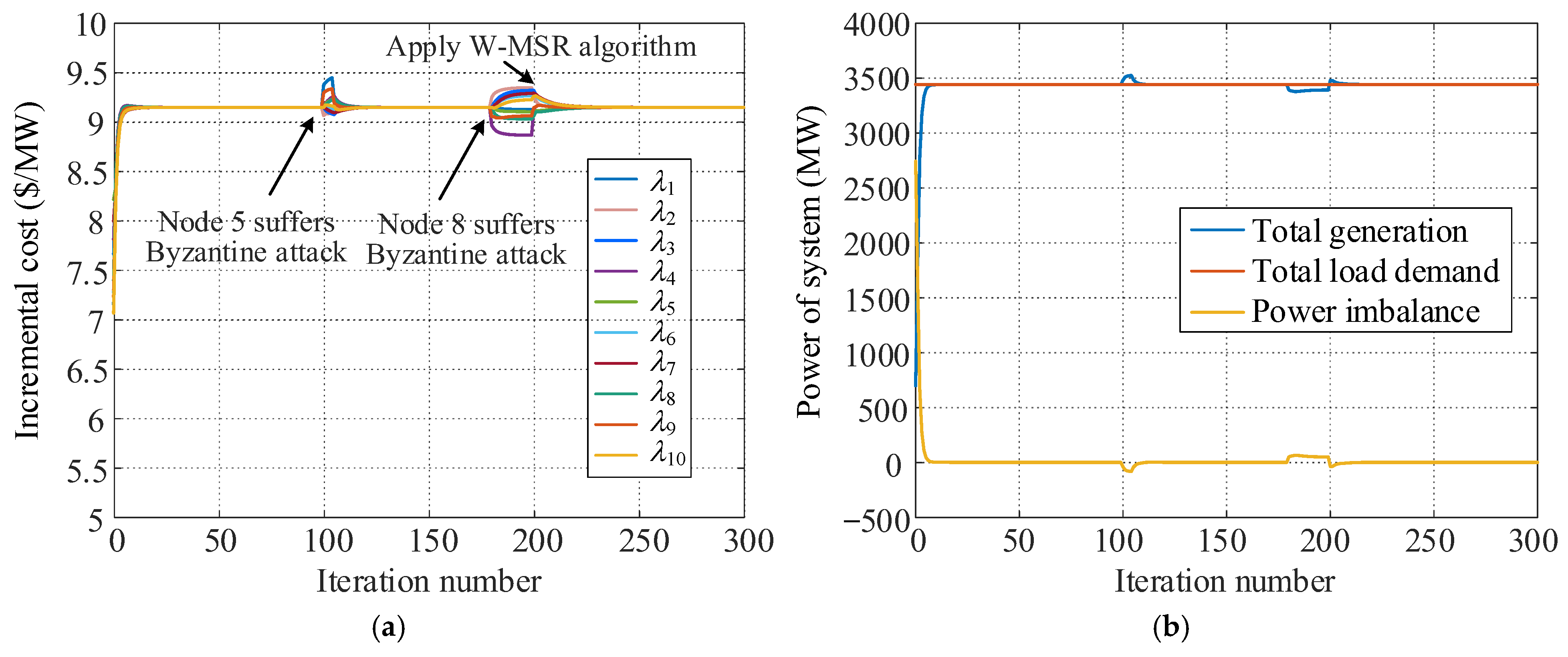
5.2.2. Simulation for Byzantine Attack
5.3. Analysis of the System with 20 Distributed Generation Units
5.3.1. Simulation for Crashed Attack
5.3.2. Simulation for Byzantine Attack
5.4. Comparative Analysis of Case Study Results
5.5. Verification of Sufficient and Necessary Conditions of Communication Network Topology
6. Conclusions
- (1)
- The distributed dispatch strategy designed in this paper, based on the W-MSR algorithm, can withstand various modes of node information attacks. It ensures that the system re-establishes power balance and operates stably at the optimal value after suffering node attacks, effectively enhancing both the security and economic efficiency of the distributed economic dispatch system.
- (2)
- The robustness of the network is suitable for measuring the performance of the communication network with an induced switching topology.
- (3)
- The condition that the communication network topology of the distributed economic dispatch system is an (F + 1, F + 1)-robust graph, which is the necessary and sufficient condition for implementing the W-MSR algorithm, provides a basis for designing a communication network for a distributed secure and economic dispatch system.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Zhang, C.; Wu, L.; Tong, Z. Economic Optimal Dispatching of Microgrid Based on Improved Finite Time Consistency. In Proceedings of the CSU-EPSA, Cologne, Germany, 4–6 July 2024; Volume 36, pp. 38–48. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Y.; Li, Z.; Jiang, T.; Li, X. Two-Stage Robust Operation of Electricity-Gas-Heat Integrated Multi-Energy Microgrids Considering Heterogeneous Uncertainties. Appl. Energy 2024, 371, 123690. [Google Scholar] [CrossRef]
- Zheng, X.; Khodayar, M.E.; Wang, J.; Yue, M.; Zhou, A. Distributionally Robust Multistage Dispatch with Discrete Recourse of Energy Storage Systems. IEEE Trans. Power Syst. 2024, 39, 6960–6973. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, X.; Zhang, W. An Improved Reinforcement Learning-Based Differential Evolution Algorithm for Combined Economic and Emission Dispatch Problems. Eng. Appl. Artif. Intell. 2025, 140, 109709. [Google Scholar] [CrossRef]
- Bai, C.; Li, Q.; Zhou, W.; Li, B.; Yin, X.; Tan, Y. Weighted Matrix Based Distributed Optimization Method for Economic Dispatch of Microgrids via Multi-Step Gradient Descent. Energy Rep. 2022, 8, 177–187. [Google Scholar] [CrossRef]
- Chen, G.; Yang, Q. An ADMM-Based Distributed Algorithm for Economic Dispatch in Islanded Microgrids. IEEE Trans. Ind. Inform. 2018, 14, 3892–3903. [Google Scholar] [CrossRef]
- Chen, Z.; Guo, C.; Dong, S.; Ding, Y.; Mao, H. Distributed Robust Dynamic Economic Dispatch of Integrated Transmission and Distribution Systems. IEEE Trans. Ind. Appl. 2021, 57, 4500–4512. [Google Scholar] [CrossRef]
- Yang, F.; Cao, J.; Ye, L.; Li, D.; Lin, S.; Zhao, Y.; Shen, Y. Incremental Cost Based Hierarchical Distributed Control Strategy for AC/DC Hybrid Microgrid. Autom. Electr. Power Syst. 2024, 48, 199–207. [Google Scholar]
- Lin, L.; Jia, Q.; Tian, S.; Liang, J.; Li, T.; Cheng, Z. Distributed Harmonic Mitigation Strategy of Distribution Network Based on Consensus Algorithm. Autom. Electr. Power Syst. 2022, 46, 109–117. [Google Scholar]
- Mao, Y.; Yu, X. A Hybrid Forecasting Approach for China’s National Carbon Emission Allowance Prices with Balanced Accuracy and Interpretability. J. Environ. Manag. 2024, 351, 119873. [Google Scholar] [CrossRef]
- Hennane, Y.; Berdai, A.; Pierfederici, S.; Meibody-Tabar, F. A Consensus-Based Control for Precise Reactive Power-Sharing in AC Microgrids. Sustain. Energy Technol. Assess. 2023, 60, 103510. [Google Scholar] [CrossRef]
- Wang, R.; Li, Q.; Zhang, B.; Wang, L. Distributed Consensus Based Algorithm for Economic Dispatch in a Microgrid. IEEE Trans. Smart Grid 2019, 10, 3630–3640. [Google Scholar] [CrossRef]
- Wu, X.; Sun, Y.; Wei, Z.; Sun, G. Distributed Hierarchical Consensus Algorithm for Economic Dispatch in Smart Grid. IET Gener. Transm. Distrib. 2019, 13, 5541–5549. [Google Scholar] [CrossRef]
- Le, J.; Zhou, Q.; Zhao, L.; Wang, Y. Research on the Real-Time Distributed Economic Dispatch Strategy for Microgrids. Energies 2019, 12, 4007. [Google Scholar] [CrossRef]
- He, Y.; Wang, W.; Wu, X. Multi-Agent Based Fully Distributed Economic Dispatch in Microgrid Using Exact Diffusion Strategy. IEEE Access 2020, 8, 7020–7031. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, Y.; Mondal, S.; Gupta, A.K. A Transfer Learning-Based Method for Cyber-Attack Tolerance in Distributed Control of Microgrids. IEEE Trans. Smart Grid 2024, 15, 1258–1270. [Google Scholar] [CrossRef]
- Liu, L.; Song, H.; Piao, X.; Wang, S.; Qu, Y. Data Protection of Distributed Economic Dispatch Based on Blockchain. Electr. Power Inf. Commun. Technol. 2022, 20, 44–52. [Google Scholar] [CrossRef]
- Huang, C.; Wang, J.; Deng, S.; Yue, D. Real-Time Distributed Economic Dispatch Scheme of Grid-Connected Microgrid Considering Cyberattacks. IET Renew. Power Gener. 2020, 14, 2750–2758. [Google Scholar] [CrossRef]
- Liu, J.; Wang, C.; Liu, J.; Xie, P. Attack Resilient Strategy for Event-Triggered Distributed Control Scheme of Multi-Energy Systems. J. Frankl. Inst. 2023, 360, 5333–5353. [Google Scholar] [CrossRef]
- Zhao, C.; He, J.; Wang, Q.-G. Resilient Distributed Optimization Algorithm Against Adversarial Attacks. IEEE Trans. Autom. Control 2020, 65, 4308–4315. [Google Scholar] [CrossRef]
- Dibaji, S.M.; Ishii, H. Consensus of Second-Order Multi-Agent Systems in the Presence of Locally Bounded Faults. Syst. Control Lett. 2015, 79, 23–29. [Google Scholar] [CrossRef]
- LeBlanc, H.J.; Zhang, H.; Koutsoukos, X.; Sundaram, S. Resilient Asymptotic Consensus in Robust Networks. IEEE J. Sel. Areas Commun. 2013, 31, 766–781. [Google Scholar] [CrossRef]
- Wang, Y.; Ishii, H. Resilient Consensus Through Event-Based Communication. IEEE Trans. Control Netw. Syst. 2020, 7, 471–482. [Google Scholar] [CrossRef]
- Tan, S.; Yang, S.; Xu, J.-X. Consensus Based Approach for Economic Dispatch Problem in a Smart Grid. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; pp. 2011–2015. [Google Scholar]
- Zhao, Y.; Chen, B.; Fan, Y.; Xin, H. Convergence Speed Analysis and Optimization for Distributed Control of Virtual Power Plant. Power Syst. Technol. 2016, 40, 2288–2295. [Google Scholar] [CrossRef]
- Zhang, Z.; Chow, M.-Y. Convergence Analysis of the Incremental Cost Consensus Algorithm Under Different Communication Network Topologies in a Smart Grid. IEEE Trans. Power Syst. 2012, 27, 1761–1768. [Google Scholar] [CrossRef]
- Sundaram, S.; Hadjicostis, C.N. Distributed Function Calculation via Linear Iterative Strategies in the Presence of Malicious Agents. IEEE Trans. Autom. Control 2011, 56, 1495–1508. [Google Scholar] [CrossRef]
- Fiore, D.; Russo, G. Resilient Consensus for Multi-Agent Systems Subject to Differential Privacy Requirements. Automatica 2019, 106, 18–26. [Google Scholar] [CrossRef]
- LeBlanc, H.J.; Koutsoukos, X.D. Consensus in Networked Multi-Agent Systems with Adversaries. In Proceedings of the 14th International Conference on Hybrid Systems: Computation and Control, Chicago, IL, USA, 12–14 April 2011; Association for Computing Machinery: New York, NY, USA, 2011; pp. 281–290. [Google Scholar]
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An Overview of Recent Progress in the Study of Distributed Multi-Agent Coordination. IEEE Trans. Ind. Inform. 2013, 9, 427–438. [Google Scholar] [CrossRef]
- Pasqualetti, F.; Bicchi, A.; Bullo, F. Consensus Computation in Unreliable Networks: A System Theoretic Approach. IEEE Trans. Autom. Control 2012, 57, 90–104. [Google Scholar] [CrossRef]
- Ren, W.; Beard, R.W.; Atkins, E.M. Information Consensus in Multivehicle Cooperative Control. IEEE Control Syst. Mag. 2007, 27, 71–82. [Google Scholar] [CrossRef]
- Xie, J.; Chen, K.; Yue, D.; Li, Y.; Wang, K.; Weng, S.; Huang, C. Distributed Economic Dispatch Based on Consensus Algorithm of Multi Agent System for Power System. Electr. Power Autom. Equip. 2016, 36, 112–117. [Google Scholar] [CrossRef]
- Binetti, G.; Davoudi, A.; Lewis, F.L.; Naso, D.; Turchiano, B. Distributed Consensus-Based Economic Dispatch with Transmission Losses. IEEE Trans. Power Syst. 2014, 29, 1711–1720. [Google Scholar] [CrossRef]








| Unit | ai (USD/MW2) | bi (USD/MW) | ci (USD) | (MW) | (MW) |
|---|---|---|---|---|---|
| G1 | 0.0038 | 6.87 | 135.88 | 75 | 500 |
| G2 | 0.0034 | 7.03 | 214.92 | 80 | 400 |
| G3 | 0.0029 | 7.58 | 108.23 | 30 | 280 |
| G4 | 0.0018 | 7.67 | 220.00 | 80 | 420 |
| G5 | 0.0016 | 8.14 | 232.56 | 50 | 350 |
| G6 | 0.0025 | 7.15 | 78.09 | 50 | 480 |
| G7 | 0.0022 | 7.86 | 234.48 | 64 | 300 |
| G8 | 0.0026 | 6.80 | 74.60 | 45 | 500 |
| G9 | 0.0033 | 5.99 | 127.69 | 74 | 400 |
| G10 | 0.0028 | 6.65 | 100.52 | 150 | 600 |
| G11 | 0.0040 | 6.32 | 128.36 | 80 | 400 |
| G12 | 0.0028 | 6.79 | 187.63 | 90 | 350 |
| G13 | 0.0033 | 6.54 | 254.23 | 75 | 450 |
| G14 | 0.0022 | 8.97 | 98.76 | 40 | 500 |
| G15 | 0.0018 | 7.32 | 118.45 | 45 | 300 |
| G16 | 0.0041 | 8.64 | 186.34 | 30 | 420 |
| G17 | 0.0035 | 7.51 | 225.79 | 65 | 600 |
| G18 | 0.0021 | 8.28 | 178.69 | 30 | 350 |
| G19 | 0.0024 | 6.97 | 169.24 | 50 | 480 |
| G20 | 0.0027 | 8.16 | 169.31 | 60 | 650 |
| Scenario | Consensus Variable (USD/MW) | Power of Each Unit (MW) | Power Imbalance (MW) |
|---|---|---|---|
| Consensus algorithm + no attack | [9.152, 9.152, 9.152, 9.152, 9.152, 9.152, 9.152, 9.152, 9.152, 9.152] | [300.285, 312.083, 271.063, 411.713, 316.302, 400.433, 293.674, 360.032, 327.601, 446.815] | 0 |
| Consensus algorithm + Crashed attack | [8.576, 8.558, 8.576, 9.051, 8.828, 8.828, 9.051, 9.204, 9.187, 9.204] | [224.448, 224.768, 171.691, 383.697, 214.949, 335.567, 270.752, 370.003, 332.824, 456.075] | 455 |
| W-MSR algorithm + Crashed attack | [9.152, 9.152, 9.152, 9.152, 9.152, 9.152, 9.152, 9.152, 9.152, 9.152] | [300.285, 312.083, 271.063, 411.713, 316.302, 400.433, 293.674, 360.032, 327.601, 446.815] | 0 |
| Scenario | Consensus Variable ($/MW) | Power of Each Unit (MW) | Power Imbalance (MW) |
|---|---|---|---|
| Consensus algorithm + no attack | [8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329] | [192.038, 191.102, 129.223, 183.192, 59.216, 235.898, 106.702, 201.825, 202.953, 299.909, 251.186, 274.909, 271.135, 40.000, 280.414, 30.000, 117.070, 30.000, 283.227, 60.000] | 0 |
| Consensus algorithm + Crashed attack | [7.892, 8.013, 7.902, 8.203, 8.046, 8.057, 8.223, 8.374, 8.345, 8.301, 8.372, 8.407, 8.450, 8.465, 8.482, 8.501, 8.504, 8.559, 8.585, 8.590] | [134.427, 144.579, 55.578, 148.020, 50.000, 181.483, 82.587, 210.374, 205.266, 294.891, 256.444, 288.731, 289.386, 40.000, 300.000, 30.000, 141.998, 66.537, 336.520, 79.628] | 103.55 |
| W-MSR algorithm + Crashed attack | [8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329, 8.329] | [192.038, 191.102, 129.223, 183.192, 59.216, 235.898, 106.702, 201.825, 202.953, 299.909, 251.186, 274.909, 271.135, 40.000, 280.414, 30.000, 117.070, 30.000, 283.227, 60.000] | 0 |
| Attack | 10 Distributed Generation Units | 20 Distributed Generation Units |
|---|---|---|
| Crashed attack | 16 | 171 |
| Byzantine attack | 23 | 31 |
| 27 | 46 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, J.; Wang, J.; Lang, H.; Wang, W. Distributed Secure Economic Dispatch Strategy Based on Robust Graph Theory and W-MSR Algorithm. Sensors 2025, 25, 2551. https://doi.org/10.3390/s25082551
Le J, Wang J, Lang H, Wang W. Distributed Secure Economic Dispatch Strategy Based on Robust Graph Theory and W-MSR Algorithm. Sensors. 2025; 25(8):2551. https://doi.org/10.3390/s25082551
Chicago/Turabian StyleLe, Jian, Jing Wang, Hongke Lang, and Weihao Wang. 2025. "Distributed Secure Economic Dispatch Strategy Based on Robust Graph Theory and W-MSR Algorithm" Sensors 25, no. 8: 2551. https://doi.org/10.3390/s25082551
APA StyleLe, J., Wang, J., Lang, H., & Wang, W. (2025). Distributed Secure Economic Dispatch Strategy Based on Robust Graph Theory and W-MSR Algorithm. Sensors, 25(8), 2551. https://doi.org/10.3390/s25082551





