Bayesian Adaptive Extended Kalman-Based Orbit Determination for Optical Observation Satellites
Abstract
1. Introduction
1.1. Related Work
1.2. Contributions in This Article
- Dynamic noise covariance adjustment: The process noise covariance matrix and observation noise covariance matrix are optimized online through adaptive factors to adapt to environmental noise fluctuations in real-time. When the observation error increases due to sudden atmospheric disturbances, BAEKF can automatically reduce the weight of the anomalous data to avoid filter dispersion.
- Bayesian a posteriori probability correction: A Bayesian inference framework is introduced to combine the a priori distribution with real-time observation to update the a posteriori probability distribution of the state estimation, effectively suppressing the linearization error accumulation. Experiments show that this method improves the position estimation accuracy by more than 30% compared with EKF in strongly nonlinear scenarios.
- Fast convergence with short-arc data: By fusing geometric constraints from multi-moment angular observations, BAEKF can achieve stable convergence of orbital parameters in a short time.
1.3. Organization of the Paper
2. Kinematic and Dynamical Model
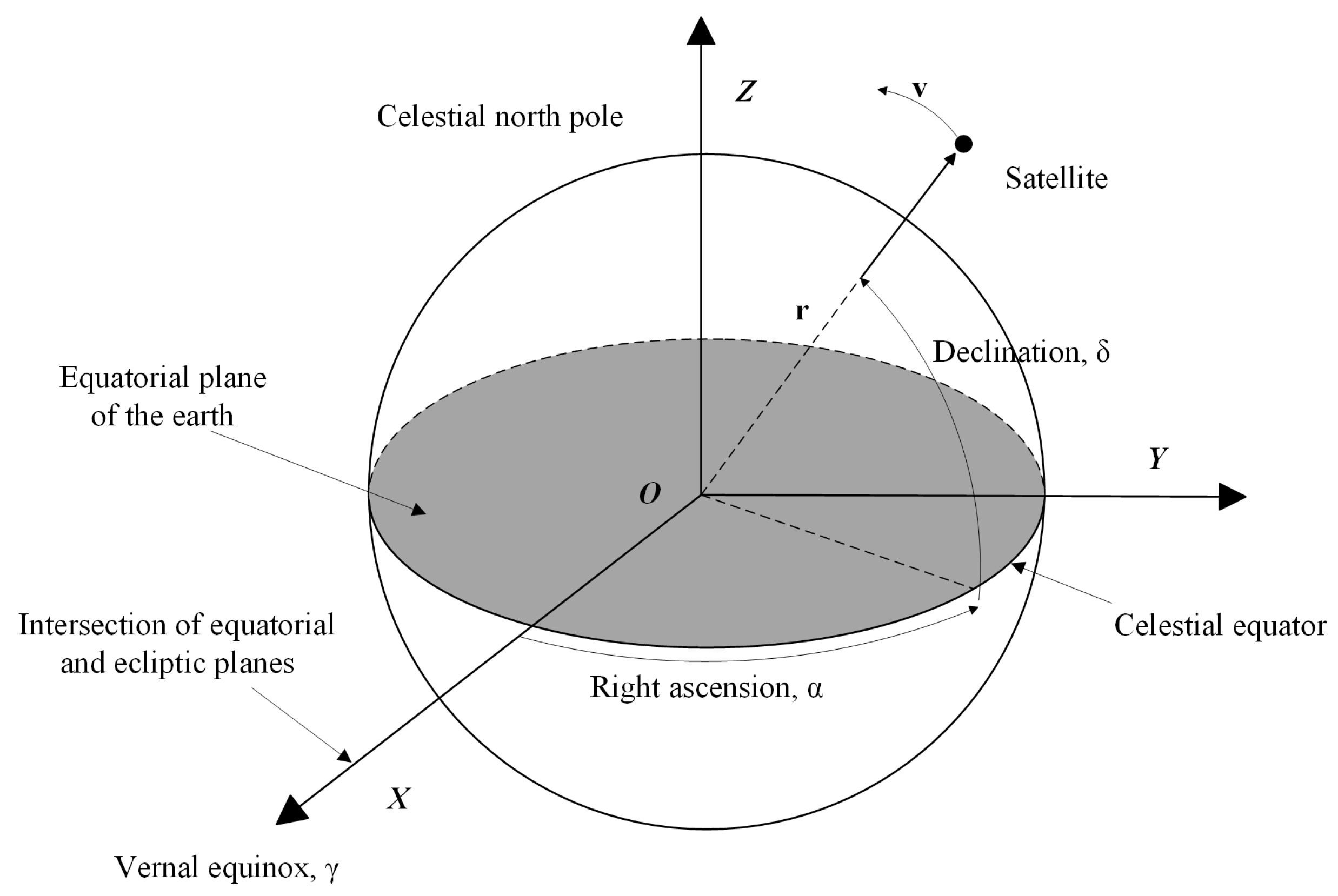
2.1. Coordinate System
2.2. Spatial Dynamics Modeling
2.3. Celestial Angle Observation Model
3. Position and Velocity Estimation
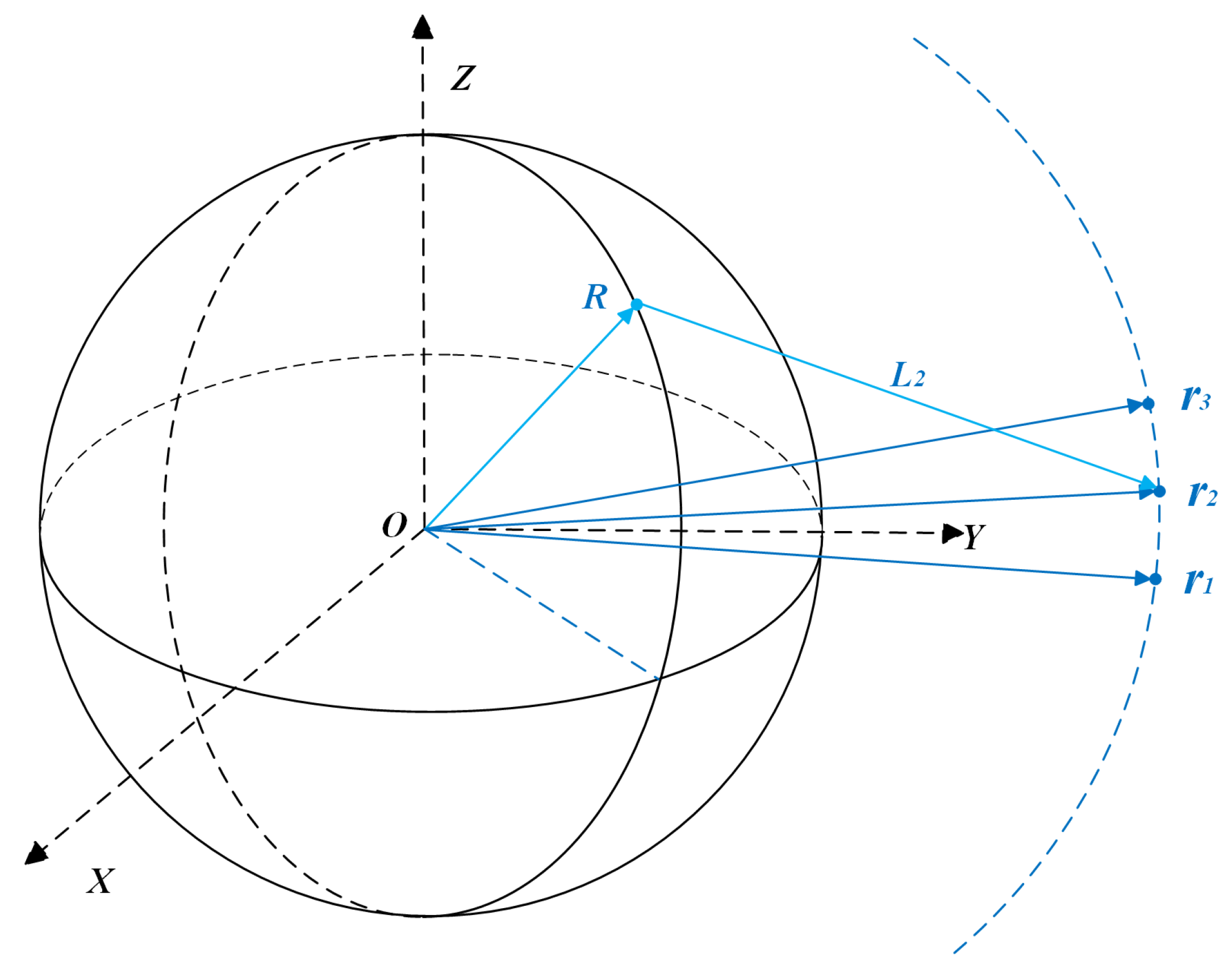
3.1. Position Vector Estimation
3.2. Velocity Vector Estimation
4. Design of Extended Kalman Filter
4.1. Initial State Estimation
4.2. Forecasting Steps
4.3. Updating Steps
5. Design of Adaptive Extended Kalman Filter
5.1. Bayesian Reasoning
- Definitional domain match: The Beta distribution is defined in the interval [0, 1], which fits the range of values of the adaptive parameters and . By limiting the range of and , it can ensure the stability of the noise covariance adjustment and avoid the parameter exceeding the reasonable range leading to numerical dispersion.
- Flexibility: The shape of the Beta distribution is controlled by hyperparameters and , allowing flexibility in expressing different prior beliefs.
- Regularization: The Beta distribution is able to avoid extreme values of and by adjusting the shape parameter, while the parameter design makes and tend to intermediate values, balancing the weights of historical information and current observations.
- Computational convenience: The Beta distribution is the conjugate prior of the binomial distribution. Although the likelihood function of observation noise in BAEKF is the Gaussian distribution, the analytical nature of the Beta distribution can still simplify the process of updating the posterior distribution. Meanwhile, combined with the maximum a posteriori estimation (MAP), the optimal parameters can be solved effectively.
5.2. Adaptive Updating Steps
5.2.1. Estimation of Process Noise
5.2.2. Estimation of Observation Noise
5.2.3. Covariance Update
5.2.4. Status Update
6. Analysis of Experiments and Results
6.1. Experimental Data
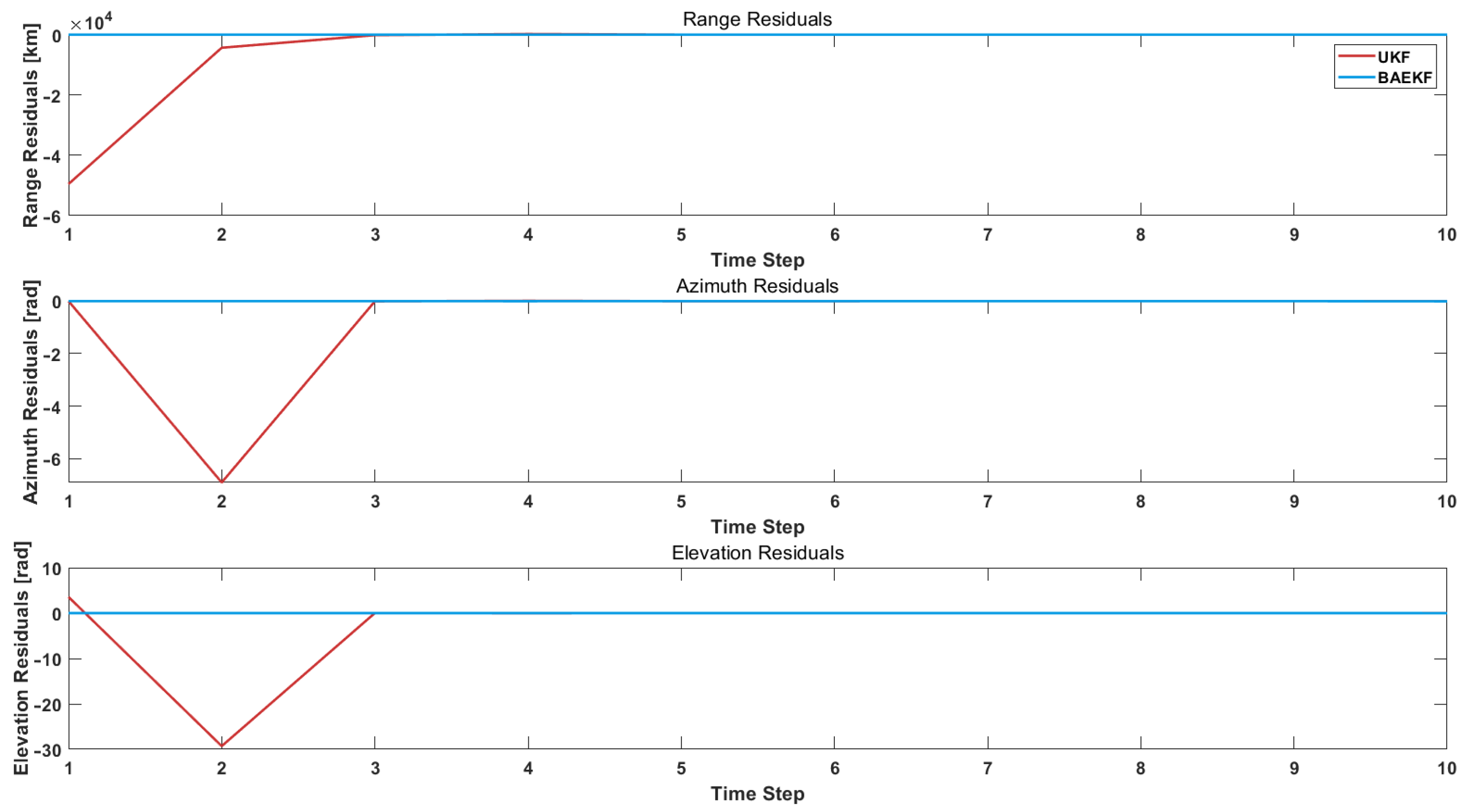
6.2. Experimental Results
6.3. Experimental Analysis
6.3.1. Comparison of Classical Differential Correction Algorithms
- Algorithm types: Classical differential correction algorithms are a class of batch algorithms that emphasize global optimization and are suitable for non-real-time tasks; BAEKF is a sequential filtering method that emphasizes real-time and is capable of dynamically updating the state estimates as new observations arrive.
- Dynamic noise adaptation: Classical differential correction algorithms assume that the statistical characteristics of noise are fixed, making it difficult to cope with dynamic noise; BAEKF adapts to noise fluctuations in real-time through adaptive noise covariance adjustment, reducing the impact of abnormal data.
- Nonlinearity handling capability: Classical differential correction algorithms deal with nonlinearities through local linearization, ignoring higher-order terms, which may lead to error accumulation; BAEKF introduces Bayesian a posteriori probability corrections to compensate for higher-order nonlinear terms and reduce errors in long-term predictions.
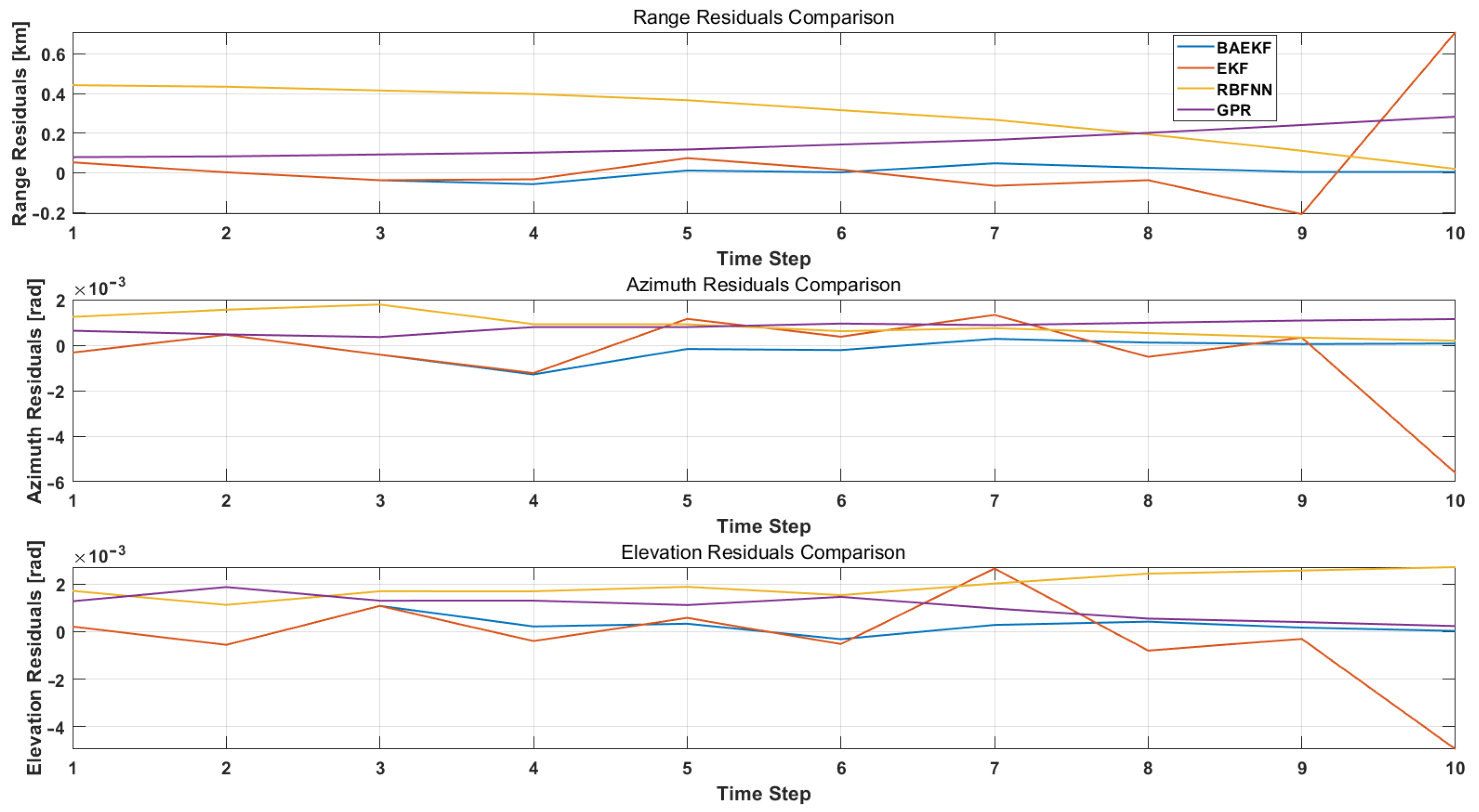
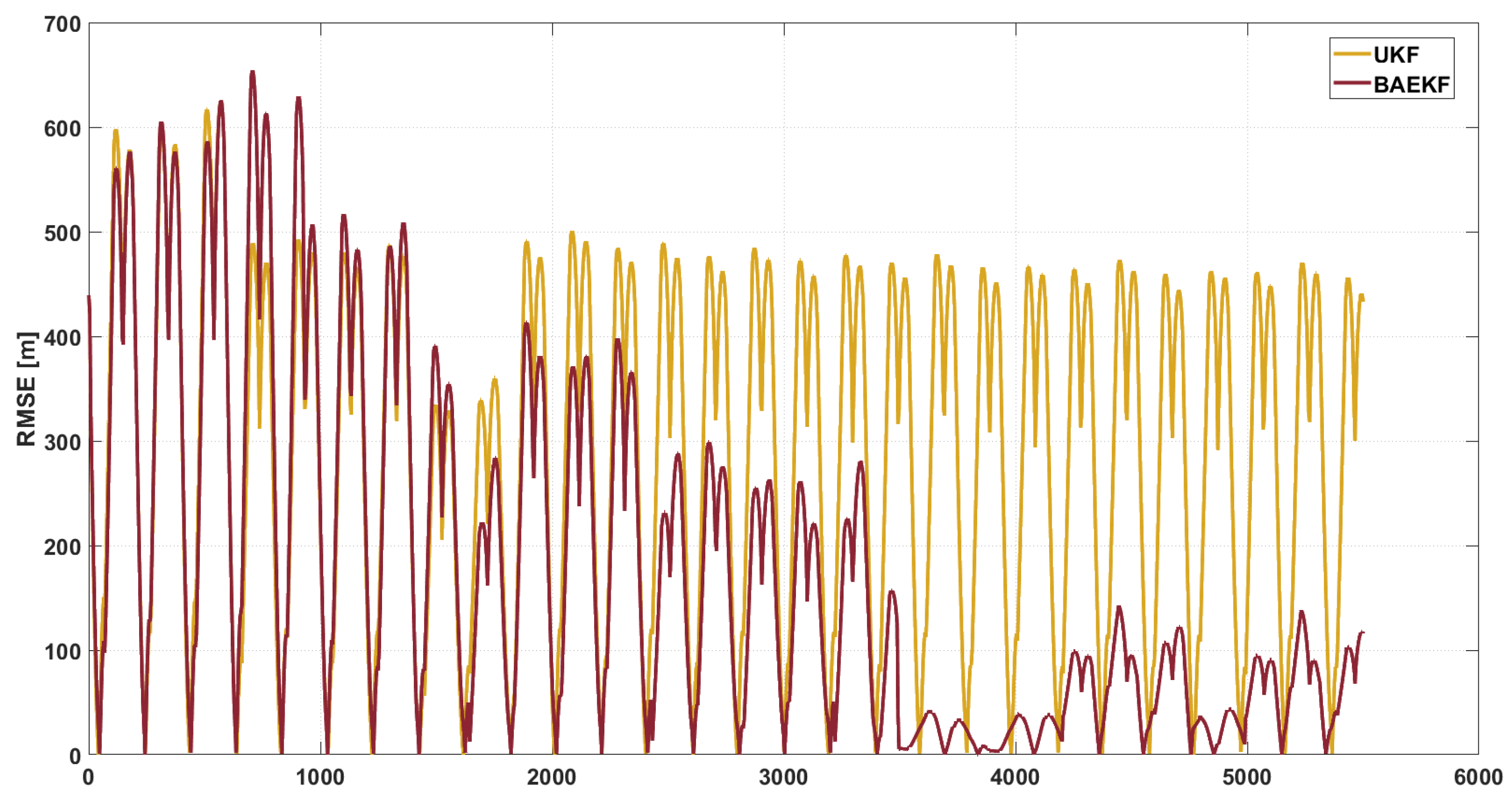
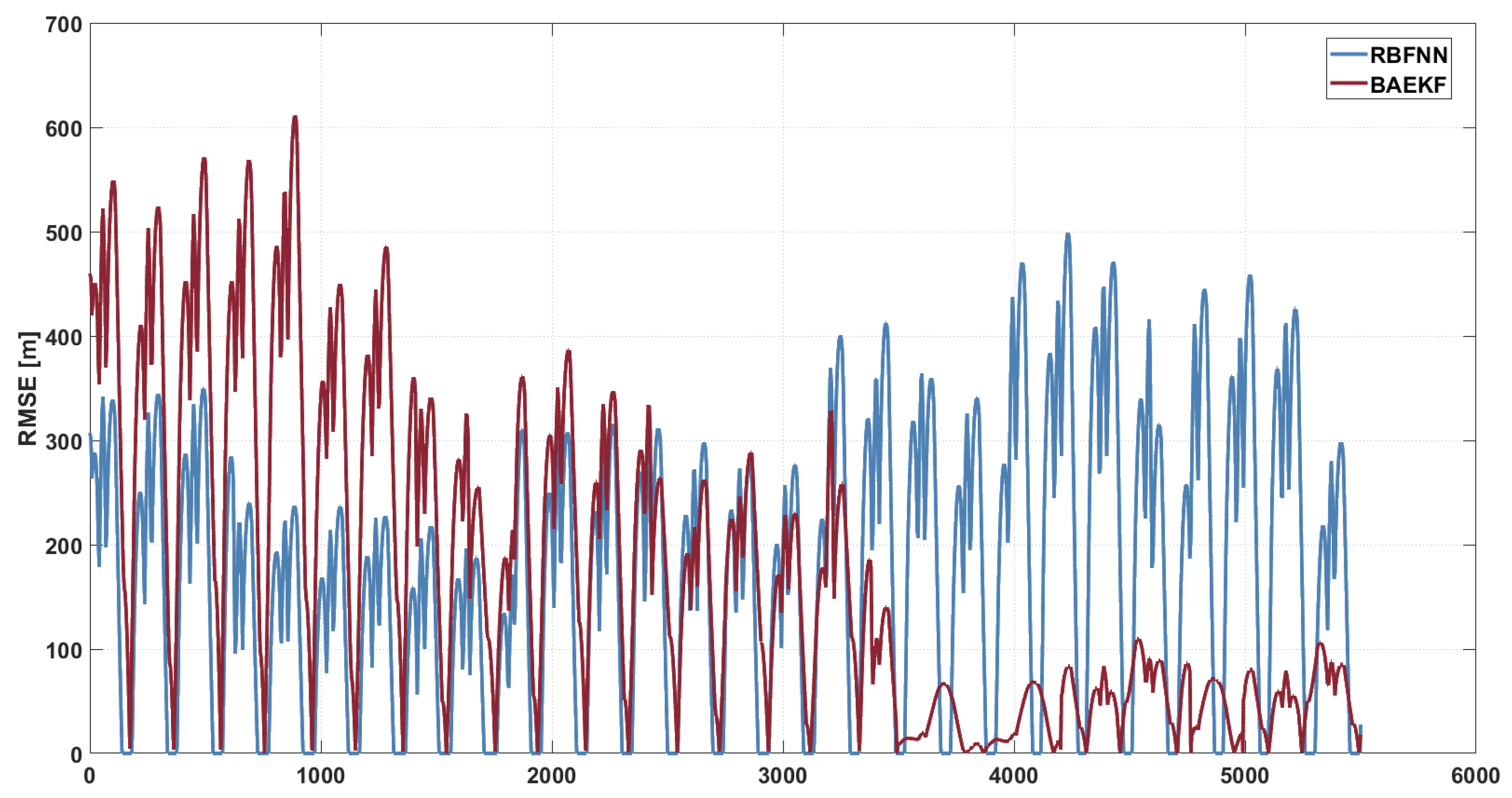
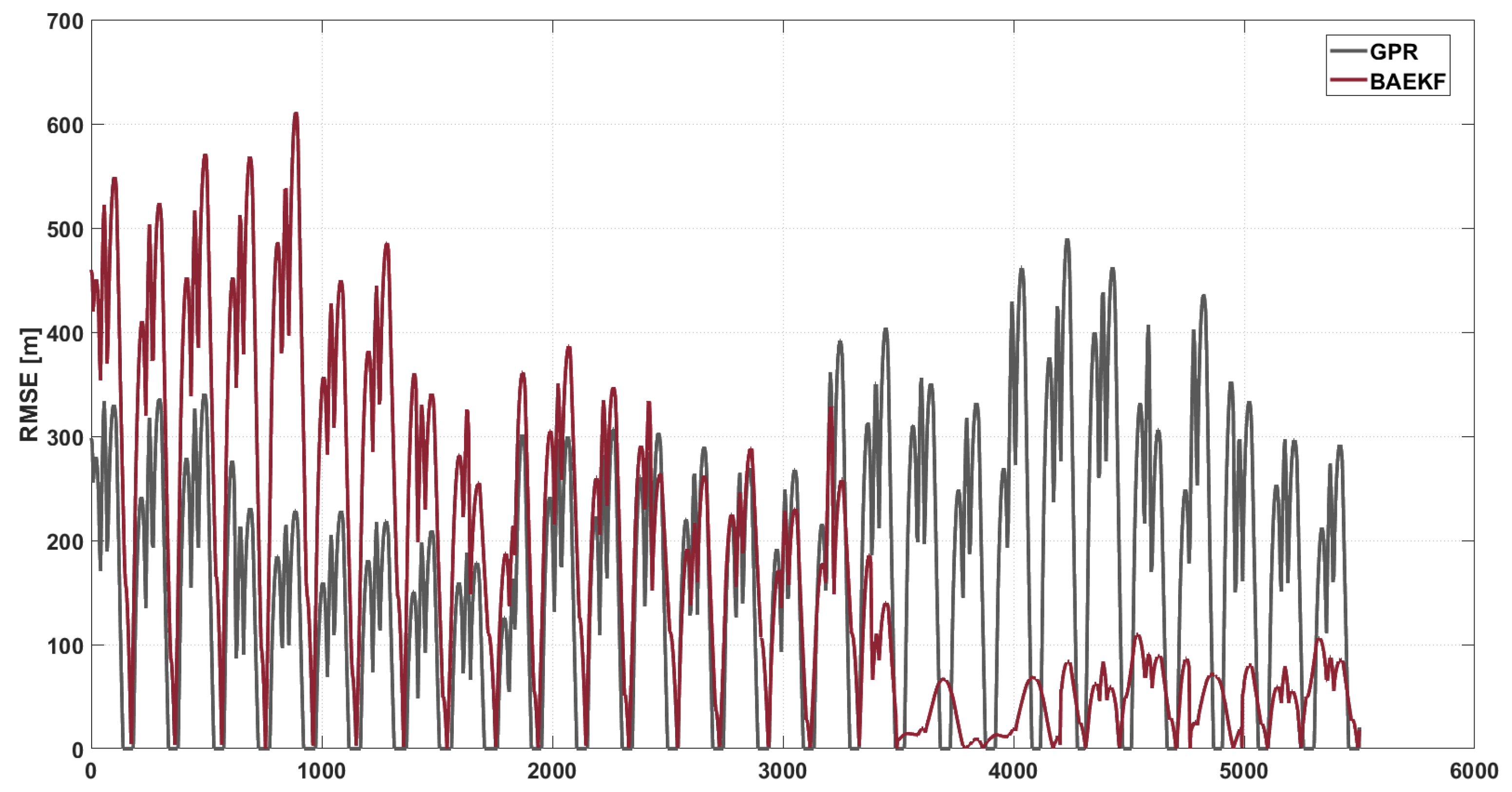
6.3.2. Comparing Modern Algorithms
| Algorithms | Average RMSE | RMSE Accuracy | Average MAE | MAE Accuracy | Residual Fluctuation |
|---|---|---|---|---|---|
| BAEKF | 120.6758 | 1 | 60.3137 | Data | 1 |
| EKF | 184.8235 | −34.71% | 108.021 | −44.16% | −40.5% |
| UKF | 194.142 | −37.83% | 115.4829 | −47.76% | – |
| RBFNN | 163.8711 | −26.37% | 96.6842 | −37.61% | −32.6% |
| GPR | 156.4762 | −22.875% | 92.3992 | −34.72% | −30.4% |
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, Y.; Cheng, Z.; Zhang, Q.H.; Zhao, Z.X. Efficacy assessment method of space object cooperative monitoring system applying fuzzy theory. Mod. Radar 2025, 1–10. [Google Scholar] [CrossRef]
- Chipade, A.; Ramanathan, V. Extended Kalman filter based statistical orbit determination for geostationary and geosynchronous satellite orbits in BeiDou constellation. Contrib. Geophys. Geod. 2021, 51, 25–46. [Google Scholar] [CrossRef]
- Romero, P.; Pablos, B.; Barderas, G. Analysis of orbit determination from Earth-based tracking for relay satellites in a perturbed areostationary orbit. Acta Astronaut. 2017, 136, 434–442. [Google Scholar] [CrossRef]
- Williams, A.; Boley, C.; Rotola, G.; Greeb, R. Sustainable skies and the Earth–space environment. Arab. J. Sci. Eng. 2023, 48, 10589–10604. [Google Scholar] [CrossRef]
- Stanislav, K.; Jiří, Š.; Matej, Z.; Roman, Ď. The Image Processing System for Ultra-Fast Moving Space Debris Objects. Nat. Sustain. 2024, 7, 228–231. [Google Scholar] [CrossRef]
- Zhang, R.; Rui, T.; Zhang, P.; Fan, L.H.; Han, J.Q.; Wang, S.Y.; Hong, J.; Lu, X.C. Optimization of ground tracking stations for BDS-3 satellite orbit determination. Adv. Space Res. 2021, 68, 4069–4087. [Google Scholar] [CrossRef]
- Kim, S.; Lim, H.; Bennett, C.J.; Lachut, M.; Jo, J.H.; Choi, J.; Choi, M.; Park, E.; Yu, S.Y.; Sung, K.P. Analysis of Space Debris Orbit Prediction Using Angle and Laser Ranging Data from Two Tracking Sites under Limited Observation Environment. Sensors 2020, 20, 1950. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Yin, X.L.; Xiao, Y.; Zhao, Z.X.; Yang, X.; Dai, C.G. Enhanced YOLOv8-based method for space debris detection using cross-scale feature fusion. Discov. Appl. Sci. 2025, 7, 95. [Google Scholar] [CrossRef]
- Liu, L.; Cao, J. Orbit determination of high-orbit space targets based on space-based optical goniometry. J. Opt. 2021, 41, 155–161. [Google Scholar] [CrossRef]
- Sergei, R.; Denise, D.; Julian, Z.; Alkahal, R.; Dhruv, U.; Mathis, B. Radial Orbit Errors of Contemporary Altimetry Satellite Orbits. Surv. Geophys. 2023, 44, 705–737. [Google Scholar] [CrossRef]
- Schrama, E. Precision orbit determination performance for CryoSat-2. Adv. Space Res. 2018, 61, 705–737. [Google Scholar] [CrossRef]
- Valli, M.; Armellin, R.; Lizia, D.P. Nonlinear filtering methods for spacecraft navigation based on differential algebra. Acta Astronaut. 2014, 94, 363–374. [Google Scholar] [CrossRef]
- Vira, D.A.; Larsen, A.B.; Skoug, M.R.; Fernes, P.A. Bayesian Model for HOPE Mass Spectrometers on Van Allen Probes. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028862. [Google Scholar] [CrossRef]
- Zhu, R.; Fu, Q.; Liu, N.; Zhao, F.; Wen, G.; Li, Y.C.; Jiang, H.L. Improved target detection method for space-based optoelectronic systems. Sci. Rep. 2024, 14, 1832. [Google Scholar] [CrossRef]
- Aarnes, H.K.; Johannes, J. The Simple Solution for Nonlinear State Estimation of Ill-Conditioned Systems: The Normalized Unscented Kalman Filter. IFAC Pap. Online 2023, 74, 5951–5956. [Google Scholar] [CrossRef]
- Gong, B.; Liu, Y.; Ning, X.; Li, S.; Ren, M. RBFNN-based angles-only orbit determination method for non-cooperative space targets. Adv. Space Res. 2024, 74, 1424–1436. [Google Scholar] [CrossRef]
- Hou, X.; Li, B.; Liu, X.; Cheng, H.; Shen, M.; Wang, P.; Xin, X. Initial orbit determination of some cislunar orbits based on short-arc optical observations. Astrodynamics 2024, 8, 455–469. [Google Scholar] [CrossRef]
- Sun, C.; Sun, Y.; Yu, X.; Fang, Q. Rapid Detection and Orbital Parameters’ Determination for Fast-Approaching Non-Cooperative Target to the Space Station Based on Fly-around Nano-Satellite. Remote Sens. 2023, 15, 1213. [Google Scholar] [CrossRef]
- Lee, E.; Park, S.; Hwang, H.; Choi, J.; Cho, S.; Jung, H. Initial orbit association and long-term orbit prediction for low earth space objects using optical tracking data. Acta Astronaut. 2020, 176, 247–261. [Google Scholar] [CrossRef]
- David, S.; Puneet, S.; Sean, O.R. Angles-Only Initial Orbit Determination via Multivariate Gaussian Process Regression. Electronics 2022, 11, 588. [Google Scholar] [CrossRef]
- DeMars, K.J.; Cheng, Y.; Jah, M.K. Collision Probability with Gaussian Mixture Orbit Uncertainty. J. Guid. Control Dyn. 2014, 37, 979–984. [Google Scholar] [CrossRef]
- Kiani, M.; Pourtakdoust, S.H. Orbit determination via adaptive Gaussian swarm optimization. J. Adv. Space Res. 2014, 55, 1028–1037. [Google Scholar] [CrossRef]
- Psiaki, M.L. Gaussian-Mixture Kalman Filter for Orbit Determination Using Angles-Only Data. J. Guid. Control Dyn. 2017, 40, 2339–2345. [Google Scholar] [CrossRef]
- Psiaki, M.L.; Weisman, R.M.; Jah, M.K. Gaussian Mixture Approximation of Angles-Only Initial Orbit Determination Likelihood Function. J. Guid. Control Dyn. 2017, 40, 2807–2819. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, T.; Lyu, Z.; Gao, D. A Virtual In-Cylinder Pressure Sensor Based on EKF and Frequency-Amplitude-Modulation Fourier-Series Method. J. Sens. 2019, 19, 3122. [Google Scholar] [CrossRef] [PubMed]
- Hassan Ayman, E.O.; Mohammed Tasnim, A.A.; Demirkol, A. Fault detection in a three-tank hydraulic system using unknown input observer and extended Kalman filter. J. Eng. Res. 2021, 9, 161–173. [Google Scholar] [CrossRef]
- György, K.; Kelemen, A.; Dávid, L. Unscented Kalman Filters and Particle Filter Methods for Nonlinear State Estimation. J. Procedia Technol. 2014, 12, 65–74. [Google Scholar] [CrossRef]
- Bai, Y.; Yan, B.; Zhou, C.; Su, T.; Jin, X. State of art on state estimation: Kalman filter driven by machine learning. J. Annu. Rev. Control 2023, 56, 100909. [Google Scholar] [CrossRef]
- Anirudh, C.; Rao, J.V.; Donghoon, K. Measurement Noise Covariance-Adapting Kalman Filters for Varying Sensor Noise Situations. Sensors 2021, 21, 8304. [Google Scholar] [CrossRef]
- Chen, J.; Jin, X.; Hou, C. Real-Time Orbit Determination of Micro–Nano Satellite Using Robust Adaptive Filtering. J. Sens. 2024, 24, 7988. [Google Scholar] [CrossRef]
- Bu, Q.C.; Chen, L.; Li, S.S. A Bayesian approach to gamma storm data processing. Prog. Astron. 2013, 31, 325–339. [Google Scholar]



| Year Month Date | Time (UTC) | Azimuth (°) | Elevation (°) |
|---|---|---|---|
| 2024 06 28 | 09: 16: 08.00 | 31.4286 | 6.3375 |
| 2024 06 28 | 09: 16: 18.00 | 32.4092 | 6.7375 |
| 2024 06 28 | 09: 16: 28.00 | 33.4119 | 7.1347 |
| 2024 06 28 | 09: 16: 38.00 | 34.4369 | 7.5292 |
| 2024 06 28 | 09: 16: 48.00 | 35.4250 | 6.3375 |
| 2024 06 28 | 09: 16: 58.00 | 36.4947 | 7.8980 |
| 2024 06 28 | 09: 17: 08.00 | 37.5875 | 8.2850 |
| 2024 06 28 | 09: 17: 18.00 | 38.7042 | 8.6673 |
| 2024 06 28 | 09: 17: 28.00 | 39.8444 | 9.0444 |
| 2024 06 28 | 09: 17: 38.00 | 41.0092 | 9.4158 |
| ONEWEB-0547 TLE Data |
|---|
| 1 56049U 23043D 25004.66144206 .00000238 00000+0 54545-3 0 9994 |
| 2 56049 87.9303 349.2857 0001740 91.7550 268.3783 13.21826925 88409 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Pang, Q.; Yin, X.; Shi, X.; Zhao, Z.; Sun, J.; Wang, J. Bayesian Adaptive Extended Kalman-Based Orbit Determination for Optical Observation Satellites. Sensors 2025, 25, 2527. https://doi.org/10.3390/s25082527
Guo Y, Pang Q, Yin X, Shi X, Zhao Z, Sun J, Wang J. Bayesian Adaptive Extended Kalman-Based Orbit Determination for Optical Observation Satellites. Sensors. 2025; 25(8):2527. https://doi.org/10.3390/s25082527
Chicago/Turabian StyleGuo, Yang, Qinghao Pang, Xianlong Yin, Xueshu Shi, Zhengxu Zhao, Jian Sun, and Jinsheng Wang. 2025. "Bayesian Adaptive Extended Kalman-Based Orbit Determination for Optical Observation Satellites" Sensors 25, no. 8: 2527. https://doi.org/10.3390/s25082527
APA StyleGuo, Y., Pang, Q., Yin, X., Shi, X., Zhao, Z., Sun, J., & Wang, J. (2025). Bayesian Adaptive Extended Kalman-Based Orbit Determination for Optical Observation Satellites. Sensors, 25(8), 2527. https://doi.org/10.3390/s25082527






