Bioimpedance Analysis of Cucumber Plants Exposed to Different Nitrogen Doses Under Greenhouse Conditions
Abstract
1. Introduction
- (1)
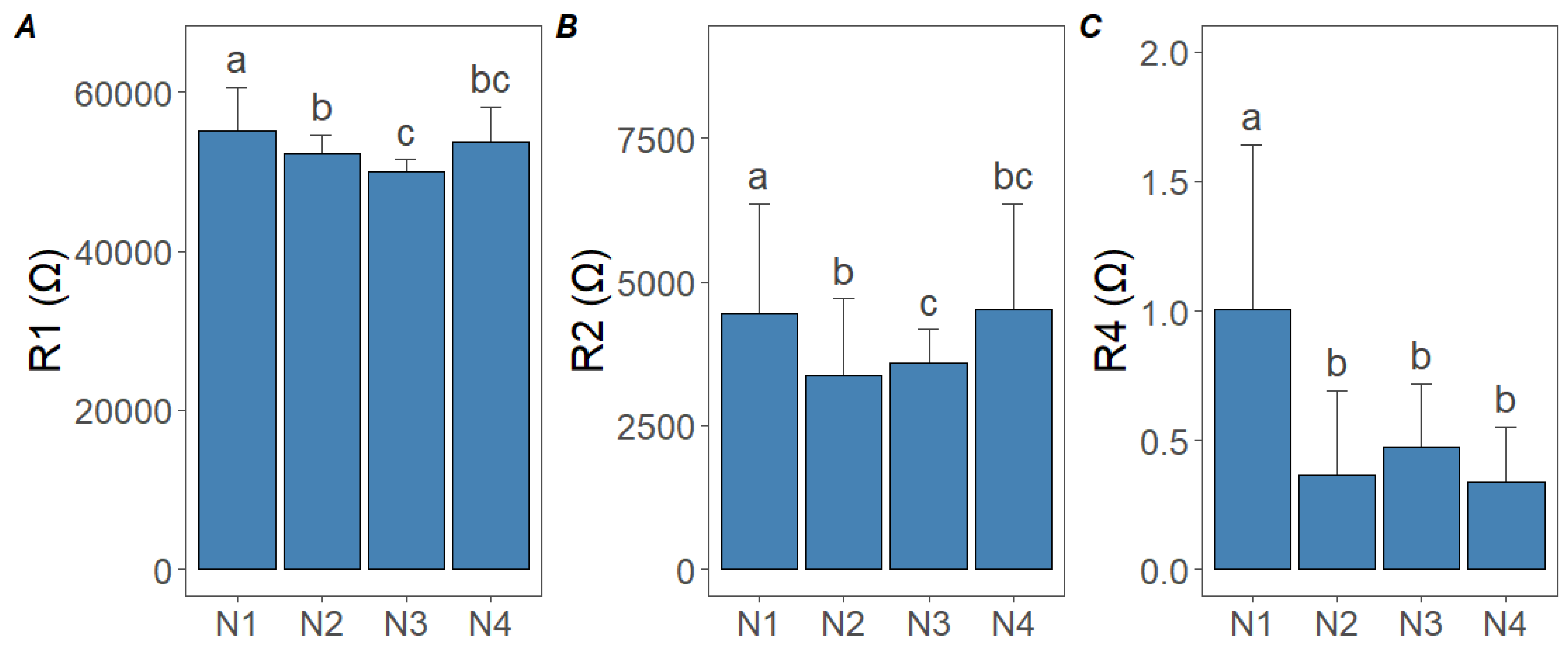
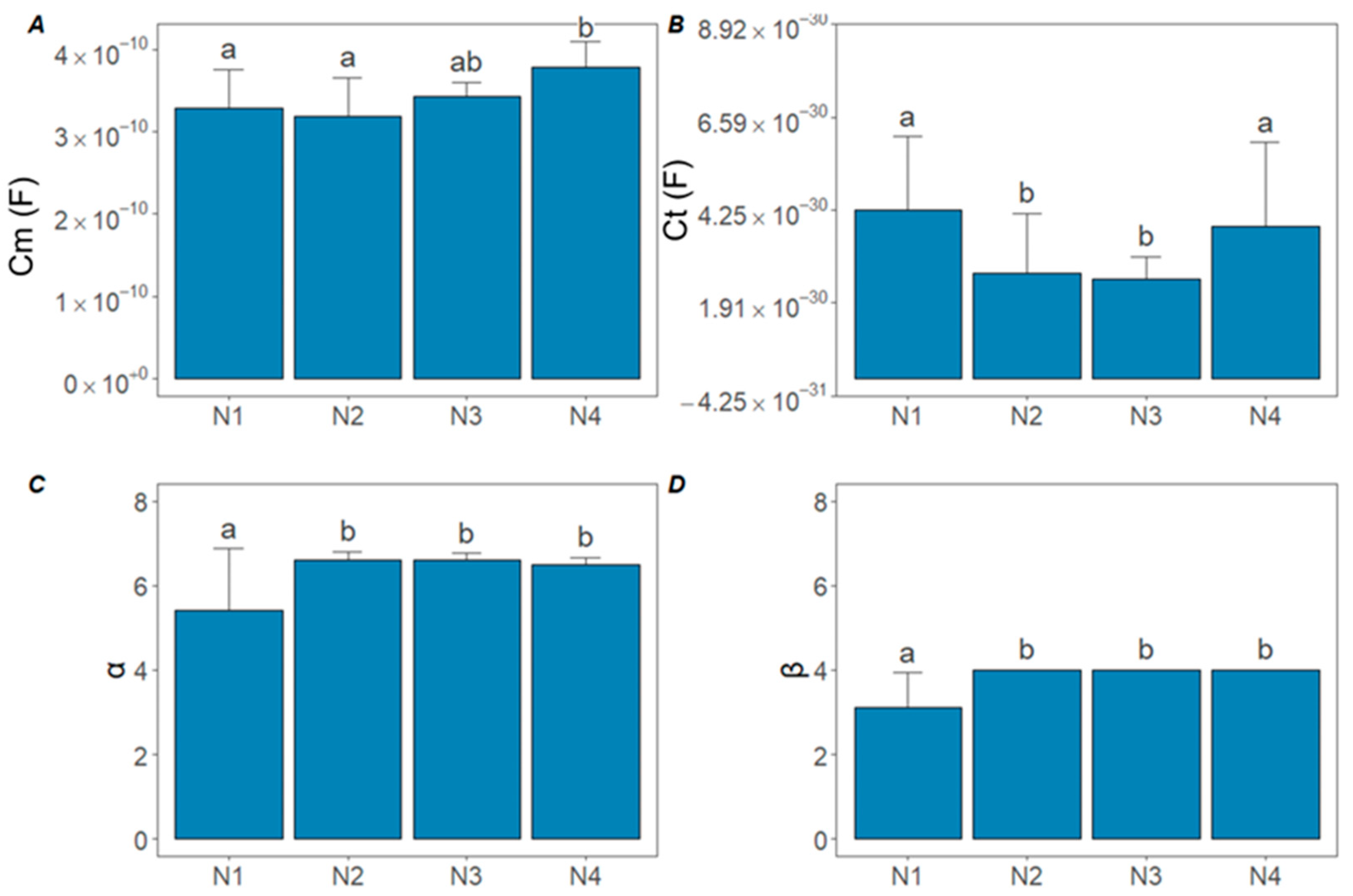
- We show that both resistance (extracellular fluid resistance, intercellular fluid resistance, and vacuole fluid resistance) and cell membrane capacitance values exhibit distinct changes with different N doses, indicating that even small changes in the NO3− and total N content of leaves can be rapidly detected using minimally invasive BIS parameters.
- (2)
- By correlating BIS-derived parameters with total N and NO3− concentrations, we establish specific threshold intervals that robustly distinguish suboptimal from near-optimal N availability in cucumber leaves.
- (3)
- Our results confirm that BIS can serve as a rapid, complementary diagnostic method alongside conventional chemical analysis, allowing timely adjustments to fertilization strategies, preventing overfertilization, and promoting more efficient N use in greenhouse cucumber production.
2. Materials and Methods
2.1. Experimental Setup and Treatments
2.2. Plant Physiological Measurements
| Determination of Plant Physiology Characteristics | |||
|---|---|---|---|
| Plant Parameter | Methods | Replication | Growth Stage |
| Leaf total N content (%) | [22] | 4 | |
| Leaf NO3− content (mg g−1 FW) | [21] | 4 | 6–7 true leaf stage of cucumber (ES2217 F1 genotype) |
| Photosynthetic pigments (mg g−1 FW) | [19] | 4 | |
| Chlorophyll Content Index (CCI, dimensionless unit) (Apogee MC-100) | [6,23] | 4 | |
2.3. Bioimpedance Spectroscopy Measurements and Plant Cell Model
2.4. Numerical Optimization-Based Parameter Extraction
2.5. Statistical Analysis
3. Results
3.1. Effect of N Treatments on Plant Physiology Parameters
3.2. Effect of N Treatments on Bioimpedance Parameters
4. Discussion
5. Conclusions and Future Work
- (1)
- BIS parameters, particularly extracellular fluid resistance and cell membrane capacitance, showed clear, statistically significant responses to different N doses. These changes reflect physiological processes such as nitrate saturation in the apoplast and membrane stability.
- (2)
- Although increasing N doses generally lowered resistance and decreased cell membrane capacitance, the total N and NO3− contents did not continue to rise indefinitely, indicating feedback suppression in NO3− uptake. This threshold effect highlights the importance of precise N management to avoid wasteful over-fertilization without gaining additional yield or quality benefits.
- (3)
- By detecting early signs of low or excess N supply, BIS measurements can complement traditional methods (e.g., Kjeldahl or NO3− assays) and help growers optimize fertilizer application.
- (4)
- While the current work focused on the 6–7 true leaf stage, future studies could map BIS responses across multiple growth phases and correlate them directly with yield metrics (e.g., fruit number, size, quality parameters). Additionally, integrating BIS data with other non-destructive diagnostic tools (e.g., hyperspectral imaging) could further refine real-time monitoring and fertilization strategies under commercial greenhouse conditions.
- (5)
- Future work will also include a more detailed investigation of the biological meaning of the α and β parameters. In our future studies, we plan to analyze these parameters more thoroughly to understand how they relate to cell membrane dynamics and other physiological processes. This deeper insight will allow us to further refine our BIS models and improve the interpretation of plant nutrient status and stress responses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Basak, R.; Wahid, K.; Dinh, A. Determination of Leaf Nitrogen Concentrations Using Electrical Impedance Spectroscopy in Multiple Crops. Remote Sens. 2020, 12, 566. [Google Scholar] [CrossRef]
- Von Wirén, N.; Gazzarrini, S.; Gojon, A.; Frommer, W.B. The Molecular Physiology of Ammonium Uptake and Retrieval. Curr. Opin. Plant Biol. 2000, 3, 254–261. [Google Scholar] [CrossRef]
- Mu, X.; Chen, Y. The Physiological Response of Photosynthesis to Nitrogen Deficiency. Plant Physiol. Biochem. 2021, 158, 76–82. [Google Scholar] [CrossRef]
- Gémes-Juhász, A.; Balogh, P.; Ferenczy, A.; Kristóf, Z. Effect of Optimal Stage of Female Gametophyte and Heat Treatment on in Vitro Gynogenesis Induction in Cucumber (Cucumis sativus L.). Plant Cell Rep. 2002, 21, 105–111. [Google Scholar] [CrossRef]
- Sabzi, S.; Pourdarbani, R.; Rohban, M.H.; García-Mateos, G.; Arribas, J.I. Estimation of Nitrogen Content in Cucumber Plant (Cucumis sativus L.) Leaves Using Hyperspectral Imaging Data with Neural Network and Partial Least Squares Regressions. Chemom. Intell. Lab. Syst. 2021, 217, 104404. [Google Scholar] [CrossRef]
- Padilla, F.M.; Peña-Fleitas, M.T.; Gallardo, M.; Thompson, R.B. Proximal Optical Sensing of Cucumber Crop N Status Using Chlorophyll Fluorescence Indices. Eur. J. Agron. 2016, 73, 83–97. [Google Scholar] [CrossRef]
- Goffart, J.P.; Olivier, M.; Frankinet, M. Crop Nitrogen Status Assessment Tools in a Decision Support System for Nitrogen Fertilization Management of Potato Crops. Horttechnology 2011, 21, 282–286. [Google Scholar] [CrossRef]
- Tomkiewicz, D.; Piskier, T. A Plant Based Sensing Method for Nutrition Stress Monitoring. Precis. Agric. 2012, 13, 370–383. [Google Scholar] [CrossRef]
- Watanabe, T.; Nakamura, N.; Sakamoto, K.; Nagata, M. Bio-Electrical Impedance Analysis of “Silk Sweet” Sweet Potato Tissues under Low-Temperature Storage Using a Novel Indicator, LTO. Biosyst. Eng. 2021, 206, 1–5. [Google Scholar] [CrossRef]
- Basak, R.; Wahid, K.A.; Dinh, A.; Soolanayakanahally, R.; Fotouhi, R.; Mehr, A.S. Rapid and Efficient Determination of Relativewater Contents of Crop Leaves Using Electrical Impedance Spectroscopy in Vegetative Growth Stage. Remote Sens. 2020, 12, 1753. [Google Scholar] [CrossRef]
- Garlando, U.; Calvo, S.; Barezzi, M.; Sanginario, A.; Ros, P.M.; Demarchi, D. Ask the Plants Directly: Understanding Plant Needs Using Electrical Impedance Measurements. Comput. Electron. Agric. 2022, 193, 106707. [Google Scholar] [CrossRef]
- Serrano-Finetti, E.; Castillo, E.; Alejos, S.; Hilario, L.L. Toward Noninvasive Monitoring of Plant Leaf Water Content by Electrical Impedance Spectroscopy. Comput. Electron. Agric. 2023, 210, 107907. [Google Scholar] [CrossRef]
- Zhang, B.; Dong, Z.; Sui, X.; Gao, J.; Feng, L. Detection of Water Content in Tomato Stems by Electrical Impedance Spectroscopy: Preliminary Study. Comput. Electron. Agric. 2024, 219, 109755. [Google Scholar] [CrossRef]
- Li, M.Q.; Li, J.Y.; Wei, X.H.; Zhu, W.J. Early Diagnosis and Monitoring of Nitrogen Nutrition Stress in Tomato Leaves Using Electrical Impedance Spectroscopy. Int. J. Agric. Biol. Eng. 2017, 10, 194–205. [Google Scholar]
- Muñoz-Huerta, R.F.; de J. Ortiz-Melendez, A.; Guevara-Gonzalez, R.G.; Torres-Pacheco, I.; Herrera-Ruiz, G.; Contreras-Medina, L.M.; Prado-Olivarez, J.; Ocampo-Velazquez, R.V. An Analysis of Electrical Impedance Measurements Applied for Plant N Status Estimation in Lettuce (Lactuca sativa). Sensors 2014, 14, 11492–11503. [Google Scholar] [CrossRef]
- Meiqing, L.; Jinyang, L.; Hanping, M.; Yanyou, W. Diagnosis and Detection of Phosphorus Nutrition Level for Solanum lycopersicum Based on Electrical Impedance Spectroscopy. Biosyst. Eng. 2016, 143, 108–118. [Google Scholar] [CrossRef]
- Jinyang, L.; Meiqing, L.; Hanping, M.; Wenjing, Z. Diagnosis of Potassium Nutrition Level in Solanum lycopersicum Based on Electrical Impedance. Biosyst. Eng. 2016, 147, 130–138. [Google Scholar] [CrossRef]
- Prasad, A.; Roy, M. Bioimpedance Analysis of Vascular Tissue and Fluid Flow in Human and Plant Body: A Review. Biosyst. Eng. 2020, 197, 170–187. [Google Scholar] [CrossRef]
- Arnon, D.I. Copper Enzymes in Isolated Chloroplasts. Polyphenoloxidase in Beta vulgaris. Plant Physiol. 1949, 24, 1–15. [Google Scholar] [CrossRef]
- Padilla, F.M.; Thompson, R.B.; Peña-Fleitas, M.T.; Gallardo, M. Reference Values for Phenological Phases of Chlorophyll Meter Readings and Reflectance Indices for Optimal N Nutrition of Fertigated Tomato. Acta Hortic. 2018, 1192, 65–72. [Google Scholar] [CrossRef]
- Hesari, N.; Szegő, A.; Mirmazloum, I.; Pónya, Z.; Kiss-Bába, E.; Kolozs, H.; Gyöngyik, M.; Vasas, D.; Papp, I. High-Nitrate-Supply-Induced Transcriptional Upregulation of Ascorbic Acid Biosynthetic and Recycling Pathways in Cucumber. Plants 2023, 12, 1292. [Google Scholar] [CrossRef] [PubMed]
- Nelson, D.W.; Sommers, L.E. Total Nitrogen Analysis of Soil and Plant Tissues. J. Assoc. Off. Anal. Chem. 1980, 63, 770–778. [Google Scholar] [CrossRef]
- Padilla, F.M.; de Souza, R.; Peña-Fleitas, M.T.; Gallardo, M.; Giménez, C.; Thompson, R.B. Different Responses of Various Chlorophyll Meters to Increasing Nitrogen Supply in Sweet Pepper. Front. Plant Sci. 2018, 9, 1752. [Google Scholar] [CrossRef] [PubMed]
- Kovács, F.; Odry, Á.; Vizvári, Z.; Kabalan, S.; Papdi, E.; Odry, P.; Juhos, K. A Novel Approach to Water Stress Assessment in Plants: New Bioimpedance Method with PSO-Optimized Cole-Cole Impedance Modeling. Comput. Electron. Agric. 2025, 234, 110167. [Google Scholar] [CrossRef]
- Vizvari, Z.; Gyorfi, N.; Maczko, G.; Varga, R.; Jakabfi-Csepregi, R.; Sari, Z.; Furedi, A.; Bajtai, E.; Vajda, F.; Tadic, V.; et al. Reproducibility Analysis of Bioimpedance-Based Self-Developed Live Cell Assays. Sci. Rep. 2024, 14, 16380. [Google Scholar] [CrossRef]
- Zhang, M.I.N.; Willison, J.H.M. Electrical Impedance Analysis in Plant Tissues: The Effect of Freeze-Thaw Injury on the Electrical Properties of Potato Tuber and Carrot Root Tissues. Can. J. Plant Sci. 1992, 72, 545–553. [Google Scholar] [CrossRef]
- Nouaze, J.C.; Kim, J.H.; Jeon, G.R.; Kim, J.H. Monitoring of Indoor Farming of Lettuce Leaves for 16 Hours Using Electrical Impedance Spectroscopy (EIS) and Double-Shell Model (DSM). Sensors 2022, 22, 9671. [Google Scholar] [CrossRef]
- Ghoneim, M.S.; Gadallah, S.I.; Said, L.A.; Eltawil, A.M.; Radwan, A.G.; Madian, A.H. Plant Stem Tissue Modeling and Parameter Identification Using Metaheuristic Optimization Algorithms. Sci. Rep. 2022, 12, 3992. [Google Scholar] [CrossRef]
- Zhang, M.I.N.; Willison, J.H.M. Electrical Impedance Analysis in Plant Tissues8. J. Exp. Bot. 1993, 44, 1369–1375. [Google Scholar] [CrossRef]
- AboBakr, A.; Said, L.A.; Madian, A.H.; Elwakil, A.S.; Radwan, A.G. Experimental Comparison of Integer/Fractional-Order Electrical Models of Plant. AEU-Int. J. Electron. Commun. 2017, 80, 1–9. [Google Scholar] [CrossRef]
- López-Villanueva, J.A.; Rodríguez Bolívar, S. Constant Phase Element in TheTime Domain: The Problem of Initialization. Energies 2022, 15, 792. [Google Scholar] [CrossRef]
- Ando, Y.; Mizutani, K.; Wakatsuki, N. Electrical Impedance Analysis of Potato Tissues during Drying. J. Food Eng. 2014, 121, 24–31. [Google Scholar] [CrossRef]
- Richardson, J.T.E. Eta Squared and Partial Eta Squared as Measures of Effect Size in Educational Research. Educ. Res. Rev. 2011, 6, 135–147. [Google Scholar] [CrossRef]
- Li, J.; Li, B.; Guan, Q.; Gao, J. Signal Molecules Controlling Nitrate Uptake by Roots. J. Plant Interact. 2022, 17, 301–308. [Google Scholar] [CrossRef]
- Hamed, S.; Altana, A.; Lugli, P.; Petti, L.; Ibba, P. Supervised Classification and Circuit Parameter Analysis of Electrical Bioimpedance Spectroscopy Data of Water Stress in Tomato Plants. Comput. Electron. Agric. 2024, 226, 109347. [Google Scholar] [CrossRef]
- Nikolic, M.; Cesco, S.; Monte, R.; Tomasi, N.; Gottardi, S.; Zamboni, A.; Pinton, R.; Varanini, Z. Nitrate Transport in Cucumber Leaves Is an Inducible Process Involving an Increase in Plasma Membrane H+-ATPase Activity and Abundance. BMC Plant Biol. 2012, 12, 66. [Google Scholar] [CrossRef]
- Azzarello, E.; Masi, E.; Mancuso, S. Electrochemical Impedance Spectroscopy. In Plant Electrophysiol. Methods Cell Electrophysiology; Springer: Berlin/Heidelberg, Germany, 2012; pp. 205–223. [Google Scholar] [CrossRef]
- Masclaux-Daubresse, C.; Daniel-Vedele, F.; Dechorgnat, J.; Chardon, F.; Gaufichon, L.; Suzuki, A. Nitrogen Uptake, Assimilation and Remobilization in Plants: Challenges for Sustainable and Productive Agriculture. Ann. Bot. 2010, 105, 1141–1157. [Google Scholar] [CrossRef]
- Tan, X.; Li, K.; Wang, Z.; Zhu, K.; Tan, X.; Cao, J. A Review of Plant Vacuoles: Formation, Located Proteins, and Functions. Plants 2019, 8, 327. [Google Scholar] [CrossRef]
- Li, S.X.; Wang, Z.H.; Stewart, B.A. Responses of Crop Plants to Ammonium and Nitrate N. Adv. Agron. 2013, 118, 205–397. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.; Yin, L.; Wang, S.; Deng, X. Alteration in Lipid Metabolism Is Involved in Nitrogen Deficiency Response in Wheat Seedlings. Plant Physiol. Biochem. 2024, 214, 108883. [Google Scholar] [CrossRef]
- Yongnian, Z.; Yinhe, C.; Yihua, B.; Xiaochan, W.; Jieyu, X. Tomato Maturity Detection Based on Bioelectrical Impedance Spectroscopy. Comput. Electron. Agric. 2024, 227, 109553. [Google Scholar] [CrossRef]
- Hamed, S.; Ibba, P.; Altana, A.; Lugli, P.; Petti, L. Towards Tomato Plant Iron Stress Monitoring Through Bioimpedance and Circuit Analysis. In Proceedings of the IEEE Conference on AgriFood Electronics (CAFE 2023), Torino, Italy, 25–27 September 2023; pp. 20–24. [Google Scholar] [CrossRef]
- O’Brien, J.A.; Vega, A.; Bouguyon, E.; Krouk, G.; Gojon, A.; Coruzzi, G.; Gutiérrez, R.A. Nitrate Transport, Sensing, and Responses in Plants. Mol. Plant 2016, 9, 837–856. [Google Scholar] [CrossRef]

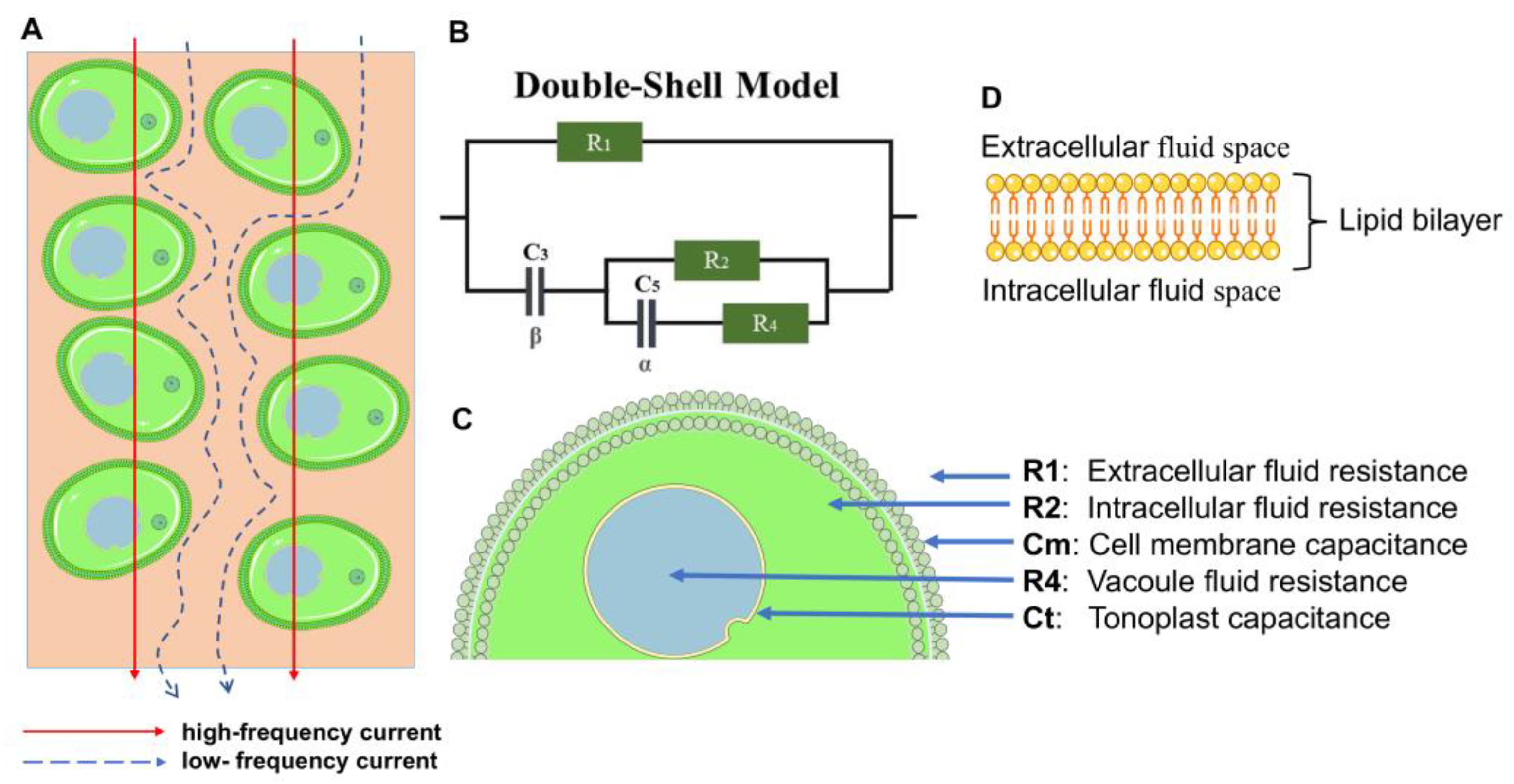
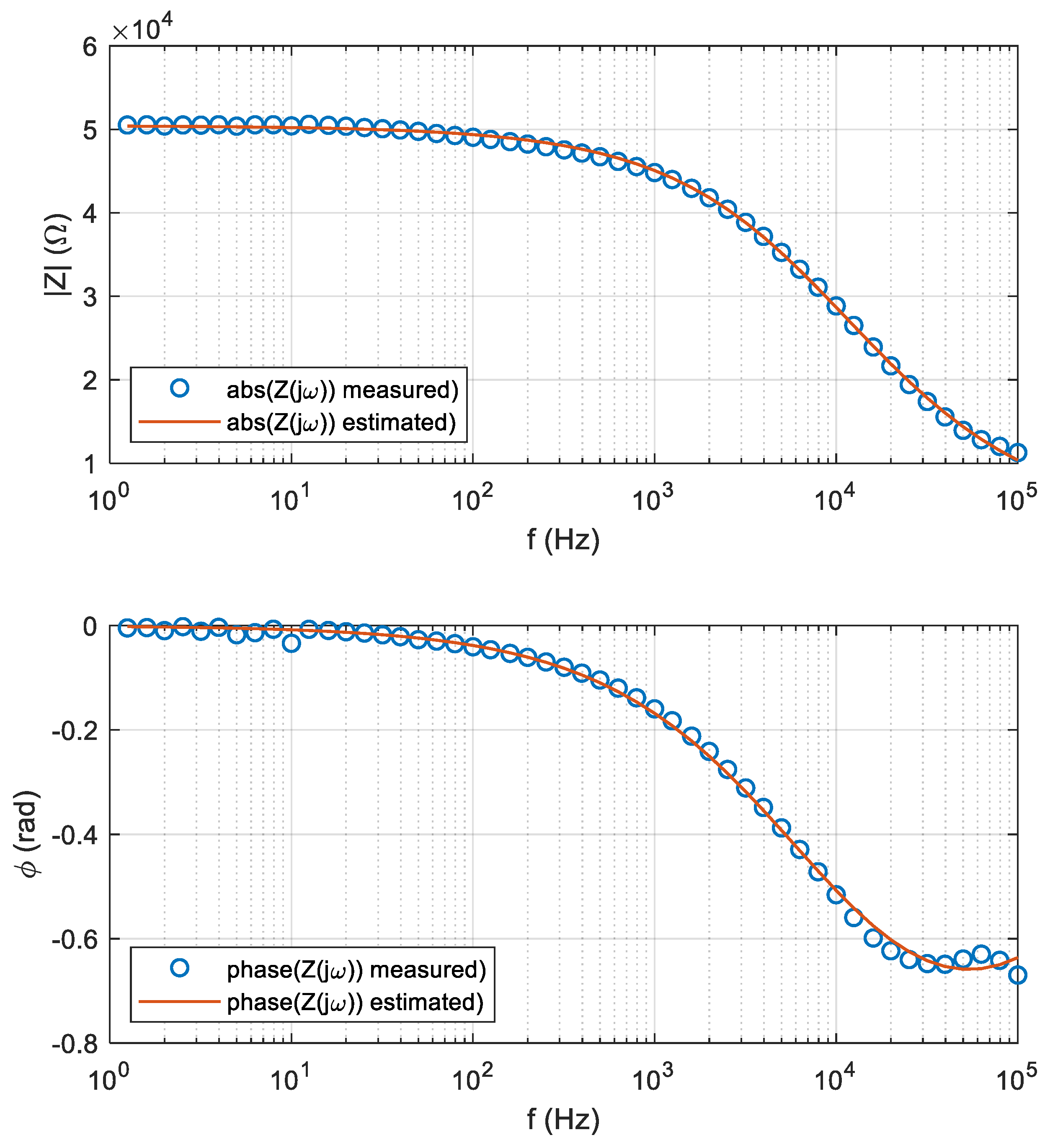
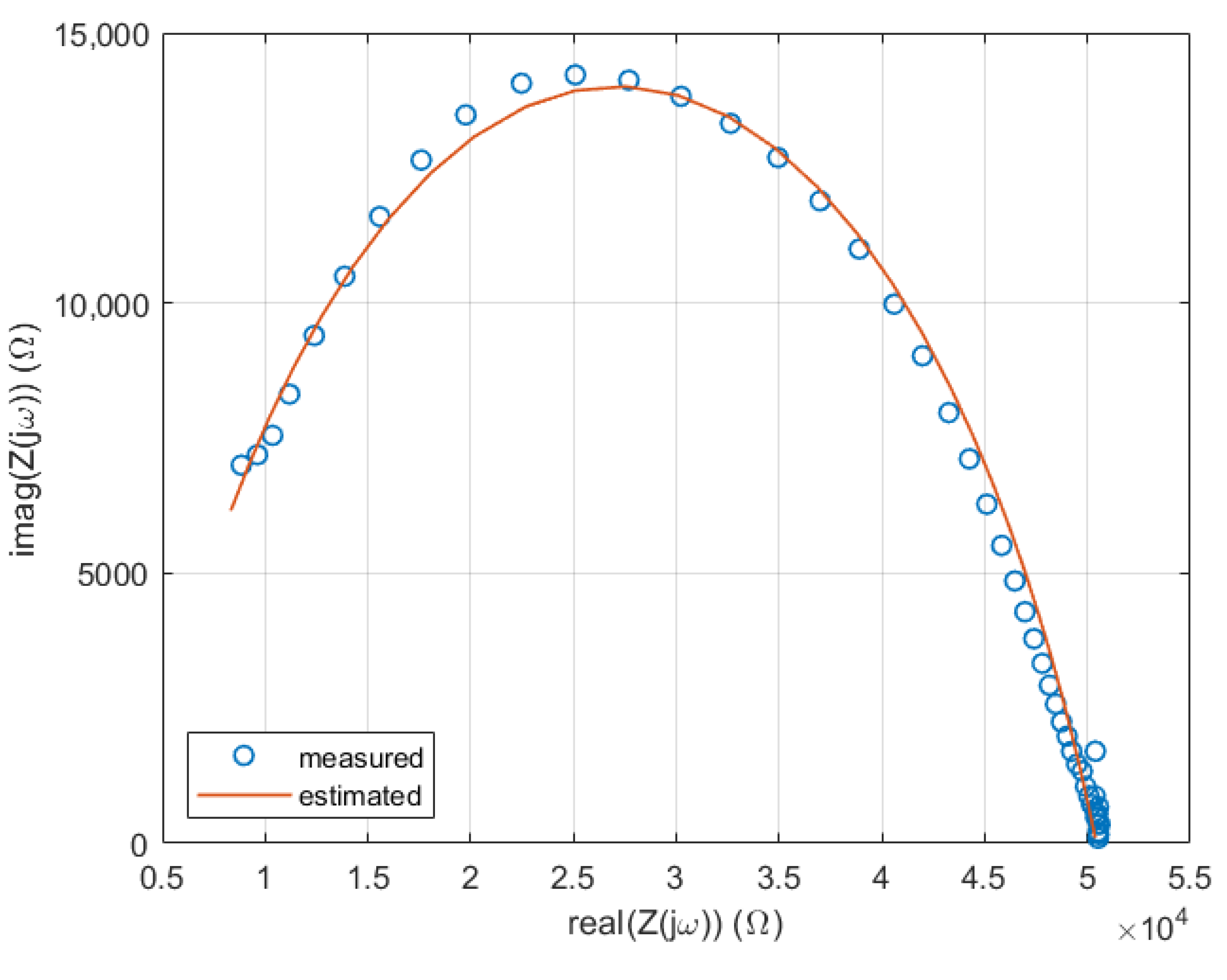
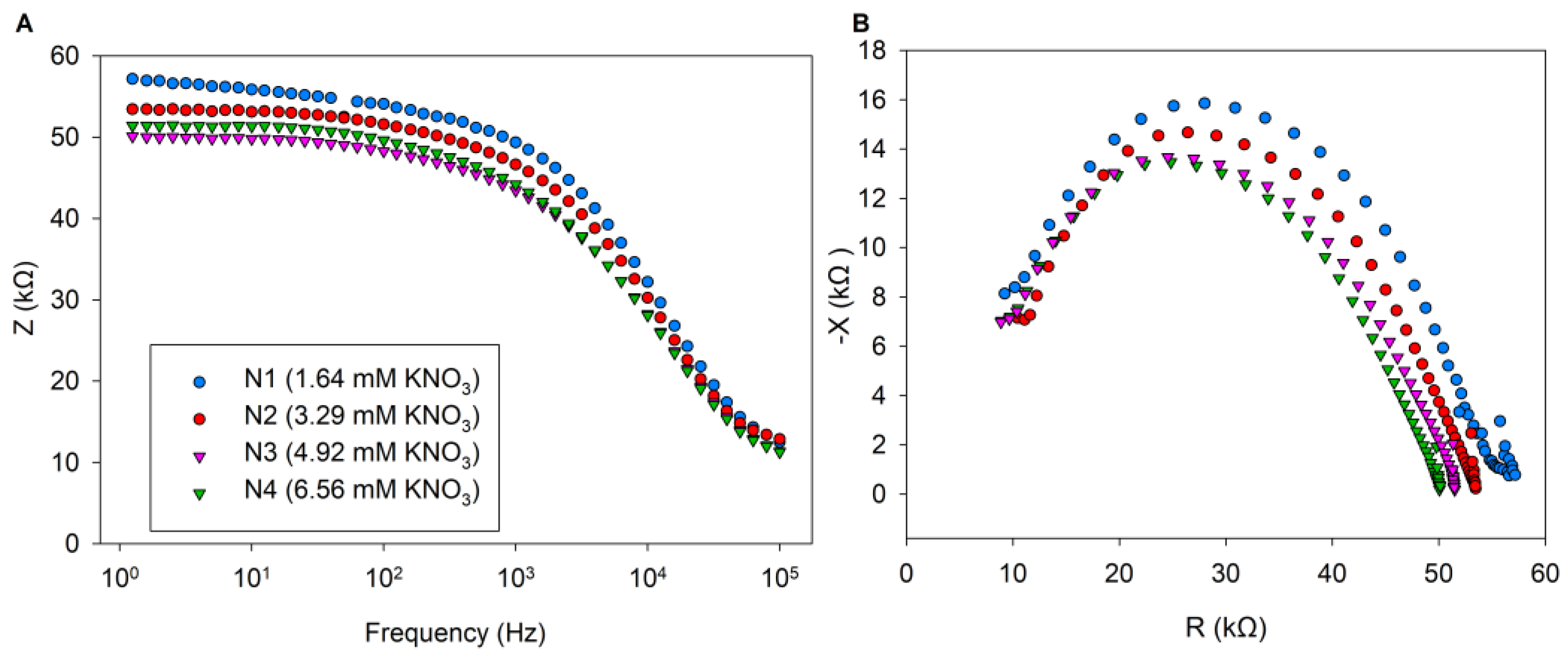

| Parameter | Initial Value | Range |
|---|---|---|
| Treatment | CCI | Total N m/m % | NO3− mg g−1 FW | Chla-a mg g−1 FW | Chla-b mg g−1 FW | Total-chl mg g−1 FW | Carotenoids mg g−1 FW |
|---|---|---|---|---|---|---|---|
| N1 | 37.93 ± 0.86 a | 4.41 ± 0.07 a | 0.37 ± 0.17 a | 3.56 ± 0.07 a | 1.15 ± 0.02 a | 4.55 ± 0.09 a | 0.63 ± 0.01 a |
| N2 | 43.33 ± 1.80 b | 4.87 ± 0.15 b | 0.43 ± 0.36 b | 4.05 ± 0.16 b | 1.31 ± 0.05 b | 5.16 ± 0.20 b | 0.71 ± 0.02 b |
| N3 | 47.33 ± 3.17 c | 5.22 ± 0.27 c | 0.47 ± 0.64 c | 4.41 ± 0.28 c | 1.43 ± 0.09 bc | 5.62 ± 0.36 c | 0.77 ± 0.04 c |
| N4 | 49.70 ± 4.46 c | 5.42 ± 0.38 c | 0.46 ± 0.89 c | 4.63 ± 0.40 c | 1.49 ± 0.12 c | 5.89 ± 0.50 d | 0.80 ± 0.06 c |
| F values | 28.03 | 25.03 | 22.03 | 28.03 | 26.03 | 28.03 | 25.03 |
| 0.72 | 0.71 | 0.69 | 0.72 | 0.60 | 0.72 | 0.52 | |
| p values | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.05 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kovács, F.; Juhos, K.; Vizvári, Z.; Odry, P.; Gyalai, I.M.; Sarcevic, P.; Odry, Á. Bioimpedance Analysis of Cucumber Plants Exposed to Different Nitrogen Doses Under Greenhouse Conditions. Sensors 2025, 25, 2486. https://doi.org/10.3390/s25082486
Kovács F, Juhos K, Vizvári Z, Odry P, Gyalai IM, Sarcevic P, Odry Á. Bioimpedance Analysis of Cucumber Plants Exposed to Different Nitrogen Doses Under Greenhouse Conditions. Sensors. 2025; 25(8):2486. https://doi.org/10.3390/s25082486
Chicago/Turabian StyleKovács, Flórián, Katalin Juhos, Zoltán Vizvári, Péter Odry, Ingrid M. Gyalai, Peter Sarcevic, and Ákos Odry. 2025. "Bioimpedance Analysis of Cucumber Plants Exposed to Different Nitrogen Doses Under Greenhouse Conditions" Sensors 25, no. 8: 2486. https://doi.org/10.3390/s25082486
APA StyleKovács, F., Juhos, K., Vizvári, Z., Odry, P., Gyalai, I. M., Sarcevic, P., & Odry, Á. (2025). Bioimpedance Analysis of Cucumber Plants Exposed to Different Nitrogen Doses Under Greenhouse Conditions. Sensors, 25(8), 2486. https://doi.org/10.3390/s25082486












