An Adaptive Signal Denoising Method Based on Reweighted SVD for the Fault Diagnosis of Rolling Bearings
Abstract
Highlights
- This paper proposed an adaptive signal denoising method based on frequency domain multipoint kurtosis (FDMK) and singular value decomposition (SVD).
- FDMK is used to identify sensitive singular components that contain fault-related information, and an estimation process is proposed to calculate the fault characteristic frequency.
- The proposed method FDMK-SVD can effectively extract fault features from raw vibration signals, even when faced with significant background noise and other interferences, enabling accurate fault diagnosis of rolling bearings.
Abstract
1. Introduction
2. Principle of SVD-Based Signal Denoising Approach
3. Reweighted Singular Value Decomposition Based on Frequency Domain Multipoint Kurtosis
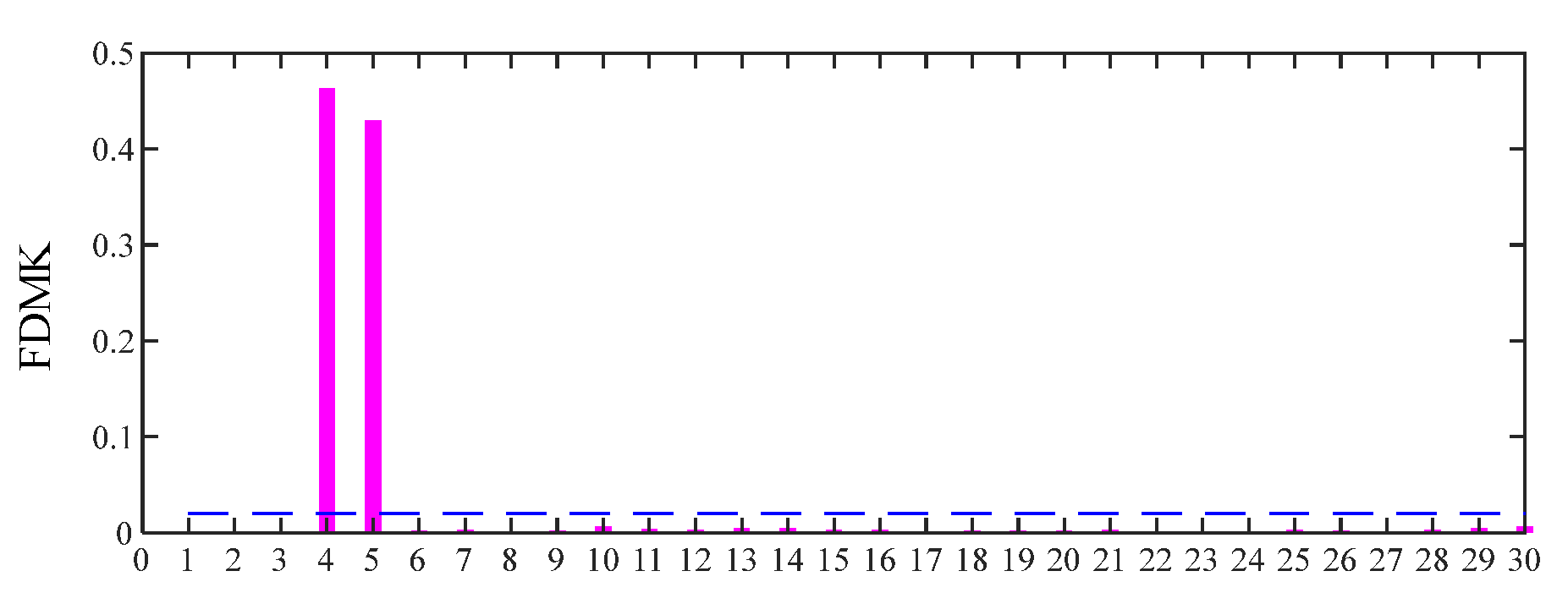
3.1. Frequency Domain Multipoint Kurtosis
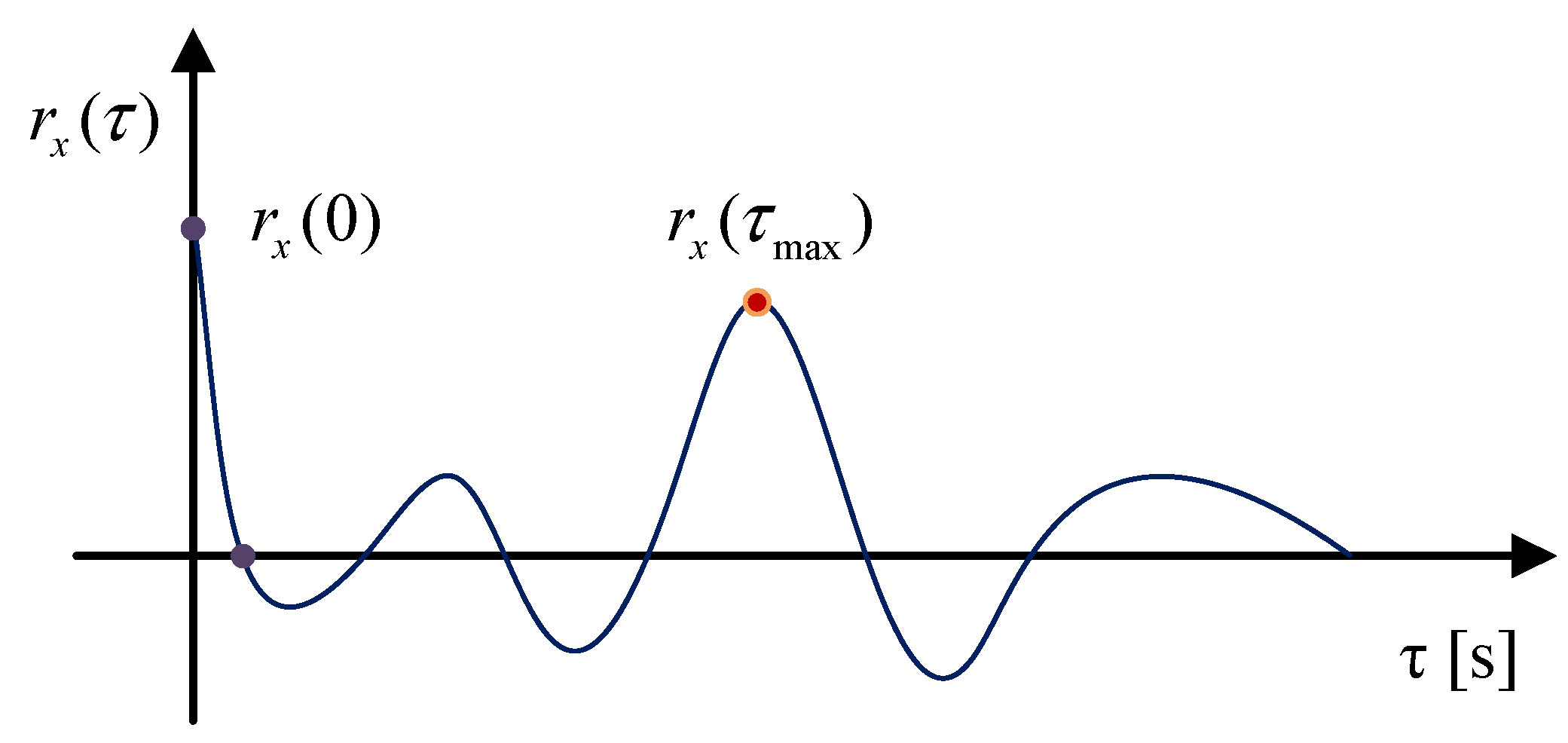
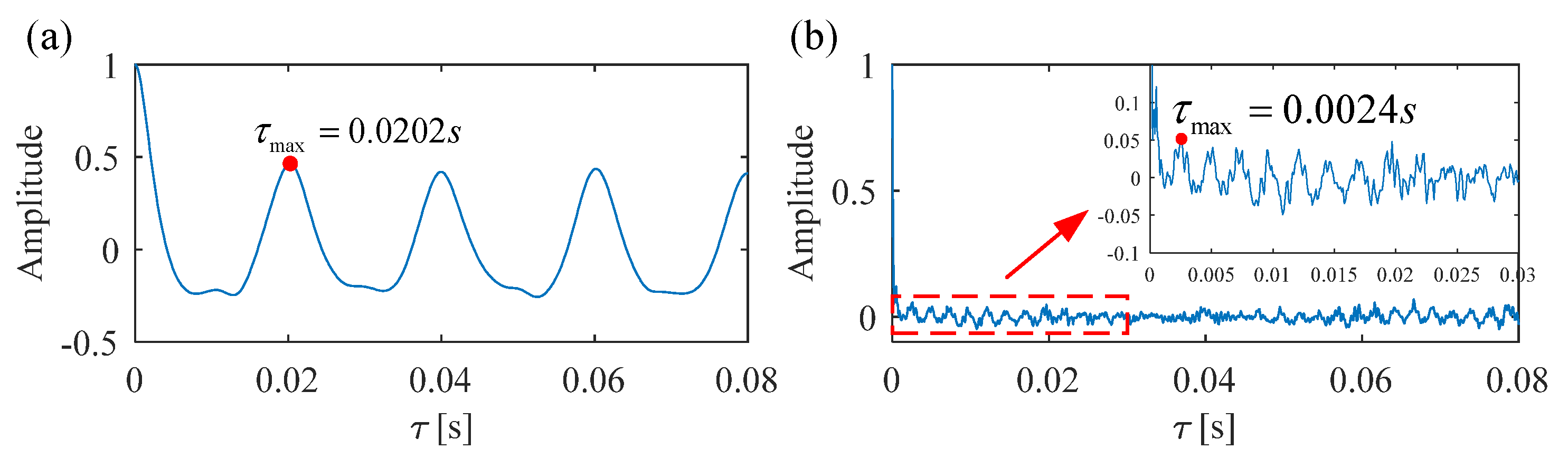
3.2. The Estimation of Fault Characteristic Frequency and Construction of Target Vector
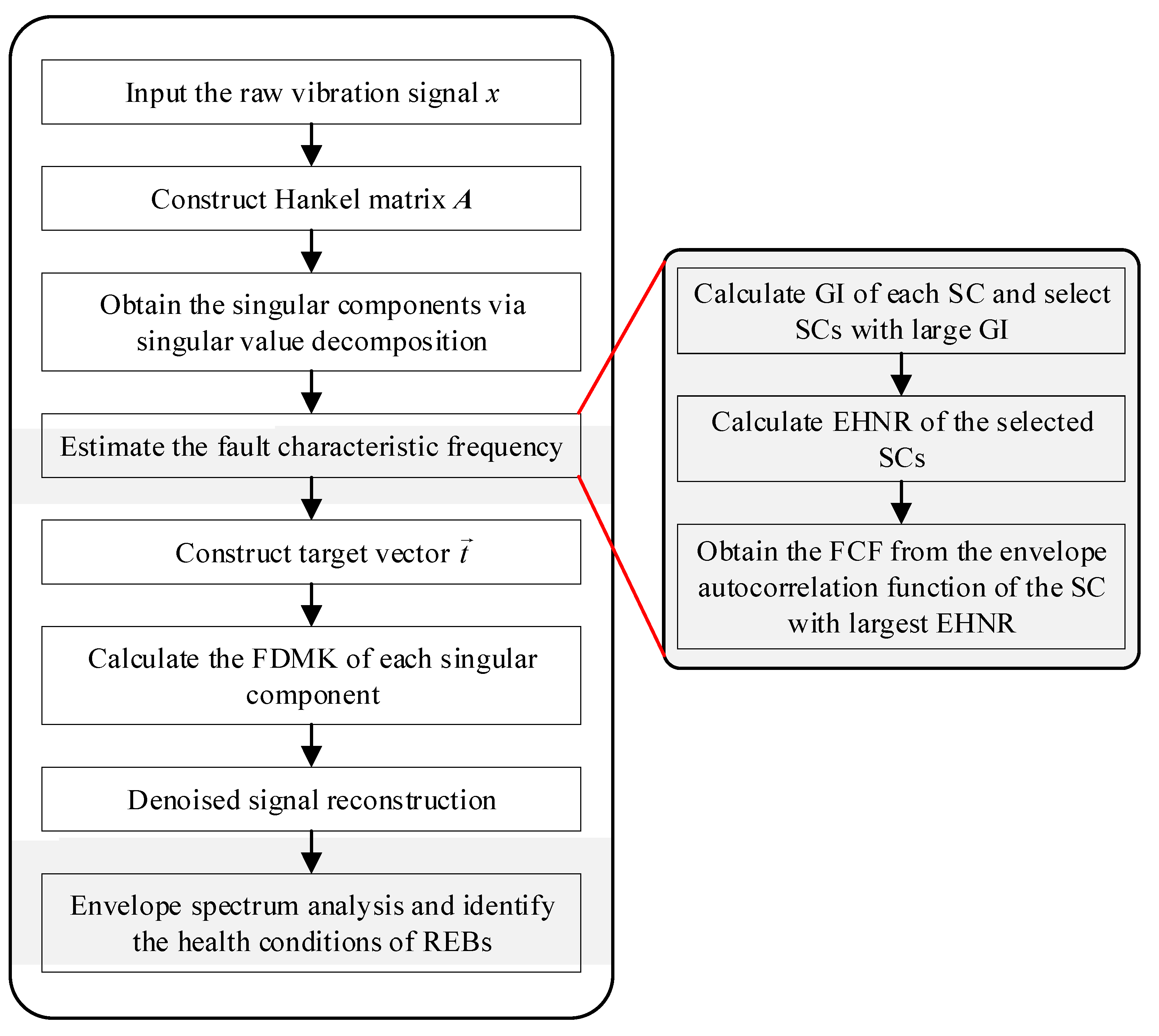
3.3. The Proposed FDMK-SVD for Fault Detection of REBs
4. Simulation Analysis
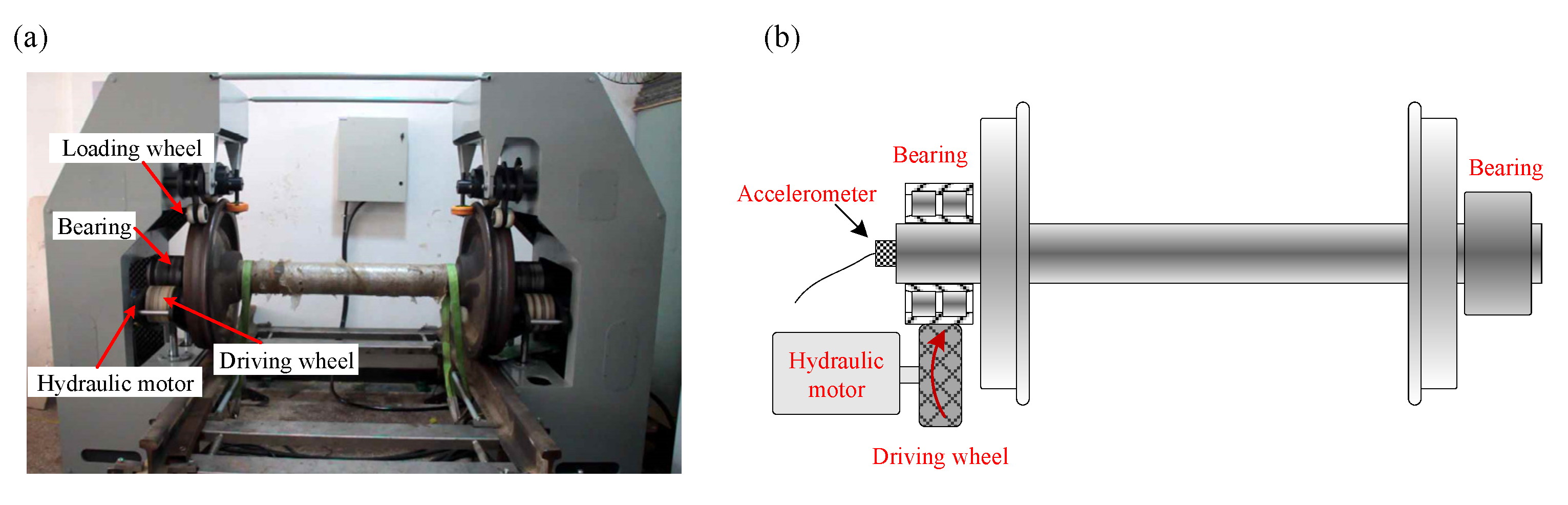
5. Experimental Verification
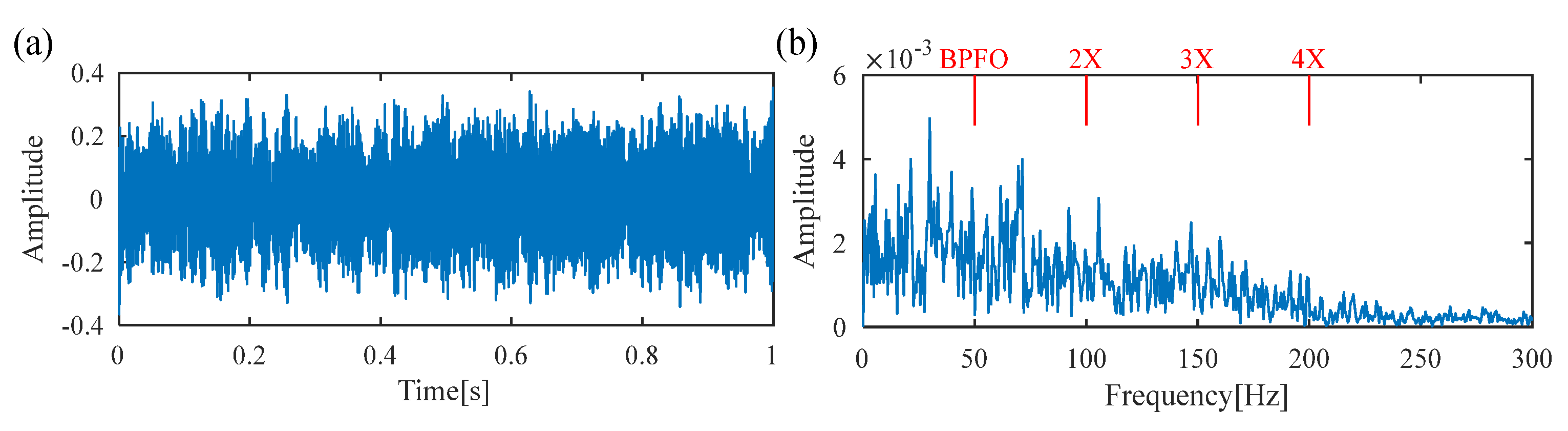
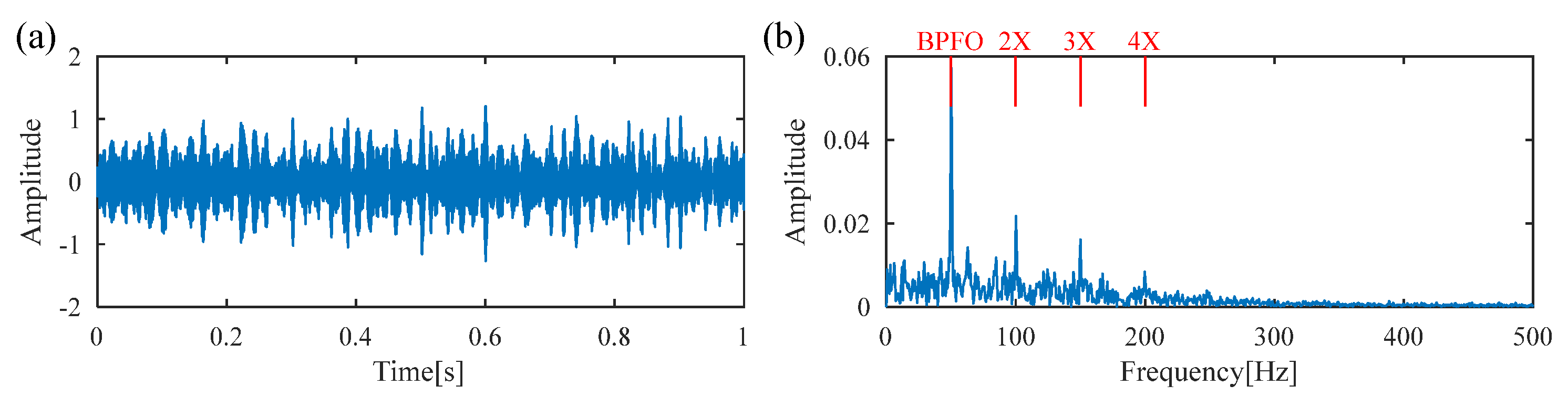
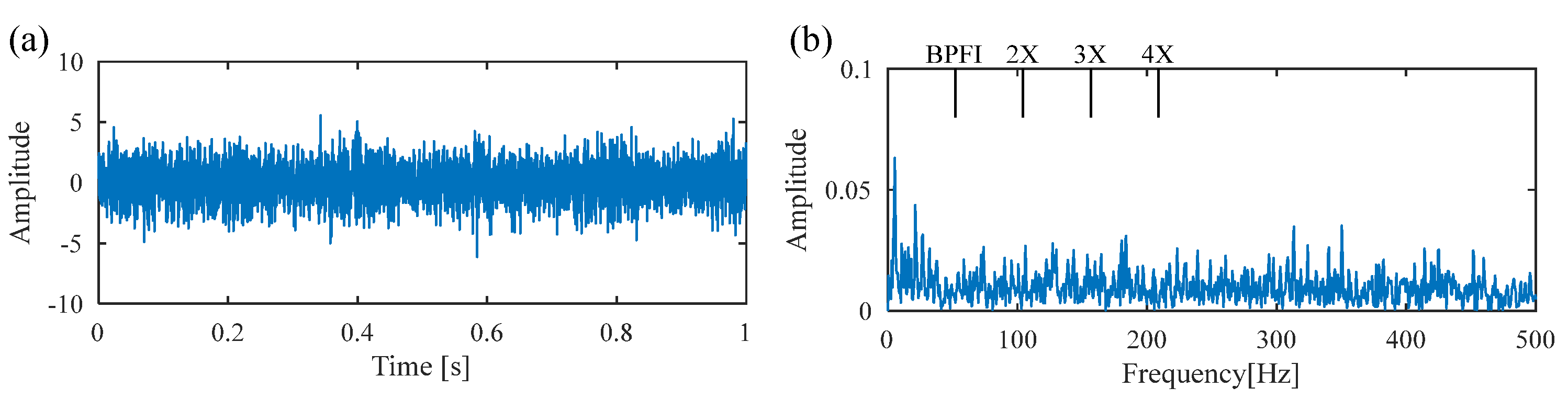
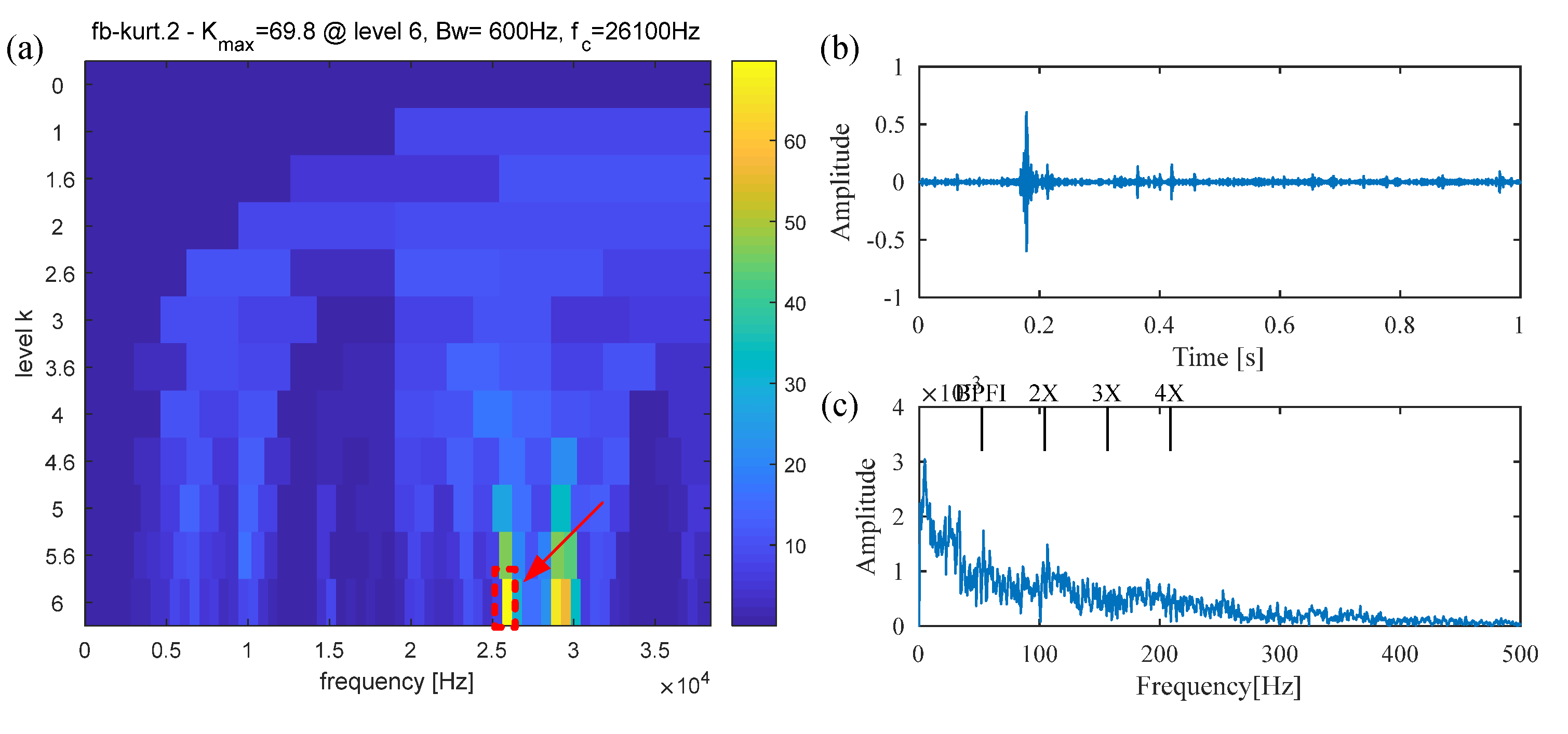
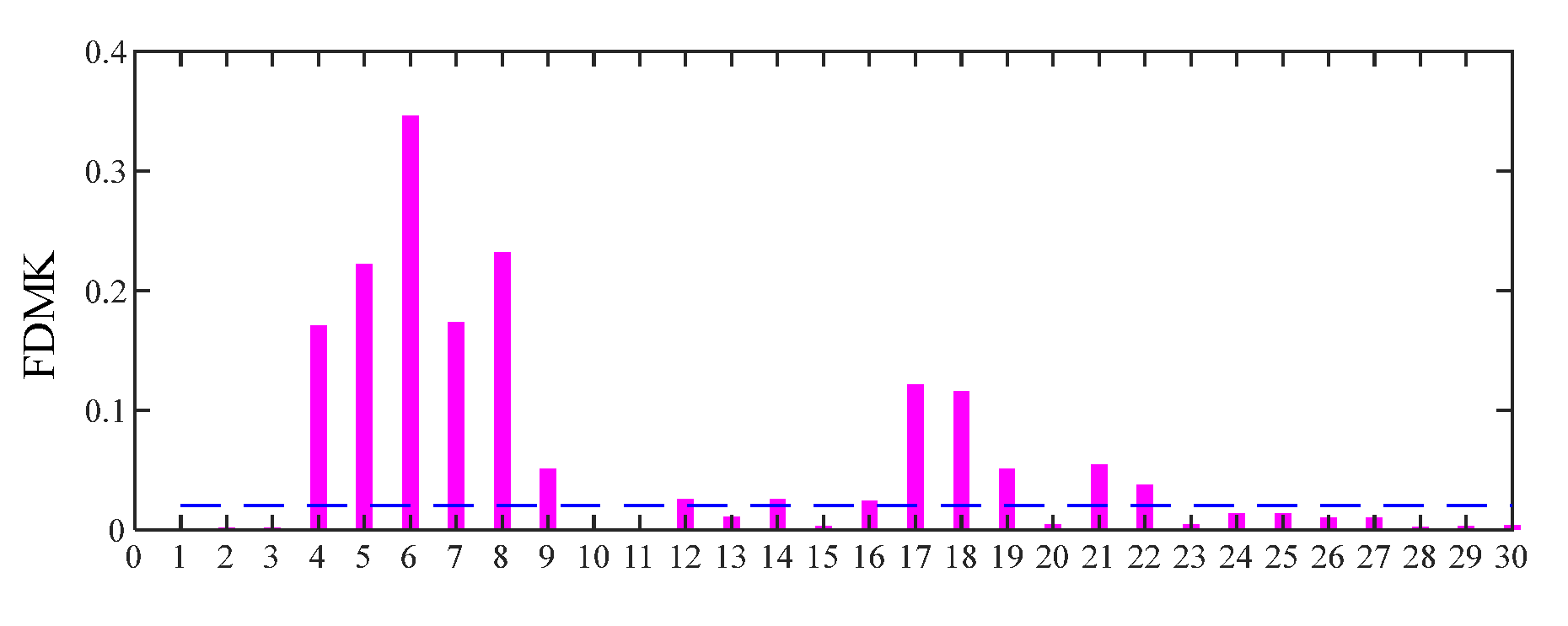
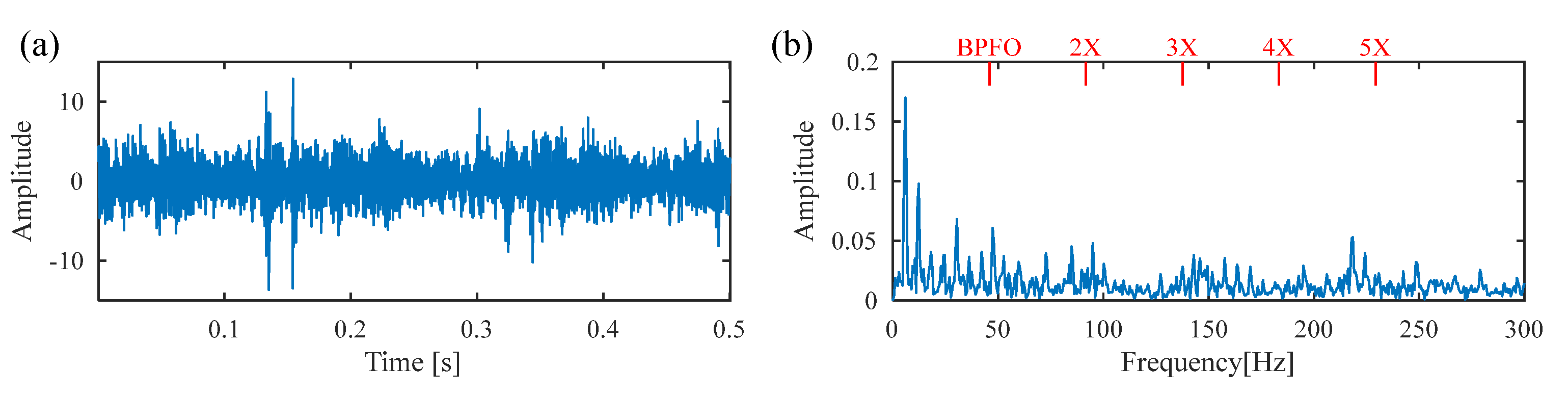
5.1. Experiment 1: The Bearing with Inner-Race-Fault
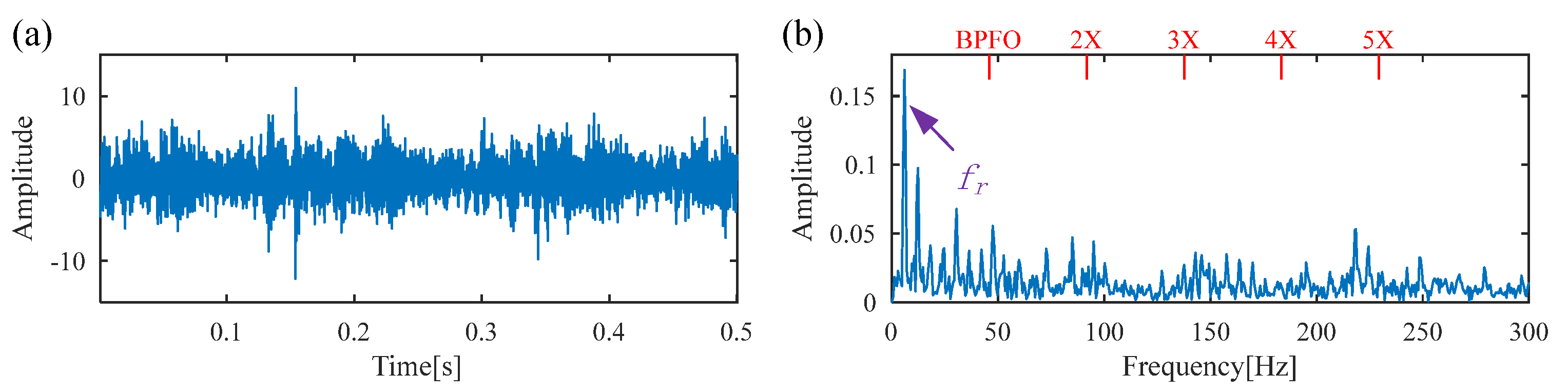
5.2. Experiment 2: The Bearing with Outer-Race Fault
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Que, H.; Liu, X.; Jin, S.; Huo, Y.; Wu, C.; Ding, C.; Zhu, Z. Partial transfer learning method based on inter-class feature transfer for rolling bearing fault diagnosis. Sensors 2024, 24, 5165. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Li, S.; Feng, K.; Sun, B.; Yang, X.; Kou, L.; Zhao, Z.; Huang, G.Q. Multiperspective temporal pooling convolutional neural networks for fault diagnosis of mechanical transmission systems. IEEE Trans. Instrum. Meas. 2025, 74, 1–12. [Google Scholar] [CrossRef]
- Shi, M.; Ding, C.; Chang, S.; Shen, C.; Huang, W.; Zhu, Z. Cross-domain class incremental broad network for continuous diagnosis of rotating machinery faults under variable operating conditions. IEEE Trans. Ind. Inform. 2024, 20, 6356–6368. [Google Scholar] [CrossRef]
- Bhattacharjee, B.; Chakraborti, P.; Choudhuri, K. Selection of suitable lubricant for sliding contact bearing and the effect of different lubricants on bearing performance: A review and recommendations. Tribol.-Finn. J. Tribol. 2020, 37, 13–25. [Google Scholar] [CrossRef]
- Ding, C.; Huang, W.; Shen, C.; Jiang, X.; Wang, J.; Zhu, Z. Synchroextracting frequency synchronous chirplet transform for fault diagnosis of rotating machinery under varying speed conditions. Struct. Health Monit. 2024, 23, 1403–1422. [Google Scholar] [CrossRef]
- Ambrozkiewicz, B.; Litak, G.; Georgiadis, A.; Syta, A.; Meier, N.; Gassner, A. Effect of radial clearance on ball bearing’s dynamics using a 2-DOF model. Int. J. Simul. Model. 2021, 20, 513–524. [Google Scholar] [CrossRef]
- Dadouche, A.; Kerrouche, R. Bearing skidding detection for high speed and aero engine applications[C]//Turbo Expo: Power for Land, Sea, and Air. Am. Soc. Mech. Eng. 2021, 85024, V09AT24A014. [Google Scholar]
- Zhang, B.; Miao, Y.; Lin, J.; Li, H. Weighted envelope spectrum based on the spectral coherence for bearing diagnosis. ISA Trans. 2022, 123, 398–412. [Google Scholar] [CrossRef]
- Mauricio, A.; Gryllias, K. Cyclostationary-based multiband envelope spectra extraction for bearing diagnostics: The combined improved envelope spectrum. Mech. Syst. Signal Process. 2021, 149, 107150. [Google Scholar] [CrossRef]
- Zhang, Q.; Ding, J.; Zhao, W. An adaptive boundary determination method for empirical wavelet transform and its application in wheelset-bearing fault detection in high-speed trains. Measurement 2021, 171, 108746. [Google Scholar] [CrossRef]
- Sun, Y.; Li, S.; Wang, Y.; Wang, X. Fault diagnosis of rolling bearing based on empirical mode decomposition and improved manhattan distance in symmetrized dot pattern image. Mech. Syst. Signal Process. 2021, 159, 107817. [Google Scholar] [CrossRef]
- Zheng, J.; Su, M.; Ying, W.; Tong, J.; Pan, Z. Improved uniform phase empirical mode decomposition and its application in machinery fault diagnosis. Measurement 2021, 179, 109425. [Google Scholar] [CrossRef]
- Miao, Y.; Li, C.; Zhang, B.; Lin, J. Application of a coarse-to-fine minimum entropy deconvolution method for rotating machines fault detection. Mech. Syst. Signal Process. 2023, 198, 110431. [Google Scholar] [CrossRef]
- Xiong, M.; Lv, Y.; Dang, Z.; Yuan, R.; Song, H. Early fault diagnosis of rolling bearings based on parameter-adaptive multipoint optimal minimum entropy deconvolution adjusted and dynamic mode decomposition. Meas. Sci. Technol. 2022, 33, 125101. [Google Scholar] [CrossRef]
- López, C.; Wang, D.; Naranjo, Á.; Moore, K.J. Box-cox-sparse-measures-based blind filtering: Understanding the difference between the maximum kurtosis deconvolution and the minimum entropy deconvolution. Mech. Syst. Signal Process. 2022, 165, 108376. [Google Scholar] [CrossRef]
- Zhao, X.; Ye, B. Similarity of signal processing effect between Hankel matrix-based SVD and wavelet transform and its mechanism analysis. Mech. Syst. Signal Process. 2009, 23, 1062–1075. [Google Scholar] [CrossRef]
- Zhao, X.; Ye, B. Singular value decomposition packet and its application to extraction of weak fault feature, Mechanical Systems and Signal Processing. Mech. Syst. Signal Process. 2016, 70, 73–86. [Google Scholar] [CrossRef]
- Golafshan, R.; Sanliturk, K.Y. SVD and Hankel matrix based de-noising approach for ball bearing fault detection and its assessment using artificial faults. Mech. Syst. Signal Process. 2016, 70, 36–50. [Google Scholar] [CrossRef]
- Cong, F.; Chen, J.; Dong, G.; Zhao, F. Short-time matrix series based singular value decomposition for rolling bearing fault diagnosis. Mech. Syst. Signal Process. 2013, 34, 218–230. [Google Scholar] [CrossRef]
- Duan, R.; Liao, Y. Impulsive feature extraction with improved singular spectrum decomposition and sparsity-closing morphological analysis. Mech. Syst. Signal Process. 2022, 180, 109436. [Google Scholar] [CrossRef]
- Jiang, H.; Jiang, Y.; Xiang, J. Method using singular value decomposition and whale optimization algorithm to quantitatively detect multiple damages in turbine blades. Struct. Health Monit. 2024, 23, 1025–1036. [Google Scholar] [CrossRef]
- Jiang, H.; Chen, J.; Dong, G.; Liu, T.; Chen, G. Study on Hankel matrix-based SVD and its application in rolling element bearing fault diagnosis. Mech. Syst. Signal Process. 2015, 52, 338–359. [Google Scholar] [CrossRef]
- Kang, J.; Kim, M. Singular value decomposition based feature extraction approaches for classifying faults of induction motors. Mech. Syst. Signal Process. 2013, 41, 348–356. [Google Scholar] [CrossRef]
- Muruganatham, B.; Sanjith, M.A.; Krishnakumar, B.; Murty, S.A.V.S. Roller element bearing fault diagnosis using singular spectrum analysis. Mech. Syst. Signal Process. 2013, 35, 150–166. [Google Scholar] [CrossRef]
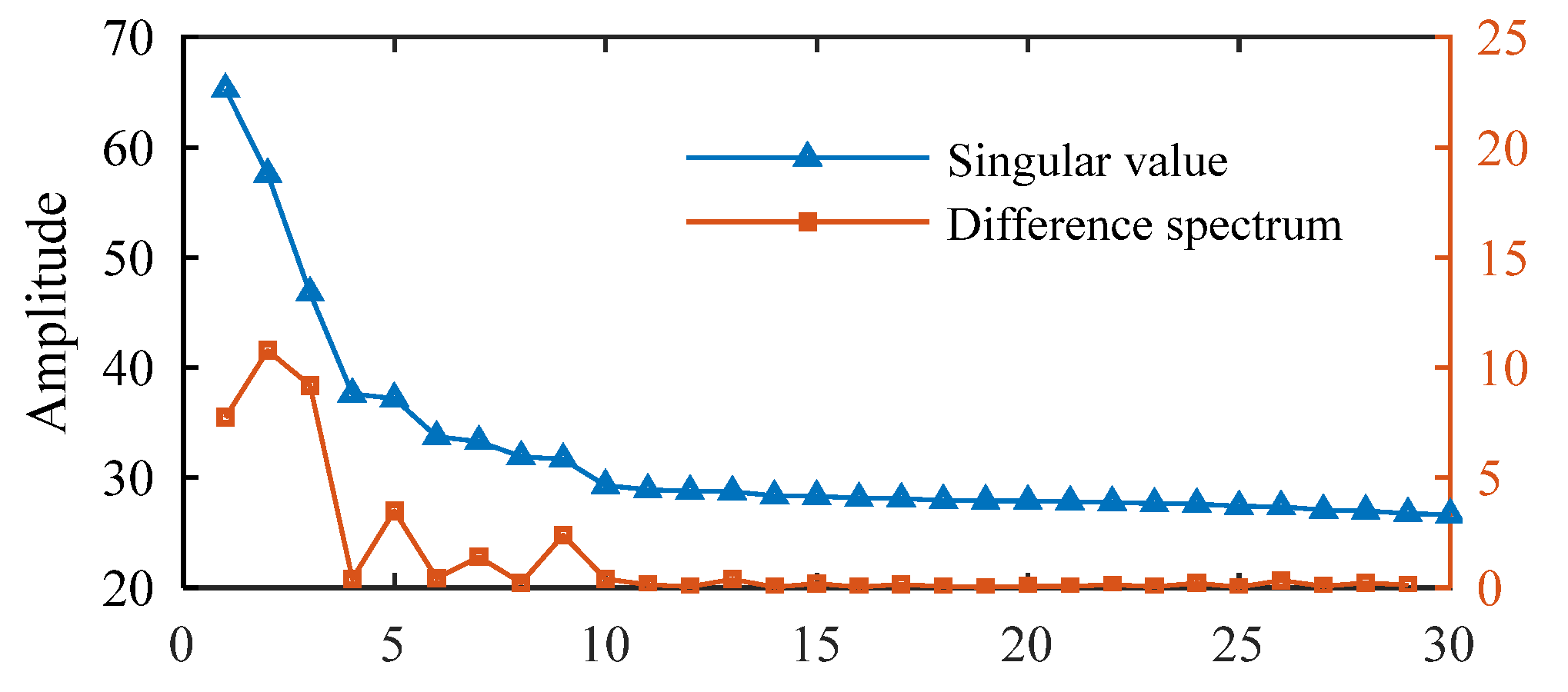
- Zhao, X.; Ye, B. Selection of effective singular values using difference spectrum and its application to fault diagnosis of headstock. Mech. Syst. Signal Process. 2011, 25, 1617–1631. [Google Scholar] [CrossRef]
- Qiao, Z.; Pan, Z. SVD principle analysis and fault diagnosis for bearings based on the correlation coefficient. Mech. Syst. Signal Process. 2015, 26, 085014. [Google Scholar] [CrossRef]
- Zhao, M.; Jia, X. A novel strategy for signal denoising using reweighted SVD and its applications to weak fault feature enhancement of rotating machinery. Mech. Syst. Signal Process. 2017, 94, 129–147. [Google Scholar] [CrossRef]
- Zhao, X.; Ye, B.; Chen, T. Difference spectrum theory of singular value and its application to the fault diagnosis of headstock of lathe. J. Mech. Eng. 2010, 46, 100–108. [Google Scholar] [CrossRef]
- Li, Q.; Weaver, B.; Chu, F.; Wang, W. A fast damping ratio identification method for rotating machinery based on the singular value of a directional power spectra density function matrix. J. Sound Vib. 2020, 488, 115630. [Google Scholar] [CrossRef]
- Su, W.; Wang, F.; Zhu, H.; Zhang, Z.; Guo, Z. Rolling element bearing faults diagnosis based on optimal Morlet wavelet filter and autocorrelation enhancement. Mech. Syst. Signal Process. 2010, 24, 1458–1472. [Google Scholar] [CrossRef]
- Kim, T.; Lee, G.; Youn, B.D. PHM experimental design for effective state separation using Jensen–Shannon divergence. Reliab. Eng. Syst. Saf. 2019, 190, 106503. [Google Scholar] [CrossRef]
- Meng, Z.; Cui, Z.; Liu, J.; Li, J.; Fan, F. Maximum cyclic Gini index deconvolution for rolling bearing fault diagnosis. IEEE Trans. Instrum. Meas. 2023, 72, 1–12. [Google Scholar] [CrossRef]
- He, W.; Jiang, Z.N.; Feng, K. Bearing fault detection based on optimal wavelet filter and sparse code shrinkage. Measurement 2009, 42, 1092–1102. [Google Scholar] [CrossRef]
- Wang, D. Some further thoughts about spectral kurtosis, spectral L2/L1 norm, spectral smoothness index and spectral Gini index for characterizing repetitive transients. Mech. Syst. Signal Process. 2018, 108, 360–368. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, Y.; Wan, F.; Chen, B.; Liu, J.; Hu, B. Adaptive filtering enhanced windowed correlated kurtosis for multiple faults diagnosis of locomotive bearings. ISA Trans. 2020, 101, 421–429. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, M.; Lin, J.; Lei, Y. Envelope harmonic-to-noise ratio for periodic impulses detection and its application to bearing diagnosis. Measurement 2016, 91, 385–397. [Google Scholar] [CrossRef]
- McDonald, G.L.; Zhao, Q. Multipoint optimal minimum entropy deconvolution and convolution fix: Application to vibration fault detection. Mech. Syst. Signal Process. 2017, 82, 461–477. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J.; Lei, Y. Application of an improved maximum correlated kurtosis deconvolution method for fault diagnosis of rolling element bearings. Mech. Syst. Signal Process. 2017, 92, 173–195. [Google Scholar] [CrossRef]
- Xu, X.; Zhao, M.; Lin, J.; Lei, Y. Periodicity-based kurtogram for random impulse resistance. Meas. Sci. Technol. 2015, 26, 085011. [Google Scholar] [CrossRef]
- Loza, C.A.; Principe, J.C. Transient model of EEG using Gini index-based matching pursuit. In Proceedings of the 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Shanghai, China, 20–25 March 2016; pp. 724–728. [Google Scholar]
- Zonoobi, D.; Kassim, A.A.; Venkatesh, Y.V. Gini index as sparsity measure for signal reconstruction from compressive samples. IEEE J. Sel. Top. Signal Process. 2011, 5, 927–932. [Google Scholar] [CrossRef]
- Miao, Y.; Zhao, M.; Lin, J. Periodicity-impulsiveness spectrum based on singular value negentropy and its application for identification of optimal frequency band. IEEE Trans. Ind. Electron. 2018, 66, 3127–3138. [Google Scholar] [CrossRef]
- Ding, C.; Zhao, M.; Lin, J. Sparse feature extraction based on periodical convolutional sparse representation for fault detection of rotating machinery. Meas. Sci. Technol. 2020, 32, 015008. [Google Scholar] [CrossRef]

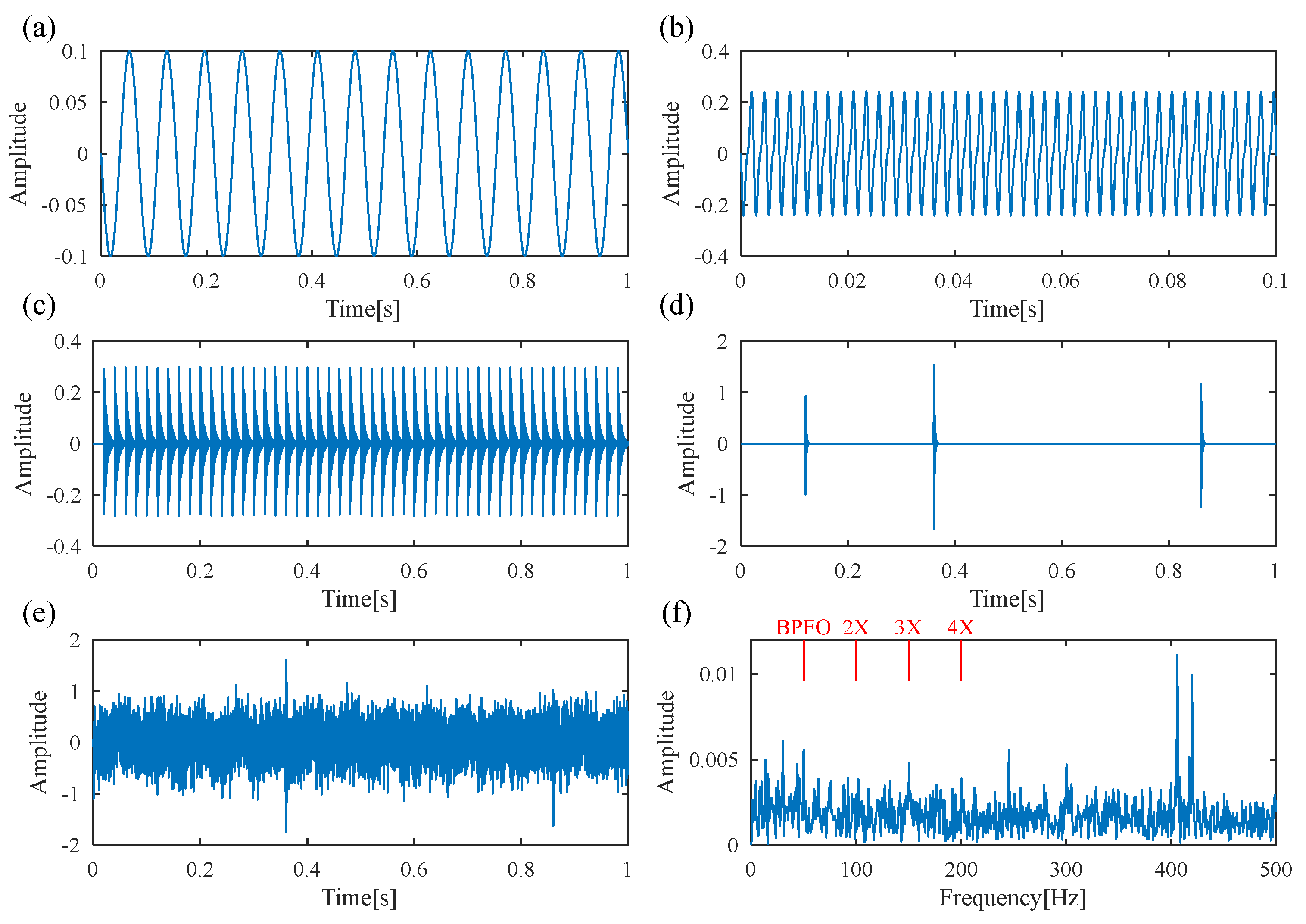
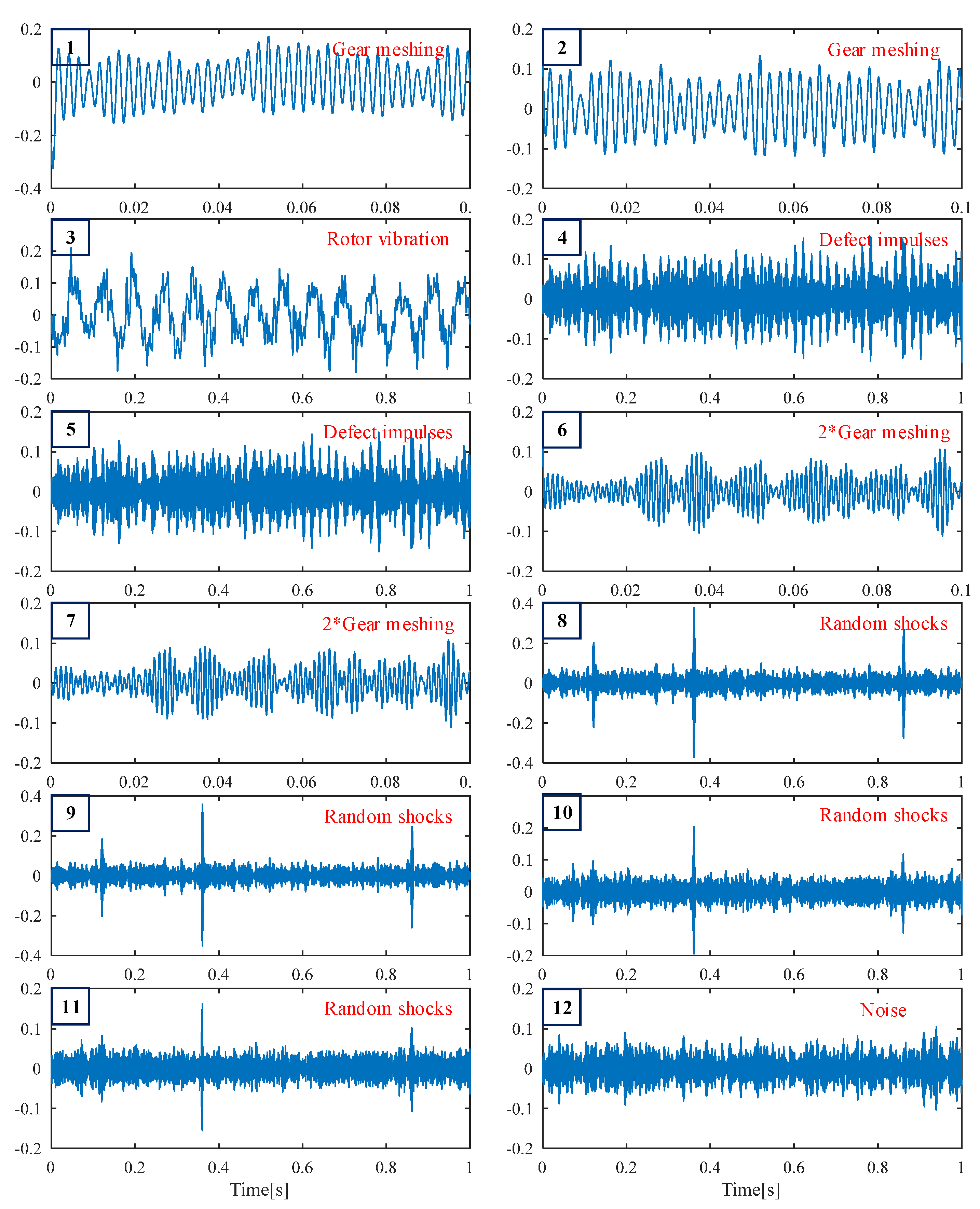







| Rotor and Shaft | Gear Meshing | Defect Impulses | Random Shocks | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f0 | A1 | α1 | T | B1 | β1 | B2 | β2 | D1 | Td | fr | αr | fr | αr |
| 14 | 0.1 | π/2 | 30 | 0.2 | π/2 | 0.08 | π/2 | 0.3 | 1/50 | 2400 | 200 | 4000 | 700 |
| Number of Rollers | Pitch Diameter (mm) | Roller Diameter (mm) | Contact Angle (Degree) |
|---|---|---|---|
| 20 | 180 | 23.775 | 9 |
| fr | BPFO | BPFI | BSF |
|---|---|---|---|
| 4.6183 | 40.1584 | 52.2083 | 17.1851 |
| fr | BPFO | BPFI | BSF |
|---|---|---|---|
| 5.2747 | 45.8657 | 59.6281 | 19.6274 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Ding, C. An Adaptive Signal Denoising Method Based on Reweighted SVD for the Fault Diagnosis of Rolling Bearings. Sensors 2025, 25, 2470. https://doi.org/10.3390/s25082470
Wang B, Ding C. An Adaptive Signal Denoising Method Based on Reweighted SVD for the Fault Diagnosis of Rolling Bearings. Sensors. 2025; 25(8):2470. https://doi.org/10.3390/s25082470
Chicago/Turabian StyleWang, Baoxiang, and Chuancang Ding. 2025. "An Adaptive Signal Denoising Method Based on Reweighted SVD for the Fault Diagnosis of Rolling Bearings" Sensors 25, no. 8: 2470. https://doi.org/10.3390/s25082470
APA StyleWang, B., & Ding, C. (2025). An Adaptive Signal Denoising Method Based on Reweighted SVD for the Fault Diagnosis of Rolling Bearings. Sensors, 25(8), 2470. https://doi.org/10.3390/s25082470







