Space Surveillance with High-Frequency Radar
Abstract
1. Introduction
2. System Description
3. Radar Product Formation
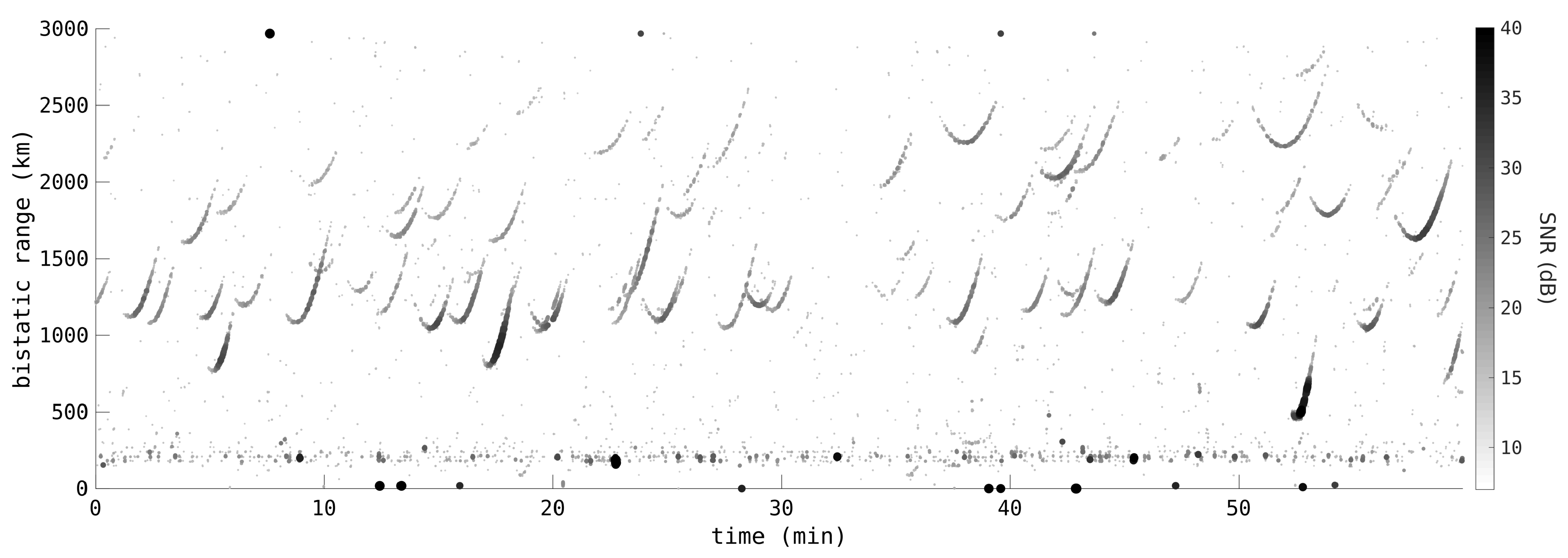
3.1. Range–Doppler Map Formation
3.2. Doppler-Walk Mitigation
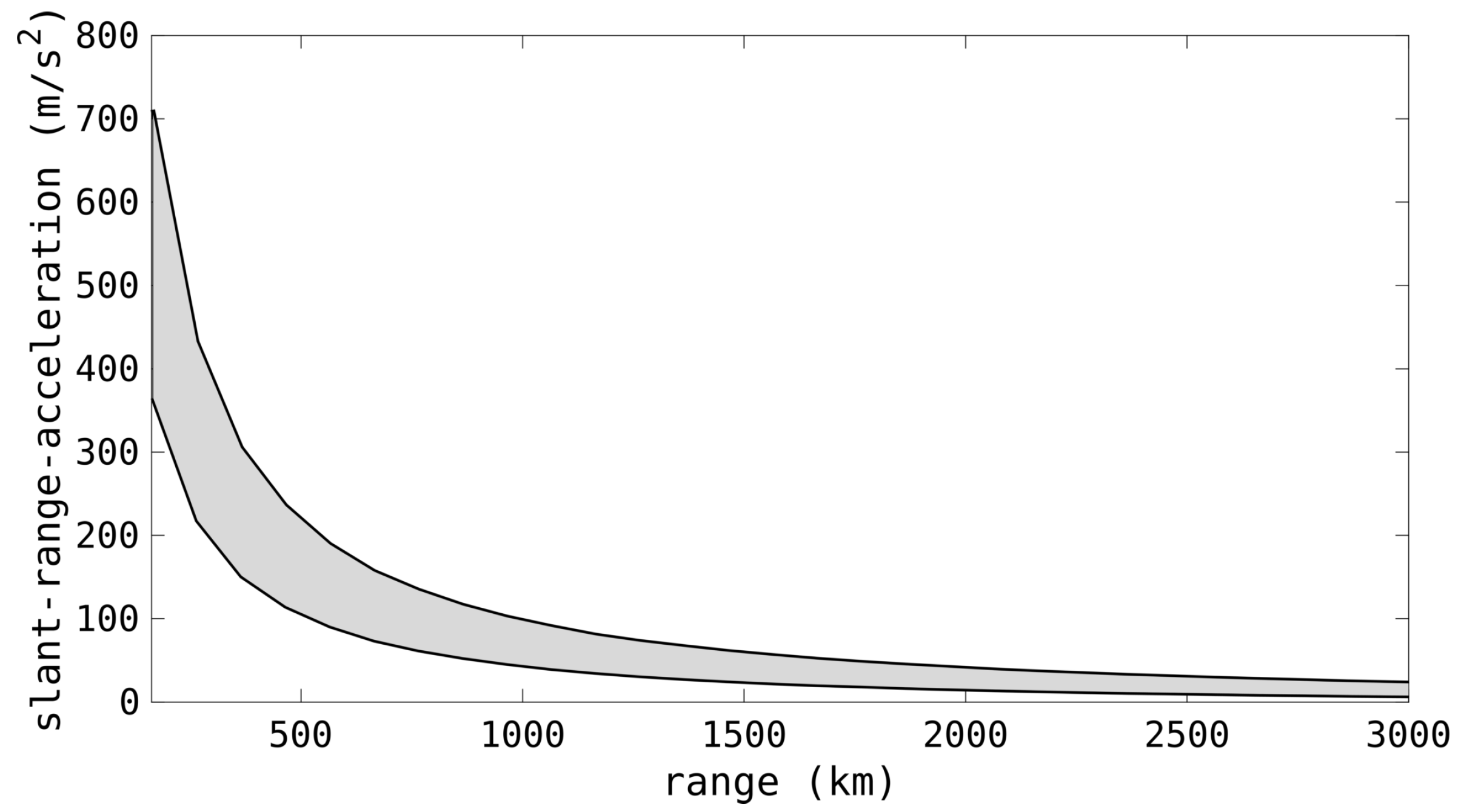
3.3. Detection Parameters
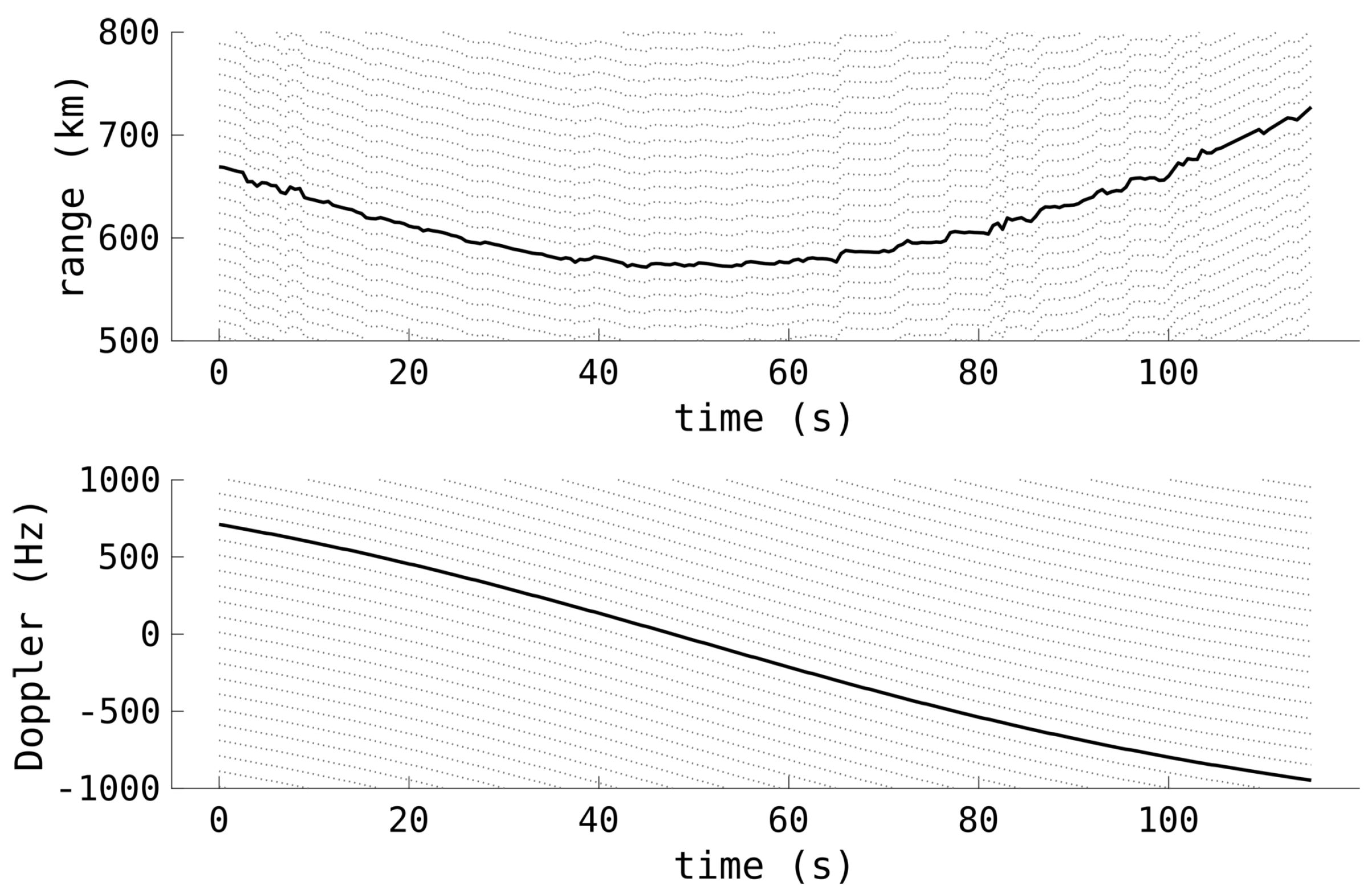
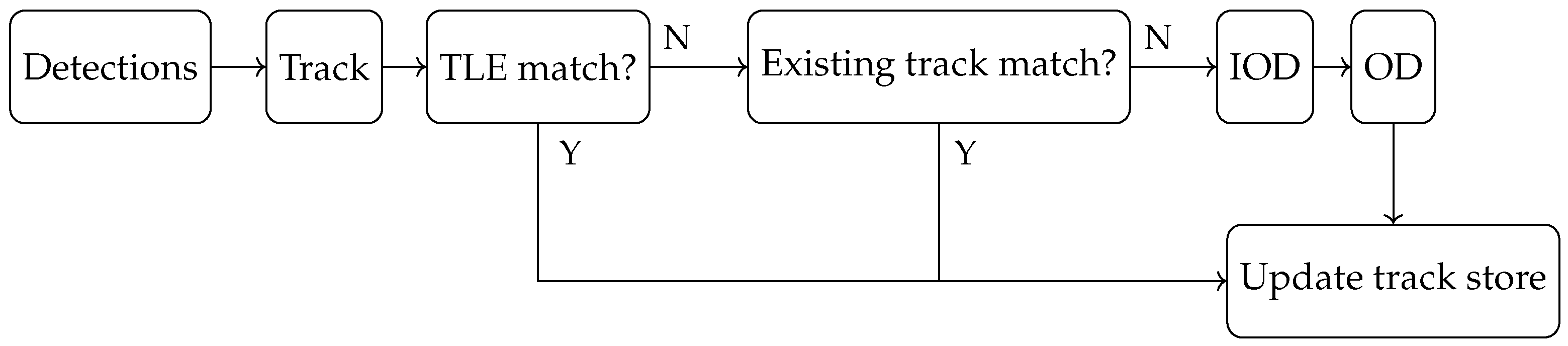
3.4. Tracking
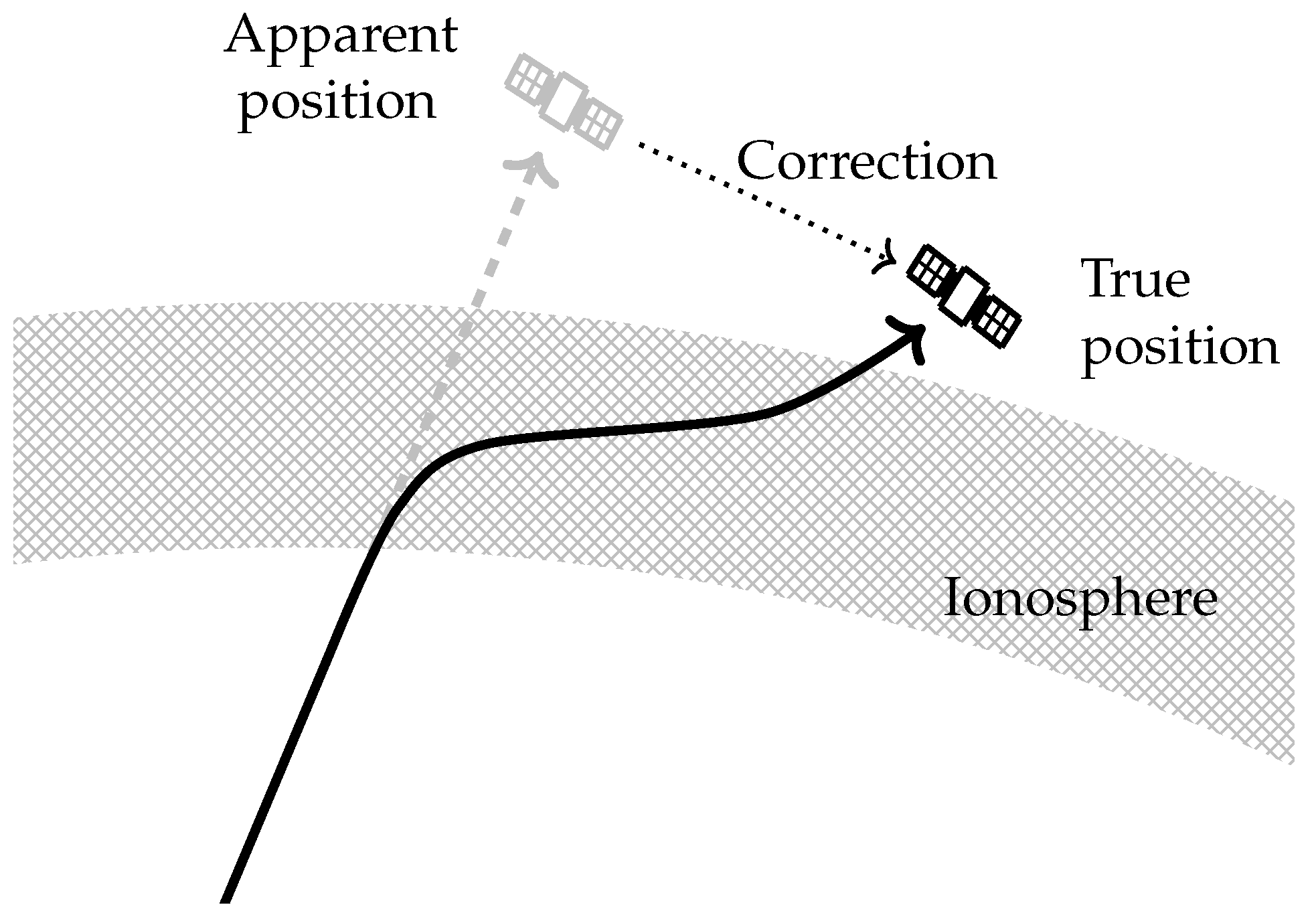
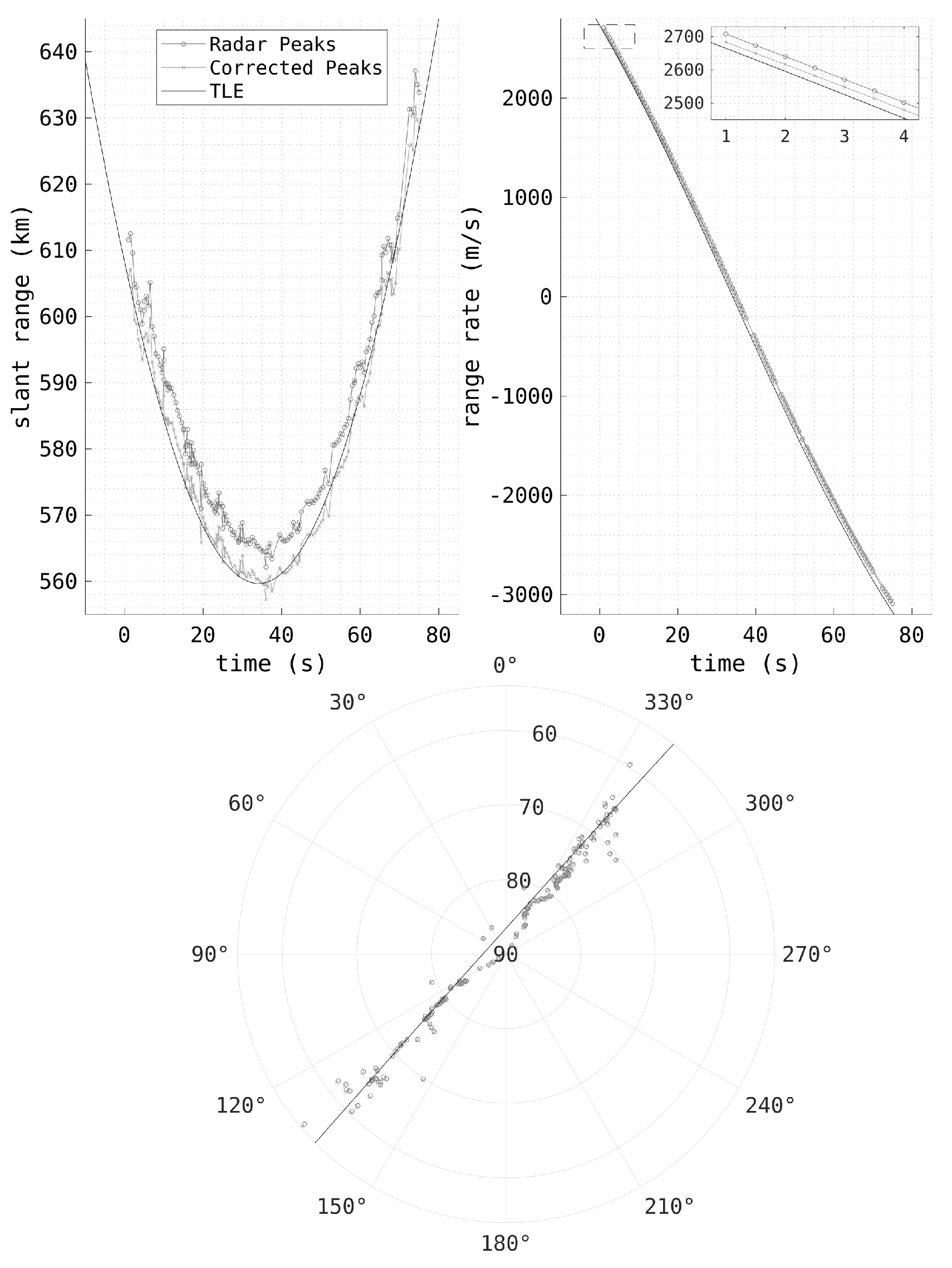
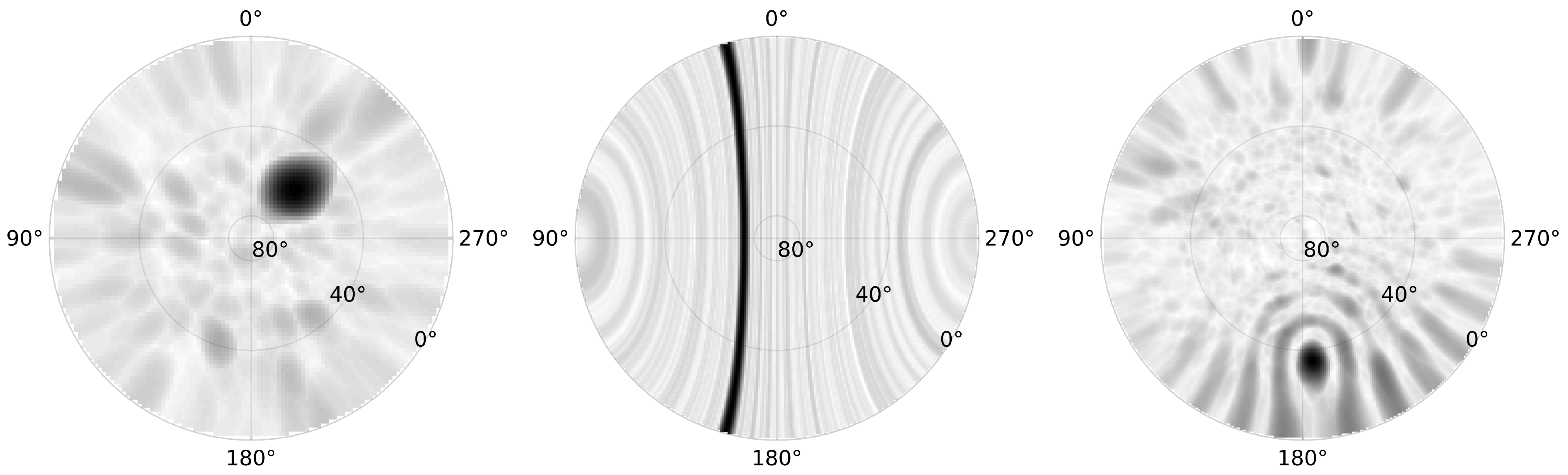
4. Correction for Ionospheric Effects
5. Space Surveillance
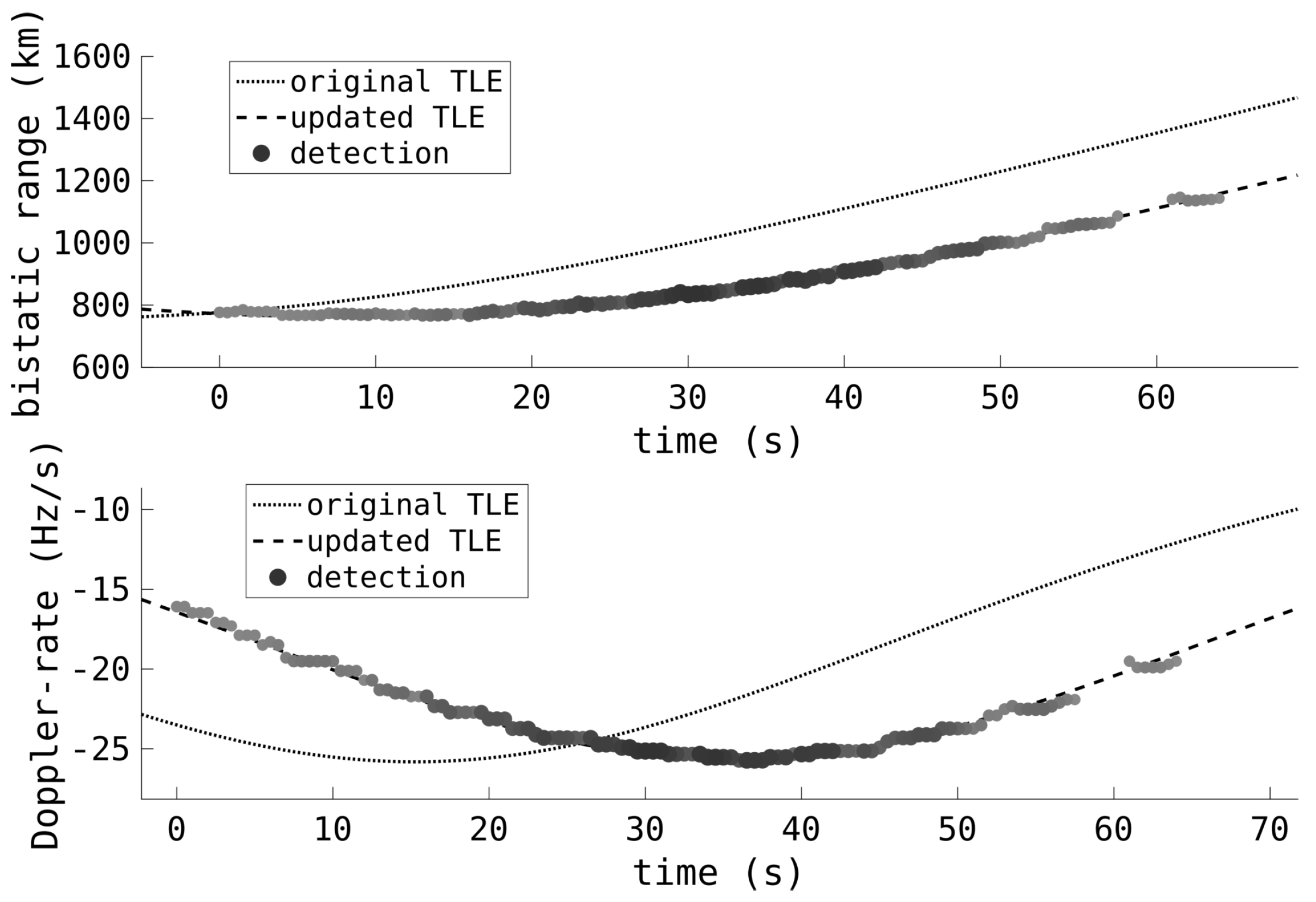
6. Orbit Determination
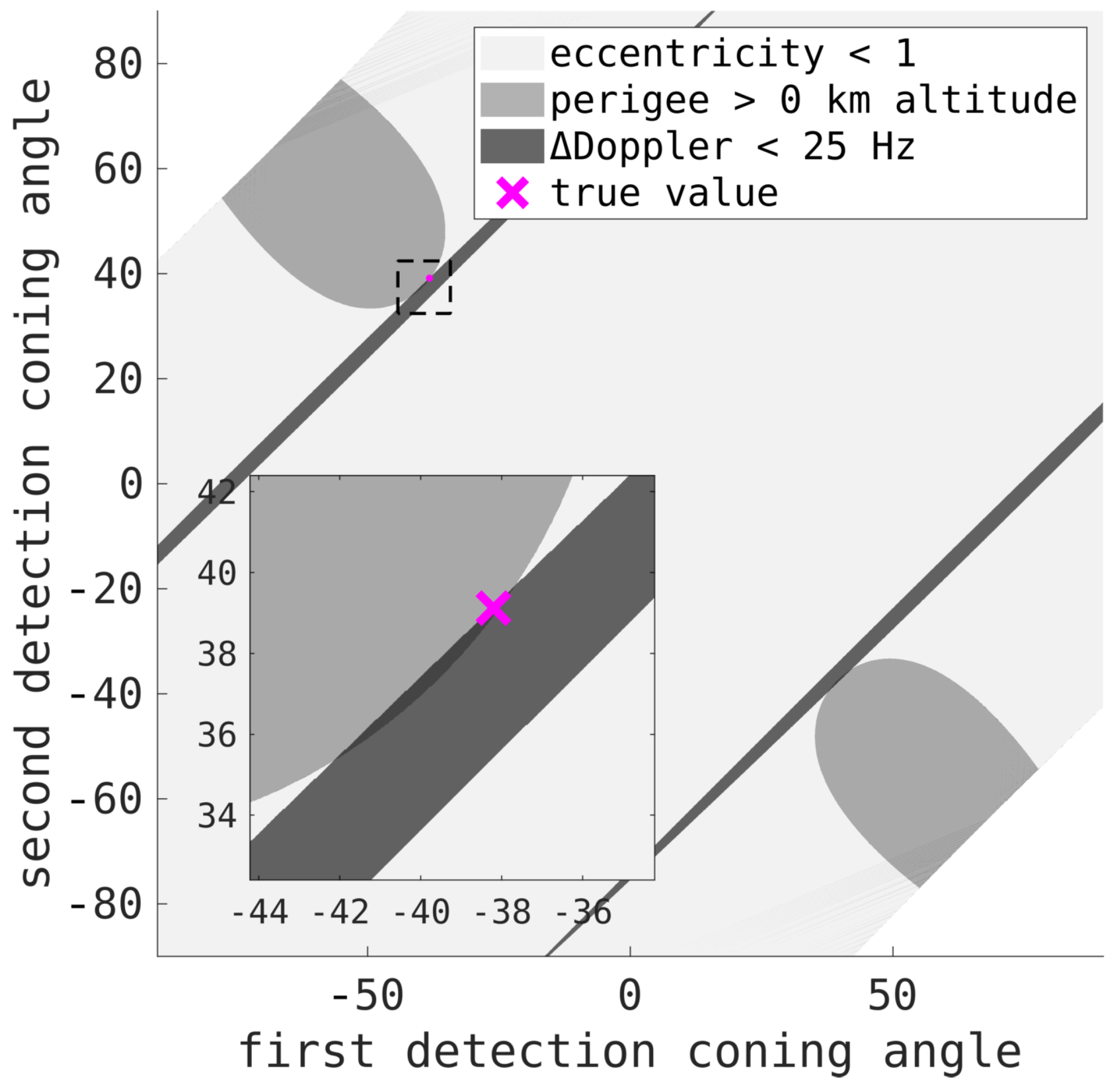
6.1. Initial Orbit Determination
6.2. Linear Array Initial Orbit Determination
6.3. Multi-Pass Orbit Determination
6.4. Linear Array Multi-Pass Orbit Determination
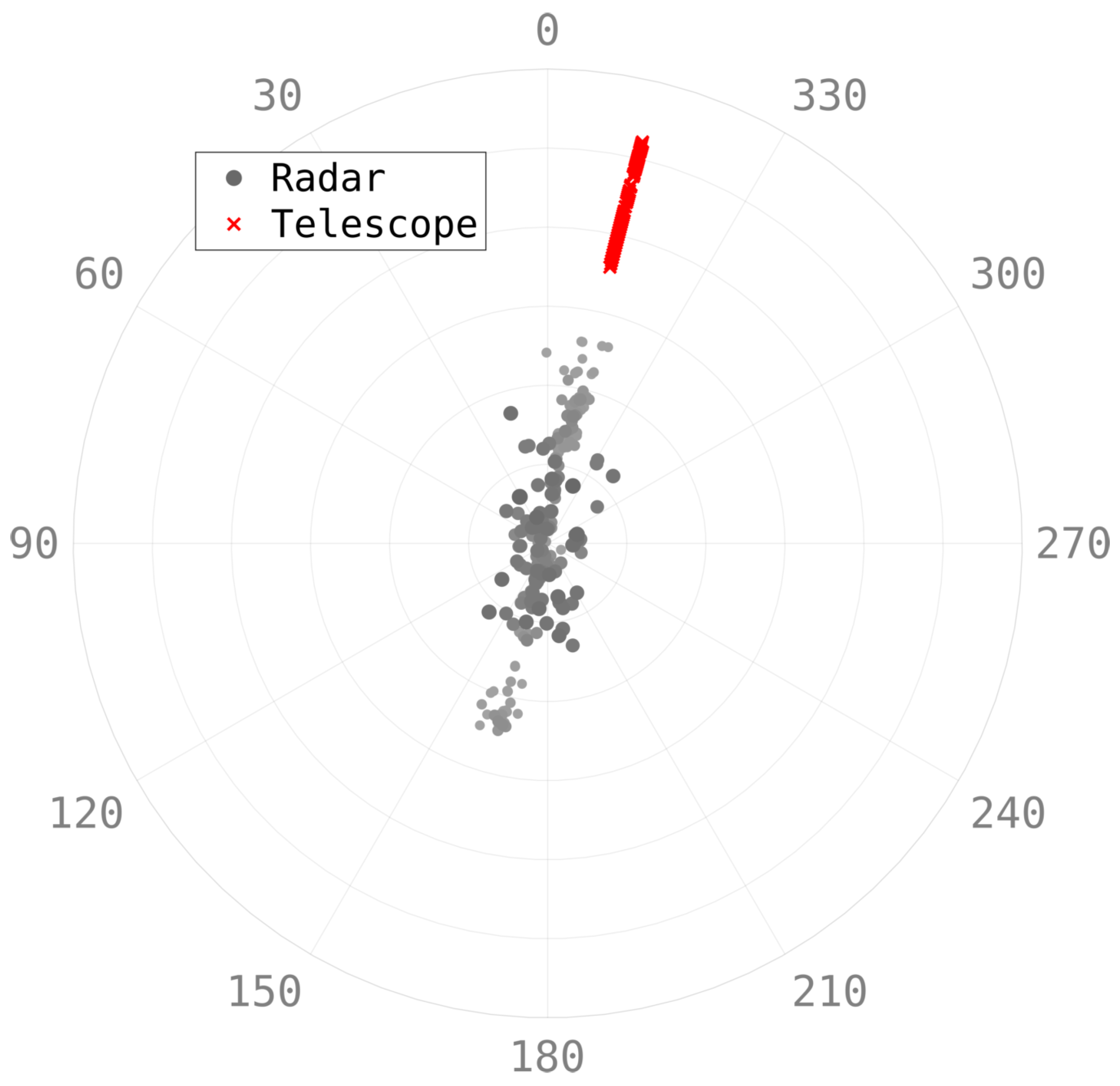
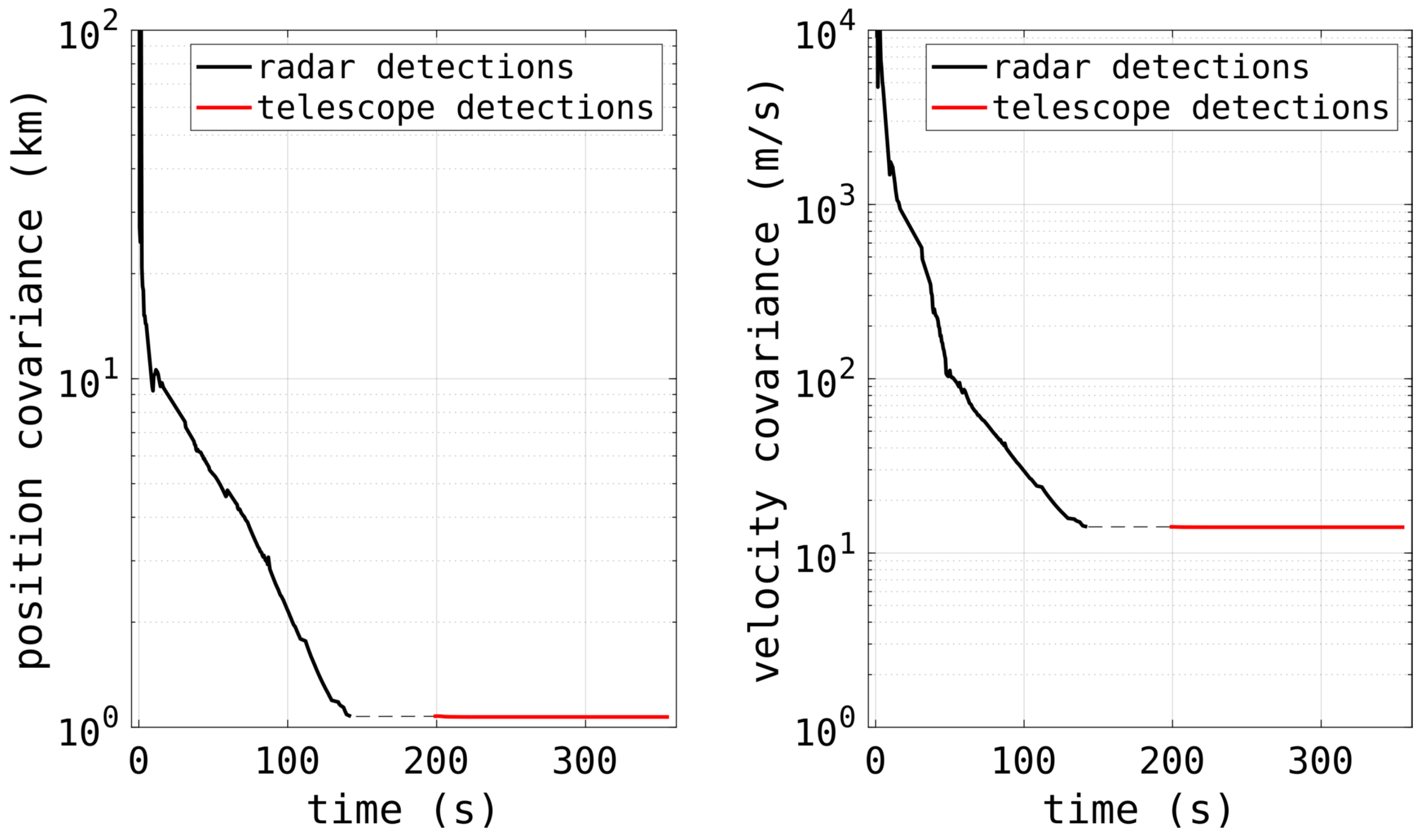
6.5. Real-Time Mid-Pass Cueing
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. DSTG Tracking Telescope

References
- Cameron, A. The Jindalee Operational Radar Network: Its Architecture and Surveillance Capability. In Proceedings of the International Radar Conference, Alexandria, VA, USA, 8–11 May 1995; pp. 692–697. [Google Scholar]
- Holdsworth, D.A.; Mulder, K.; Turley, M.D.E. Jindalee Operational Radar Network: New Growth from Old Roots. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York, NY, USA, 21–25 March 2022; pp. 1–6. [Google Scholar]
- Anderson, S.; Edwards, P.; Marrone, P.; Abramovich, Y. Investigations with SECAR—A Bistatic HF Surface Wave Radar. In Proceedings of the 2003 International Conference on Radar, Adelaide, SA, Australia, 3–5 September 2003; IEEE: Piscataway, NJ, USA, 2003. IEEE Cat. No. 03EX695. pp. 717–722. [Google Scholar]
- Holdsworth, D.A.; Reid, I.M.; Cervera, M.A. Buckland Park All-Sky Interferometric Meteor Radar. Radio Sci. 2004, 39, 1–12. [Google Scholar]
- Singer, W.; Latteck, R.; Holdsworth, D. A New Narrow Beam Doppler Radar at 3 MHz for Studies of the High-Latitude Middle Atmosphere. Adv. Space Res. 2008, 41, 1488–1494. [Google Scholar]
- Chisham, G.; Lester, M.; Milan, S.; Freeman, M.; Bristow, W.; Grocott, A.; McWilliams, K.; Ruohoniemi, J.; Yeoman, T.; Dyson, P.L.; et al. A Decade of the Super Dual Auroral Radar Network (SuperDARN): Scientific Achievements, New Techniques and Future Directions. Surv. Geophys. 2007, 28, 33–109. [Google Scholar]
- Frazer, G.J.; Williams, C.G. Decametric Radar for Missile Defence. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Neale, B. CH―The First Operational Radar. Gec J. Res. 1985, 3, 73–83. [Google Scholar]
- Griffiths, H. The German WW2 HF Radars Elefant and See-Elefant. IEEE Aerosp. Electron. Syst. Mag. 2013, 28, 4–12. [Google Scholar] [CrossRef]
- Griffiths, H.; Willis, N. Klein Heidelberg—The First Modern Bistatic Radar System. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1571–1588. [Google Scholar] [CrossRef]
- Bowser, C.A.; Busch, H. Radar Telemetry Observations for Two Saturn Launch Vehicles; ITT Electro-Physics., Inc.: Stamford, CT, USA, 1966. [Google Scholar]
- Sinnott, D.H. The Development of Over-the-Horizon Radar in Australia; Defence Science and Technology Organisation (Australia): Canberra, Australia, 1988. [Google Scholar]
- Frazer, G.J.; Boashash, B. Section 14.4-High-Frequency Radar Measurements of a Ballistic Missile Using the WVD. In Time-Frequency Signal Analysis and Processing, 2nd ed.; Boashash, B., Ed.; Academic Press: Oxford, UK, 2016; pp. 793–856. [Google Scholar]
- Frazer, G.J.; Anderson, S.J. Wigner-Ville Analysis of HF Radar Measurement of an Accelerating Target. In Proceedings of the ISSPA ’99—Fifth International Symposium on Signal Processing and its Applications, Brisbane, QLD, Australia, 22–25 August 1999; IEEE Cat. No.99EX359. Volume 1, pp. 317–320. [Google Scholar]
- Headrick, J.; Curley, S.; Thorp, M.; Ahearn, J.; Utley, F.; Headrick, W.; Rohlfs, D.C. A Madre Evaluation Report 3. Detection and Analysis of AMR Test 6210; Technical Report 1316; Naval Research Laboratory: Washington, DC, USA, 1962. [Google Scholar]
- Colbert, M.J. An Analysis of the Potential for Using Over-the-Horizon Radar Systems for Space Surveillance; Air Force Institute of Technology: Wright-Patterson Air Force Base, OH, USA, 2004. [Google Scholar]
- Henault, S.; Czarnowske, K.; Antar, Y.M.M. Multifunction Over-the-Horizon Radar for Space Domain Awareness. In Proceedings of the 2024 18th European Conference on Antennas and Propagation (EuCAP), Glasgow, UK, 17–22 March 2024; pp. 1–5. [Google Scholar]
- Henault, S.; Czarnowske, K.; Antar, Y.M. Space Domain Awareness Using Over-the-Horizon Radar. IEEE Trans. Radar Syst. 2025, 3, 349–359. [Google Scholar] [CrossRef]
- Frazer, G.J.; Meehan, D.H.; Warne, G.M. Decametric Measurements of the ISS Using an Experimental HF Line-of-Sight Radar. In Proceedings of the 2013 International Conference on Radar, Adelaide, Australia, 9–12 September 2013; pp. 173–178. [Google Scholar]
- Frazer, G.; Rutten, M.; Cheung, B.; Cervera, M. Orbit Determination Using a Decametric Line-of-Sight Radar. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 10–13 September 2013. [Google Scholar]
- Czarnowske, K.A. Space Domain Awareness Using High Frequency Line of Sight and Ionospheric Correction Methods; Royal Military College of Canada: Kingston, ON, Canada, 2023. [Google Scholar]
- Holdsworth, D.A.; Spargo, A.J.; Reid, I.M.; Adami, C. Low Earth Orbit Object Observations Using the Buckland Park VHF Radar. Radio Sci. 2020, 55, e2019RS006873. [Google Scholar]
- Heading, E.; Nguyen, S.T.; Holdsworth, D.; Reid, I.M. Micro-Doppler Signature Analysis for Space Domain Awareness Using VHF Radar. Remote. Sens. 2024, 16, 1354. [Google Scholar]
- Holdsworth, D.A.; Spargo, A.J.; Reid, I.M.; Adami, C.L. Space Domain Awareness Observations Using the Buckland Park VHF Radar. Remote. Sens. 2024, 16, 1252. [Google Scholar] [CrossRef]
- Frazer, G.J. Forward-Based Receiver Augmentation for OTHR. In Proceedings of the 2007 IEEE Radar Conference, Waltham, MA, USA, 17–20 April 2007; IEEE: Piscataway, NJ, USA, 2007; pp. 373–378. [Google Scholar]
- Saillant, S.; Bok, D.; Molinié, J.-P.; Leventis, A.; Samczynski, P.; Brouard, P.; Saverino, A.L.; Capria, A.; Paichard, Y. iFURTHER Project-A Cognitive Network of HF Radars for Europe Defence. In Proceedings of the 2023 IEEE International Radar Conference (RADAR), Sydney, Australia, 6–10 November 2023; pp. 1–6. [Google Scholar]
- Abratkiewicz, K.; Samczyński, P.; Mazurek, G.; Bartoszewski, M.; Julczyk, J. Passive Radar Using a Non-Cooperative Over-the-Horizon Radar as an Illuminator-First Results. In Proceedings of the 2024 IEEE Radar Conference (RadarConf24), Denver, CO, USA, 6–10 May 2024; pp. 1–6. [Google Scholar]
- Bok, D.; Brouard, P.; Saverino, A.L.; Capria, A.; Abratkiewicz, K.; Molinié, J.-P.; Pisciottano, I.; Ippolito, A.; Samczyński, P.; Vandewalle, S.; et al. Key Challenges in True Multistatic OTH Radar Concepts Based on HF-Radar in iFURTHER. In Proceedings of the RADAR 2024, Rennes, France, 21–25 October 2024. [Google Scholar]
- USSPACECOM. Space-Track. Available online: https://www.space-track.org (accessed on 2 April 2025).
- Rowland, J.; McKnight, D.; Pino, B.; Reihs, B.; Stevenson, M. A worldwide network of radars for space domain awareness in low earth orbit. In Proceedings of the Advanced Maui Optical And Space Surveillance Technologies Conference (AMOS), Maui, HI, USA, 14–17 September 2021. [Google Scholar]
- Th, M.; Eglizeaud, J.; Bouchard, J. GRAVES: The new French system for space surveillance. In Proceedings of the 4th European Conference On Space Debris, ESA/ESOC, Darmstadt, Germany, 18–20 April 2005. [Google Scholar]
- Saillant, S. Bistatic space-debris surveillance radar. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–4. [Google Scholar]
- Wilden, H.; Kirchner, C.; Peters, O.; Ben Bekhti, N.; Brenner, A.; Eversberg, T. GESTRA —A phased-array based surveillance and tracking radar for space situational awareness. In Proceedings of the 2016 IEEE International Symposium On Phased Array Systems and Technology (PAST), Waltham, MA, USA, 18–21 October 2016; pp. 1–5. [Google Scholar]
- Gomez, R.; Besso, P.; Pinna, G.; Alessandrini, M.; Salmeron, J.; Prada, M. Initial operations of the breakthrough Spanish Space Surveillance and Tracking Radar (S3TSR) in the European context. In Proceedings of the 1st ESA NEO and Debris Detection Conference, Darmstadt, Germany, 22–24 January 2019; pp. 22–24. [Google Scholar]
- Cutajar, D.; Magro, A.; Borg, J.; Zarb Adami, K.; Bianchi, G.; Bortolotti, C.; Cattani, A.; Fiocchi, F.; Lama, L.; Maccaferri, A.; et al. A real-time space debris detection system for BIRALES. In Proceedings of the International Astronautical Congress: IAC Proceedings, Bremen, Germany, 1–5 October 2018; pp. 1–9. [Google Scholar]
- Bianchi, G.; Naldi, G.; Fiocchi, F.; Di Lizia, P.; Bortolotti, C.; Mattana, A.; Maccaferri, A.; Magro, A.; Roma, M.; Schiaffino, M.; et al. A new concept of bi-static radar for space debris detection and monitoring. In Proceedings of the 2021 International Conference On Electrical, Computer, Communications And Mechatronics Engineering (ICECCME), Mauritius, 7–8 October 2021; pp. 1–6. [Google Scholar]
- Tingay, S.; Kaplan, D.; McKinley, B.; Briggs, F.; Wayth, R.; Hurley-Walker, N.; Kennewell, J.; Smith, C.; Zhang, K.; Arcus, W.; et al. On the detection and tracking of space debris using the Murchison Widefield Array. I. Simulations and test observations demonstrate feasibility. Astron. J. 2013, 146, 103. [Google Scholar] [CrossRef]
- Palmer, J.; Hennessy, B.; Rutten, M.; Merrett, D.; Tingay, S.; Kaplan, D.; Tremblay, S.; Ord, S.; Morgan, J.; Wayth, R. Surveillance of Space using passive radar and the Murchison Widefield Array. In Proceedings of the 2017 IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 1715–1720. [Google Scholar]
- Malanowski, M.; Jędrzejewski, K.; Misiurewicz, J.; Kulpa, K.; Gromek, A.; Kłos, J.; Droszcz, A.; Pożoga, M. Passive radar based on LOFAR radio telescope for air and space target detection. In Proceedings of the 2021 IEEE Radar Conference (RadarConf21), Atlanta, GA, USA, 8–14 May 2021; pp. 1–6. [Google Scholar]
- Finch, D.; Palmer, J.; White, B.; Nguyen, S. Passive Radar for Launch and Re-Entry Support. In Proceedings of the Advanced Maui Optical And Space Surveillance (AMOS) Technologies Conference, Kihei, HI, USA, 17–20 September 2024; p. 91. [Google Scholar]
- Frazer, G.J.; Williams, C.G.; Yardley, H. Energy-Budget Analysis of a 2-D High-Frequency Radar Incorporating Optimum Beamforming. In Proceedings of the 2016 IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–6. [Google Scholar]
- Jonker, J.; Cervera, M.; Holdsworth, D.; Neudegg, D.; Harris, T.; MacKinnon, A.; Reid, I. Impact of Ionospheric Doppler Perturbations on Space Domain Awareness Observations. In Proceedings of the 2023 IEEE International Radar Conference (RADAR), Sydney, Australia, 6–10 November 2023; pp. 1–6. [Google Scholar]
- Hennessy, B.; Holdsworth, D.A.; Yardley, H.; Debnam, R.; Warne, G.; Jessop, M. Effects of Range Doppler-Rate Coupling on High Frequency Chirp Radar for Accelerating Targets. In Proceedings of the 2023 IEEE International Radar Conference (RADAR), Sydney, Australia, 6–10 November 2023; pp. 1–6. [Google Scholar]
- Hennessy, B.; Yardley, H.; Holdsworth, D.A.; Debnam, R.; Jessop, M.; Warne, G. Velocity Ambiguity Resolution Using Opposite Chirprates with LFM Radar. In Proceedings of the 2023 IEEE International Radar Conference (RADAR), Sydney, Australia, 6–10 November 2023; pp. 1–6. [Google Scholar]
- Jonker, J.; Cervera, M.; Harris, T.; Holdsworth, D.; MacKinnon, A.; Neudegg, D.; Reid, I. Doppler Variations in Radar Observations of Resident Space Objects: Likely Ionospheric Pc1 Plasma Waves. Adv. Space Res. 2024, 74, 2430–2451. [Google Scholar] [CrossRef]
- Camilleri, T.A.; Cervera, M.A. Ionospheric Corrections for HF LOS Satellite Observations at Solar Minimum. In Proceedings of the URSI AP-RASC 2025, Sydney, Australia, 17–22 August 2025. [Google Scholar]
- Klauder, J.R.; Price, A.; Darlington, S.; Albersheim, W.J. The Theory and Design of Chirp Radars. Bell Syst. Tech. J. 1960, 39, 745–808. [Google Scholar] [CrossRef]
- Fitzgerald, R.J. Effects of Range-Doppler Coupling on Chirp Radar Tracking Accuracy. IEEE Trans. Aerosp. Electron. Syst. 1974, AES-10, 528–532. [Google Scholar] [CrossRef]
- Stein, S. Algorithms for Ambiguity Function Processing. IEEE Trans. Acoust. Speech Signal Process. 1981, 29, 588–599. [Google Scholar] [CrossRef]
- Stove, A.G. Linear FMCW Radar Techniques. In IEE Proceedings F (Radar and Signal Processing); IET: Stevenage, UK, 1992; Volume 139, pp. 343–350. [Google Scholar]
- Turley, M.D. Hybrid CFAR techniques for HF radar. In Radar Systems (RADAR 97); IEE: London, UK, 1997; pp. 36–40. [Google Scholar]
- Kelly, E.J. The Radar Measurement of Range, Velocity and Acceleration. IRE Trans. Mil. Electron. 1961, MIL-5, 51–57. [Google Scholar] [CrossRef]
- Kelly, E.J.; Wishner, R.P. Matched-Filter Theory for High-Velocity, Accelerating Targets. IEEE Trans. Mil. Electron. 1965, 9, 56–69. [Google Scholar] [CrossRef]
- McGeogh, J.; Jensen, G. Acceleration and Velocity Processing of HF Radar Signals; Technical Report 6611; Naval Research Laboratory: Washington, DC, USA, 1967. [Google Scholar]
- Jensen, G.; McGeogh, J.; Veeder, J. Results of Acceleration and Velocity Processing of HF Radar Signals from Missile Launches. Part 1. Observations of ETR Tests 2949, 6075, and 3635. Technical Report 6476; Naval Research Laboratory: Washington, DC, USA, 1966; Volume 6075. [Google Scholar]
- Jensen, G.; McGeogh, J.; Veeder, J. Results of Acceleration and Velocity Processing of HF Radar Signals from Missile Launches. Part 2. Observations of ETR Tests 0169, and 3670; Technical Report 6485; Naval Research Laboratory: Washington, DC, USA, 1966. [Google Scholar]
- Hennessy, B.; Tingay, S.; Hancock, P.; Young, R.; Tremblay, S.; Wayth, R.B.; Morgan, J.; McSweeney, S.; Crosse, B.; Johnston-Hollitt, M.; et al. Improved Techniques for the Surveillance of the Near Earth Space Environment with the Murchison Widefield Array. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Hennessy, B.; Gustainis, D.; Misaghi, N.; Young, R.; Somers, B. Deployable Long Range Passive Radar for Space Surveillance. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York, NY, USA, 21–25 March 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–6. [Google Scholar]
- Jędrzejewski, K.; Kulpa, K.; Malanowski, M.; Pożoga, M.; Wójtowicz, P. Exploring the Feasibility of Detecting LEO Space Objects in Passive Radar Without Prior Orbit Parameter Information. In Proceedings of the 2024 IEEE Radar Conference (RadarConf24), Denver, CO, USA, 6–10 May 2024; pp. 1–6. [Google Scholar]
- Klare, J.; Behner, F.; Carloni, C.; Cerutti-Maori, D.; Fuhrmann, L.; Hoppenau, C.; Karamanavis, V.; Laubach, M.; Marek, A.; Perkuhn, R.; et al. The Future of Radar Space Observation in Europe—Major Upgrade of the Tracking and Imaging Radar (TIRA). Remote. Sens. 2024, 16, 4197. [Google Scholar] [CrossRef]
- Kohlleppel, R. Extent of Observation Parameters in Space Surveillance by Radar. In Proceedings of the 2018 19th International Radar Symposium (IRS), Bonn, Germany, 20–22 June 2018; pp. 1–7. [Google Scholar]
- Howard, S.D. (DSTG, Edinburgh, SA, Australia). Details on range-Doppler coupling with accelerating radar returns. Private communication, 2024. [Google Scholar]
- Martín-Pastor, A.; Narvaez-Rodriguez, R. New Properties about the Intersection of Rotational Quadratic Surfaces and Their Applications in Architecture. Nexus Netw. J. 2019, 21, 175–196. [Google Scholar] [CrossRef]
- Streit, R.L.; Luginbuhl, T.E. Maximum Likelihood Method for Probabilistic Multihypothesis Tracking. In Signal and Data Processing of Small Targets 1994; SPIE: Bellingham, WA, USA, 1994; Volume 2235, pp. 394–405. [Google Scholar]
- Guier, W.H.; Weiffenbach, G.C. The Doppler Determination of Orbits; Technical Report. Applied Physics Laboratory; The Johns Hopkins University: Baltimore, MD, USA, 1959. [Google Scholar]
- Cervera, M.; Harris, T. Modeling Ionospheric Disturbance Features in Quasi-Vertically Incident Ionograms Using 3-D Magnetoionic Ray Tracing and Atmospheric Gravity Waves. J. Geophys. Res. Space Phys. 2014, 119, 431–440. [Google Scholar] [CrossRef]
- Bilitza, D.; Pezzopane, M.; Truhlik, V.; Altadill, D.; Reinisch, B.W.; Pignalberi, A. The International Reference Ionosphere Model: A Review and Description of an Ionospheric Benchmark. Rev. Geophys. 2022, 60, e2022RG000792. [Google Scholar]
- Bilitza, D.; Rawer, K.; Pallaschke, S. Study of Ionospheric Models for Satellite Orbit Determination. Radio Sci. 1988, 23, 223–232. [Google Scholar] [CrossRef]
- Bennett, J. The Calculation of Doppler Shifts Due to a Changing Ionosphere. J. Atmos. Terr. Phys. 1967, 29, 887–891. [Google Scholar] [CrossRef]
- SpaceFest Gets Underway at Woomera. Australian Defence Magazine 2019. Available online: https://www.australiandefence.com.au/defence/cyber-space/spacefest-gets-underway-at-woomera (accessed on 2 April 2025).
- Vallado, D.A.; McClain, W.D. Fundamentals of Astrodynamics and Applications; Space Technology Library; Springer: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Pirovano, L.; Principe, G.; Armellin, R. Data association and uncertainty pruning for tracks determined on short arcs. In Celestial Mechanics And Dynamical Astronomy; Springer: Berlin/Heidelberg, Germany, 2020; Volume 132, pp. 1–23. [Google Scholar]
- Pastor, A.; Sanjurjo-Rivo, M.; Escobar, D. Track-to-track association methodology for operational surveillance scenarios with radar observations. CEAS Space J. 2023, 15, 535–551. [Google Scholar]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hennessy, B.; Rutten, M.; Young, R.; Tingay, S.; Summers, A.; Gustainis, D.; Crosse, B.; Sokolowski, M. Establishing the Capabilities of the Murchison Widefield Array as a Passive Radar for the Surveillance of Space. Remote. Sens. 2022, 14, 2571. [Google Scholar]
- Vierinen, J.; Kastinen, D.; Markkanen, J.; Grydeland, T.; Kero, J.; Horstmann, A.; Hesselbach, S.; Kebschull, C.; Røynestad, E.; Krag, H. 2018 Beam-Park Observations of Space Debris with the EISCAT Radars. In Proceedings of the 1st ESA NEO and Debris Detection Conference, Darmstadt, Germany, 22–24 January 2019. [Google Scholar]
- Escobal, P. Methods of Orbit Determination; John Wiley & Sons: Hoboken, NJ, USA, 1965. [Google Scholar]
- Izzo, D. Revisiting Lambert’s Problem. Celest. Mech. Dyn. Astron. 2015, 121, 1–15. [Google Scholar]
- White, K.; Cook, D.; Kharabash, S.; Kumar, A.; Fok, V.; Webb, C.; Bawden, P.; Alvino, J.; Gaetjens, H.; See, K.; et al. An Australian Experimental SDA System: RED STAR. In Proceedings of the Advanced Maui Optical and Space Surveillance (AMOS) Technologies Conference, Kihei, HI, USA, 17–20 September 2024; p. 146. [Google Scholar]
- Maisonobe, L.; Pommier, V.; Parraud, P. Orekit: An Open Source Library for Operational Flight Dynamics Applications. In Proceedings of the 4th International Conference on Astrodynamics Tools and Techniques, European Space Agency Paris, Madrid, Spain, 3–6 May 2010; pp. 3–6. [Google Scholar]
- Eastment, J.; Ladd, D.; Walden, C.; Donnelly, R.; Ash, A.; Harwood, N.; Smith, C.; Bennett, J.; Ritchie, I.; Rutten, M.; et al. Technical Description of Radar and Optical Sensors Contributing to Joint UK-Australian Satellite Tracking, Data-Fusion and Cueing Experiment. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 9–12 September 2014; Curran Associates, Inc.: Red Hook, NY, USA, 2014; Volume 1, p. 12. [Google Scholar]
- Hobson, T.; Clarkson, I.; Bessell, T.; Rutten, M.; Gordon, N.; Moretti, N.; Morreale, B. Catalogue Creation for Space Situational Awareness with Optical Sensors. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Maui, HI, USA, 20–23 September 2016. [Google Scholar]
- Moretti, N.; Rutten, M.; Bessell, T.; Morreale, B. Autonomous Space Object Catalogue Construction and Upkeep Using Sensor Control Theory. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conf.(AMOS), Maui, HI, USA, 19–22 September 2017. [Google Scholar]
- Wallace, P. TPOINT—Telescope Pointing Analysis System; Starlink User Note 100; ADS: Harvard, UK, 1994. [Google Scholar]











Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hennessy, B.; Yardley, H.; Debnam, R.; Camilleri, T.A.; Spencer, N.K.; Holdsworth, D.A.; Warne, G.; Cheung, B.; Kharabash, S. Space Surveillance with High-Frequency Radar. Sensors 2025, 25, 2302. https://doi.org/10.3390/s25072302
Hennessy B, Yardley H, Debnam R, Camilleri TA, Spencer NK, Holdsworth DA, Warne G, Cheung B, Kharabash S. Space Surveillance with High-Frequency Radar. Sensors. 2025; 25(7):2302. https://doi.org/10.3390/s25072302
Chicago/Turabian StyleHennessy, Brendan, Heath Yardley, Rob Debnam, Tristan A. Camilleri, Nicholas K. Spencer, David A. Holdsworth, Goeff Warne, Brian Cheung, and Sergey Kharabash. 2025. "Space Surveillance with High-Frequency Radar" Sensors 25, no. 7: 2302. https://doi.org/10.3390/s25072302
APA StyleHennessy, B., Yardley, H., Debnam, R., Camilleri, T. A., Spencer, N. K., Holdsworth, D. A., Warne, G., Cheung, B., & Kharabash, S. (2025). Space Surveillance with High-Frequency Radar. Sensors, 25(7), 2302. https://doi.org/10.3390/s25072302




