Noninvasive Glucose Measurements in Tissue Simulating Phantoms Using a Solid-State Near-Infrared Sensor
Abstract
1. Introduction
2. Experimental
2.1. Reagents
2.2. Tissue Simulating Phantom Construction
2.3. Instrumentation and Data Acquisition
2.3.1. Early-Stage Laser Prototype Spectrometer
2.3.2. TTT-2500 Spectrometer
2.4. Temperature Control and Collection of Spectra
2.5. Data Transformation
3. Results and Discussion
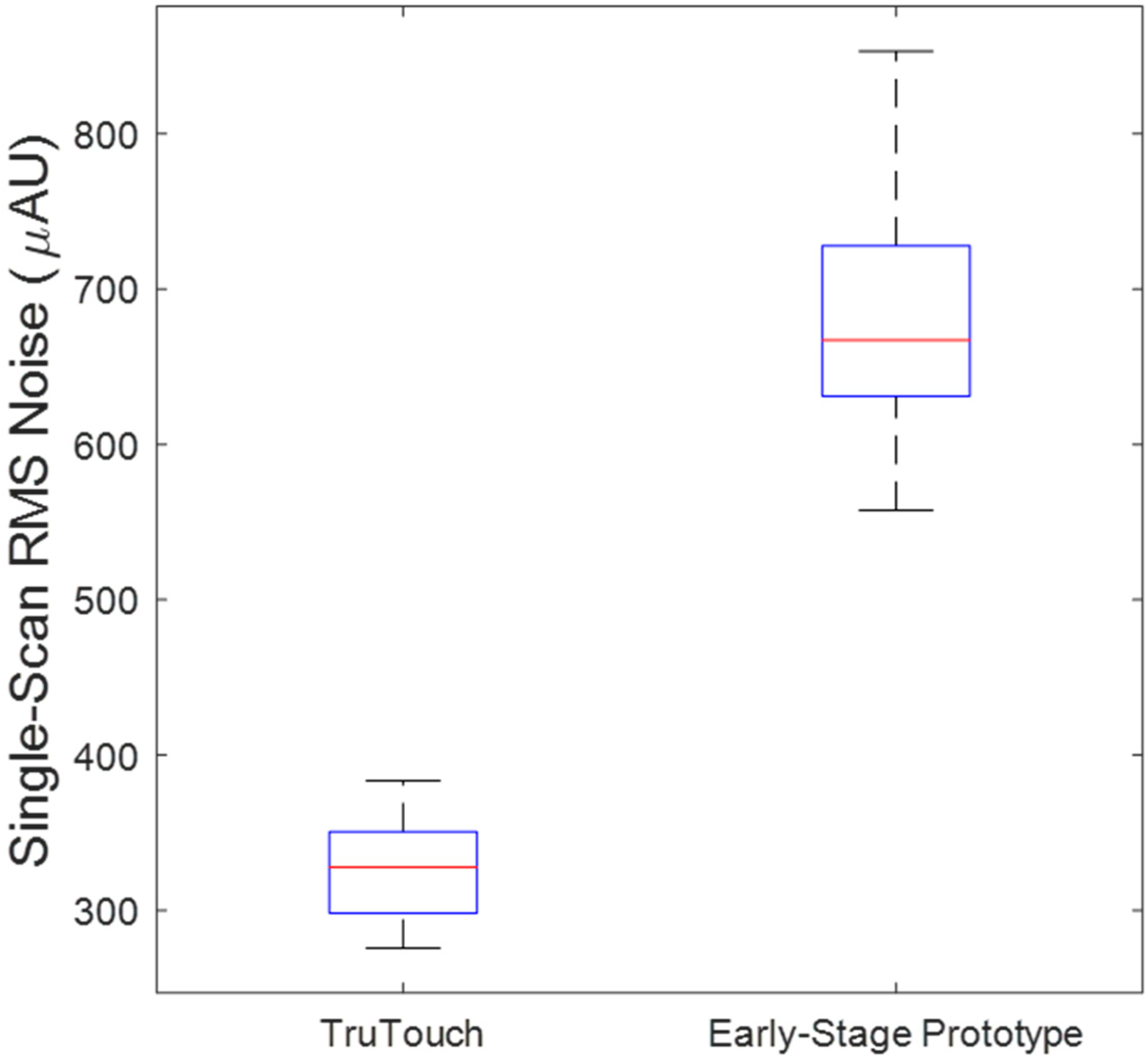
3.1. Comparison of the Spectral Datasets
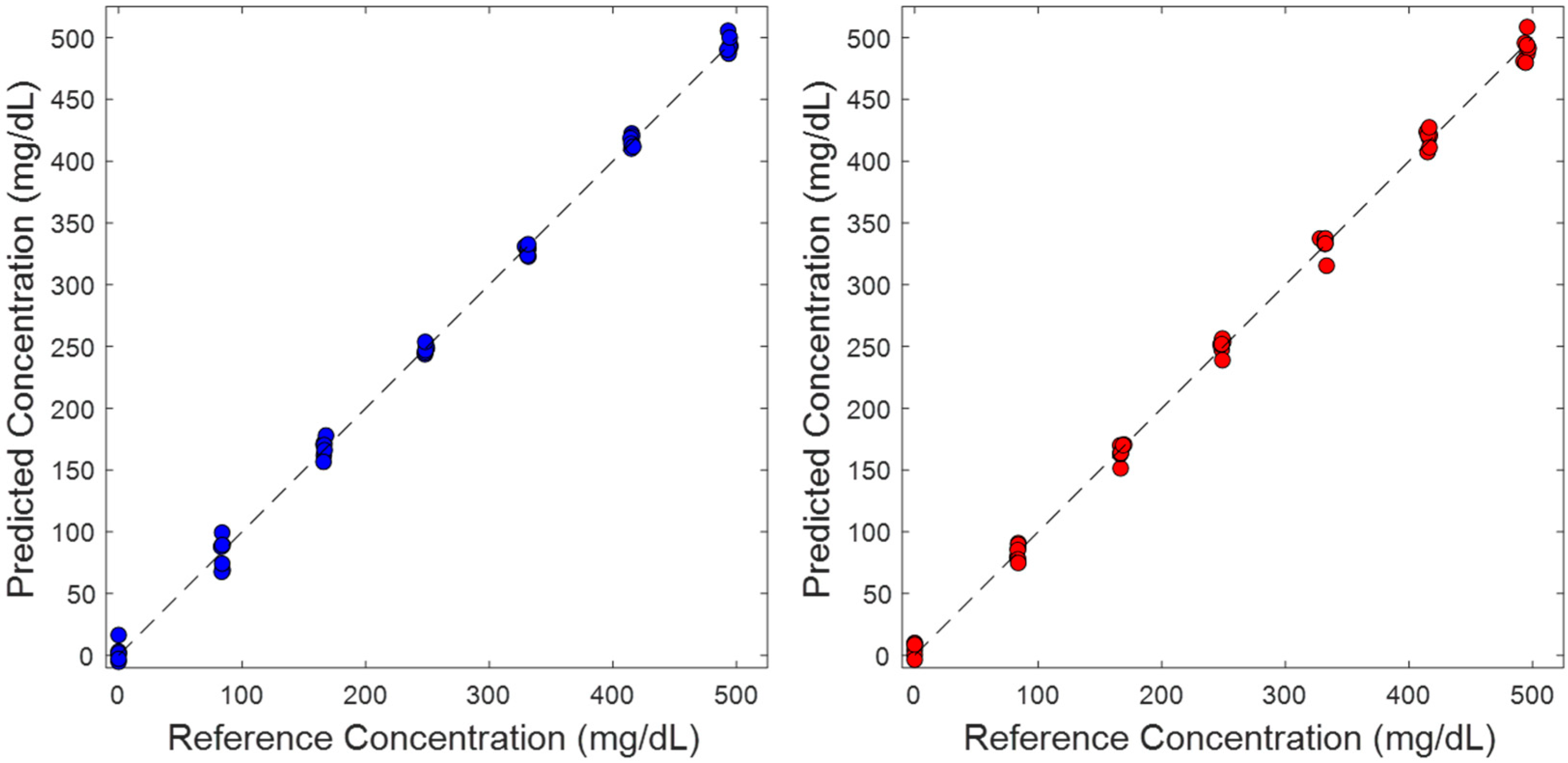
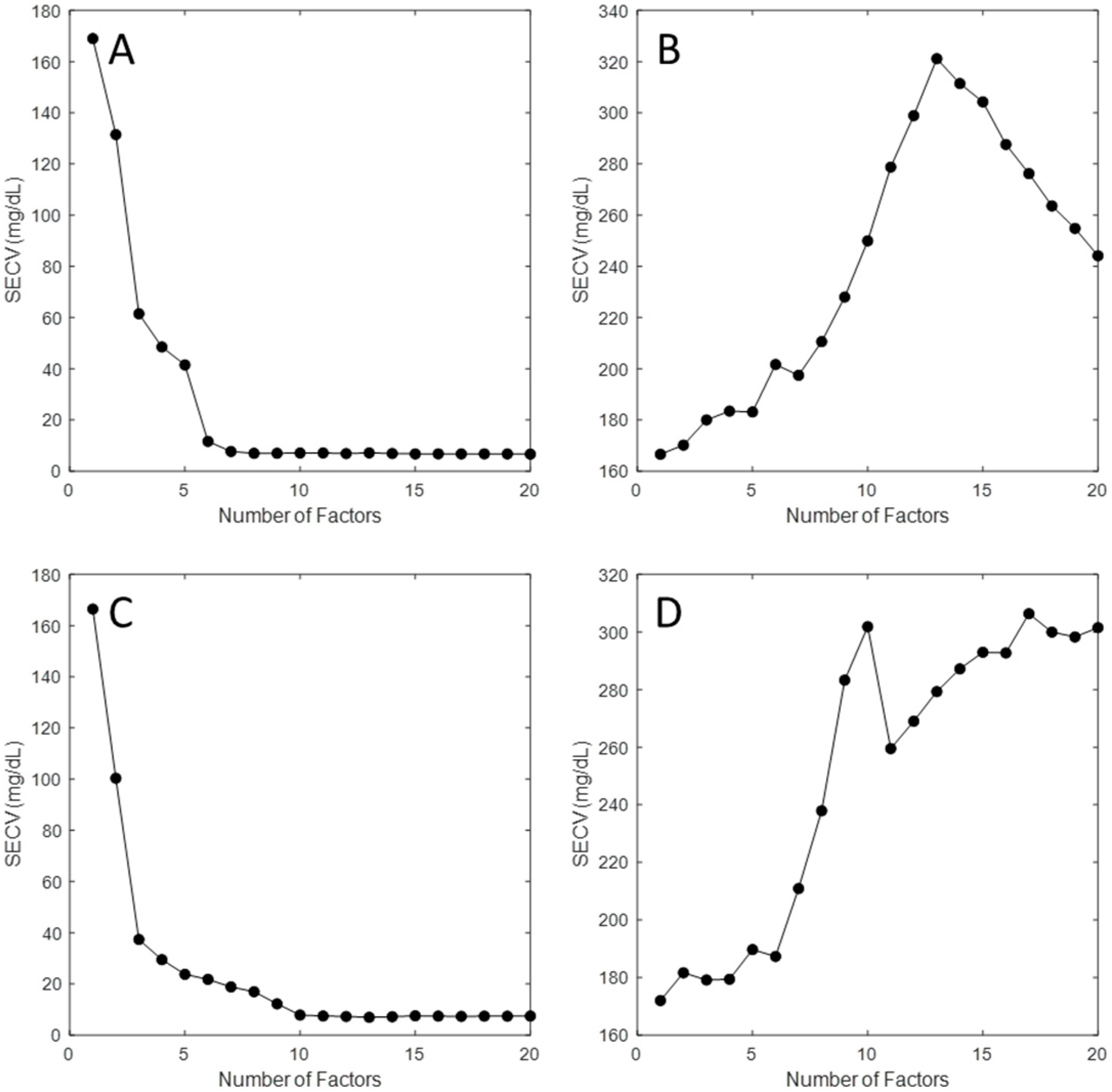
3.2. Partial Least Squares Analysis
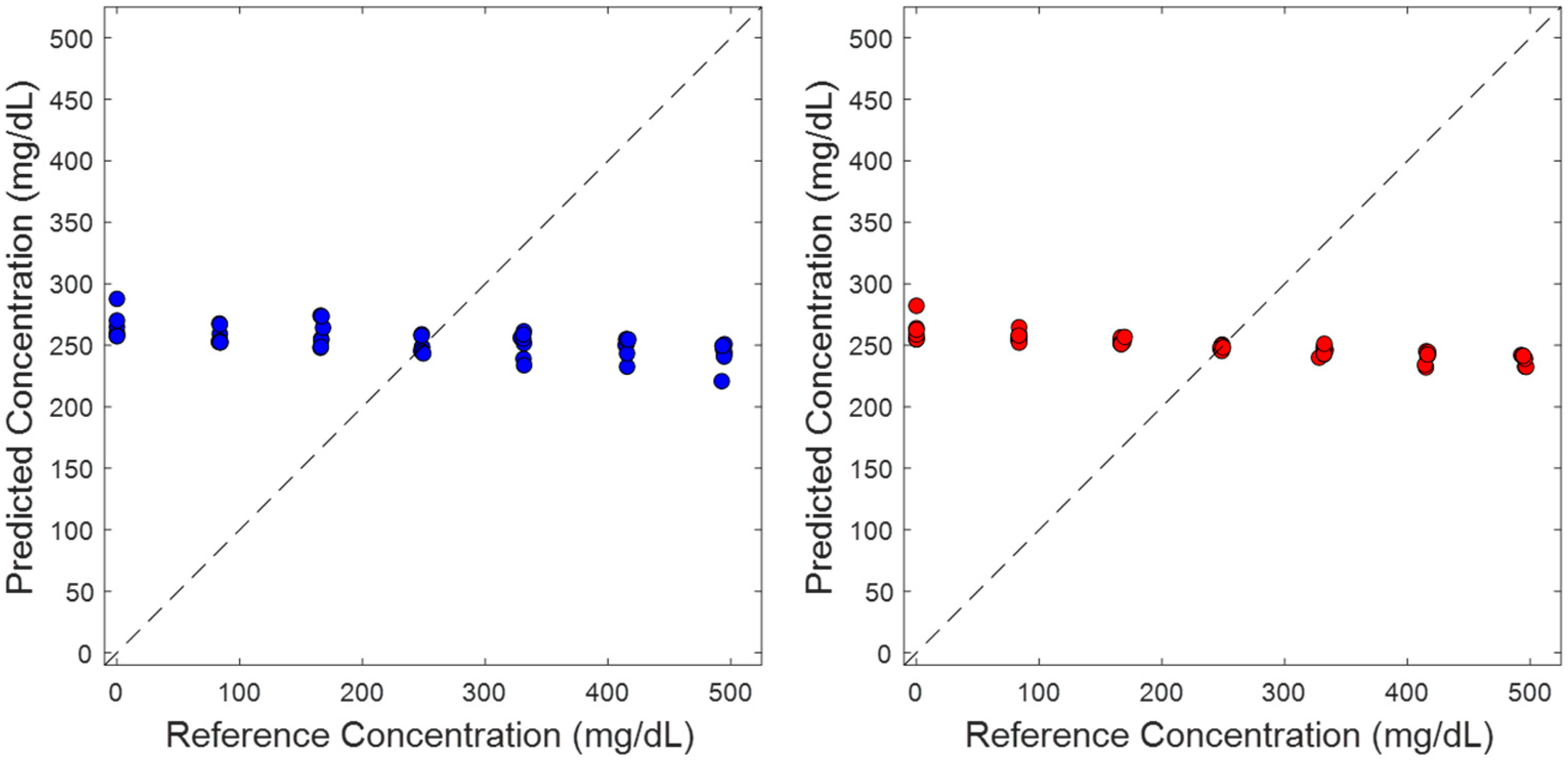
3.3. Impact of Additional Random Noise
3.4. Randomized Glucose Concentration Assignments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Magliano, D.J.; Boyko, E.J. IDF Diabetes Atlas, 10th ed.; International Diabetes Federation: Brussels, Belgium, 2021. [Google Scholar]
- Mayeda, L.; Katz, R.; Ahmad, I.; Bansal, N.; Batacchi, Z.; Hirsch, I.B.; Robinson, N.; Trence, D.L.; Zelnick, L.; de Boer, I.H. Glucose Time in Range and Peripheral Neuropathy in Type 2 Diabetes Mellitus and Chronic Kidney Disease. BMJ Open Diabetes Res. Care 2020, 8, e000991. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Wang, C.; Shen, Y.; Chen, L.; Zhang, L.; Cai, J.; Lu, W.; Zhu, W.; Hu, G.; Xia, T.; et al. Time in Range in Relation to All-Cause and Cardiovascular Mortality in Patients with Type 2 Diabetes: A Prospective Cohort Study. Diabetes Care 2021, 44, 549–555. [Google Scholar] [CrossRef] [PubMed]
- Ong, W.M.; Chua, S.S.; Ng, C.J. Barriers and Facilitators to Self-Monitoring of Blood Glucose in People with Type 2 Diabetes Using Insulin: A Qualitative Study. Patient Prefer. Adherence 2014, 8, 237–246. [Google Scholar] [PubMed]
- Park, J.J.; Guttmann-Bauman, I.; Chun, A.; Pandharpurkar, T.H.; Mullin, R. Patient-Reported Barriers to Continuous Glucose Monitor Usage. Diabetes 2023, 72, 723-P. [Google Scholar]
- Kovatchev, B.P. Metrics for Glycaemic Control-From HbA1c to Continuous Glucose Monitoring. Nat. Rev. Endocrinol. 2017, 13, 425–436. [Google Scholar] [PubMed]
- Nguyen, M.; Han, J.; Spanakis, E.K.; Kovatchev, B.P.; Klonoff, D.C. A Review of Continuous Glucose Monitoring-Based Composite Metrics for Glycemic Control. Diabetes Technol. Ther. 2020, 22, 613–622. [Google Scholar] [PubMed]
- Trisha, S.; Zhang, J.Y.; Thomas, A.; Arnold, M.A.; Vetter, B.N.; Heinemann, L.; Klonoff, D.C. Products for Monitoring Glucose Levels in the Human Body with Noninvasive Optical, Noninvsive Fluid Sampling, or Minimally Invasive Technologies. J. Diabetes Sci. Technol. 2021, 16, 168–214. [Google Scholar]
- Moses, J.C.; Adibi, S.; Wickramasinghe, N.; Nguyen, L.; Angelova, M.; Islam, S.M.S. Non-invasive Blood Glucose Monitoring Technology in Diabetes Management: Review. mHealth 2024, 10, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.L. The Pursuit of Noninvasive Glucose:” Hunting the Deceitful Turkey”, 6th ed. 2018. Available online: https://www.nivglucose.com/ (accessed on 25 August 2018).
- Griffiths, P.R.; de Haseth, J.A. Fourier Transform Infrared Spectrometry, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Klonoff, D.C.; Nguyen, K.T.; Xu, N.Y.; Arnold, M.A. Noinvasive Glucose Monitoring: In God We Trust-All Others Bring Data. J. Diabetes Sci. Technol. 2021, 15, 1211–1215. [Google Scholar] [CrossRef] [PubMed]
- Viana, F.A.C. A Tutorial on Latin Hypercube Design of Experiments. Qual. Reliab. Engng. Int. 2016, 32, 1975–1985. [Google Scholar]
- Ridder, T.D.; Steeg, B.J.V.; Laaksonen, B.D. Comparison of Spectroscopically Measured Tissue Alcohol Concentration to Blood and Breath Alcohol Measurements. J. Biomed. Opt. 2009, 14, 054039. [Google Scholar] [PubMed]
- Hazen, K.H.; Arnold, M.A.; Small, G.W. Temperature-Insensitive Near-Infrared Spectroscopic Measurement of Glucose in Aqueous Solution. Appl. Spectrosc. 1994, 48, 477–483. [Google Scholar]
- Fortmann-Roe, S. Understanding the Bias-Variance Tradeoff. Available online: https://scott.fortmann-roe.com/docs/BiasVariance.html (accessed on 10 December 2023).
- American Diabetes Association Professional Practice Committee. Glycemic Goals and Hypoglycemia: Standards of Care in Diabetes-2025. Diabetes Care 2025, 48, S128–S145. [Google Scholar] [CrossRef] [PubMed]
- Holt, R.I.G.; DeVries, J.H.; Hess-Fischl, A.; Hirsch, I.B.; Klupa, T.; Ludwig, B.; Norgaard, K.; Pettus, J.; Renard, E.; Skyler, J.S.; et al. The Management of Type 1 Diabetes in Adults. A Consensus Report by the American Diabetes Association (ADA) and the European Association for the Study of Diabetes (EASD). Diabetes Care 2021, 44, 2589–2625. [Google Scholar] [CrossRef] [PubMed]

| Glucose | 0 | 82.5 | 167.5 | 250 | 332.5 | 417.5 | 500 |
| Polystyrene beads | 1466 | 1588 | 1712 | 1734 | 1956 | 2078 | 2200 |
| Instrument | TTT-2500 | Early-Stage Prototype |
|---|---|---|
| Spectral range (nm) | 1551–2378 | 1401–2238 |
| Number of factors | 8 | 10 |
| SECV (mg/dL) | 6.62 | 7.82 |
| Regression slope | 0.998 (±0.006) | 0.998 (±0.007) |
| Regression intercept | 1.0 (±2) | 1.0 (±2) |
| Coefficient of determination, R2 | 0.998 | 0.998 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kauffman, A.B.; Shakya, R.; Yu, S.; Arnold, M.A. Noninvasive Glucose Measurements in Tissue Simulating Phantoms Using a Solid-State Near-Infrared Sensor. Sensors 2025, 25, 2238. https://doi.org/10.3390/s25072238
Kauffman AB, Shakya R, Yu S, Arnold MA. Noninvasive Glucose Measurements in Tissue Simulating Phantoms Using a Solid-State Near-Infrared Sensor. Sensors. 2025; 25(7):2238. https://doi.org/10.3390/s25072238
Chicago/Turabian StyleKauffman, Ariel B., Ruben Shakya, Shuai Yu, and Mark A. Arnold. 2025. "Noninvasive Glucose Measurements in Tissue Simulating Phantoms Using a Solid-State Near-Infrared Sensor" Sensors 25, no. 7: 2238. https://doi.org/10.3390/s25072238
APA StyleKauffman, A. B., Shakya, R., Yu, S., & Arnold, M. A. (2025). Noninvasive Glucose Measurements in Tissue Simulating Phantoms Using a Solid-State Near-Infrared Sensor. Sensors, 25(7), 2238. https://doi.org/10.3390/s25072238






