Real-Time Sensor for Measuring the Surface Temperature of Thermal Protection Structures Based on the Full-Time Domain Temperature Inversion Method
Abstract
Highlights:
- Real-time implementation of a full-time domain method (TIM-AB) is achieved by an overlapping sliding window method.
- The optimal window duration is equal to the thermal hysteresis time, and the effect of noise on the inversion accuracy can be effectively reduced by Savitzky-Golay filtering.
- The surface temperature of TPSs can be calculated by real-time inversion using the TIM-AB method.
- It is proved that the proposed method has great potential for engineering applications.
Abstract
1. Introduction
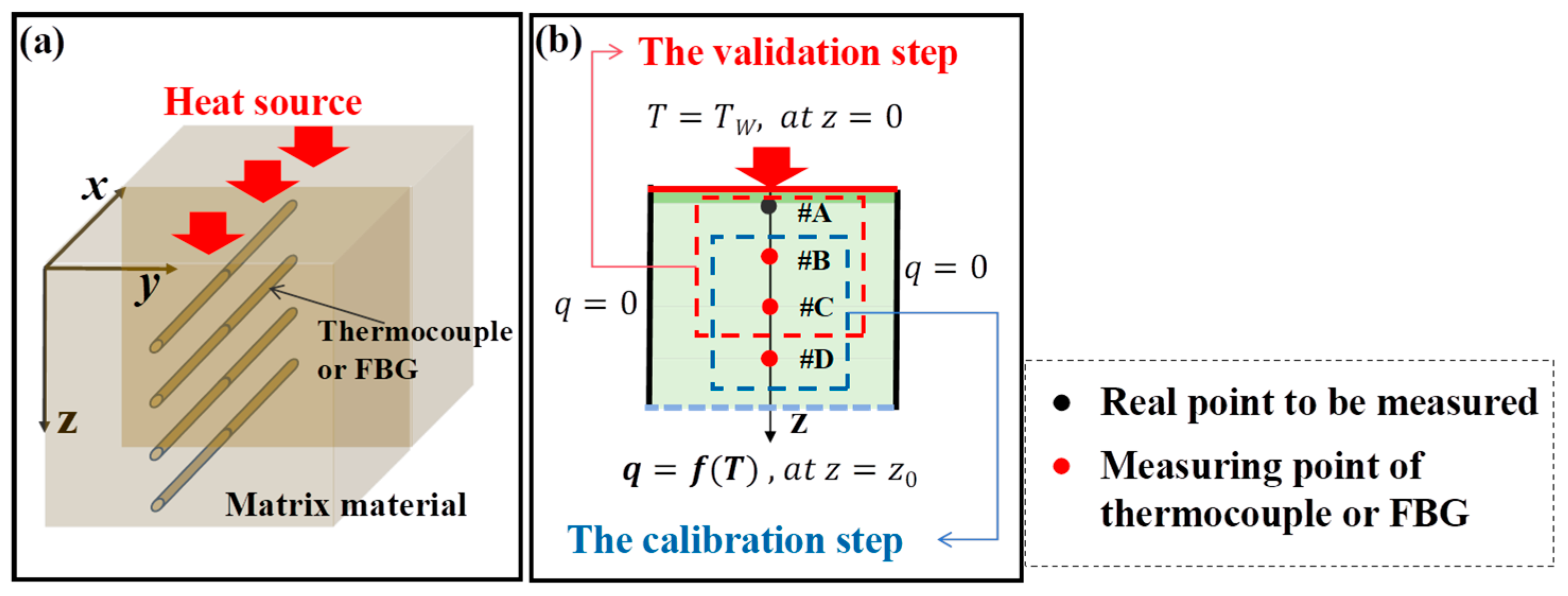
2. Real-Time Implementation of TIM-AB
2.1. The Temperature Inversion Method with Adaptive Boundary
2.2. The Implementation Method of Real-Time Inversion
3. Feasibility Analysis of Real-Time Inversion
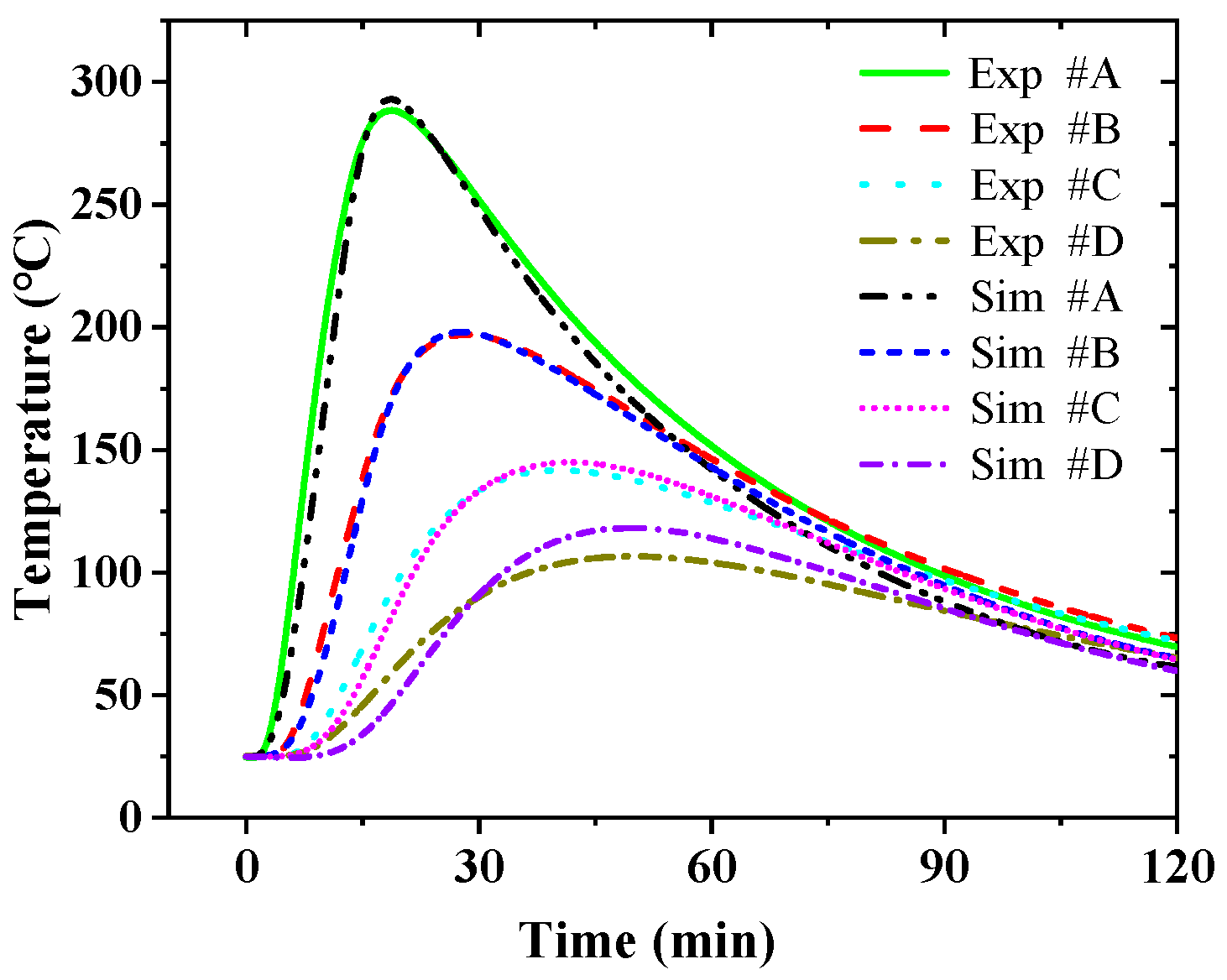
3.1. Surface Temperature Estimation by TIM-AB Method
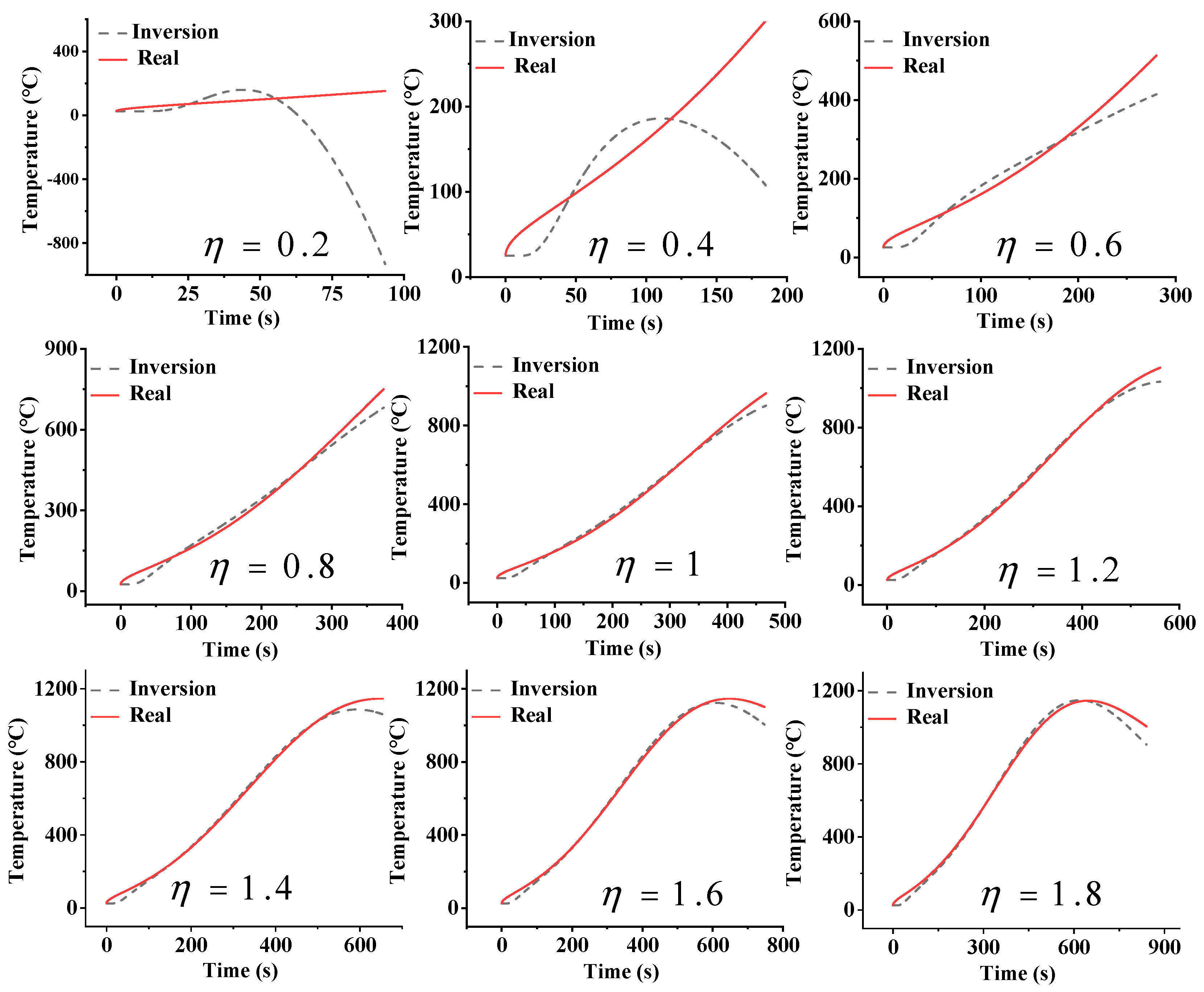
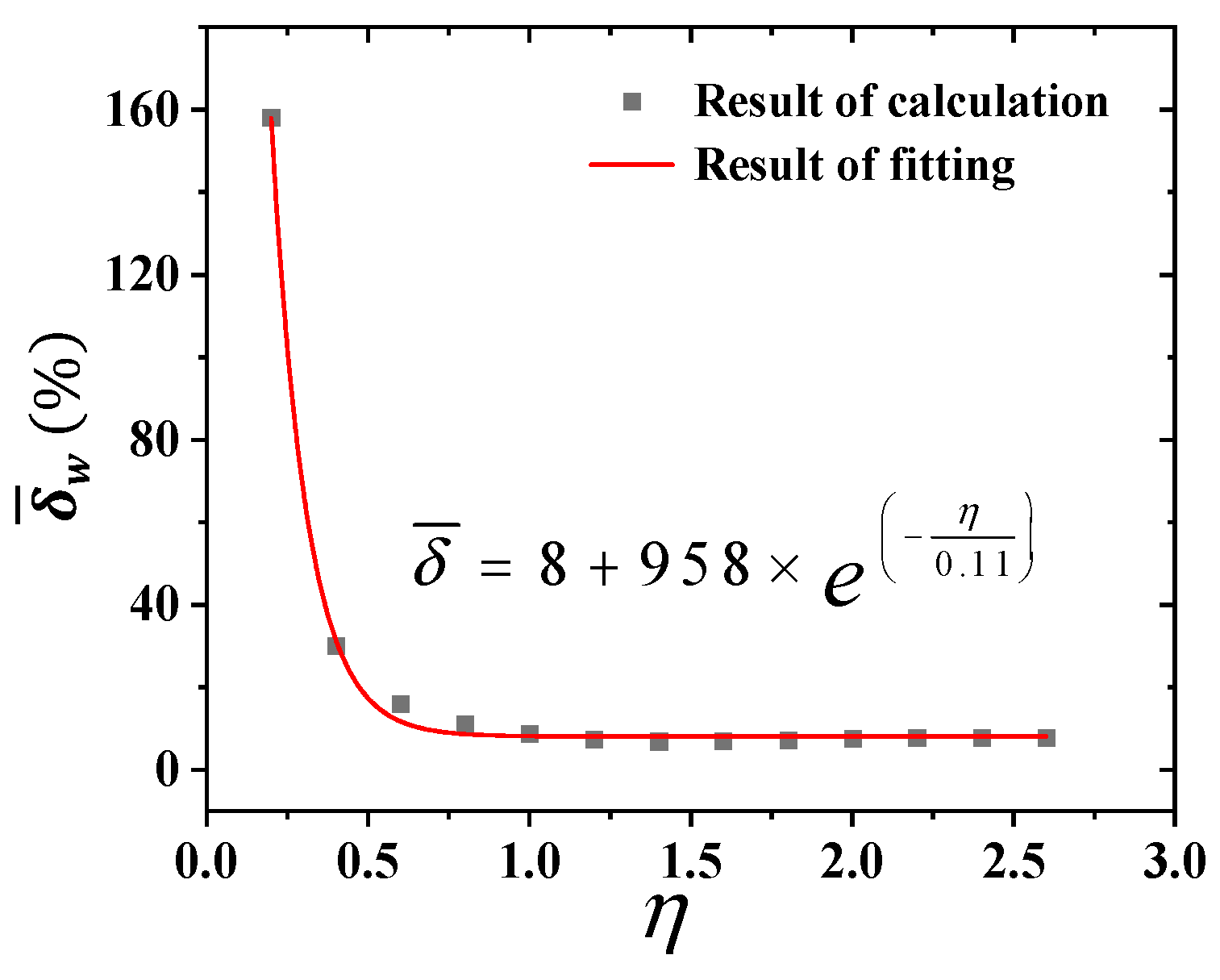
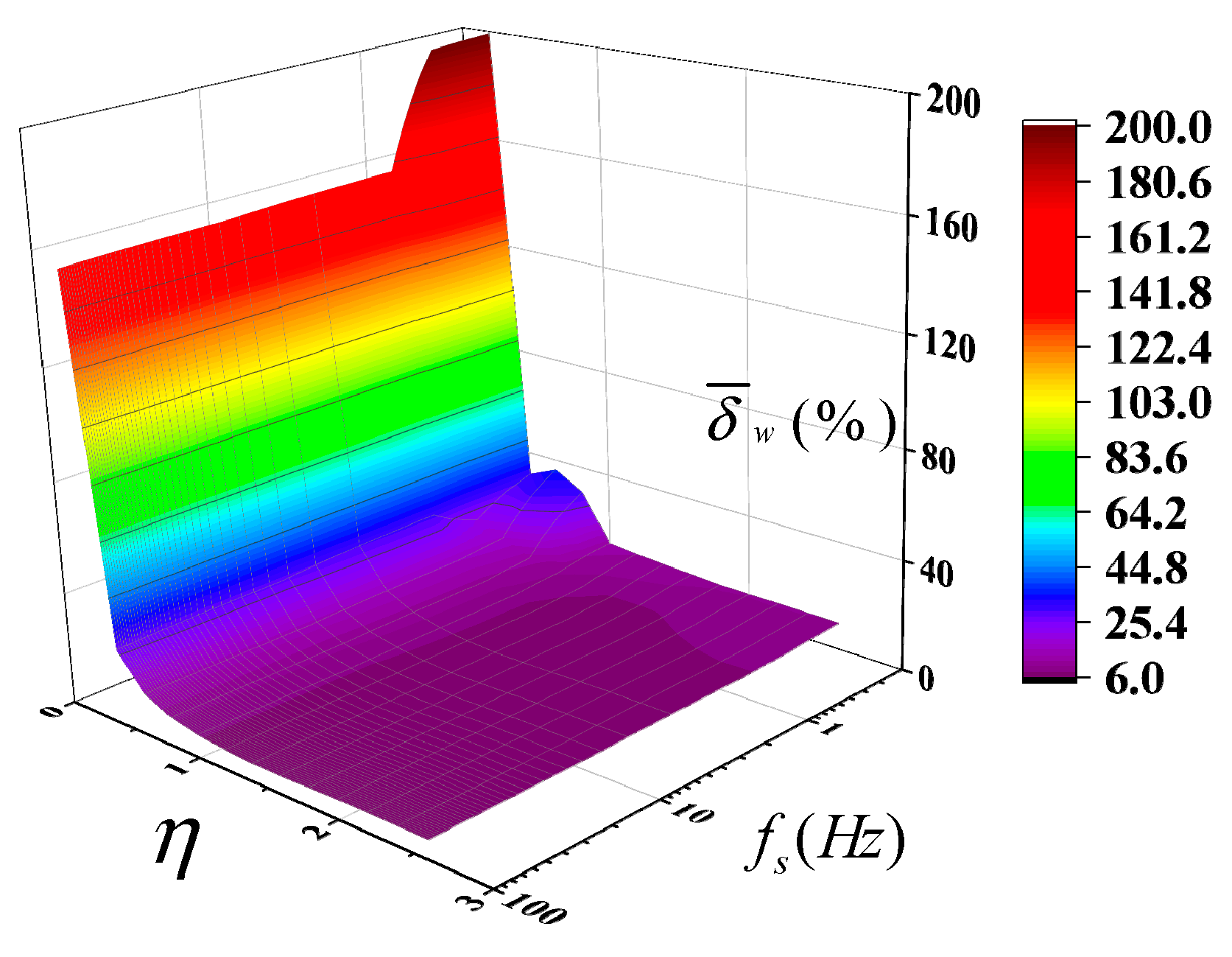
3.2. The Relationship Between Moving Window Size and the Thermal Hysteresis Time
3.3. The Influence of the Slide Step of Window
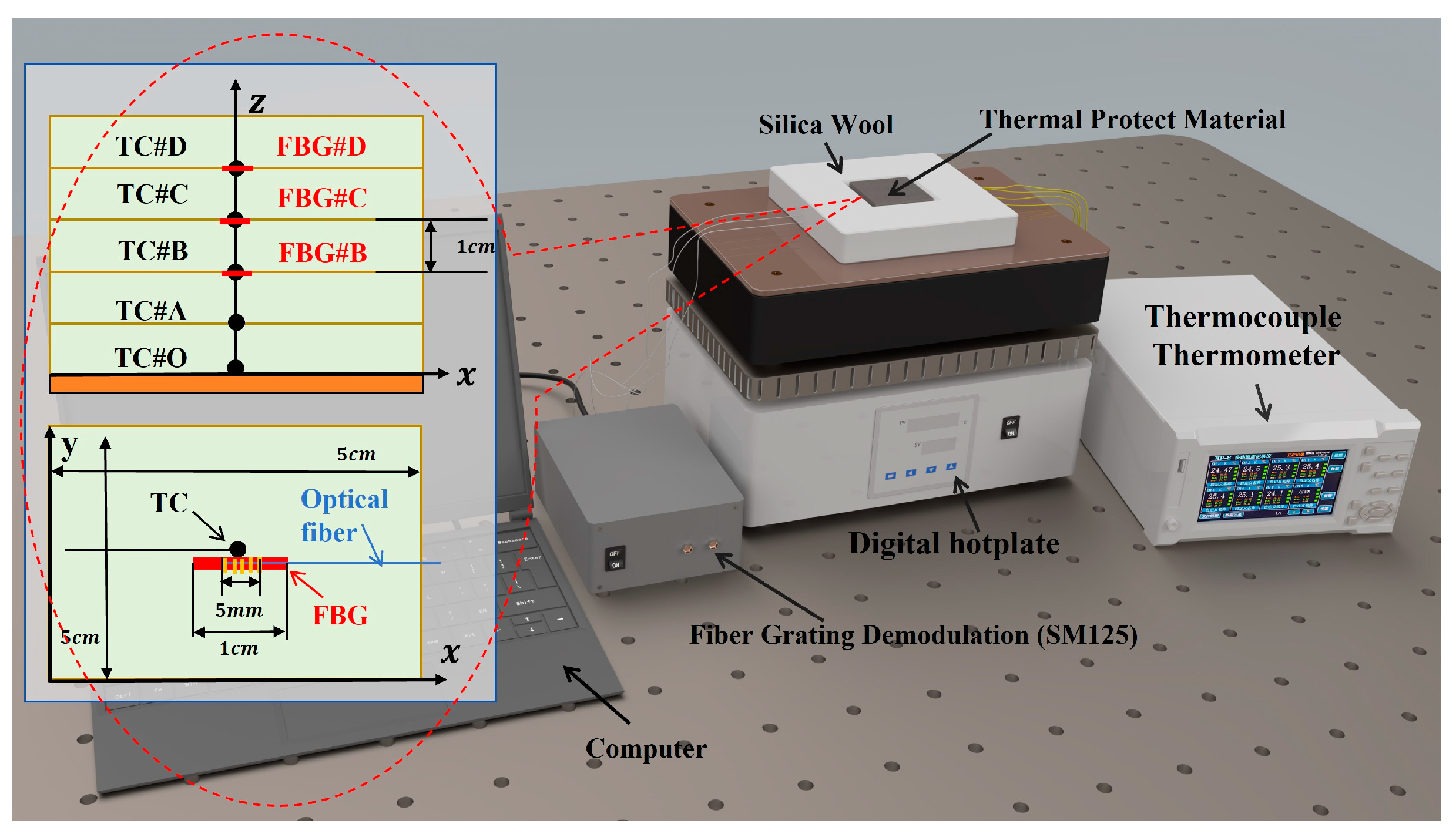
4. Real-Time Inversion of Surface Temperature of the TPS Under Transient Thermal Shock
4.1. Experimental Method
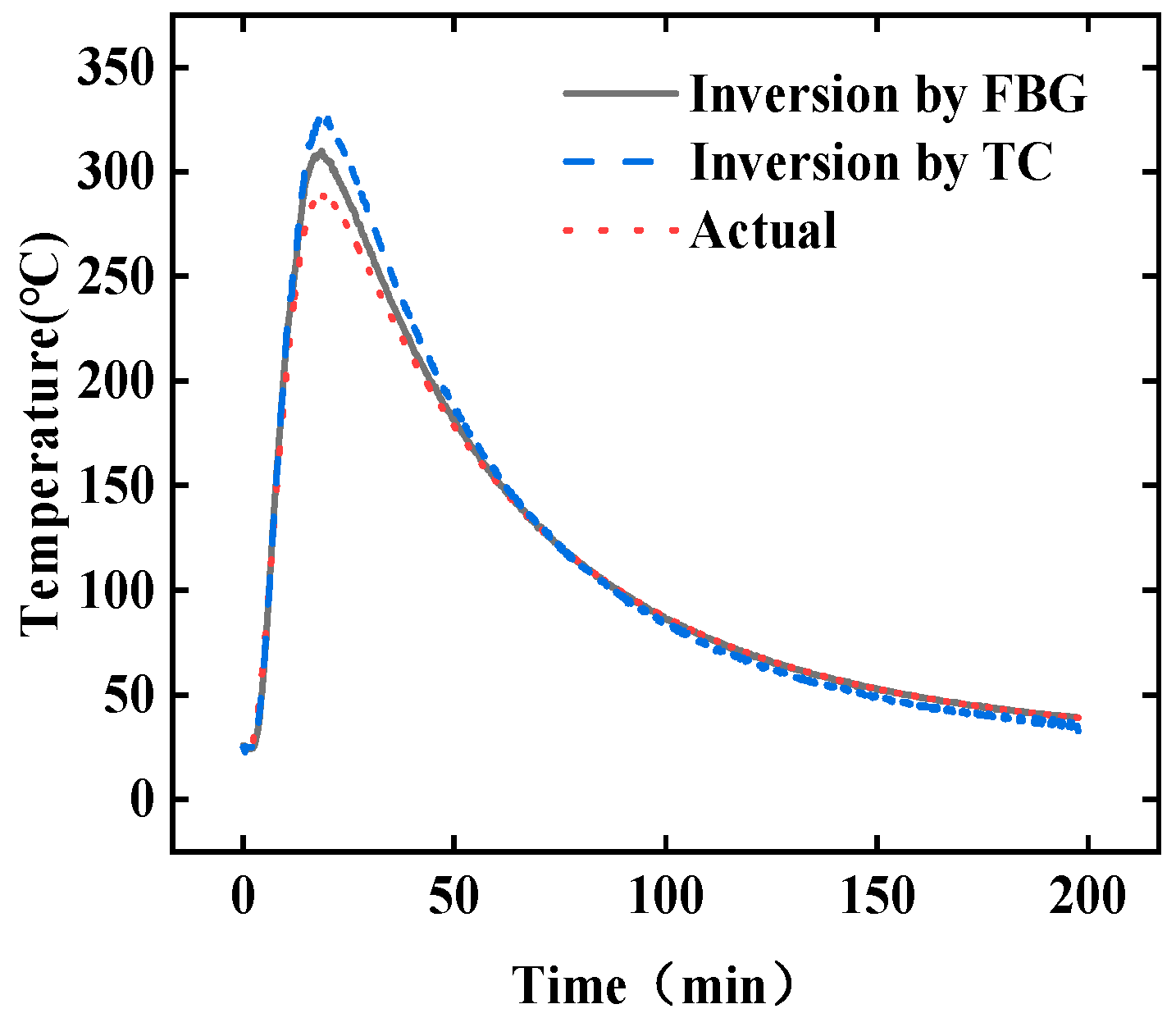
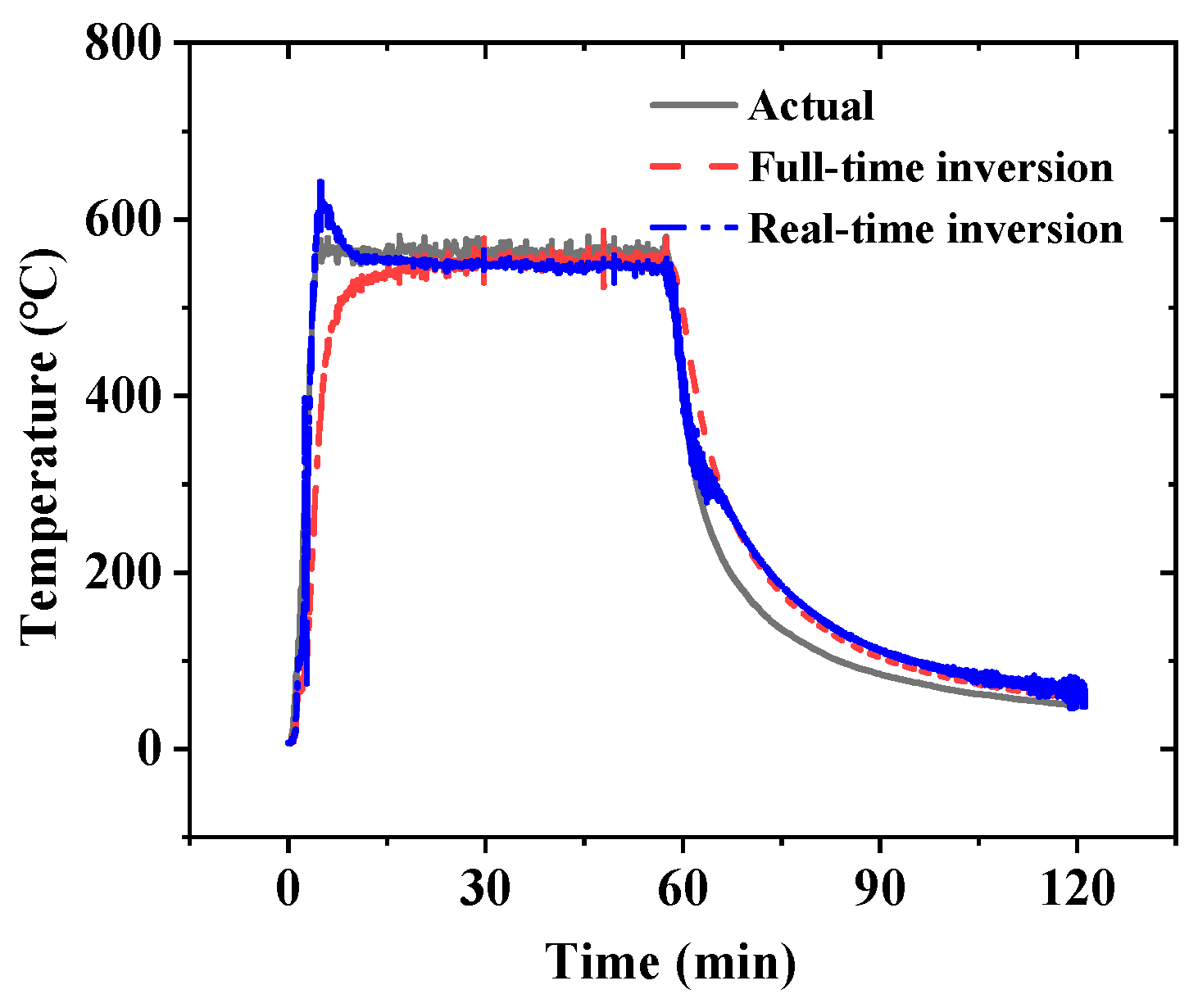
4.2. Comparison of Full-Time Inversion and Real-Time Inversion
4.3. The Influence of Measurement Uncertainty on Real-Time Inversion
4.4. The Influence of Data Noise on the Real-Time Inversion
5. Comparison
6. Conclusions
- (1)
- Numerical simulations analyzed the relationship between inversion accuracy and moving window size under Gaussian thermal shock. The results show the mean relative error of real-time inversion has an exponential relationship with the moving window size, with the optimal duration of window being 1 time that of the thermal hysteresis time. When the window slide step is smaller than the sensor’s data collection per unit time, the stack size scarcely affects inversion accuracy. For insulation materials with a large thermal hysteresis time, as long as the thermocouple sampling frequency exceeds 1 Hz, the influence of sampling frequency on the inversion accuracy is minimal, and the material’s surface temperature can be effectively retrieved.
- (2)
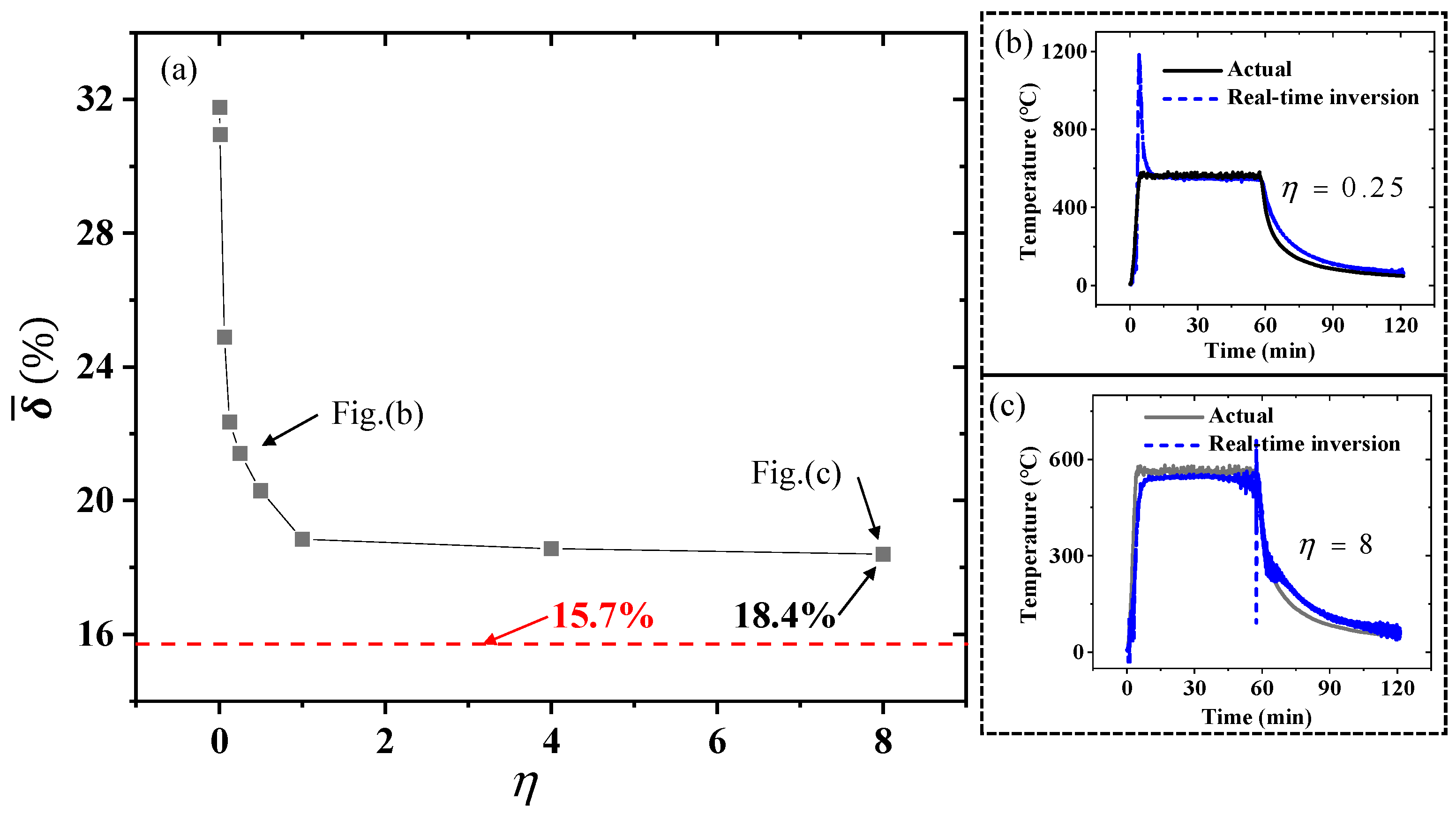
- Experiments using a quartz lamp heater for lateral heating of the TPS verified that the real-time inversion method can accurately invert the surface temperature of the TPS materials using real data. Without noise filtering, the mean relative error of real-time inversion is 18.8%, higher than the 15.7% error of full-time domain inversion. Data noise from electromagnetic interference and other factors significantly can increase the inversion error.
- (3)
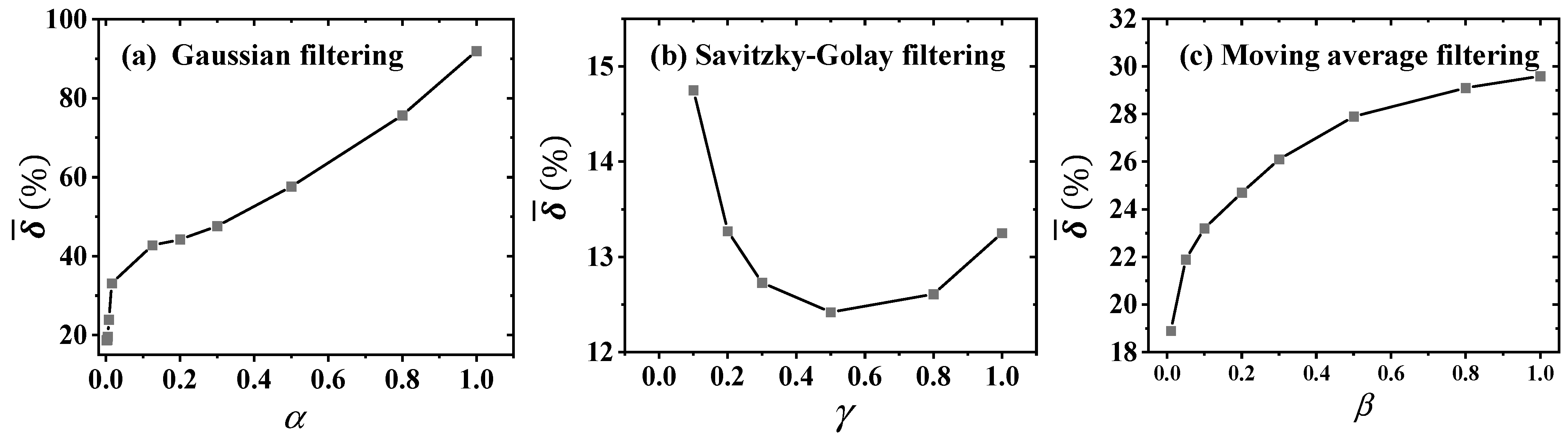
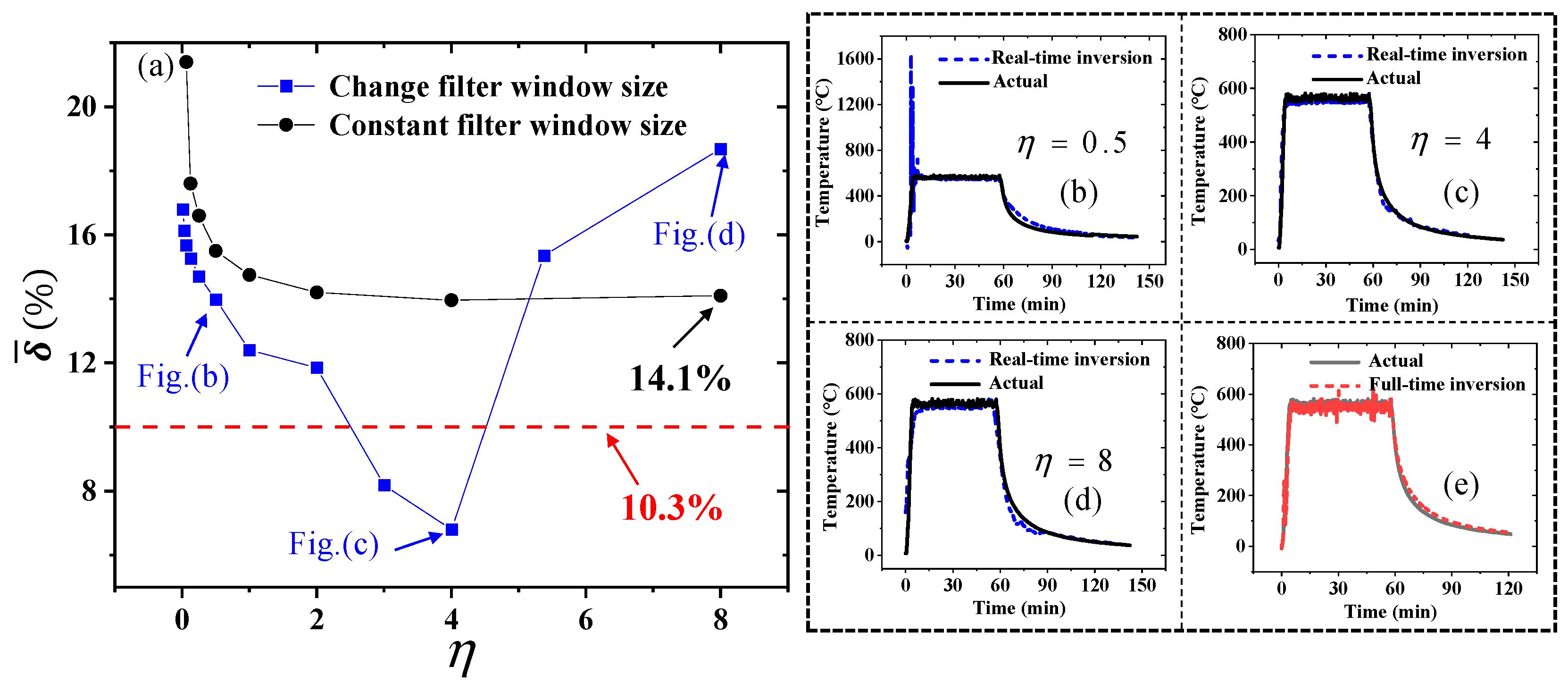
- Three noise filtering methods, Gaussian, Savitzky-Golay, and moving average, are compared, with Savitzky-Golay proving the most effective. When the noise filtering window size is constant, the inversion error remains exponentially related to the moving window size. However, when the noise filtering window size varies, no monotonic relationship exists between the inversion error and moving window size. By adjusting the noise filtering window size, real-time inversion accuracy is significantly enhanced, reducing the mean relative error to 6.7%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| TPS | Thermal Protection Structure |
| IHCP | Inverse Heat Conduction Problem |
| TIM-AB | Temperature Inversion Method with Adaptive Boundary |
| ARX | Auto-Regression with eXtra |
| FBG | Fiber Bragg Grating |
| TC | Thermocouple |
References
- Zhang, S.; Zhang, Z.; Wang, Y.; Zheng, H. Design and performance verification of thermal protection structure of high temperature probe in aeroengine. Appl. Therm. Eng. 2024, 253, 123745. [Google Scholar] [CrossRef]
- Sapozhnikov, S.Z.; Mityakov, V.Y.; Mityakov, A.V.; Mozhaĭskiĭ, S.A. Gradient-type sensors for heat flux measurements high temperatures. Tech. Phys. Lett. 2008, 34, 815–817. [Google Scholar]
- Trubachev, S.A.; Korobeinichev, O.P.; Shmakov, A.G.; Sagitov, A.R. Method of heat flux measurement in solid fuel flames using semiconductor sensors. Combust. Explos. Shock Waves 2024, 60, 185–192. [Google Scholar]
- Sakharov Valerii, A.; Popov Pavel, A.; Monakhov Nikolai, A. Heat flux measurements of high speed flow around an axisymmetric body using sensors based on anisotropic thermoelements. St. Petersburg Polytech. Univ. J. Phys. Math. 2023, 63, 450–455. [Google Scholar]
- Le, V.T.; Ha, S.; Ha, N.; Goo, N.S. Advanced sandwich structures for thermal protection systems in hypersonic vehicles: A review. Compos. Part B Eng. 2021, 226, 109301. [Google Scholar]
- Wang, F.; Zhang, P.; Wang, Y.; Sun, C.; Xia, X. Real-time identification of severe heat loads over external interface of lightweight thermal protection system. Therm. Sci. Eng. Prog. 2022, 37, 101583. [Google Scholar]
- Nenarokomov, A.V.; Alifanov, O.M.; Budnik, S.A.; Netelev, A.V. Research and development of heat flux sensor for ablative thermal protection of spacecrafts. Int. J. Heat Mass Transf. 2016, 97, 990–1000. [Google Scholar]
- Tallman, T.N.; Frueh, S.; Lin, C.; Wertz, J.; Cherry, M.; Apostolov, Z.D.; Rueschhoff, L.M. The electrical response of refractory carbon/carbon composites to high-temperature ablation: A pathway to embedded sensing in extreme environments. Compos. Part B Eng. 2023, 264, 110922. [Google Scholar] [CrossRef]
- Sobota, T.; Taler, D.; Taler, J. Measurement of the temperature of the fluid inside the tube based on the temperature measurement of the thermally insulated outer surface. Int. J. Heat Mass Transf. 2024, 228, 125622. [Google Scholar]
- Chen, S.; Su, Z.; Dai, M.; Xue, C.; Tao, J.; Hai, Z. A General Super-Resolution Approach Integrating Physical Information for Temperature Field Measurement. Sensors 2024, 24, 7445. [Google Scholar] [CrossRef]
- Oliveira, A.V.S.; Avrit, A.; Gradeck, M. Thermocouple response time estimation and temperature signal correction for an accurate heat flux calculation in inverse heat conduction problems. Int. J. Heat Mass Transf. 2021, 185, 122398. [Google Scholar]
- Mohebbi, F. Explicit Sensitivity Coefficients for Estimation of Temperature-Dependent Thermophysical Properties in Inverse Transient Heat Conduction Problems. Computation 2020, 8, 95. [Google Scholar] [CrossRef]
- Kumar, S.; Mahulikar, S.P. Reconstruction of aero-thermal heating and thermal protection material response of a Reusable Launch Vehicle using inverse method. Appl. Therm. Eng. 2016, 103, 344–355. [Google Scholar]
- Brociek, R.; Hetmaniok, E.; Słota, D. Reconstruction of aerothermal heating for the thermal protection system of a reusable launch vehicle. Appl. Therm. Eng. 2023, 219, 119405. [Google Scholar]
- Jiang, X.; Wang, X.; Wen, Z.; Wang, H. Resolution-independent generative models based on operator learning for physics-constrained Bayesian inverse problems. Comput. Methods Appl. Mech. Eng. 2024, 420, 116690. [Google Scholar]
- Gu, J.h.; Hong, M.; Yang, Q.Q.; Heng, Y. A fast inversion approach for the identification of highly transient surface heat flux based on the generative adversarial network. Appl. Therm. Eng. 2023, 220, 119765. [Google Scholar]
- Santos, J.A.; Oliveira, J.R.F.; do Nascimento, J.G.; Fernandes, A.P.; Guimaraes, G. Simultaneous estimation of thermal properties via measurements using one active heating surface and Bayesian inference. Int. J. Therm. Sci. 2021, 172, 107304. [Google Scholar]
- Tian, J.M.; Chen, B.; Zhou, Z.F. Methodology of surface heat flux estimation for 2D multi-layer mediums. Int. J. Heat Mass Transf. 2017, 114, 675–687. [Google Scholar]
- Wu, T.; Zhang, C.; Ji, H.; Zhang, Y.; Tao, C.; Qiu, J. Heat Flux Identification of Aircraft Structure with Artificial Neural Network Compensation. J. Thermophys. Heat Transf. 2023, 37, 523–533. [Google Scholar]
- Cebo-Rudnicka, A.; Malinowski, Z. Identification of heat flux and heat transfer coefficient during water spray cooling of horizontal copper plate. Int. J. Therm. Sci. 2019, 145, 106038. [Google Scholar]
- Samadi, F.; Woodbury, K.; Kowsary, F. Optimal combinations of Tikhonov regularization orders for IHCPs. Int. J. Therm. Sci. 2020, 161, 106697. [Google Scholar] [CrossRef]
- Uyanna, O.; Najafi, H.; Rajendra, B. An inverse method for real-time estimation of aerothermal heating for thermal protection systems of space vehicles. Int. J. Heat Mass Transf. 2021, 177, 121482. [Google Scholar] [CrossRef]
- Najafi, H.; Woodbury, K.A.; Beck, J.V.; Keltner, N.R. Real-time heat flux measurement using directional flame thermometer. Appl. Therm. Eng. 2015, 86, 229–237. [Google Scholar] [CrossRef]
- Najafi, H.; Woodbury, K.A.; Beck, J.V. A filter based solution for inverse heat conduction problems in multi-layer mediums. Int. J. Heat Mass Transf. 2015, 83, 710–720. [Google Scholar] [CrossRef]
- Cebula, A.; Taler, J. Determination of transient temperature and heat flux on the surface of a reactor control rod based on temperature measurements at the interior points. Appl. Therm. Eng. 2014, 63, 158–169. [Google Scholar] [CrossRef]
- Khatoon, S.; Phirani, J.; Bahga, S.S. Fast Bayesian inference for inverse heat conduction problem using polynomial chaos and Karhunen–Loeve expansions. Appl. Therm. Eng. 2023, 219, 119616. [Google Scholar] [CrossRef]
- Qi, H.; Wen, S.; Wang, Y.F.; Ren, Y.T.; Wei, L.Y.; Ruan, L.M. Real-time reconstruction of the time-dependent heat flux and temperature distribution in participating media by using the Kalman filtering technique. Appl. Therm. Eng. 2019, 157, 113667. [Google Scholar] [CrossRef]
- Zheng, Y.; Yin, Z. Cutting temperature field online reconstruction using temporal convolution and deep learning networks. Int. J. Heat Mass Transf. 2025, 241, 126766. [Google Scholar] [CrossRef]
- Wan, S.; Wang, K.; Xu, P.; Huang, Y. Numerical and experimental verification of the single neural adaptive PID real-time inverse method for solving inverse heat conduction problems. Int. J. Heat Mass Transf. 2022, 189, 122657. [Google Scholar] [CrossRef]
- Najafi, H.; Woodbury, K.A. Online heat flux estimation using artificial neural network as a digital filter approach. Int. J. Heat Mass Transf. 2015, 91, 808–817. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, Q.; Ma, H.; Chen, S.; Fei, Q. Transfer machine learning framework for efficient full-field temperature response reconstruction of thermal protection structures with limited measurement data. Int. J. Heat Mass Transf. 2025, 242, 126785. [Google Scholar]
- Zhang, L.; Li, L.; Ju, H.; Zhu, B. Inverse identification of interfacial heat transfer coefficient between the casting and metal mold using neural network. Energy Convers. Manag. 2010, 51, 1898–1904. [Google Scholar]
- He, Z.; Ni, F.; Wang, W.; Zhang, J. A physics-informed deep learning method for solving direct and inverse heat conduction problems of materials. Mater. Today Comm. 2021, 28, 102719. [Google Scholar]
- Nakamura, T.; Kamimura, Y.; Igawa, H.; Morino, Y. Inverse analysis for transient thermal load identification and application to aerodynamic heating on atmospheric reentry capsule. Aerosp. Sci. Technol. 2014, 38, 48–55. [Google Scholar] [CrossRef]
- Woodbury, K.A.; Beck, J.V.; Najafi, H. Filter solution of inverse heat conduction problem using measured temperature history as remote boundary condition. Int. J. Heat Mass Transf. 2014, 72, 139–147. [Google Scholar]
- Huang, W.; Li, J.; Liu, D. Real-Time Solution of Unsteady Inverse Heat Conduction Problem Based on Parameter-Adaptive PID with Improved Whale Optimization Algorithm. Energies 2022, 16, 225. [Google Scholar] [CrossRef]
- Najafi, H.; Woodbury, K.A.; Beck, J.V. Real time solution for inverse heat conduction problems in a two-dimensional plate with multiple heat fluxes at the surface. Int. J. Heat Mass Transf. 2015, 91, 1148–1156. [Google Scholar] [CrossRef]
- Deng, S.; Hwang, Y. Applying neural networks to the solution of forward and inverse heat conduction problems. Int. J. Heat Mass Transf. 2006, 49, 4732–4750. [Google Scholar]
- Zhao, X.; Jin, K.Z.; Yan, M.Y.; Nan, P.Y.; Zhou, F.; Xin, G.G.; Lim, K.; Ahmad, H.; Zhang, Y.P.; Yang, H.Z. Inverse heat transfer for real-time thermal evaluation of aircraft thermal protection structure with embedded FBG sensors. Appl. Therm. Eng. 2025, 260, 124869. [Google Scholar]
- Kalberla, P.M.W.; Haud, U. Properties of cold and warm HI gas phases derived from a Gaussian decomposition of HI4PI data. Astron. Astrophys. 2018, 619, A58. [Google Scholar]
- Li, W.; Sigmund, O.; Zhang, X.S. Analytical realization of complex thermal meta-devices. Nat. Commun. 2024, 15, 5527. [Google Scholar] [PubMed]
- Ali, M.A.; Shimoda, M. Toward multiphysics multiscale concurrent topology optimization for lightweight structures with high heat conductivity and high stiffness using MATLAB. Struct. Multidiscip. Optim. 2022, 65, 207. [Google Scholar]
- Li, W.; Huang, J.; Zhang, Z.; Wang, L.; Huang, H.; Liang, J. A model for thermal protection ablative material with local thermal non-equilibrium and thermal radiation mechanisms. Acta Astronaut. 2021, 183, 101–111. [Google Scholar]
- Feng, J.; Liu, M.; Ma, S.; Yang, J.; Mo, W.; Su, X. Micro-nano scale heat transfer mechanisms for fumed silica based thermal insulating composite. Int. Commun. Heat Mass Transf. 2020, 110, 104392. [Google Scholar]
- Tychanicz-Kwiecień, M.; Wilk, J.; Gil, P. Review of high-temperature thermal insulation materials. J. Thermophys. Heat Transf. 2019, 33, 271–284. [Google Scholar]






| Reference | Key Approach for Solving IHCP | Features and Functions |
|---|---|---|
| [22] | Tikhonov regularization | Suitable for 1-D heat transfer of a multilayer medium; Robust noise resistance; Near real time, 17 s delay. |
| [24] | Tikhonov digital filter | Suitable for 1-D heat transfer of multilayer medium; Near real time. |
| [28] | Rapid computation combined with hybrid neural networks | Suitable for 2-D heat transfer; Based on algorithm pre-training; Real time, Second delay. |
| [34] | Sequential Function Specification and Truncated Singular Value Decomposition | Suitable for 2-D heat transfer; Stable thermal parameters required. |
| [35] | Tikhonov digital filter | Suitable for 1-D heat transfer; Near real time. |
| This paper | The Auto-Regression with eXtra and Overlapping Sliding Window | Suitable for 1-D heat transfer; No thermal parameters required; Robust noise resistance; Real time, less than 1 s delay. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhao, X.; Wei, X.; Nan, P.; Zhou, F.; Xin, G.; Lim, K.-S.; Zhang, Y.; Yang, H. Real-Time Sensor for Measuring the Surface Temperature of Thermal Protection Structures Based on the Full-Time Domain Temperature Inversion Method. Sensors 2025, 25, 2227. https://doi.org/10.3390/s25072227
Liu Y, Zhao X, Wei X, Nan P, Zhou F, Xin G, Lim K-S, Zhang Y, Yang H. Real-Time Sensor for Measuring the Surface Temperature of Thermal Protection Structures Based on the Full-Time Domain Temperature Inversion Method. Sensors. 2025; 25(7):2227. https://doi.org/10.3390/s25072227
Chicago/Turabian StyleLiu, Yuhao, Xiong Zhao, Xiangyu Wei, Pengyu Nan, Fan Zhou, Guoguo Xin, Kok-Sing Lim, Yupeng Zhang, and Hangzhou Yang. 2025. "Real-Time Sensor for Measuring the Surface Temperature of Thermal Protection Structures Based on the Full-Time Domain Temperature Inversion Method" Sensors 25, no. 7: 2227. https://doi.org/10.3390/s25072227
APA StyleLiu, Y., Zhao, X., Wei, X., Nan, P., Zhou, F., Xin, G., Lim, K.-S., Zhang, Y., & Yang, H. (2025). Real-Time Sensor for Measuring the Surface Temperature of Thermal Protection Structures Based on the Full-Time Domain Temperature Inversion Method. Sensors, 25(7), 2227. https://doi.org/10.3390/s25072227






