Optimization of a Time-of-Arrival-Ridge Estimation Iterative Model for Ultra-Wideband Positioning in a Long Linear Area
Abstract
Highlights
- A high-precision UWB+TOA-RR positioning algorithm is proposed, incorporating Ridge estimation and equivalent weights to improve localization accuracy in long linear areas.
- The TOA-RR model achieves a positioning accuracy of approximately 0.5 m, significantly outperforming conventional TOA-LS and TOA-R models in long linear environments.
- This study resolves the challenge of inaccurate UWB localization in long linear areas, such as tunnels and corridors, providing a robust solution for high-precision indoor positioning.
- The proposed TOA-RR algorithm enhances the stability and accuracy of UWB localization, making it suitable for practical applications in challenging environments.
Abstract
1. Introduction
1.1. Related Work
- (1)
- In the domain of optimizing UWB equipment layout schemes and exploring UWB-based combination positioning methods, several scholars have conducted studies and achieved more favorable outcomes.
- (2)
- Numerous scholars carried out optimizations of UWB solution models, yielding positive application outcomes.
- (3)
- Furthermore, the research into UWB technology has yielded promising results in the field of long linear underground tunnel localization.
1.2. Motivation and Contribution
1.3. Outline of the Paper
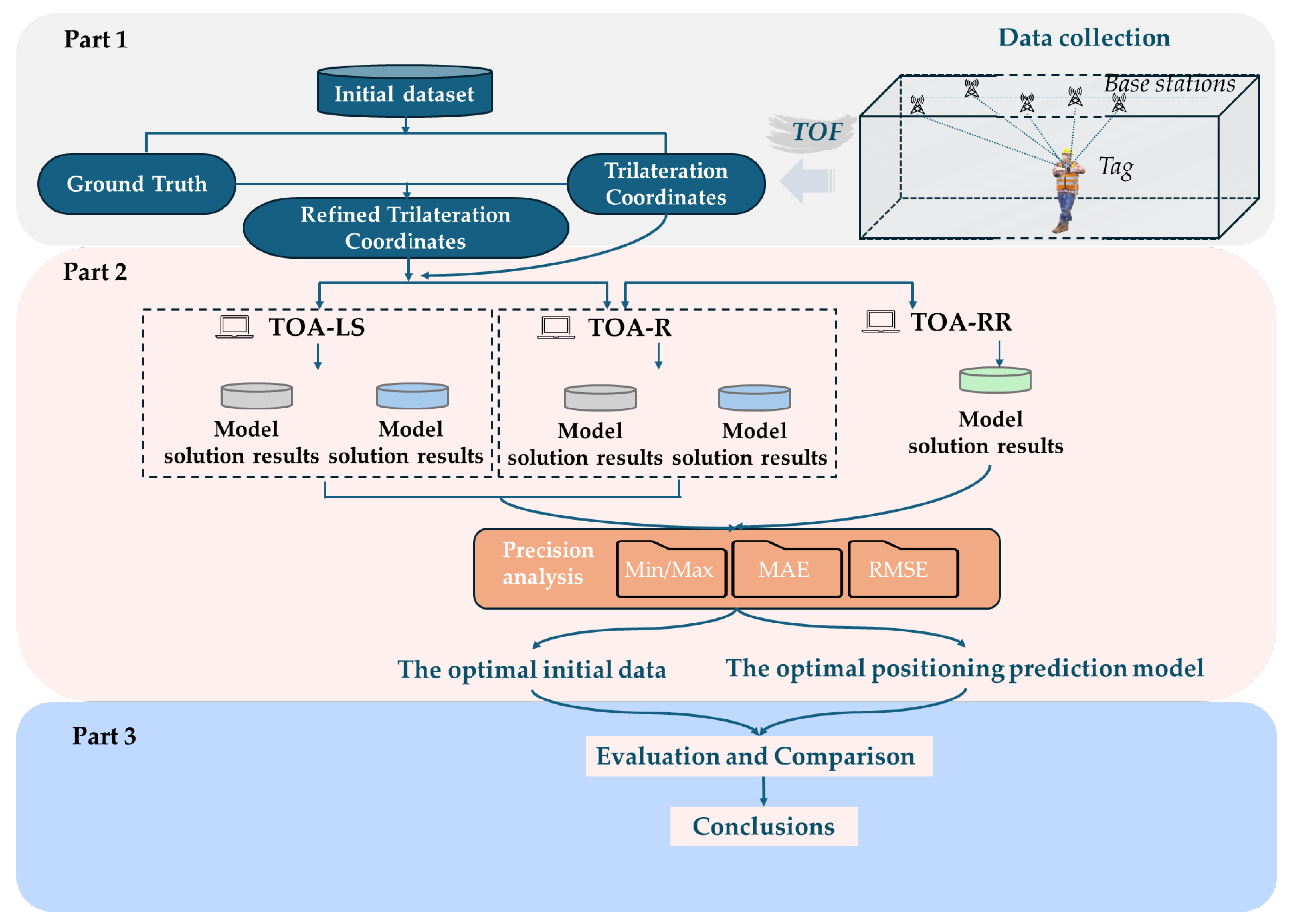
2. Optimization of UWB Positioning Calculation Models
2.1. TOA-LS (Least Squares Model)
2.2. TOA-R (Ridge Estimation Model)
2.3. TOA-RR (Ridge Estimation Iterative Model)
3. Test Scheme
3.1. Test Site and Equipment
3.2. Data Acquisition and Preprocessing
- (1)
- Distance measurement between the base station and the tag
- (2)
- Estimation of the approximate coordinates of the pending tags
3.3. Test Procedures
4. Results and Discussion
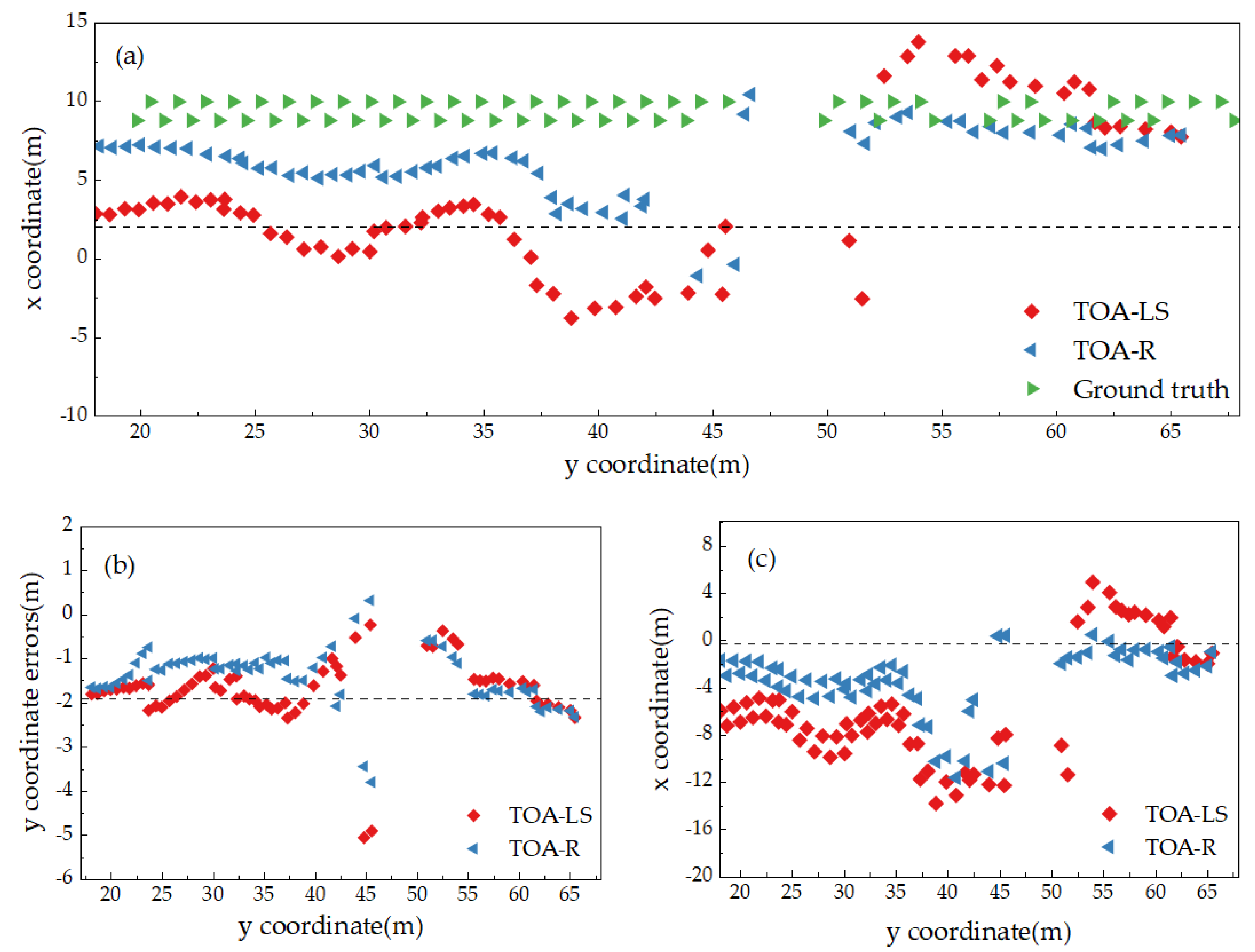
4.1. Comparison of TOA-LS Model and TOA-R Model of Which the Trilateral Intersection Coordinates Are Used as the Initial Values
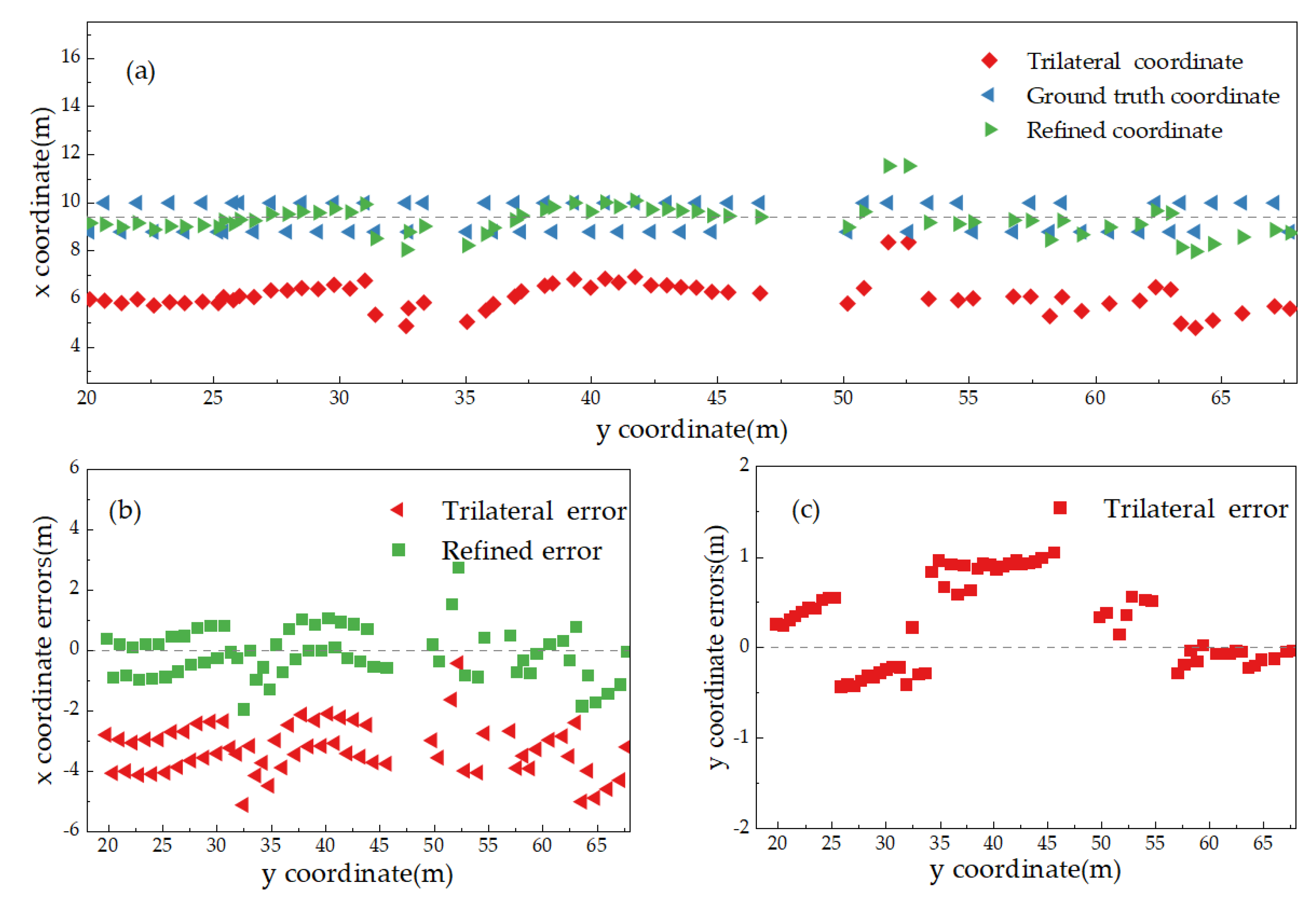
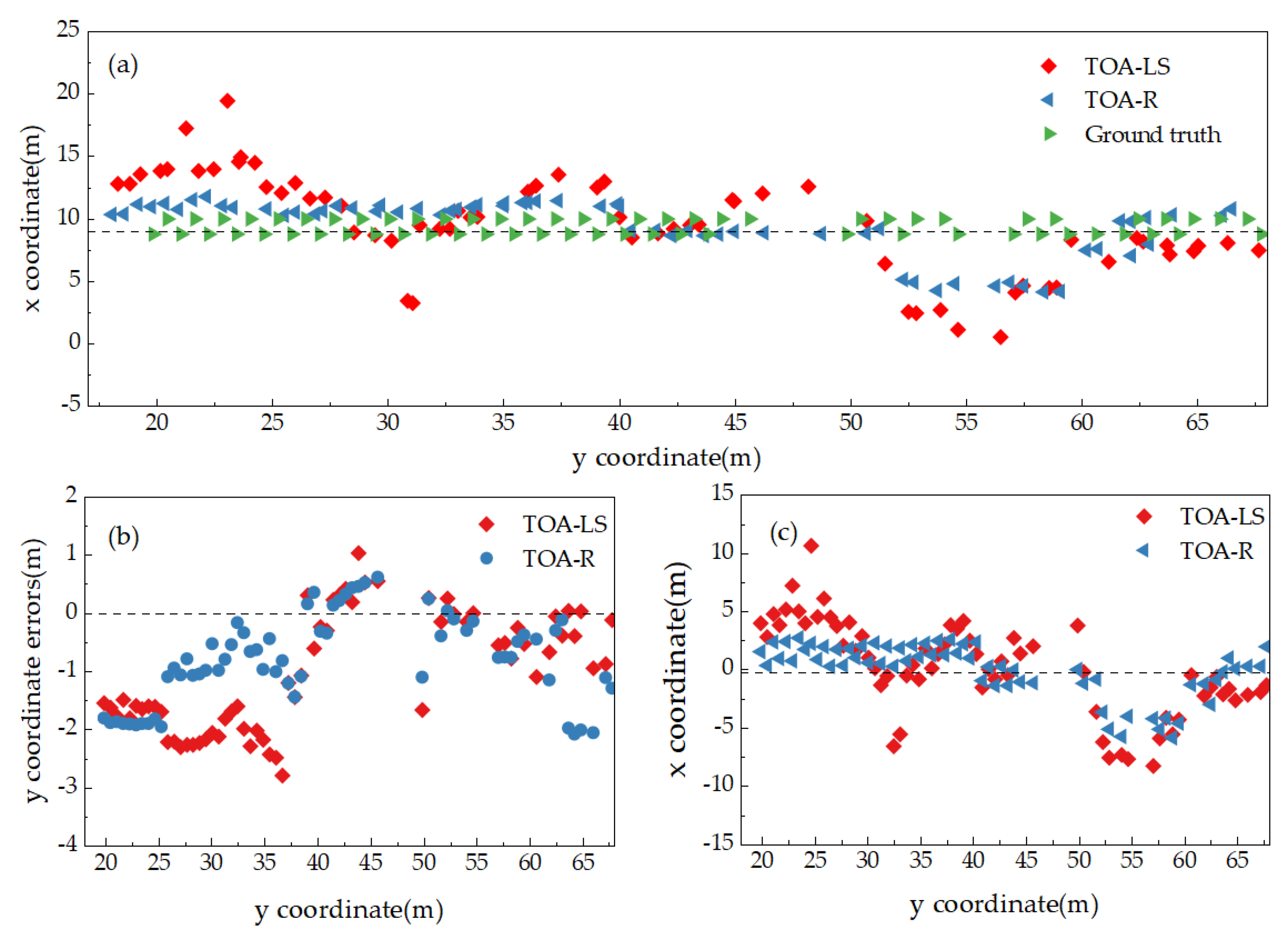
4.2. Comparison of TOA-LS Model and TOA-R Model of Which the Refined Trilateral Intersection Coordinates Are Used as the Initial Values
4.3. Comparison of the TOA-RR Iterative Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, R.; Guo, G.; Chen, L.; Niu, X. Research and Application Status and development trend of indoor high-precision positioning technology. J. Wuhan Univ. (Inf. Sci. Ed.) 2023, 48, 1591–1600. [Google Scholar] [CrossRef]
- Leitch, S.G.; Ahmed, Q.Z.; Abbas, W.B.; Hafeez, M.; Laziridis, P.I.; Sureephong, P.; Alade, T. On Indoor Localization Using WiFi, BLE, UWB, and IMU Technologies. Sensors 2023, 23, 8598. [Google Scholar] [CrossRef] [PubMed]
- Mazhar, F.; Khan, M.G.; Sällberg, B. Precise Indoor Positioning Using UWB: A Review of Methods, Algorithms and Implementations. Wireless Pers. Commun. 2017, 97, 4467–4491. [Google Scholar] [CrossRef]
- Coppens, D.; Shahid, A.; Lemey, S.; Herbruggen, B.V.; Marshall, C.; Poorter, E.D. An Overview of UWB Standards and Organizations (IEEE 802.15.4, FiRa, Apple): Interoperability Aspects and Future Research Directions. IEEE Access 2022, 10, 70219–70241. [Google Scholar] [CrossRef]
- Bastiaens, S.; Gerwen, J.V.V.; Macoir, N.; Deprez, K.; Cock, C.D.; Joseph, W.; Poorter, E.D.; Plets, D. Experimental Benchmarking of Next-Gen Indoor Positioning Technologies (Unmodulated) Visible Light Positioning and Ultra-Wideband. IEEE Internet Things J. 2022, 9, 17858–17870. [Google Scholar] [CrossRef]
- Li, C.; Tanghe, E.; Martens, L.; Romme, J.; Singh, G.; Poorter, E.D.; Joseph, W. Device-Free Pedestrian Tracking Using Low-Cost Ultrawideband Devices. IEEE Trans. Instrum. Meas. 2022, 71, 1–4. [Google Scholar] [CrossRef]
- Deng, W.; Li, J.; Tang, Y.; Zhang, X. Low-Complexity Joint Angle of Arrival and Time of Arrival Estimation of Multipath Signal in UWB System. Sensors 2023, 23, 6363. [Google Scholar] [CrossRef]
- Alsindi, N.A.; Alavi, B.; Pahlavan, K. Measurement and Modeling of Ultrawideband TOA-Based Ranging in Indoor Multipath Environments. IEEE Trans. Veh. Technol. 2008, 58, 1046–1058. [Google Scholar] [CrossRef]
- Chong, Y.; Xu, X.; Guo, N.; Shu, L.; Zhang, Q.; Yu, Z.; Wen, T. Cooperative Localization of Firefighters Based on Relative Ranging Constraints of UWB and Autonomous Navigation. Electronics 2023, 12, 1181. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Q.; Li, Z.; Mi, J.; Zhang, K. Research on High Precision Positioning Method for Pedestrians in Indoor Complex Environments Based on UWB/IMU. Remote Sens. 2023, 15, 3555. [Google Scholar] [CrossRef]
- Park, J.; Nam, S.; Choi, H.; Ko, Y.; Ko, Y.-B. Improving deep learning-based UWB LOS/NLOS identification with transfer learning: An empirical approach. Electronics 2020, 9, 1714. [Google Scholar] [CrossRef]
- Lou, P.; Zhao, Q.; Zhang, X.; Li, D.; Hu, J. Indoor Positioning System with UWB Based on a Digital Twin. Sensors 2022, 22, 5936. [Google Scholar] [CrossRef]
- Yan, J.; Yang, C.; Fan, W.; Zheng, Y.; Li, J.; Gao, Z. GNSS/UWB Integrated Positioning with Robust Helmert Variance Component Estimation. Adv. Space Res. 2024, 73, 2532–2547. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, T.; Fu, Y. Design of two-dimensional accurate positioning integrated base station based on TOF/PDOA algorithm. Coal Mine Mach. 2023, 44, 24–27. [Google Scholar] [CrossRef]
- Ali, R.; Liu, R.; Nayyar, A.; Qureshi, B.; Cao, Z. Tightly Coupling Fusion of UWB Ranging and IMU PDR for Indoor Localization. IEEE Access 2021, 9, 164206–164222. [Google Scholar] [CrossRef]
- Si, M.; Wang, Y.; Zhou, N.; Seow, C.; Siljak, H. A Hybrid Indoor Altimetry Based on Barometer and UWB. Sensors 2023, 23, 4180. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, A.; Sui, X.; Wang, C.; Wang, S.; Gao, J.; Shi, Z. Improved-UWB/LiDAR-SLAM Tightly Coupled Positioning System with NLOS Identification Using a LiDAR Point Cloud in GNSS-Denied Environments. Remote Sens. 2022, 14, 1380. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, L.; Kuang, Z.; Kuang, Z.; Shen, X.; Zhang, Z. LS location algorithm of UWB node in non-line-of-sight environment. J. Guilin Univ. Technol. 2022, 42, 736–741. [Google Scholar]
- Wang, G.; Jiao, L.; Cao, X.-H. Research on indoor 3D positioning Algorithm based on least square Method. Comput. Technol. Dev. 2020, 30, 69–73. [Google Scholar]
- Perakis, H.; Gikas, V.; Retscher, G. Development of Advanced Positioning Techniques of UWB/Wi-Fi RTT Ranging for Personal Mobility Applications. Sensors 2024, 24, 7520. [Google Scholar] [CrossRef]
- Zhu, C.; Yang, J. A TOF and TDOA joint localization Algorithm based on weighted Centroid. J. Zhengzhou Univ. (Eng.) 2023, 44, 50–55. [Google Scholar] [CrossRef]
- Zhao, K.; Zhao, T.; Zheng, Z.; Yu, C.; Ma, D.; Rabie, K.; Kharel, R. Optimization of Time Synchronization and Algorithms with TDOA Based Indoor Positioning Technique for Internet of Things. Sensors 2020, 20, 6513. [Google Scholar] [CrossRef]
- Qian, J. Indoor positioning accuracy analysis of NLOS UWB by weighted least squares. Geospat. Inf. 2023, 21, 86–88. [Google Scholar]
- Liu, G.; Lu, L. Passive localization by weighted least squares combined genetic algorithm. Comput. Syst. Appl. 2023, 32, 173–180. [Google Scholar] [CrossRef]
- Poulose, A.; Han, D.S. UWB Indoor Localization Using Deep Learning LSTM Networks. Appl. Sci 2020, 10, 6290. [Google Scholar] [CrossRef]
- Si, L.; Wang, Z.; Wei, D.; Gu, J.; Zhang, P. Fusion Positioning of Mobile Equipment in Underground Coal Mine Based on Redundant IMUs and UWB. IEEE Trans. Ind. Inform. 2024, 20, 5946–5958. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, S.; Yao, J.; Gu, C. Integrated Positioning System of Unmanned Automatic Vehicle in Coal Mines. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, S.; Li, H.; Gu, C.; Jiang, H.; Meng, D. Accurate integrated position measurement system for mobile applications in GPS-denied coal mine. ISA Trans. 2023, 139, 621–634. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]







| Base Station Name | X Coordinate (m) | Y Coordinate (m) |
|---|---|---|
| B1 | 9.620 | 13.610 |
| B2 | 9.620 | 37.560 |
| B3 | 9.620 | 72.770 |
| B4 | 7.896 | 24.984 |
| B5 | 7.971 | 55.404 |
| Model | Error in the x Coordinate (m) | Error in the y Coordinate (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| MinAE | MaxAE | MAE | RMSE | MinAE | MaxAE | MAE | RMSE | |
| TOA-LS | 0.4341 | 13.7390 | 6.5375 | 7.3834 | 0.2231 | 5.0378 | 1.7043 | 1.8619 |
| TOA-R | 0.0330 | 11.0531 | 3.1715 | 3.8568 | 0.0779 | 3.7878 | 1.4000 | 1.5255 |
| Model | Error in the x Coordinate (m) | Error in the y Coordinate (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| MinAE | MaxAE | MAE | RMSE | MinAE | MaxAE | MAE | RMSE | |
| TOA-LS | 0.0678 | 10.6881 | 3.1626 | 3.9490 | 0.0080 | 2.7858 | 1.1605 | 1.4242 |
| TOA-R | 0.0152 | 5.8418 | 1.7764 | 2.2697 | 0.0461 | 2.0778 | 0.9104 | 1.1040 |
| Model | Error in the x Coordinate (m) | Error in the y Coordinate (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| MinAE | MaxAE | MAE | RMSE | MinAE | MaxAE | MAE | RMSE | |
| TOA-RR | 0.4676 | 5.3673 | 2.0905 | 2.3047 | 0.1736 | 3.7820 | 1.2739 | 1.4529 |
| Refined-TOA-RR | 0.0543 | 2.8949 | 1.3241 | 1.5347 | 0.0095 | 1.4357 | 0.5272 | 0.6443 |
| Model | Error in the x Coordinate (m) | Error in the y Coordinate (m) | Euclidean Error (m) | ||||
|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | Median | 75% Percentiles | 90% Percentiles | |
| TOA-LS | 6.5375 | 7.3834 | 1.7043 | 1.8619 | 6.9069 | 8.9860 | 11.6416 |
| TOA-R | 3.1715 | 3.8568 | 1.4000 | 1.5255 | 3.3675 | 4.4076 | 5.7558 |
| TOA-RR | 2.0905 | 2.3047 | 1.2739 | 1.4529 | 2.4599 | 3.0460 | 3.5038 |
| Refined TOA-LS | 3.1626 | 3.949 | 1.1605 | 1.4242 | 3.0694 | 4.8854 | 6.6519 |
| Refined TOA-R | 1.7764 | 2.2697 | 0.9104 | 1.104 | 2.0719 | 2.6008 | 4.1243 |
| Refined TOA-RR | 1.3241 | 1.5347 | 0.5272 | 0.6443 | 1.5373 | 1.9557 | 2.5864 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Li, M.; Wang, J.; Duan, A.; Sun, H.; Meng, Q. Optimization of a Time-of-Arrival-Ridge Estimation Iterative Model for Ultra-Wideband Positioning in a Long Linear Area. Sensors 2025, 25, 2229. https://doi.org/10.3390/s25072229
Li M, Li M, Wang J, Duan A, Sun H, Meng Q. Optimization of a Time-of-Arrival-Ridge Estimation Iterative Model for Ultra-Wideband Positioning in a Long Linear Area. Sensors. 2025; 25(7):2229. https://doi.org/10.3390/s25072229
Chicago/Turabian StyleLi, Mengqian, Mingduo Li, Jinhua Wang, Aoze Duan, Haotian Sun, and Qinggang Meng. 2025. "Optimization of a Time-of-Arrival-Ridge Estimation Iterative Model for Ultra-Wideband Positioning in a Long Linear Area" Sensors 25, no. 7: 2229. https://doi.org/10.3390/s25072229
APA StyleLi, M., Li, M., Wang, J., Duan, A., Sun, H., & Meng, Q. (2025). Optimization of a Time-of-Arrival-Ridge Estimation Iterative Model for Ultra-Wideband Positioning in a Long Linear Area. Sensors, 25(7), 2229. https://doi.org/10.3390/s25072229




