Reversible Watermarking for Electrocardiogram Protection
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Description
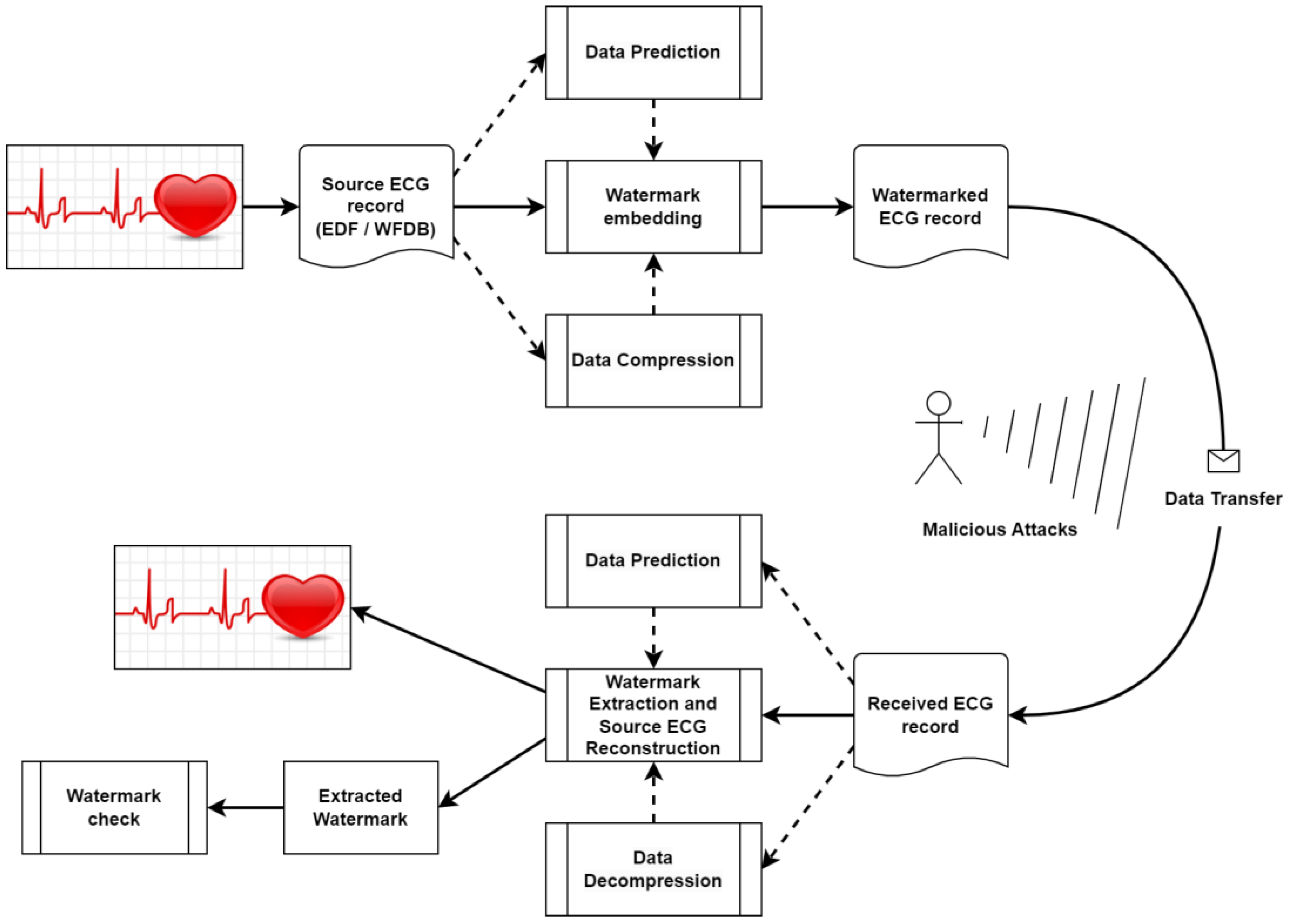
2.2. General Reversible Watermarking Scheme
2.3. Reversible Contrast Mapping Difference Expansion
2.4. Integer Transform-Based Difference Expansion
2.5. Prediction Error Expansion
2.6. Lossless Compression-Based Watermarking
2.7. Prediction Algorithms
2.7.1. Neighbor-Based Prediction
2.7.2. Inter-Lead Prediction
2.7.3. Physical Signal Prediction
2.7.4. Compression Algorithms
2.8. Data and Metrics
2.8.1. Performance Metrics
2.8.2. Database
3. Results
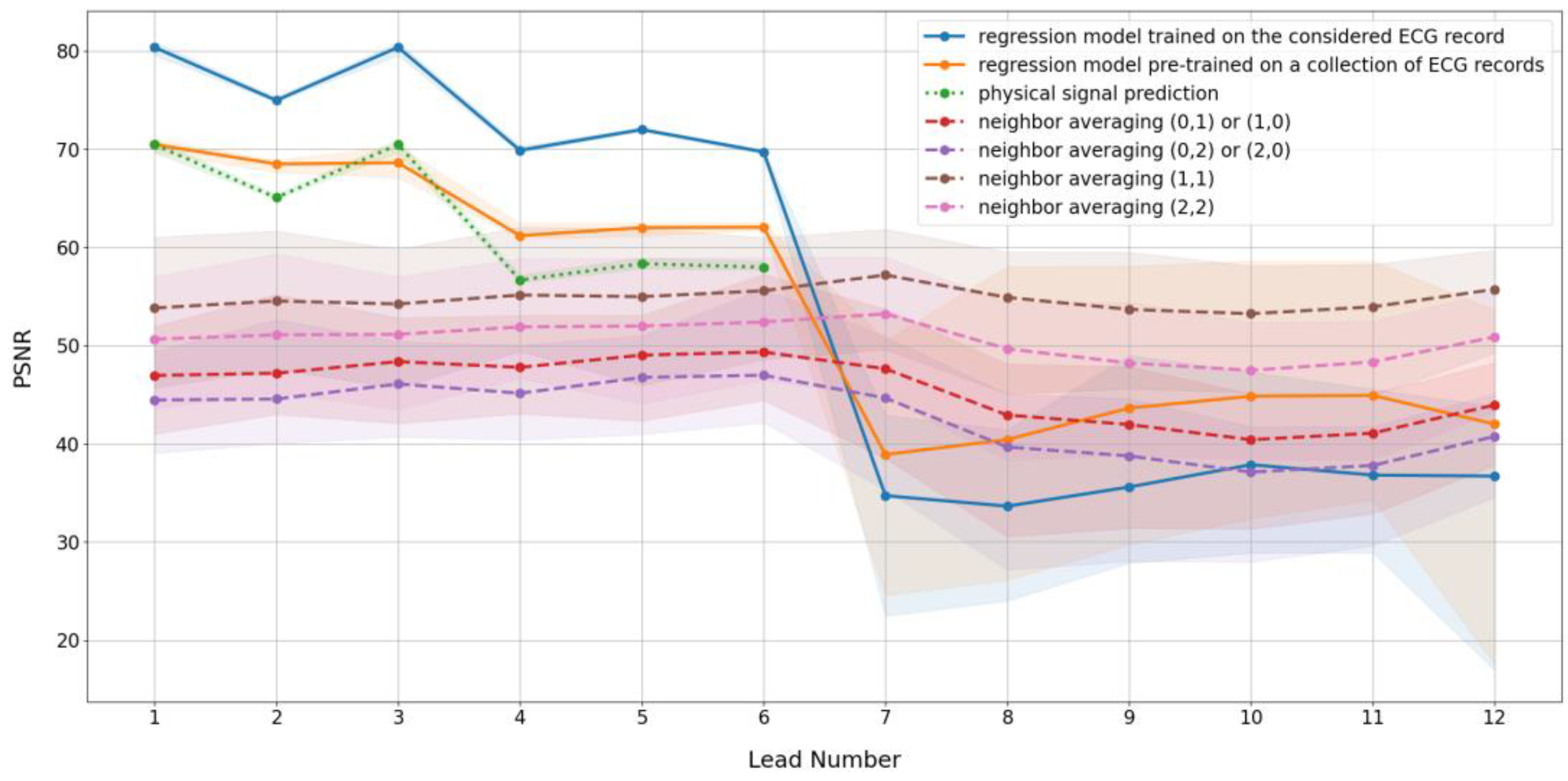
3.1. Prediction Algorithm Comparison
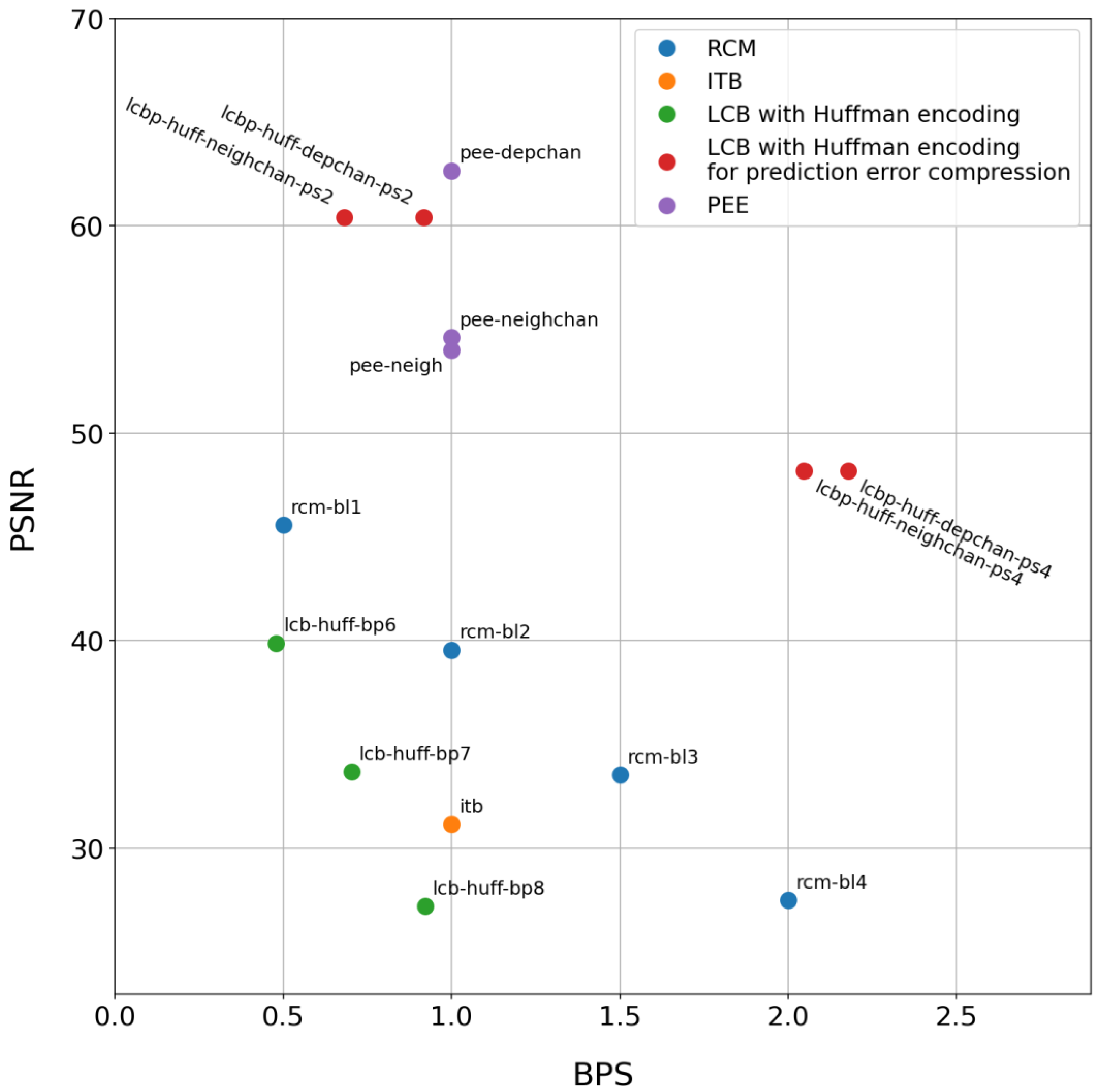
3.2. Compression Algorithm Comparison
3.3. Performance Comparison
3.4. Final Outcomes
4. Conclusions
- If minimizing container distortion is critical, one should use PEE algorithms (with prediction based on adjacent samples or linear-dependence formulas) or LCBP (featuring Huffman coding and a low number of modified bit planes). This situation may arise, for instance, when a physician performs a preliminary ECG analysis before extracting the watermark and restoring the signal’s original appearance.
- If a high and predictable embedding capacity is more important, applying the RCM-DE method with a larger number of bits per pair of container samples or the ITB-DE algorithm is advisable. A significant embedding capacity might be required, for example, if error-correcting coding is implemented to ensure accurate container recovery even after any distortions or interference during file transmission or storage.
- If a compromise is needed, then LCBP with Huffman coding and a higher number of modified bit planes should be used. However, if simplicity of implementation and low computational complexity are prioritized, as well as the option to embed in all channels simultaneously, one can opt for ITB-DE or RCM-DE with a smaller number of bits per pair of container samples
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kumar, S.; Rajpal, A.; Sharma, N.K.; Rajpal, S.; Nayyar, A.; Kumar, N. ROSEmark: Robust semi-blind ECG watermarking scheme using SWT-DCT framework. Digit. Signal Process. 2022, 129, 103648. [Google Scholar] [CrossRef]
- Khaldi, A.; Kafi, M.R.; Meghni, B. Electrocardiogram signal security by digital watermarking. J. Ambient Intell. Humaniz. Comput. 2022, 14, 13901–13913. [Google Scholar]
- Sanivarapu, P.V.; Rajesh, K.N.V.P.S.; Reddy, N.V.R.; Reddy, N.C.S. Patient data hiding into ECG signal using watermarking in transform domain. Phys. Eng. Sci. Med. 2020, 43, 213–226. [Google Scholar]
- Tseng, K.K.; He, X.; Kung, W.M.; Chen, S.T.; Liao, M.; Huang, H.N. Wavelet-Based Watermarking and Compression for ECGSignals with Verification Evaluation. Sensors 2014, 14, 3721–3736. [Google Scholar]
- Engin, M.; Çıdam, O.; Engin, E.Z. Wavelet Transformation Based Watermarking Technique for Human Electrocardiogram (ECG). J. Med. Syst. 2005, 29, 589–594. [Google Scholar] [PubMed]
- Sharma, N.; Anand, A.; Singh, A.K.; Agrawal, A.K. Optimization based ECG watermarking in RDWT-SVD domain. Multimed. Tools Appl. 2021, 82, 5031–5047. [Google Scholar]
- Duy, T.P.; Tran, D.; Ma, W. An intelligent learning-based watermarking scheme for outsourced biomedical time series data. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017. [Google Scholar]
- Duy, T.P.; Tran, D.; Ma, W. A proposed pattern recognition framework for EEG-based smart blind watermarking system. In Proceedings of the 2016 23rd International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016. [Google Scholar]
- Pham, T.D.; Tran, D.; Ma, W. A Proposed Blind DWT-SVD Watermarking Scheme for EEG Data. Lect. Notes Comput. Sci. 2015, 9492, 69–76. [Google Scholar]
- Nguyen, H.N.; Pham, T.D.; Nguyen, H.T.H. Right protection mechanism based on optimal robust watermarking for shared EEG data. In Proceedings of the 2020 RIVF International Conference on Computing and Communication Technologies (RIVF), Ho Chi Minh, Vietnam, 14–15 October 2020. [Google Scholar]
- Bhalerao, S.; Ansari, I.A.; Kumar, A. Reversible ECG Watermarking for Ownership Detection, Tamper Localization, and Recov-ery. Circuits Syst. Signal Process. 2022, 41, 5134–5159. [Google Scholar]
- Tripathi, P.M.; Kumar, A.; Komaragiri, R.; Kumar, M. Watermarking of ECG signals compressed using Fourier decomposition method. Multimed. Tools Appl. 2022, 81, 19543–19557. [Google Scholar]
- Kumar, A.; Ranganatham, R.; Singh, S.; Komaragiri, R.; Kumar, M. A robust digital ECG signal watermarking and compression using biorthogonal wavelet transform. Res. Biomed. Eng. 2021, 37, 79–85. [Google Scholar]
- Bhalerao, S.; Ansari, I.A.; Kumar, A.; Jain, D.K. A reversible and multipurpose ECG data hiding technique for telemedicine applications. Pattern Recognit. Lett. 2019, 125, 463–473. [Google Scholar] [CrossRef]
- Coltuc, D.; Chassery, J.-M. Very Fast Watermarking by Reversible Contrast Mapping. IEEE Signal Process. Lett. 2007, 14, 255–258. [Google Scholar] [CrossRef]
- Meng, L.; Liu, L.; Tian, G.; Wang, X. An adaptive reversible watermarking in IWT domain. Multimed. Tools Appl. 2021, 80, 711–735. [Google Scholar] [CrossRef]
- Bote-Curiel, L.; Muñoz-Romero, S.; Gerrero-Curieses, A.; Rojo-Álvarez, J.L. Deep Learning and Big Data in Healthcare: A Double Review for Critical Beginners. Appl. Sci. 2019, 9, 2331. [Google Scholar] [CrossRef]
- Kligfield, P.; Gettes, L.S.; Bailey, J.J.; Childers, R.; Deal, B.J.; Hancock, E.W.; Van Herpen, G.; Kors, J.A.; Macfarlane, P.; Mirvis, D.M.; et al. Recommendations for the Standardization and Interpretation of the Electrocardiogram: Part I: The Electrocardio-gram and Its Technology: A Scientific Statement From the American Heart Association Electrocardiography and Arrhythmias Committee, Council on Clinical Cardiology; the American College of Cardiology Foundation; and the Heart Rhythm Society Endorsed by the International Society for Computerized Electrocardiology. Circulation 2007, 115, 1306–1324. [Google Scholar] [CrossRef]
- Rao, C.R.; Toutenburg, H. Linear Models and Generalizations: Least Squares and Alternatives; Springer Series in Statistics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2008. [Google Scholar]
- Meek, S. ABC of clinical electrocardiography: Introduction. I—Leads, rate, rhythm, and cardiac axis. BMJ 2002, 324, 415–418. [Google Scholar] [CrossRef]
- Morgado, E.; Alonso-Atienza, F.; Santiago-Mozos, R.; Barquero-Pérez, Ó.; Silva, I.; Ramos, J.; Mark, R. Quality Estimtion of the Electrocardiogram Using Cross-Correlation among Leads. BioMed. Eng. OnLine 2015, 14, 59. [Google Scholar] [CrossRef]
- Robinson, A.H.; Cherry, C. Results of a prototype television bandwidth compression scheme. Proc. IEEE 1967, 55, 356–364. [Google Scholar] [CrossRef]
- Vitter, J.S. Algorithm 673: Dynamic Huffman coding. ACM Trans. Math. Softw. 1989, 15, 158–167. [Google Scholar] [CrossRef]
- Zheng, J.; Guo, H.; Chu, H. A Large Scale 12-Lead Electrocardiogram Database for Arrhythmia Study. Available online: https://physionet.org/content/ecg-arrhythmia/1.0.0/ (accessed on 22 February 2025).
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, E215–E220. [Google Scholar] [CrossRef]
- Perez, M.V.; Mahaffey, K.W.; Hedlin, H.; Rumsfeld, J.S.; Garcia, A.; Ferris, T.; Balasubramanian, V.; Russo, A.M.; Rajmane, A.; Cheung, L.; et al. Large-Scale Assessment of a Smartwatch to Identify Atrial Fibrillation. N. Engl. J. Med. 2019, 381, 1909–1917. [Google Scholar] [CrossRef] [PubMed]
- Wagner, G.S.; Strauss, D.G. Marriott’s Practical Electrocardiography, 12th ed.; LWW: Baltimore, MD, USA, 2013. [Google Scholar]
- Ecg-Watermarking. Available online: https://github.com/snowwm/ecg-watermarking/ (accessed on 22 February 2025).


| # | Notation | Description |
|---|---|---|
| 1 | Regression by file | Training a separate regression model for each ECG file, where one lead is used for prediction and the remaining leads are used for model training |
| 2 | Regression by collection of files | Training a common regression model for a collection of ECG files, where one lead is used for prediction and the remaining leads are used for model training |
| 3 | Physical prediction | Physical prediction using formulas from Section 2.7.3 |
| 4 | Neighbor averaging (1,0) or (0,1) | or |
| 5 | Neighbor averaging (2,0) or (0,2) | or |
| 6 | Neighbor averaging (1,1) | |
| 7 | Neighbor averaging (2,2) |
| Notation | Embedding Method | Prediction Method | Compression Method | Parameters Used |
|---|---|---|---|---|
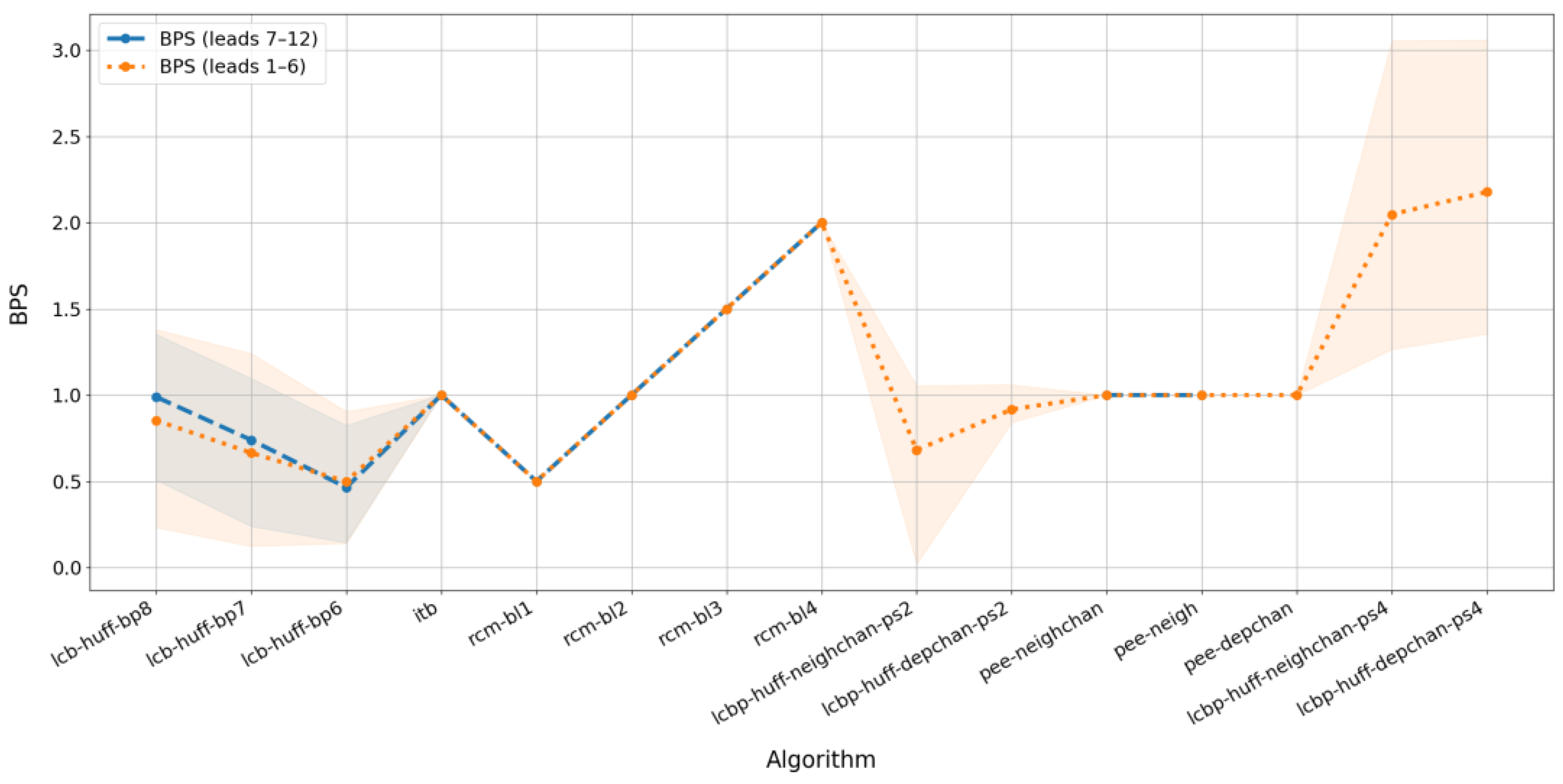
| lcb-huff-bp8 lcb-huff-bp7 lcb-huff-bp6 | LCB | - | Huffman | The number after the letters “bp” indicates the number of the lower of the two successive bit planes that were compressed and overwritten. Obviously, in practice, the bit planes have to be chosen based on the required balance between BPS and PSNR. |
| itb | ITB | - | - | Method has no adjustable parameters |
| rcm-bl1 rcm-bl2 rcm-bl3 rcm-bl4 | RCM | - | - | The number after the letters “bl” means the number of digital signal bits built into one pair of host signal samples. In this case, BPS is equal to half of this number |
| lcbp-huff-neighchan-ps2 | LCBP | neighchan * | The suffix “ps2” means that two bit planes are used to record the compressed prediction errors. To minimize distortion, it is reasonable to use the least significant bit planes. | |
| lcbp-huff-depchan-ps2 | depchan * | Huffman | ||
| lcbp-huff-depchan-ps4 | depchan * | |||
| pee-neighchan | PEE | neighchan * | These combinations differ in prediction methods. The neighbor prediction algorithm is used only here because it is not applicable to the prediction error compression method (LCBP). | |
| pee-neigh | neigh * | - | ||
| pee-depchan | depchan * | |||
| lcbp-huff-neighchan-ps4 | LCBP | neighchan * | Huffman | The “ps4” suffix means that four bit planes are used to record the compressed prediction errors, which significantly increases the embedding volume compared to the two-plane option. |
| lcbp-huff-depchan-ps4 | depchan * |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreev, P.; Denisova, A.; Fedoseev, V. Reversible Watermarking for Electrocardiogram Protection. Sensors 2025, 25, 2185. https://doi.org/10.3390/s25072185
Andreev P, Denisova A, Fedoseev V. Reversible Watermarking for Electrocardiogram Protection. Sensors. 2025; 25(7):2185. https://doi.org/10.3390/s25072185
Chicago/Turabian StyleAndreev, Pavel, Anna Denisova, and Victor Fedoseev. 2025. "Reversible Watermarking for Electrocardiogram Protection" Sensors 25, no. 7: 2185. https://doi.org/10.3390/s25072185
APA StyleAndreev, P., Denisova, A., & Fedoseev, V. (2025). Reversible Watermarking for Electrocardiogram Protection. Sensors, 25(7), 2185. https://doi.org/10.3390/s25072185






