Predicting Restroom Dirtiness Based on Water Droplet Volume Using the LightGBM Algorithm
Abstract
1. Introduction
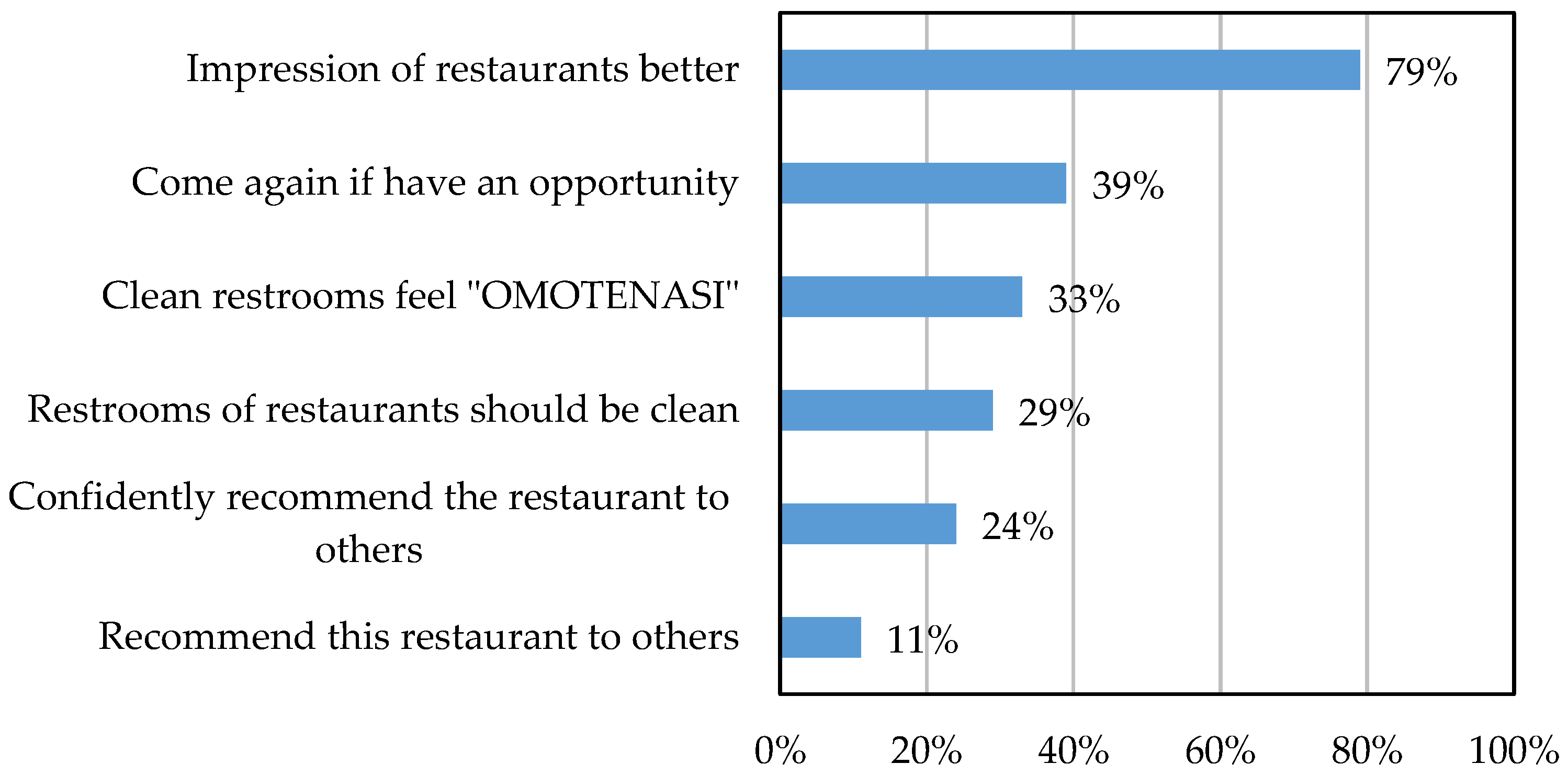
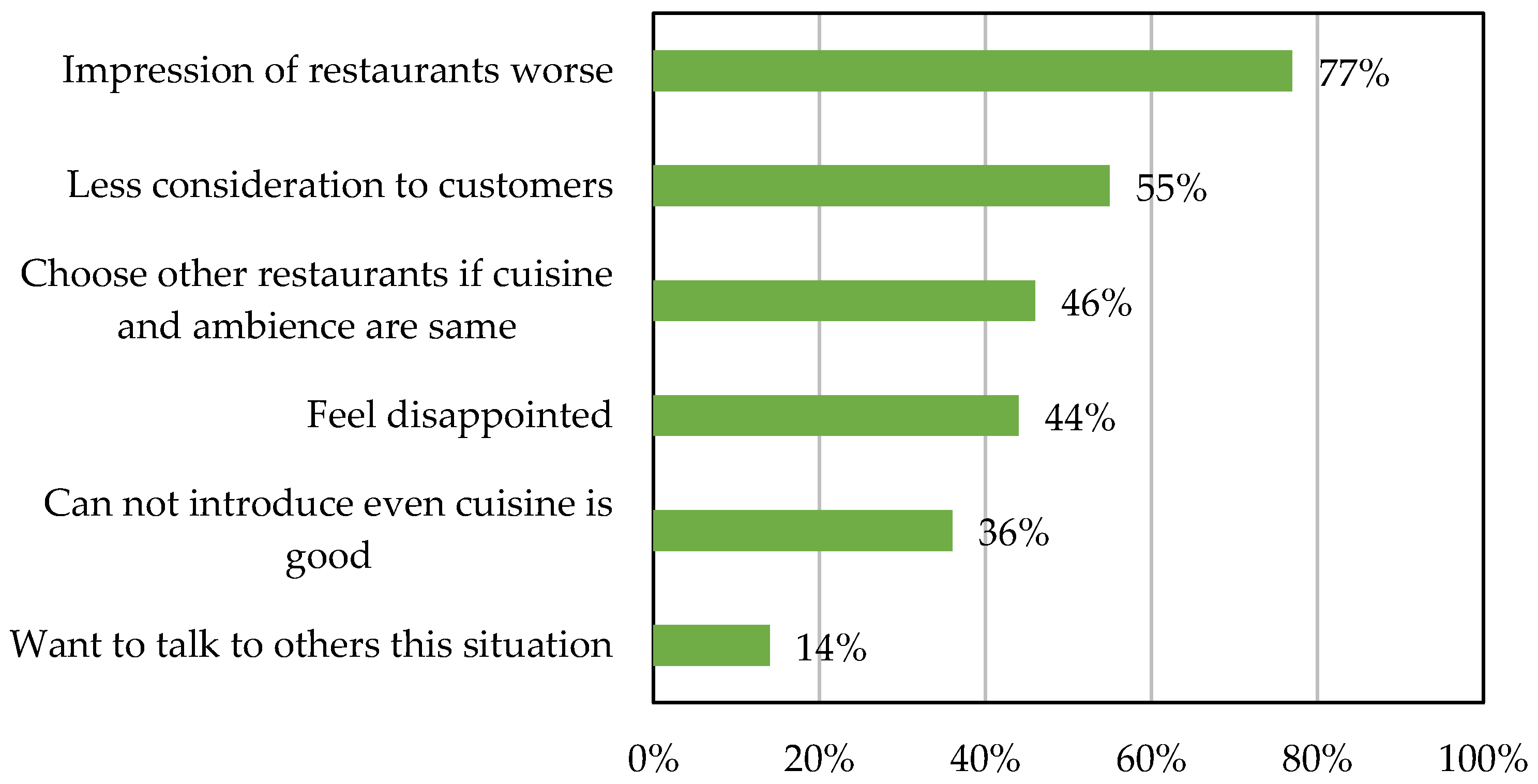
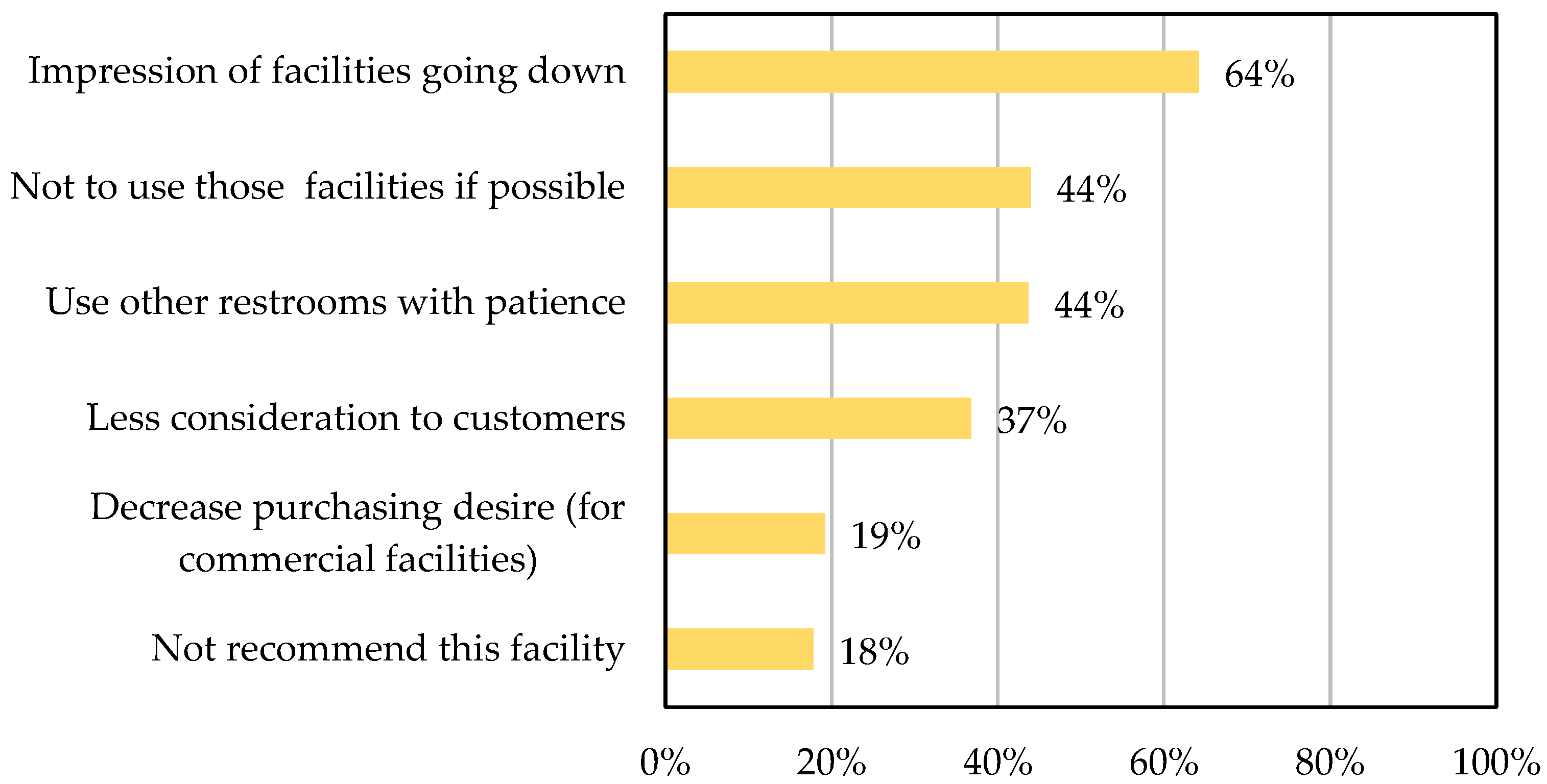
1.1. Current Issues Faced by Cleaning Companies
1.2. Solution for Restroom Cleaning Issues
2. Dirtiness Quantification Method
2.1. Definition of Dirtiness
2.2. Overview of Method
3. In Situ Experiment and Results
3.1. Preparation of Water Droplet Images
3.2. Data Collection
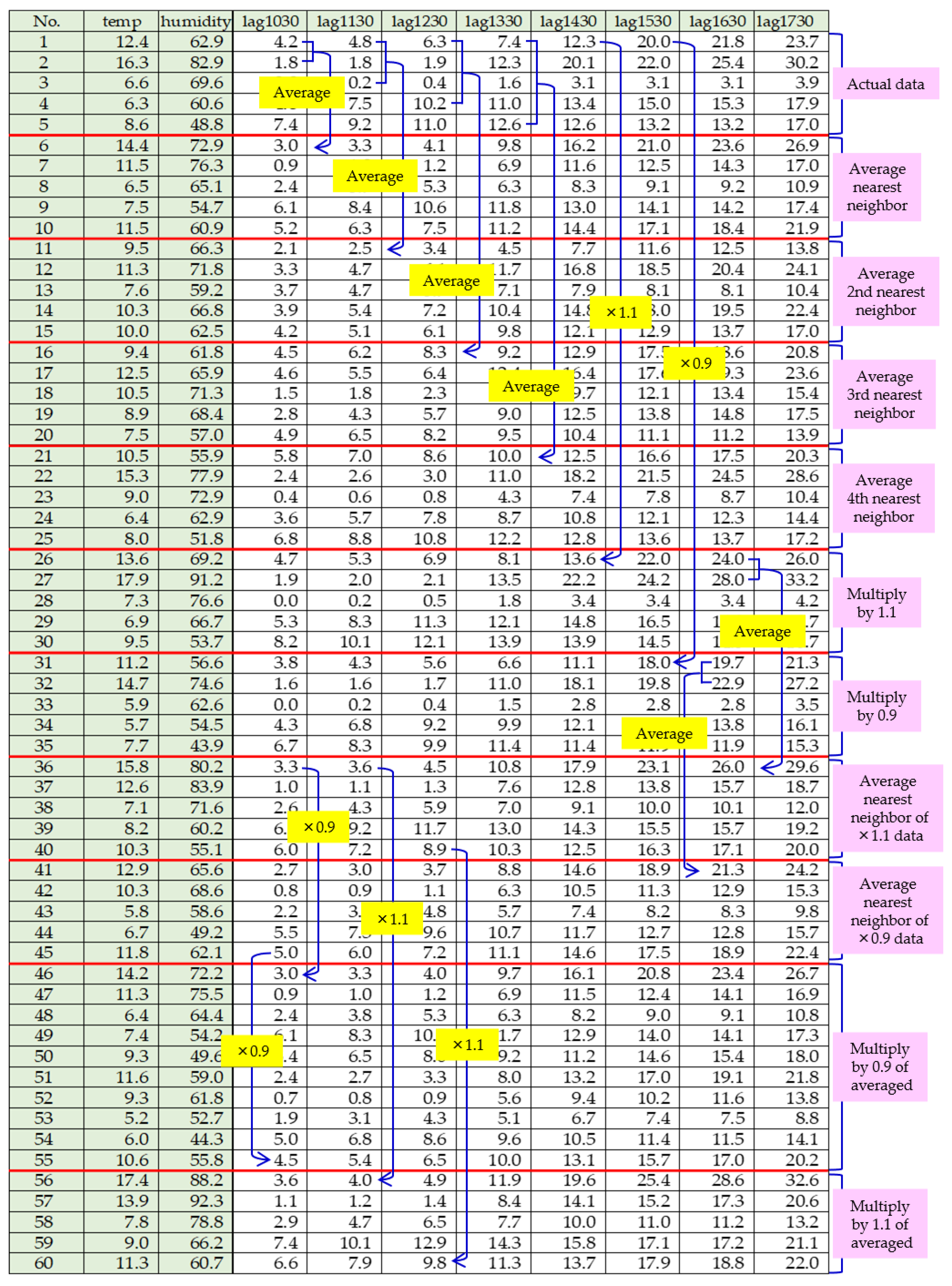
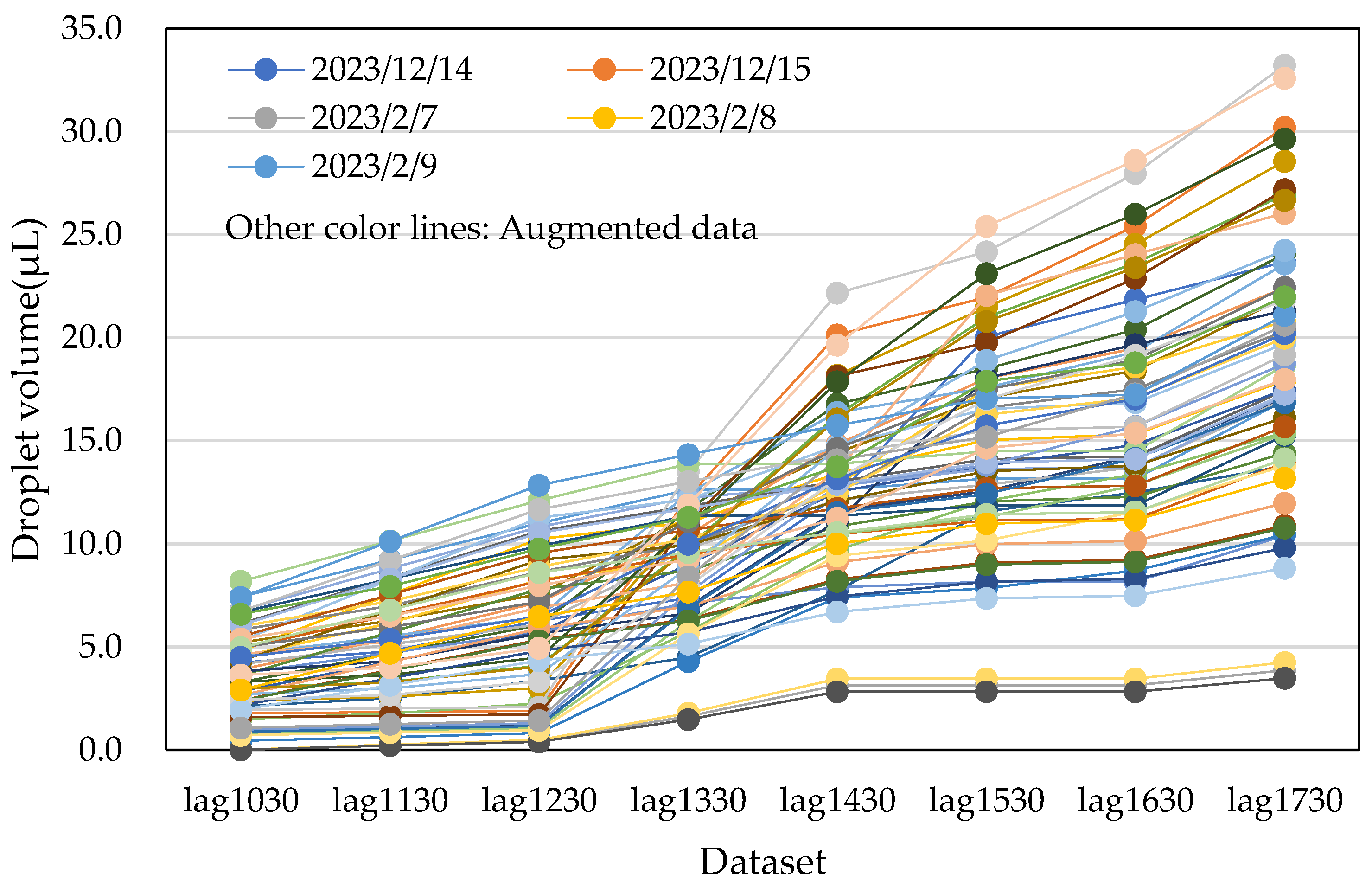
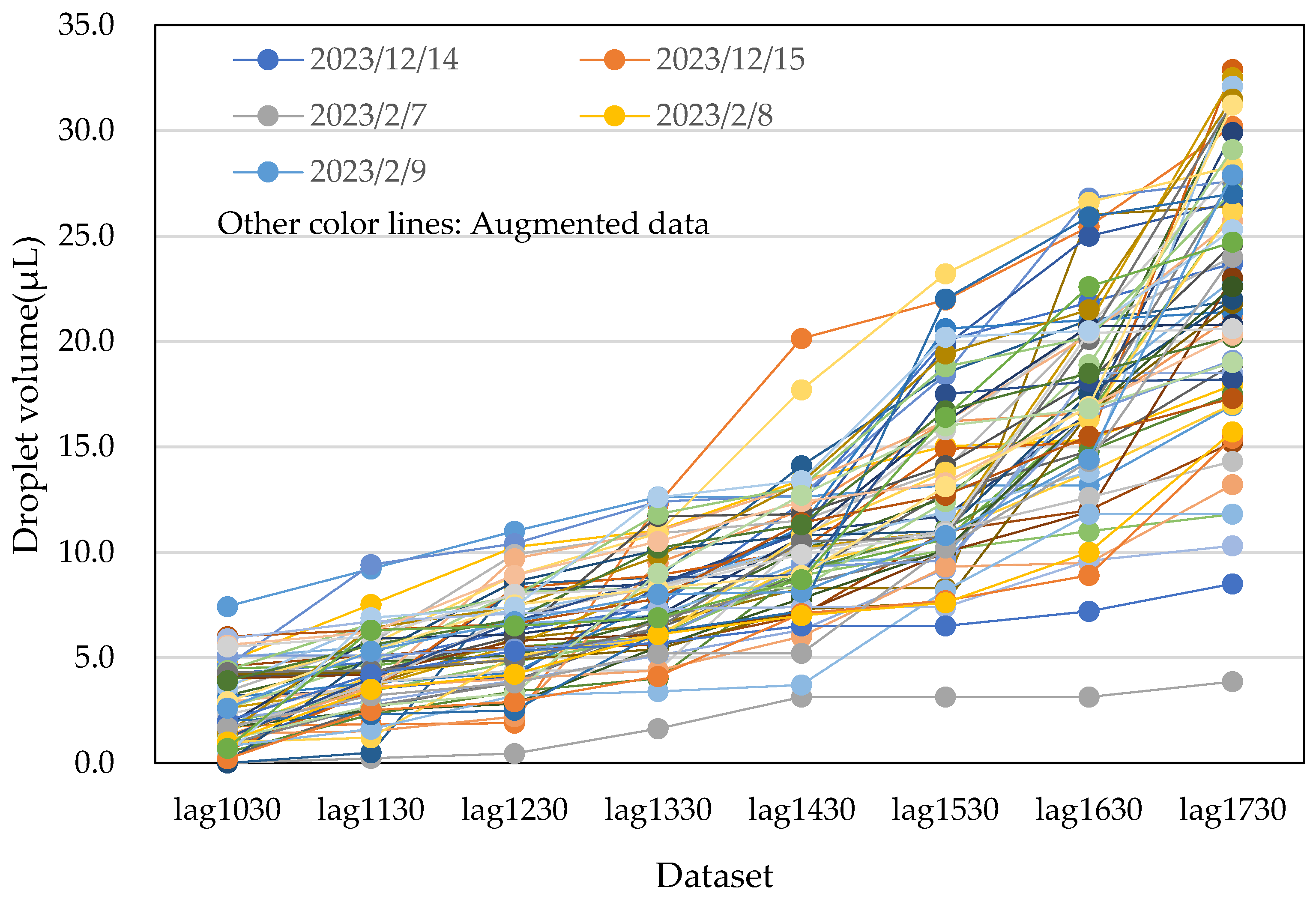
3.3. Data Augmentation
- Averaging and scaling method: This approach involved successively taking averages of two nearest neighbouring data points, two second-nearest neighbouring data points, and so on. These averages were then multiplied by 0.9 and 1.1, and the process was repeated. This method generated three sets of augmented data by expanding the margins of the minimum and maximum values.
- Random number generation method: In this method, random numbers were generated between the maximum and minimum values for each dataset.
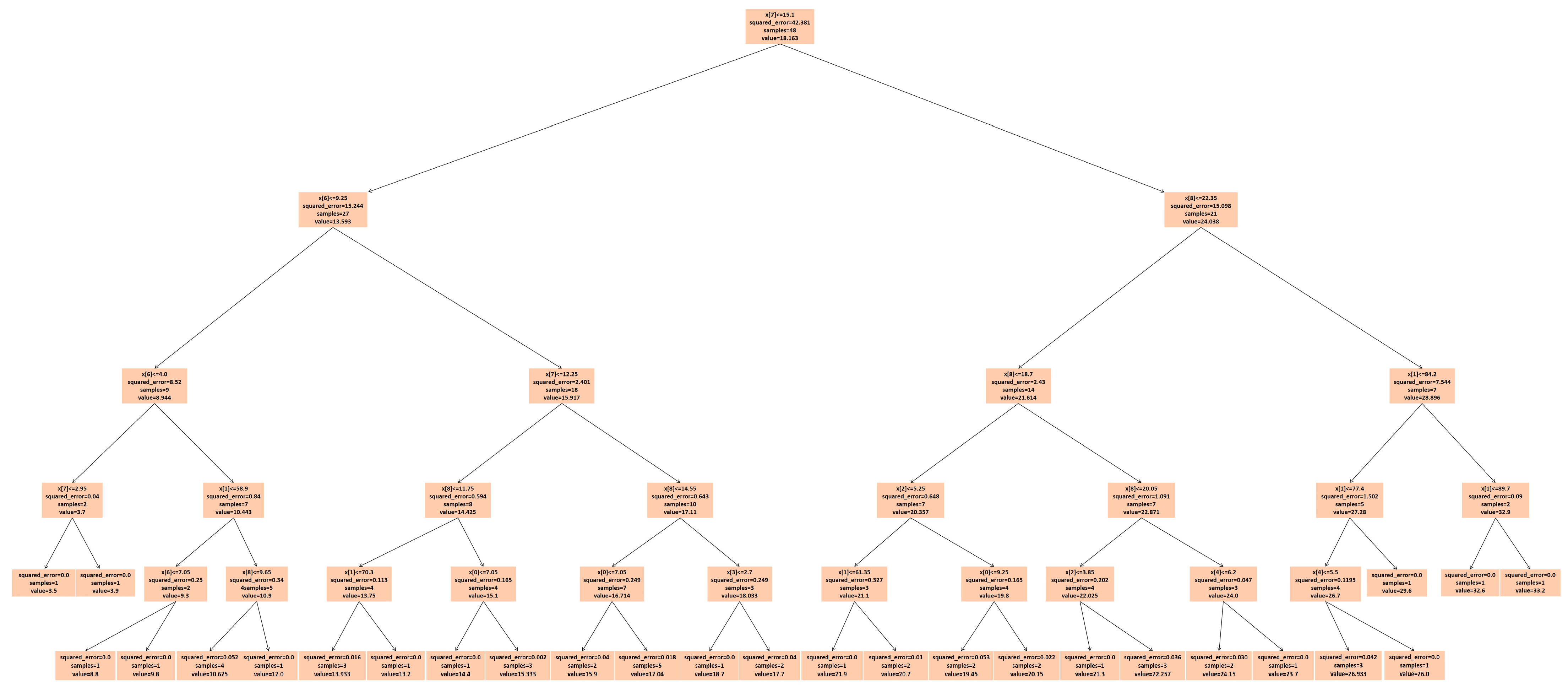
3.4. Water Droplet Volume Prediction
4. Results and Discussion
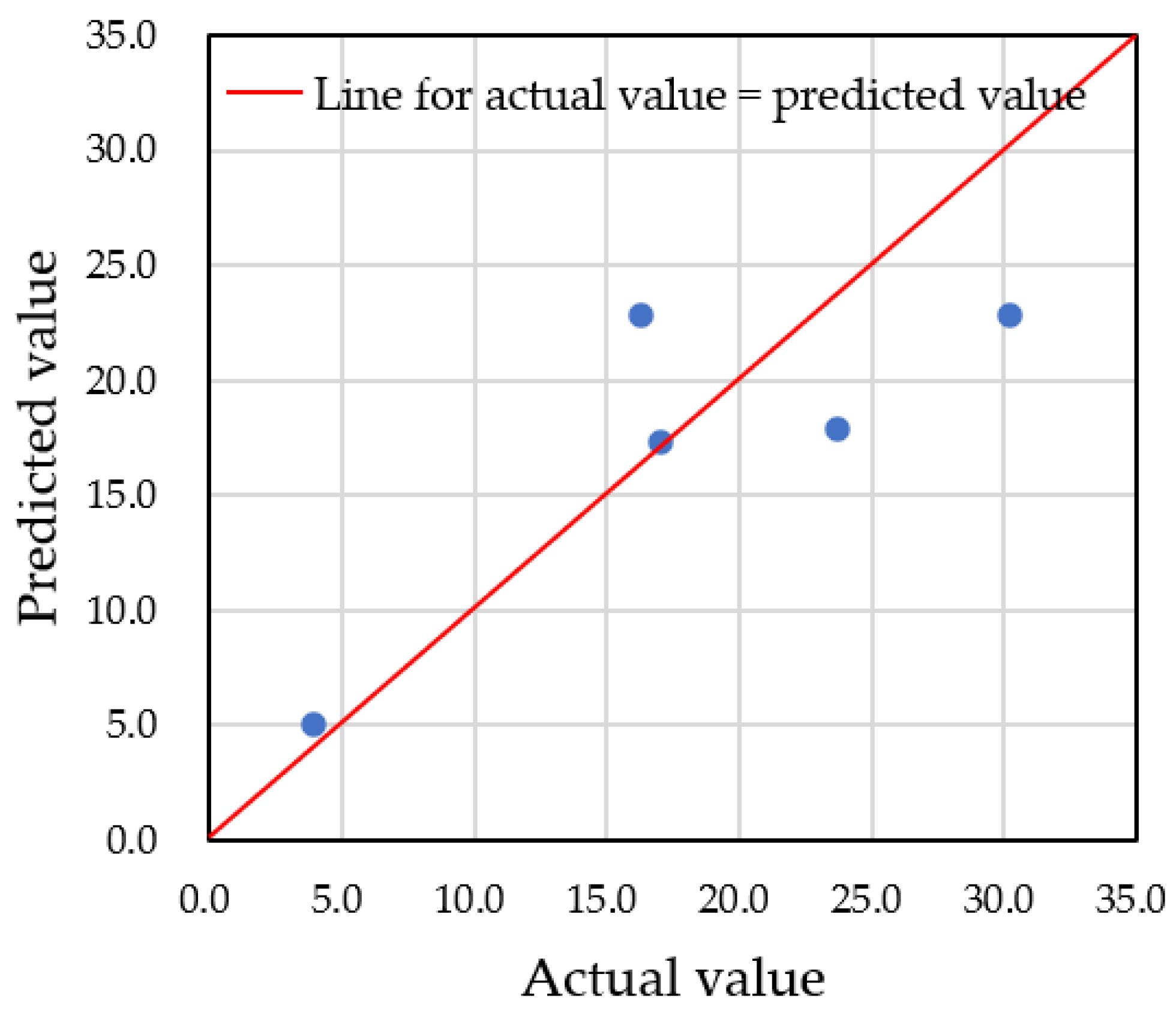
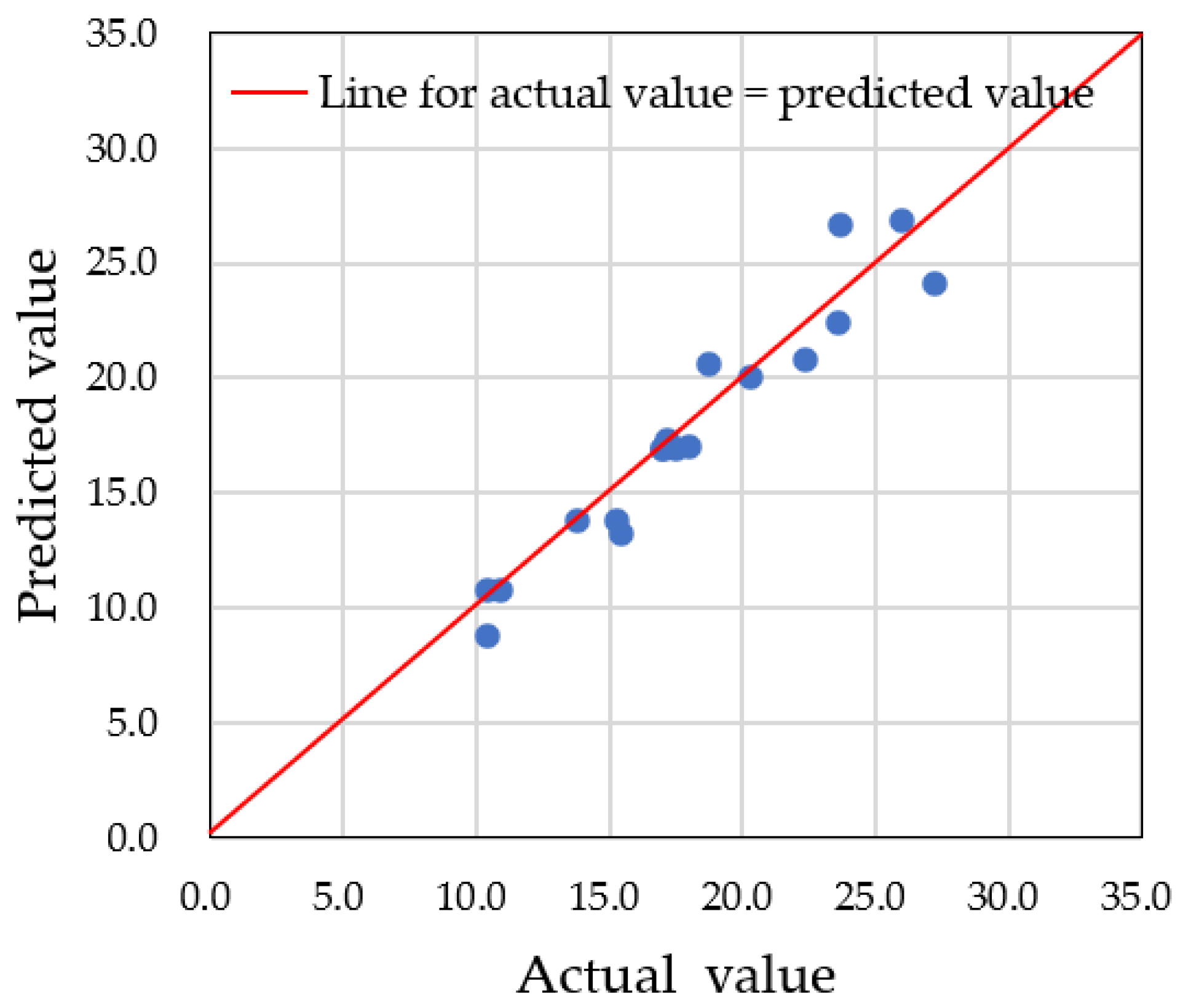
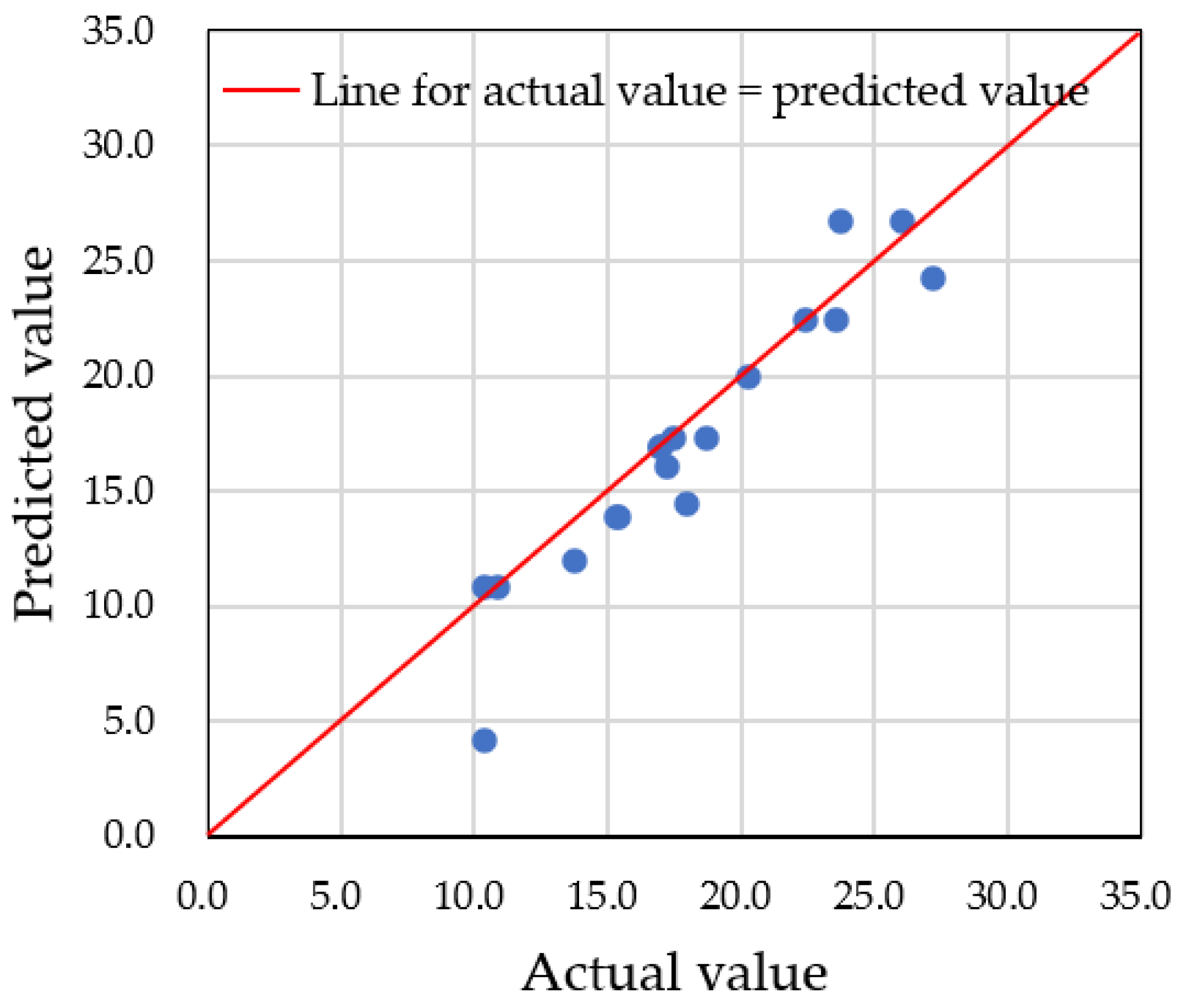
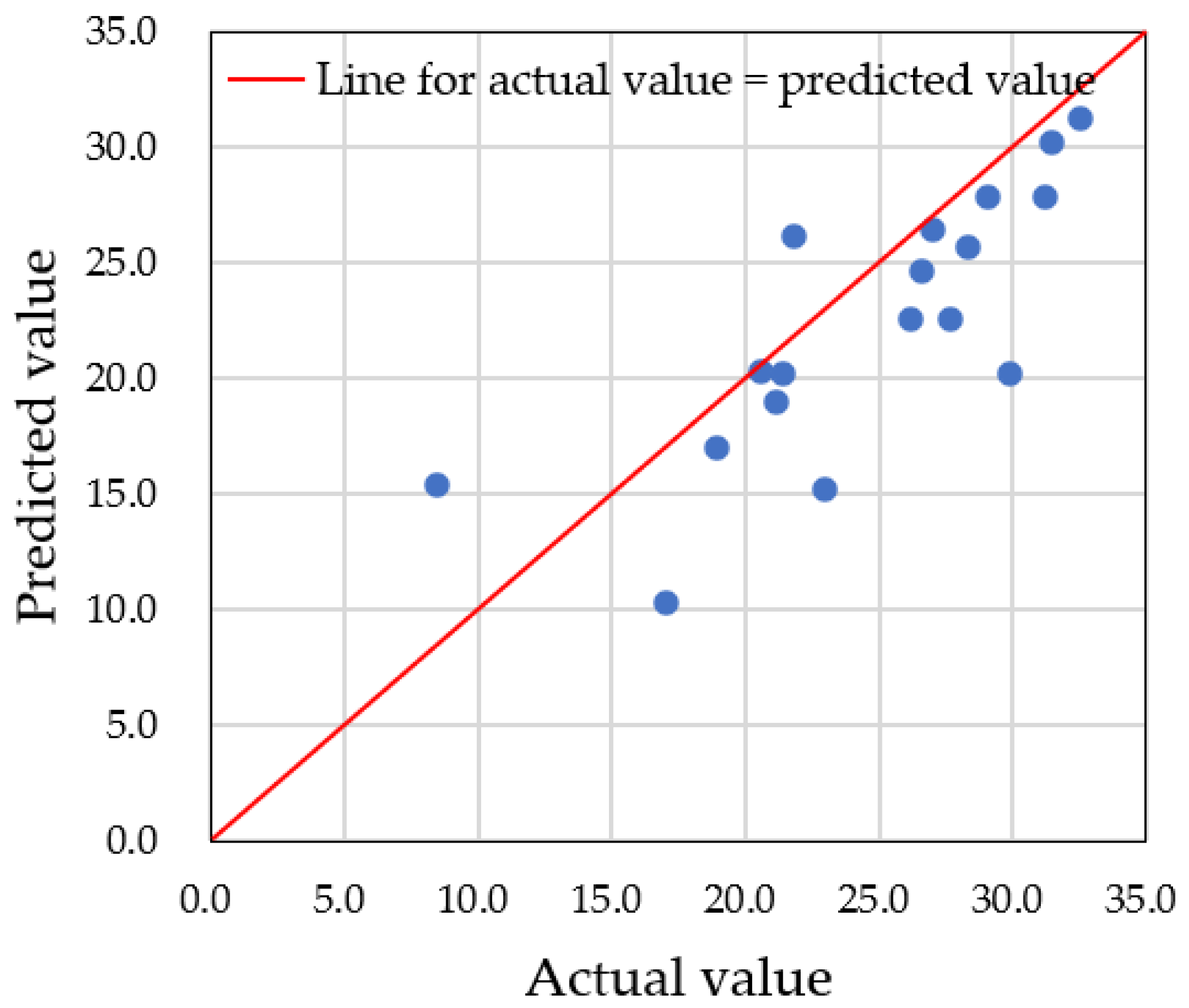
4.1. Prediction Using Actual Data
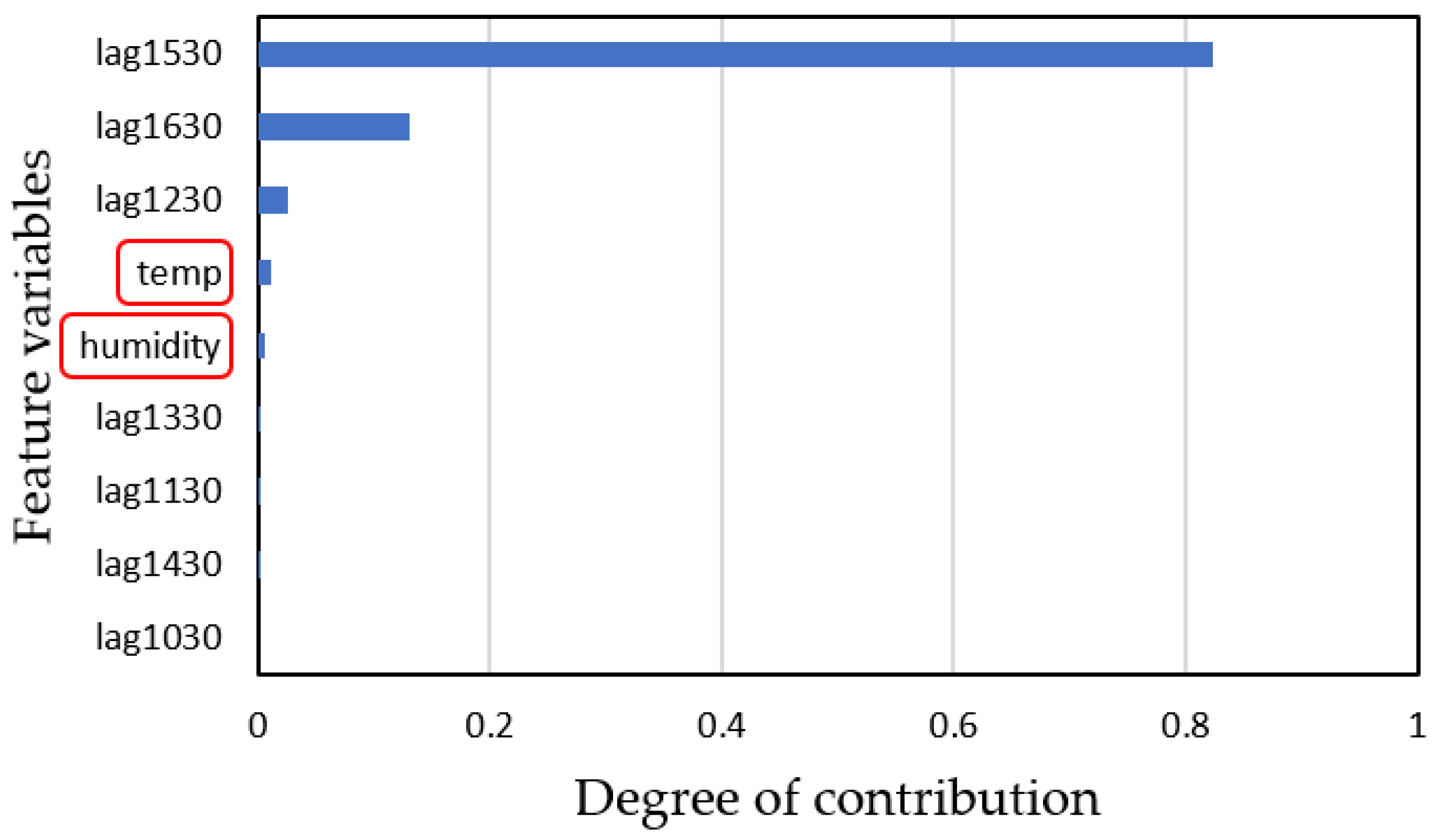
4.2. Setting Hyperparameters of LightGBM
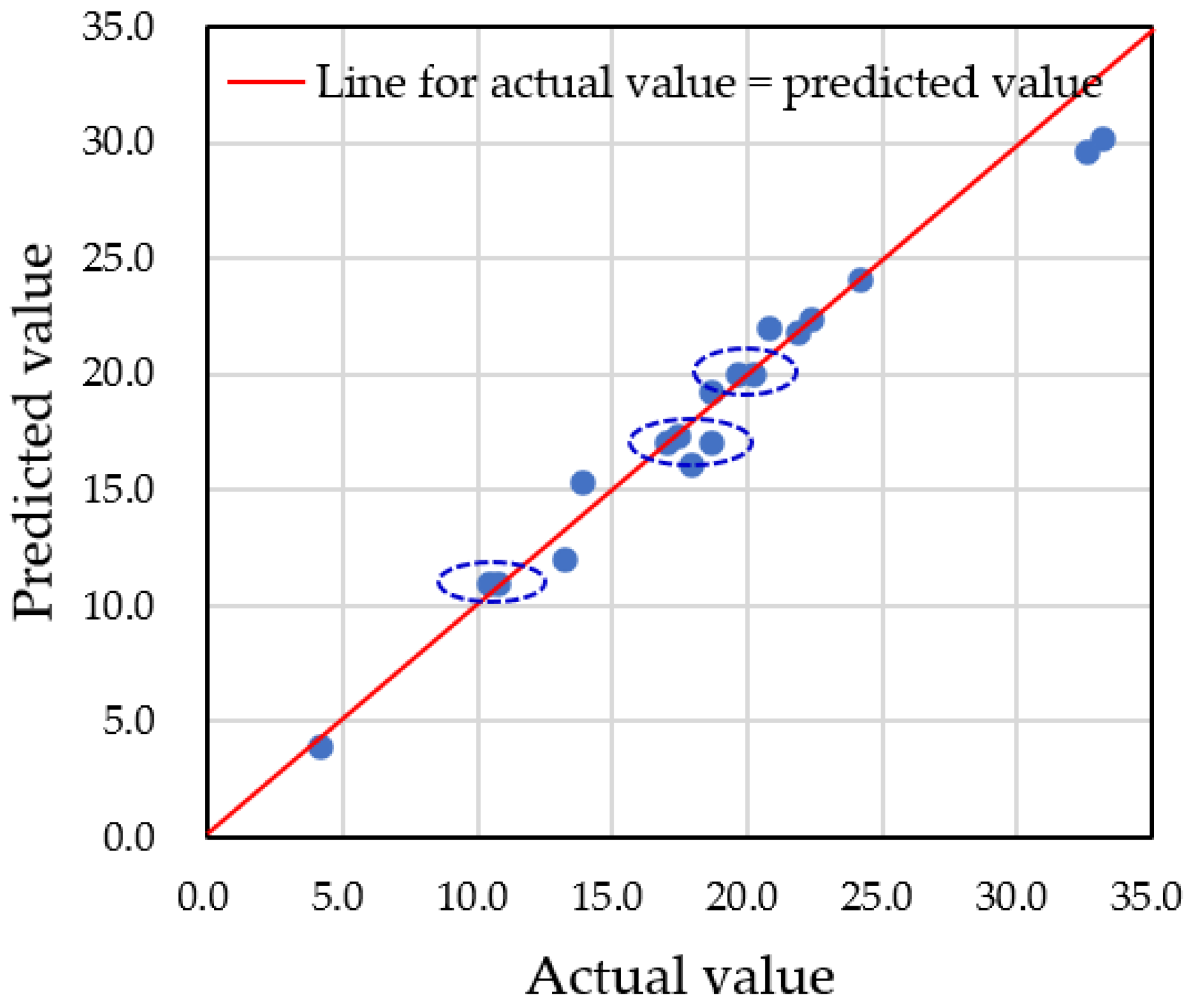
4.3. Differences in Prediction Accuracy with Augmented Data
5. Conclusions
6. Future Study
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, H.; Bachman, J.R. Examining Customer Perceptions of Restaurant Restroom Cleanliness and Their Impact on Satisfaction and Intent to Return. J. Foodserv. Bus. Res. 2019, 22, 191–208. [Google Scholar] [CrossRef]
- Afacan, Y.; Gurel, M.O. Public Toilets: An Exploratory Study on the Demands, Needs, and Expectations in Turkey. Environ. Plan. B Plan. Des. 2015, 42, 242–262. [Google Scholar] [CrossRef]
- Hartigan, S.M.; Bonnet, K.; Chisholm, L.; Kowalik, C.; Dmochowski, R.R.; Schlundt, D.; Reynolds, W.S. Why Do Women Not Use the Bathroom? Women’s Attitudes and Beliefs on Using Public Restrooms. Int. J. Environ. Res. Public Health 2020, 17, 2053. [Google Scholar] [CrossRef] [PubMed]
- Jayasinghe, L.; Wijerathne, N.; Yuen, C.; Zhang, M. Feature Learning and Analysis for Cleanliness Classification in Restrooms. IEEE Access 2019, 7, 14871–14882. [Google Scholar] [CrossRef]
- Lewkowitz, S.; Gilliland, J. A Feminist Critical Analysis of Public Toilets and Gender: A Systematic Review. Urban Aff. Rev. 2024, 61, 282–309. [Google Scholar] [CrossRef]
- TOTO LTD. Customer Awareness Survey of Restaurant Restrooms. Available online: https://jp.toto.com/products/machinaka/restaurantquestionnaires/ (accessed on 8 December 2024).
- Aica Kogyo Company, Limited. Survey on Awareness About Comfort of Restrooms. Available online: https://www.aica.co.jp/news/detail/post_143.html (accessed on 8 December 2024).
- Lokman, A.; Ramasamy, R.K.; Ting, C.Y. Scheduling and Predictive Maintenance for Smart Toilet. IEEE Access 2023, 11, 17983–17999. [Google Scholar] [CrossRef]
- Raendran, V.; Ramasamy, R.K.; Rosdi, I.S.; Ab Razak, R.; Fauzi, N.M. IoT Technology for Facilities Management: Understanding end User Perception of the Smart Toilet. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 353–359. [Google Scholar] [CrossRef]
- Vision Sensing Co., Ltd. InGaAs Near Infrared Camera NIR640SN. Available online: https://www.vision-sensing.jp/en/catalog/catalog_all_en.pdf (accessed on 8 December 2024).
- Forestier, G.; Petitjean, F.; Dau, H.A.; Webb, G.I.; Keogh, E. Generating Synthetic Time Series to Augment Sparse Datasets. In Proceedings of the IEEE International Conference on Data Mining (ICDM), New Orleans, LA, USA, 17–21 November 2017; pp. 865–870. [Google Scholar] [CrossRef]
- Morel, M.; Achard, C.; Kulpa, R.; Dubuisson, S. Time-Series Averaging Using Constrained Dynamic Time Warping Tolerance. Pattern Recognit. 2018, 74, 77–89. [Google Scholar] [CrossRef]
- Petitjean, F.; Gançarski, K. A Global Averaging Method for Dynamic Time Warping, with Applications to Clustering. Pattern Recognit. 2011, 44, 678–693. [Google Scholar] [CrossRef]
- Künsch, H.R. The Jackknife and the Bootstrap for General Stationary Observations. Ann. Stat. 1989, 17, 1217–1241. [Google Scholar] [CrossRef]
- Vogel, R.M.; Shallcross, A.L. The Moving Blocks Bootstrap Versus Parametric Time Series Models. Water Resour. Res. 1996, 32, 1875–1882. [Google Scholar] [CrossRef]
- Hidalgo, J. An Alternative Bootstrap to Moving Blocks for Time Series Regression Models. J. Econom. 2003, 117, 369–399. [Google Scholar] [CrossRef]
- Radovanov, B.; Marcikić, A. A Comparison of Four Different Block Bootstrap Methods. Croat. Oper. Res. Rev. 2014, 5, 189–202. [Google Scholar] [CrossRef]
- Lin, Z.; Jain, A.; Wang, C.; Fanti, G.; Sekar, V. Using GANs for Sharing Networked Time Series Data: Challenges, Initial Promise, and Open Questions. In Proceedings of the IMC ’20: Proceedings of the ACM Internet Measurement Conference, Virtual, 27–29 October 2020; Association for Computing Machinery: New York, NY, USA, 2020; pp. 464–483. [Google Scholar] [CrossRef]
- Brophy, E.; Wang, Z.; She, Q.; Ward, T. Generative Adversarial Networks in Time Series: A Systematic Literature Review. ACM Comput. Surv. 2023, 55, 1–31. [Google Scholar] [CrossRef]
- Lin, Z.; Jain, A.; Wang, C.; Fanti, G.; Sekar, V. Generating High-Fidelity, Synthetic Time Series Datasets with Doppelganger. arXiv 2019, arXiv:1909.13403. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the 31st Conference on Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 1–9. [Google Scholar]
- Yan, J.; Xu, Y.; Cheng, Q.; Jiang, S.; Wang, Q.; Xiao, Y.; Ma, C.; Yan, J.; Wang, X. LightGBM: Accelerated Genomically Designed Crop Breeding through Ensemble Learning. Genome Biol. 2021, 22, 1–24. [Google Scholar] [CrossRef]
- Cao, Q.; Wu, Y.; Yang, J.; Yin, J. Greenhouse Temperature Prediction Based on Time-Series Features and LightGBM. Appl. Sci. 2023, 13, 1610. [Google Scholar] [CrossRef]
- Khan, A.A.; Chaudhari, O.; Chandra, R. A Review of Ensemble Learning and Data Augmentation Models for Class Imbalanced Problems: Combination, Implementation and Evaluation. Expert Syst. Appl. 2024, 244, 122778. [Google Scholar] [CrossRef]
- Zhang, D.; Gong, Y. The Comparison of LightGBM and XGBoost Coupling Factor Analysis and Prediagnosis of Acute Liver Failure. IEEE Access 2020, 8, 220990–221003. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Hewamalage, H.; Bergmeir, C.; Bandara, K. Recurrent Neural Networks for Time Series Forecasting: Current Status and Future Directions. Int. J. Forecast. 2021, 37, 388–427. [Google Scholar] [CrossRef]
- Amalou, I.; Mouhni, N.; Abdali, A. Multivariate Time Series Prediction by RNN Architectures for Energy Consumption Forecasting. Energy Rep. 2022, 8, 1084–1091. [Google Scholar] [CrossRef]
- Selvin, S.; Vinayakumar, R.; Gopalakrishnan, E.A.; Menon, V.K.; Soman, K.P. Stock Price Prediction Using LSTM, RNN and CNN-Sliding Window Model. In Proceedings of the International Conference on Advances in Computing, Communications and Informatics, Udupi, India, 13–16 September 2017; pp. 1643–1647. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [PubMed]
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A Review on the Long Short-Term Memory Model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar]
- Staudemeyer, R.C.; Morris, E.R. Understanding LSTM—A Tutorial into Long Short-Term Memory Recurrent Neural Networks. arXiv 2019, arXiv:1909.09586. [Google Scholar]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) Network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Gers, F.A.; Schmidhuber, J.; Cummins, F. Learning to Forget: Continual Prediction with LSTM. Neural Comput. 2000, 12, 2451–2471. [Google Scholar] [CrossRef]
- Nelson, D.M.; Pereira, A.C.; De Oliveira, R.A. Stock Market’s Price Movement Prediction with LSTM Neural Networks. In Proceedings of the International Joint Conference on Neural Networks, Anchorage, AK, USA, 14–19 May 2017; pp. 1419–1426. [Google Scholar]
- Dey, R.; Salem, F.M. Gate-Variants of Gated Recurrent Unit (GRU) Neural Networks. In Proceedings of the IEEE 60th International Midwest Symposium on Circuits and Systems, Medford, MA, USA, 6–9 August 2017; pp. 1597–1600. [Google Scholar] [CrossRef]
- Fu, R.; Zhang, Z.; Li, L. Using LSTM and GRU Neural Network Methods for Traffic Flow Prediction. In Proceedings of the 31st Youth Academic Annual Conference of Chinese Association of Automation, Wuhan, China, 1–13 November 2016; pp. 324–328. [Google Scholar]





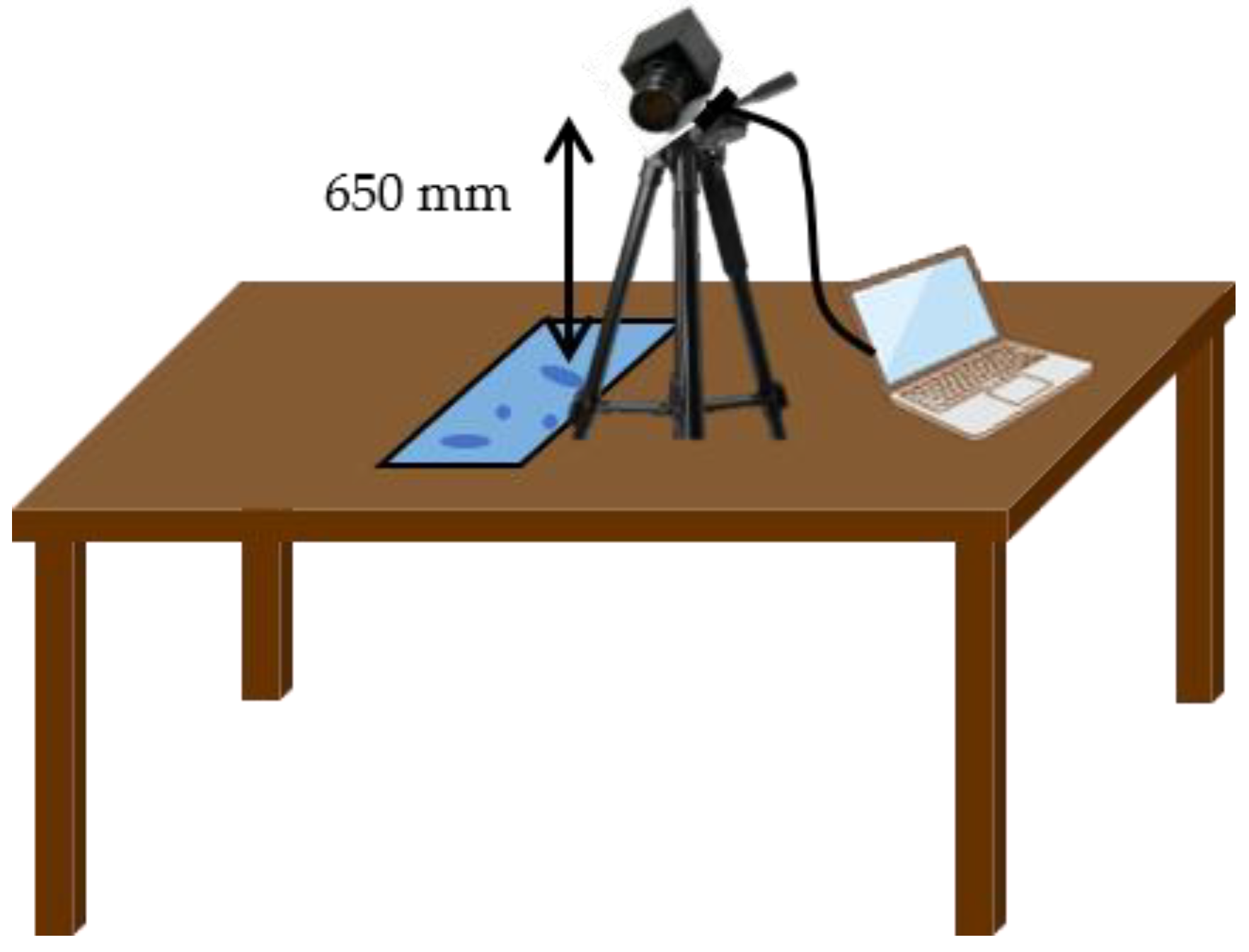

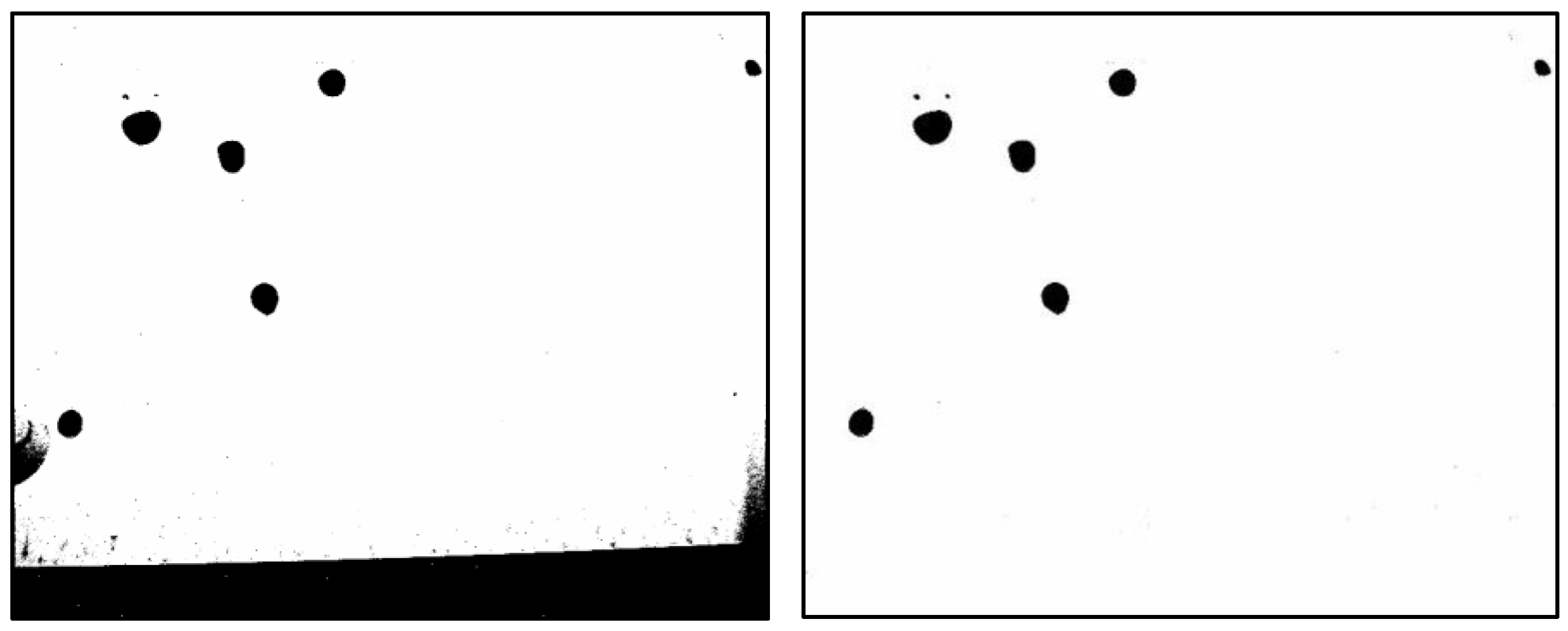






| Image Sensor | InGaAs |
| Number of pixels | 640 × 512 pixels |
| Wavelength sensitivity | 0.9–1.7 µm |
| Frame rate | 98 fps |
| Camera dimensions | 61 × 59 × 81 mm (width × height × depth) (without the lens) |
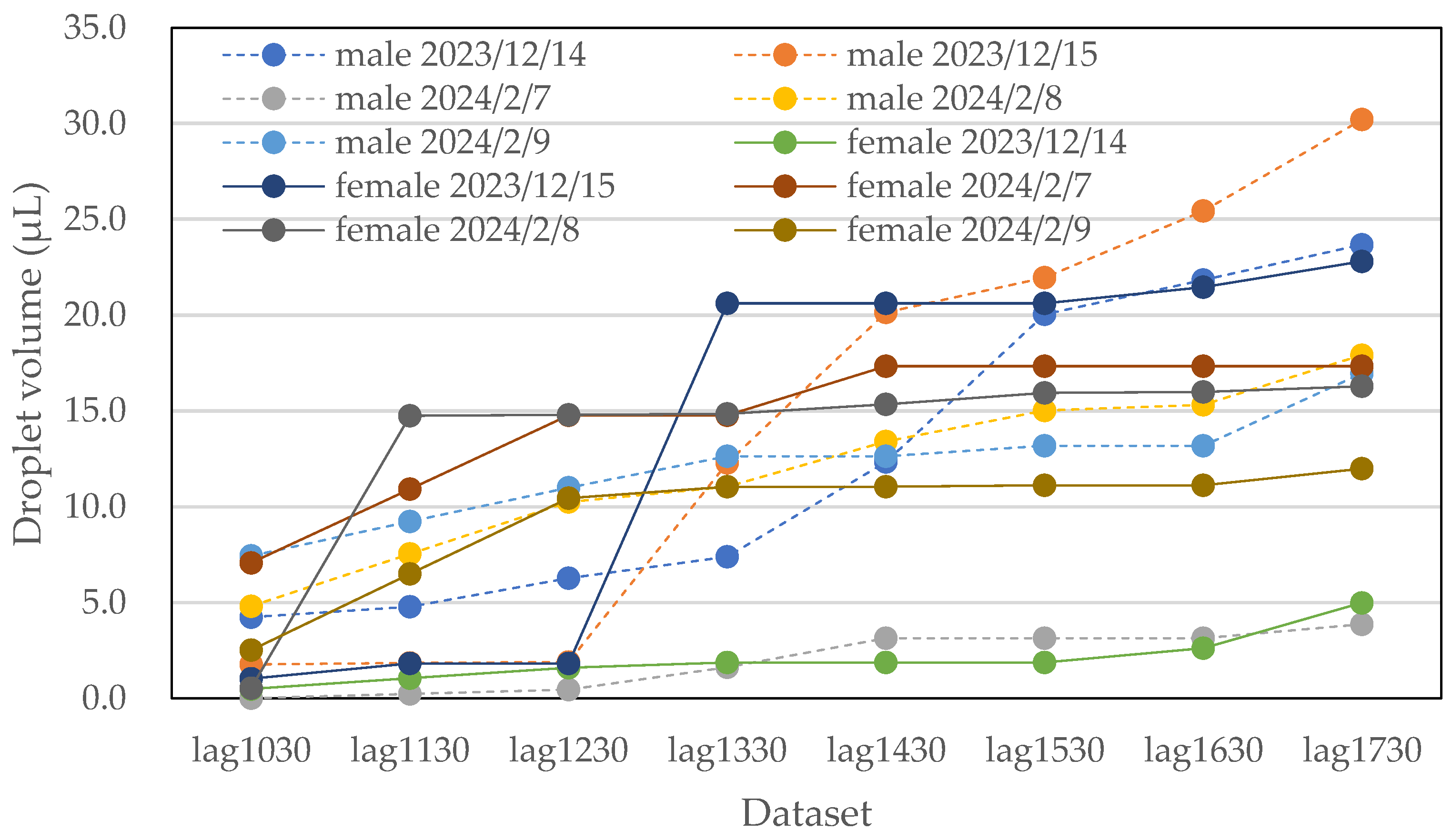
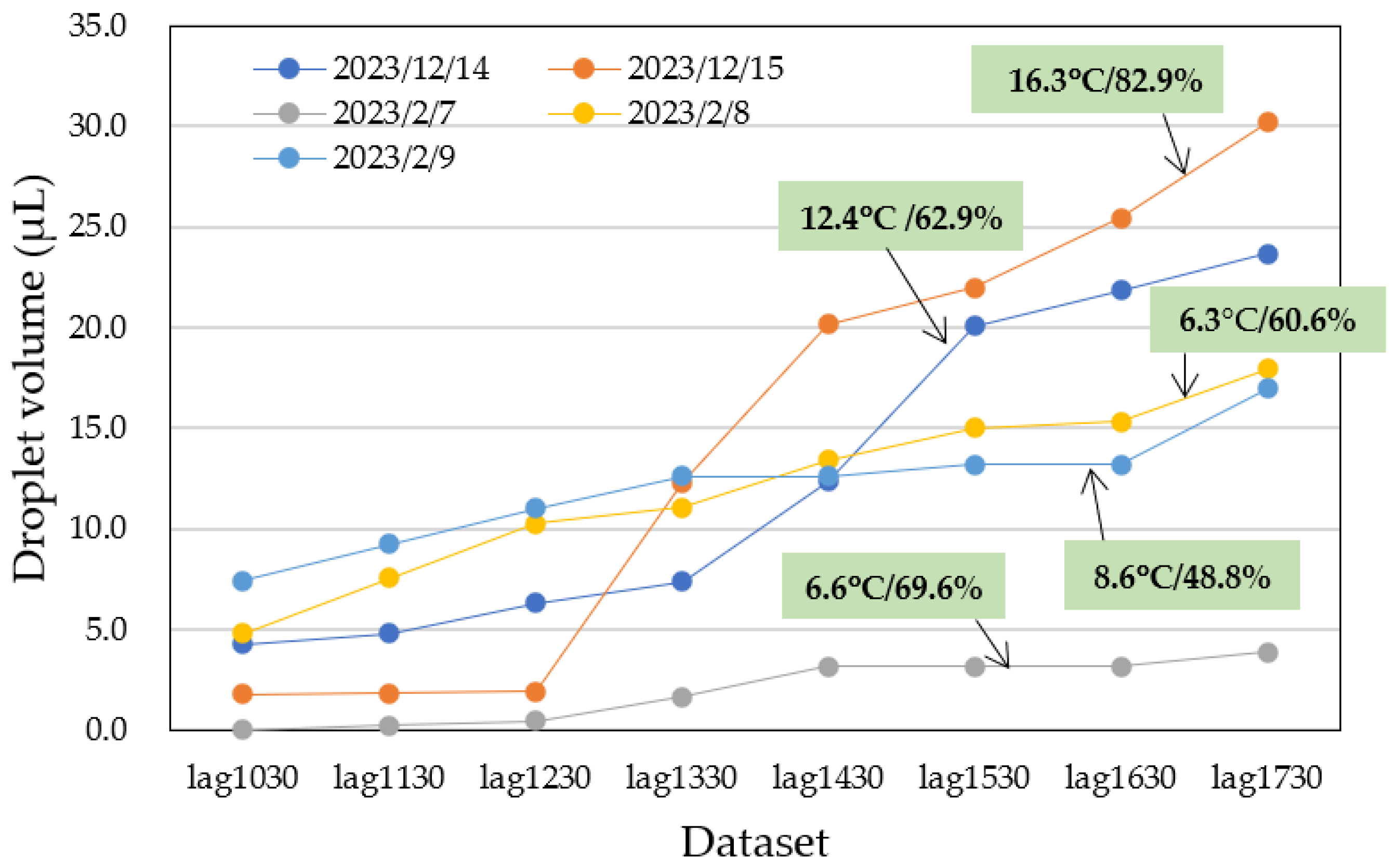
| Sex | Temperature (°C) | Humidity (%) | lag1030 (μL) | lag1130 (μL) | lag1230 (μL) | lag1330 (μL) | lag1430 (μL) | lag1530 (μL) | lag1630 (μL) | lag1730 (μL) |
|---|---|---|---|---|---|---|---|---|---|---|
| Male | 12.4 | 62.9 | 4.2 | 4.8 | 6.3 | 7.4 | 12.3 | 20.0 | 21.8 | 23.7 |
| Male | 16.3 | 82.9 | 1.8 | 1.8 | 1.9 | 12.3 | 20.1 | 22.0 | 25.4 | 30.2 |
| Male | 6.6 | 69.6 | 0.0 | 0.2 | 0.4 | 1.6 | 3.1 | 3.1 | 3.1 | 3.9 |
| Male | 6.3 | 60.6 | 4.8 | 7.5 | 10.2 | 11.0 | 13.4 | 15.0 | 15.3 | 17.9 |
| Male | 8.6 | 48.8 | 7.4 | 9.2 | 11.0 | 12.6 | 12.6 | 13.2 | 13.2 | 17.0 |
| Female | 12.4 | 62.9 | 0.5 | 1.0 | 1.6 | 1.9 | 1.9 | 1.9 | 2.6 | 5.0 |
| Female | 16.3 | 82.9 | 1.0 | 1.8 | 1.8 | 20.6 | 20.6 | 20.6 | 21.5 | 22.8 |
| Female | 6.6 | 69.6 | 7.1 | 10.9 | 14.8 | 14.8 | 17.3 | 17.3 | 17.3 | 17.3 |
| Female | 6.3 | 60.6 | 0.5 | 14.7 | 14.8 | 14.8 | 15.3 | 15.9 | 16.0 | 16.3 |
| Female | 8.6 | 48.8 | 2.5 | 6.5 | 10.5 | 11.0 | 11.0 | 11.1 | 11.1 | 12.0 |
| No. | lag1030 | lag1130 | lag1230 | lag1330 | lag1430 | lag1530 | lag1630 | lag1730 |
|---|---|---|---|---|---|---|---|---|
| 1 | 4.2 | 4.8 | 6.3 | 7.4 | 12.3 | 20.0 | 21.8 | 23.7 |
| 2 | 1.8 | 1.8 | 1.9 | 12.3 | 20.1 | 22.0 | 25.4 | 30.2 |
| 3 | 0.0 | 0.2 | 0.4 | 1.6 | 3.1 | 3.1 | 3.1 | 3.9 |
| 4 | 4.8 | 7.5 | 10.2 | 11.0 | 13.4 | 15.0 | 15.3 | 17.9 |
| 5 | 7.4 | 9.2 | 11.0 | 12.6 | 12.6 | 13.2 | 13.2 | 17.0 |
| 6 | 4.5 | 4.6 | 5.5 | 6.0 | 9.1 | 10.6 | 16.5 | 26.2 |
| 7 | 3.2 | 3.4 | 8.2 | 8.5 | 11.0 | 11.7 | 16.6 | 29.9 |
| 8 | 4.6 | 5.1 | 5.5 | 5.6 | 7.0 | 11.0 | 12.0 | 15.2 |
| 9 | 0.3 | 2.6 | 3.9 | 6.4 | 8.9 | 12.8 | 14.8 | 18.9 |
| 10 | 1.2 | 3.7 | 5.9 | 6.6 | 8.3 | 8.3 | 26.0 | 26.4 |
| 11 | 0.0 | 0.5 | 8.5 | 8.8 | 14.1 | 18.5 | 21.0 | 21.9 |
| 12 | 3.2 | 4.8 | 5.1 | 6.8 | 10.1 | 12.6 | 17.7 | 31.3 |
| 13 | 4.6 | 9.4 | 10.4 | 12.4 | 12.7 | 18.4 | 26.8 | 27.6 |
| 14 | 1.4 | 1.5 | 2.2 | 9.5 | 12.0 | 16.2 | 16.6 | 21.2 |
| 15 | 3.4 | 5.7 | 9.9 | 10.9 | 11.5 | 13.9 | 20.6 | 24.0 |
| 16 | 1.5 | 4.1 | 5.0 | 6.1 | 9.4 | 10.9 | 13.8 | 17.0 |
| 17 | 5.0 | 5.5 | 6.6 | 7.0 | 9.5 | 9.8 | 17.6 | 22.9 |
| 18 | 1.9 | 3.4 | 4.8 | 6.0 | 8.9 | 10.1 | 11.0 | 11.8 |
| 19 | 0.7 | 3.5 | 4.1 | 8.4 | 10.9 | 19.8 | 25.0 | 26.6 |
| 20 | 0.6 | 3.4 | 8.3 | 8.9 | 10.1 | 14.9 | 15.2 | 32.9 |
| 21 | 0.9 | 2.7 | 3.8 | 6.8 | 8.5 | 10.0 | 16.6 | 27.7 |
| 22 | 2.6 | 3.6 | 5.6 | 8.4 | 10.2 | 11.0 | 20.8 | 32.5 |
| 23 | 3.1 | 3.8 | 4.3 | 7.7 | 11.2 | 20.6 | 21.0 | 21.4 |
| 24 | 0.5 | 2.3 | 3.4 | 4.0 | 9.1 | 11.1 | 14.8 | 17.5 |
| 25 | 2.1 | 2.9 | 3.9 | 5.1 | 6.3 | 9.2 | 18.5 | 18.5 |
| 26 | 2.9 | 3.6 | 9.7 | 11.0 | 13.2 | 16.2 | 20.3 | 25.7 |
| 27 | 2.3 | 3.8 | 4.4 | 4.4 | 10.5 | 15.8 | 20.7 | 28.1 |
| 28 | 3.7 | 5.6 | 8.9 | 10.9 | 17.7 | 23.2 | 26.6 | 28.3 |
| 29 | 3.6 | 6.6 | 7.2 | 8.4 | 10.3 | 11.9 | 13.8 | 32.1 |
| 30 | 2.6 | 4.8 | 8.1 | 8.3 | 8.3 | 12.4 | 18.9 | 29.1 |
| 31 | 1.8 | 5.9 | 6.1 | 7.0 | 10.7 | 16.2 | 20.7 | 20.8 |
| 32 | 4.0 | 4.2 | 5.8 | 6.1 | 7.1 | 10.0 | 11.9 | 23.0 |
| 33 | 4.1 | 4.3 | 6.0 | 11.7 | 11.8 | 14.1 | 18.1 | 24.6 |
| 34 | 4.2 | 4.3 | 4.9 | 5.4 | 7.3 | 7.6 | 16.6 | 21.8 |
| 35 | 0.0 | 5.1 | 8.6 | 10.1 | 10.8 | 11.0 | 17.5 | 22.0 |
| 36 | 1.7 | 2.5 | 2.8 | 5.5 | 7.8 | 10.1 | 16.6 | 22.6 |
| 37 | 5.1 | 5.1 | 5.4 | 5.9 | 9.3 | 9.6 | 16.6 | 19.1 |
| 38 | 1.3 | 3.6 | 4.0 | 4.4 | 6.0 | 9.3 | 9.5 | 13.2 |
| 39 | 1.6 | 3.7 | 7.0 | 8.4 | 10.1 | 11.0 | 12.6 | 14.3 |
| 40 | 1.0 | 1.2 | 5.1 | 5.9 | 10.8 | 13.8 | 16.3 | 26.2 |
| 41 | 0.8 | 1.6 | 3.2 | 3.4 | 3.7 | 8.2 | 11.8 | 11.8 |
| 42 | 4.4 | 6.6 | 7.9 | 11.8 | 13.1 | 18.8 | 20.2 | 27.1 |
| 43 | 1.2 | 4.0 | 6.7 | 8.8 | 8.9 | 17.5 | 18.1 | 18.2 |
| 44 | 6.0 | 6.3 | 6.6 | 7.8 | 11.4 | 12.7 | 15.5 | 17.3 |
| 45 | 4.3 | 4.4 | 4.9 | 6.4 | 10.5 | 10.7 | 20.1 | 31.3 |
| 46 | 1.4 | 6.4 | 7.4 | 9.8 | 13.3 | 19.4 | 21.5 | 31.5 |
| 47 | 2.0 | 2.3 | 2.5 | 6.2 | 7.2 | 22.0 | 25.9 | 27.0 |
| 48 | 3.9 | 5.6 | 6.8 | 10.2 | 11.3 | 16.7 | 18.5 | 20.2 |
| 49 | 5.9 | 6.7 | 7.1 | 7.3 | 7.4 | 7.4 | 9.6 | 10.3 |
| 50 | 5.6 | 6.2 | 8.9 | 10.5 | 12.4 | 13.3 | 16.9 | 20.3 |
| 51 | 5.5 | 6.0 | 8.0 | 8.3 | 9.9 | 10.9 | 20.4 | 20.6 |
| 52 | 2.9 | 5.3 | 7.5 | 8.3 | 8.9 | 13.1 | 16.9 | 31.2 |
| 53 | 0.4 | 6.9 | 7.4 | 12.6 | 13.4 | 20.2 | 20.5 | 25.3 |
| 54 | 1.1 | 2.7 | 3.3 | 9.0 | 12.7 | 16.0 | 16.8 | 19.0 |
| 55 | 2.0 | 4.2 | 5.3 | 5.7 | 6.5 | 6.5 | 7.2 | 8.5 |
| 56 | 0.2 | 2.5 | 2.9 | 4.1 | 7.1 | 7.7 | 8.9 | 15.4 |
| 57 | 1.7 | 3.2 | 3.8 | 5.2 | 5.2 | 10.2 | 14.3 | 24.0 |
| 58 | 1.0 | 3.5 | 4.2 | 6.1 | 7.0 | 7.6 | 10.0 | 15.7 |
| 59 | 2.6 | 5.3 | 6.7 | 8.0 | 8.1 | 10.8 | 14.4 | 27.9 |
| 60 | 0.7 | 6.3 | 6.5 | 6.9 | 8.7 | 16.4 | 22.6 | 24.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurose, S.; Moriwaki, H.; Matsunaga, T.; Lee, S.-S. Predicting Restroom Dirtiness Based on Water Droplet Volume Using the LightGBM Algorithm. Sensors 2025, 25, 2186. https://doi.org/10.3390/s25072186
Kurose S, Moriwaki H, Matsunaga T, Lee S-S. Predicting Restroom Dirtiness Based on Water Droplet Volume Using the LightGBM Algorithm. Sensors. 2025; 25(7):2186. https://doi.org/10.3390/s25072186
Chicago/Turabian StyleKurose, Sumio, Hironori Moriwaki, Tadao Matsunaga, and Sang-Seok Lee. 2025. "Predicting Restroom Dirtiness Based on Water Droplet Volume Using the LightGBM Algorithm" Sensors 25, no. 7: 2186. https://doi.org/10.3390/s25072186
APA StyleKurose, S., Moriwaki, H., Matsunaga, T., & Lee, S.-S. (2025). Predicting Restroom Dirtiness Based on Water Droplet Volume Using the LightGBM Algorithm. Sensors, 25(7), 2186. https://doi.org/10.3390/s25072186






