Blind Interference Suppression with Uncalibrated Phased-Array Processing †
Abstract
1. Introduction
1.1. Problem Overview
- Spread-spectrum communications which generally distribute the information rate disproportionately across the bandwidth so as to minimize the statistical impact of interference;
- Successive interference cancellation which seeks to iteratively remove interference through estimation and subtraction;
- Spectral white-space estimation methods which attempt to locate (and possibly predict) which frequency bands are available, often using non-contiguous spectrum waveforms;
- Multi-antenna methods which include an entire array of techniques to provide spatial diversity.
1.2. Traditional Beamforming Methods
1.3. Non-Beamforming Methods
2. Materials and Methods
2.1. Overview
2.2. Analysis Polyphase Filterbank Channelizers
2.3. Synthesis Polyphase Filterbank Channelizers
2.4. Almost-Perfect Reconstruction
- suppressing non-adjacent channels;
- canceling aliasing between the overlapping pass-bands of adjacent channels.
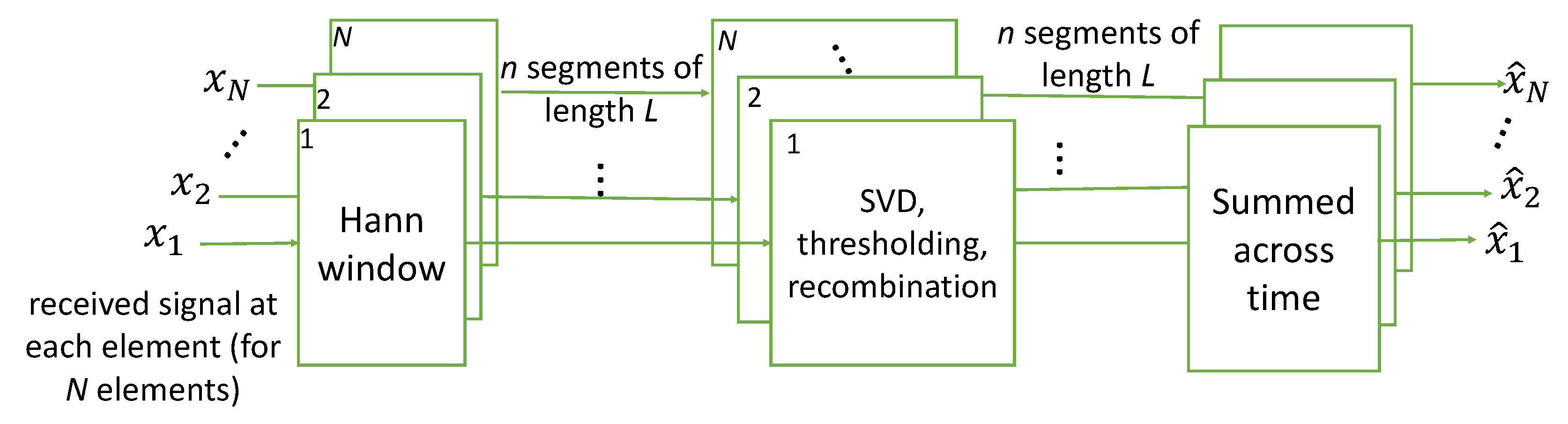
2.5. SVD Reconstruction
2.6. Signal of Interest Enhancement
2.7. Singular Value Selection
2.8. Configuration Order
- The data are passed through N identical PFB analysis filterbanks with M channels.
- Each of the M filtered outputs across the N sensors are then processed using SVD reconstruction to remove the interference.
- The resulting data are synthesized using a bank of M synthesis filters.
- Finally, the data are combined across sensors using the Rayleigh quotient.

- The complex valued matrix R has the dimensions , where N is the number of antenna elements (or sensors), and k is the number of samples in the buffer.
- The matrix R is filtered through an analysis filterbank defined by an M-band channelizer, whose output is oversampled by a factor of 2. This process outputs a sequence of matrices for , where m corresponds to the band number. Each matrix has the dimensions , where is the block size after decimation.
- Each matrix is windowed by a periodic, L-point Hann window into framed segments, which have a segment overlap of 50% and sample length L. That is to say, for every sensor with the indices , the newly framed counterpart is , where f is the frame index, which continues to iterate until it segments the entire matrix . The total number of frames is heavily dependent upon L and the amount of overlap.
- For each frame, the resulting matrix —for band number —has the size . As noted by its size, contains the framed data from all N sensors.
- The matrix is then processed—and interfering signals are removed—using SVD reconstruction.
- The frames are linearly combined to reconstruct each , which has the same shape as (). Given the type of window and the amount of overlap, would be perfectly reconstructed in the time domain if singular values had not been removed from . As such, the newly reconstructed is with the nuisance signals mostly, if not completely, removed.
- Each is synthesized through its own synthesis filter (M synthesis filters in total) to produce the matrix , which has the shape .
- The data from all of the sensors in are combined, using weights defined by the Rayleigh quotient, into a single vector , which is k samples long.
- The probability of packet error is analyzed by attempting to decode the packet in .
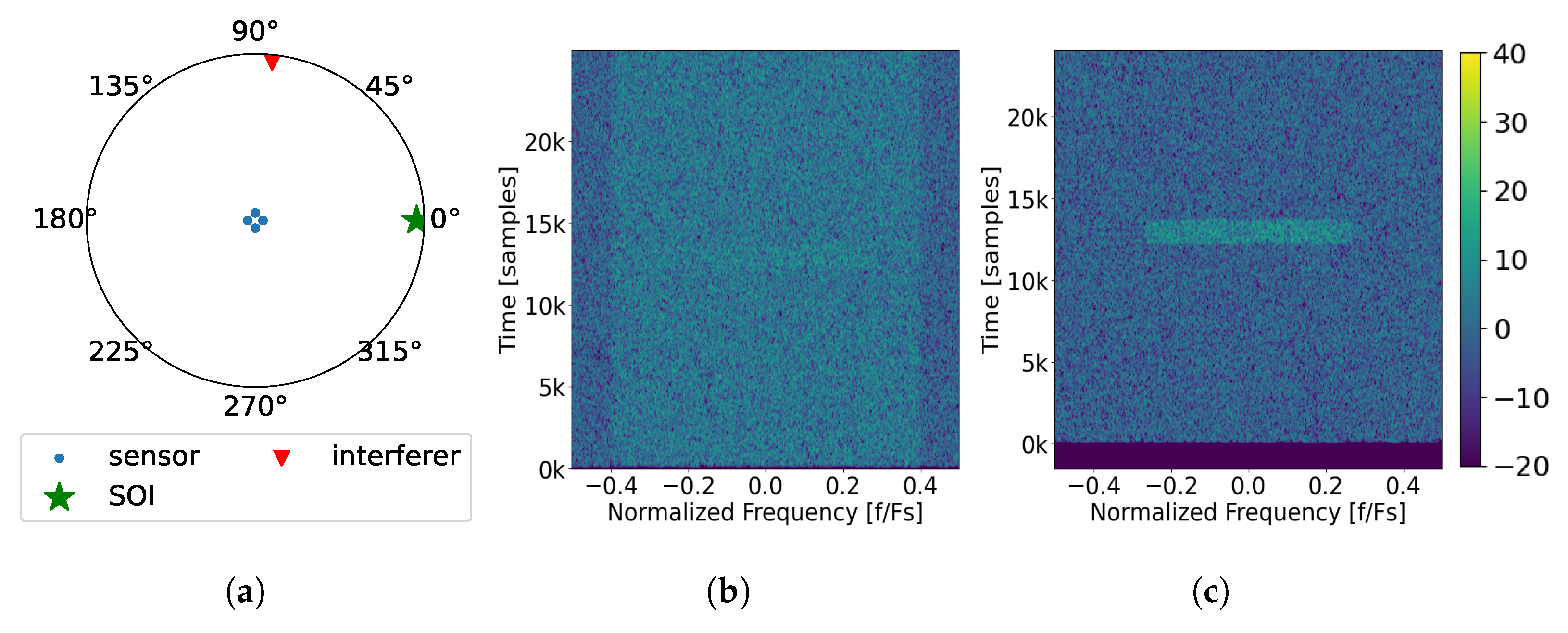
2.9. Simulated Single Packet Scenarios
2.9.1. Scenario 1: Three Interference Sources
- There is a processing delay in the output incurred by both the PFB channelizer as well as the windowing function, which is visible in the output plot.
- The majority of SOI experiences 6 dB enhancement by coherently combining the antenna elements as made evident by its higher power level in the output plot; however, because of interference C, it cannot be decoded.
- Interferences A and B can be successfully removed with minimal impact on SOI, but interference C cannot. While all of the interfering signals are frequency-separable and thus can be processed relatively independently, since interference C comes from the same DOA as SOI, the interference cannot be separated from SOI. This is due to them both sharing the same eigenspace and thus singular values. The only way to potentially decode SOI is to allow the sub-band containing interference C to be notched out, which will introduce some ISI and performance degradation.
- Due to how close the DOA of interference A is to the DOA of SOI, the power of SOI is lowered in the particular sub-band where the interference is removed.
- Unlike with interference A, SOI does not show signs of reduced power in the same band where interference B is removed. This is due to the DOA of the interference being sufficiently removed from that of SOI, so they do not share singular values (or similar eigenspace). Thus, the interference can be removed without visibly impairing the power of SOI.
2.9.2. Scenario 2: Narrowband Noise Interference Sources
- Overall, the majority of the SOI has a 6 dB improvement.
- The narrowband noise interference is successfully removed; however, like with interference A from Scenario 1, in the sub-bands where the narrowband noise interference used to be, SOI is slightly reduced in power. This is likely due to the DOA of the interference being close enough to SOI’s DOA such that SOI and the interference share singular values and have similar eigenspaces.

2.9.3. Scenario 3: Wideband Noise Interference Sources
- Once again, SOI is shown to have the same 6 dB enhancement as in previous scenarios.
- The wideband interference is successfully removed with minimal disturbance to SOI as it arrives from an entirely different direction than SOI.
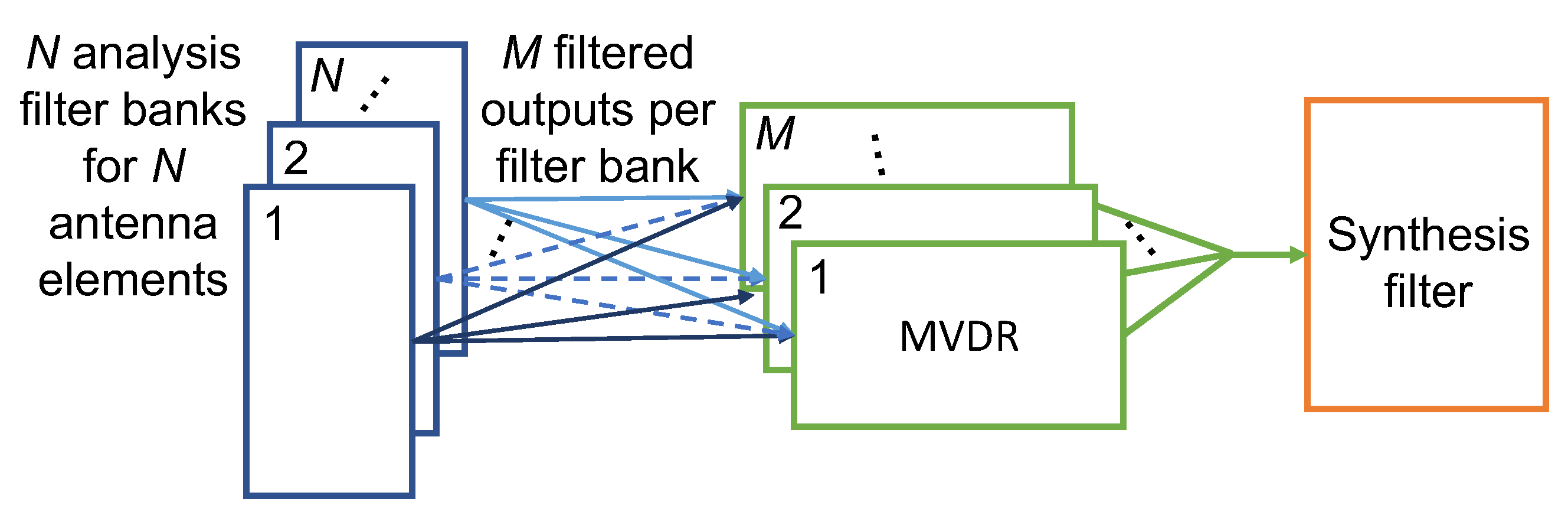
2.10. MVDR
- 5.
- MVDR is performed on the matrix Am. The result is the vector of length .
- 6.
- The frames are then linearly combined to reconstruct .
- 7.
- The probability of packet error is analyzed by attempting to decode the packet in .
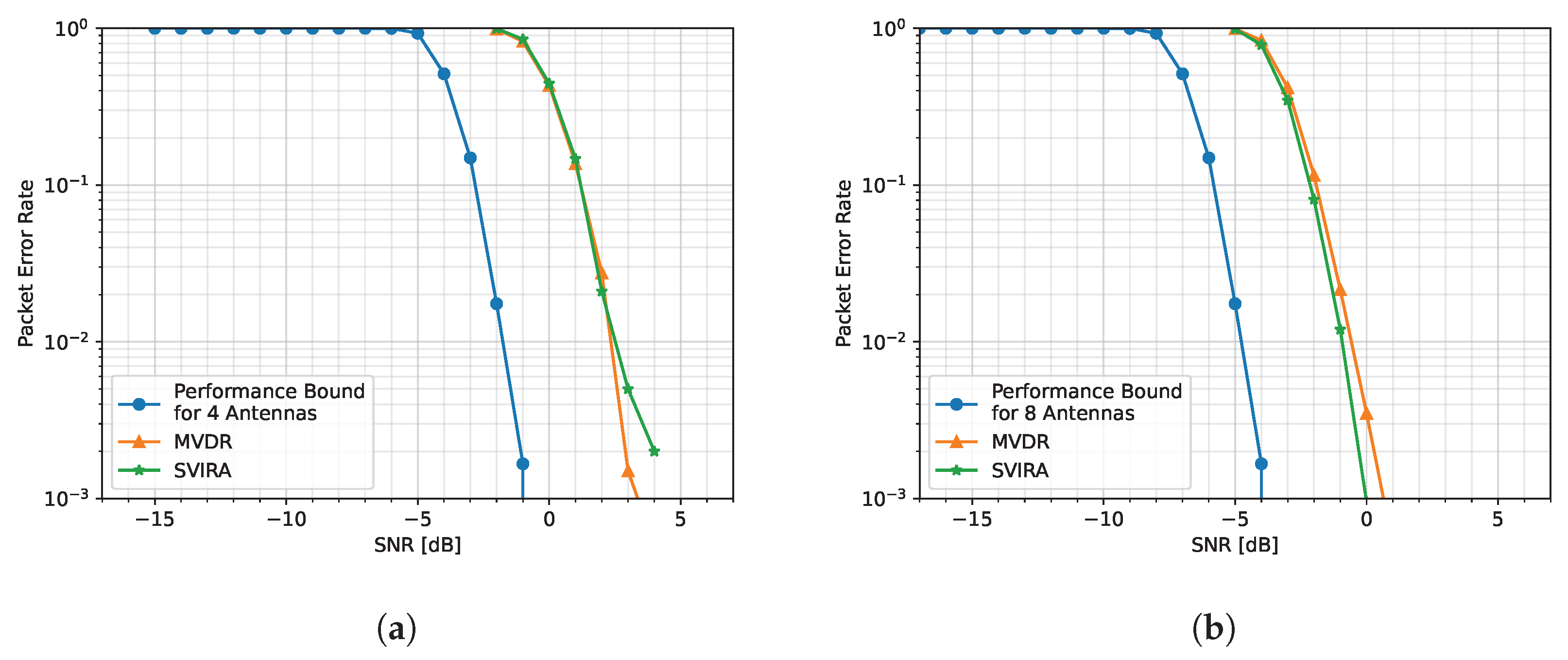
2.11. Simulated Comparison to MVDR
2.12. Key Technical Contributions
- Works with legacy waveforms.
- Operates without precise antenna configuration knowledge.
- Can remove more interference sources than degrees of freedom afforded by the phased array with frequency separability.
- Does not require estimation of interference number or types.
- Able to achieve a similar PER performance as MVDR.
3. Experimentation
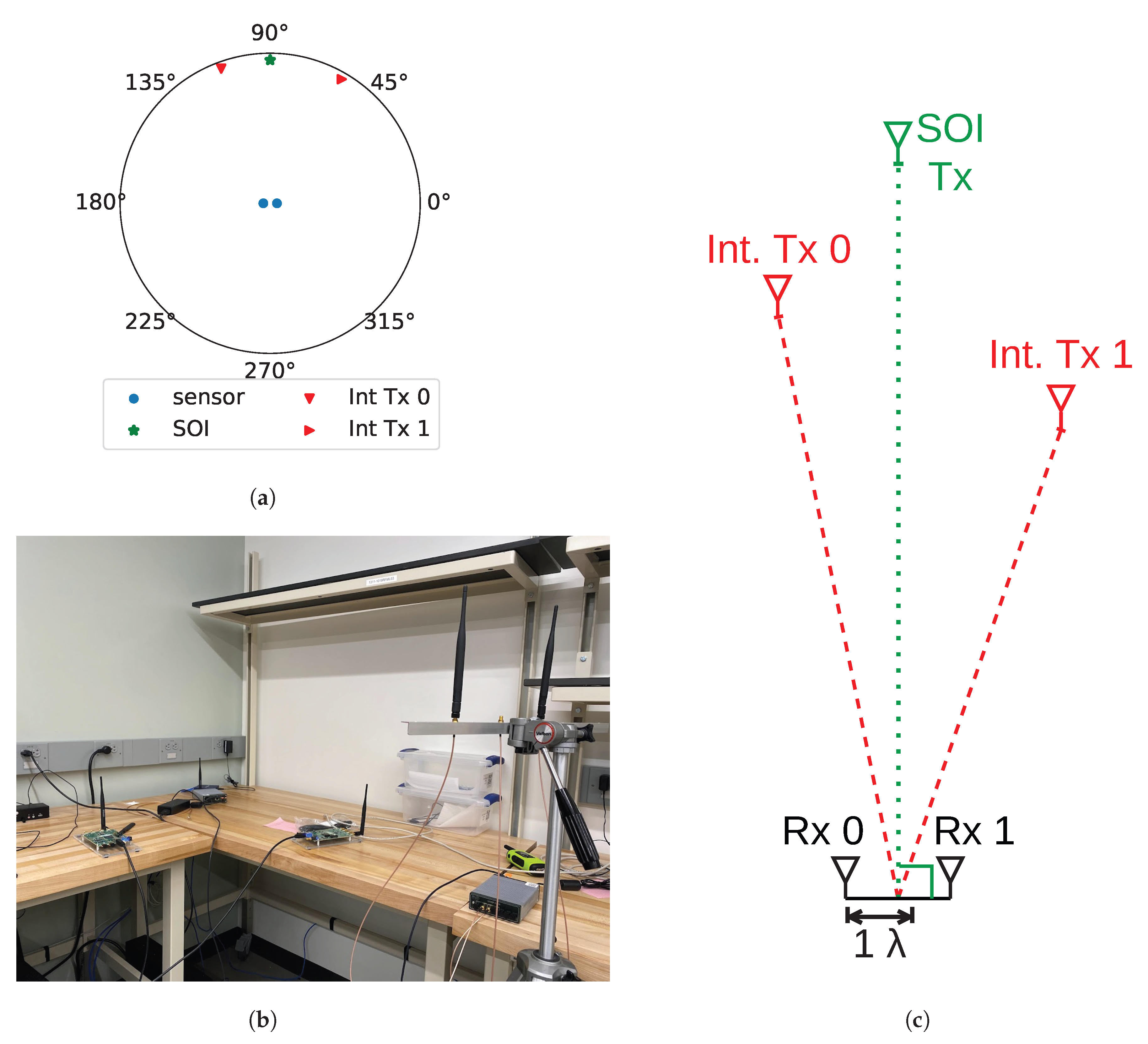
3.1. Hardware Setup and Description
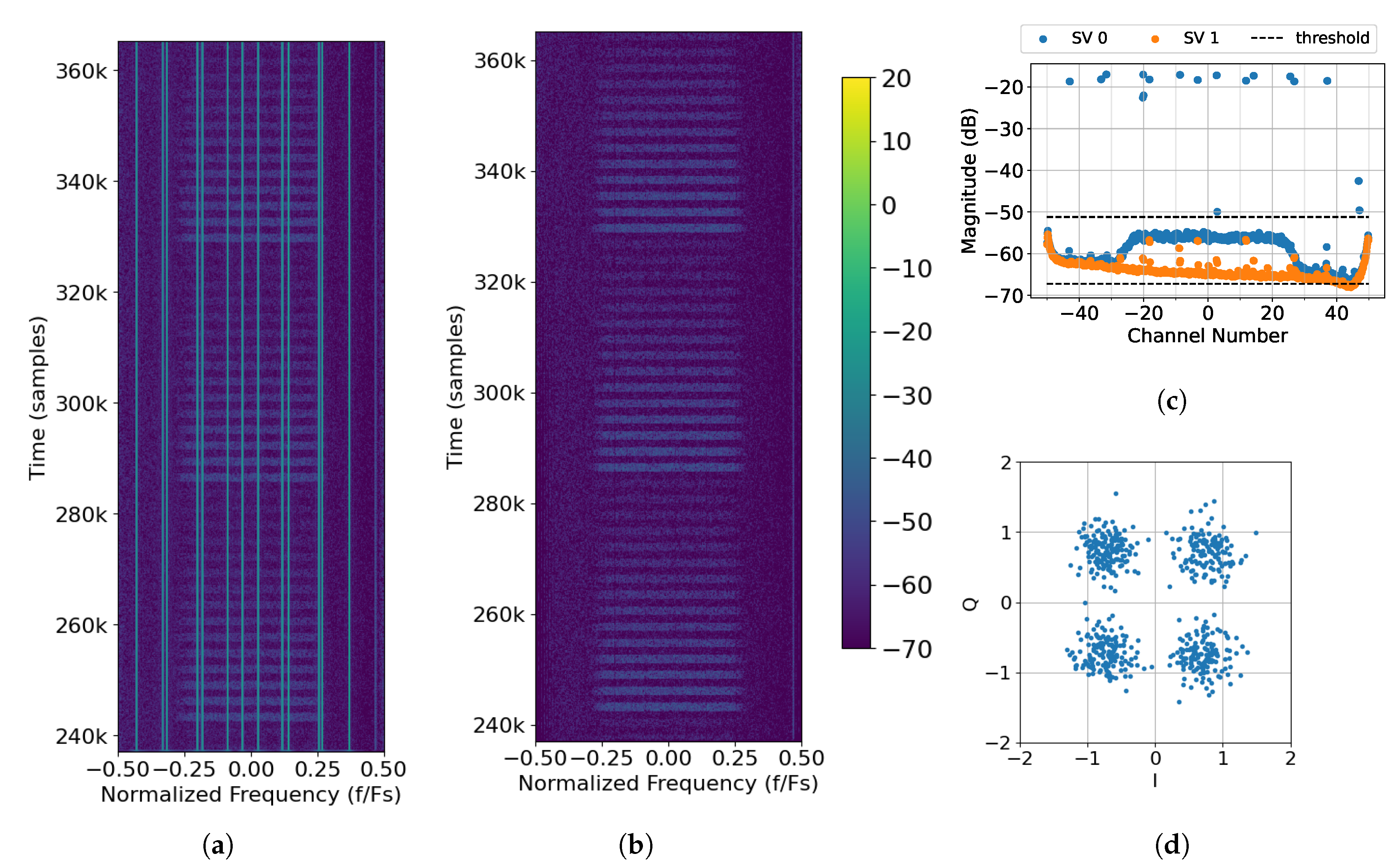
3.2. Data Collection Setup
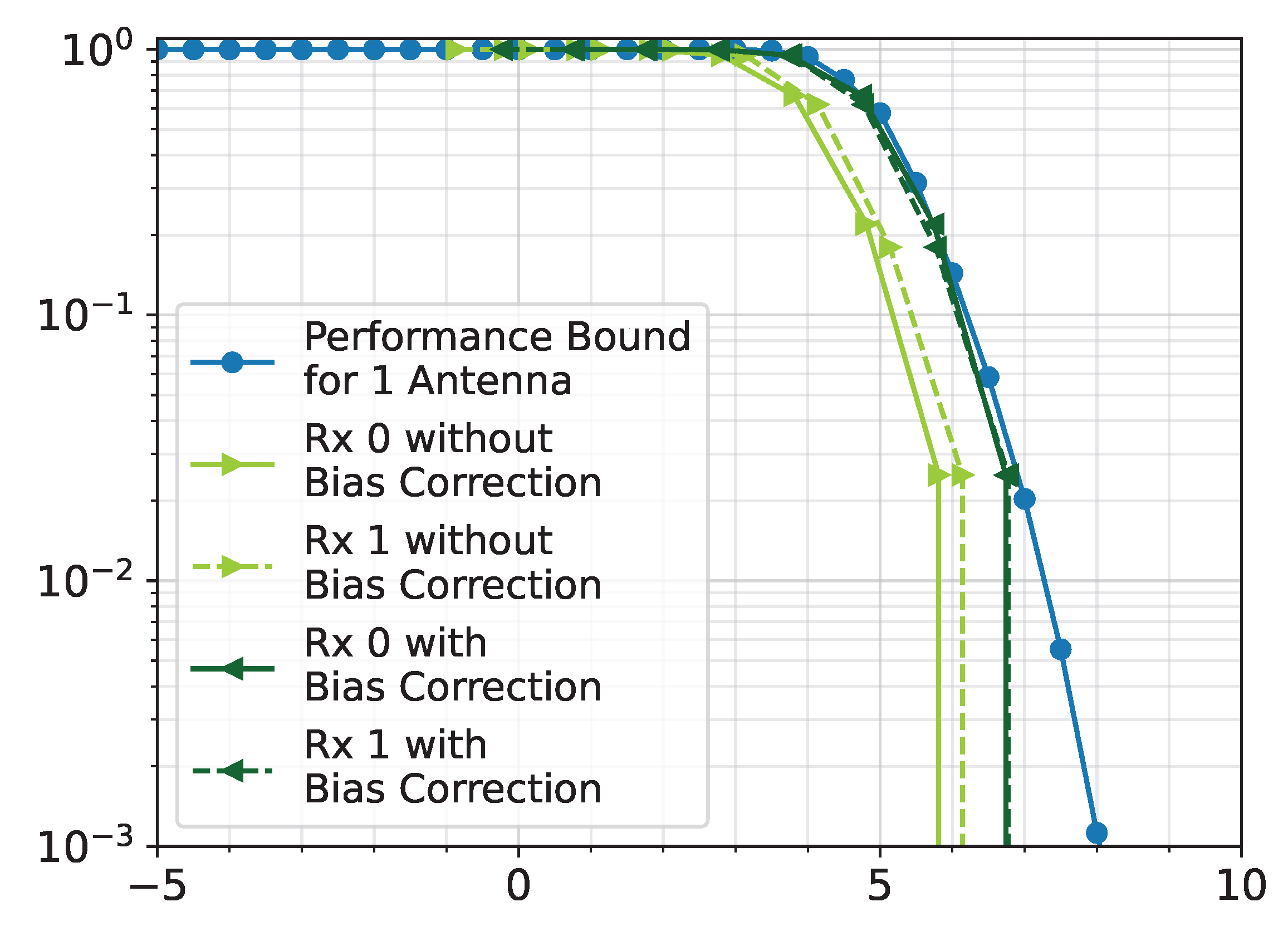
3.3. SNR and Gain Calibration

- Find the EVM of each packet.
- Estimate the SNR of each packet.
- For each packet, determine the difference between the EVM and estimated SNR.
- Take the median of the differences as the bias.
- Add the bias to the estimated SNR.
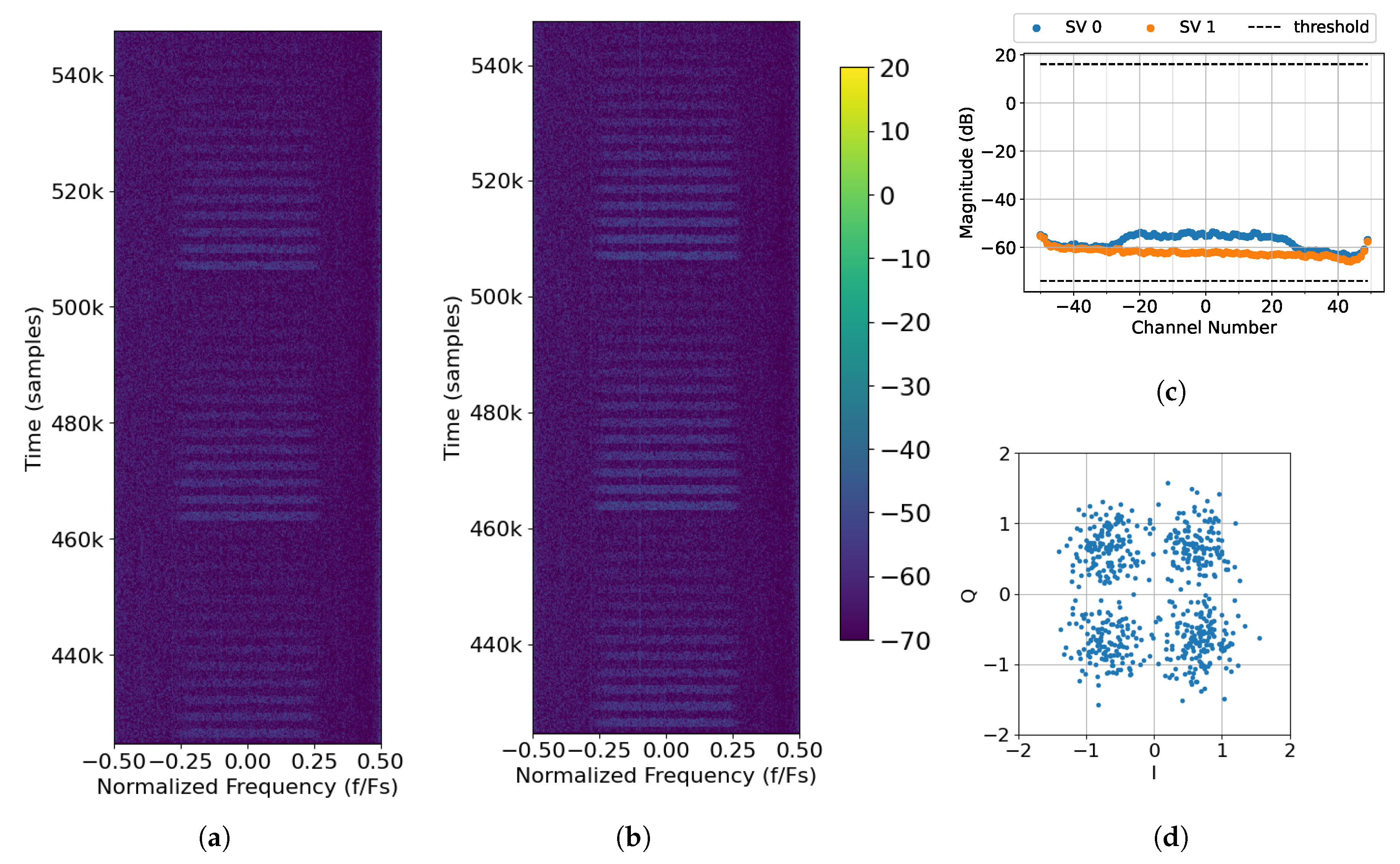
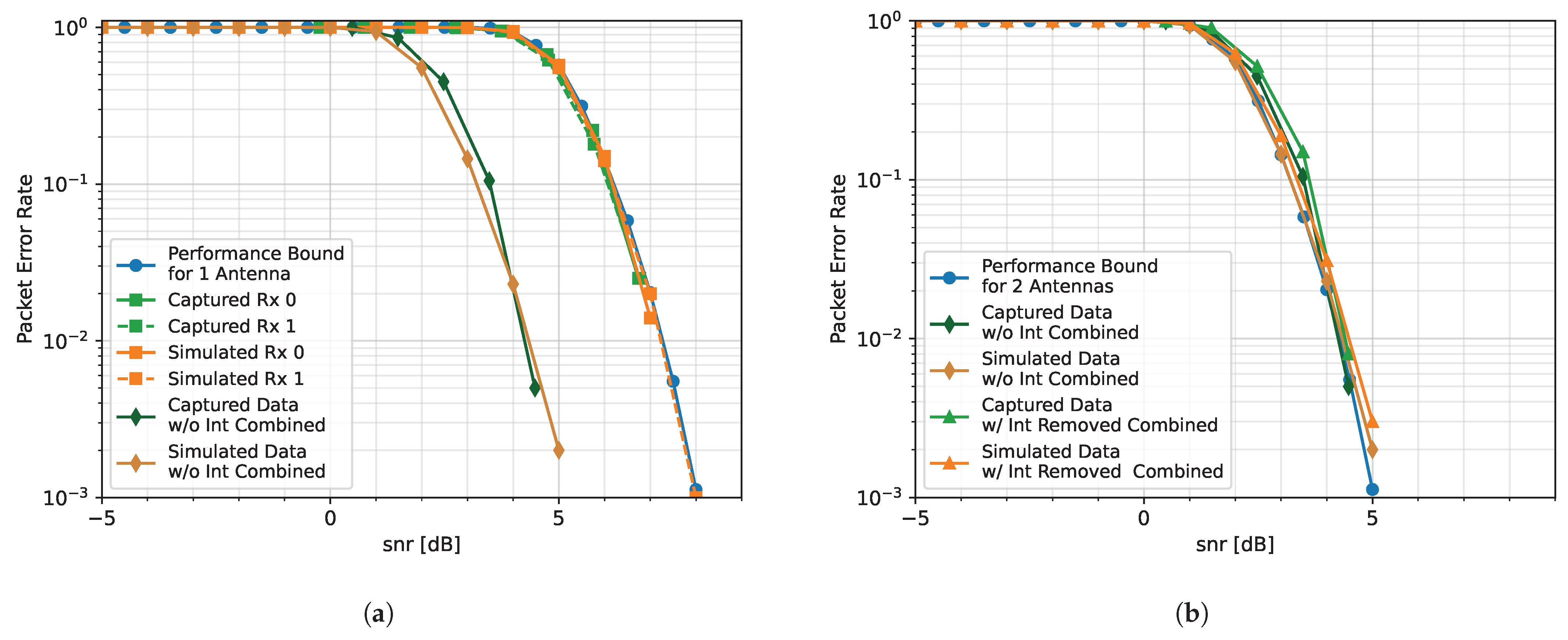
4. Experimental Results
4.1. No Interference Source
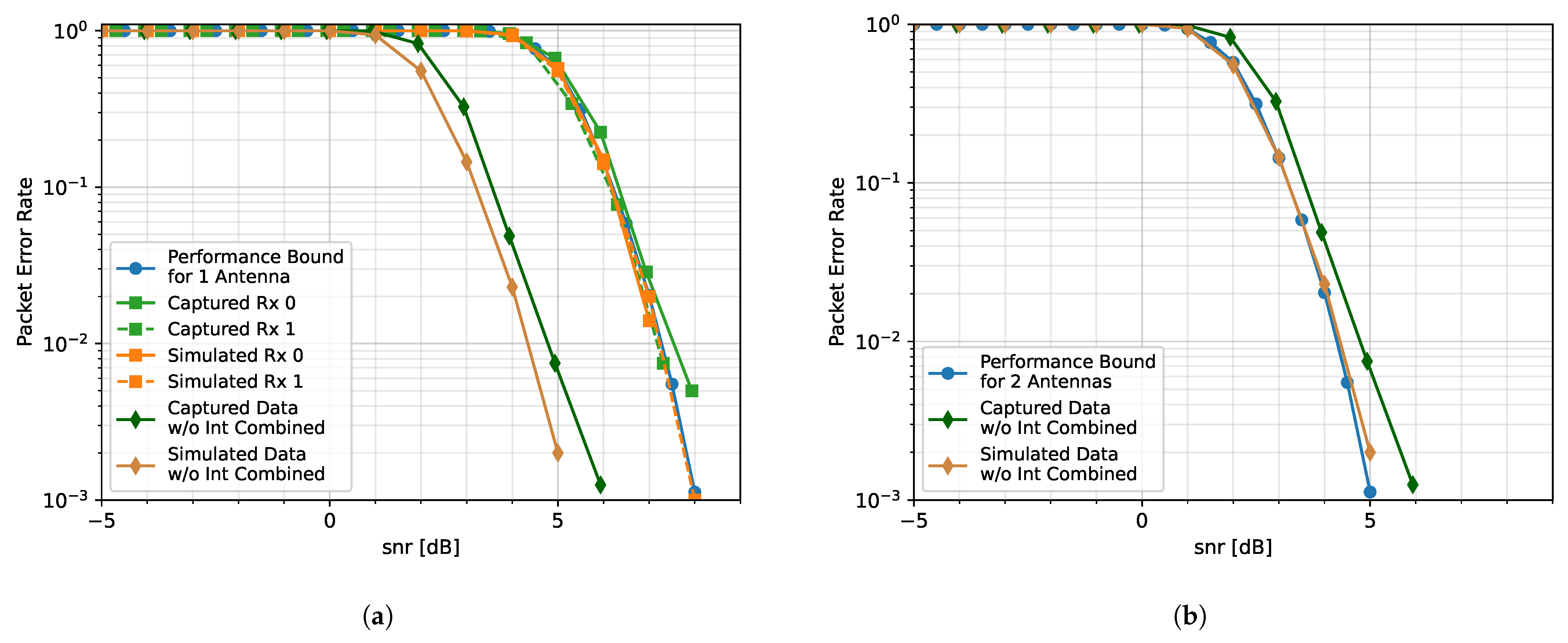
4.2. One Interference Source Case
4.3. Two Interference Sources Case
5. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| M | the number of sub-channels in channelizer |
| N | the number of antenna elements (“sensors”) |
| h0 | the channelizer prototype filter |
| 2L | the block size for processing SVD, consistent with L for Hann window |
| xi(n,m) | i is the element index; n is the time index; m is the channel index |
| AWGN | additive white Gaussian noise |
| CCI | co-channel interference |
| CMA | constant modulus algorithm |
| CNN | convolutional neural network |
| CSV | composite steering vector |
| dB | decibels |
| DFT | discrete Fourier transform |
| DOA | direction of arrival |
| EM | electromagnetic |
| EVM | error vector magnitude |
| FCC | Federal Communications Commission |
| FFT | fast Fourier transform |
| IoT | Internet of Things |
| IQR | interquartile range |
| ISI | intersymbol interference |
| ISM | industrial, scientific, and medical |
| LO | local oscillator |
| LMS | least mean-squares |
| MUSIC | multiple signal classification |
| MVDR | minimum variance distortionless response |
| OFDM | orthogonal frequency-division multiplexing |
| probability density function | |
| PER | packet error rate |
| PFB | polyphase filterbank |
| PSD | power spectral density |
| RQ | Rayleigh quotient |
| QPSK | quaternary phase-shift keying |
| RFFE | radio frequency front end |
| RFID | radio frequency identification |
| RLS | recursive least-squares |
| SCORE | spectral self-coherent restoral |
| SDR | software-defined radio |
| SIC | successive interference cancellation |
| SINR | signal-to-interference-plus-noise ratio |
| SNR | signal-to-noise ratio |
| SOI | signal of interest |
| STAP | space–time adaptive processing |
| SV | singular value |
| SVD | singular value decomposition |
| SVIRA | singular value interference removal algorithm |
| UCA | uniform circular array |
| USRP | universal software radio peripheral |
References
- Code of Federal Regulations. Title 47, Chapter 1, Subchapter A, Part 15. 1989. Available online: https://www.ecfr.gov/current/title-47/chapter-I/subchapter-A/part-15 (accessed on 28 March 2023).
- Capon, J. High-resolution frequency-wavenumber spectrum analysis. Proc. IEEE 1969, 57, 1408–1418. [Google Scholar]
- Song, X.; Wang, J.; Han, Y.; Xue, Y. A recursive algorithm to robust adaptive beamforming and diagonal loading. In Proceedings of the 2006 6th World Congress on Intelligent Control and Automation, Dalian, China, 21–23 June 2006; Volume 1, pp. 2268–2271. [Google Scholar]
- Ding, Y.; Li, Z. A blind beamforming algorithm based on time-frequency analysis technology. In Proceedings of the 2021 6th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 9–11 April 2021; pp. 367–371. [Google Scholar]
- Lee, J.H.; Jeong, Y.S.; Cho, S.W.; Yeo, W.Y.; Pister, K.S. Application of the Newton method to improve the accuracy of TOA estimation with the beamforming algorithm and the MUSIC algorithm. Prog. Electromagn. Res. 2011, 116, 475–515. [Google Scholar]
- Basha, T.G.; Sridevi, P.; Prasad, M.G. Beam forming in smart antenna with precise direction of arrival estimation using improved MUSIC. Wirel. Pers. Commun. 2013, 71, 1353–1364. [Google Scholar]
- Ahmed, I.; Koushik, B.A.; Kumar, G.C.; Neethu, S. Simulation of Direction of Arrival Using MUSIC Algorithm and Beamforming using Variable Step Size LMS Algorithm. In Proceedings of the 2022 IEEE Microwaves, Antennas, and Propagation Conference (MAPCON), Bangalore, India, 12–16 December 2022; pp. 993–997. [Google Scholar]
- Eireiner, T.; Muller, T.; Luy, J.F.; Owens, F. Implementation of a smart antenna system with an improved NCMA algorithm. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, 2003, Philadelphia, PA, USA, 8–13 June 2003; Volume 3, pp. 1529–1532. [Google Scholar]
- Ahmed, B.I.; Jabeen, F. Blind adaptive beamforming simulation using NCMA for smart antenna. In Proceedings of the 2017 IEEE 7th International Advance Computing Conference (IACC), Hyderabad, India, 5–7 January 2017; pp. 492–495. [Google Scholar]
- Qin, B.; Cai, Y.; Champagne, B.; Zhao, M. Complexity reduction techniques for blind adaptive beamforming in OFDM antenna arrays. In Proceedings of the 2014 Sixth International Conference on Wireless Communications and Signal Processing (WCSP), Hefei, China, 23–25 October 2014; pp. 1–6. [Google Scholar]
- Ranganathan, V.; Prabha, G.; Narayanankutty, K. Constant modulus hybrid recursive and least mean squared algorithm performance comparable to unscented Kalman filter for blind beamforming. In Proceedings of the 2016 IEEE Annual India Conference (INDICON), Bangalore, India, 16–18 December 2016; pp. 1–4. [Google Scholar]
- Agee, B.G.; Schell, S.V.; Gardner, W.A. Spectral self-coherence restoral: A new approach to blind adaptive signal extraction using antenna arrays. Proc. IEEE 1990, 78, 753–767. [Google Scholar]
- Zhang, W.; Liu, W. Low-complexity blind beamforming based on cyclostationarity. In Proceedings of the 2012 Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 1–5. [Google Scholar]
- Kim, J.H.; Seo, Y.K.; Kwon, S.Y.; Kim, H.N.; Park, J.O.; Kang, H.J.; Kim, J.Y.; Mun, B.H. Blind beamforming based on Multi-target SCORE with a DMP algorithm. In Proceedings of the International Conference on Electronics, Information and Communication (ICEIC), Auckland, New Zealand, 22–25 January 2019. [Google Scholar]
- Koldovskỳ, Z.; Tichavskỳ, P.; Kautskỳ, V. Orthogonally constrained independent component extraction: Blind MPDR beamforming. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 1155–1159. [Google Scholar]
- Zhang, L.; Liao, B.; Huang, L.; Guo, C. An eigendecomposition-based approach to blind beamforming in a multipath environment. IEEE Commun. Lett. 2016, 21, 322–325. [Google Scholar]
- Xie, Z.; Fan, C.; Zhu, J.; Deng, Y.; Huang, X. Improved Blind Beamforming for Multipath Signals in Complex Interference Environment. In Proceedings of the 2020 IEEE 5th International Conference on Signal and Image Processing (ICSIP), Nanjing, China, 23–25 October 2020; pp. 639–643. [Google Scholar]
- Zhao, B.; Yang, J.A.; Zhang, M. Research on blind source separation and blind beamforming. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 7, pp. 4389–4393. [Google Scholar] [CrossRef]
- Wang, C.; Tang, J. Blind beamforming technique for reception of multipath coherent signals. IEEE Commun. Lett. 2016, 20, 1453–1456. [Google Scholar]
- Ramezanpour, P.; Rezaei, M.J.; Mosavi, M.R. Deep-learning-based beamforming for rejecting interferences. IET Signal Process. 2020, 14, 467–473. [Google Scholar]
- Jo, M.J.; Lee, G.W.; Moon, J.M.; Cho, C.; Kim, H.K. Estimation of MVDR Beamforming Weights Based on Deep Neural Network. In Proceedings of the Audio Engineering Society Convention 145, New York, NY, USA, 17–20 October 2018. [Google Scholar]
- Kim, H.; Kang, K.; Shin, J.W. Factorized MVDR Deep Beamforming for Multi-Channel Speech Enhancement. IEEE Signal Process. Lett. 2022, 29, 1898–1902. [Google Scholar] [CrossRef]
- Miridakis, N.I.; Vergados, D.D. A Survey on the Successive Interference Cancellation Performance for Single-Antenna and Multiple-Antenna OFDM Systems. IEEE Commun. Surv. Tutor. 2013, 15, 312–335. [Google Scholar] [CrossRef]
- Kohno, R. Spatial and temporal communication theory using adaptive antenna array. IEEE Pers. Commun. 1998, 5, 28–35. [Google Scholar] [CrossRef]
- Wang, K.; Wang, L.; Han, C. Joint space and time domain processing for DOA estimation. In Proceedings of the 2015 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Ningbo, China, 19–22 September 2015; pp. 1–4. [Google Scholar]
- Zhang, Y.; Yang, K.; Amin, M.G.; Karasawa, Y. Performance analysis of subband arrays. IEICE Trans. Commun. 2001, 84, 2507–2515. [Google Scholar]
- Vaidyanathan, P.P. Multirate Systems and Filter Banks; Prentice Hall: Hoboken, NJ, USA, 1998. [Google Scholar]
- Harris, F.J. Multirate Signal Processing for Communication Systems, 2nd ed.; River Publishers: Aalborg, Denmark, 2021. [Google Scholar]
- Proakis, J.G.; Manolakis, D.G. Digital Signal Processing: Principles, Algorithms, and Applications; Pearson Education: London, UK, 2007; Chapter 11; pp. 794–795. [Google Scholar]
- Proakis, J.G.; Salehi, M. Digital Communications; McGraw Hill Education: New York, NY, USA, 2018; p. 1087. [Google Scholar]
- Kolman, B.; Hill, D.R. 8.2 Spectral Decomposition and Singular Value Decomposition. In Elementary Linear Algebra; Pearson Education: London, UK, 2008; pp. 488–500. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2013; Chapter 1; pp. 234–239. [Google Scholar]
- Vorobyov, S.A. Principles of minimum variance robust adaptive beamforming design. Signal Process. 2013, 93, 3264–3277. [Google Scholar] [CrossRef]
- Ettus Research. USRP E-320. 2023. Available online: https://www.ettus.com/all-products/usrp-e320/ (accessed on 6 April 2023).





| Requires Knowledge of Array Configuration | Requires Estimation of SOI DOA | Requires Estimation of Number of Signals | Algorithm Complexity per Input | |
|---|---|---|---|---|
| MVDR | Yes | Yes | No | |
| MUSIC | Yes | Yes | No | |
| Eigen-based | No | No | Yes | |
| SVIRA | No | No | No |
| Number of Sweeps | Transmission Gain Range per Sweep (dB) | Number of Tones | Number of Interference Sources | M | B | Thresholds (dB) | |
|---|---|---|---|---|---|---|---|
| File 8 (Trans. A) | 800 | −8 to −22 | 0 | 0 | 96 | 64 | −1, 80 |
| File 27 (Trans. A) | 200 | −10 to −24 | 0 | 0 | 96 | 64 | −1, 80 |
| File 27 (Trans. B) | 500 | −10 to −24 | 8 | 1 | 370 | 128 | −1, 25 |
| File 41 (Trans. A) | 800 | −8 to −22 | 0 | 0 | 96 | 64 | −1, 80 |
| File 41 (Trans. B) | 1000 | −8 to −22 | 13 | 2 | 800 | 320 | −1, 15 |
| Number of Sweeps | SNR Range per Sweep (dB) | Number of Tones | Number of Interference Sources | M | B | Thresholds (dB) | |
|---|---|---|---|---|---|---|---|
| File 4 | 1000 | −5 to 8 | 0 | 0 | 96 | 64 | −1, 80 |
| File 5 | 1000 | −5 to 9 | 8 | 1 | 370 | 128 | −1, 25 |
| File 6 | 1000 | −5 to 8 | 13 | 2 | 800 | 320 | −1, 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lusk, L.O.; Gaeddert, J.D. Blind Interference Suppression with Uncalibrated Phased-Array Processing. Sensors 2025, 25, 2125. https://doi.org/10.3390/s25072125
Lusk LO, Gaeddert JD. Blind Interference Suppression with Uncalibrated Phased-Array Processing. Sensors. 2025; 25(7):2125. https://doi.org/10.3390/s25072125
Chicago/Turabian StyleLusk, Lauren O., and Joseph D. Gaeddert. 2025. "Blind Interference Suppression with Uncalibrated Phased-Array Processing" Sensors 25, no. 7: 2125. https://doi.org/10.3390/s25072125
APA StyleLusk, L. O., & Gaeddert, J. D. (2025). Blind Interference Suppression with Uncalibrated Phased-Array Processing. Sensors, 25(7), 2125. https://doi.org/10.3390/s25072125






