Influence of Sampling Rate on Wearable IMU Orientation Estimation Accuracy for Human Movement Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Measurement Systems
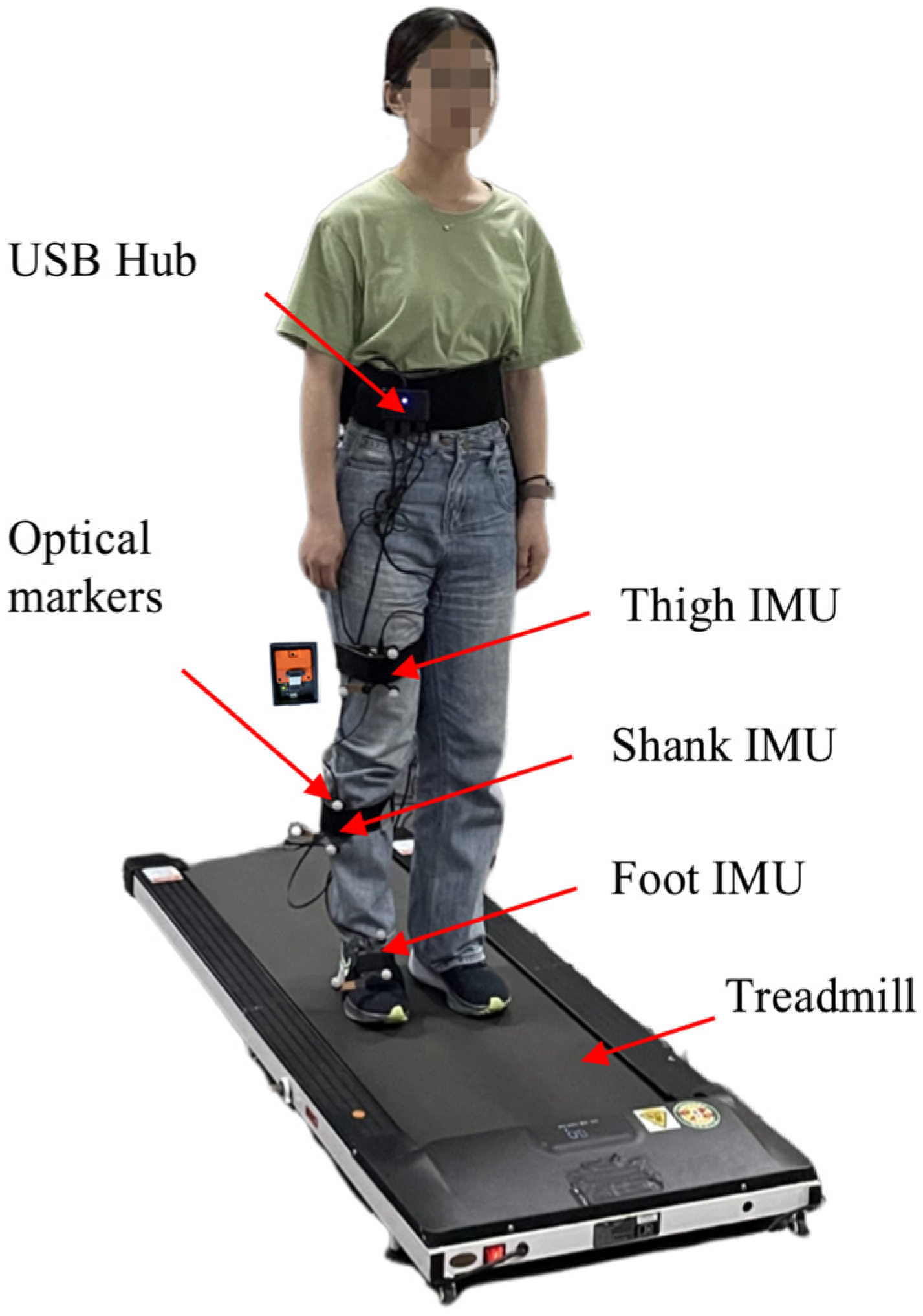
2.1.1. Experimental Setup for Human Subjects Test
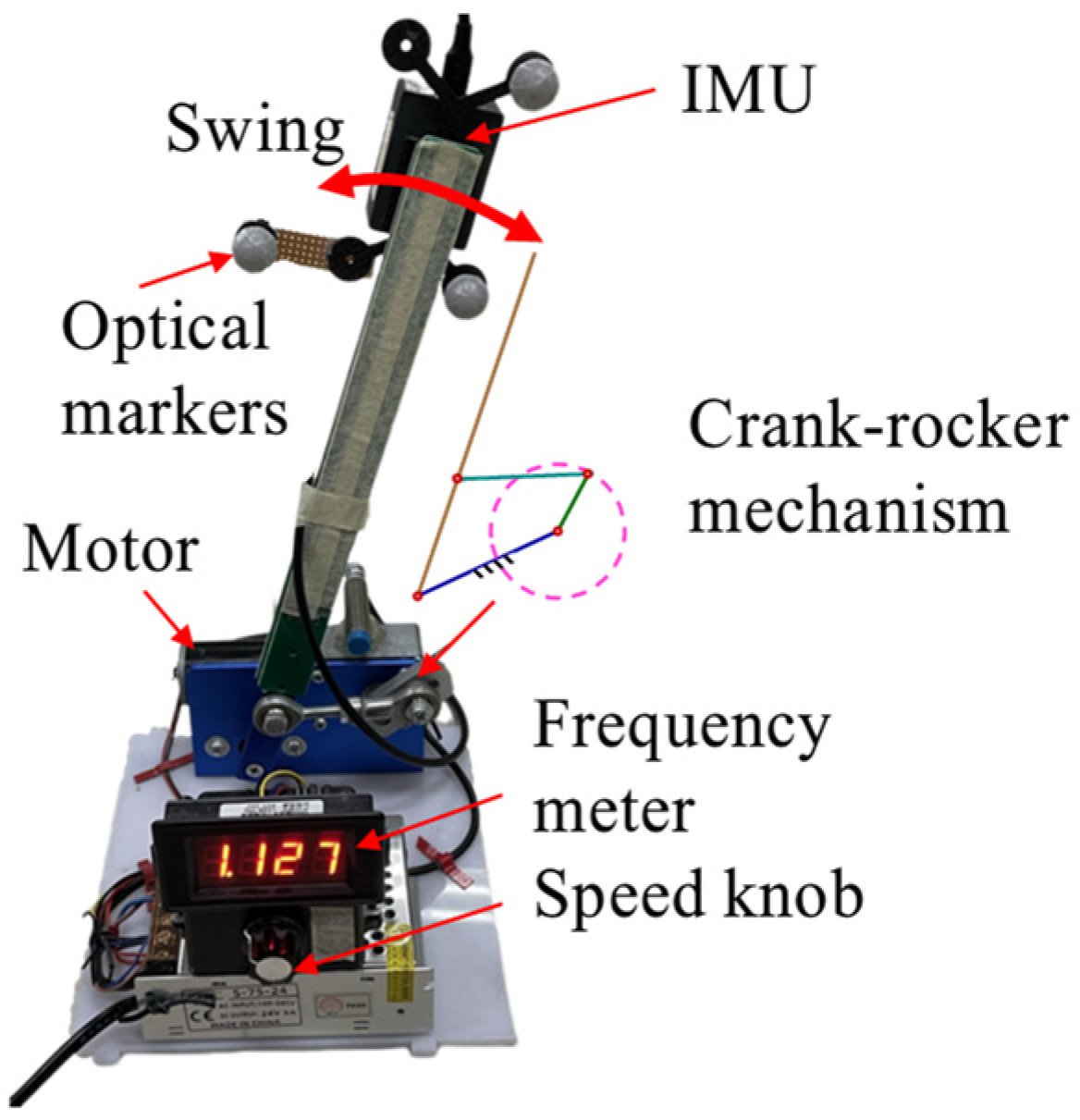
2.1.2. Experimental Setup for Cyclic Movements Test
2.2. Experimental Protocol
2.2.1. Orientation Estimation on Human Subjects
2.2.2. Orientation Estimation on the Motion Testbed
2.3. Sensor Fusion Algorithms
- Quaternion addition-based integration method () [17]
- 2.
- Quaternion multiply based integration method ()
2.4. Data Analysis
3. Results
3.1. Walking and Running Experiments
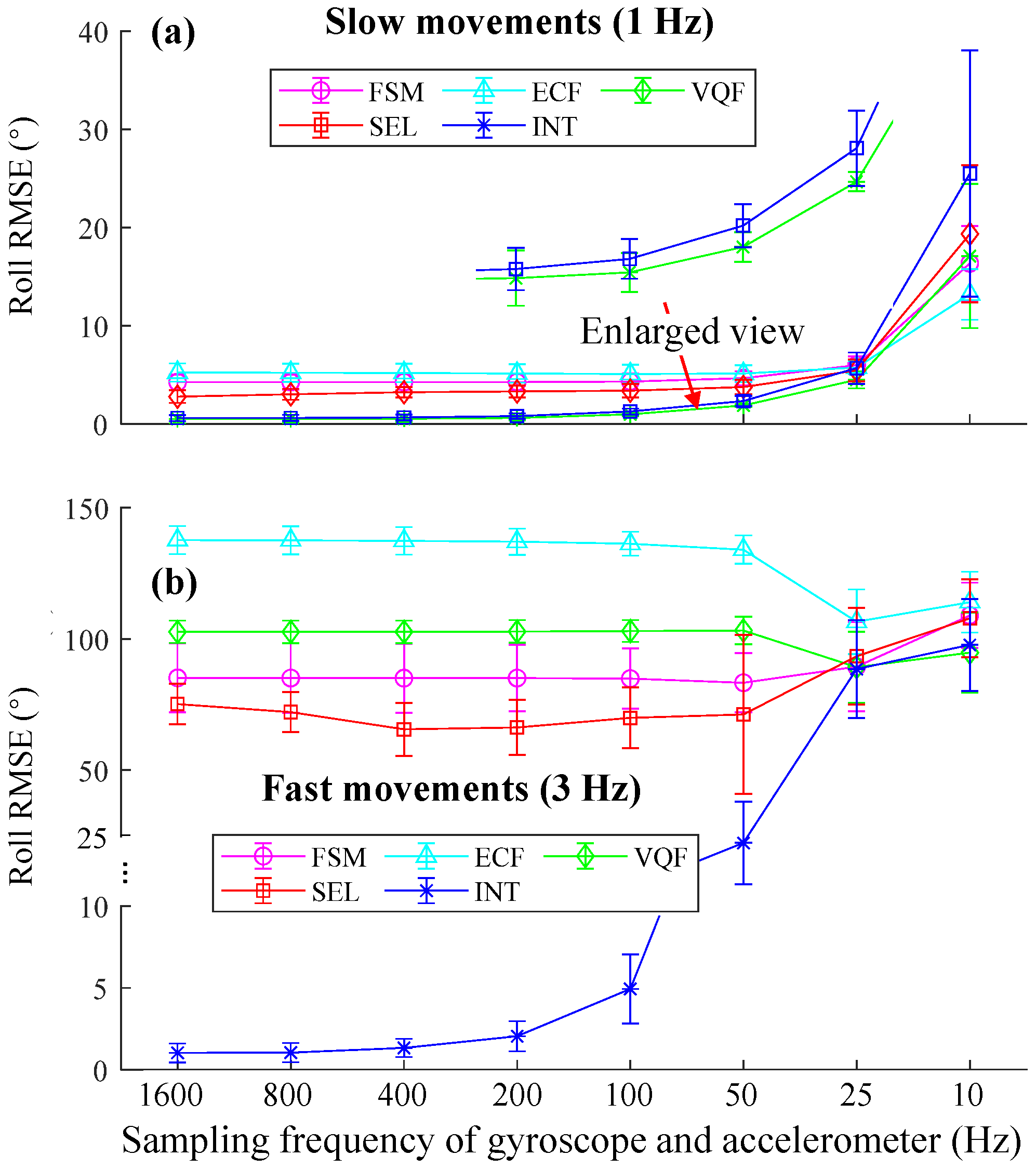
3.2. Motion Testbed Experiments
3.3. Detailed Analysis of Orientation Estimation
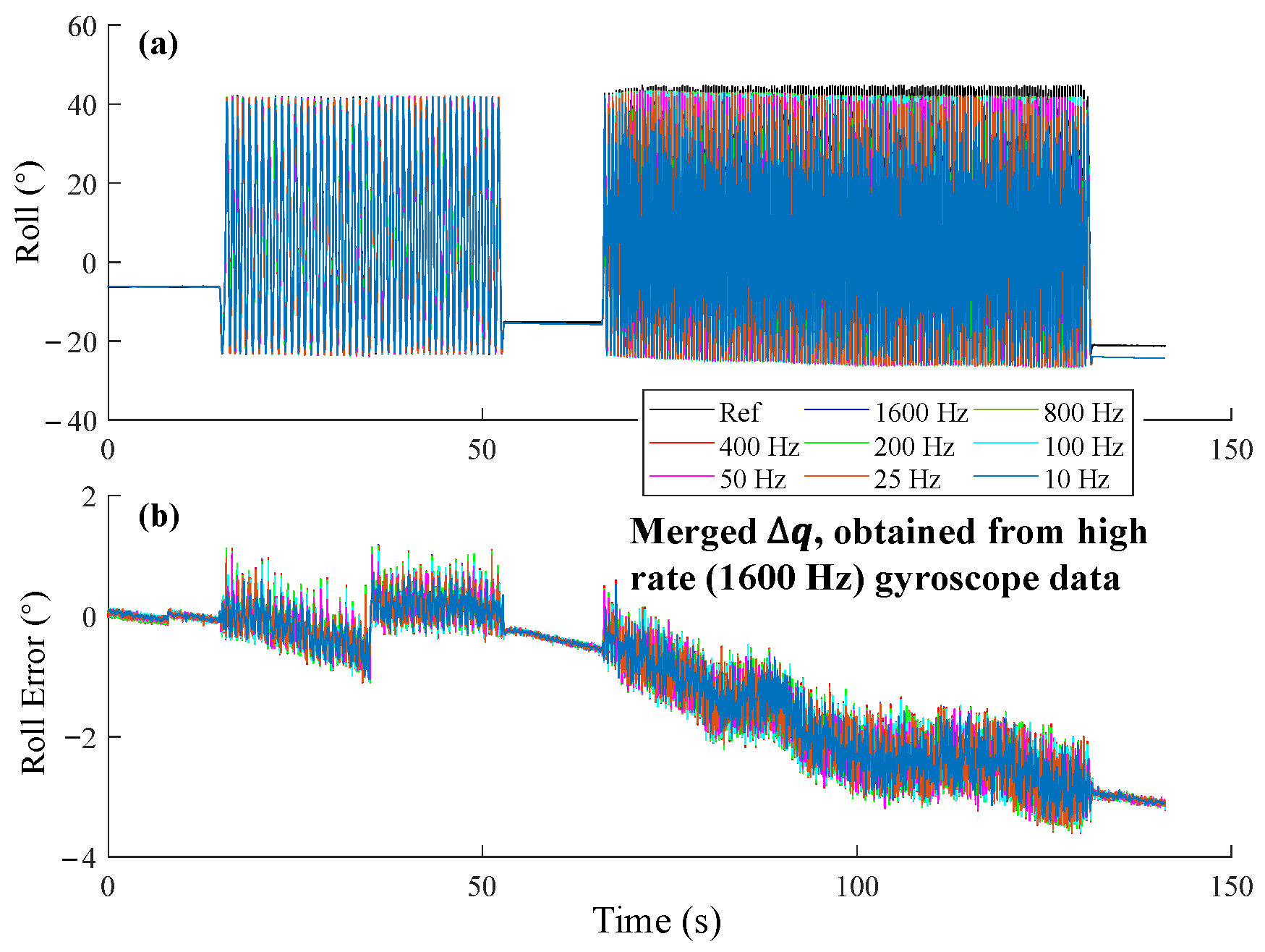
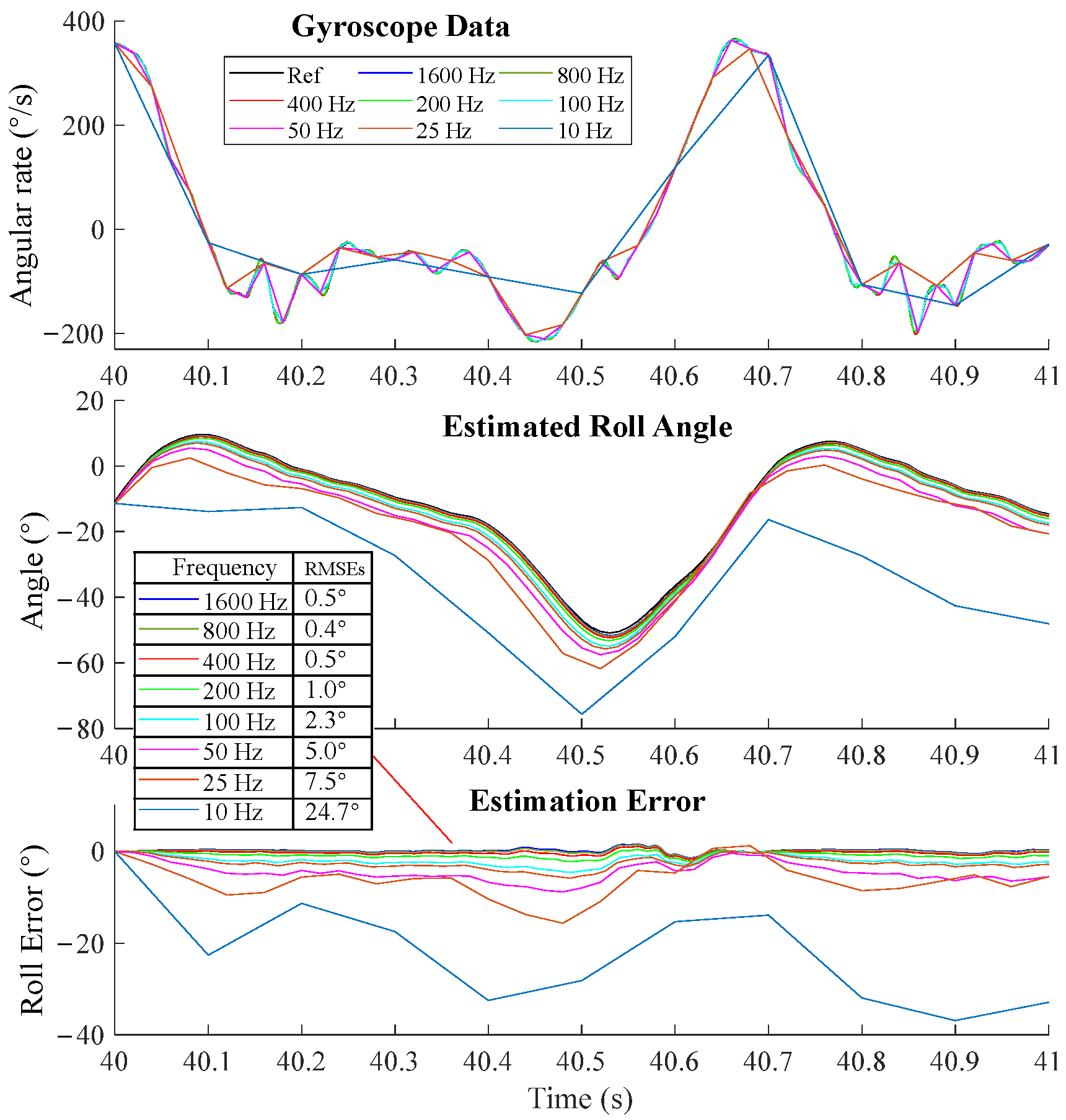
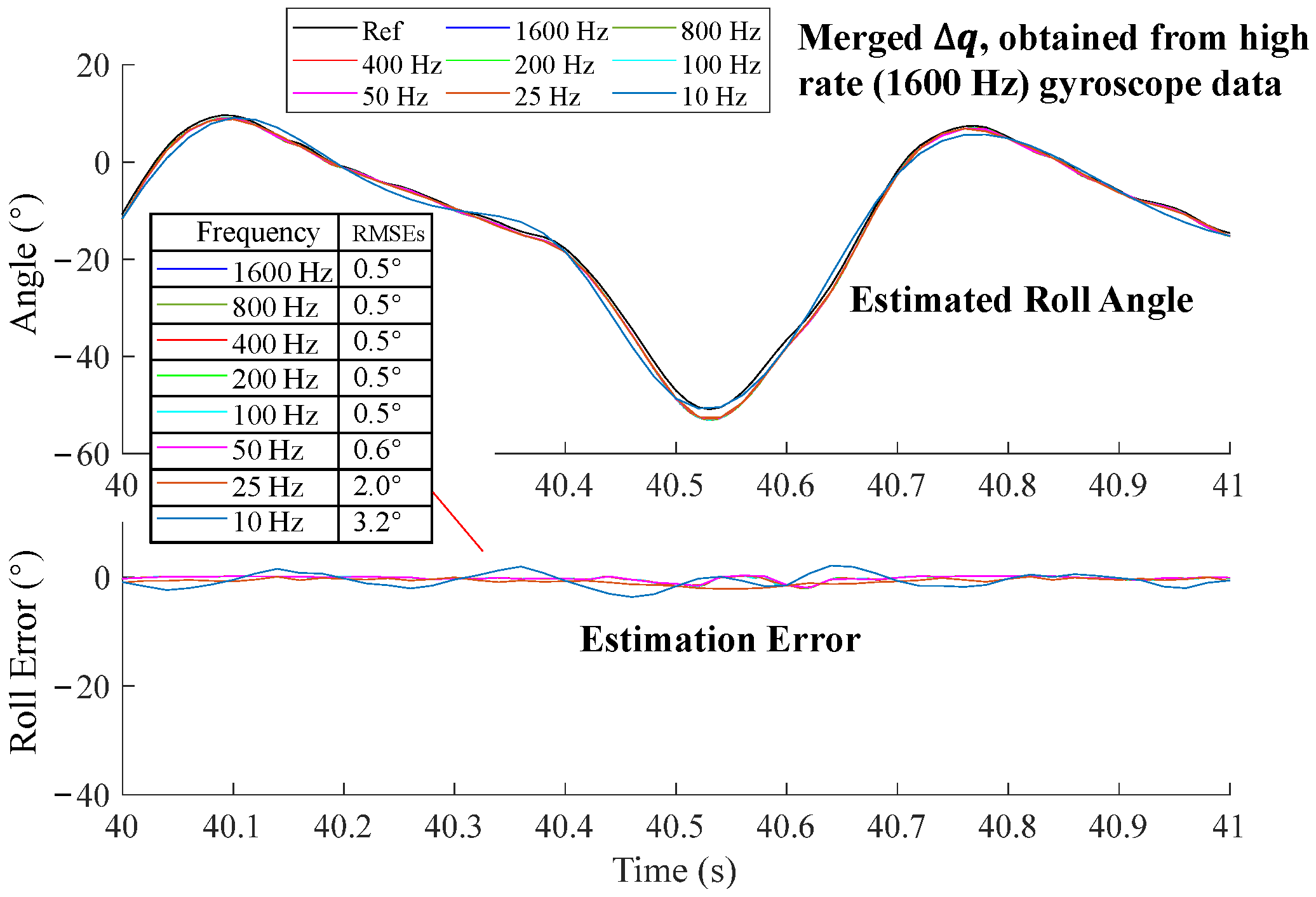
3.3.1. Orientation Estimation During a Short Period (1 s~2 s)
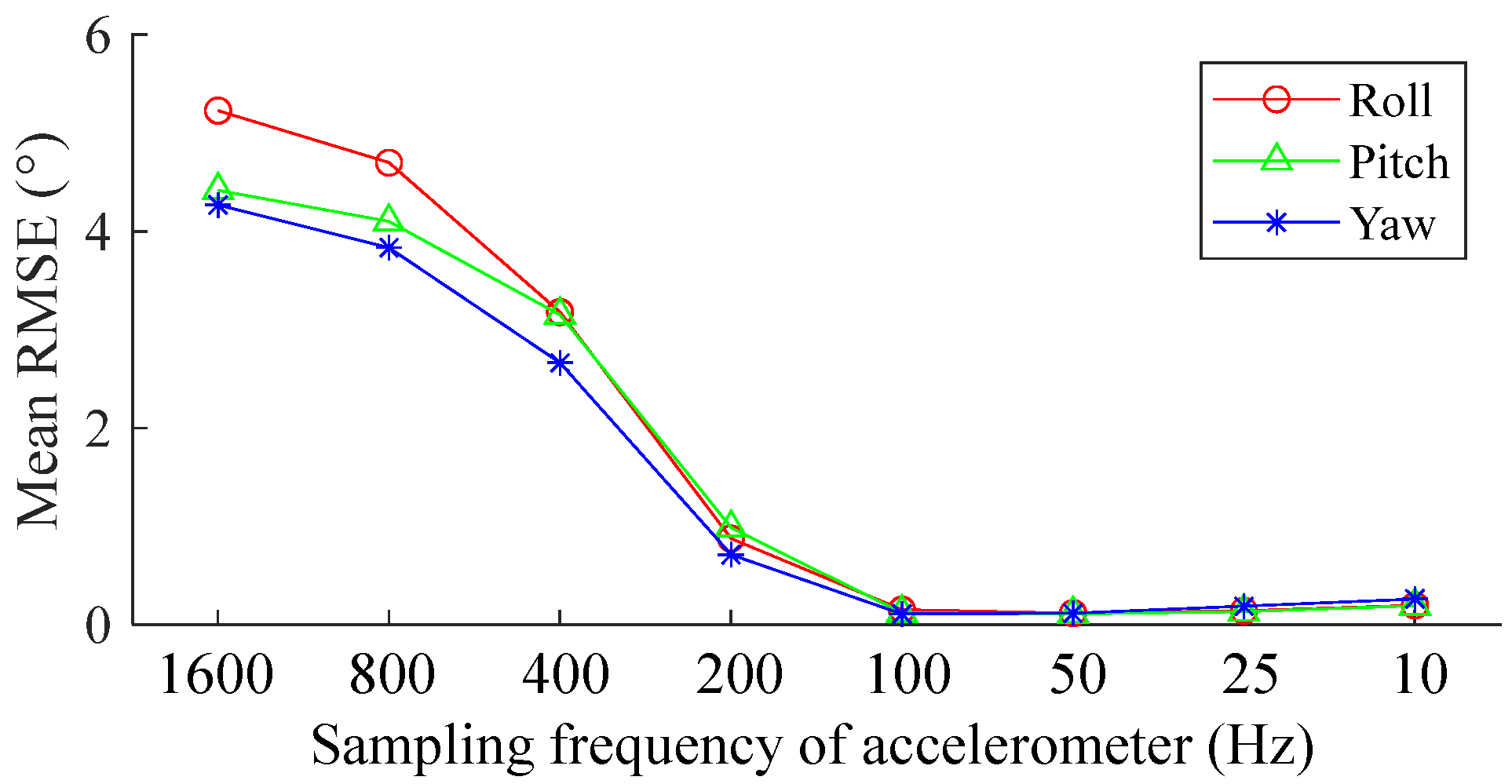
3.3.2. Influence of the Sampling Rate of Accelerometer
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Picerno, P.; Iosa, M.; D’souza, C.; Benedetti, M.G.; Paolucci, S.; Morone, G. Wearable inertial sensors for human movement analysis: A five-year update. Expert Rev. Med. Devices 2021, 18, 79–94. [Google Scholar] [CrossRef]
- Majumder, S.; Deen, M.J. Wearable IMU-Based System for Real-Time Monitoring of Lower-Limb Joints. IEEE Sens. J. 2021, 21, 8267–8275. [Google Scholar] [CrossRef]
- Kong, W.; Sessa, S.; Cosentino, S.; Zecca, M.; Saito, K.; Wang, C.; Imtiaz, U.; Lin, Z.; Bartolomeo, L.; Ishii, H.; et al. Development of a real-time IMU-based motion capture system for gait rehabilitation. In Proceedings of the 2013 IEEE International Conference on Robotics and Biomimetics (Robio), Shenzhen, China, 12–14 December 2013; pp. 2100–2105. [Google Scholar]
- Dahl, K.D.; Dunford, K.M.; Wilson, S.A.; Turnbull, T.L.; Tashman, S. Wearable sensor validation of sports-related movements for the lower extremity and trunk. Med. Eng. Phys. 2020, 84, 144–150. [Google Scholar] [CrossRef] [PubMed]
- Dadashi, F.; Mariani, B.; Rochat, S.; Büla, C.J.; Santos-Eggimann, B.; Aminian, K. Gait and Foot Clearance Parameters Obtained Using Shoe-Worn Inertial Sensors in a Large-Population Sample of Older Adults. Sensors 2014, 14, 443–457. [Google Scholar] [CrossRef]
- Dowling, A.V.; Favre, J.; Andriacchi, T.P. Inertial Sensor-Based Feedback Can Reduce Key Risk Metrics for Anterior Cruciate Ligament Injury During Jump Landings. Am. J. Sports Med. 2012, 40, 1075–1083. [Google Scholar] [CrossRef] [PubMed]
- Pratt, K.A.; Sigward, S.M. Detection of Knee Power Deficits Following Anterior Cruciate Ligament Reconstruction Using Wearable Sensors. J. Orthop. Sports Phys. Ther. 2018, 48, 895–902. [Google Scholar] [CrossRef]
- Yin, Z.-X.; Xu, H.-M. A wearable rehabilitation game controller using IMU sensor. In Proceedings of the 4th IEEE International Conference on Applied System Innovation 2018 (IEEE ICASI 2018), Chiba, Japan, 13–17 April 2018; pp. 1060–1062. [Google Scholar]
- Nazarahari, M.; Noamani, A.; Ahmadian, N.; Rouhani, H. Sensor-to-body calibration procedure for clinical motion analysis of lower limb using magnetic and inertial measurement units. J. Biomech. 2019, 85, 224–229. [Google Scholar] [CrossRef]
- McGrath, T.; Stirling, L. Body-Worn IMU-Based Human Hip and Knee Kinematics Estimation during Treadmill Walking. Sensors 2022, 22, 2544. [Google Scholar] [CrossRef]
- Fan, B.; Li, Q.; Liu, T. Improving the accuracy of wearable sensor orientation using a two-step complementary filter with state machine-based adaptive strategy. Meas. Sci. Technol. 2018, 29, 115104. [Google Scholar]
- Benoussaad, M.; Sijobert, B.; Mombaur, K.; Coste, C.A. Robust Foot Clearance Estimation Based on the Integration of Foot-Mounted IMU Acceleration Data. Sensors 2016, 16, 12. [Google Scholar] [CrossRef]
- Ju, H.; Lee, M.S.; Park, S.Y.; Song, J.W.; Park, C.G. A pedestrian dead-reckoning system that considers the heel-strike and toe-off phases when using a foot-mounted IMU. Meas. Sci. Technol. 2016, 27, 015702. [Google Scholar] [CrossRef]
- Nazarahari, M.; Rouhani, H. 40 years of sensor fusion for orientation tracking via magnetic and inertial measurement units: Methods, lessons learned, and future challenges. Inf. Fusion 2021, 68, 67–84. [Google Scholar] [CrossRef]
- Poddar, S.; Kumar, V.; Kumar, A. A Comprehensive Overview of Inertial Sensor Calibration Techniques. J. Dyn. Syst. Meas. Control. Trans. ASME 2017, 139, 011006. [Google Scholar] [CrossRef]
- Sabatini, A.M. Estimating Three-Dimensional Orientation of Human Body Parts by Inertial/Magnetic Sensing. Sensors 2011, 11, 1489–1525. [Google Scholar] [CrossRef]
- Madgwick, S.O.H.; Harrison, A.J.L.; Vaidyanathan, R. Estimation of IMU and MARG orientation using a gradient descent algorithm. In Proceedings of the 2011 IEEE International Conference on Rehabilitation Robotics, Zurich, Switzerland, 29 June–1 July 2011; p. 5975346. [Google Scholar] [CrossRef]
- Madgwick, S.O.H.; Wilson, S.; Turk, R.; Burridge, J.; Kapatos, C.; Vaidyanathan, R. An Extended Complementary Filter for Full-Body MARG Orientation Estimation. IEEE-ASME Trans. Mechatron. 2020, 25, 2054–2064. [Google Scholar] [CrossRef]
- Nazarahari, M.; Rouhani, H. Sensor fusion algorithms for orientation tracking via magnetic and inertial measurement units: An experimental comparison survey. Inf. Fusion 2021, 76, 8–23. [Google Scholar] [CrossRef]
- Laidig, D.; Seel, T. VQF: Highly accurate IMU orientation estimation with bias estimation and magnetic disturbance rejection. Inf. Fusion 2023, 91, 187–204. [Google Scholar] [CrossRef]
- De Vries, W.H.K.; Veeger, H.E.J.; Baten, C.T.M.; van der Helm, F.C.T. Magnetic distortion in motion labs, implications for validating inertial magnetic sensors. Gait Posture 2009, 29, 535–541. [Google Scholar] [CrossRef]
- Xsens Technologies B.V. Magnetic Field Mapper Documentation; Xsens Technologies B.V.: Enschede, The Netherlands, 2019. [Google Scholar]
- Caruso, M.; Sabatini, A.M.; Laidig, D.; Seel, T.; Knaflitz, M.; Della Croce, U.; Cereatti, A. Analysis of the Accuracy of Ten Algorithms for Orientation Estimation Using Inertial and Magnetic Sensing under Optimal Conditions: One Size Does Not Fit All. Sensors 2021, 21, 2543. [Google Scholar] [CrossRef]
- Romijnders, R.; Warmerdam, E.; Hansen, C.; Welzel, J.; Schmidt, G.; Maetzler, W. Validation of IMU-based gait event detection during curved walking and turning in older adults and Parkinson’s Disease patients. J. Neuroeng. Rehabil. 2021, 18, 28. [Google Scholar] [CrossRef]
- Del Rosario, M.B.; Lovell, N.H.; Redmond, S.J. Quaternion-Based Complementary Filter for Attitude Determination of a Smartphone. IEEE Sens. J. 2016, 16, 6008–6017. [Google Scholar] [CrossRef]
- Riddick, R.; Smits, E.; Faber, G.; Shearwin, C.; Hodges, P.; van den Hoorn, W. Estimation of human spine orientation with inertial measurement units (IMU) at low sampling rate: How low can we go? J. Biomech. 2023, 157, 111726. [Google Scholar] [CrossRef] [PubMed]
- Williamson, J.; Qi, L.; Lu, F.; Mohrman, W.; Li, K.; Dick, R.; Shang, L. Data sensing and analysis: Challenges for wearables. In Proceedings of the 20th Asia and South Pacific Design Automation Conference, Chiba, Japan, 19–22 January 2015; pp. 136–141. [Google Scholar]
- Carratù, M.; Iacono, S.D.; Hoang, M.L.; Pietrosanto, A. Energy characterization of attitude algorithms. In Proceedings of the 2019 IEEE 17th International Conference on Industrial Informatics (INDIN), Helsinki, Finland, 22–25 July 2019; pp. 1585–1590. [Google Scholar]
- Zhu, K.; Li, D.; Li, J.; Shull, P.B. Real-time IMU-Based Kinematics in the Presence of Wireless Data Drop. IEEE J. Biomed. Health Inform. 2024, 28, 6512–6524. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, Z.; Li, J.; Cangelosi, A.; Yang, C. Demonstration Learning and Generalization of Robotic Motor Skills Based on Wearable Motion Tracking Sensors. IEEE Trans. Instrum. Meas. 2023, 72, 2519515. [Google Scholar] [CrossRef]
- Fan, B.; Li, Q.; Liu, T. How Magnetic Disturbance Influences the Attitude and Heading in Magnetic and Inertial Sensor-Based Orientation Estimation. Sensors 2018, 18, 76. [Google Scholar] [CrossRef]
- Ligorio, G.; Sabatini, A.M. A Novel Kalman Filter for Human Motion Tracking With an Inertial-Based Dynamic Inclinometer. IEEE Trans. Biomed. Eng. 2015, 62, 2033–2043. [Google Scholar] [CrossRef]
- Bailey, J.P.; Mata, T.; Mercer, J. Is the Relationship Between Stride Length, Frequency, and Velocity Influenced by Running on a Treadmill or Overground? Int. J. Exerc. Sci. 2017, 10, 1067–1075. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, T.; Koh, M.W.P.; Hu, M.; Murata, H.; Hisano, G.; Ichimura, D.; Hobara, H. Effects of step frequency during running on the magnitude and symmetry of ground reaction forces in individuals with a transfemoral amputation. J. Neuroeng. Rehabil. 2022, 19, 33. [Google Scholar] [CrossRef]
- Laidig, D.; Weygers, I.; Bachhuber, S.; Seel, T. VQF: A Milestone in Accuracy and Versatility of 6D and 9D Inertial Orientation Estimation. In Proceedings of the 2022 25th International Conference on Information Fusion (Fusion 2022), Linköping, Sweden, 4–7 July 2022. [Google Scholar]
- Seel, T.; Ruppin, S. Eliminating the Effect of Magnetic Disturbances on the Inclination Estimates of Inertial Sensors. IFAC Pap. 2017, 50, 8798–8803. [Google Scholar] [CrossRef]
- Guo, S.; Wu, J.; Wang, Z.; Qian, J. Novel MARG-Sensor Orientation Estimation Algorithm Using Fast Kalman Filter. J. Sens. 2017, 2017, 8542153. [Google Scholar] [CrossRef]
- Han, S.; Wang, J. A Novel Method to Integrate IMU and Magnetometers in Attitude and Heading Reference Systems. J. Navig. 2011, 64, 727–738. [Google Scholar] [CrossRef]
- Lee, J.K.; Choi, M.J. Effect of Strapdown Integration Order and Sampling Rate on IMU-Based Attitude Estimation Accuracy. Sensors 2018, 18, 2775. [Google Scholar] [CrossRef]
- Qureshi, U.; Golnaraghi, F. An Algorithm for the In-Field Calibration of a MEMS IMU. IEEE Sens. J. 2017, 17, 7479–7486. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, T.; Wang, M.; Wang, J.; Li, Y. A High-Order Coning Error Compensation Algorithm Under High Rate Maneuvering. IEEE Sens. J. 2020, 20, 208–218. [Google Scholar] [CrossRef]
- Wang, M.; Wu, W.; Wang, J.; Pan, X. High-order attitude compensation in coning and rotation coexisting environment. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1178–1190. [Google Scholar] [CrossRef]
- Pfau, T.; Reilly, P. How low can we go? Influence of sample rate on equine pelvic displacement calculated from inertial sensor data. Equine Vet. J. 2021, 53, 1075–1081. [Google Scholar] [CrossRef]
- Potter, M.V.; Ojeda, L.V.; Perkins, N.C.; Cain, S.M. Effect of IMU Design on IMU-Derived Stride Metrics for Running. Sensors 2019, 19, 2601. [Google Scholar] [CrossRef]




| Algorithm | Parameters |
|---|---|
| FSM [11] Fan et al. | . |
| ECF [18] Madgwick et al. | |
| VQF [20] Laidig and Seel | Parameters are the same as the default values in the open-source code. |
| SEL [36] Seel and Ruppin | tauAcc = 1, tauMag = 3, zeta = 0, accRating = 1. |
| INT [39] | The initial Euler angles were calculated using accelerometer and magnetometer data during the static period. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, B.; Zhang, L.; Cai, S.; Du, M.; Liu, T.; Li, Q.; Shull, P. Influence of Sampling Rate on Wearable IMU Orientation Estimation Accuracy for Human Movement Analysis. Sensors 2025, 25, 1976. https://doi.org/10.3390/s25071976
Fan B, Zhang L, Cai S, Du M, Liu T, Li Q, Shull P. Influence of Sampling Rate on Wearable IMU Orientation Estimation Accuracy for Human Movement Analysis. Sensors. 2025; 25(7):1976. https://doi.org/10.3390/s25071976
Chicago/Turabian StyleFan, Bingfei, Luobin Zhang, Shibo Cai, Mingyu Du, Tao Liu, Qingguo Li, and Peter Shull. 2025. "Influence of Sampling Rate on Wearable IMU Orientation Estimation Accuracy for Human Movement Analysis" Sensors 25, no. 7: 1976. https://doi.org/10.3390/s25071976
APA StyleFan, B., Zhang, L., Cai, S., Du, M., Liu, T., Li, Q., & Shull, P. (2025). Influence of Sampling Rate on Wearable IMU Orientation Estimation Accuracy for Human Movement Analysis. Sensors, 25(7), 1976. https://doi.org/10.3390/s25071976







