Efficient Multi-Sensor Fusion for Cooperative Autonomous Vehicles Leveraging C-ITS Infrastructure and Machine Learning
Abstract
1. Introduction
2. Related Work
3. Proposed Method
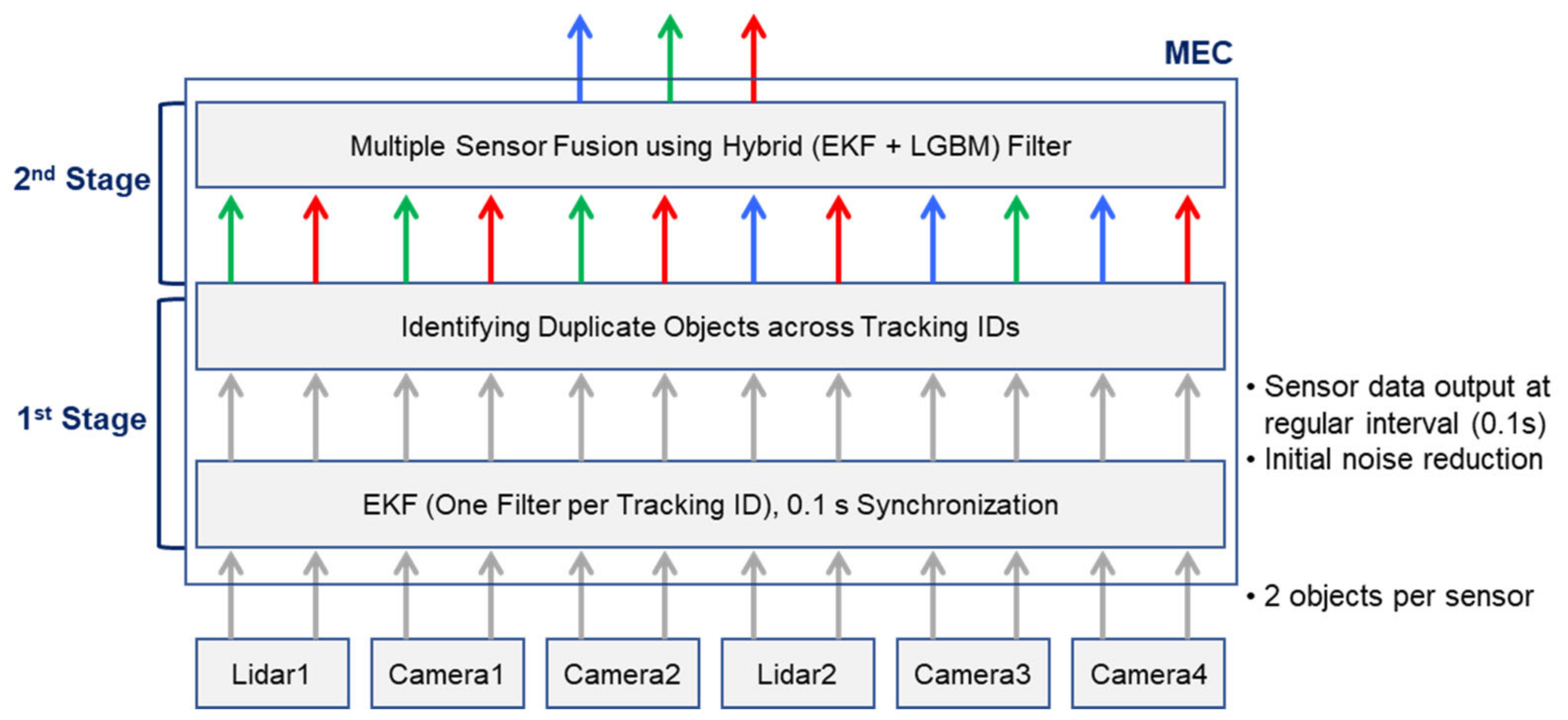
3.1. Overall Architecture and Process of the Two-Stage Fusion Method
3.2. LGBM-Augmented Extended Kalman Filter for Robust Trajectory Estimation
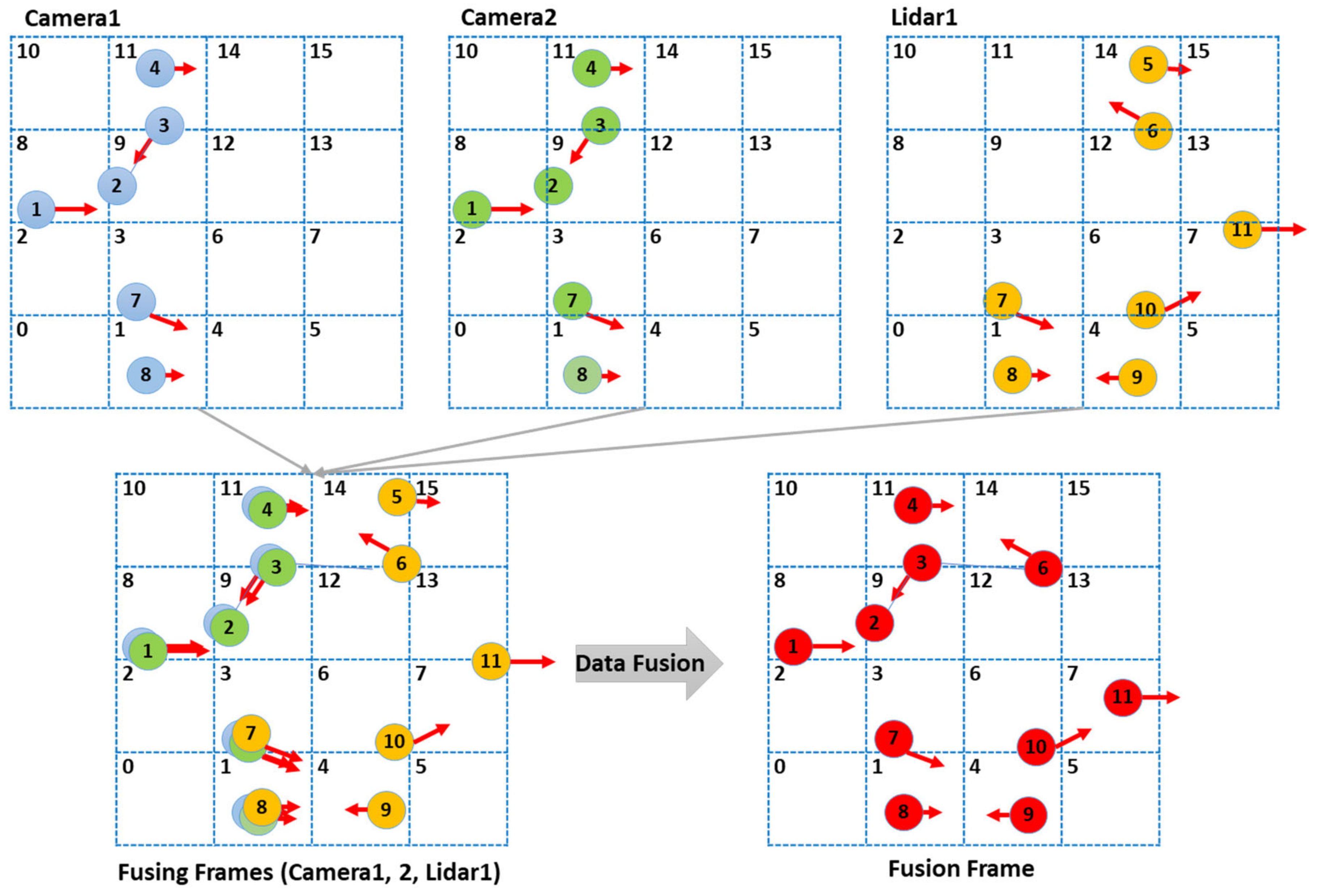
3.3. Grid Indexing for Object Identification
3.4. Data Fusion
4. Performance Evaluation
4.1. Experimental Environments and Methods
4.2. Experiments for Detecting Duplicate Objects
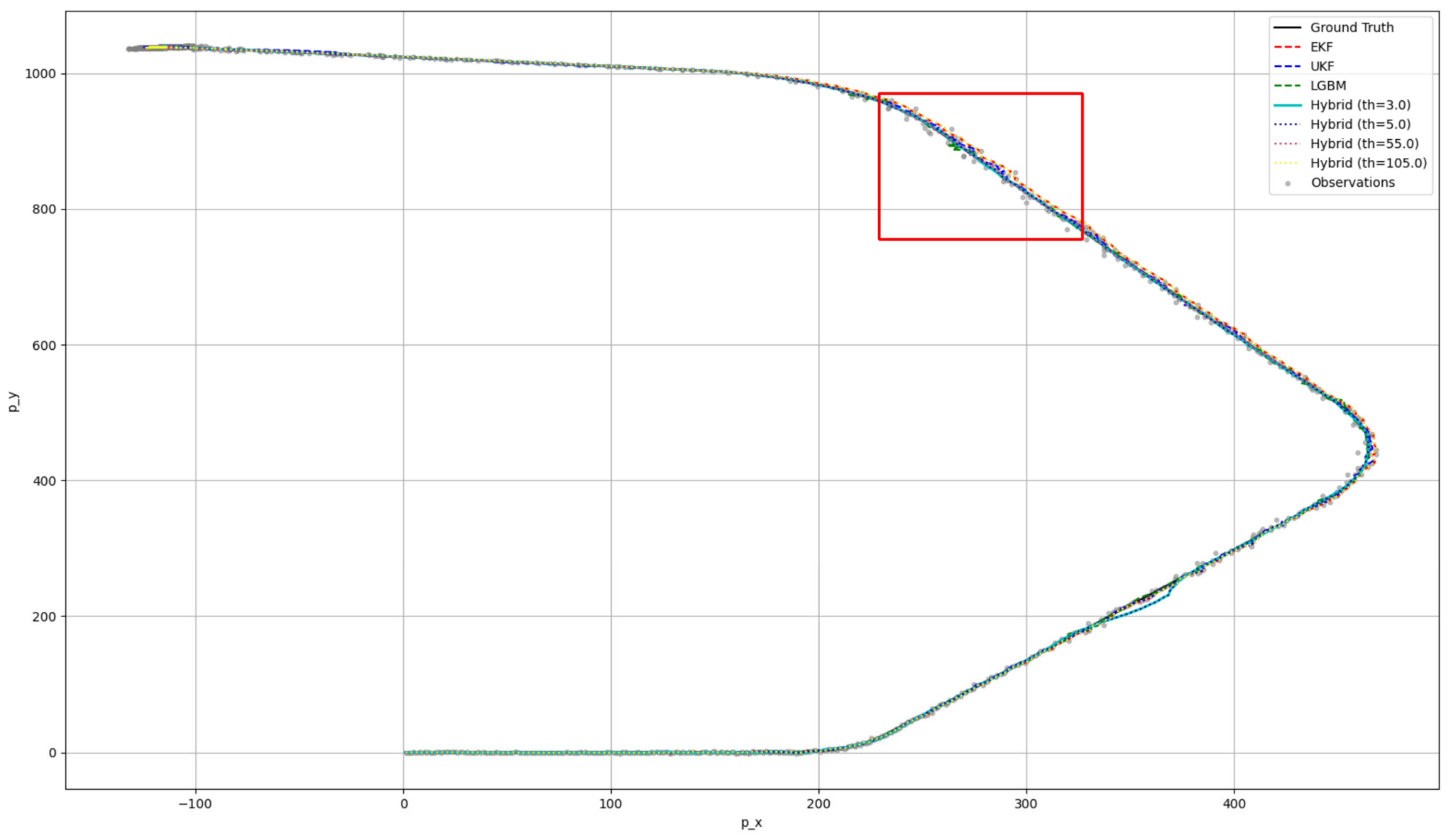
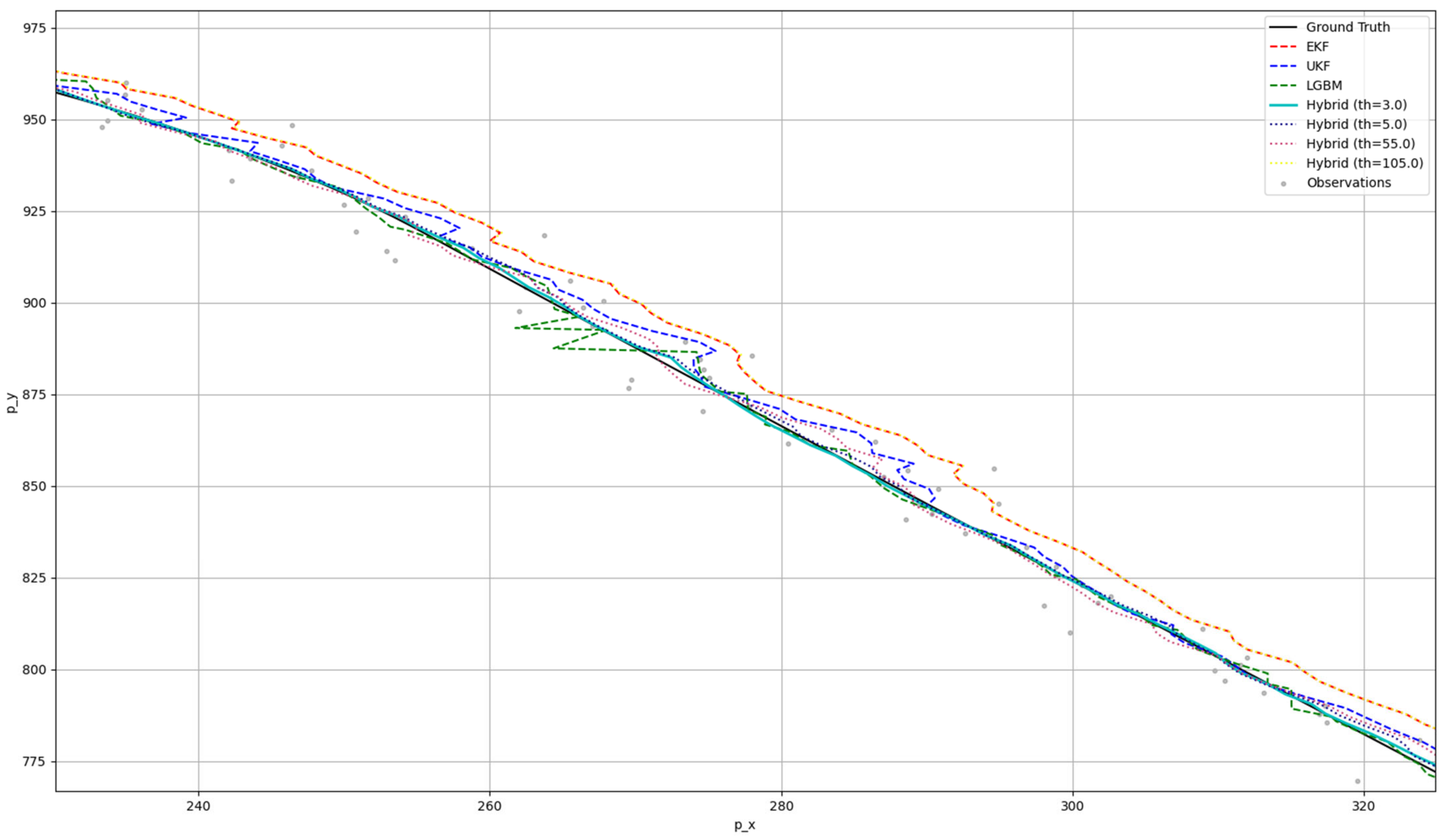
4.3. Data Fusion Experiment Using Synthetic Data and Real Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ji, S.; Mun, C. Design and Performance Analysis of 5G NR V2X-Based Sensor Data Sharing System. J. KIIT 2023, 21, 129–135. [Google Scholar] [CrossRef]
- Yusuf, S.A.; Khan, A.; Souissi, R. Vehicle-to-Everything (V2X) in the Autonomous Vehicles Domain–A Technical Review of Communication, Sensor, and AI Technologies for Road User Safety. Transp. Res. Interdiscip. Perspect. 2024, 23, 100980. [Google Scholar]
- Čvek, K.; Mostarac, M.; Miličević, K. Impact of Different Noise Distributions in the Application of Kalman Filter in Sensor Fusion. In Proceedings of the 2022 International Conference on Smart Systems and Technologies (SST), Osijek, Croatia, 19–21 October 2022; pp. 203–207. [Google Scholar] [CrossRef]
- Xu, Z.; Zhao, S.; Zhang, R. An Efficient Multi-Sensor Fusion and Tracking Protocol in a Vehicle-Road Collaborative System. IET Commun. 2021, 15, 2330–2341. [Google Scholar] [CrossRef]
- Bai, S.; Lai, J.; Lyu, P. A Novel Plug-and-Play Factor Graph Method for Asynchronous Absolute/Relative Measurements Fusion in Multisensor Positioning. IEEE Trans. Ind. Electron. 2023, 70, 940–951. [Google Scholar] [CrossRef]
- Laidouni, M.Z.; Bondžulić, B.; Bujaković, D. Multisensor Image Fusion: Dataset, Methods, and Performance Evaluation. J. Opt. Therm. Eng. 2024, 23, 319–327. [Google Scholar] [CrossRef]
- Tong, J.; Liu, C.; Bao, J. A Novel Ensemble Learning-Based Multisensor Information Fusion Method for Rolling Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2023, 72, 9501712. [Google Scholar] [CrossRef]
- Yuan, Y.; Yu, F.; Zong, H. Multisensor Integrated Autonomous Navigation Based on Intelligent Information Fusion. J. Spacecr. Rockets 2024, 61, 702–713. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; Technical Report 95-041; University of North Carolina: Chapel Hill, NC, USA, 2001. [Google Scholar]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Advances in Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2017; Volume 30, pp. 3146–3154. [Google Scholar]
- Liu, F.; Liu, Y.; Sun, X.; Sang, H. A New Multi-Sensor Hierarchical Data Fusion Algorithm Based on Unscented Kalman Filter for the Attitude Observation of the Wave Glider. Appl. Ocean Res. 2021, 109, 102562. [Google Scholar] [CrossRef]
- Tian, K.; Radovnikovich, M.; Cheok, K. Comparing EKF, UKF, and PF Performance for Autonomous Vehicle Multi-Sensor Fusion and Tracking in Highway Scenario. In Proceedings of the 2022 IEEE International Systems Conference (SysCon), Montréal, QC, Canada, 25–28 April 2022; pp. 1–6. [Google Scholar]
- Wang, Y.; Xie, C.; Liu, Y.; Zhu, J.; Qin, J. A Multi-Sensor Fusion Underwater Localization Method Based on Unscented Kalman Filter on Manifolds. Sensors 2024, 24, 6299. [Google Scholar] [CrossRef] [PubMed]
- Ye, L. An Efficient Indexing Maintenance Method for Grouping Moving Objects with Grid. Procedia Environ. Sci. 2011, 11, 486–492. [Google Scholar] [CrossRef]
- Li, C.; Feng, Y. Algorithm for Analyzing N-Dimensional Hilbert Curve. In Proceedings of the 2005 International Conference on Computational Science and Its Applications, Singapore, 9–12 May 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 657–662. [Google Scholar] [CrossRef]




| Symbols | Definition |
|---|---|
| State vector at time k (e.g., position and velocity). | |
| Control input (e.g., accelerations, wheel commands). | |
| State transition matrix. | |
| Control–input matrix. | |
| Process noise covariance. | |
| Observation model mapping xk to the measurement space. | |
| Measurement noise covariance. | |
| Sensor measurement at time k. | |
| Error covariance of the state estimate at time k. |
| Category | 500 Objects Processing Time (ms) | ||
|---|---|---|---|
| 1 Thread | 4 Threads | 8 Threads | |
| Proposed method | 0.03 | 0.02 | 0.007 |
| Sequential comparison | 59.46 | N/A | N/A |
| Noise Scale | Error Mean (m) | Error Std (m) |
|---|---|---|
| 0.5 | 1.779 | 1.529 |
| 1 | 3.559 | 3.058 |
| 2 | 7.118 | 6.116 |
| 3 | 10.676 | 9.174 |
| Noise Scale | Best Parameters | |
|---|---|---|
| 0.5 | EKF UKF LGBM Hybrid | q_scale = 2.0, r_scale = 0.1 q_scale = 0.1, r_scale = 0.1 learning_rate = 0.1, max_depth = 7 alpha = 0.5, beta = 1.0 |
| 1 | EKF UKF LGBM Hybrid | q_scale = 2.0, r_scale = 0.1 q_scale = 0.1, r_scale = 0.5 learning_rate = 0.1, max_depth = 7 alpha = 1.5, beta = 1.0 |
| 2 | EKF UKF LGBM Hybrid | q_scale = 2.0, r_scale = 0.1 q_scale = 0.1, r_scale = 0.5 learning_rate = 0.1, max_depth = 7 alpha = 1.5, beta = 0.5 |
| 3 | EKF UKF LGBM Hybrid | q_scale = 2.0, r_scale = 0.1 q_scale = 0.1, r_scale = 1.0 learning_rate = 0.1, max_depth = 7 alpha = 1.5, beta = 1.0 |
| Noise Scale | Approach | RMSE (m) | MSE (m) | MAE (m) | Avg Time per Step (ms) |
|---|---|---|---|---|---|
| 0.5 | ekf | 2.541 | 6.457 | 1.838 | 0.00004 |
| ukf | 0.662 | 0.438 | 0.38 | 0.0002 | |
| lgbm | 0.59 | 0.347 | 0.158 | 0.004 | |
| hybrid (th = 5.0) | 0.602 | 0.362 | 0.36 | 0.0002 | |
| 1.0 | ekf | 2.688 | 7.227 | 1.857 | 0.00004 |
| ukf | 1.513 | 2.29 | 0.81 | 0.0002 | |
| lgbm | 0.535 | 0.286 | 0.148 | 0.003 | |
| hybrid (th = 35.0) | 1.101 | 1.213 | 0.682 | 0.0002 | |
| hybrid (th = 45.0) | 1.159 | 1.342 | 0.705 | 0.0002 | |
| hybrid (th = 55.0) | 1.272 | 1.617 | 0.761 | 0.0001 | |
| hybrid (th = 65.0) | 1.417 | 2.006 | 0.838 | 0.0001 | |
| 2.0 | ekf | 3.219 | 10.363 | 2.083 | 0.0001 |
| ukf | 2.455 | 6.029 | 1.349 | 0.0005 | |
| lgbm | 0.417 | 0.174 | 0.129 | 0.004 | |
| hybrid (th = 95.0) | 2.08 | 4.33 | 1.293 | 0.0003 | |
| hybrid (th = 105.0) | 2.119 | 4.491 | 1.314 | 0.0002 | |
| hybrid (th = 115.0) | 2.114 | 4.469 | 1.321 | 0.0002 | |
| hybrid (th = 125.0) | 2.19 | 4.795 | 1.368 | 0.0002 | |
| hybrid (th = 135.0) | 2.245 | 5.04 | 1.401 | 0.0002 | |
| hybrid (th = 145.0) | 2.369 | 5.614 | 1.476 | 0.0002 | |
| 3.0 | ekf | 4.0 | 16.003 | 2.543 | 0.00005 |
| ukf | 3.873 | 14.999 | 2.123 | 0.0002 | |
| lgbm | 0.394 | 0.156 | 0.122 | 0.004 | |
| hybrid (th = 325.0) | 3.364 | 11.32 | 2.112 | 0.0002 | |
| hybrid (th = 345.0) | 3.384 | 11.453 | 2.123 | 0.0002 | |
| hybrid (th = 365.0) | 3.38 | 11.424 | 2.119 | 0.0001 | |
| hybrid (th = 385.0) | 3.409 | 11.623 | 2.126 | 0.0001 | |
| hybrid (th = 405.0) | 3.467 | 12.02 | 2.167 | 0.0001 |
| Approach | RMSE (m) | MSE (m) | MAE (m) |
|---|---|---|---|
| Original Observation Values | 2.107 | 44.397 | 0.985 |
| Hybrid (th = 20.0) | 1.364 | 18.607 | 0.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwak, J.; Jeon, H.; Song, S. Efficient Multi-Sensor Fusion for Cooperative Autonomous Vehicles Leveraging C-ITS Infrastructure and Machine Learning. Sensors 2025, 25, 1975. https://doi.org/10.3390/s25071975
Kwak J, Jeon H, Song S. Efficient Multi-Sensor Fusion for Cooperative Autonomous Vehicles Leveraging C-ITS Infrastructure and Machine Learning. Sensors. 2025; 25(7):1975. https://doi.org/10.3390/s25071975
Chicago/Turabian StyleKwak, Jiwon, Hayoung Jeon, and Seokil Song. 2025. "Efficient Multi-Sensor Fusion for Cooperative Autonomous Vehicles Leveraging C-ITS Infrastructure and Machine Learning" Sensors 25, no. 7: 1975. https://doi.org/10.3390/s25071975
APA StyleKwak, J., Jeon, H., & Song, S. (2025). Efficient Multi-Sensor Fusion for Cooperative Autonomous Vehicles Leveraging C-ITS Infrastructure and Machine Learning. Sensors, 25(7), 1975. https://doi.org/10.3390/s25071975






