Temporal Features-Fused Vision Retentive Network for Echocardiography Image Segmentation
Abstract
1. Introduction
- (1)
- We propose the Temporal Feature Fusion Module (TFFM) based on temporal–channel self-attention. It fuses the temporal and channel dimensions and applies self-attention to the fused dimension to capture the inter-frame correlations in echocardiography images. Additionally, we introduce a channel aggregation module that extracts complementary interaction information between channels to reallocate features of the fused channels. This module summarizes the features of multiple frames and enhances the features of ambiguous regions in key frames caused by noise and artifacts.
- (2)
- We introduce the Vision RetNet as the encoder in echocardiography segmentation. Vision RetNet constructs a spatial decay matrix by introducing explicit spatial prior information through the Manhattan distance, extending the retention mechanism used for one-dimensional sequences to two-dimensional images. Therefore, Vision RetNet can learn spatial correlations in the image effectively.
- (3)
- We propose an end-to-end video sequence segmentation model that combines the advantages of the two modules mentioned above, achieving competitive performance compared to existing models on the EchoNet-Dynamic dataset and the CAMUS dataset.
2. Related Work
2.1. Semantic Segmentation in Cardiac Images
2.2. Medical Image Segmentation with Inter-Frame Correlations
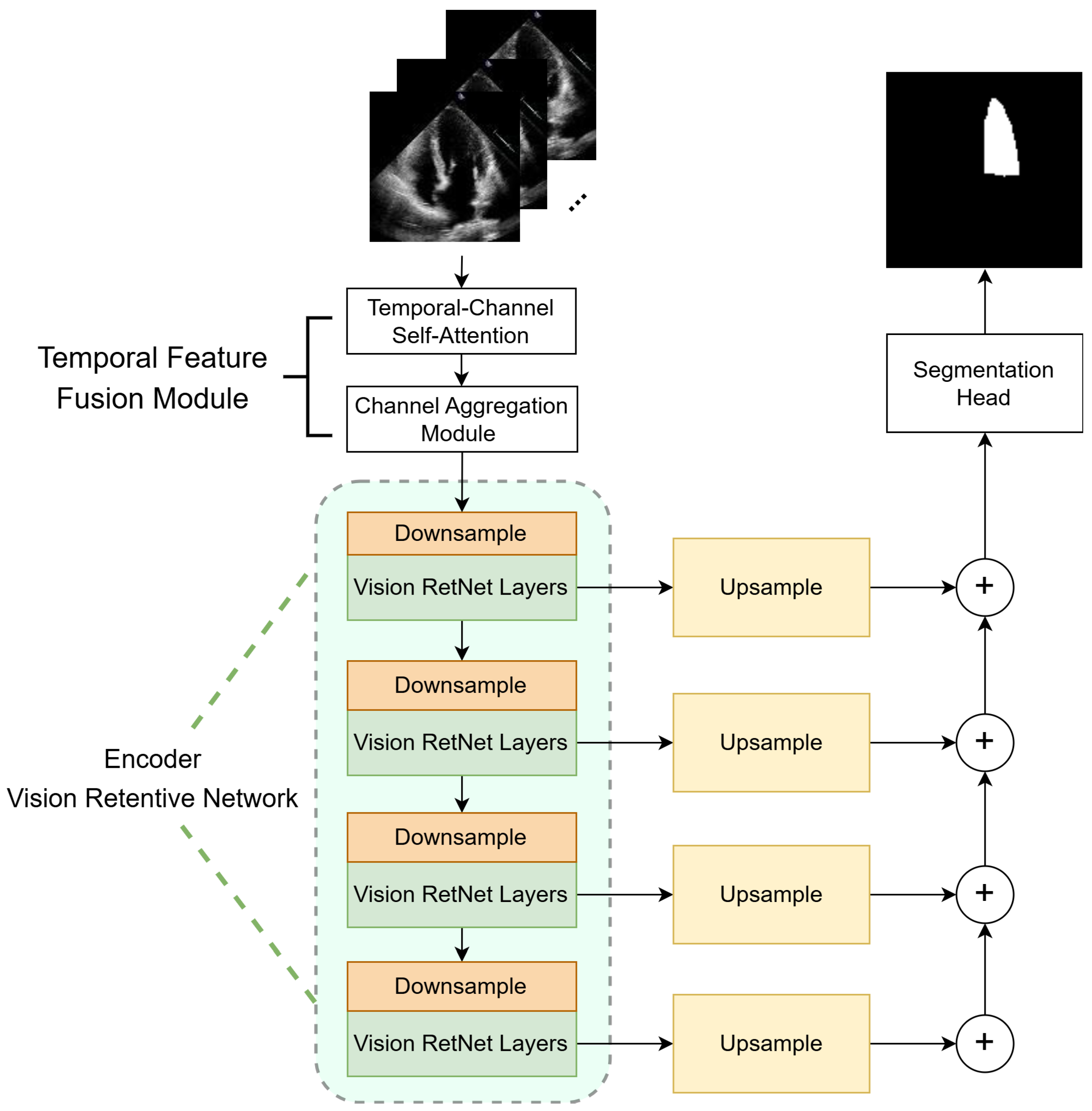
3. Methods
3.1. Temporal Feature Fusion Module
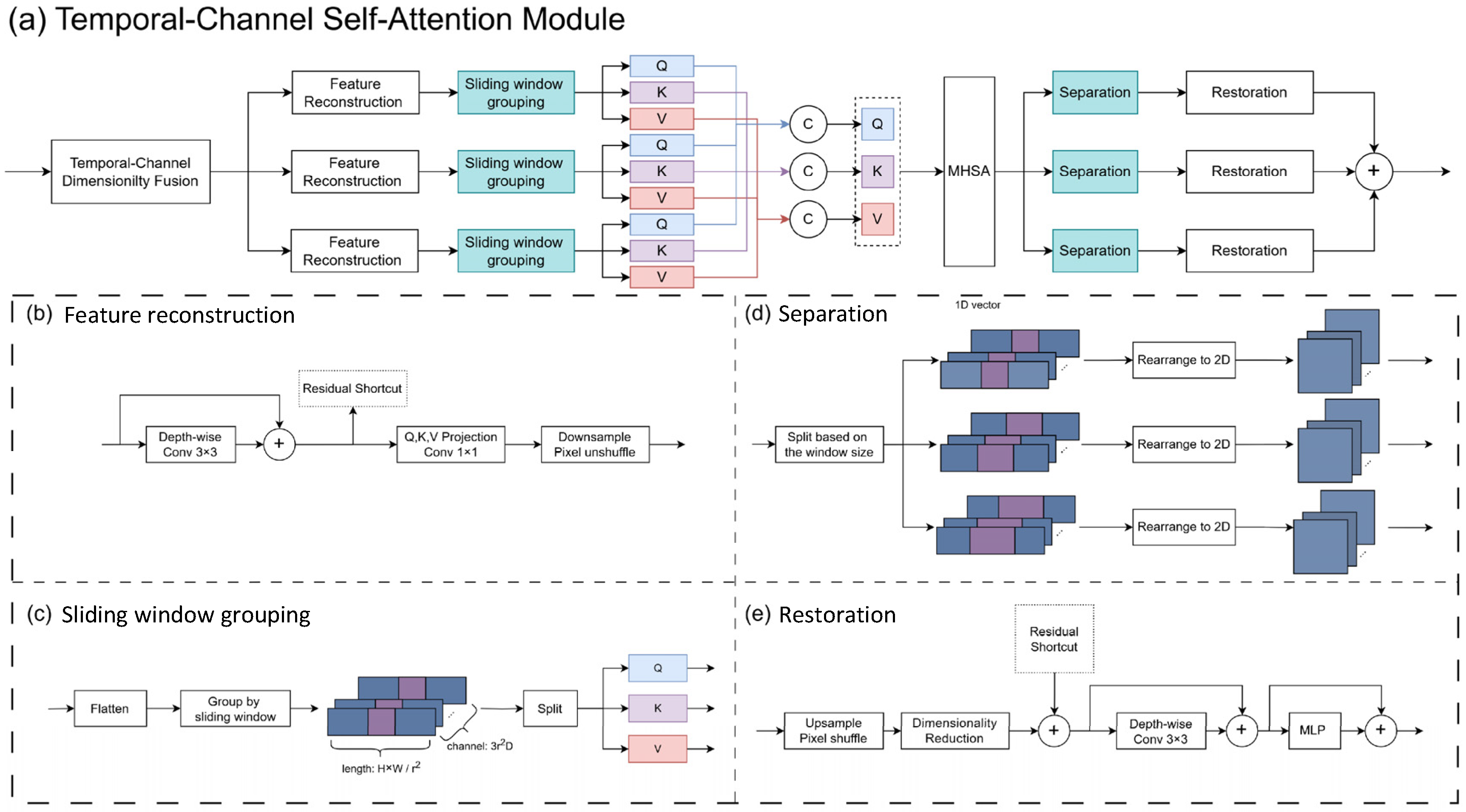
3.1.1. Temporal–Channel Self-Attention (TCSA)
3.1.2. Channel Aggregation Module (CA)
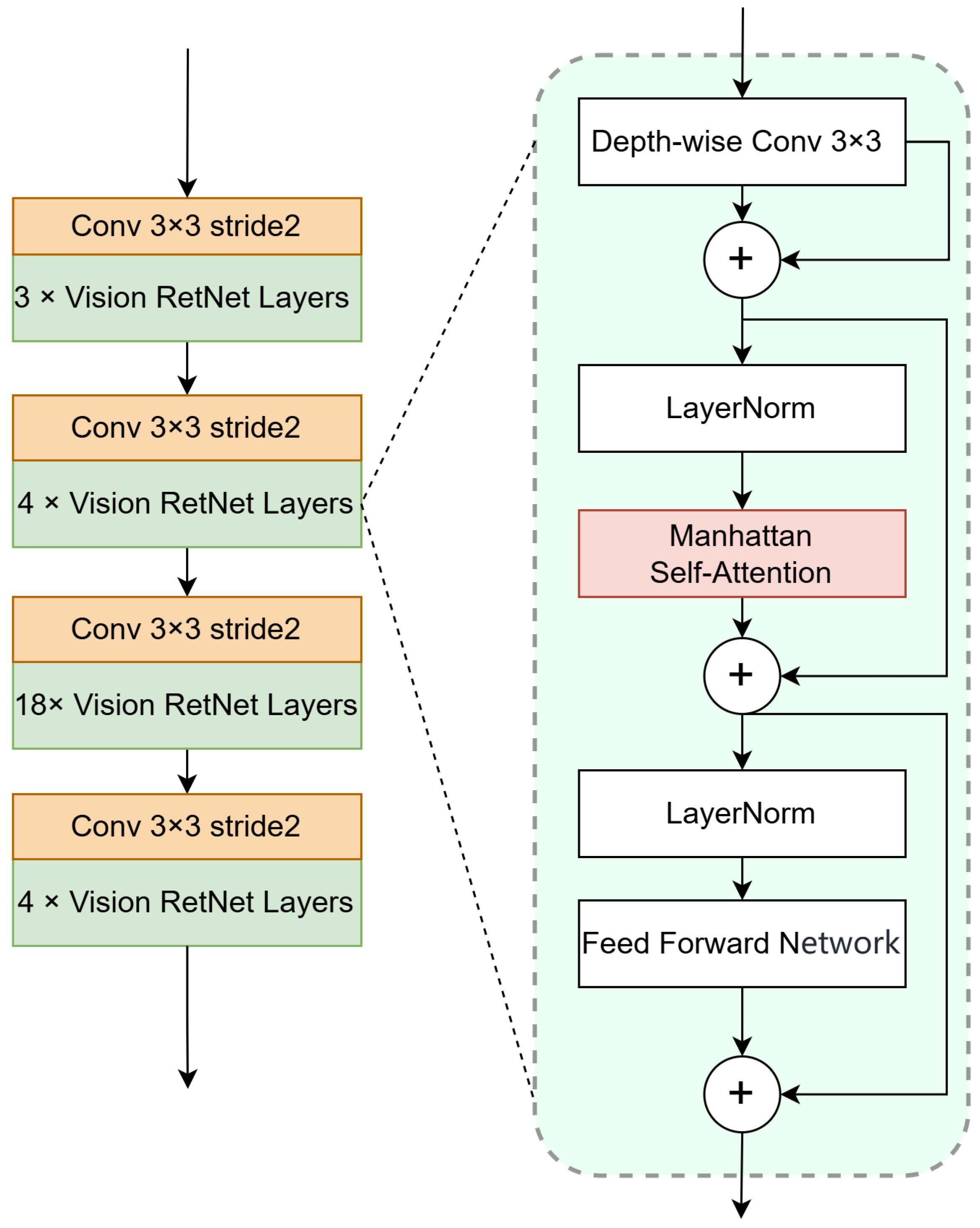
3.2. Vision Retentive Network Encoder
3.2.1. Manhattan Self-Attention
3.2.2. Encoder Architecture
3.2.3. Computational Complexity Analysis
4. Experiments
4.1. Dataset
4.2. Evaluation Metrics
4.3. Implementation Details
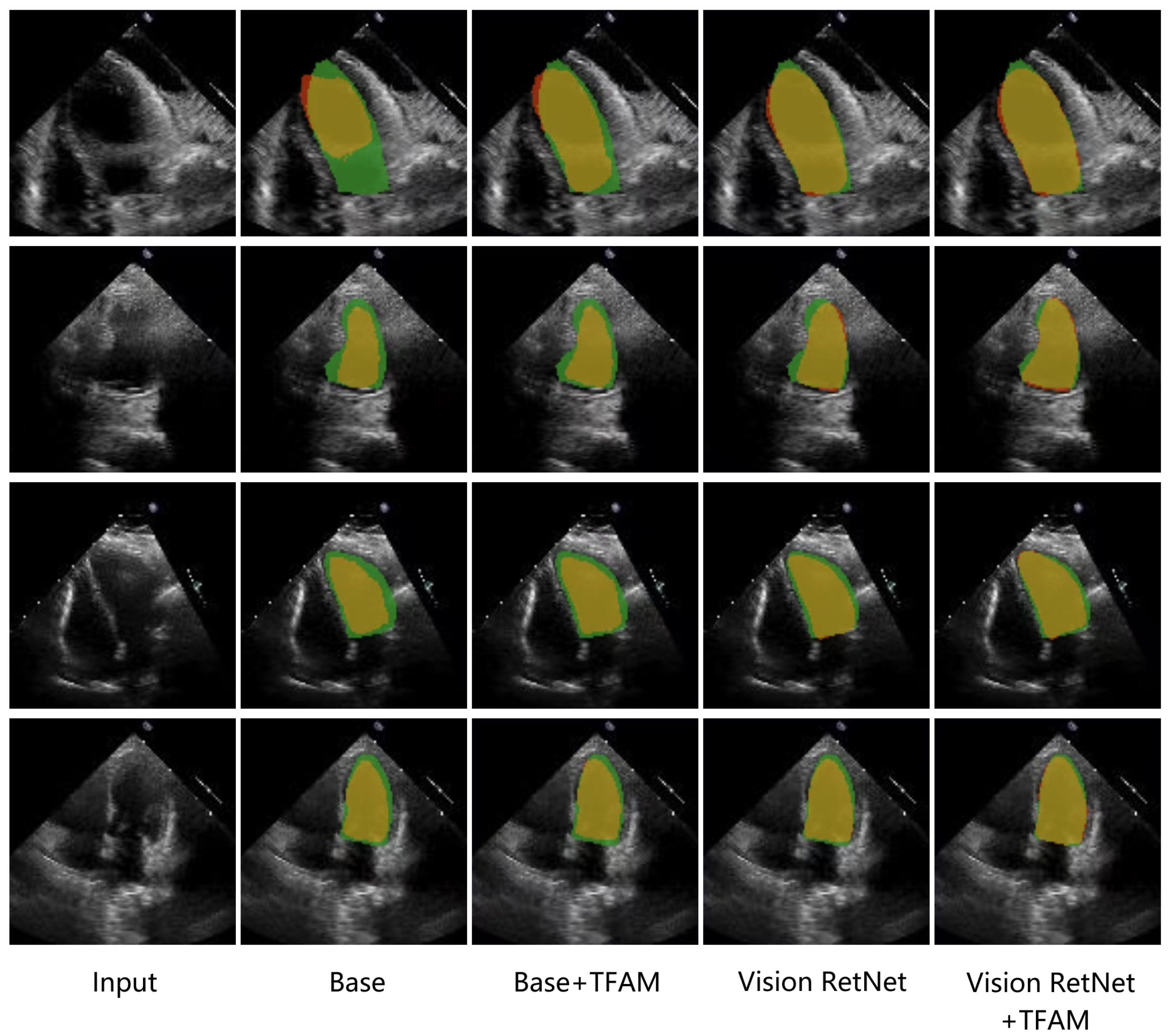
4.4. Experimental Results
4.4.1. Comparison with Other Methods
4.4.2. Ablation Study
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CVD | Cardiovascular Disease |
| LV | Left Ventricle |
| ED | End-Diastole |
| ES | End-Systole |
| CNN | Convolutional Neural Network |
| CT | Computed Tomography |
| MRI | Magnetic Resonance Imaging |
| RetNet | Retentive Network |
| FPN | Feature Pyramid Network |
| LSTM | Long Short-Term-Memory |
| TFFM | Temporal Feature Fusion Module |
| Conv | Convolution |
| DWConv | Depth-Wise Convolution |
| TCSA | Temporal–Channel Self-Attention |
| CA | Channel Aggregation |
| MaSA | Manhattan Self-Attention |
| 2D | 2-Dimensional |
| 1D | 1-Dimensional |
| DSC | Dice Similarity Coefficient |
| HD95 | The 95th percentile of the Hausdorff Distance |
| GCN | Graph Convolution Network |
Appendix A. Python Environment of Our Method
| Python Packages | Versions |
|---|---|
| Python | 3.8.19 |
| albumentations | 1.3.0 |
| eniops | 0.7.0 |
| Medpy | 0.5.2 |
| monai | 1.4.0 |
| mmcv | 2.2.0 |
| mmengine | 0.10.2 |
| mmsegmentation | 1.2.2 |
| numpy | 1.24.4 |
| pandas | 2.0.3 |
| pillow | 10.4.0 |
| scikit-image | 0.23.2 |
| scikit-learn | 1.5.0 |
| scipy | 1.13.1 |
| SimpleITK | 2.3.0 |
| torch | 2.4.0 |
| torchvision | 0.19.0 |
References
- Di Cesare, M.; Perel, P.; Taylor, S.; Kabudula, C.; Bixby, H.; Gaziano, T.A.; McGhie, D.V.; Mwangi, J.; Pervan, B.; Narula, J.; et al. The heart of the world. Glob. Heart 2024, 19, 11. [Google Scholar] [CrossRef] [PubMed]
- Silva, J.F.; Silva, J.M.; Guerra, A.; Matos, S.; Costa, C. Ejection Fraction Classification in Transthoracic Echocardiography Using a Deep Learning Approach. In Proceedings of the 2018 IEEE 31st International Symposium on Computer-Based Medical Systems (CBMS), Karlstad, Sweden, 18–21 June 2018; pp. 123–128. [Google Scholar] [CrossRef]
- Norris, R.M.; White, H.D.; Cross, D.B.; Wild, C.J.; Whitlock, R.M. Prognosis after recovery from myocardial infarction: The relative importance of cardiac dilatation and coronary stenoses. Eur. Heart J. 1992, 13, 1611–1618. [Google Scholar] [CrossRef]
- Cui, R.; He, W.; Huang, J.; Zhang, J.; Zhang, H.; Liang, S.; He, Y.; Liu, Z.; Gao, S.; He, Y.; et al. Spatial temporal graph convolution network for the analysis of regional wall motion in left ventricular opacification echocardiography. Biomed. Signal Process. Control 2025, 103, 107391. [Google Scholar] [CrossRef]
- Yao, G.H.; Deng, Y.; Liu, Y.; Xu, M.J.; Zhang, C.; Deng, Y.B.; Ren, W.D.; Li, Z.A.; Tang, H.; Zhang, Q.B.; et al. Echocardiographic measurements in normal Chinese adults focusing on cardiac chambers and great arteries: A prospective, nationwide, and multicenter study. J. Am. Soc. Echocardiogr. 2015, 28, 570–579. [Google Scholar] [CrossRef]
- Frangi, A.F.; Niessen, W.J.; Viergever, M.A. Three-dimensional modeling for functional analysis of cardiac images, a review. IEEE Trans. Med Imaging 2001, 20, 2–5. [Google Scholar] [CrossRef] [PubMed]
- Huang, Q.; Sun, J.; Ding, H.; Wang, X.; Wang, G. Robust liver vessel extraction using 3D U-Net with variant dice loss function. Comput. Biol. Med. 2018, 101, 153–162. [Google Scholar] [CrossRef]
- Chen, W.; Liu, B.; Peng, S.; Sun, J.; Qiao, X. S3D-UNet: Separable 3D U-Net for brain tumor segmentation. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries, Proceedings of the 4th International Workshop, BrainLes 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 16 September 2018; Revised Selected Papers, Part II 4; Springer: Berlin/Heidelberg, Germany, 2019; pp. 358–368. [Google Scholar]
- Abraham, N.; Khan, N.M. A novel focal tversky loss function with improved attention u-net for lesion segmentation. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 683–687. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015; Proceedings, Part III 18. Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Vaswani, A. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 1. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-unet: Unet-like pure transformer for medical image segmentation. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 205–218. [Google Scholar]
- Gao, Y.; Zhou, M.; Metaxas, D.N. UTNet: A hybrid transformer architecture for medical image segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, 27 September–1 October 2021; Proceedings, Part III 24. Springer: Berlin/Heidelberg, Germany, 2021; pp. 61–71. [Google Scholar]
- Hatamizadeh, A.; Tang, Y.; Nath, V.; Yang, D.; Myronenko, A.; Landman, B.; Roth, H.R.; Xu, D. Unetr: Transformers for 3d medical image segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 3–8 January 2022; pp. 574–584. [Google Scholar]
- Cui, R.; Liang, S.; Zhao, W.; Liu, Z.; Lin, Z.; He, W.; He, Y.; Du, C.; Peng, J.; Huang, H. A Shape-Consistent Deep-Learning Segmentation Architecture for Low-Quality and High-Interference Myocardial Contrast Echocardiography. Ultrasound Med. Biol. 2024, 50, 1602–1610. [Google Scholar] [CrossRef]
- Sun, Y.; Dong, L.; Huang, S.; Ma, S.; Xia, Y.; Xue, J.; Wang, J.; Wei, F. Retentive network: A successor to transformer for large language models. arXiv 2023, arXiv:2307.08621. [Google Scholar]
- Fan, Q.; Huang, H.; Chen, M.; Liu, H.; He, R. Rmt: Retentive networks meet vision transformers. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 11–15 June 2024; pp. 5641–5651. [Google Scholar]
- Leclerc, S.; Smistad, E.; Pedrosa, J.; Østvik, A.; Cervenansky, F.; Espinosa, F.; Espeland, T.; Berg, E.A.R.; Jodoin, P.M.; Grenier, T.; et al. Deep learning for segmentation using an open large-scale dataset in 2D echocardiography. IEEE Trans. Med. Imaging 2019, 38, 2198–2210. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: 4th International Workshop, DLMIA 2018, and 8th International Workshop, ML-CDS 2018, Held in Conjunction with MICCAI 2018, Granada, Spain, 20 September 2018; Proceedings 4. Springer: Berlin/Heidelberg, Germany, 2018; pp. 3–11. [Google Scholar]
- Leclerc, S.; Smistad, E.; Østvik, A.; Cervenansky, F.; Espinosa, F.; Espeland, T.; Berg, E.A.R.; Belhamissi, M.; Israilov, S.; Grenier, T.; et al. LU-Net: A multistage attention network to improve the robustness of segmentation of left ventricular structures in 2-D echocardiography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2020, 67, 2519–2530. [Google Scholar] [CrossRef] [PubMed]
- Moradi, S.; Oghli, M.G.; Alizadehasl, A.; Shiri, I.; Oveisi, N.; Oveisi, M.; Maleki, M.; Dhooge, J. MFP-Unet: A novel deep learning based approach for left ventricle segmentation in echocardiography. Phys. Medica 2019, 67, 58–69. [Google Scholar] [CrossRef]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Ali, Y.; Janabi-Sharifi, F.; Beheshti, S. Echocardiographic image segmentation using deep Res-U network. Biomed. Signal Process. Control 2021, 64, 102248. [Google Scholar] [CrossRef]
- Zhang, H.; Cai, Z. ConvNextUNet: A small-region attentioned model for cardiac MRI segmentation. Comput. Biol. Med. 2024, 177, 108592. [Google Scholar] [CrossRef]
- Ouyang, D.; He, B.; Ghorbani, A.; Lungren, M.P.; Ashley, E.A.; Liang, D.H.; Zou, J.Y. Echonet-dynamic: A large new cardiac motion video data resource for medical machine learning. In Proceedings of the NeurIPS ML4H Workshop, Vancouver, BC, Canada, 14 December 2019; pp. 1–11. [Google Scholar]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Liu, F.; Wang, K.; Liu, D.; Yang, X.; Tian, J. Deep pyramid local attention neural network for cardiac structure segmentation in two-dimensional echocardiography. Med. Image Anal. 2021, 67, 101873. [Google Scholar] [CrossRef]
- Deng, K.; Meng, Y.; Gao, D.; Bridge, J.; Shen, Y.; Lip, G.; Zhao, Y.; Zheng, Y. Transbridge: A lightweight transformer for left ventricle segmentation in echocardiography. In Proceedings of the Simplifying Medical Ultrasound: Second International Workshop, ASMUS 2021, Held in Conjunction with MICCAI 2021, Strasbourg, France, 27 September 2021; Proceedings 2. Springer: Berlin/Heidelberg, Germany, 2021; pp. 63–72. [Google Scholar]
- Thomas, S.; Gilbert, A.; Ben-Yosef, G. Light-weight spatio-temporal graphs for segmentation and ejection fraction prediction in cardiac ultrasound. In Proceedings of the MICCAI, Singapore, 18–22 September 2022. [Google Scholar]
- Zeng, Y.; Tsui, P.H.; Pang, K.; Bin, G.; Li, J.; Lv, K.; Wu, X.; Wu, S.; Zhou, Z. MAEF-Net: Multi-attention efficient feature fusion network for left ventricular segmentation and quantitative analysis in two-dimensional echocardiography. Ultrasonics 2023, 127, 106855. [Google Scholar] [CrossRef]
- Chen, E.; Cai, Z.; Lai, J.h. Weakly supervised semantic segmentation of echocardiography videos via multi-level features selection. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Shenzhen, China, 14–17 October 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 388–400. [Google Scholar]
- Ahn, S.S.; Ta, K.; Thorn, S.; Langdon, J.; Sinusas, A.J.; Duncan, J.S. Multi-frame attention network for left ventricle segmentation in 3D echocardiography. In Proceedings of the Medical Image Computing and Computer Assisted Intervention–MICCAI 2021: 24th International Conference, Strasbourg, France, 27 September–1 October 2021; Proceedings, Part I 24. Springer: Berlin/Heidelberg, Germany, 2021; pp. 348–357. [Google Scholar]
- Yuan, R.; Xu, J.; Li, X.; Zhang, Y.; Feng, R.; Zhang, X.; Zhang, T.; Gao, S. Medseq: Semantic segmentation for medical image sequences. In Proceedings of the 2022 IEEE International Conference on Bioinformatics and Biomedicine (BIBM), Las Vegas, NV, USA, 6–8 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1356–1361. [Google Scholar]
- Zeng, C.; Yang, X.; Smithard, D.; Mirmehdi, M.; Gambaruto, A.M.; Burghardt, T. Video-SwinUNet: Spatio-temporal Deep Learning Framework for VFSS Instance Segmentation. In Proceedings of the 2023 IEEE International Conference on Image Processing (ICIP), Kuala Lumpur, Malaysia, 8–11 October 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 2470–2474. [Google Scholar]
- Li, M.; Zeng, D.; Xie, Q.; Xu, R.; Wang, Y.; Ma, D.; Shi, Y.; Xu, X.; Huang, M.; Fei, H. A deep learning approach with temporal consistency for automatic myocardial segmentation of quantitative myocardial contrast echocardiography. Int. J. Cardiovasc. Imaging 2021, 37, 1967–1978. [Google Scholar] [CrossRef]
- Lin, Z.; Tsui, P.H.; Zeng, Y.; Bin, G.; Wu, S.; Zhou, Z. CLA-U-Net: Convolutional Long-short-term-memory Attention-gated U-Net for Automatic Segmentation of the Left Ventricle in 2-D Echocardiograms. In Proceedings of the 2022 IEEE International Ultrasonics Symposium (IUS), Venice, Italy, 10–13 October 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–4. [Google Scholar]
- Li, S.; Wang, Z.; Liu, Z.; Tan, C.; Lin, H.; Wu, D.; Chen, Z.; Zheng, J.; Li, S.Z. Moganet: Multi-order gated aggregation network. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2023. [Google Scholar]
- Ren, S.; Zhou, D.; He, S.; Feng, J.; Wang, X. Shunted self-attention via multi-scale token aggregation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–20 June 2022; pp. 10853–10862. [Google Scholar]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef]
- Ye, Z.; Kumar, Y.J.; Song, F.; Li, G.; Zhang, S. Bi-DCNet: Bilateral Network with Dilated Convolutions for Left Ventricle Segmentation. Life 2023, 13, 1040. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Wu, H.; Zeng, R.; Qin, J. MemSAM: Taming Segment Anything Model for Echocardiography Video Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 17–21 June 2024; pp. 9622–9631. [Google Scholar]




| Model | Architecture | DSC (%) ↑ | HD95 (Pixels) ↓ | Params (MB) |
|---|---|---|---|---|
| U-Net | CNN | 91.36 | 4.98 | 9.5 |
| UNETR | CNN+Transformer | 92.43 | 3.06 | 87.5 |
| SwinUNet | Transformer | 92.67 | 2.92 | 27.1 |
| TransUNet | CNN+Transformer | 92.93 | 2.84 | 105.1 |
| DeepLabV3 | CNN | 92.68 | 2.83 | 39.6 |
| nnUNet | CNN | 92.86 | - | 7.37 |
| Bi-DCNet | CNN | 92.28 | - | - |
| EchoGraphs | CNN+GCN | 92.10 | - | 27.1 |
| MemSAM | Segment Anything | 92.78 | 4.57 | - |
| Ours | CNN+RetNet | 93.17 | 2.72 | 35.2 |
| Model | Architecture | DSC (%) ↑ | HD95 (Pixels) ↓ |
|---|---|---|---|
| U-Net | CNN | 92.17 | 7.12 |
| UNETR | CNN+Transformer | 92.45 | 7.37 |
| SwinUNet | Transformer | 92.56 | 6.82 |
| TransUNet | CNN+Transformer | 93.42 | 6.07 |
| DeepLabV3 | CNN | 92.91 | 6.57 |
| nnUNet | CNN | 93.33 | - |
| MemSAM | Segment Anything | 93.31 | 4.57 |
| Ours | CNN+RetNet | 93.70 | 5.81 |
| Setting | DSC (%) ↑ | HD95 (Pixels) ↓ |
|---|---|---|
| Baseline(UNETR) | 92.43 | 3.06 |
| Baseline+TFFM | 92.49 | 3.04 |
| Baseline+Vision RetNet | 92.95 | 2.72 |
| Vision RetNet+TFFM | 93.17 | 2.72 |
| Setting | DSC (%) ↑ | HD95 (Pixels) ↓ |
|---|---|---|
| UNet (no self-attention) | 92.17 | 7.12 |
| TransUNet | 93.42 | 6.07 |
| TransUNet+TCSA | 93.50 | 6.07 |
| TransUNet+CA | 93.46 | 6.07 |
| TransUNet+TFFM | 93.53 | 6.06 |
| UNETR | 92.45 | 7.37 |
| UNETR+TCSA | 92.53 | 7.37 |
| UNETR+CA | 92.48 | 7.37 |
| UNETR+TFFM | 92.55 | 7.37 |
| Vision RetNet | 93.40 | 5.81 |
| Vision RetNet+TCSA | 93.61 | 5.80 |
| Vision RetNet+CA | 93.45 | 5.81 |
| Vision RetNet+TFFM | 93.70 | 5.81 |
| 3rd Stage | DSC (%) ↑ | FLOPs (G) |
|---|---|---|
| Original MaSA | 93.63 | 412.6 |
| Decomposed MaSA | 93.60 | 340.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z.; Cui, R.; Ning, L.; Peng, J. Temporal Features-Fused Vision Retentive Network for Echocardiography Image Segmentation. Sensors 2025, 25, 1909. https://doi.org/10.3390/s25061909
Lin Z, Cui R, Ning L, Peng J. Temporal Features-Fused Vision Retentive Network for Echocardiography Image Segmentation. Sensors. 2025; 25(6):1909. https://doi.org/10.3390/s25061909
Chicago/Turabian StyleLin, Zhicheng, Rongpu Cui, Limiao Ning, and Jian Peng. 2025. "Temporal Features-Fused Vision Retentive Network for Echocardiography Image Segmentation" Sensors 25, no. 6: 1909. https://doi.org/10.3390/s25061909
APA StyleLin, Z., Cui, R., Ning, L., & Peng, J. (2025). Temporal Features-Fused Vision Retentive Network for Echocardiography Image Segmentation. Sensors, 25(6), 1909. https://doi.org/10.3390/s25061909






