A Circularly Polarized Broadband Composite Spiral Antenna for Ground Penetrating Radar
Abstract
1. Introduction
2. Theory of Spiral Antenna
3. Antenna Design
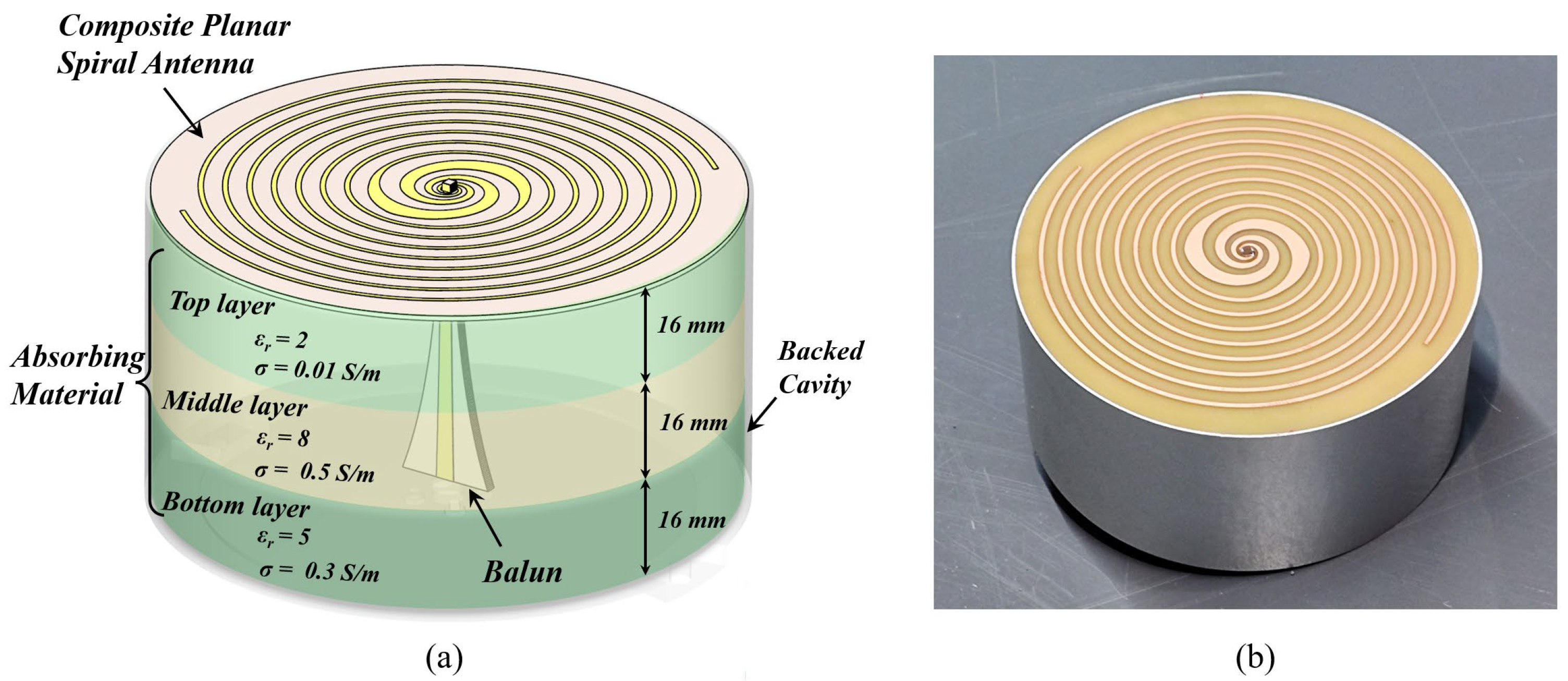
3.1. Composite Planar Spiral Antenna
3.2. Balun
3.3. Backed Cavity
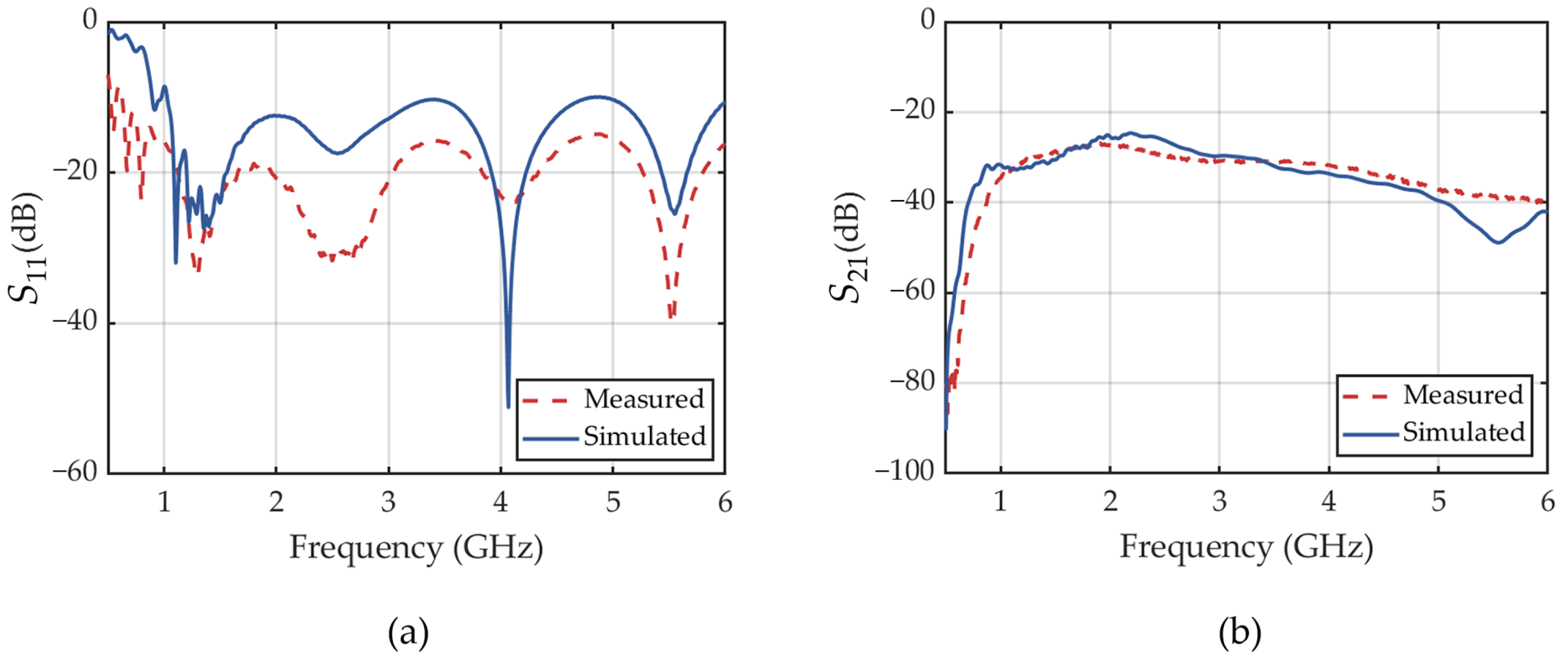
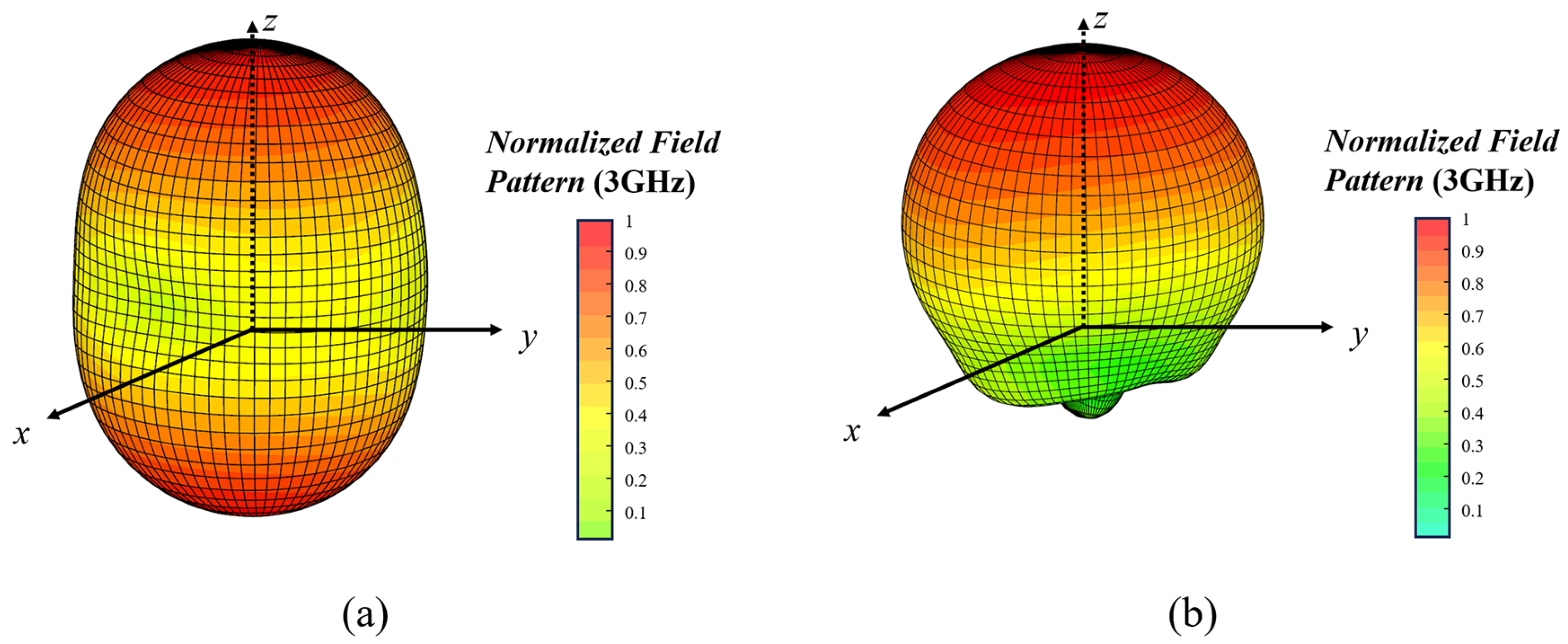
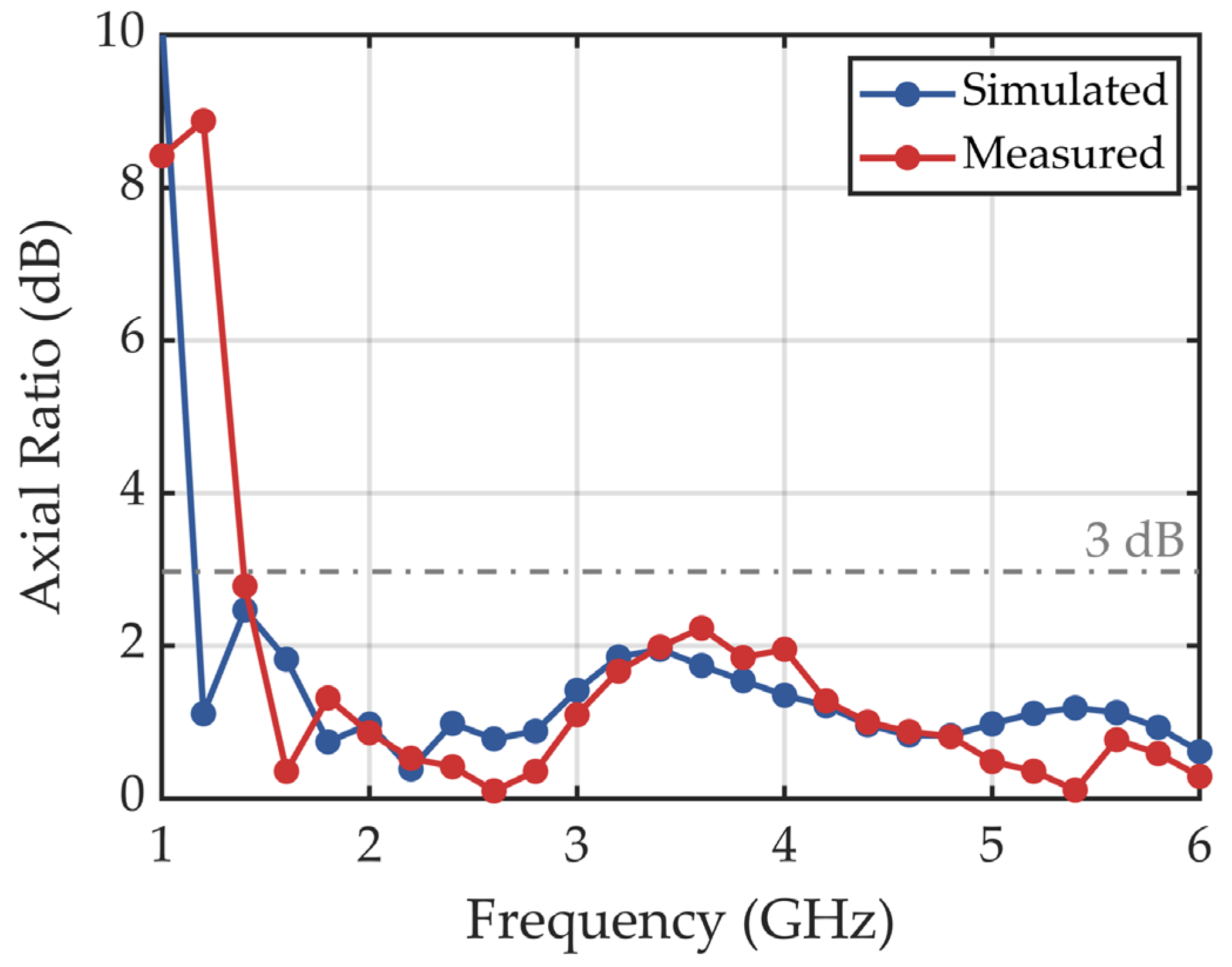
4. Antenna Evaluation
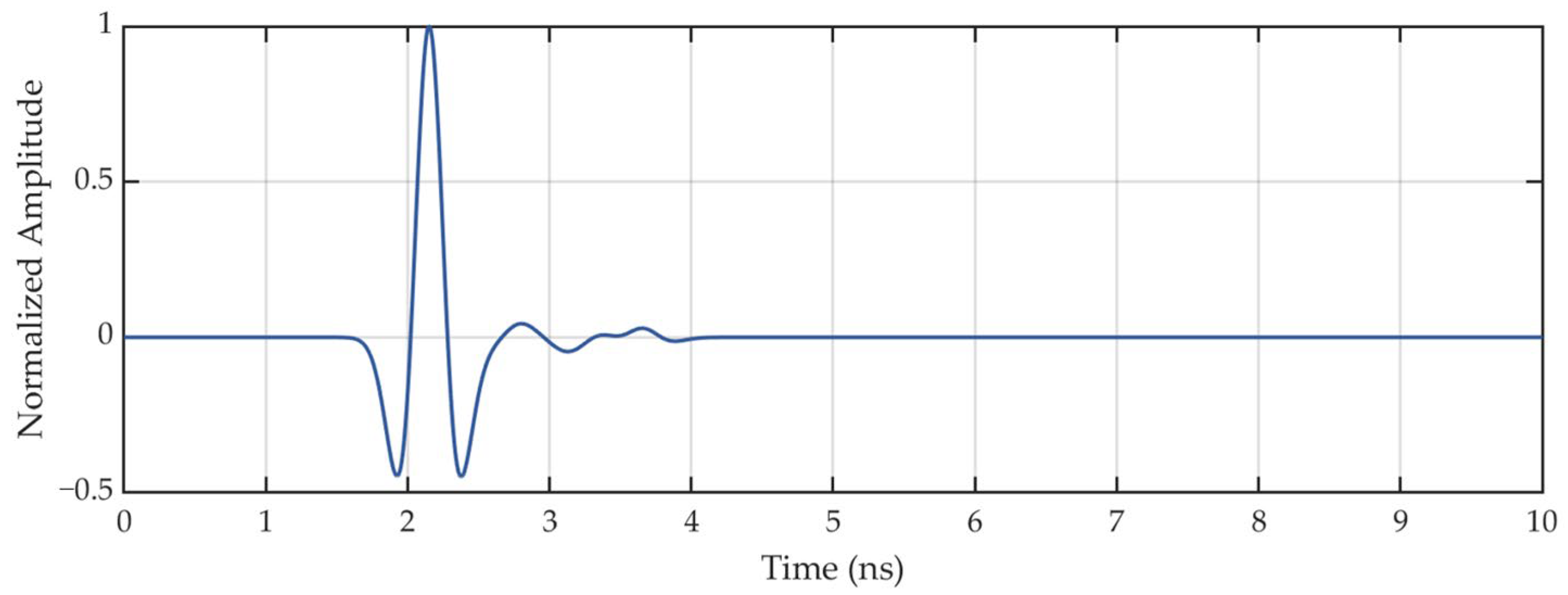
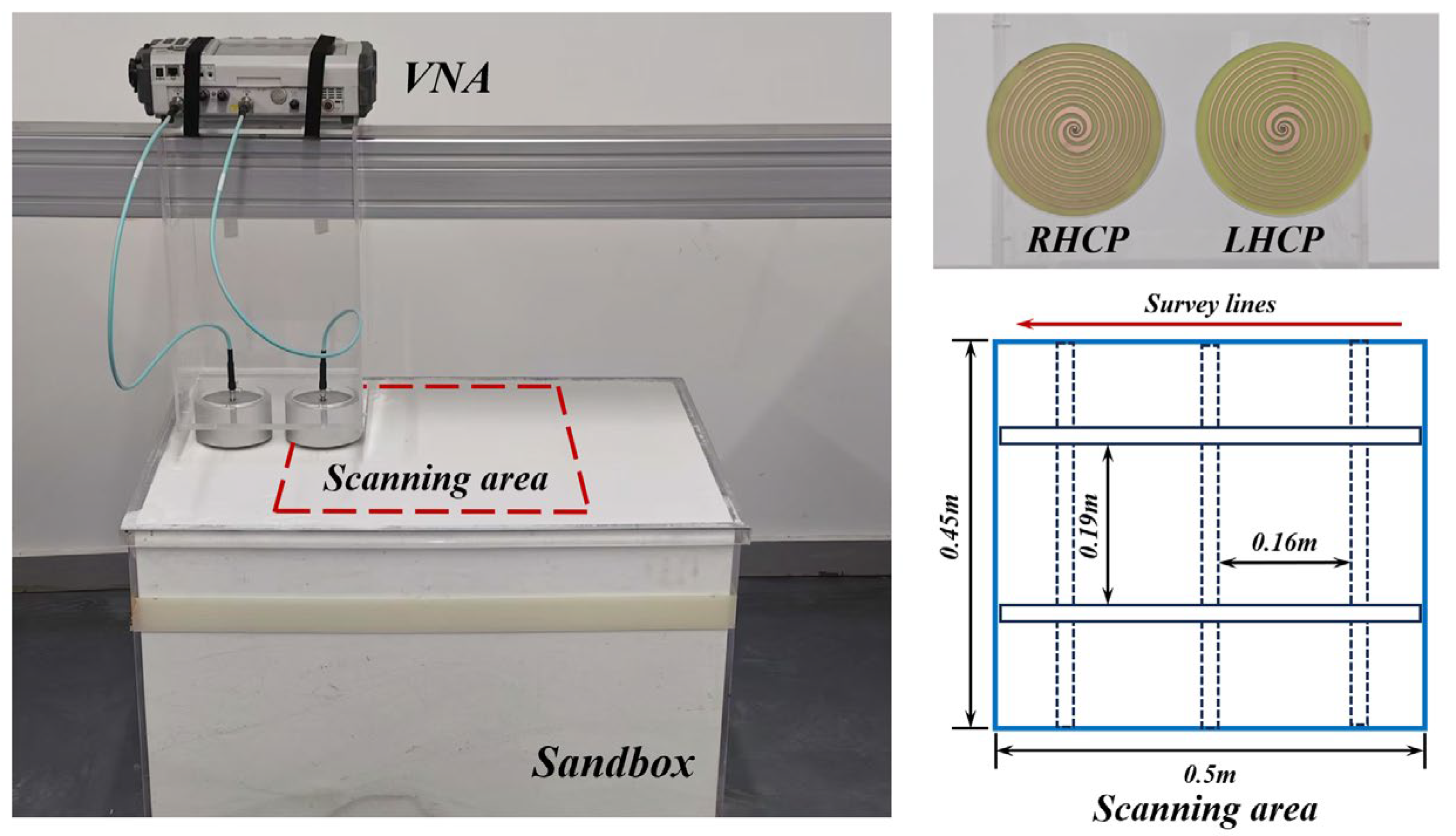
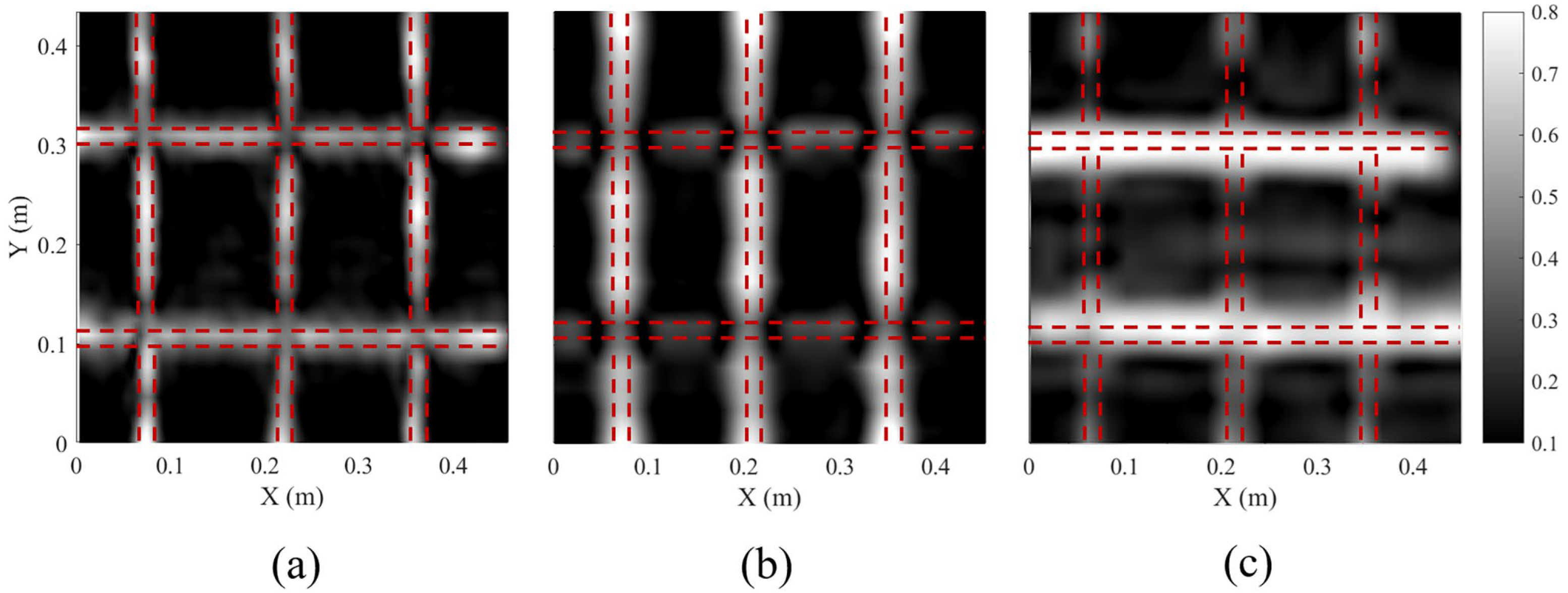
5. Three-Dimensional GPR Measurement
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GPR | Ground Penetrating Radar |
| VNA | Vector Network Analyzer |
| LHCP | Left-Hand Circularly Polarized |
| RHCP | Right-Hand Circularly Polarized |
| AR | Axial Ratio |
Appendix A. Deconvolution Method
References
- Daniels, D. Ground Penetrating Radar; The Institution of Electrical Engineers: London, UK, 2004. [Google Scholar]
- Jol, H.M. Ground Penetrating Radar Theory and Applications; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Gao, X.; Podd, F.J.W.; Van Verre, W.; Daniels, D.J.; Peyton, A.J. Investigating the performance of bi-static GPR antennas for near-surface object detection. Sensors 2019, 19, 170. [Google Scholar] [CrossRef] [PubMed]
- Rial, F.I.; Lorenzo, H.; Pereira, M.; Armesto, J. Analysis of the emitted wavelet of high-resolution bowtie GPR antennas. Sensors 2009, 9, 4230–4246. [Google Scholar] [CrossRef] [PubMed]
- Roberts, R.L.; Daniels, J.J. Analysis of GPR polarization phenomena. J. Environ. Eng. Geophys. 1996, 1, 139–157. [Google Scholar] [CrossRef]
- Liu, H.; Zhao, J.; Sato, M. A hybrid dual-polarization GPR system for detection of linear objects. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 317–320. [Google Scholar] [CrossRef]
- Feng, X.; Yu, Y.; Liu, C.; Fehler, M. Subsurface polarimetric migration imaging for full polarimetric ground-penetrating radar. Geophys. J. Int. 2015, 202, 1324–1338. [Google Scholar] [CrossRef]
- Chi-Chih, C.; Higgins, M.B.; Neill, K.O.; Detsch, R. Ultrawide-bandwidth fully-polarimetric ground penetrating radar classification of subsurface unexploded ordnance. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1221–1230. [Google Scholar] [CrossRef]
- Neill, K.O.; Haider, S.A.; Geimer, S.D.; Paulsen, K.D. Effects of the ground surface on polarimetric features of broadband radar scattering from subsurface metallic objects. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1556–1565. [Google Scholar] [CrossRef]
- Sassen, D.S.; Everett, M.E. 3D polarimetric GPR coherency attributes and full-waveform inversion of transmission data for characterizing fractured rock. Geophysics 2009, 74, J23–J34. [Google Scholar] [CrossRef]
- Zhou, H.; Feng, X.; Dong, Z.; Liu, C.; Liang, W.; An, Y. Local freeman decomposition for robust imaging and identification of subsurface anomalies using misaligned full-polarimetric GPR data. Remote Sens. 2022, 14, 804. [Google Scholar] [CrossRef]
- Zeng, Z.; Li, J.; Huang, L.; Feng, X.; Liu, F. Improving target detection accuracy based on multipolarization MIMO GPR. IEEE Trans. Geosci. Remote Sens. 2015, 53, 15–24. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, Y.; Tian, Q.; Wang, X.; Meng, H. Analysis and simulation of a sequential rotationally excited circular polarized multi-dipole array for a bi-static antenna GPR for deep exploration. Remote Sens. 2023, 15, 1134. [Google Scholar] [CrossRef]
- Sun, H.-H.; Lee, Y.H.; Luo, W.; Ow, L.F.; Yusof, M.L.; Yucel, A.C. Compact dual-polarized vivaldi antenna with high gain and high polarization purity for GPR applications. Sensors 2021, 21, 503. [Google Scholar] [CrossRef]
- Liu, H.; Zhong, J.; Ding, F.; Meng, X.; Liu, C.; Cui, J. Detection of early-stage rebar corrosion using a polarimetric ground penetrating radar system. Constr. Build. Mater. 2022, 317, 125768. [Google Scholar] [CrossRef]
- Liu, H.; Huang, X.; Han, F.; Cui, J.; Spencer, B.F.; Xie, X. Hybrid polarimetric GPR calibration and elongated object orientation estimation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2080–2087. [Google Scholar] [CrossRef]
- Grigoor-Feghi, N.; Masoumi, R.; Kazemi, R. Development of a fully planar logarithmic spiral antenna with integrated balun in UWB GPR systems for landmines detection. Electromagnetics 2022, 42, 559–570. [Google Scholar] [CrossRef]
- Dyson, J. The equiangular spiral antenna. IRE Trans. Antennas Propag. 1959, 7, 181–187. [Google Scholar] [CrossRef]
- Fu, W.; Lopez, E.R.; Rowe, W.S.T.; Ghorbani, K. A planar dual-arm equiangular spiral antenna. IEEE Trans. Antennas Propag. 2010, 58, 1775–1779. [Google Scholar] [CrossRef]
- Eubanks, T.W.; Chang, K. A compact parallel-plane perpendicular-current feed for a modified equiangular spiral antenna. IEEE Trans. Antennas Propag. 2010, 58, 2193–2202. [Google Scholar] [CrossRef]
- Kaiser, J. The Archimedean two-wire spiral antenna. IRE Trans. Antennas Propag. 1960, 8, 312–323. [Google Scholar] [CrossRef]
- Nakano, H.; Mimnaki, H.; Yamauchi, J.; Hirose, K. A low profile Archimedean spiral antenna. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Ann Arbor, MI, USA, 28 June–2 July 1993; Volume 451, pp. 450–453. [Google Scholar]
- Etellisi, E.A.; Elmansouri, M.A.; Filipovic, D.S. Wideband monostatic simultaneous transmit and receive (STAR) Antenna. IEEE Trans. Antennas Propag. 2016, 64, 6–15. [Google Scholar] [CrossRef]
- McFadden, M.; Scott, W.R. Analysis of the equiangular spiral antenna on a dielectric substrate. IEEE Trans. Antennas Propag. 2007, 55, 3163–3171. [Google Scholar] [CrossRef]
- Nakano, H.; Kikkawa, K.; Kondo, N.; Iitsuka, Y.; Yamauchi, J. Low-profile equiangular spiral antenna Backed by an EBG reflector. IEEE Trans. Antennas Propag. 2009, 57, 1309–1318. [Google Scholar] [CrossRef]
- Pan, T.; Dai, L.; Chen, S.; Yan, Z.; Lin, Y. Low-impedance flexible Archimedean-equiangular spiral antenna. IEEE Antennas Wirel. Propag. Lett. 2019, 18, 1789–1793. [Google Scholar] [CrossRef]
- Nakano, H.; Nogami, K.; Arai, S.; Mimaki, H.; Yamauchi, J. A spiral antenna backed by a conducting plane reflector. IEEE Trans. Antennas Propag. 1986, 34, 791–796. [Google Scholar] [CrossRef]
- Zhong, Y.W.; Yang, G.M.; Mo, J.Y.; Zheng, L.R. Compact circularly polarized Archimedean spiral antenna for ultrawideband communication applications. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 129–132. [Google Scholar] [CrossRef]
- Shih, T.Y.; Behdad, N. A compact, broadband spiral antenna with unidirectional circularly polarized radiation patterns. IEEE Trans. Antennas Propag. 2015, 63, 2776–2781. [Google Scholar] [CrossRef]
- Schreider, L.; Begaud, X.; Soiron, M.; Perpere, B.; Renard, C. Broadband Archimedean spiral antenna above a loaded electromagnetic band gap substrate. IET Microw. Antennas Propag. 2007, 1, 212–216. [Google Scholar] [CrossRef]
- O’Brien, J.M.; Grandfield, J.E.; Mumcu, G.; Weller, T.M. Miniaturization of a spiral antenna using periodic Z-plane meandering. IEEE Trans. Antennas Propag. 2015, 63, 1843–1848. [Google Scholar] [CrossRef]
- Okamura, S.; Takahashi, K.; Sato, M. Non-destructive inspection of buildings using radar polarimetry. In Proceedings of the 2013 Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Tsukuba, Japan, 23–27 September 2013; pp. 122–125. [Google Scholar]
- Lee, J.H.; Hwang, J.M.; Choi, D.H.; Park, S.O. Noninvasive biosignal detection radar system using circular polarization. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 400–404. [Google Scholar] [CrossRef]
- Yousefzadeh, M.; Ebrahimzadeh, R.; Zakeri, B.; Talbi, L.; Hettak, K.; Boutayeb, H. Design of automotive radar antenna for covering middle- and long-range with dual-circular polarization. IEEE Trans. Antennas Propag. 2024, 72, 7504–7514. [Google Scholar] [CrossRef]
- Nord, M.E.; Ainsworth, T.L.; Jong-Sen, L.; Stacy, N.J.S. Comparison of compact polarimetric synthetic aperture radar modes. IEEE Trans. Geosci. Remote Sens. 2009, 47, 174–188. [Google Scholar] [CrossRef]
- Balanis, C.A. Antenna Theory: Analysis and Design, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Booker, H.G. Slot aerials and their relation to complementary wire aerials (Babinet’s principle). J. Inst. Electr. Eng.-Part IIIA Radiolocation 1946, 93, 620–626. [Google Scholar] [CrossRef]
- Milligan, T.A. Modern Antenna Design; John Wiley & Sons: Hoboken, NY, USA, 2005. [Google Scholar]
- Zhao, Y.; Hu, W. Design of a UWB unidirectional radiation compound spiral antenna. In Proceedings of the 2015 IEEE 6th International Symposium on Microwave, Antenna, Propagation, and EMC Technologies (MAPE), Shanghai, China, 28–30 October 2015; pp. 158–161. [Google Scholar]
- Wadell, B.C. Transmission Line Design Handbook; Artech house: Boston, MA, USA, 1991. [Google Scholar]
- Yao, H.; Yang, J.; Li, H.; Xu, J.; Bi, K. Optimal design of multilayer radar absorbing materials: A simulation-optimization approach. Adv. Compos. Hybrid Mater. 2023, 6, 43. [Google Scholar] [CrossRef]
- Pozar, D.M. Microwave Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Mallat, S.G.; Zhang, Z. Matching pursuits with time-frequency dictionaries. IEEE Trans. Signal Process. 1993, 41, 3397–3415. [Google Scholar] [CrossRef]
- Gao, S.; Luo, Q.; Zhu, F. Circularly Polarized Antennas; John Wiley & Sons: West Sussex, UK, 2014. [Google Scholar]
- Toh, B.Y.; Cahill, R.; Fusco, V.F. Understanding and measuring circular polarization. IEEE Trans. Educ. 2003, 46, 313–318. [Google Scholar] [CrossRef]
- Liu, H.; Chen, Z.; Lu, H.; Han, F.; Liu, C.; Li, J.; Cui, J. Migration of ground penetrating radar with antenna radiation pattern correction. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3500805. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, B.; Ding, F.; Li, J.; Meng, X.; Liu, C.; Shi, R. Enhanced imaging of reinforcement by dual-polarization ground penetrating radar. Prog. Geophys. 2024. Available online: https://kns.cnki.net/kcms/detail/11.2982.P.20241227.1354.006.html (accessed on 16 March 2025).


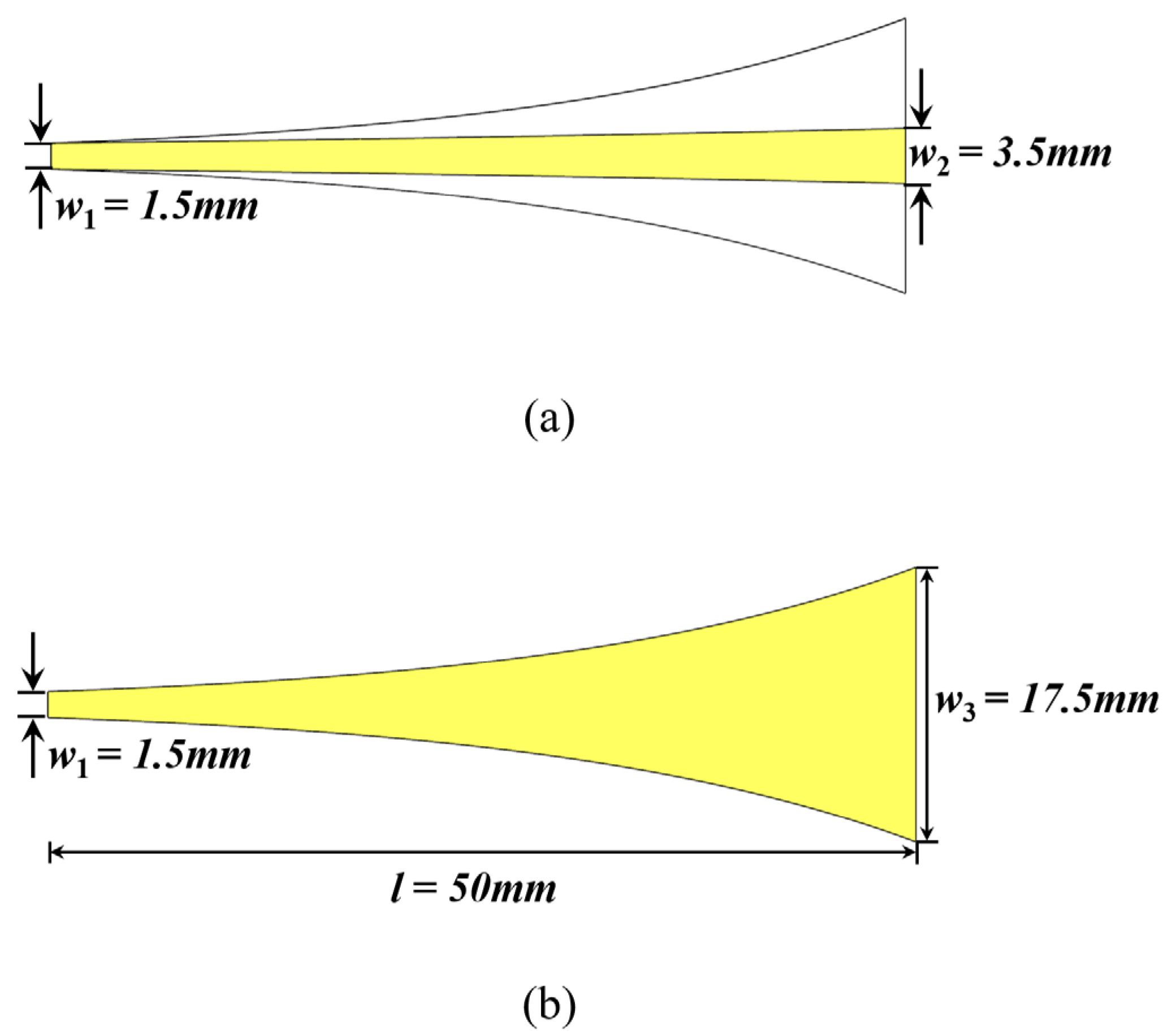


| Equiangular Spiral Structure | Archimedean Spiral Structure | |
|---|---|---|
| Starting radius (r0) | 1.5 mm | 14 mm |
| Starting angle (θ0) | 0° | 0° |
| Azimuthal angle (θ) | 720° | 1800° |
| Growth rate (a) | 0.221 | 9 |
| Line width | - | 1 mm |
| Reference | S11 Bandwidth (GHz) | AR | Size (mm2) | Fractional Bandwidth (%) |
|---|---|---|---|---|
| [20] | 3.95~10.6 | >3 dB in the whole band | 59.94 × 59.94 × 1.14 | 91.4 |
| [23] | 0.8~3.5 | <3 dB (0.5~2.5 GHz) | 152.4 × 152.4 × 15 | 125.6 |
| [26] | 2.5~4.5 | <3 dB (2.5–4.5 GHz) | 38.2 × 38.2 × 10 | 57.1 |
| [28] | 1.9~8.5 | <3 dB (2–6 GHz) | 36 × 36 × 20 | 126.9 |
| [31] | 0.8~3 | <3 dB (1.5~3 GHz) | 76.2 × 76.2 × 38.1 | 115.8 |
| [39] | 5~20 | <5 dB (5~20 GHz) | 50 × 50 × 23 | 120 |
| This work | 1~6 | <3 dB (1~6 GHz) | 111.5 × 111.5 × 51.8 | 142.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhang, S.; Wu, P.; Meng, X.; Zhou, J.; Du, Y. A Circularly Polarized Broadband Composite Spiral Antenna for Ground Penetrating Radar. Sensors 2025, 25, 1890. https://doi.org/10.3390/s25061890
Liu H, Zhang S, Wu P, Meng X, Zhou J, Du Y. A Circularly Polarized Broadband Composite Spiral Antenna for Ground Penetrating Radar. Sensors. 2025; 25(6):1890. https://doi.org/10.3390/s25061890
Chicago/Turabian StyleLiu, Hai, Shangyang Zhang, Pei Wu, Xu Meng, Junyong Zhou, and Yanliang Du. 2025. "A Circularly Polarized Broadband Composite Spiral Antenna for Ground Penetrating Radar" Sensors 25, no. 6: 1890. https://doi.org/10.3390/s25061890
APA StyleLiu, H., Zhang, S., Wu, P., Meng, X., Zhou, J., & Du, Y. (2025). A Circularly Polarized Broadband Composite Spiral Antenna for Ground Penetrating Radar. Sensors, 25(6), 1890. https://doi.org/10.3390/s25061890








