Adaptive Distributed Student’s T Extended Kalman Filter Employing Allan Variance for UWB Localization
Abstract
1. Introduction
- We design a distributed UWB localization strategy for mobile objects, utilizing a distributed filter structure. The system employs multiple local filters to estimate the target’s position by fusing distance measurements. The main filter then combines these outputs to compute the final position.
- An adaptive Allan variance computation method was derived, where Allan variance is calculated based on noise estimation from the previous moment.
- Building on the distributed UWB localization scheme and Allan variance method, we propose the adaptive distributed Student’s t EKF. This method uses a t distribution to model the noise, and the main filter fuses the local filter outputs to compute the final result, with Allan variance assisting the local filter.
- Experimental results, supported by rigorous statistical analyses, demonstrate the superior efficiency and effectiveness of the proposed algorithms, which significantly outperform traditional methods.
2. Problem Formulation
2.1. UWB Localization with the Adaptive Distributed Student’s T Extended Kalman Filter Scheme
2.2. Problem Formulation
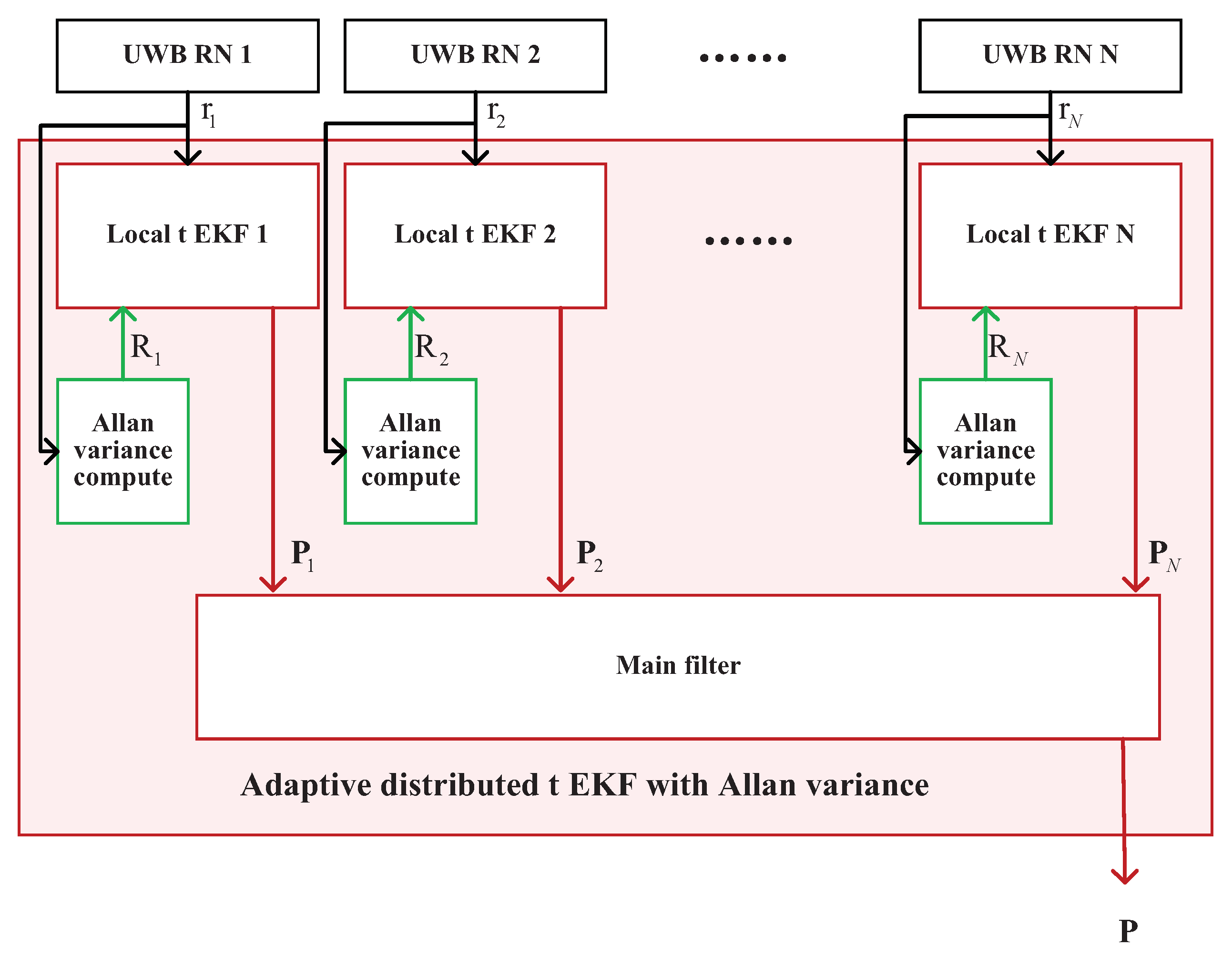
3. Adaptive Distributed Student’s T EKF
3.1. Allan Variance
3.2. Distributed Student’s T EKF
3.3. Adaptive Distributed Student’s T Filter
| Algorithm 1: Adaptive distributed Student’s t extended Kalman filter for model (2) and (3) |
 |
4. Test and Discussion
4.1. UWB Mobile Robot Localization
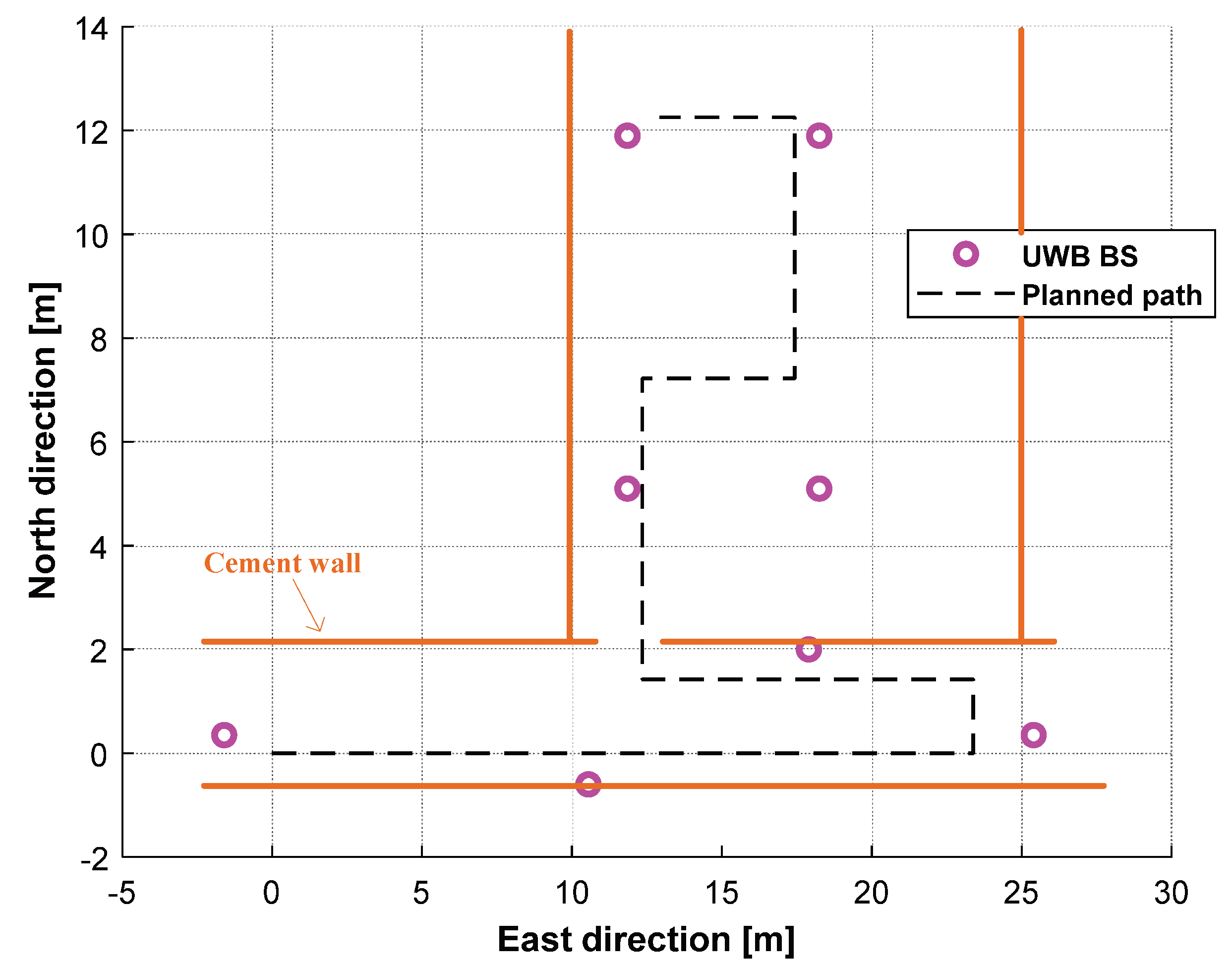
4.2. UWB Robotic Dog Localization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANFIS | Adaptive-Network Fuzzy Inference System |
| AUVs | Autonomous Underwater Vehicles |
| BDS | BeiDou Navigation Satellite System |
| BN | Blind Node |
| DRKF | Dual-Rate Kalman Filter |
| DOF | Degrees of Freedom |
| EKF | Extended Kalman Filter |
| GAF | Gramian Angular Field |
| GLONASS | Global Navigation Satellite System |
| GNSS | Global Navigation Satellite System |
| GPS | Global Positioning System |
| LS | Least Squares |
| RFID | Radio Frequency Identification |
| RMSE | Root Mean Square Error |
| SP | Static Person |
| SPL | Static Person Localization |
| TJU-1 | Tianjin University-1 |
| NARX | Nonlinear Autoregressive Exogenous model |
| NLOS | Non-Line-Of-Sight |
| Probability Density Function | |
| UWB | Ultrawide Band |
| BS | Base Station |
References
- Luo, R.; Lai, C. Enriched Indoor Map Construction Based on Multisensor Fusion Approach for Intelligent Service Robot. IEEE Trans. Ind. Electron. 2012, 59, 3135–3145. [Google Scholar] [CrossRef]
- Xu, Y.; Wan, D.; Bi, S.; Guo, H.; Zhuang, Y. A FIR filter assisted with the predictive model and ELM integrated for UWB-based quadrotor aircraft localization. Satell. Navig. 2023, 4, 2. [Google Scholar] [CrossRef]
- He, Z.; Chen, W.; Yang, Y.; Weng, D.; Cao, N. Maritime Ship Target Imaging with GNSS-Based Passive Multistatic Radar. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–18. [Google Scholar] [CrossRef]
- Cheng, J.; Liu, W.; Zhang, X.; Wang, F.; Li, Z.; Tang, C.; Pan, J.; Chang, Z. On-board validation of BDS-3 autonomous navigation using inter-satellite link observations. J. Geod. 2023, 7, 71. [Google Scholar] [CrossRef]
- Gong, X.; Zhang, W.; Wang, Q.; Wang, F.; Li, X.; Sang, J.; Liu, W. Precise real-time navigation of the small TJU-1 satellite using GPS, GLONASS and BDS. Measurement 2022, 204, 112090. [Google Scholar] [CrossRef]
- Zhuang, Y.; Hua, L.; Wang, Q.; Cao, Y.; Thompson, J.S. Visible Light Positioning and Navigation Using Noise Measurement and Mitigation. IEEE Trans. Veh. Technol. 2019, 68, 11094–11106. [Google Scholar] [CrossRef]
- Ma, H.; Ma, Z.; Gao, L.Y. RFID-enabled localization system for mobile robot in the workshop. Int. J. Technol. Res. Appl. 2023, 13, 135–147. [Google Scholar] [CrossRef]
- Chatzistefanou, A.; Tzitzis, A.; Megalou, S.; Sergiadis, G.; Dimitriou, A. Target Localization by Mobile Handheld UHF RFID Reader and IMU. IEEE J. Radio Freq. Identif. 2022, 6, 426–438. [Google Scholar] [CrossRef]
- Miesen, R.; Kirsch, F.; Vossiek, M. UHF RFID Localization Based on Synthetic Apertures. IEEE Trans. Autom. Sci. Eng. 2013, 10, 807–815. [Google Scholar] [CrossRef]
- Xu, Y.; Zang, X.; Shmaliy, Y.S.; Yu, J.; Zhuang, Y.; Sun, M. UWB-Based Robot Localization Using Distributed Adaptive EFIR Filtering. IEEE Internet Things J. 2024, 11, 30704–30713. [Google Scholar] [CrossRef]
- Deng, B.; Xu, T.; Yan, M. UWB NLOS Identification and Mitigation Based on Gramian Angular Field and Parallel Deep Learning Model. IEEE Sens. J. 2023, 23, 28513–28525. [Google Scholar] [CrossRef]
- Kocur, D.; Porteleky, T.; Svecova, M.; Svingal, M.; Fortes, J. A Novel Signal Processing Scheme for Static Person Localization Using M-sequence UWB Radars. IEEE Sens. J. 2021, 21, 20296–20310. [Google Scholar] [CrossRef]
- Zhao, S.; Huang, B.; Shmaliy, Y.S. Bayesian state estimation on finite horizons: The case of linear state–space model. Automatica 2017, 85, 91–99. [Google Scholar] [CrossRef]
- Zhao, S.; Huang, B.; Liu, F. Linear Optimal Unbiased Filter for Time-Variant Systems Without Apriori Information on Initial Conditions. IEEE Trans. Autom. Control 2016, 62, 882–887. [Google Scholar] [CrossRef]
- Han, S.; Wang, J. Integrated GPS/INS navigation system with dual-rate Kalman Filter. GPS Solut. 2012, 16, 389–404. [Google Scholar] [CrossRef]
- Liang, K.; Hao, S.; Yang, Z.; Wang, J. A Multi-Global Navigation Satellite System (GNSS) Time Transfer Method with Federated Kalman Filter (FKF). Sensors 2023, 23, 5328. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Xia, X.; Zheng, Z.; Ma, J. GNSS/IMU/LiDAR fusion for vehicle localization in urban driving environments within a consensus framework. Mech. Syst. Signal Process. 2023, 205, 110862. [Google Scholar] [CrossRef]
- Zhao, W.; Zhao, H.; Liu, G.; Zhang, G. ANFIS-EKF-Based Single-Beacon Localization Algorithm for AUV. Remote Sens. 2022, 14, 5281. [Google Scholar] [CrossRef]
- Feng, N.; Li, K.; Huang, Z.; Wei, Z.; Wang, W.; Zhao, J. NISAC-EKF: An integrated localization deployment algorithm for UAV swarms based on NARX and EKF. Phys. Commun. 2024, 64, 102310. [Google Scholar] [CrossRef]
- Roth, M.; Ozkan, E.; Gustafsson, F. A Student’s t filter for heavy tailed process and measurement noise. In Proceedings of the International Conference on Acoustics, Speech, and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar]



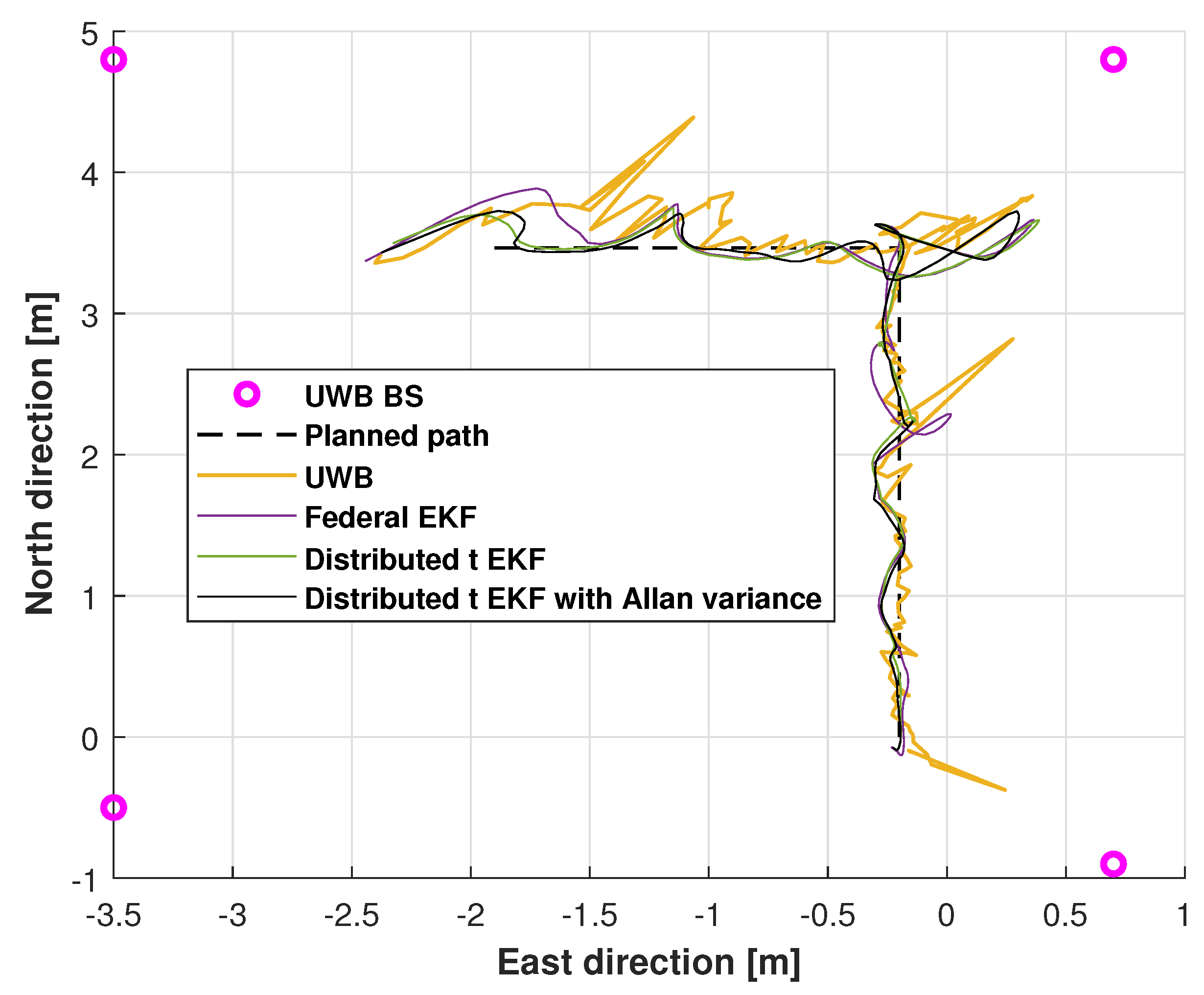

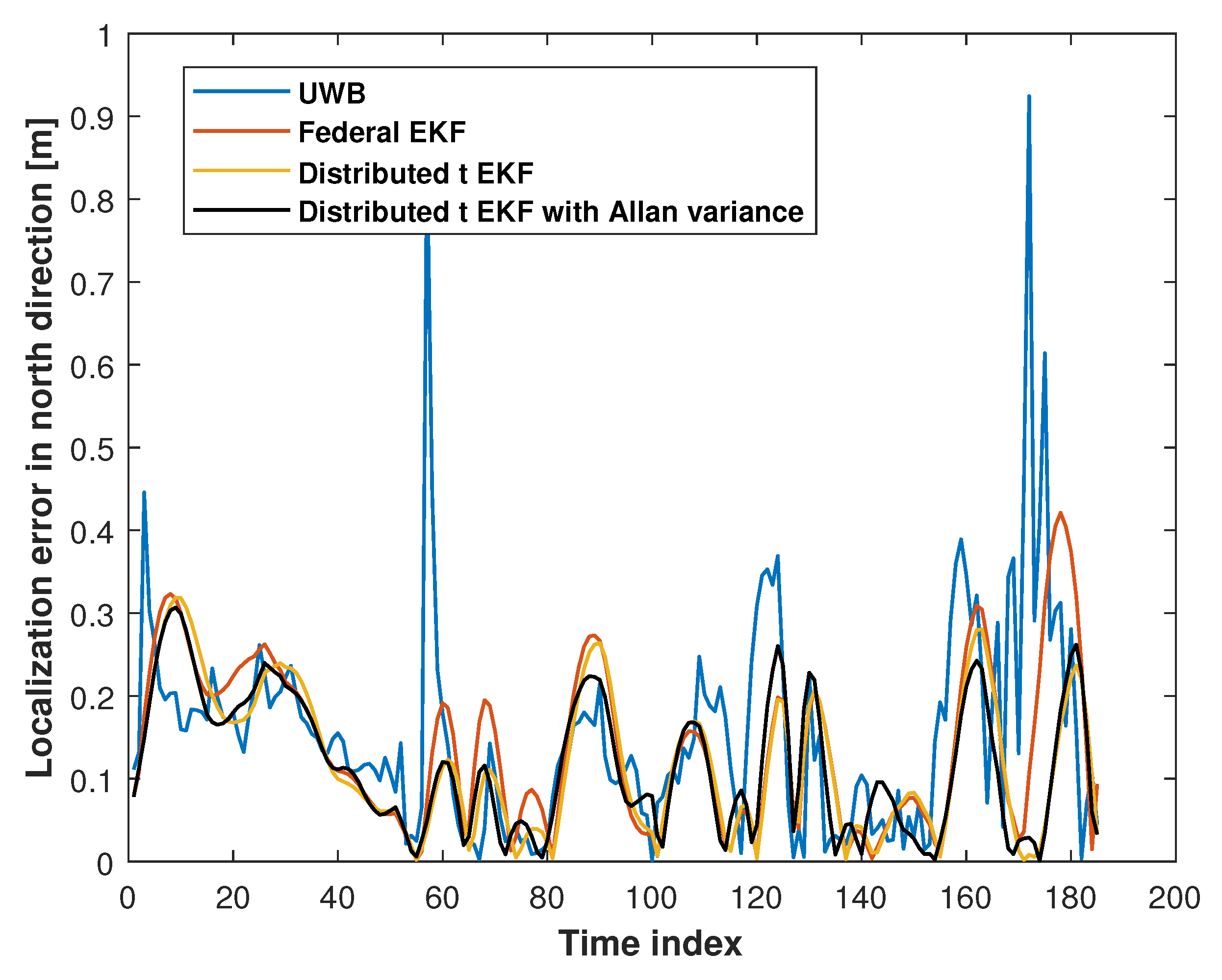


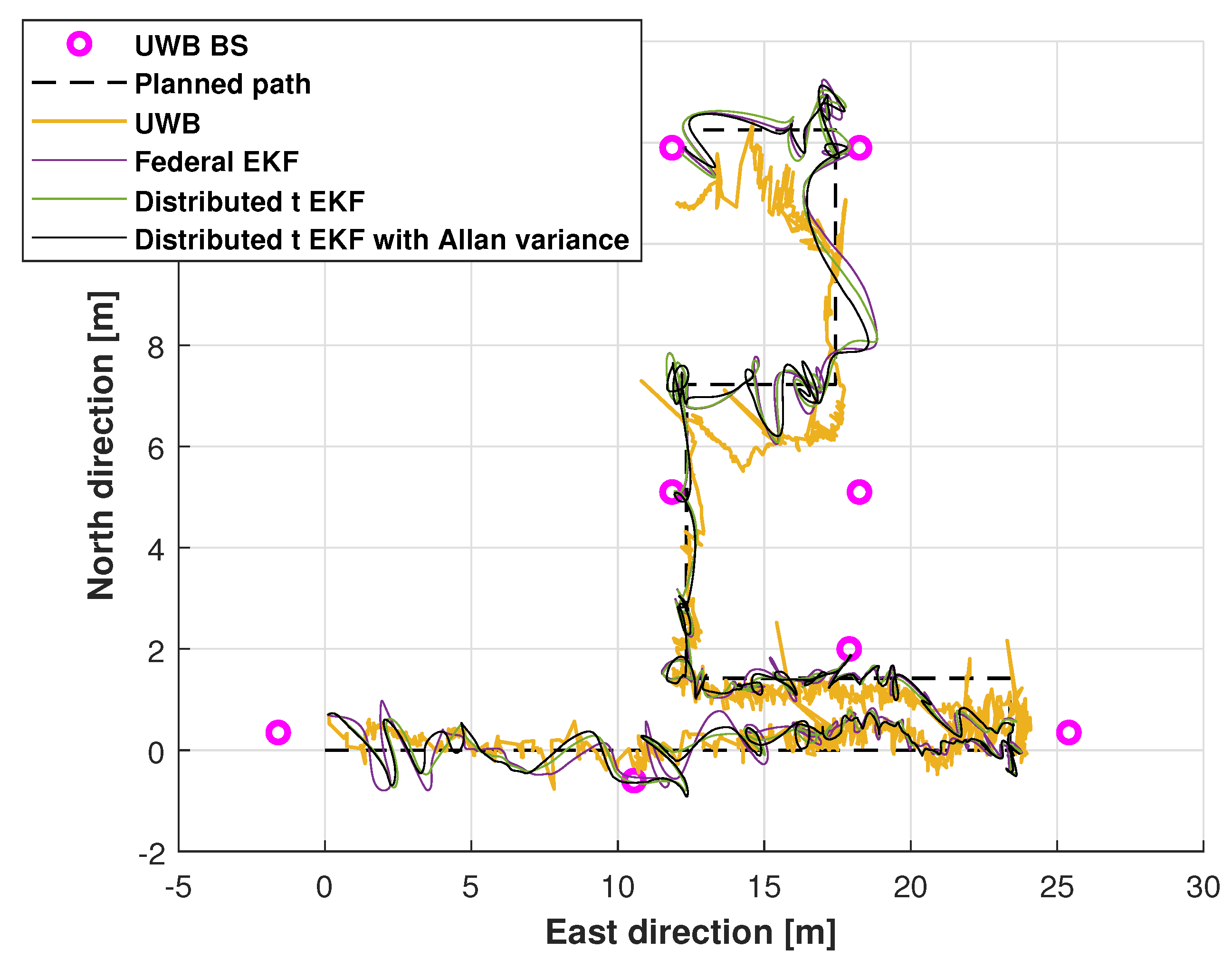

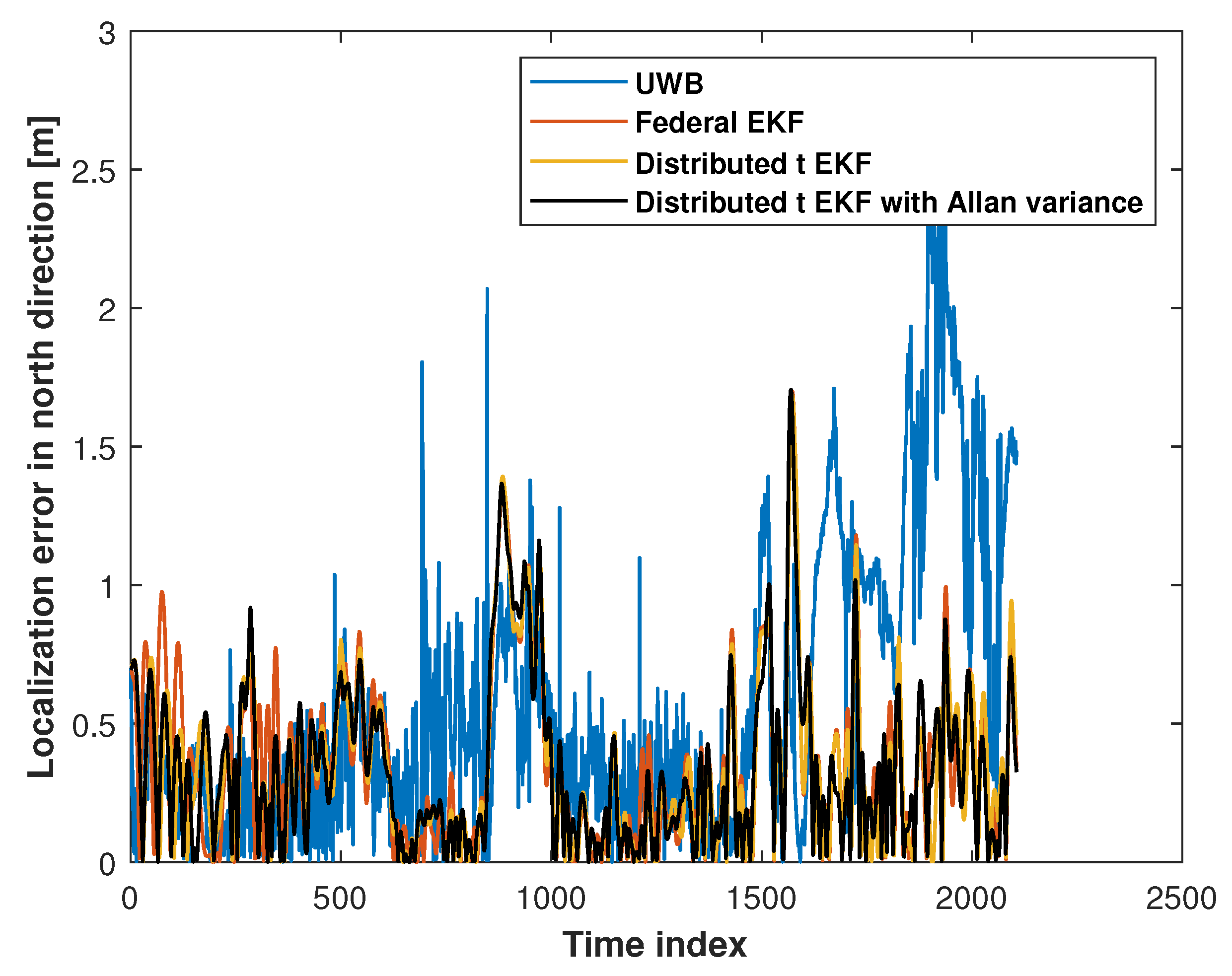
| Methods | East Position | North Position | Mean |
|---|---|---|---|
| UWB | 0.182 | 0.205 | 0.194 |
| Federal EKF | 0.161 | 0.170 | 0.166 |
| Distributed t EKF | 0.155 | 0.146 | 0.151 |
| Adaptive distributed t EKF with Allan variance | 0.145 | 0.142 | 0.144 |
| Methods | East Position | North Position | Mean |
|---|---|---|---|
| UWB | 0.568 | 0.764 | 0.666 |
| Federal EKF | 0.475 | 0.474 | 0.476 |
| Distributed t EKF | 0.500 | 0.458 | 0.479 |
| Adaptive distributed t EKF with Allan variance | 0.468 | 0.451 | 0.459 |
| Methods | East Position | North Position | Mean |
|---|---|---|---|
| UWB | 0.661 | 0.613 | 0.637 |
| Federal EKF | 0.624 | 0.611 | 0.618 |
| Distributed t EKF | 0.644 | 0.603 | 0.623 |
| Adaptive distributed t EKF with Allan variance | 0.625 | 0.599 | 0.612 |
| Methods | First Time | Second Time | Mean |
|---|---|---|---|
| UWB | 0.666 | 0.637 | 0.652 |
| Federal EKF | 0.476 | 0.618 | 0.547 |
| Distributed t EKF | 0.479 | 0.623 | 0.551 |
| Adaptive distributed t EKF with Allan variance | 0.459 | 0.612 | 0.535 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Yang, M.; Zang, X.; Deng, L.; Li, M.; Xu, Y.; Sun, M. Adaptive Distributed Student’s T Extended Kalman Filter Employing Allan Variance for UWB Localization. Sensors 2025, 25, 1883. https://doi.org/10.3390/s25061883
Gao Y, Yang M, Zang X, Deng L, Li M, Xu Y, Sun M. Adaptive Distributed Student’s T Extended Kalman Filter Employing Allan Variance for UWB Localization. Sensors. 2025; 25(6):1883. https://doi.org/10.3390/s25061883
Chicago/Turabian StyleGao, Yanli, Maosheng Yang, Xin Zang, Lei Deng, Manman Li, Yuan Xu, and Mingxu Sun. 2025. "Adaptive Distributed Student’s T Extended Kalman Filter Employing Allan Variance for UWB Localization" Sensors 25, no. 6: 1883. https://doi.org/10.3390/s25061883
APA StyleGao, Y., Yang, M., Zang, X., Deng, L., Li, M., Xu, Y., & Sun, M. (2025). Adaptive Distributed Student’s T Extended Kalman Filter Employing Allan Variance for UWB Localization. Sensors, 25(6), 1883. https://doi.org/10.3390/s25061883






