1. Introduction
The power converter, as a core component of motor drive systems, is widely used in fields such as electric vehicles, renewable energy generation, and rail transportation. During operation, the power converter often needs to switch frequently between the rectifier and inverter states, which may lead to faults under multi-conditions. Therefore, the ability to quickly and accurately diagnose faults in power converters across multi-conditions is essential for ensuring the safe operation of motor drive systems.
Power converter faults are primarily classified into short-circuit (SC) faults and open-circuit (OC) faults, which are manifested by the failure of internal power devices such as an insulated gate bipolar transistor (IGBT) [
1]. The main causes of SC faults can be divided into two aspects. On one hand, abnormal Pulse Width Modulation (PWM) control signals may lead to SC faults. On the other hand, IGBT breakdown may occur under high-stress conditions such as over-voltage, over-current, or excessive junction temperature. When an SC fault occurs, protective devices within the power converter, such as circuit breakers or fast-acting fuses, are activated to isolate the failed component and shut down the power converter [
2]. The primary cause of OC faults is IGBT thermal fatigue failure, in which failure of internal solder layers or bonding wires prevents the IGBT from conducting current [
3]. Once an OC fault occurs, the output current of the power converter becomes distorted and unbalanced; this does not trigger protective devices but severely reduces the output power quality and may even lead to secondary faults [
4]. This paper focuses on the diagnosis of OC faults in the power converter.
For OC faults, current diagnosis methods mainly include model-based methods [
5,
6,
7], signal-based methods [
8,
9,
10], and data-driven methods [
11,
12,
13]. Model-based methods require the establishment of mathematical models that characterize the physical behavior of the actual system. By observing and calculating the residuals between the measured values of the actual system and the simulated values from the mathematical model, the current state of the system can be assessed. In reference [
14], the current residual is calculated by comparing the actual current path with the estimated current path, and faults are identified based on characteristic residual patterns. In reference [
15], the extended Kalman filter is adjusted by measuring currents on both the battery and capacitor sides until the residual falls below a set correction threshold, and fault detection and localization are achieved by determining whether the maximum correction count or correction values on the faulted side exceed the threshold. In reference [
16], output current and its rate of change are used as fault detection variables, while the sum of phase current and neutral point voltage residuals is used for fault localization. In reference [
17], a process of state augmentation and nonsingular coordinate transformation was designed for the observation system to address misdiagnosis issues arising from interactions between different fault types. Model-based methods generally offer high diagnosis accuracy; however, establishing mathematical models for complex systems is challenging. Furthermore, when system parameters change, the model needs to be redefined.
An IGBT OC fault leads to voltage oscillations at the load end of the power converter and introduces significant harmonics in the output current. Fault diagnosis methods based on observing these signal variations are referred to as signal-based methods. When an OC fault occurs in the IGBT, the current path in its corresponding bridge arm changes. Reference [
18] proposes diagnosing inverter OC faults by utilizing changes in the current path under effective vector coordinates. Reference [
19] designed a normalized cost function for detecting OC faults and used the current mean and phase angle for fault localization. In addition to current detection, voltage signals can also be used to diagnose IGBT OC faults. Reference [
20] utilizes the similarity of capacitor voltages under fault and normal conditions in modular multilevel converters, employing a correlation coefficient for early-stage fault localization. Reference [
21] performs fault diagnosis based on the characteristic that the common-mode voltage of an inverter remains equal during normal operation and reduces fault miss-detection rates by injecting active common-mode voltage. Reference [
22] proposed a fault diagnosis method based on the dynamic characteristics of midpoint voltage and a fault-tolerant control strategy based on Complementary Switch Blocking, which mitigates fault impacts by blocking gate drive signals of the complementary switch. Reference [
23] processes three-phase voltage signals using ensemble empirical mode decomposition, breaking them down into intrinsic mode functions and calculating their norm entropy to characterize fault signal statistics. However, in practical applications, current signals are susceptible to load effects, reducing diagnosis accuracy and increasing diagnosis time. Voltage-based methods often require additional sensors, raising operational and maintenance costs.
Data-driven methods build fault diagnosis models by training on large amounts of historical data to establish a mapping relationship between fault features and fault modes. Once the model detects abnormal data, it can quickly identify the fault type using previously learned knowledge, completing the diagnosis process. For online fault diagnosis applications, the model needs to respond rapidly to fault signals. Numerous studies have aimed to improve diagnosis speed and efficiency to meet real-time requirements. For IGBT OC faults in three-phase PWM inverters, Reference [
24] designed an ensemble classifier based on the Extreme Learning Machine with a reliability mechanism and used a Random Vector Functional Link (RVFL) network to identify fault features, reducing diagnosis time. Building on this, reference [
25] proposed an RVFL network based on the Fast Fourier Transform and Relief algorithm to prevent misdiagnosis due to similar fault features. Reference [
26] introduced a diagnosis method for IGBT OC faults in Neutral Point Clamped (NPC) three-level inverters, using Independent Component Analysis and Joint Approximate Diagonalization algorithms to separate fault signals, allowing for more precise identification of complex fault patterns. Reference [
27] proposed a fault detection and localization method based on the Entropy of Wavelet Packets feature extraction and Support Vector Machine (SVM) to diagnose IGBT OC faults in multilevel inverters. Reference [
28] considered the multi-scale characteristics of fault signals and developed a fault diagnosis algorithm based on multi-scale Approximate Entropy, Dempster–Shafer evidence theory, and Deng entropy fusion, effectively addressing conflicts and uncertainties among features and enhancing the mutual benefits of features across different scales.
The aforementioned methods demonstrate rapid processing speeds and high accuracy in diagnosing OC faults, they still rely on feature extraction algorithms to derive various characteristics from the raw signals. The diagnosis efficacy of these methods is significantly constrained by the selection process of features based on individual expert experience. This human intervention not only adds to operational complexity but may also introduce the risk of misjudgment. In contrast, deep neural networks possess exceptional feature parsing and selection capabilities, allowing them to automatically identify and select optimal fault features based on internal signal correlations, thereby enhancing the accuracy and reliability of fault diagnosis [
29,
30]. Reference [
31] proposed a deep convolutional network model based on the inception module, which can automatically extract and identify fault features in three-phase PWM converters, applicable in both inverter and rectifier states. Reference [
32] eliminated redundant features and sampling points through correlation analysis, followed by wavelet transformation to further compress feature data, accelerating the training process of deep feedforward networks. Reference [
33] combined neural network models with classification algorithms, achieving rapid fault feature identification along the time dimension using an improved Long Short-Term Memory (LSTM) network, while employing SVM to classify the outputs of the enhanced LSTM, thus addressing the interpretability issues of neural network outputs. Reference [
34] introduced a wide residual network model based on incremental learning, which combines the automatic feature extraction capability of residual networks with the incremental learning ability of generalized learning systems, allowing for incremental learning of new data without retraining the model. To tackle the challenges of extracting fault features from NPC inverters under non-stationary conditions, reference [
35] proposed a fault diagnosis method based on attention collaborative stacked LSTM (ASLSTM) networks, which extracts highly discriminative features from multi-source time series data, improving the stability of fault diagnosis for NPC inverters.
All of the aforementioned models diagnose OC faults in power converters by analyzing current or voltage signals. However, in practice, these signals are usually affected by the electromagnetic environment and produce burrs, spikes, and other disturbances, which may reduce the diagnostic accuracy of the models. Fractional order gradient descent is an optimization method based on fractional order calculus, which allows for the incorporation of historical information during the gradient update, thereby enhancing the model’s learning capability. Compared to traditional integer-order gradient descent, fractional order gradient descent can adjust the optimization path of the neural network model through non-integer-order gradients, improve global search capabilities, and thus enhance the model’s robustness against noise. Reference [
36] proposed an optimizer based on fractional order momentum gradient descent, which enables the neural network model to better converge to the global optimal solution, and improves the fault diagnosis accuracy under small sample datasets. Reference [
37] employed the long-term memory property of Caputo–Fabrizio fractional order derivatives to solve the local dependence and singularity problems of traditional integer orders in practical applications, and improved the extraction effect of weak fault signals. Reference [
38] utilizes the fractional order chaotic system to map the original vibration signals into the three-dimensional chaotic space, constructs a 3D dynamic error phase map with obvious differentiation ability, and realizes the rapid classification of fault signals.
Although neural networks exhibit high accuracy in fault diagnosis, when the operating state of the power converter changes, the neural network model needs to be retrained on new fault features, which leads to a decrease in diagnosis accuracy. Therefore, this paper proposes a lifelong learning-enabled fractional order-convolutional encoder model that can continuously learn the open-circuit fault characteristics of the power converter under multi-conditions. This model maintains high diagnostic accuracy for all faults, highlighting its significant research implications and practical applications. The contributions of this paper are as follows:
1. A convolutional encoder model was constructed for learning and diagnosing OC faults in the power converter. The time series features of three-phase current fault signals and the relative positional relationships between each phase signal are automatically extracted by the convolutional module. The encoder module is utilized to identify and classify these features, enabling the automatic learning and diagnosis of fault samples.
2. Fractional order is utilized to optimize the convolutional encoder model. This model improves the optimization process of backpropagation by incorporating fractional order, allowing it to fully consider the historical gradient information when updating, and is conducive to capturing long-term dependencies in time-series data. Additionally, the smooth gradient update path reduces the oscillations during the optimization process, facilitating stable convergence to the global optimal solution and improving robustness against anomalous noise.
3. A multilevel lifelong learning framework is designed to enable the model to continuously learn from new fault samples. Limit the range of updates during which the model parameters learn new tasks by incorporating a resilient regularization penalty term into the loss function. In addition, a random small number of samples from previous tasks are inserted into the new fault samples and by learning the soft labels from earlier tasks to improve the stability and accuracy of the model under different tasks.
2. Fault Analysis
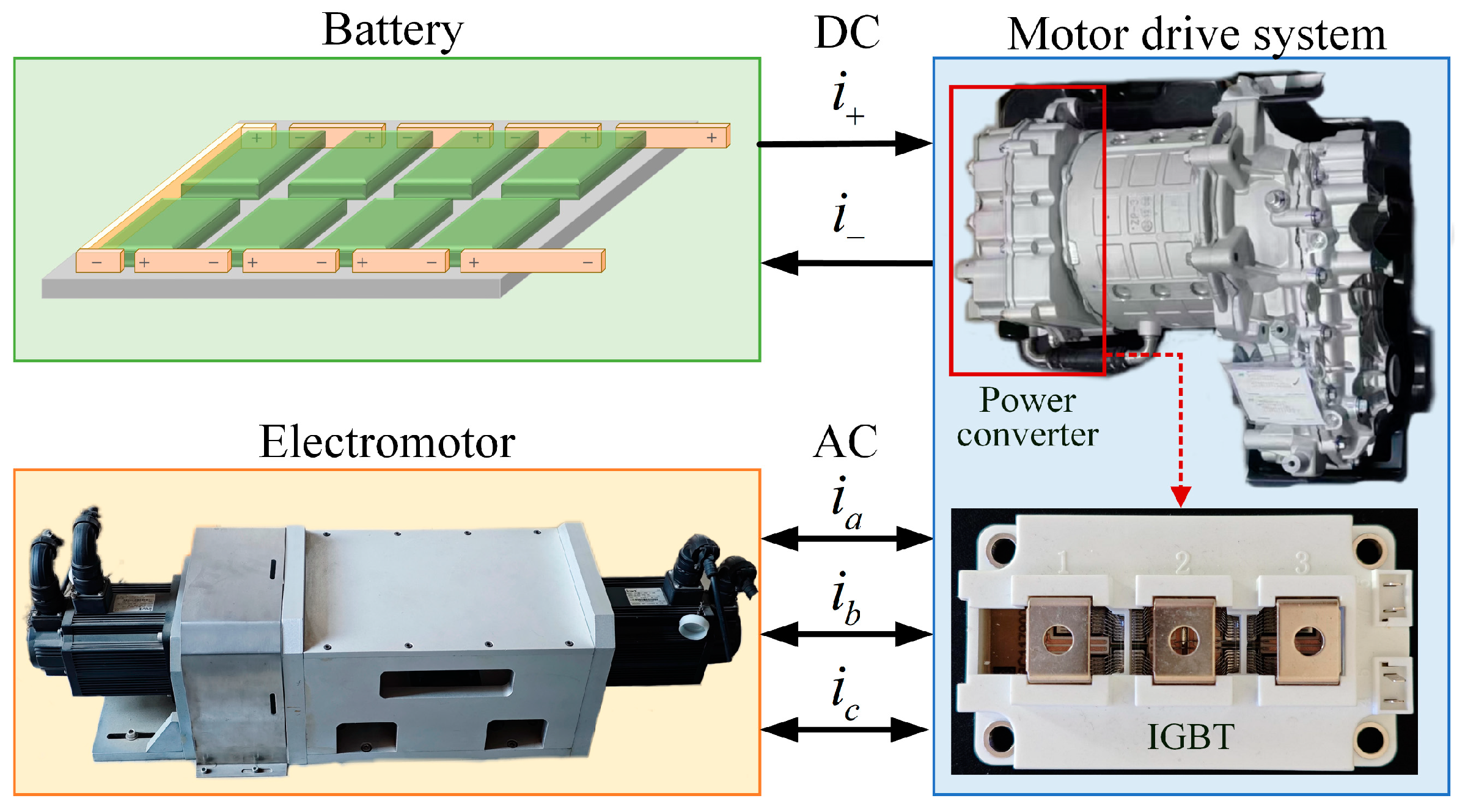
The structure of the motor drive system is shown in
Figure 1, consisting mainly of a battery, power converter, and motor. When the system operates the motor, the power converter works in the inverter state, converting the electric energy from direct current (DC) to alternating current (AC) and delivering it to the motor. Conversely, when the system is in a braking state, the motor operates in generator mode, outputting three-phase AC to the power converter. At this time, the power converter works in a rectifier state, converting the three-phase AC into DC and storing it in the battery. Therefore, during the operation of the motor drive system, the power converter continuously alternates between rectifier and inverter state.
The circuit structure of the power converter is shown in
Figure 2. The DC power source
VD, capacitor
C1, and resistor
R1 form an equivalent DC power source responsible for supplying and storing electrical energy.
Sx and
Dx (
x = 1, 2, …, 6) represent IGBT and Fast Recovery Diode (FRD), respectively. The three-phase bridge circuit consists of six pairs of IGBT with anti-parallel FRD. The three-phase AC,
ik (
k =
a,
b,
c), flows through the LCL filter—comprising an inductor-capacitor-inductor configuration—before being supplied to the motor. The LCL filter comprises inductors
L1 and
L2, resistor
R2, and capacitor
C2. The six pairs of IGBT in the three-phase bridge circuit are turned on and off in a specific pattern by the PWM control system, enabling bidirectional energy conversion between AC and DC. The signal acquisition module captures the system’s three-phase currents using current sensors. In rectification mode, the sensor captures the power converter’s bridge arm current
I1 as the fault diagnosis signal, and in inverter mode, it captures the load-side current
I2. An IGBT OC fault causes them to remain off, independent of PWM control, leading to current distortions that vary with converter operating conditions and motor types, such as AC Induction Motors (ACIM) or Permanent Magnet Synchronous Machines (PMSMs) in electric vehicles. This study thus examines the approach for diagnosing IGBT OC faults in the power converter under multi-conditions and motors.
In practical applications, diagnosing single or double OC faults is more practical as the probability of multiple OC faults occurring simultaneously is very low. This helps to identify and locate the failed device in time, preventing the fault from spreading to other parts of the system, which could result in secondary failures or even system paralysis. Furthermore, the OC fault diagnosis approach proposed in this paper is not restricted to a specific circuit topology or a particular model of IGBT device. This is because the approach can automatically learn and recognize fault characteristics from the signal. And no matter which topology or device, the occurrence of an OC fault will produce distinct abnormal features in the current or voltage signal. Consequently, the approach is universal and can be extended to new power converters with redundant designs or more switching devices, thus providing theoretical support and technical guarantee to improve the safety and reliability of the overall system. Based on the multi-conditions of the power converter and various motors, four distinct operating tasks can be classified, as shown in
Table 1.
The simulation circuit is constructed using the MATLAB/Simulink R2022b platform according to the circuit topology of
Figure 2 to simulate the current waveforms of the power converter when OC failure occurs under different tasks, and the parameters of the simulation circuit are shown in
Table 2. The MATLAB/Simulink R2022b software is developed by MathWorks Incorporated (Natick, MA, USA).
2.1. Fault Analysis of the Power Converter Working Under Inverter Condition
When the power converter operates in the inverter state, energy transfers from the DC to the AC side. During normal operation, the output currents ia, ib, and ic are balanced three-phase currents. To examine the waveform changes, phase A current ia is used as an example. In the first half of the ia cycle, S4 remains off while S1, controlled by the PWM controller, alternates on and off in a set pattern, outputting a PWM square wave voltage with amplitude VD and positive polarity to phase A. This PWM square wave voltage, acting on an inductive load, produces a sinusoidal current ia in phase A, where ia > 0. In the second half-cycle, the pattern is reversed, with S1 off and S4 controlled by PWM, resulting in a sinusoidal current ia with negative polarity.
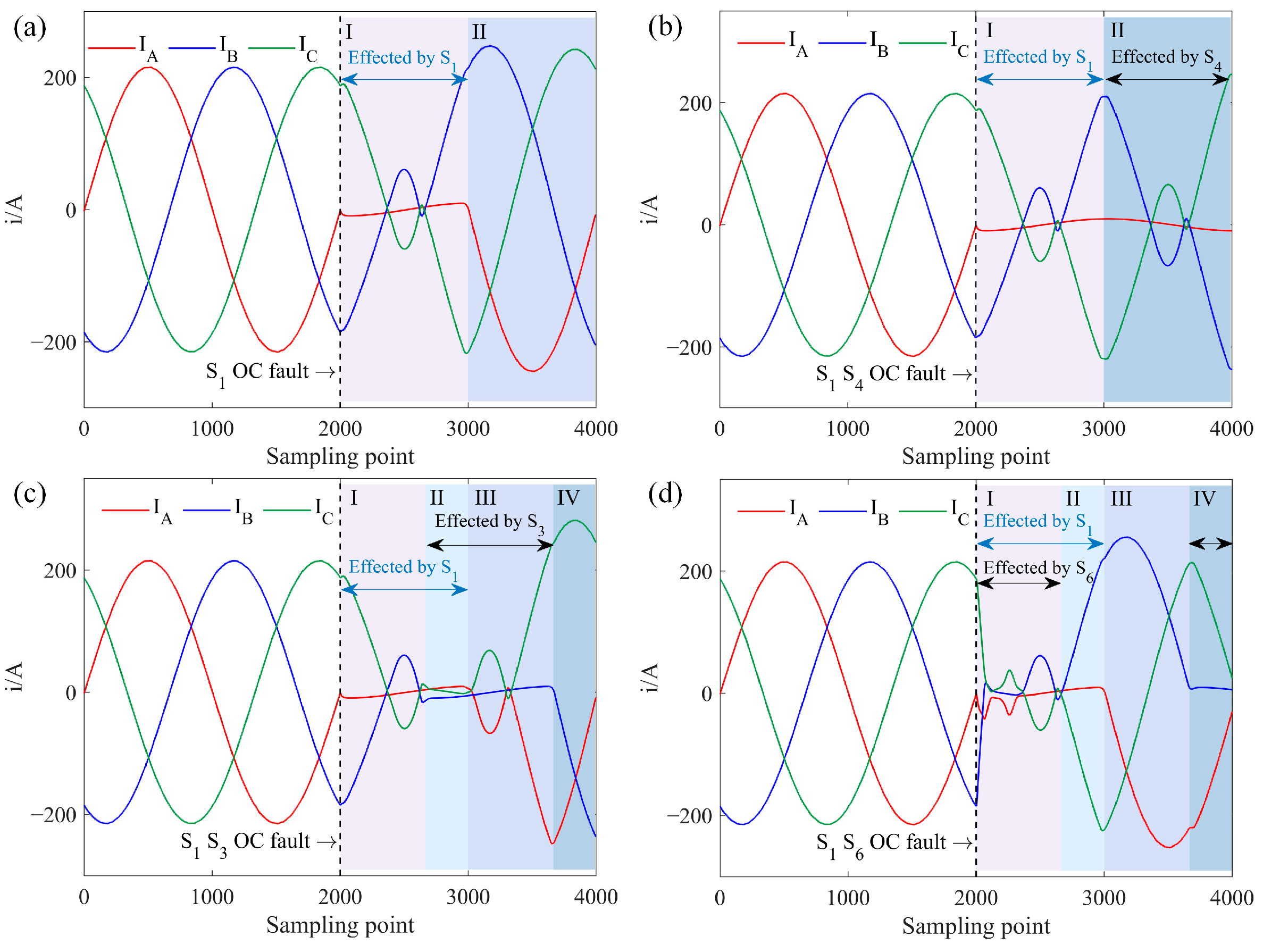
For Task A, with an ACIM, the three-phase current simulated waveform with an OC fault in
S1 is shown in
Figure 3a. In the second cycle, when
S1 fails, it is effectively off, and with
S1 also off, the DC side voltage cannot reach the AC side through phase A, leading to
ia = 0 in the first half-cycle. The resulting unbalanced power among the three phases distorts the currents in the non-faulted phases
ib and
ic, causing harmonic generation and amplitude increase. If
S4 experiences an OC fault, there will be no current output in the second half of
ia. Similar current waveform changes occur in phases B and C with single IGBT OC faults.
Dual IGBT OC faults can occur in three configurations: (1) faults in the same-phase IGBTs, (2) faults in different-phase IGBTs in the same half-bridge, and (3) faults in different-phase IGBTs in different half-bridges.
Figure 3b shows the three-phase current simulated waveform with OC faults in
S1 and
S4, representing same-phase faults. Since
S1 and
S4 affect separate halves of the
ia cycle independently, the fault waveform appears as a superposition of two symmetrical single IGBT faults in phase A, resulting in zero current in phase A while currents
ib and
ic remain opposite.
Figure 3c illustrates the three-phase current simulated waveform when
S1 and
S3 experience faults, representing different-phase faults within the same half-bridge. In the three-phase bridge circuit, any two phases in the same half-bridge have a 120
◦ phase difference. Since each phase IGBT conducts over a 180
◦ interval, overlapping occurs when a dual OC fault happens in the same half-bridge. Based on the distinct distortions, the three-phase current waveform is divided into four segments. Segment I is affected only by
S1, and Segment III only by
S3, behaving as single IGBT faults. Segment II shows overlapping effects from
S1 and
S3 faults, with both phases A and B OC, and
ia =
ib =
ic = 0 due to the three-phase current vector sum equaling zero. Segment IV remains unaffected by faults.
S1 and
S6 represent faults in different phases and half-bridges, with a 120
◦ phase overlap. Their dual fault three-phase current simulated waveform is shown in
Figure 3d. Segments II and IV are influenced by individual IGBT faults, while Segment III remains fault-free. Segment I reflects overlapping effects from both
S1 and
S6 faults, resulting in
ia = 0 and
ib = −
ic. Due to the increased current magnitude in phases B and C, the rapid current drop induces intense oscillations and distortion.
For Task C, with a PMSM, a typical three-phase current simulated waveform under an OC fault is shown in
Figure 4. Similarly to the previous analysis, a single IGBT OC fault results in no current in the affected phase for half of the cycle, while the currents in the other phases become distorted.
Figure 4a illustrates the three-phase current simulated waveform with an OC fault in
S1. In cases of dual IGBT OC faults, the analysis depends on whether there is an overlap in the faulted phases. Non-overlapping segments behave as single IGBT faults, while overlapping segments follow the same analysis as Task A. However, due to the differences in motor type and control strategy, the current distortions resulting from IGBT faults vary compared to other tasks.
2.2. Fault Analysis of Power Converter Working Under Rectifier Condition
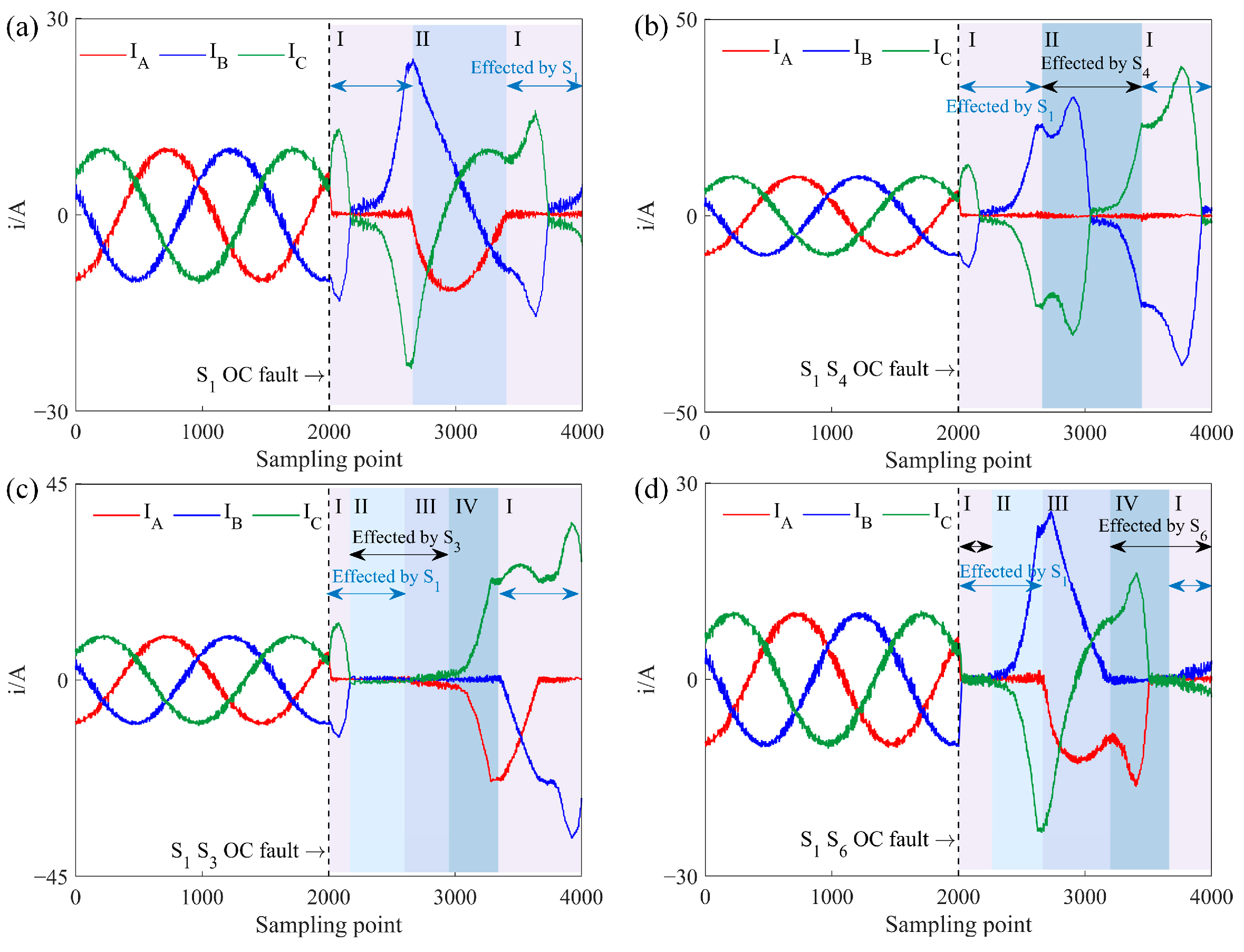
When the power converter operates in a rectifier state, energy flows from the AC to the DC side. For Task B, where the motor is an ACIM, a typical three-phase current simulated waveform under an OC fault is shown in
Figure 5. When the rectifier is operating normally, symmetrical three-phase voltage at the AC side generates symmetrical three-phase current through the load inductance.
Taking A-phase current
ia as an example, the three-phase current simulated waveform under a single IGBT OC fault is analyzed. When
ia > 0, the current flows through
D1 to the DC side or returns to the AC side through
S4. When
ia < 0, the current flows back to the AC side via either
S1 or
D4. Thus, an OC fault in
S1 affects only the
ia < 0 part, as shown in
Figure 5a, where
ia = 0 during this period due to the lack of return current through
S1. When the A-phase voltage reaches the lowest value among the three phases,
D4 conducts to carry the current back to the motor. In the latter half-cycle of
ia, two no-current intervals appear since
D4 turns off when other diodes are conducting. Due to the constant vector sum of the three-phase currents, some distortion also occurs in
ib and
ic.
The types of dual IGBT OC faults in a rectifier state are similar to those in an inverter state.
Figure 5b shows the three-phase current simulated waveform for an OC fault in the A-phase IGBT, where only
D1 and
D4 conduct, causing four zero-current intervals in
ia over one cycle. As IGBTs in the same phase sequence do not conduct simultaneously, no overlap occurs in fault effects, so the other two-phase currents remain distorted but do not reach zero.
Figure 5c shows the case where upper-bridge IGBTs in A-phase and B-phase experience OC faults. Segments I and III are impacted by individual IGBT faults, similar to a single IGBT OC fault waveform. Segment II remains unaffected, operating normally. In Segment IV, both
S1 and
S3 OC are in OC, resulting in zero intervals for both
ia and
ib. Since
ic > 0,
D2 remains at positive voltage and cannot conduct, meaning
D4 and
D6 do not turn off simultaneously, allowing at least two phases to conduct current. This fault waveform can be seen as an overlap of the individual
S1 and
S3 faults.
Figure 5d presents the scenario of a simultaneous OC fault in upper-bridge IGBT
S1 of A-phase and lower-bridge IGBT
S6 of B-phase. Segment I is fault-free, and Segment II involves only the
S6 fault. In Segment III,
ia ≤ 0 and with
S1 in fault, A-phase current only flows through
D4. Likewise, with
ib ≥ 0 and
S6 in fault, B-phase current can only pass through
D3, preventing A- and B-phases from forming a current loop, meaning they do not conduct simultaneously during this stage. When
ic < 0,
S5 conducts while
S2 is off, forming a current loop between B- and C-phases through
D3 and
S5, resulting in
ia = 0 and
ib = −
ic. When
ic ≥ 0,
S2 conducts while
S5 is off, forming a loop between A- and B-phases through
S2 and
D4, making
ib = 0 and
ia = −
ic. Segment IV experiences only a single IGBT fault but with an increase in current amplitude across all phases.
For Task D, where the motor is a PMSM operating in a rectifier state, a typical OC fault three-phase current simulated waveform is shown in
Figure 6. Unlike the previous analysis, an OC fault does not cause segments of the current to reach zero. Instead, it leads to an imbalance in the three-phase power. This imbalance disrupts the symmetry of the current waveform, which can significantly affect the performance of the PMSM and lead to irregularities in power flow within the system.
The above content analyzed the four typical types of faults in the power converter under different operational tasks. Extending this analysis to all phases of IGBTs results in a total of 85 distinct fault types, as summarized in
Table 3. Unique labels are assigned to each type of fault and used for neural network model training.
3. Approach
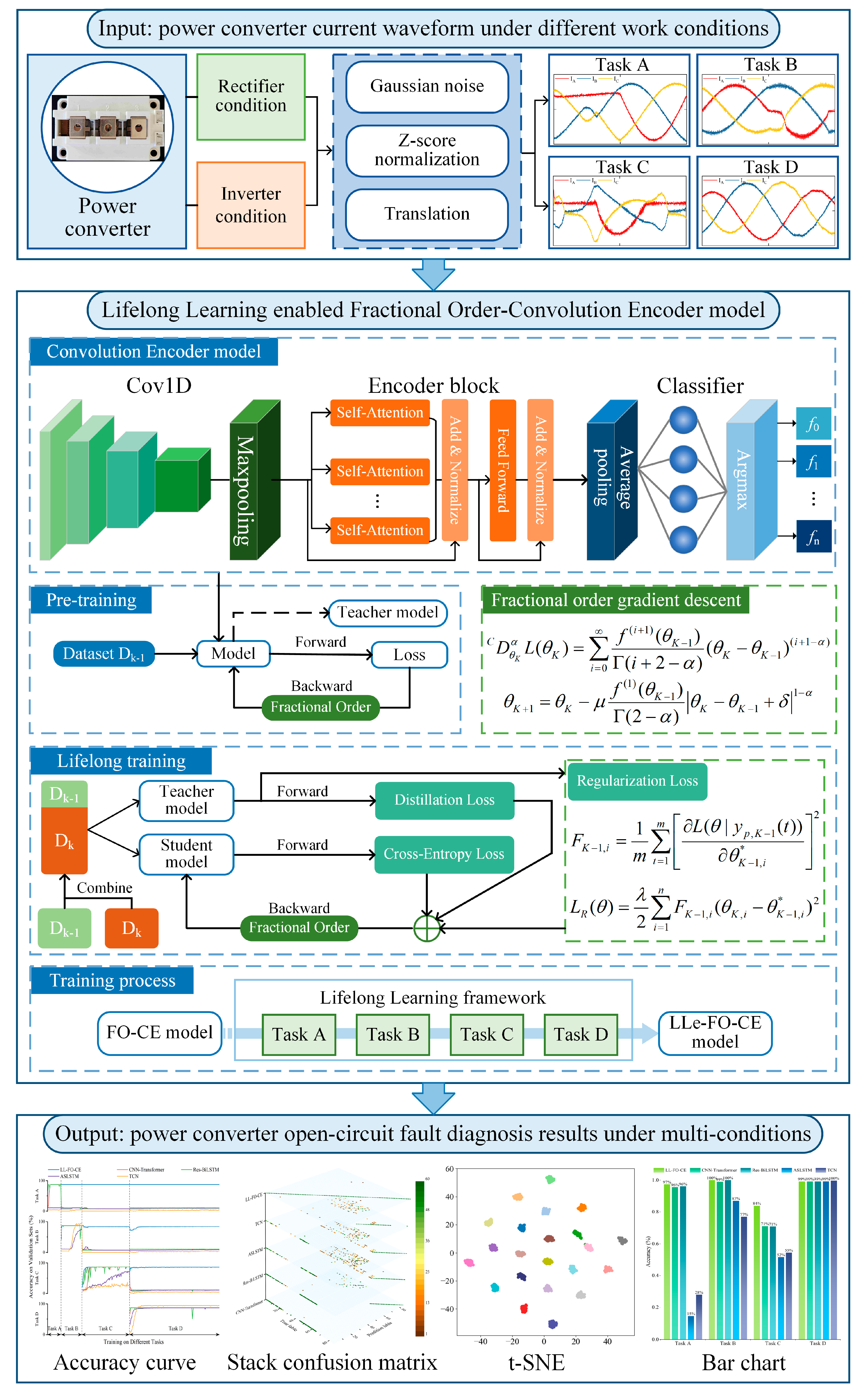
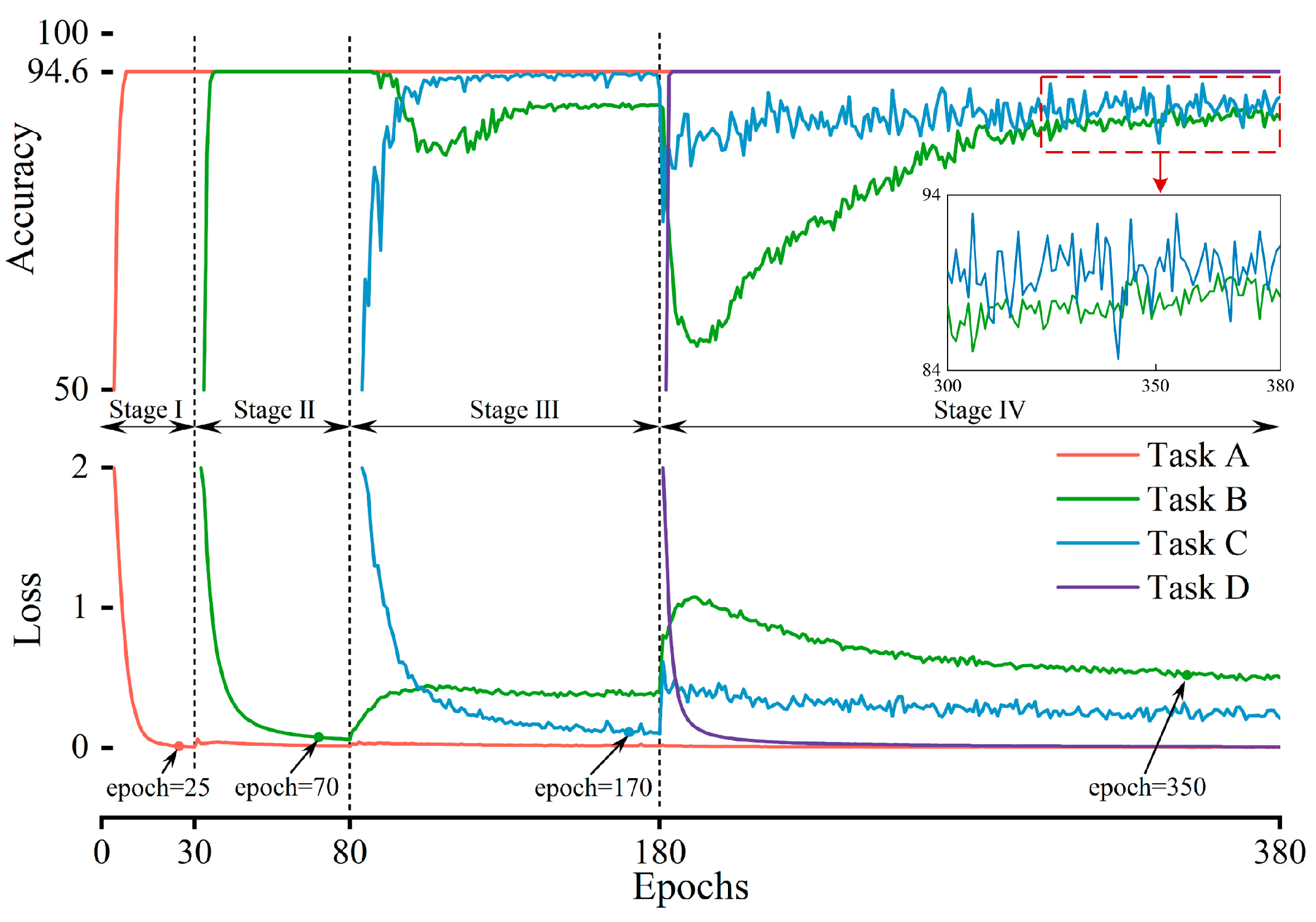
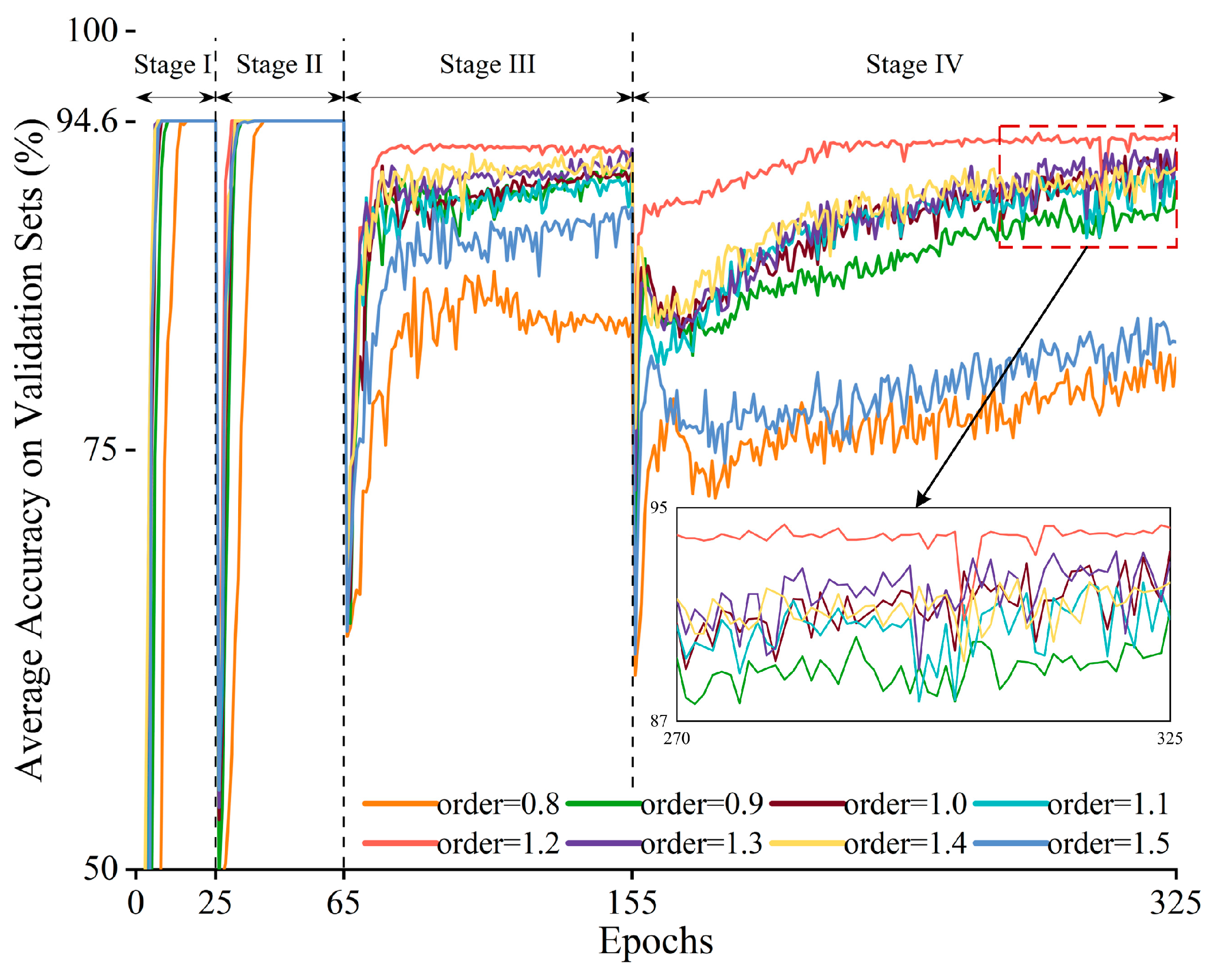
A lifelong learning-enabled fractional order-convolutional encoder (LL-FO-CE) model is proposed, with a flowchart shown in
Figure 7. The proposed model is capable of continuously learning the three-phase current signals of a power converter across four different task types and accurately diagnosing faults in all previously learned tasks.
A simulation circuit is built on the MATLAB/Simulink platform, and a single cycle of current signals is collected while the power converter is operating stably, denoted as
Ioriginal. To enhance the model’s generalization ability and robustness, data preprocessing is applied to the raw signals. Since OC faults in the power converter occur randomly and may appear at any point within a cycle, the original sample data are shifted along the time dimension to simulate current signals with faults occurring at different times. The data are cyclically shifted by a fixed step size, as shown in (1).
The vector
Ij,shifted represents the
j-th shifted sample, where
xt is the sample point and
p is the shifting step size. The shifted sample obtained is then used as the base sample for the next shift, with this process repeated until all data have been cycled through, ultimately yielding a total of
j groups of fault samples. However, in practical applications, current signals are often affected by noise during acquisition. To simulate this interference, a random Gaussian white noise is applied to each sample group, as shown in (2).
where
μ is the mean of the Gaussian distribution,
σ2 is the variance, and
c is the noise amplification factor. Setting
μ = 0,
σ2 = 1 and
c = 10, we obtain the noise-augmented fault sample
Ij,noise. Given the large values in the original data, to prevent disproportionately large features from skewing the training results, the data are standardized using the Z-Score, as shown in (3).
where
Ij represents the fault sample after data preprocessing, while
μI is the mean of
Ij,noise, and
σI is the standard deviation of
Ij,noise. Finally, by merging all the fault samples, we obtain the dataset
I of three-phase current signals from the power converter under four different tasks, as shown in (4).
The dataset
I will be used for training and testing the LL-FO-CE model. The first part of the model is the convolutional module, which is designed to extract features from the data, as shown in (5) and (6) [
39].
where
Hconv is the output of the convolutional layer, and
Hpool is the output of the max-pooling layer. After the three-phase current signal samples are input into the model, they undergo multiple layers of 1D convolution and max-pooling to thoroughly extract the features of the fault samples. The hidden feature outputs from the convolutional module are then fed into the encoder module. First, the variables undergo positional encoding, as shown in (7)–(9) [
40].
where
pos represents the position of each sample point in the sequence,
d is the dimensionality of the position vector, which corresponds to the number of channels in the feature map output from the convolutional module, and
i is the index of the dimension of the position vector. Then, the attention weights for the features are calculated using self-attention, as shown in (10) [
41].
√
dk is the scaling factor, which helps prevent the vanishing gradients caused by excessively large products.
Q,
K, and
V represent the Query, Key, and Value vectors in self-attention, as shown in (11)–(13).
WQ,
WK, and
WV are the weight parameter matrices, which are updated through model training. Then, by utilizing the multi-head attention mechanism, the model computes attention in parallel across different subspaces, as shown in (14).
The calculation formula for the
i-th self-attention head is shown in (15).
The output of each encoder layer will pass through a feedforward neural network consisting of two linear transformations and a nonlinear activation function, as shown in (16).
W and
b are the weight parameter matrix and bias parameter of the feedforward neural network, respectively, while
max represents the activation function. The encoder module is composed of multiple identical encoders stacked together, with each layer including multi-head self-attention and a feedforward neural network. Thus, the output of a single-layer encoder can be expressed, as shown in (17) and (18).
Z represents the output of the multi-head attention,
Z′ denotes the output of the encoder, and
LayerNorm refers to layer normalization. The output of the encoder module is then passed through a fully connected layer, mapping it to the dimensionality of the number of classes, as shown in (19).
Hfc represents the hidden state output from the fully connected layer, while
Wfc and
bfc denote the weight parameter matrix and the bias parameter vector, respectively. Finally, the hidden state is transformed into a probability distribution using the
Softmax function, and the final classification result is determined through
Argmax, as shown in (20) and (21).
The equations above outline the fundamental architecture and the forward propagation process of the proposed model. In the backpropagation and parameter update phase of the model, the fractional order derivative is utilized to optimize the gradient descent process [
36]. The Caputo fractional order gradient descent is given by (22).
CD is the Caputo fractional operator,
L(
θ) is the loss function,
α is the order of the fractional derivative, and
I is the smallest integer greater than
α; thus,
I − 1 <
α <
I.
θ represents the neural network parameters, and
Γ is the Gamma function. When
I = 1 and 0 <
α < 1, the expression is given by (23).
When
I = 2, and 1 <
α < 2, the expression becomes (24).
Therefore, the expression for the fractional order when 0 <
α < 2 is given by (25).
By applying the Taylor series expansion to (25) up to the first term, we obtain the fractional order loss function for the case when 0 <
α < 2, as shown in (26).
δ is a small positive number introduced to prevent division by zero. Therefore, the parameter update expression based on the fractional order gradient descent is shown in (27).
This method allows the neural network to update parameters using fractional order gradients during backpropagation, enabling the model to quickly find the global optimal solution and avoid getting trapped in local optima.
The above process allows the model to train optimally for fault diagnosis tasks in a single state of the power converter. However, when the state changes, the model will be unable to recognize new fault features and will need to be retrained with new fault samples. To enable the model to continue learning new fault samples, a multilevel lifelong learning framework has been designed. This framework includes randomly inserting samples from previous tasks into the new batch of training data, learning soft labels from previous tasks, and adding a regularization penalty term to the loss function.
First, a replay buffer containing randomly selected fault samples from previous tasks is constructed, as shown in (28) [
42].
Ij represents the fault samples from Task A, where
j is a random number in the interval (1,
m), and
m is the total number of samples in Task A. This operation is performed at the beginning of each iteration cycle when the model is learning a new task, to update the samples in the replay buffer. The samples from
DA,re are combined with the current batch of training data
DB, as shown in (29).
DAB contains samples from both the previous Task A and the current Task B, which are used for model training. To maintain consistency across the two different tasks, the model learns the soft labels from the previous task, as shown in (30) [
43].
LCE is the cross-entropy loss function, while
LKL denotes the Kullback–Leibler (KL) divergence loss function. The
σ represents the
Softmax function, and
yT and
yS refer to the model’s predictions on the previous task and the current task, respectively.
β is a weight parameter, and
T is the temperature coefficient. The loss
LKD consists of two parts: one is the hard target loss
LCE, which measures the discrepancy between the model’s predictions on the current task and the true labels. The other part is the soft target loss
LKL, which indicates the difference between the model’s output on the previous task and the soft labels. By adjusting the size of
β, the model’s focus during the learning of new tasks can be controlled. A larger
β places more emphasis on retaining previous knowledge, while a smaller
β favors the learning of the new task. The temperature coefficient
T is used to regulate the difficulty of learning the knowledge from previous tasks; a larger
T facilitates the acquisition of knowledge from earlier tasks.
To mitigate the model’s forgetting speed regarding previous tasks, a regularization penalty term that measures the importance of the model parameters is added to the loss function. For Task D, the optimal parameters
θ should maximize the conditional probability
P(
θ|
D), which can be expressed using Bayes’ theorem as (31) [
44].
DA and
DB are two distinct tasks that make up Task D. Since
DA and
DB are independent of each other, we obtain (32).
Under the given parameters, log
P(
DB|
θ) represents the loss function for Task
DB, denoted as −
LB(
θ), and log
P(
DB) is a constant. Thus, the optimization objective is expressed as (33).
Simplifying the right side of the equation yields (34).
For the posterior probability
P(
θ|
DA), it can be approximated as a Gaussian distribution that conforms to the prior probability
P(
DA|
θ). Let
f(
θ) = log
P(
DA|
θ), and expand it up to the third term at the optimal parameter
θ*A using the Taylor formula, as shown in (35).
Since
θ*A is the optimal solution for
f(
θ), it follows that
f′(
θ*A) = 0. Substituting the probability density function of
f(
θ) gives us (36).
By solving, we obtain
μ =
θ*A and
δ2 = −1/
f″(
θ*A). Substituting these into (34) gives us the expression shown in (37).
log [1/(√2
π)
δ] is a constant. Based on the optimization objective, we can construct the loss function
LREG as shown in (38).
where
f″(
θ*A) can be represented by the diagonal elements of the Fisher information matrix −
FA,i, as shown in (39) [
45].
θ*A represents the network parameters of the neural network on Task
DA,
yp,A(
t) is the predicted value on
DA, and
m is the total amount of data in
DA. By calculating the partial derivative of the loss function of all predicted values with respect to the network parameters
θ*A, the importance of weight
FA,i of the parameters for Task
DA can be obtained. The neural network will continue training on Task
DB, and the loss function will be constructed by incorporating
FA,i as shown in (40).
The loss function
LKD is combined with
LREG, and the parameters of the LL-FO-CE model are updated through fractional-order gradient descent during backpropagation, resulting in the parameter update expression as shown in (41).
5. Semi-Physical Experiments
To further verify the reliability of the proposed fault diagnosis method, a semi-physical virtual simulation system for power converter fault diagnosis has been established using the OPAL-RT OP4510 real-time simulator, a Tektronix (Beaverton, OR, USA) oscilloscope, and a desktop computer equipped with an AMD R5-7500F CPU, an RTX 4060 Ti GPU, and 32 GB of RAM. The CPU is manufactured by Advanced Micro Devices, Inc. (Santa Clara, CA, USA), while the GPU is produced by NVIDIA Corporation (Santa Clara, CA, USA). The experimental setup is shown in
Figure 15. The OPAL-RT OP4510 is used to generate the control signals and run the simulation model, which operates on RT-LAB, the industrial-grade real-time simulation system developed by OPAL-RT (Montreal, QC, Canada). The oscilloscope monitors and collects the current signals generated by the OP4510 in real time, producing waveform files. The desktop computer is used to run the fault diagnosis program.
The workflow of the semi-physical virtual simulation experiment system is as follows: First, build and compile the simulation model file according to the RT-LAB standard on the computer. Next, transfer the compiled file to the OP4510 real-time simulation platform. After that, start the simulation model on the OP4510 and perform the corresponding control operations on the model. At the same time, an oscilloscope is used to monitor and collect the current signal, generating the corresponding current waveform file. During this process, the computer will run the fault diagnosis program synchronously to analyze the waveform data generated by the oscilloscope in depth, so as to realize the accurate detection of faults and the precise location of the failed device.
The real-time emulator OP4510 generates and controls PWM signals to drive a power converter emulation circuit. In this circuit, each IGBT device corresponds to a specific PWM signal. When all PWM signals are functioning normally, the power converter maintains a stable operating state. However, if a PWM signal is disconnected, the corresponding IGBT device will enter a shutdown state, thereby simulating an OC fault scenario of the power converter in real applications. The system adopts the double closed-loop control method based on the
d-q rotating coordinate system, which is mainstream in the engineering field. The main parameter settings are detailed in
Table 5 to ensure the accuracy and stability of the system control.
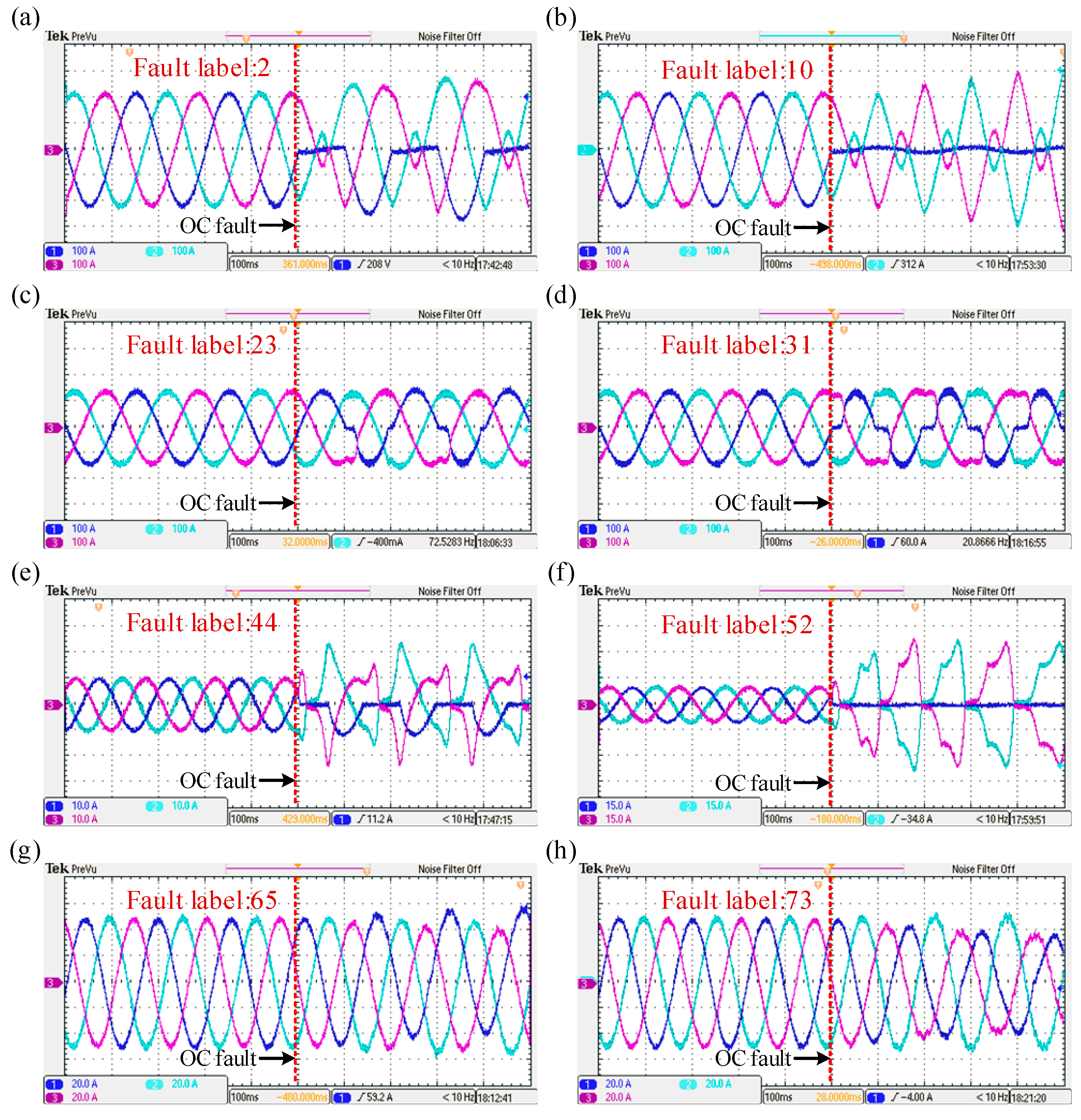
A validation set of three-phase current data, encompassing 85 fault categories, was obtained through the semi-physical virtual simulation system. Each fault category includes 60 sets of three-phase current signal samples, with eight typical fault waveforms illustrated in
Figure 16. In comparison to the Simulink simulation waveforms, these waveforms exhibit noticeable burrs and noise interference, which may increase the difficulty of fault diagnosis.
Four evaluation metrics are used to assess the effectiveness of fault diagnosis: accuracy, precision, recall, and F1 score. Accuracy represents the number of correctly diagnosed samples as a proportion of the total number of samples, reflecting the overall effectiveness of the fault diagnosis results, as shown in (42).
where
TP is the number of samples correctly diagnosed as positive classes, which means that no faulty samples were correctly diagnosed.
TN is the number of samples correctly diagnosed as negative classes, which means that faulty samples were correctly diagnosed.
The precision indicates the proportion of samples predicted by the model to belong to each category that actually do belong to that category. It is used to measure the accuracy of the model’s predictions for each category. The global precision is calculated by Macro-Average as shown in (43).
where
TPi denotes the number of samples correctly predicted by the model to be in category
i,
FPi denotes the number of samples incorrectly predicted by the model to be in category
i, and
N represents the total number of samples across all categories. Macro-Averaging is applicable when the number of samples is equal for all categories and their importance is considered uniform.
Recall indicates, for each category, the proportion of samples that correctly belong to that category and are correctly predicted by the model as being in that category. It is used to measure the model’s ability to recognize each category. The global recall is calculated by Macro-Average as in (44).
F1 Score is the harmonic mean of precision and recall, providing a more comprehensive assessment of the model’s performance metrics in terms of precision and recall. The global F1 Score is calculated by Macro-Average as in (45).
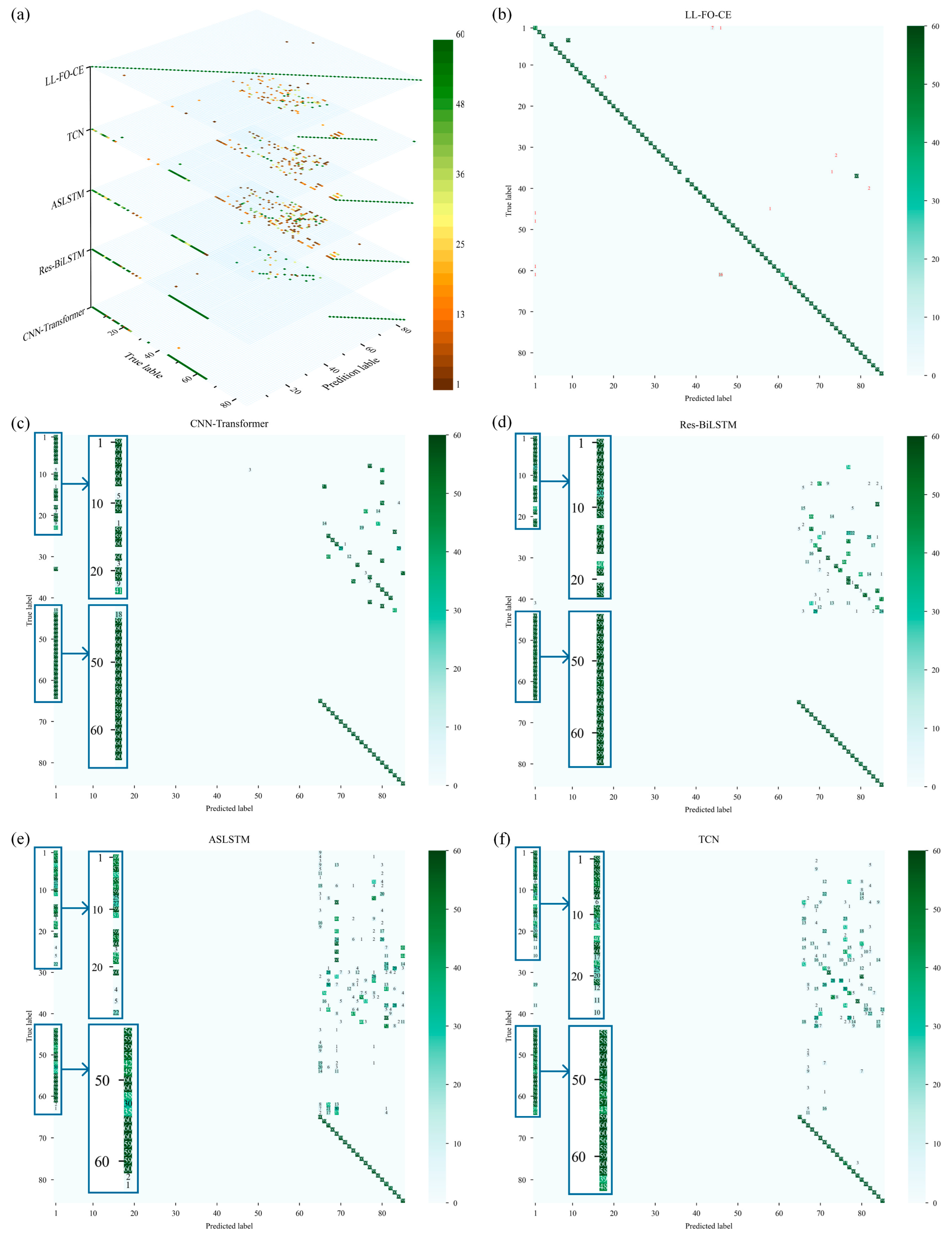
The models were permitted to make ten predictions on the validation set, and their fault diagnosis performance was evaluated using the aforementioned metrics. The results are presented in
Figure 17, and
Table 6 displays the average of accuracy, precision, recall, and F1 score for each model based on ten predictions across various tasks.
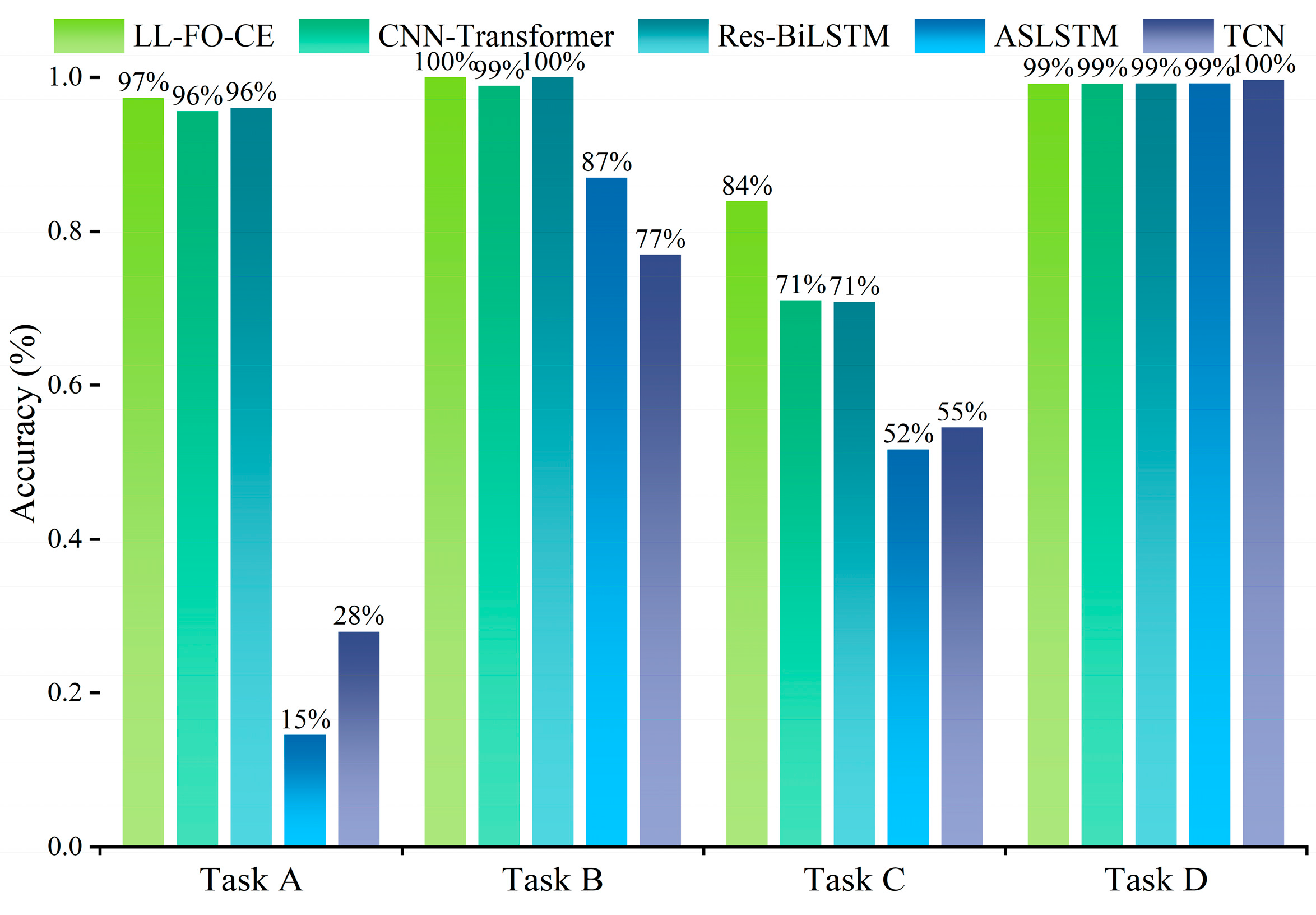
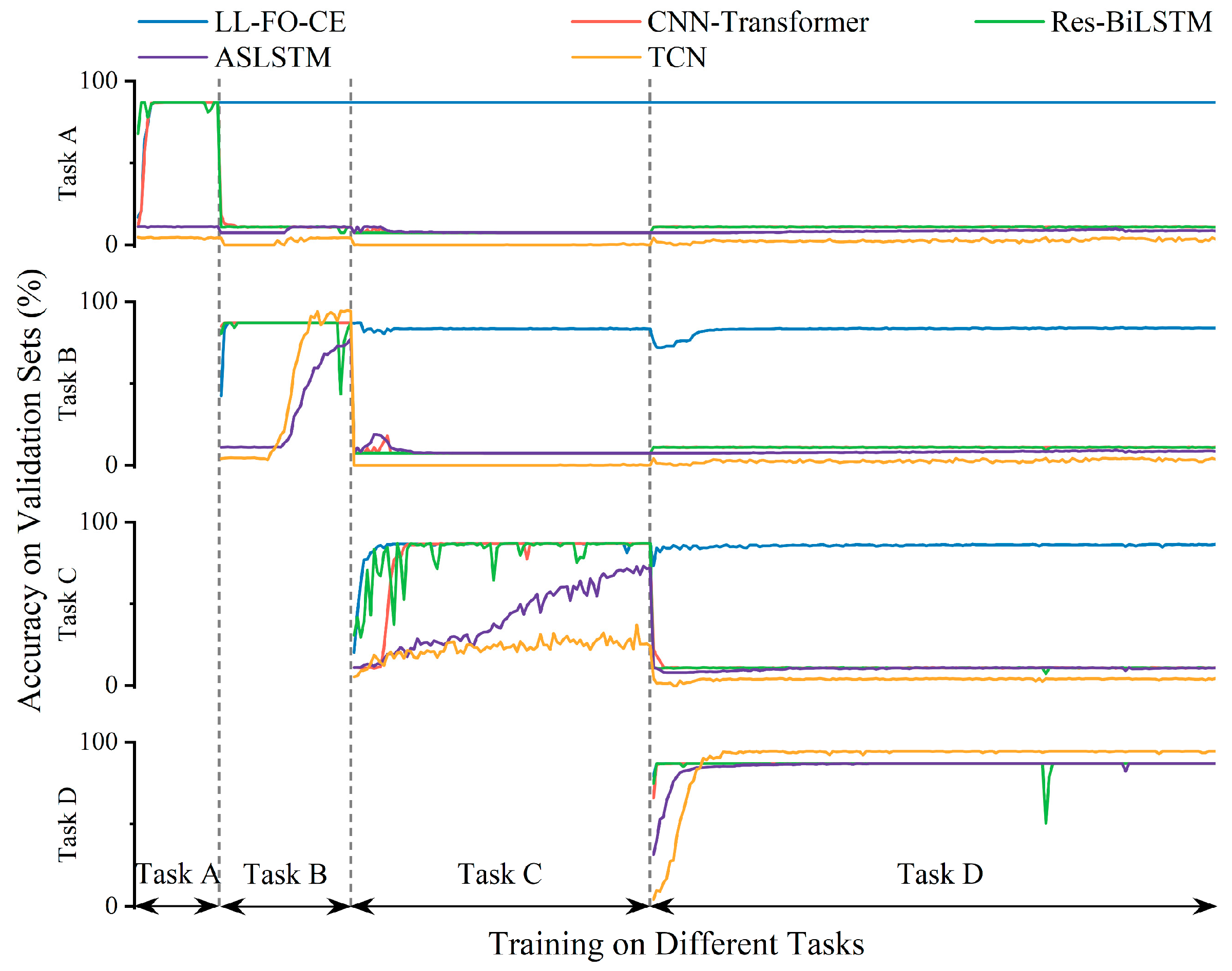
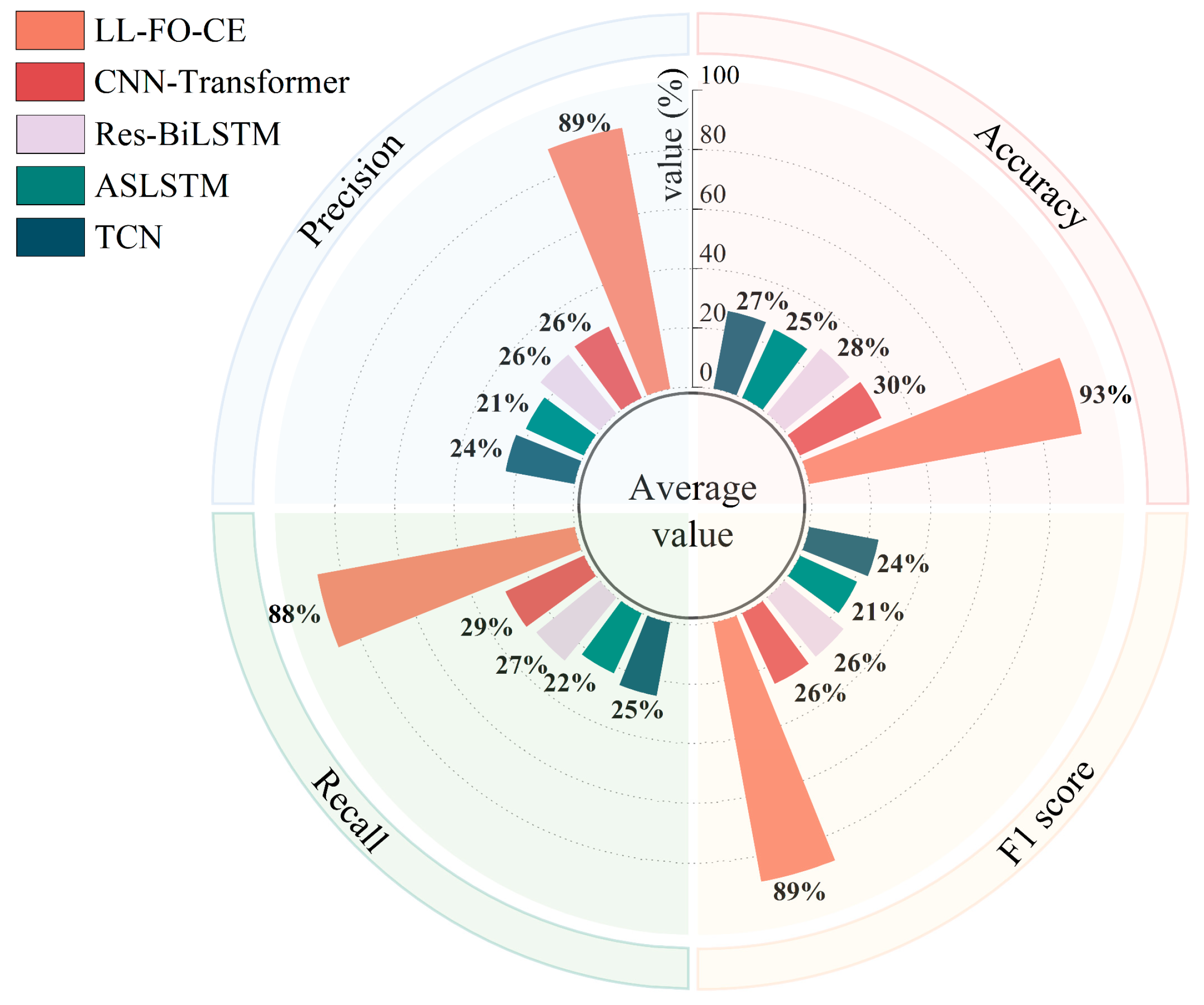
For Task A, Task B, and Task C, the accuracy of LL-FO-CE is 92.9%, 94.5%, and 87.9%, respectively, which shows the best performance among all models. The precision, recall, and F1 scores also represent the highest values across all models, indicating strong diagnosis accuracy and fault identification capability. In contrast, the other models struggled with fault recognition and diagnosis on the validation set for the first three tasks. This limitation arose because they could not maintain long-term memory of different tasks and gradually forgot the knowledge of previous tasks while continuously learning new tasks.
For Task D, the accuracy of LL-FO-CE, CNN-Transformer, Res-BiLSTM, ASLSTM, and TCN are 98.5%, 98%, 97.1%, 94.3%, and 92.9%, respectively. The precision scores are 98.6%, 98.1%, 98%, 92.1%, and 92.3%, respectively. The recall scores are 98.5%, 98%, 97.1%, 90.8%, and 92.4%. The F1 scores are 98.5%, 98.1%, 97.6%, 90.8%, and 92.2%, respectively. All models demonstrate improved performance on this task because Task D is the final task to be learned. However, the presence of disturbances in the fault sample waveforms results in a certain degree of degradation in the diagnosis performance of the other models. LL-FO-CE enhances the backpropagation optimization process through fractional order derivatives, which are highly robust, thereby maintaining superior diagnosis performance compared to other SOTA models when applied to actual fault waveforms with disturbances.
Figure 17 illustrates the overall average of 10 predictions made by each model across all tasks in the validation set. The different colored areas represent various metrics, while distinct colored bars indicate different models. For all 85 fault categories, LL-FO-CE demonstrates optimal performance across all metrics, achieving an average diagnosis accuracy of 93%. The other models, which can only perform better on Task D, exhibit performance averages ranging from 20% to 30% across all tasks. This figure visualizes the performance disparity between the proposed model and other SOTA models in the validation set, highlighting the advantages of the proposed model in diagnosing power converter faults under varying conditions.